Following the idea of modeling surface tension with a continuum method in [
19], we calculate the surface tension force via
, where
and
are surface curvature as well as normal at SPH particle
i (superscripts denote particle indices). Furthermore,
is a constant surface tension parameter, measured in
, which depends on the simulated fluid. As mentioned above, we thus have to approximate curvature as well as normal direction per particle. Our proposed method is organized in three major algorithmic steps. First, particles in an SPH simulation are classified into two groups—surface and non-surface particles. Second, the normal vector is estimated for all surface particles. This makes use of a Monte Carlo technique to locally estimate an integral, taking into account neighboring particles. Due to the probabilistic nature of Monte Carlo computations, the resulting normal vectors are additionally smoothed. Thirdly, following a similar Monte Carlo strategy, we estimate local curvature, again only for the classified surface particles, also with a subsequent smoothing step. The described process can be applied to 2D or 3D scenes. In addition, the number of random samples, and thus the accuracy, can automatically be adjusted according to the simulation time step. Employing the computed data, the surface tension forces per particle can be determined. The individual steps are described in detail in the following.
3.1. Particle Classification
The main idea of classifying particles is to reduce the computation time of the surface tension calculation. We aim to achieve this by excluding (ideally all) non-surface particles from the calculation. Doing so should not affect the overall result since for the latter the surface tension force should be zero anyhow. In contrast, it is crucial for the correctness of the result that no surface particle be misclassified (i.e., there should be no false negatives). Incorrect classification of non-surface particles as surface ones (i.e., false positives) should be minimized, but does not affect the correctness of the fluid dynamics.
To properly classify the particles, we experimented with defining various feature spaces. Optimally, this should only depend on the local geometry. As possible features, we examined, for instance, the summation of neighborhood masses, using various weighting kernels. However, it turned out that good results could already be achieved by mapping fluid particles into a simple 2-dimensional feature space. The first component of this space is given by the mass-weighted average distance of particles in a local neighborhood:
where
m and
are masses and positions of particles
i and
j, respectively. The neighborhood is defined by the (user-selected) SPH kernel radius
h; thus each particle
i has associated neighbor particles
j, at distances smaller than
h. Please note that we normalize by dividing the mass-weighted average by
h, thus making the feature independent of kernel size. For the second feature dimension, we just employ the number of neighbors per particle
.
Next, in order to train a classifier, we have to generate fluid simulation data, and determine for each particle which class it belongs to. The latter training data classification step is done employing a similar strategy as followed for our normal and curvature estimation, as outlined in
Section 3.2 and
Section 3.4. We randomly generate samples on a sphere enclosing a particle and determine coverage of these by neighboring spheres. To achieve high accuracy in this classification, we employ a very large number of samples. In addition, any incorrect classification of a particle as surface (i.e., false positives) in this step, can potentially be remedied by checking for full sphere coverage. Further details of the underlying Monte Carlo strategy will be presented below. Simulations to create the training data have been performed using the SPlisHSPlasH framework [
7]. Scenes with particle numbers between 2K and 30K are employed. Different particle configurations, obstacles, boundaries, and gravity forces are used, to ensure broad coverage. Thus generated, and initially classified, particles are plotted in our 2-dimensional feature space in
Figure 2 (left). Please note that using the described features, the two particle classes already exhibit a reasonable separation. It becomes apparent that a linear classifier may already suffice for the classification task.
For the classification step machine learning strategies can be employed. Since we initially worked in higher-dimensional feature spaces, we decided to use a neural network classifier. Nevertheless, as discussed above, moving to a 2-dimensional feature space turned out to be sufficient for our purpose. We still do employ a neural network as linear classifier; however, using a simpler approach, such as for instance support vector machines would also be adequate. In this context, it should be noted that some recent work explored the use of machine learning in fluid simulation, albeit only for obtaining solutions to the Navier–Stokes equations, instead of performing the task of classifying particles (e.g., [
20,
21,
22,
23]). In our technique, we effectively obtain a line separating the two classes in the feature space. However, since we strive to minimize (i.e., optimally avoid) false negatives, we opted to shift the line by a distance
d along the ordinate, such that no false positives remain (i.e., with respect to the training data). The obtained linear classifier (
) is then applied in any new fluid simulation, dividing particles into surface and non-surface ones, progressively per time step. As visualized in
Figure 2 (right), the selection of parameter d affects the particle classification, which will be discussed further below.
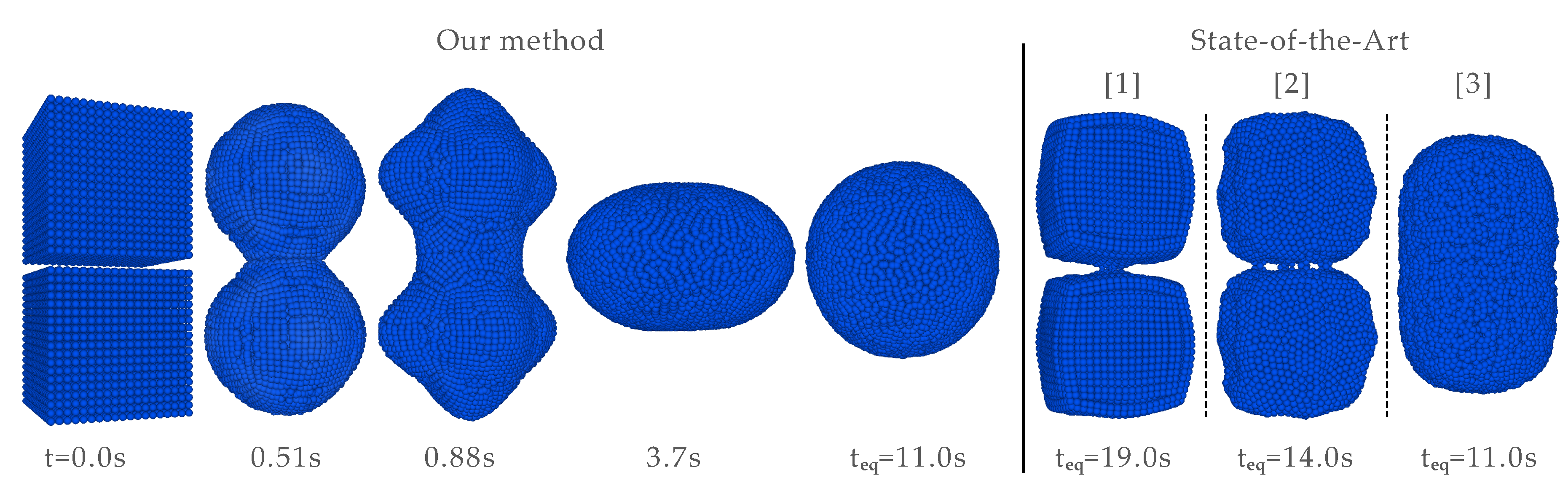
Applying this approach in our later tests, we did not encounter any false negatives in those simulations, also with different particle configurations and geometries. Still, false positives do result. In the experiments outlined in
Section 4 the method yielded on average 0.014% false positives in the Droplet, 5.66% in the Dambreak, and 4.75% in the Crown splash test scenario, respectively. Still, the method proved to work fast and be robust with regard to false negatives. The performance of the method is three orders of magnitudes faster than the timings reported by [
3] for a double dambreak scenario.
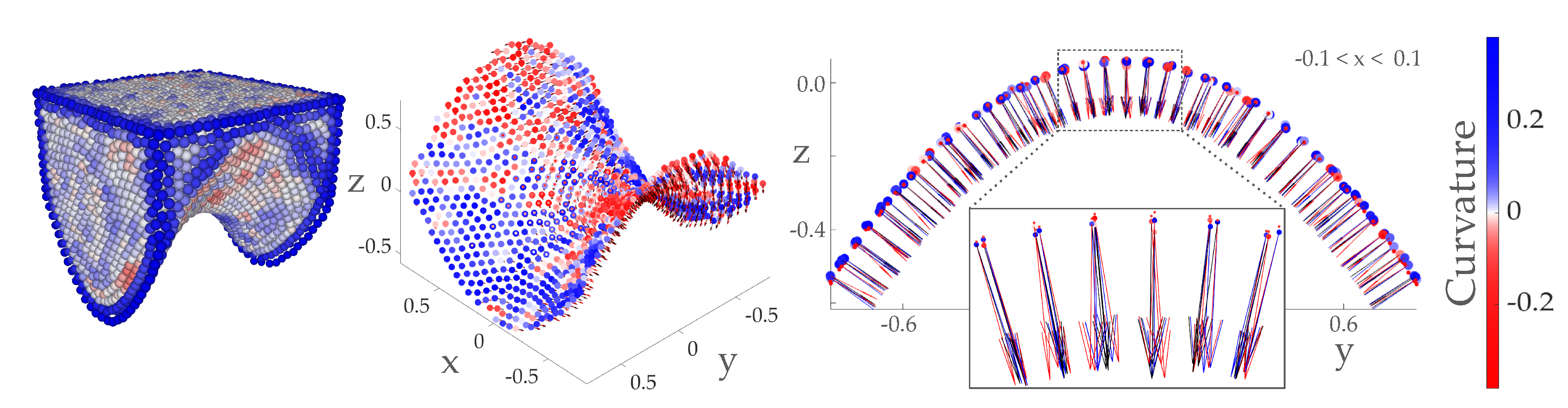
As a further well-defined testcase, we also examined the classification for the example of a hyperbolic paraboloid. For this shape the normals and curvatures are analytically known, both positives as well as negatives being present. To obtain a matching SPH particle system for the analytic surface, we employed the paraboloid function to define a fluid container as an OBJ triangle-mesh geometry. The bottom of this container geometry is set to the shape of the paraboloid. Given this boundary mesh, we then carried out an SPH simulation using the Implicit Incompressible SPH [
24], with constant step size of
. The simulation was run until the system converged to a steady state, providing particles in the container, including the bottom. The particles classified as surface particles in the resulting SPH system are extracted and cropped for further comparison and analysis. Snapshots of the simulation, as well as the cropped region of surface particles at the container’s bottom are visualized in
Figure 3 (note that also curvature computed for the particles is indicated). To visualize the curvature we employ a blue-white-red color-map, with an optional
scale revealing variations in small number regions.
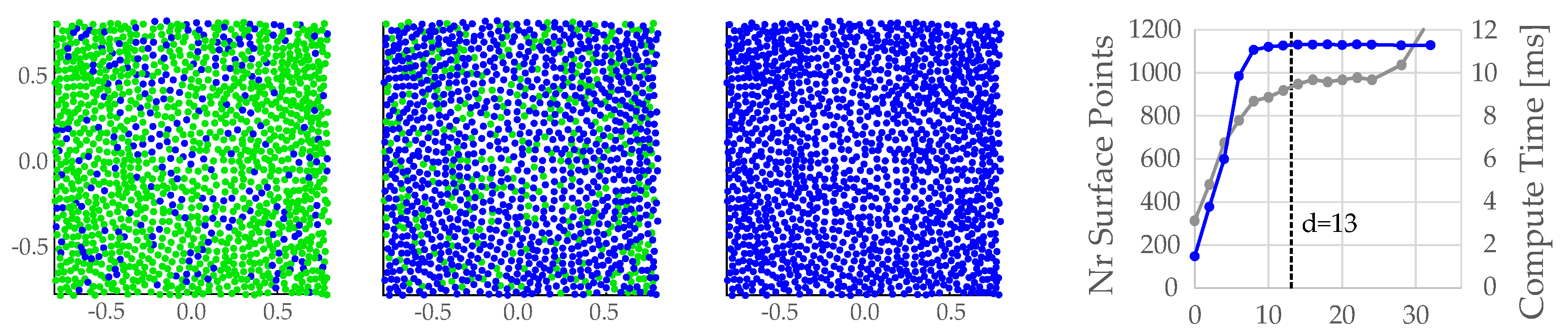
On this dataset, we examined the effect of the shift parameter
d in the linear classifier.
Figure 4 illustrates how points located near the surface in the cropped section were classified. Results are shown for the paraboloid setup, with increasing
d: the smaller the parameter the less surface points are correctly classified (note that all should be classified as surface points for this cropped part). In this special case, a value of about
performed well, since the number of classified surface points as well as the computation time per simulation time step plateaued at this value. Please note that a lower value leads to faster computation times by avoiding re-classification in the Monte Carlo process. Nevertheless, low values may lead to incorrect classifications, wherefore a higher value should be preferable.
3.2. Normal Calculation
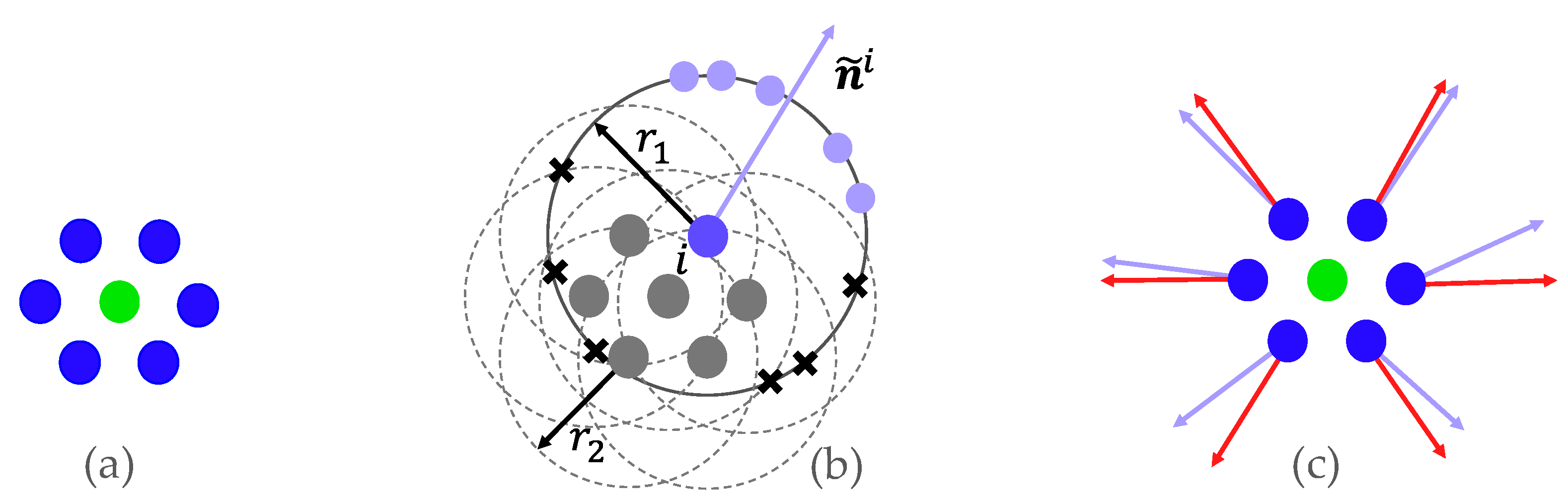
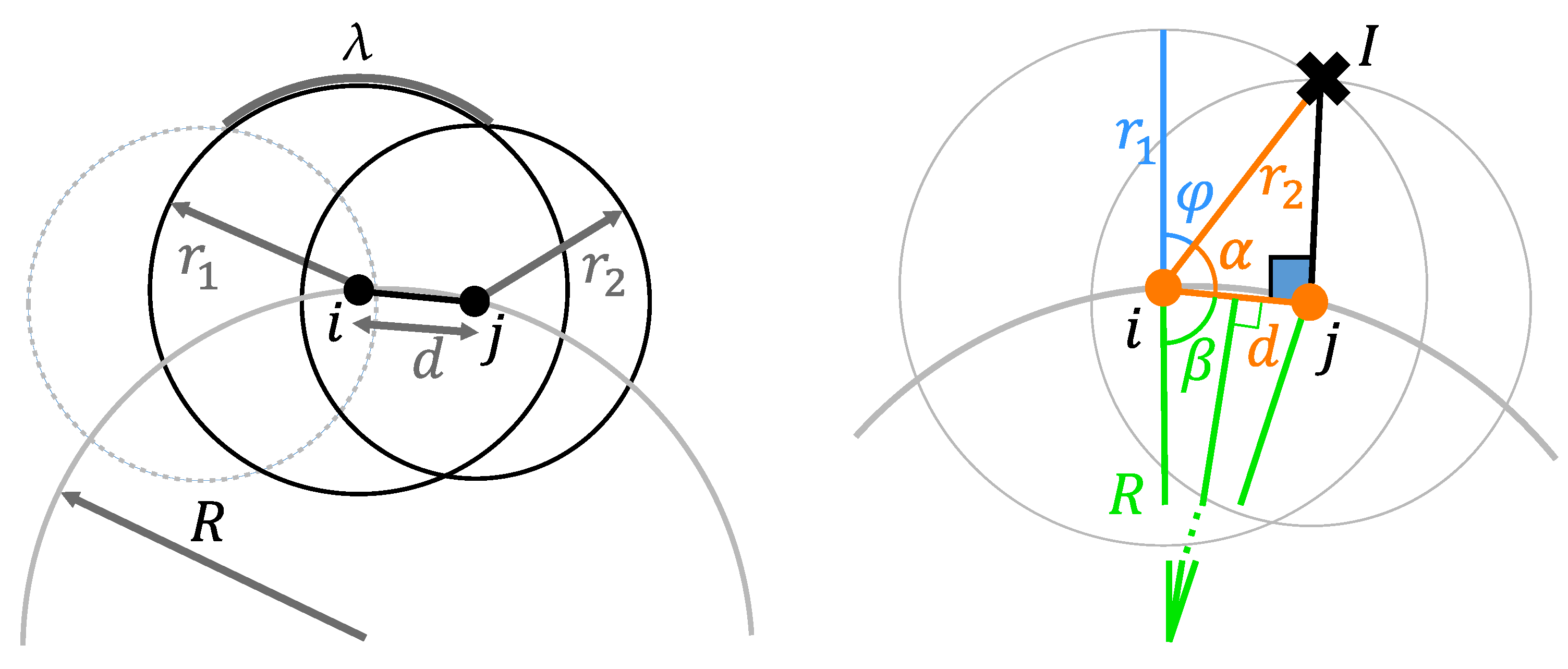
Once the classification has been finalized, we have to compute the surface normals, as well as the curvatures, per particle. Since we do not make use of any smoothed field in the fluid we have to calculate both values using only the geometry as input. Both calculations follow a similar notion, wherefore, the general idea of both will be outlined first. The following will address the 3D case, but the concept applies analogously to 2D. The key idea in both cases is to first assume a sphere of radius around a considered surface particle at position . The radius will always be selected equal to the SPH kernel size h. Next, additional spheres of radius are considered, with their respective centers given by all neighboring particles at position (i.e., all surface and non-surface ones combined). For this, the neighborhood of a particle is again given according to kernel radius h. Also, note that is usually smaller than . The neighboring spheres will overlap the initial sphere , located at particle i, thus leaving a smaller spherical area that is not overlapped, i.e., not within the neighbor spheres.
Since we work with incompressible or weakly compressible SPH particle distributions the density of the point cloud has to be nearly constant. Thus, it can be conjectured that the surface normal
at the particle will point towards the centroid of the non-overlapped spherical area on the sphere. In addition, as will be discussed in more detail below, we also found that the fraction of the sphere that has not been covered is related to the surface curvature at that point. The area of the sphere that is not overlapped by the neighboring ones can be calculated with a spherical integral. However, this integral can be computationally very expensive to determine exactly, wherefore we propose to estimate it using a Monte Carlo integration strategy. With regard to the normal computation, we first generate
uniformly distributed random sample points
on the surface of sphere
of particle
i. Initially, the positions are determined accordingly to a uniform random distribution. Below we will also examine other sampling strategies. Of the generated particles, we will next only consider those that are not inside of any neighboring sphere
. For our following derivations, we will represent this with a binary function:
Based on this, we obtain a first estimate of the surface normal:
Elements in this computation process are visualized in
Figure 5b. Also note that non-surface particles will be assigned with a zero vector. Due to the probabilistic nature of our method, discontinuities in the estimated normal field may be encountered; especially, at lower sampling numbers. However, the normal field should be as smooth as possible on the surface of the fluid. Therefore, we propose to carry out an additional smoothing step. First, we compute a weighted average of all neighboring surface particle normals, based on the results obtained in the previous step:
employing a weight kernel
W, again with kernel radius
h:
Also note again that the normals of non-surface particles have been set to zero in the previous step. The final smoothed surface particle normal is then obtained by a weighted average of both computed temporary normals:
where
is a user selected interpolation parameter. For all our computations we have set it to 0.5; this yielded, for instance for the paraboloid test case, stable and plausible curvature values in the calculations below. Also, for this geometry variation of
did not result in a strong influence on the angular error as well as the computation time. The outcome of the normal smoothing process is also illustrated in
Figure 5c. Further note that this smoothing step can be repeated several times.
To evaluate the accuracy of the proposed normal estimation process we carried out comparisons between analytically defined and our estimated normals. As error measure we determine the angle between the vectors via
, where
is the estimated normal and
the analytically correct one. In our first test case, we obtained the latter for the geometry of a 2D circle; a random 2D point cloud is generated by uniformly sampling the geometry. Next, due to the random nature of our estimation process, we determine as final error value the average of 100 computations. The results of this study are summarized in
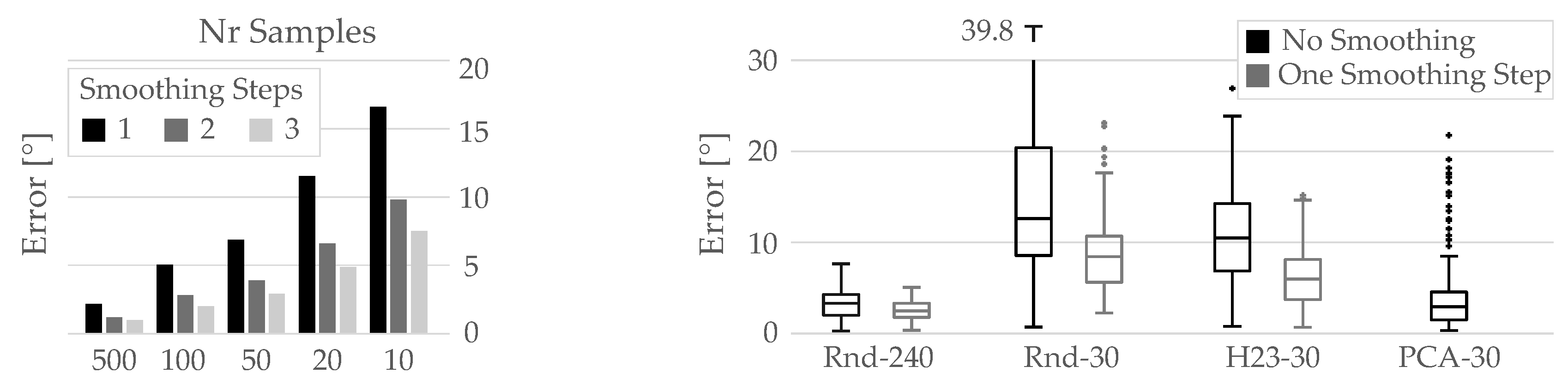
Figure 6 (left). As can be seen, the average error depends both on the number of samples as well as on the number of smoothing steps. The higher the number of sampling points, the more accurate the approximation becomes; while additional smoothing improves the estimates, by filtering out noise incurred by the representation as a point cloud.
A second, more comprehensive analysis in 3D has also been carried out, using the previously described hyperbolic paraboloid test case. We compared the estimated normals to the analytically defined ones. In addition, we also compute the error metric for an alternative sampling approach using a pseudo-random Halton sampling (described in detail below). Finally, for further evaluation we also compute normals on the point cloud via a principal component analysis (PCA) in a local neighborhood, similar to [
25]. For the latter, the mean center
of a surface point neighborhood is computed and used to determine the normal
as the minor Eigenvector of the local (weighted) covariance matrix
:
with
W the cubic support kernel and
r the support radius. Please note that in contrast to the Monte Carlo normal the orientation is not known. For our experiment, we set the orientation according to the Monte Carlo normals.
Figure 6 (right) shows the error mean and standard deviation for three sampling methods, examining also the effect of smoothing and the number of samples, for the paraboloid test case. The angular error is low at
° for high sample counts. Employing a PCA normal computation also leads to good accuracy, but takes about
additional computation time in the paraboloid experiment.
3.3. Sampling Scheme
As indicated above, akin to the notion of importance sampling, we explored possibly improvements of the naive uniformly distributed random Monte Carlo sampling. The first straightforward improvement is to employ pre-computed instead of run-time generated random spherical direction vectors. The former can be stored in look-up tables. We employed
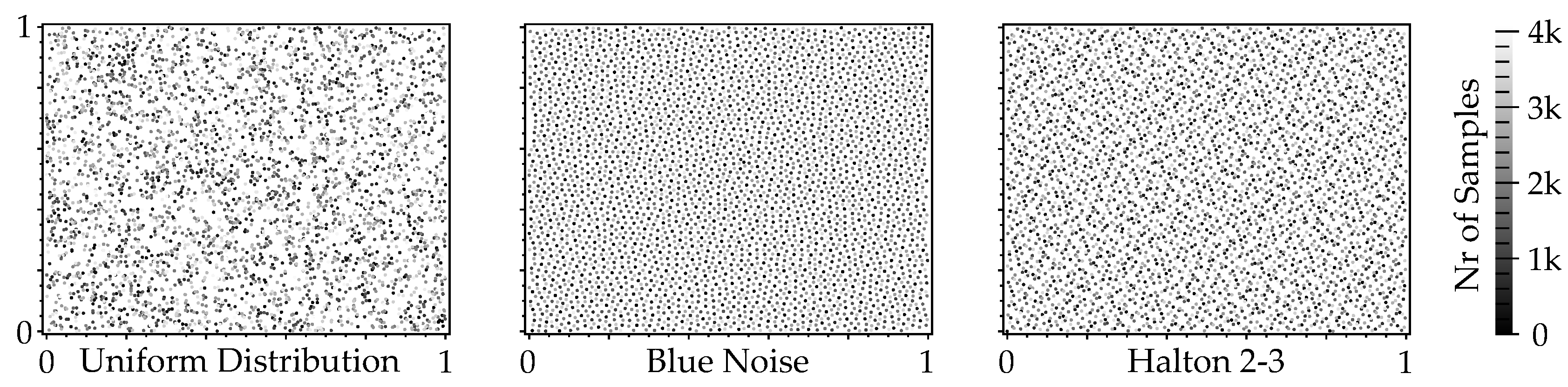
single precision pre-computed direction vectors. Values are accessed with a modulo index operation. Please note that the quality of the results correlate with precision and table size. Secondly, we also tested pseudo-random schemes that provide more homogeneous sample distributions. We tested various Halton sequences [
26] as well as blue noise sampling (see
Figure 7). For the former, the 2–3 scheme in 2D provided the best results. For the latter we employed the implementation of [
27], which realizes a Poisson distribution on Wang tiles [
28].
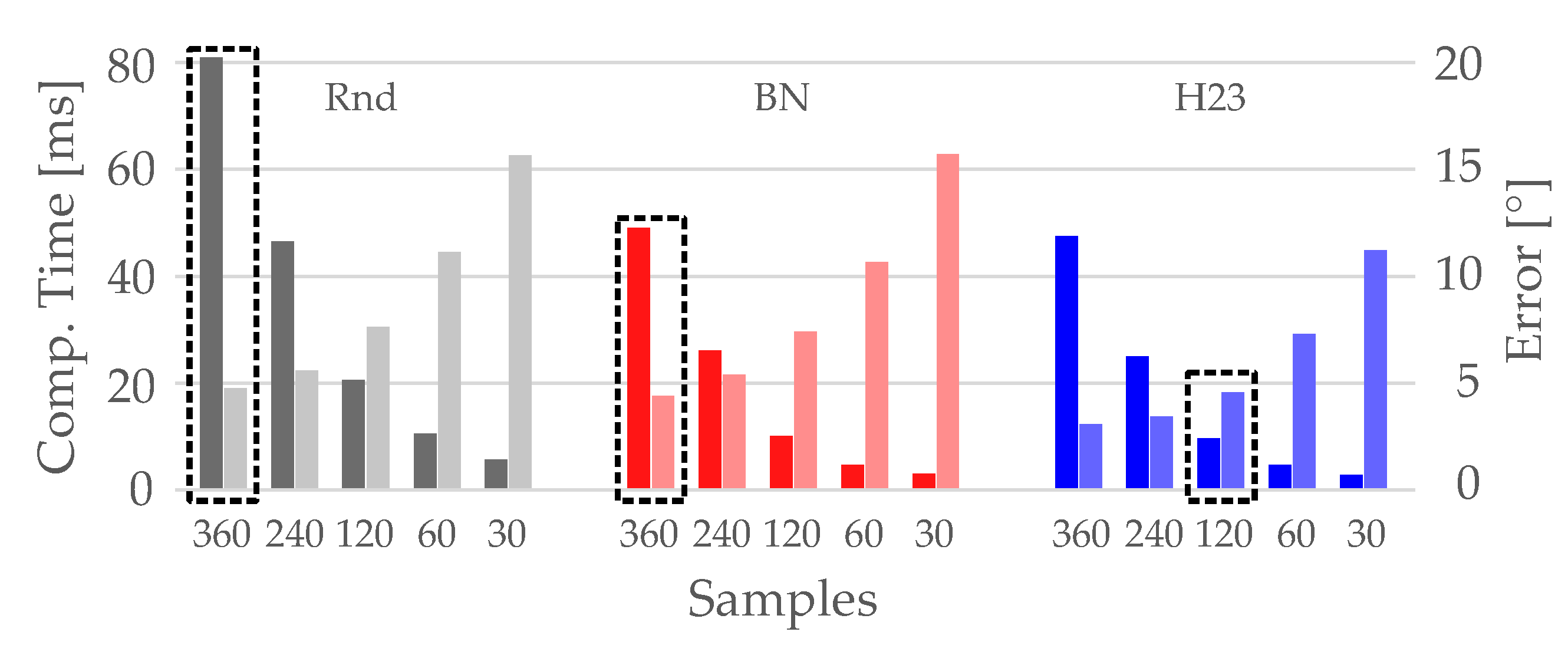
As best performing scheme we selected the Halton 2-3 (
) scheme for further analysis. Using a look-up table as well as reducing the number of samples results in a speedup; mainly due to the more robust homogeneous sample distribution. We further also examined the effect of the number of samples in this context. For our paraboloid test geometry, we calculated the mean angular error of the Monte Carlo (MC) normals to the analytic normals; in addition, also the surface computation time was measured. Both are averaged over 100 steady state simulation steps. In
Figure 8 the results are shown for uniform distribution
, blue noise
, and
. To reach a small mean angular error below 5°
requires about 360 samples (note values marked by dashed boxes). Using
the speed up due to using a look-up table can be seen. Nevertheless, obtaining errors below 5° still requires 360 samples. Switching to
allows reducing the samples to 120 for a comparable error, yielding a good speedup of
.
3.4. Curvature Calculation
The surface curvature of a 3D surface is locally given by two values, also known as principal curvatures [
29]. These are defined as the eigenvalues of the shape operator at a point on the surface. By averaging the two we obtain the mean curvature
. Gaussian and mean curvature estimation fail with point clouds including noise. We have found that it is possible to establish a direct relation between the mean curvature and the fraction of a sphere that is not covered by neighboring ones, via the process outlined above. We begin by noting that the fraction of the uncovered surface area of a sphere, using the mapping function (
2), is given by:
where
is a sphere surface location with spherical coordinates
and
. As before, instead of attempting to compute this value exactly, we will approximate it, for a particle
i, based on random samples following a Monte Carlo integration strategy:
As will be seen later, it is possible to estimate from , which itself can be determined from the randomly sampled points . Please note that . We will first derive the underlying relationship in 2D, and later extend to 3D.
3.4.1. Relationship in 2D
The following derivation is explained while closely referring to the illustration and notation in
Figure 9. We start with assuming in 2D a circular outline (shown on the bottom in gray), representing a shape for which the curvature should be determined. The circle has a radius of
, and thus the sought curvature
is given in this case analytically by the reciprocal
. However, later the formalism should be applied to any arbitrary shape or curve, based on randomly sampled locations.
First, in order to render our derivation independent of particle size, we will attempt to estimate an adjusted curvature parameter
, considering correspondingly also an adapted
. With this in mind, as a starting point for examining in this case the relationship between
and
, we will begin with deriving a lower bound
, i.e., in 2D the minimal arc that would not be covered by neighboring circles. For this, first consider a particle
i on the circular outline. We associate with this particle again a circle
, with radius
, and center
. Next, consider additional neighboring particles
j, akin to what was discussed above; to these again correspond circles
with centers
, all with the same radius
, overlapping circle
. Please note that the maximal overlap will result for those particles
j that are also located on the circular outline; in 2D there would be two of these, next to particle
i. Thus, we have to find the geometrical relationship at which circle
around such a particle
j would cover a maximal arc on
. When the circles overlap, we can find two intersection points; denoting the outer one as
, the maximum coverage will result when the vector between
and
is perpendicular to the vector between
and
; see also
Figure 9 (right). In this situation, the angle between the normal at particle
i and the vector between
and
is given as
. Also note that this angle can be obtained via:
where angles
and
are defined based on the chord between the particle positions, as depicted. Also note that the distance between the latter is given as:
According to the geometric configuration, both angles can be obtained via:
Finally, due to having two neighboring particles in symmetric configuration, we have to consider
for the non-covered arc. Overall, we obtain
. Using the previous equations, we obtain a closed form solution, independent of the sign of the curvature:
where the adjusted curvature is related to the ratio of the radii
and the minimal covered fraction
, which we approximate via random sampling.
3.4.2. Relationship in 3D
In 3D we follow a similar derivation. As before, we attempt to do this via estimating the ratio of a minimal, uncovered spherical surface area to the complete surface of a sphere. Again, we assume a particle
i on this surface, surrounded by several particles
j, for which again local spheres of radius
and
are defined. In 3D the uncovered spherical surface area
will be a spherical cap, which is given analytically. A cap on a sphere with radius
, defined by a projected solid angle
is given as:
As in the 2D case, we compute
based on the non-covered surface area:
Thus, rearranging the terms we can also in 3D express the adjusted curvature analytically:
again depending on the ratio of
and
, which we can estimate. For our implementation, and the later test scenarios we employed the ratio
, which generally yielded optimal performance. In line with this, in another example scene, i.e., the zero gravity droplet, artifacts were encountered when reducing the value to
; particles occasionally became disconnected from the surface and remained as outliers. In contrast, the paraboloid case did allow for lower ratios of
and
. Nevertheless, using the above ratio was the most robust over all test cases.
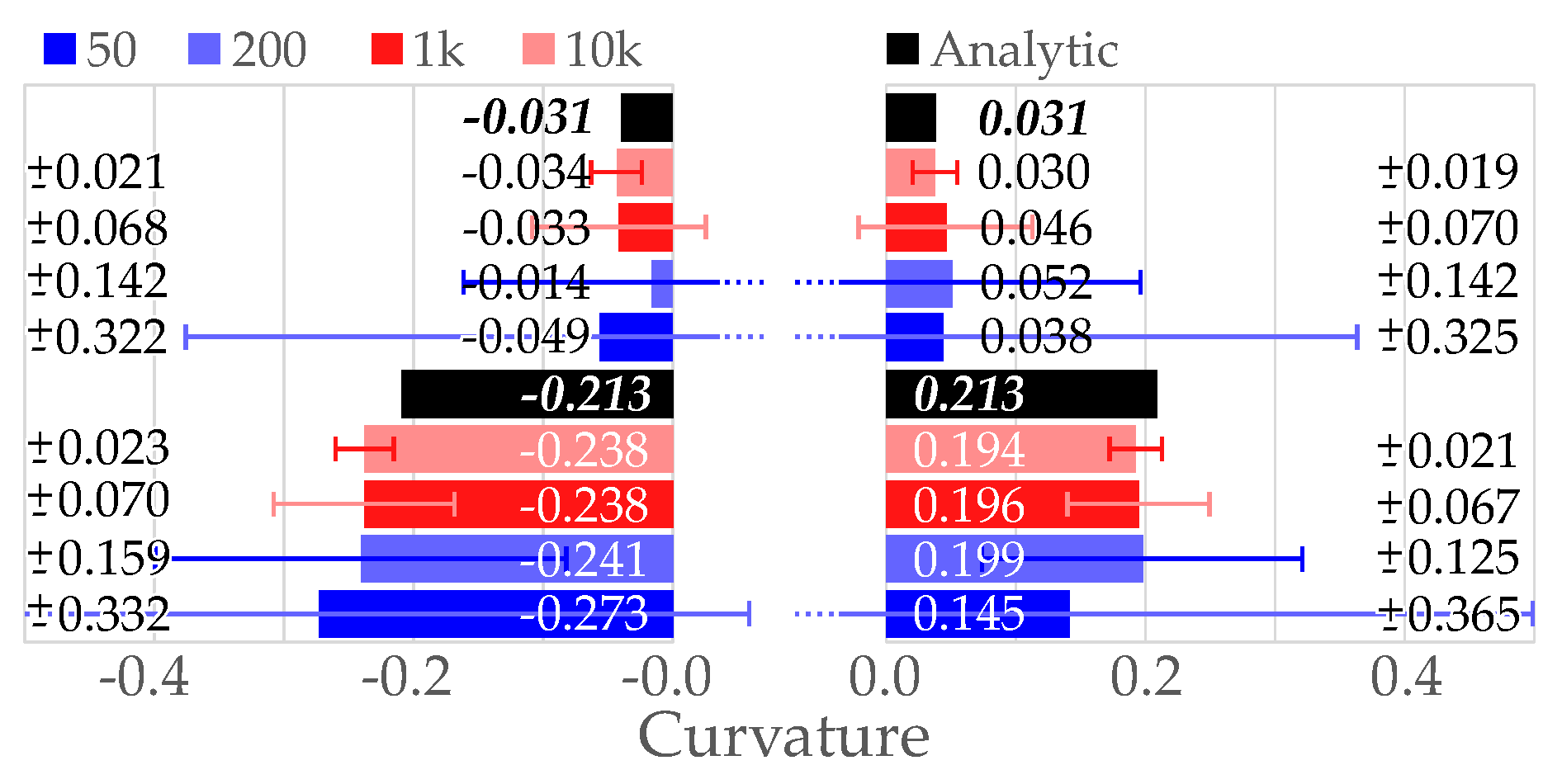
To evaluate our curvature estimation method, we compare our approximations with analytically defined mean curvature values. The latter can, for instance, be obtained in closed form for any point on an ellipsoid [
30]. Thus, we create an ellipsoidal point cloud, for which we obtain our estimate, and compare to the ground truth. Due to the stochastic nature of our method, we determine the mean and the standard deviation for 40 measurements. Moreover, note that accuracy again depends on the number of samples, wherefore we also tested our method for different amounts of such samples. The results of this validation are compiled in
Figure 10. As can be seen, for smaller curvatures our estimation approaches the correct solution, independent of the curvature sign. Moreover, even for a small number of samples our estimated average curvature is close to the correct solution. Nevertheless, the standard deviation is large for small sample numbers, but can be reduced by increasing the number of samples. In addition, we found that for larger curvatures, also larger errors in the mean curvature resulted. This is due to the sphere radius
becoming closer to actual surface features.
Finally, it should be noted that our initial development of the method was in 2D. There, the circle segment shown in
Figure 9 (left) can efficiently be computed analytically. Nevertheless, in 3D the matching computation of a spherical segment becomes more difficult and costly, wherefore we introduced the Monte Carlo approach.
3.4.3. Curvature Smoothing and Adaptive Sampling
Similar to the normal field, the curvature field should also be smooth along the surface. The probabilistic nature of the estimation process may also introduce artifacts. Thus, we again suggest to apply one or more smoothing steps, averaging computed curvatures in a local neighborhood. Furthermore, as already seen in
Figure 6, the accuracy of Monte Carlo approaches will depend on the number of samples. A straightforward approach could be to employ a constant number at all times; however, we have found that adapting the number according to the underlying numerical simulation is advantageous. The idea is inspired by the Courant–Friedrichs–Lewy (CFL) condition [
1], which relates numerical time step, spatial discretization, and propagation velocity. According to this, solution time steps in SPH algorithms are often adaptively adjusted; commonly based on forces or velocities of the fluid particles. Along this line, we propose to adjust the number of random sampling points used per time step as
, with time step
and user-selected proportionality constant
. The latter can be considered to be a sampling density factor, its value representing a trade-off between accuracy and computation speed. We have achieved good results with setting this parameter to 10,000–100,000. Our adaptive sampling makes the total number of samples per particle over a simulation time period independent of the numerical time step size.