RNN-ABC: A New Swarm Optimization Based Technique for Anomaly Detection
Abstract
1. Introduction
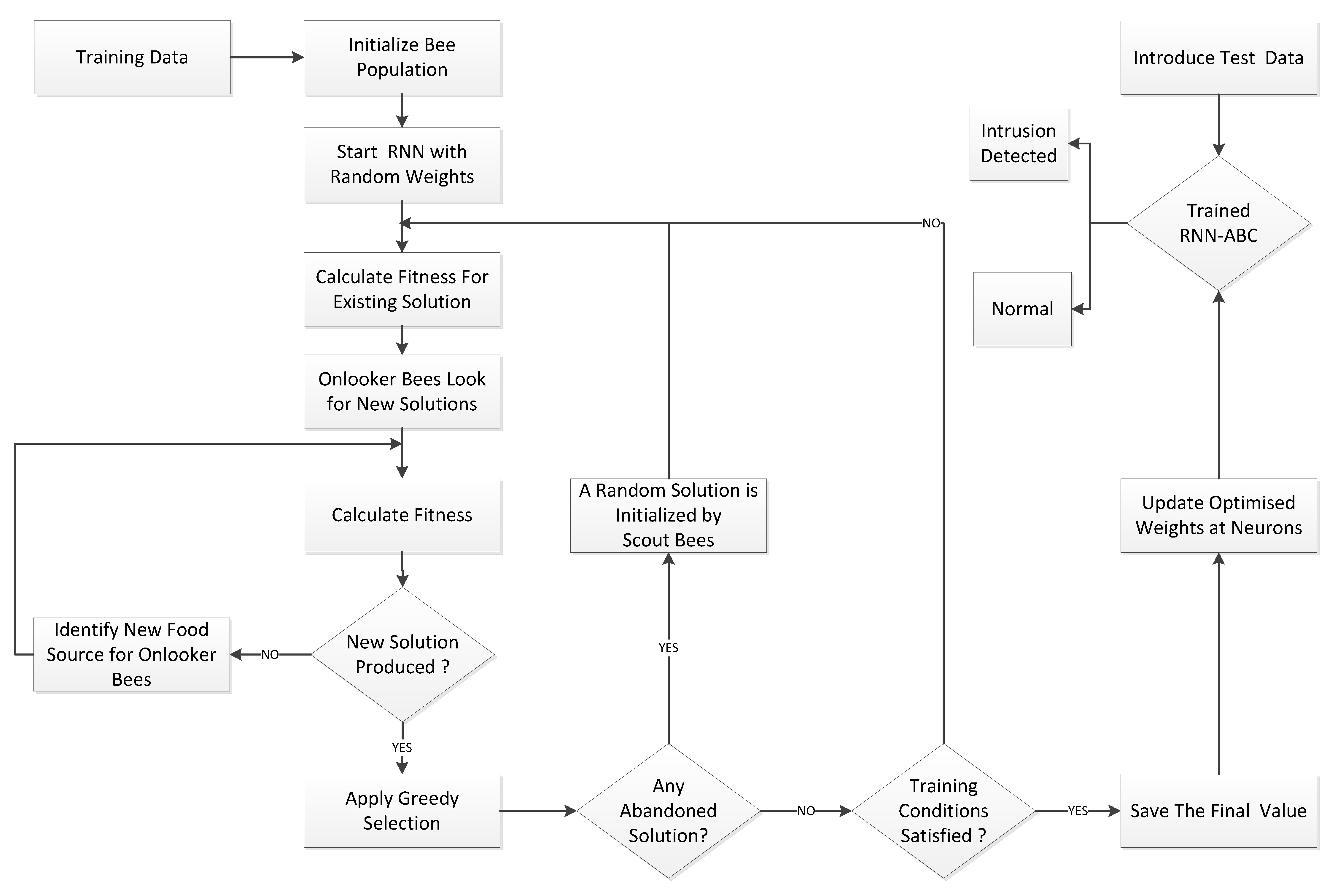
- For the development of a novel attack prediction paradigm, a new intrusion detection system using random neural networks and an artificial bee colony algorithm (RNN-ABC) is proposed.
- The performance of the previously published RNN-IDS is further extended to investigate and compare with the proposed random neural network intrusion detection system (RNN-ABC) using a number of colony sizes, food sources, iterations, and employed bees.
- Results are further extended and error rates are compared on different learning rates for both RNN-IDS and RNN-ABC, using mean of mean squared error (MMSE), standard deviation of mean squared error (SDMSE), best mean squared error (BMSE), and worst mean squared error (WMSE).
2. Preliminary Work
2.1. Random Neural Network Model
- It can reach neuron with probability as an excitation signal.
- It can reach neuron with probability as an inhibitory signal.
- It can depart the neural network with probability .
2.2. Gradient Descent Algorithm
3. Proposed Random Neural Network-Based Artificial Bee Colony Optimization (RNN-ABC)
- Step I: Initialize a population of solutions , which are randomly generated by scout bees using the equationwhere denotes the value of a food source, which ranges from , where PS represents the colony (population) size of the bee colony. Each existing solution is a D-dimensional search space of the parameters to be optimized.
- Step II: Assess the existing population using the default function.
- Step III: Start training the random neural network (RNN), where each solution is formulated using input layer neurons , hidden layer neurons , and output layer neurons of the model. The D-dimensional search space is calculated using the expressionDuring the training phase, as the weight is randomly distributed among neurons, the food position in the entire population is , where .Furthermore,
- -
- is a positive potential of mutual weight distribution between neurons i and h of layer 0 and layer 1;
- -
- is a positive potential of mutual weight distribution between neurons h and o of layer 1 and layer 2;
- -
- is a negative potential of mutual weight distribution between neurons i and h of layer 0 and layer 1; and
- -
- is a negative potential of mutual weight distribution between neurons h and o of layer 1 and layer 2.
- Step IV: Evaluation of the fitness () of population using objective function:
- Step V: Calculate the new solution, , as identified by the onlooker bees, and evaluate the fitness of the new source.where
- -
- ;
- -
- are randomly chosen indexes; and
- -
- is used to control the difference between two neighbour food sources, based on their fitness value.
- Step VI: Start the greedy selection process.
- Step VII: Calculate the probability value of the solution by using Equation (15) and normalize it into the interval [0,1]:
- Step VIII: Onlooker bees find new solution based on the probability .
- Step IX: Calculate the new fitness value .
- Step X: Re-apply the greedy selection process.
- Step XI: Scout bee to abandon food source if profitability of solution is not improved. New random value is generated using Equation (11).
- Step XII: Store the best solution and erase the previous value, based on fitness.
- Step XIII: Repeat Step IV for a new feasible solution, until maximum iterations or unchanged value of mean square error (MSE) is reached.
3.1. Data Set for Training and Testing
3.2. Feature Extraction
3.3. Data Encoding and Normalization
4. Results
4.1. Sensitivity
4.2. Specificity
4.3. False Negative Rate
4.4. False Positive Rate
4.5. Positive Predictive Value
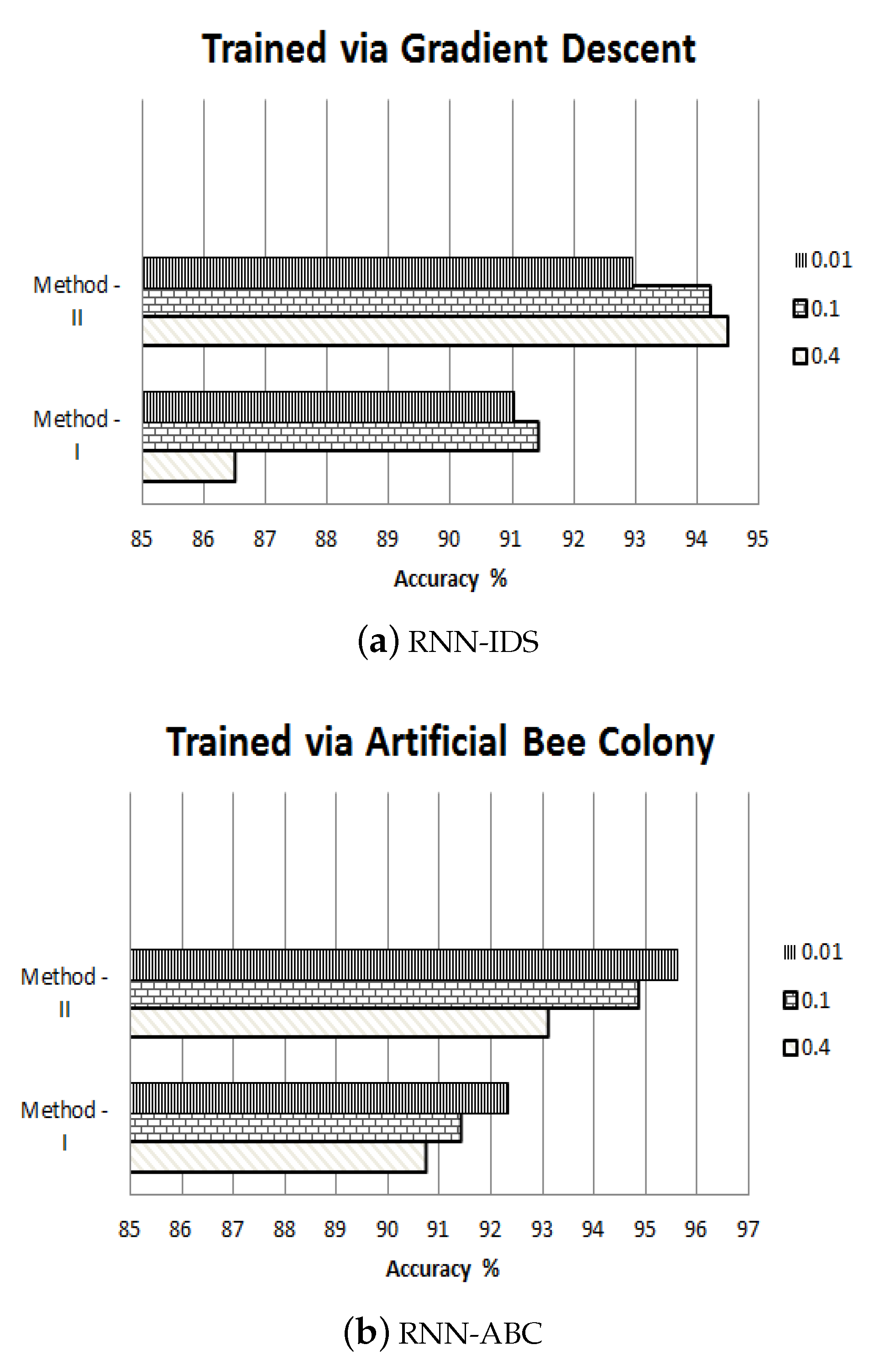
4.6. Accuracy
4.7. Method-I GD
4.8. Method-II GD
4.9. Method-I ABC
4.10. Method-II ABC
5. Conclusions
- To extend our current work for multi-class attack detection with RNN-ABC using other optimization parameters.
- To apply machine learning to design context-aware access-controlled systems which would open the gate for a lot of research opportunities and help to develop and secure several applications, such as IoT, communication systems, and healthcare applications.
- To protect the system from misled prediction, we would like to enhance the capability of RNN-ABC by training it to detect adversarial attacks. This can be achieved by reinforcement mechanisms to improve data reconciliation during the measurement phase of the data set. The performance against adversaries can also be improved using compartmentalization, traffic normalization, applying bifurcating analysis techniques, active mapping, and so on.
Author Contributions
Funding
Conflicts of Interest
References
- Qureshi, A.U.H.; Larijani, H.; Ahmad, J.; Mtetwa, N. A Heuristic Intrusion Detection System for Internet-of-Things (IoT). In Proceedings of the Intelligent Computing—Proceedings of the Computing Conference, London, UK, 16–17 July 2019; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Kayes, A.S.M.; Rahayu, W.; Dillon, T.S. Critical situation management utilizing IoT-based data resources through dynamic contextual role modelling and activation. Computing 2019, 101, 743–772. [Google Scholar] [CrossRef]
- Kayes, A.; Rahayu, W.; Dillon, T.; Chang, E.; Han, J. Context-aware access control with imprecise context characterization for cloud-based data resources. Future Gener. Comput. Syst. 2019, 93, 237–255. [Google Scholar] [CrossRef]
- Iyengar, A.; Kundu, A.; Pallis, G. Healthcare Informatics and Privacy. IEEE Internet Comput. 2018, 22, 29–31. [Google Scholar] [CrossRef]
- Xiao, L.; Wan, X.; Lu, X.; Zhang, Y.; Wu, D. IoT Security Techniques Based on Machine Learning: How Do IoT Devices Use AI to Enhance Security? IEEE Signal Process. Mag. 2018, 35, 41–49. [Google Scholar] [CrossRef]
- Significant Cyber Incidents. Available online: https://www.csis.org/programs/technology-policy-program/significant-cyber-incidents (accessed on 13 August 2019).
- Liu, Q.; Li, P.; Zhao, W.; Cai, W.; Yu, S.; Leung, V.C.M. A Survey on Security Threats and Defensive Techniques of Machine Learning: A Data Driven View. IEEE Access 2018, 6, 12103–12117. [Google Scholar] [CrossRef]
- Mirjalili, S. Genetic Algorithm. In Evolutionary Algorithms and Neural Networks: Theory and Applications; Springer International Publishing: Cham, Switzerland, 2019; pp. 43–55. [Google Scholar] [CrossRef]
- Kennedy, J. Swarm Intelligence. In Handbook of Nature-Inspired and Innovative Computing: Integrating Classical Models with Emerging Technologies; Zomaya, A.Y., Ed.; Springer US: Boston, MA, USA, 2006; pp. 187–219. [Google Scholar]
- Li, X.; Clerc, M. Swarm Intelligence. In Handbook of Metaheuristics; Gendreau, M., Potvin, J.Y., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 353–384. [Google Scholar]
- Qureshi, A.; Larijani, H.; Ahmad, J.; Mtetwa, N. A Novel Random Neural Network Based Approach for Intrusion Detection Systems. In Proceedings of the 10th Computer Science and Electronic Engineering (CEEC), Colchester, UK, 19–21 September 2018; pp. 50–55. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Farnaaz, N.; Jabbar, M. Random Forest Modeling for Network Intrusion Detection System. Procedia Comput. Sci. 2016, 89, 213–217. [Google Scholar] [CrossRef]
- Kwon, D.; Kim, H.; Kim, J.; Suh, S.C.; Kim, I.; Kim, K.J. A survey of deep learning-based network anomaly detection. In Cluster Computing; Springer: Cham, Switzerland, 2017; pp. 1–13. [Google Scholar]
- Yin, C.; Zhu, Y.; Fei, J.; He, X. A Deep Learning Approach for Intrusion Detection Using Recurrent Neural Networks. IEEE Access 2017, 5, 21954–21961. [Google Scholar] [CrossRef]
- Ingre, B.; Yadav, A. Performance analysis of NSL-KDD dataset using ANN. In Proceedings of the International Conference on Signal Processing and Communication Engineering Systems, Guntur, India, 2–3 January 2015; pp. 92–96. [Google Scholar] [CrossRef]
- Gelenbe, E. Random Neural Networks with Negative and Positive Signals and Product Form Solution; MIT Press: Cambridge, MA, USA, 1989. [Google Scholar] [CrossRef]
- Emmanuel, R.; Clark, C.; Ahmadinia, A.; Javed, A.; Gibson, D.; Larijani, H. Experimental testing of a random neural network smart controller using a single zone test chamber. IET Netw. 2015, 4, 350–358. [Google Scholar] [CrossRef]
- Ahmad, J.; Larijani, H.; Emmanuel, R.; Mannion, M.; Javed, A.; Phillipson, M. Energy demand prediction through novel random neural network predictor for large non-domestic buildings. In Proceedings of the Annual IEEE International Systems Conference (SysCon), Montreal, QC, Canada, 24–27 April 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Javed, A.; Larijani, H.; Ahmadinia, A.; Emmanuel, R.; Mannion, M.; Gibson, D. Design and Implementation of a Cloud Enabled Random Neural Network-Based Decentralized Smart Controller With Intelligent Sensor Nodes for HVAC. IEEE Internet Things J. 2017, 4, 393–403. [Google Scholar] [CrossRef]
- Saeed, A.; Ahmadinia, A.; Javed, A.; Larijani, H. Intelligent Intrusion Detection in Low-Power IoTs. ACM Trans. Internet Technol. 2016, 16, 1–25. [Google Scholar] [CrossRef]
- Javed, A.; Larijani, H.; Ahmadinia, A.; Gibson, D. Smart Random Neural Network Controller for HVAC Using Cloud Computing Technology. IEEE Trans. Ind. Inform. 2017, 13, 351–360. [Google Scholar] [CrossRef]
- Adeel, A.; Larijani, H.; Ahmadinia, A. Random neural network based novel decision making framework for optimized and autonomous power control in LTE uplink system. Phys. Commun. 2016, 19, 106–117. [Google Scholar] [CrossRef]
- Abdelbaki, H.; Gelenbe, E.; EL-Khamy, S. Analog hardware implementation of the random neural network model. In Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium, Como, Italy, 27 July 2000; Volume 4, pp. 197–201. [Google Scholar] [CrossRef]
- Mohamed, S.; Rubino, G. A study of real-time packet video quality using random neural networks. IEEE Trans. Circuits Syst. Video Technol. 2002, 12, 1071–1083. [Google Scholar] [CrossRef]
- Mahmod, M.; Alnaish, Z.; Al-Hadi, I.A.A. Hybrid intrusion detection system using artificial bee colony algorithm and multi-layer perceptron. Int. J. Comput. Sci. Inf. Secur. 2015, 13, 1. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- NSL-KDD—Datasets—Research—Canadian Institute for Cybersecurity. Available online: http://www.unb.ca/cic/datasets/nsl.html (accessed on 3 May 2018).
- Bajaj, K.; Pradesh, H.; Arora, A.; University, C. Improving the Intrusion Detection using Discriminative Machine Learning Approach and Improve the Time Complexity by Data Mining Feature Selection Methods. Int. J. Comput. Appl. 2013, 76, 975–8887. [Google Scholar] [CrossRef]
- Javed, A.; Larijani, H.; Ahmadinia, A.; Emmanuel, R.; Emmanuel, R. Random neural network learning heuristics. Probab. Eng. Inf. Sci. 2017, 31, 1–21. [Google Scholar] [CrossRef]

| Dataset Type | Instance | Normal Patterns | Attack Patterns (%) |
|---|---|---|---|
| NSL-KDD Train20 | 25,192 | 13,499 | 46.6 |
| NSL-KDD Train+ | 125,973 | 67,343 | 46.5 |
| NSL-KDD Test+ | 22,544 | 9711 | 56.9 |
| NSL-KDD Test− | 11,850 | 2152 | 81.8 |
| Optimization Parameters | Value |
|---|---|
| Bee Colony Size | 20 |
| Food Sources | 10 |
| Employed Bees | 10 |
| Maximum Iterations | 100 |
| Learning Rates | ||||||
|---|---|---|---|---|---|---|
| Gradient Decent | Method I | Method II | ||||
| 0.4 | 0.1 | 0.01 | 0.4 | 0.1 | 0.01 | |
| Sensitivity | 91.72 | 93.36 | 94.24 | 94.79 | 95.31 | 95.60 |
| Specificity | 24.8 | 42.56 | 55.86 | 59.62 | 72.88 | 69.68 |
| False Negative Rate (FNR) | 8.28 | 5.76 | 6.64 | 5.21 | 5.04 | 4.40 |
| Flase Positive Rate (FPR) | 75.18 | 57.44 | 44.14 | 40.38 | 27.12 | 30.22 |
| Positive Predictive Value (PPV) | 93.63 | 96.60 | 96.95 | 97.81 | 98.67 | 98.62 |
| Accuracy | 86.5 | 91.42 | 91.02 | 92.95 | 94.21 | 94.50 |
| Learning Rates | ||||||
|---|---|---|---|---|---|---|
| Performance Metrics | Method I | Method II | ||||
| 0.4 | 0.1 | 0.01 | 0.4 | 0.1 | 0.01 | |
| MMSE | ||||||
| SDMSE | ||||||
| BMSE | ||||||
| WMSE | ||||||
| Learning Rates | ||||||
|---|---|---|---|---|---|---|
| Artificial Bee Colony | Method I | Method II | ||||
| 0.4 | 0.1 | 0.01 | 0.4 | 0.1 | 0.01 | |
| Sensitivity | 92.27 | 93.10 | 93.98 | 94.13 | 95.20 | 95.84 |
| Specificity | 71.15 | 67.10 | 64.78 | 70.70 | 72.77 | 77.88 |
| False Negative Rate (FNR) | 7.73 | 6.90 | 6.02 | 587 | 4.80 | 4.16 |
| False Positive Rate (FPR) | 28.85 | 32.90 | 35.22 | 29.30 | 27.29 | 22.12 |
| Positive Predictive Value (PPV) | 97.64 | 97.62 | 97.79 | 98.21 | 98.24 | 99.05 |
| Accuracy | 90.75 | 91.42 | 92.32 | 93.10 | 94.84 | 95.62 |
| Learning Rates | ||||||
|---|---|---|---|---|---|---|
| Performance Metrics | Method I | Method II | ||||
| 0.4 | 0.1 | 0.01 | 0.4 | 0.1 | 0.01 | |
| MMSE | ||||||
| SDMSE | ||||||
| BMSE | ||||||
| WMSE | ||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qureshi, A.-U.-H.; Larijani, H.; Mtetwa, N.; Javed, A.; Ahmad, J. RNN-ABC: A New Swarm Optimization Based Technique for Anomaly Detection. Computers 2019, 8, 59. https://doi.org/10.3390/computers8030059
Qureshi A-U-H, Larijani H, Mtetwa N, Javed A, Ahmad J. RNN-ABC: A New Swarm Optimization Based Technique for Anomaly Detection. Computers. 2019; 8(3):59. https://doi.org/10.3390/computers8030059
Chicago/Turabian StyleQureshi, Ayyaz-Ul-Haq, Hadi Larijani, Nhamoinesu Mtetwa, Abbas Javed, and Jawad Ahmad. 2019. "RNN-ABC: A New Swarm Optimization Based Technique for Anomaly Detection" Computers 8, no. 3: 59. https://doi.org/10.3390/computers8030059
APA StyleQureshi, A.-U.-H., Larijani, H., Mtetwa, N., Javed, A., & Ahmad, J. (2019). RNN-ABC: A New Swarm Optimization Based Technique for Anomaly Detection. Computers, 8(3), 59. https://doi.org/10.3390/computers8030059







