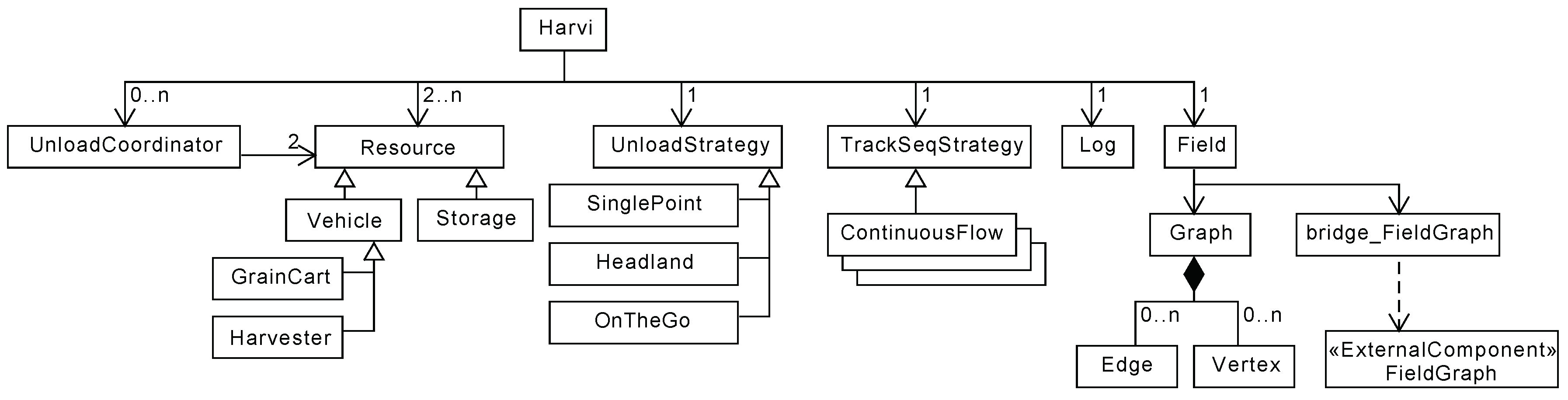
1. Introduction
The agricultural sector evolved to achieve a massive increase in productivity, for the sector demands have grown, and inexpensive and high-quality food is a requirement. In the agricultural domain, harvesting is the process of gathering a ripe crop from the fields, and it has a huge impact on productivity. The increases in harvest productivity are predicted [
1] to emerge from better planning and optimisation of the interaction between the different resources involved in the harvesting operations. Current industrial-level harvesting operations involve advanced logistics, which produce a plan in the form of a choreography to be performed by human-operated vehicles during the harvest process.
The sketch in
Figure 1 provides an abstraction of a harvest process. In it, the typical vehicles involved in a harvest are displayed: combines, service units, and trucks; each indicated by labels numbered: 1, 2, and 4 respectively. Combines are vehicles reaping the crop from the field while storing the yield in a local bin. For small fields, a single combine may be used, but in larger fields, the use of multiple combines is common practice. To optimise the harvest process time and vehicle usage, the combine may use an auger (an Archimedes’ screw kind of conveyor) to unload the bin content, while it reaps the field. Unloads are part of the plan, as depicted by number 3 in
Figure 1. The plan designates a service unit and ensures an adequate (side-by-side) and timely route synchronisation between the two vehicles. After the unloads, the service units unload the grain to on-road trucks, and become free to service another combine.
The grand vision, where a farmer stands in front of a field supervising the result of an automated harvest process, is not far from what current technology allows [
2]. Nevertheless, practice shows there are still several technological and social challenges to overcome. On the social side, one is faced with rooted practices and novelty aversion from the practitioners. On the technological side, the modern tools and concepts take a long time to get ready to perform efficiently in the field.
This paper reports on part of the results of a three-year project named “off-line and on-line logistics planning of harvesting processes” where Aarhus University and the company AGCO A/S worked together to address the practical technological challenges faced by the next generation harvest logistic systems. The project produced prototypes for the systems involved in harvest logistics optimisation including both an off-line simulation tool, where a harvest operation can be setup and several parameters explored and optimized by means of simulation (indicated by 6 in
Figure 1), and a real-time guidance system that provides guidance in the form of routes that the operators should follow during the actual harvest process (indicated by 5 in
Figure 1).
The prototypes served as mock-up realisations of a harvest logistics solution and enabled us to produce field experiments. The experiments involved vehicles uploading controller area network (CAN) bus data to our prototype which in turn issued route plans in the form of GPS coordinate waypoints to be followed. From the experiments, valuable feedback was collected to improve the robustness of the prototypes and add operator driven usability features to the prototypes.
During the course of the harvest process, deviations are likely to occur due to a biologically varying environment. For instance, yield may be different than expected and vary across the field, causing the bin of the combine to be filled faster or slower than expected. This type of deviation might make the planned route invalid because the bin could become full faster than anticipated, potentially leaving the combine in a position where unloading is not feasible. Therefore it is crucial to be able to cope with this type of deviation.
Besides the environmental factors, the guidance system is also challenged by the human driver, for the human control of harvesting machinery is naturally coarse, and vehicle manoeuvring in the field has hard limitations. Small positional deviations compared to the planned route will occur because of this manoeuvring. Such small deviations should be tolerated and should not trigger a replanning. However, a driver may follow a route that is different from the planned one, and in this case the logistics system should trigger a replanning. Therefore, a deviation addressing mechanism is an essential usability and user-acceptance feature of a guidance solution, as human operators expect flexibility and tolerance from such a system.
To cope with deviations we devised a novel software architecture, the harvest coach architecture (HCA), adapting the fault tolerance architecture from the domain of fault tolerance control [
3]. In that domain a system controller operates at two different execution levels. Without faulty conditions, the control is performed at the base level, which is labelled as the execution level. In case a fault is diagnosed, the system enters into a supervisory execution level which has the logic to diagnose the situation and adapts the controller system which operates under the degraded conditions.
In our software architecture there is also the notion of two execution levels. At the execution level there is the “harvest logistics system” (HLS) (In previous publications it was termed both as a “centralised control algorithm” or as a “master algorithm”. In this paper we unify these in the HLS keyword, avoiding the duplication and also highlighting the disconnection with the “master algorithm” concept as defined in the machine learning field.) which deploys an initial harvest plan tuned for a best case scenario in terms of the field conditions. The execution level was previously developed as reported in [
4,
5,
6,
7], and, before our additions, implemented a stepwise loop reading the values for the several vehicle parameters (e.g., GPS position, bin level) in the field and issuing the routes to be shown to the operators in thin clients to be carried in cabins of the vehicles.
At the supervision level there is what we term the “harvest coach” (HC) which diagnoses differences from the planned operations (for instance, low-yield in a patch of land assumed to be highly productive at the offline setup stage) using “harvest deviation monitors” (HDMs) and deploys a novel “plan” (system) that mitigates the encountered “deviation” (fault). The proposed deviation-tolerant architecture finds the optimal continuation plan given the deviation. Our solution abstracts the computation of the new plan as there are vast works regarding optimality, and the computation of an optimal continuation plan after a deviation is a rich and complex research field in itself [
8,
9].
To exercise our HCA software solution, we chose to focus into position deviations and yield deviations, as both are expected to happen when using the HLS, although only the position deviations were experimentally tested in the field. In this paper, a definition for the two kinds of deviations is given in the forms of Equations (
1) and (
4), which we described in
Section 4 and
Section 5 respectively.
In addition, we developed artefacts to avoid redundant replanning actions, and to cover the cases where the particular deviation instance is known to be tolerable. For instance, the introduction of a position validity measure (defined by (
2) in (
4)), a division of the harvest process plan into phases, and an automaton to infer the current plan phase from the data collected in the field allowed us to discard redundant deviations.
The HLS prototype was extended with the HCA, and was put to the test in several infield experiments where the system was used to guide a test driver operating a combine vehicle retrofitted with the prototype. The results of such experiments provide a positive review to the application of the HCA and we summarise the main outcomes in this paper. We expect our architecture and results to be useful to a broader audience, and in particular we believe they may be useful in the development of systems where deviations play a role.
In a first implementation, the HCA solution was non-interactive and worked in auto mode. Infield tests showed that the user would not be aware that a deviation is happening and the plan was changed. Moreover, at points the user could be interested in keeping the original plan, although deviating for the route. Therefore, we added interactive elements to the HCA. Deviations were signalled from the HC to the operator and approval was first obtained before issuing a new plan.
Our goal as the academic partner in the joint research project was to use a model-driven approach system design to build prototypes of the different components of the envisioned system. Preference was given to the usage of open source software platforms, except for the combine harvester and gateway component that were provided by the industrial partner.
Our architecture is built on top of a prototype reported in previous publications. In [
4,
5], the authors reported on how optimisation algorithms for different aspects of the harvest operation can be combined through the usage of a combination of design patterns and a formal Vienna developed method (VDM) model. This paper is based on the same model, but we added the deviation mechanism to allow replanning, and ensure the plan is updated throughout the whole harvest process.
In [
6], the technical details of the main component in the harvest logistics prototype are described. In particular, the paper exposes reasons for the choice of a sequential execution model and the model evolution throughout project timeline. The paper is suited for an audience with expertise in VDM and contains no details in terms of the harvest coach architecture which in turn is the focus of out paper and the proposed architecture.
In [
7,
10], the reader may find details about the process of unit testing the prototypes developed. One paper uses the harvest logistics prototype as a case study and test to the improvements of the VDM testing support, the other uses it as an example of distributed system modeling. Furthermore, Tran-Jørgensen et al. [
10] reports a number of 134 unit tests for the HLS system VDM model and how they are performed. In contrast to such works, our architecture provides a solution to the deployment of the prototype in the field, and we focus on providing the details on the construction of the solution itself.
Fault tolerance and industrial grade system solutions are abundant, yet deviation-tolerance poses a more challenging research problem to the designer of a guidance solution, and seems to us far from being solved, in particular in the harvesting domain. In fact, we have not found any other literature that address this particular problem. Our approach is to port concepts from the domain of fault-tolerant control systems [
3] into the architecture, yet the result is not a traditional fault-tolerant controller, because a deviation occurs not as a fault of a component (e.g., GPS receiver failure) or human fault, but as a deviation from the harvest plan. The harvest logistic control system components are assumed to be up and running both before, during, and after a deviation happens.
In
Section 2, an introduction to the stepwise control loop and the HLS prototypes is framed in a broad setting. In
Section 3, the high-level details of the HCA in terms of a feedback loop control system are introduced. In
Section 4 and
Section 5, the different deviation scenarios considered and how to take the human-in-the-loop aspects into account are described. Then
Section 6 presents more details regarding our particular prototype implementation, especially the changes performed to the previously existing VDM model. In
Section 7, the performance of the HCA in different tests performed in a real agricultural field facility of Aarhus University is reported. Finally, in
Section 8 we provide a discussion of the infield experiments and the outcomes of the addition of the HCA to our prototype.
2. The Harvester Logistics System Prototype
In this section, we provide a high-level description of the behaviour of the real-time guidance system prototype. We focus on the essential components of the HLS prototype, i.e., the ones involved in the actual harvest operations, and on how each plays a role in the final behaviour of the system. The essential components are:
Thin client: a standard tablet/smartphone hosting a GUI, which was developed during the project, and provides guidance to the combine and service unit operators. The guidance consists of showing a map view displaying the plan produced by the HLS in the form of routes/synchronisation points to be followed.
Combine: standard harvester machine manufactured by AGCO and operated by a licensed driver with the support of our thin client prototype.
Combine gateway: AGCO proprietary hardware equipment with navigation and internet connection, which we used to upload controller area network (CAN) bus data from the combine to a cloud server which our own HLS prototype had access to.
Cloud server: a standard desktop computer hosting both:
- -
the HLS prototype,
- -
a standard publish-subscriber service for communication over the network,
- -
and the back end web-services for the thin clients to run in tablets.
As we focus on deviations (user/process specific faults) and not on fault tolerance (missing messages/faulty sensor) we assume all the components work under normal conditions and will then treat them as black-boxes, except for the HLS prototype which is the only box that is relevant for the deviations.
The HLS prototype, given its criticality, was developed following the VDM [
11]. The method prescribes the development of state-based and object-oriented models in the VDM formal modelling language and has been previously extensively applied in the development of high-level controllers. The HLS model implements a stepwise loop which, for clarity, in this section, is described in terms of a feedback loop in the notation of control systems and we refer the reader interested in the VDM details to [
4,
5,
6] and in
Section 6.
The abstract behaviour of the real-time guidance prototype is depicted in
Figure 2. In it, the HLS and its environment are depicted. The HLS reads the desired state of the field
f from the setup and outputs a route
r in the form of the next waypoints that need to be reached by an operator.
At each instant the HLS measures the available field parameters (e.g., vehicles GPS coordinates, grain intake, level of bin), computes the remainder of the field as the error , and outputs new routes by discarding the waypoints that were already reached. The diagram assumes there is only one operator in the field, but by replicating the operator box and its connections one obtains the system diagram by simple refinement.
The vehicle operator (the human-in-the-loop element) steers the vehicle to follow the route r and changes the state of the field and its position y through its output u. In the best-case scenario the operator is attempting to minimise the error between the operator measurement of the current vehicle trajectory and the expected route r. It was a requirement of our project that the HLS must be able to operate without relying on additional sensors to measure the field status y. The measurements rely on the sensor information already available from the CAN bus, from which we obtain the measured outcomes of the expected process state.
If the plan is not followed, a deviation occurs and this affects the continuation of the plan. A deviation occurrence at some time instant translates to the measurement of a value for a parameter in the field that does not match the value expected by the plan f. For instance, the measured value for the position of the combine by the measurements of CAN bus data component (e.g., combine report a position inferred to be at row X) may differ from the value that was expected by the plan (e.g., according to the planned route f, the combine is expected be positioned at row Y). In that case the previously deployed route r is compromised, and the HLS component had no logic to produce either a continuation route r from that moment on, or a new plan f.
To illustrate what is meant by measuring the process state, consider the estimation of the geographical position of a combine in a field (a geolocation), which is essential in the detection of position deviations. The estimation dataflow is depicted in
Figure 3. The combine is equipped with a gateway providing latitude
and longitude
coordinates in the form of geographic coordinates
in a sphere, which traverse the network to reach the HLS prototype.
To be used in route planning, the spherical geographical coordinates must be projected into coordinates of a plane, because the problems to be solved while computing routes (e.g. distances, angles, …) are easy to solve using the plane Euclidean geometry. In our work, the coordinate projection is based on a standard Universal Transverse Mercator projection as the one that can be found in [
12], and is abstracted as a mathematical function
providing coordinates in terms of an easting
and northing
value.
Yet the precision of positioning systems is far too refined in the context of manoeuvring tonne weighing vehicles in a farming field, thus we convert the coordinates using a snap to grid () projection. The produces an easting and a northing value, projecting the plane coordinates to the nearest plane coordinates of a grid/mesh defining the expected routes in the graph.
Given that the routes in the grid structure are defined in terms of traversing an edge in a predefined direction, we use another projection to convert the grid coordinates into a triple recording an edge (token unique identifier) e, a direction (forward or backward) d, and a progress (percentage of edge traversed) p. The projection coordinates simplify the monitoring of deviations, as the computation relies on comparing the edge identifiers, direction tokens, and progress numbers.
Having defined the dataflow of vehicles data, we can now provide an illustration of how to produce the measurements of the process status y without relying in extra sensors. Let us consider the estimation of the amount of yield to be reaped in the field position corresponding to some edge e. Our experiments show one is able to infer the changes in the state of the harvest process y with sufficient accuracy by correlating the status of the combine variables related to grain intake (position of the header, grain intake in kg/L) and the time-series of triples , which is reported while traversing the edge e, under the assumption that there is a clear monotonic increase of the progress p, converging to a value of 100%. Nonetheless, the sparse investment in sensors leads to higher complexity, when one needs to decide whether an operator not following the routes prescribed by the plan does so due to either better situational awareness or mistake.
3. The Harvest Coach Architecture
In this section, we present a high-level description of the devised HCA deviation-tolerance architecture. Because of its generic aspect, the high-level details of the HCA are described in terms of a feedback loop, since the HCA may be useful to apply in a broader scope. The description also emphasises the addition we made to the previously stage of development of the system prototype, corresponding to the HLS as described in
Figure 2, where a deviation would lead to a fail state, and block the system progress.
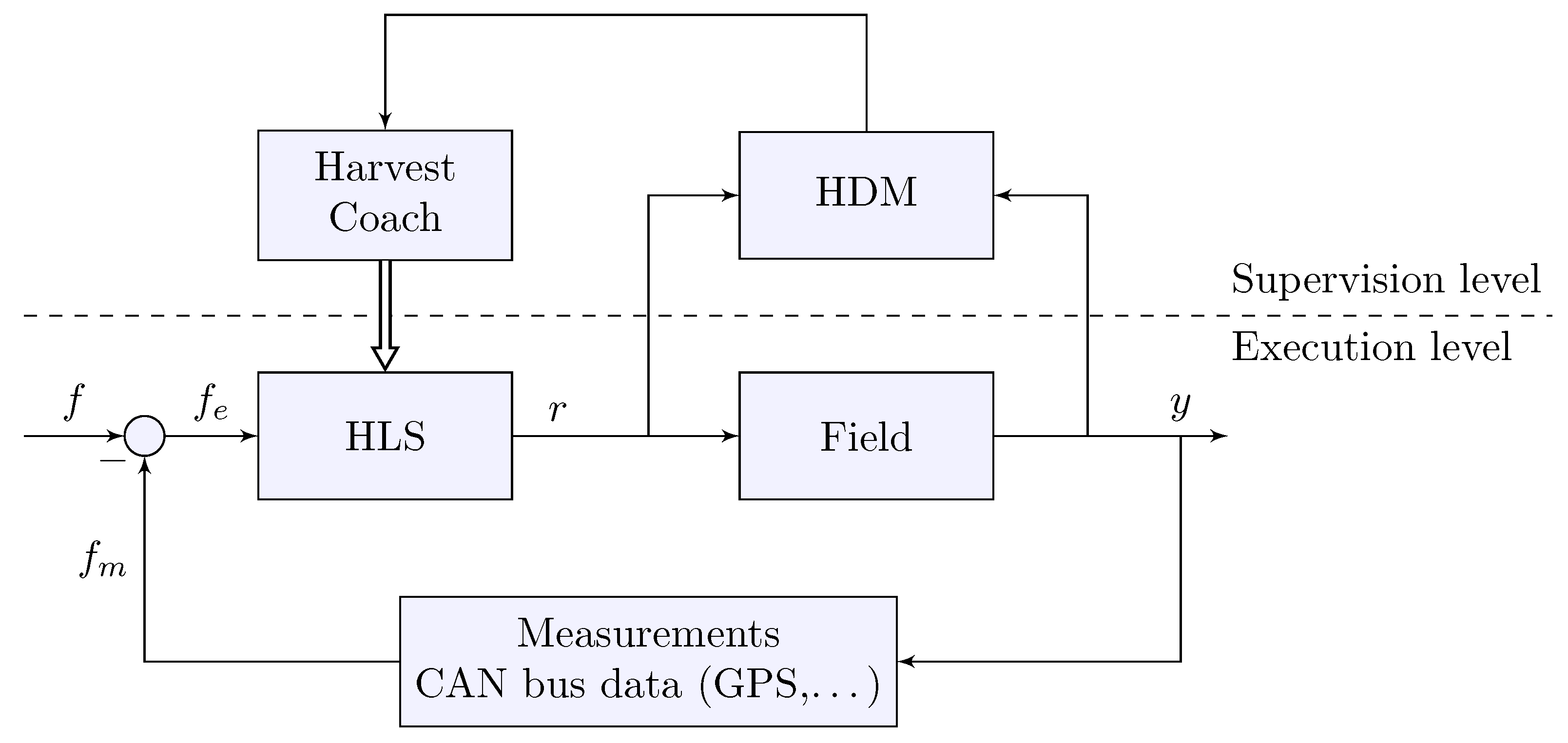
The modification to the existing HLS prototype is shown in
Figure 4, and consists of two new components: the harvest coach and the HDM. The addition of the new components introduce the notion of run levels, which are highlighted by the dashed line dividing
Figure 4 horizontally. The run levels are defined in the same way that fault tolerance architectures define them:
Execution level: the base operational level for the system, where the best case scenario conditions are met and where the operators in the field follow the routes deployed by the HLS, which in turn simply updates the plan progress.
Supervision level: where the HC runs when a deviation occurs and where the HDMs run periodically. This is a critical run level ensuring the deviations are detected and action is taken accordingly, when appropriate.
The execution level has a trapping mechanism allowing the execution to be switched into the supervision level. This switch of level gave rise to the idea of a coach, because beyond an update of the simulation model state, the operation decisions rely on a centralised component running at another level with a global view of the field, which is itself responsible for making changes to a plan during the harvest operation.
At the execution level one finds the HLS and a loop identical to the one in
Figure 2, where the field component in
Figure 4 abstracts the inner loop in
Figure 2, which in turn corresponds to an abstraction of the physical harvest elements comprising both the piece of land holding the crop and also the vehicles and other assets. As in
Figure 2 the route variables
r are generated to perform the expected field harvest
f, and the route is input to the field elements producing an update to the field elements variables
y.
To be able to detect deviations the HDM receives both the route r to be followed and the field measured values as input. When a violation of the expected values is observed, the HDM relays such an event to the HC by triggering its execution and trapping the execution to the supervision most critical level.
The execution of the HC performs the necessary operations to decide whether the deviation demands a new plan generation or if it is possible to continue to operate. The logic built-in at the HC level is designed according to the definitions in a deviations catalogue to be understood as the deviations the HC is able to manage and what are the actions to be taken when a deviation is detected.
In the case of a critical deviation (e.g., position Y when expecting to be in position X), which demands a re-optimisation and issuing a different route r the HC deploys a new HLS component as illustrated by the thick arrow and the execution goes back to the lower level. The new version of the HLS component is tuned to produce a route r which fits the deviating state for the current field measurement containing the deviating parameter (for instance, in our running example, a liaison route from position Y to X may be issued as a mitigation).
The issuing of a new plan is not immediate, as it could erroneously be inferred from the double arrow in the diagram in
Figure 4. Diagnosed deviations for which a new plan is required are transmitted to the driver via the thin clients, so the drivers have the last decision on whether a new plan should be put in place or not.
The next two sections provide a low-level account on two kinds of deviation present in the deviation catalogue: position and yield deviations, and illustrate the nuts and bolts involved in addressing the specific deviations. For the implementation details of the high-level HCA in terms of the operational VDM model please confer
Section 6.
4. Position Deviations
In a position deviation, there is a discrepancy between the reported position of a vehicle and the expected position according to the plan. As described in
Section 2, the variables from the field
y are processed to obtain
, the measured field values, and the geolocation sub-system produces triples
, which define the reported position of a vehicle. Assuming the planned position is given by the triple
, we define a position deviation in (
1). The definition states a deviation occurs when the reported position edge or the direction of the vehicle differ from the planned ones, or the distance between the progress and the planned progress is greater then the arithmetic precision
of the computing platform hosting the HLS:
Minor position deviations occur frequently, because it is both unreasonable to expect vehicles can be steered to follow the route with infinite accuracy and to assume no event leading to a deliberate decision by the operator to deviate from the planned route happens. From an analysis of field data, the position deviations can be sorted into one of the following exclusive categories:
Negotiation/manoeuvring deviations: occurring when the driving of the machinery demands a temporary deviation from the plan. The typical example is a need to reverse and back off in order to align a vehicle with the planned driving direction, or during transition between edges.
Situational awareness deviations: these occur when the driver detects conditions in the field that the HLS system is neither aware of nor able to detect. The typical example is a patch of land without crop or an obstacle in the path.
User error deviations: these occur when (possibly by mistake) the plan is not followed but due to the operations specificities it is not recommended to reverse/manoeuvre back to the position expected in the original plan. The typical example is the entrance in a different work row than the one planned.
To make the system user-friendly and minimise user interactions, the harvest deviation monitors evaluate if the deviations detected by Evaluating (
1) are critical to the plan or if they can be considered in the Category 1. In that case, a re-plan is not triggered and user interaction is delayed until either a deviation of Category 2 or 3 occurs.
Due to the project requirements, the evaluation of the severity of the criticality depends on the inference of the situation in the field rather than on the inspection of the situation via the addition of extra sensors. Therefore, in
Section 4.1,
Section 4.2,
Section 4.3 we introduce the software mechanisms devised to classify deviations, and in
Section 4.4 we describe the classification.
4.1. Position Validity
Our first change to the HLS model was the introduction of a validity measure for the position measurement allowing the inference of off-field manoeuvring. As the existing HLS system uses a
to project map coordinates
into the internal graph representation’s coordinates
, the manoeuvring outside the field leads to deviation triggering. To filter those cases, we measure the distance between the GPS coordinates and the coordinates in the grid, and a position is assumed to be valid if the distance lies within a certain bound. In our case studies, a bound of
has shown to be a good cut-off value, and when (
1) is conjunct with (
2) several non-critical deviations are discarded.
Although a measure of validity is enough to avoid triggering a deviation when vehicles manoeuvre outside the field boundaries, there are several other cases where the deviation criticality depends both on the position in the field and also on the phase of the harvest process.
4.2. Plan Phase Structure
In our abstract setting, a harvest plan consists of a route for each of the vehicles, and each route is defined as a sequence of waypoints whereto a vehicle should be driven, and is interspersed with waypoints prescribing the position where vehicles/resources synchronise to perform unloads and transfer bin contents. We consider a harvest plan is divided into three phases:
Open field: occurring between the start of the harvest process and the completion of harvesting the headlands (boundary/perimeter around an agricultural field).
Harvest rows: the harvesting of the parallel rows, which constitute the traditional field crop arrangement
Finalise: all the activities/planned waypoints (unload the bin, drive to depot, …) to be completed after the finishing of the work rows.
To keep track of the execution status of each of the plan phases, we divide each of the first two phases into a sub-phase Init to be set if the corresponding plan phase was commanded but there is no evidence the operation is being executed, and a sub-phase Exec set whenever the measurements indicate that the plan phase is underway, yet the plan phase cannot be measured by adding an extra piece of technology and demands the inference of its approximate value.
4.3. Harvest Plan Tracking Automaton
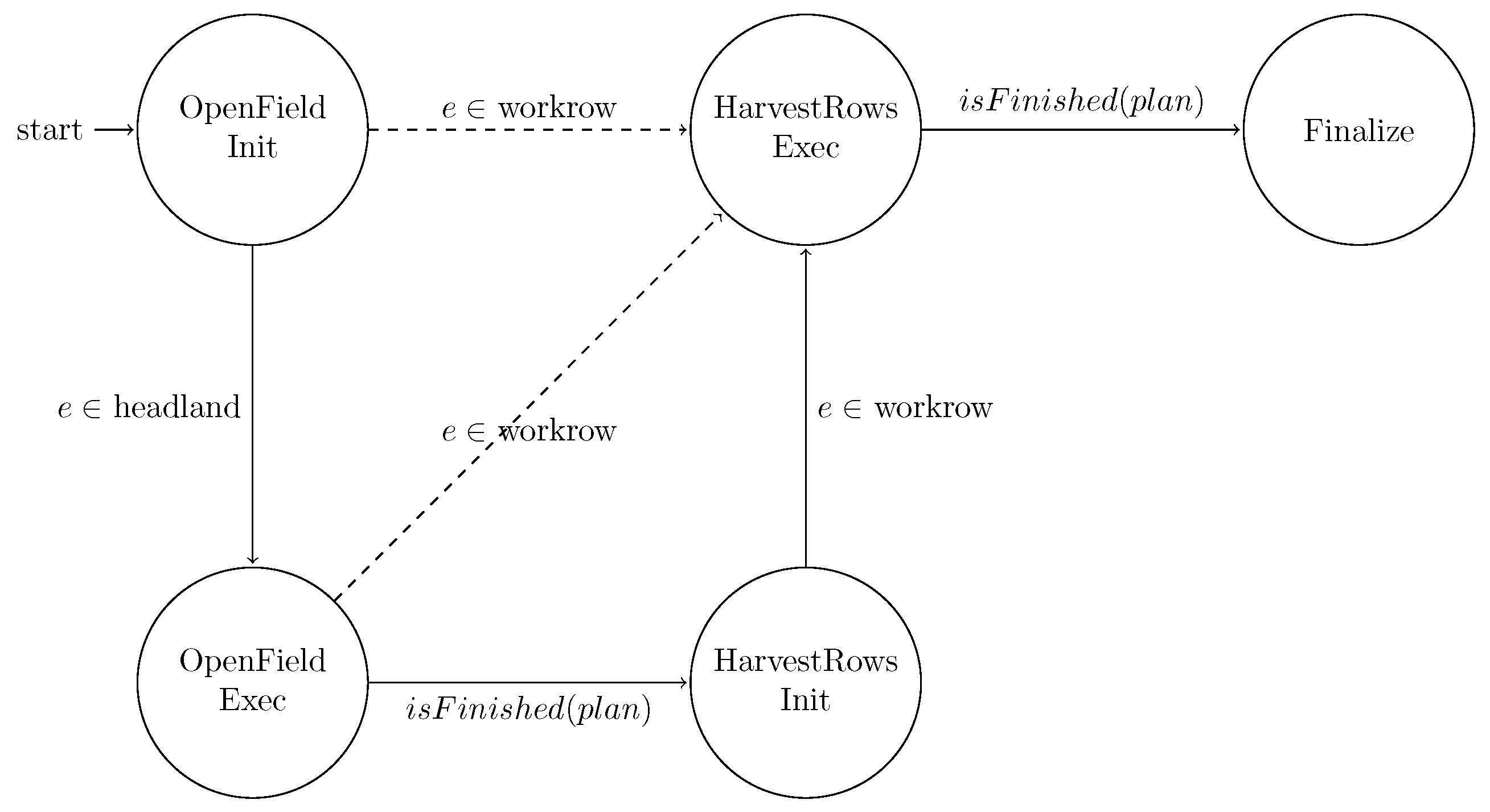
To infer the plan phase approximation, we use an automaton which is used to keep track of the harvest progress based on the reported positions and other measured parameters. The states of the automaton reflect the different phases of the harvest process domain, whether the phase is already under execution, or it was just initialised/dispatched. The automaton transitions are performed at the happening of two types of event:
a new vehicle position is measured by the system,
the planned waypoints for a phase are completed, and this event sets the predicate isFinished(plan) to true.
The transitions of the automaton are depicted in
Figure 5, and, for each state, a transition depends on the type of the edge
e in the position and the value of the isFinished(plan) predicate. The set of edges
e is partitioned into a disjoint union of the sets: headland and workrow, and such partition is used to decide whether a position inferred edge
e belongs to a headland e ∈ headland, or a work row e ∈ workrow, or is a connecting edge (Connecting edges are not relevant for the automaton state transition, but are important to have in mind for
Section 4.4). At the harvest process start the automaton is set in the initial state OpenField/Init and the state progresses until the finalise state where the plan is expected to be fully/completely executed.
The dashed transitions of the automaton reflect the need to cope with deviations. For instance, the transition from the OpenField/Exec state to the HarvestRows/Exec if the position inferred edge e ∈ workrow is measured is one such example. Such a transition reflects the case where the open field phase of the plan is considered as finished by the driver, for instance, in case the driver becomes aware that the remainder waypoints of the plan for the open field phase do not result in yield, for instance due to the absence of crop in the corresponding patch of the field. In such situations, the driver may directly start harvesting the work rows and the automaton must skip the HarvestRows/Init state. The described abnormal transition configures a Category 2 deviation, thus causing the HC to be triggered and the deviation to be treated by among other actions discarding all non-achieved waypoints for the Open Field phase.
4.4. Position Deviation Classification
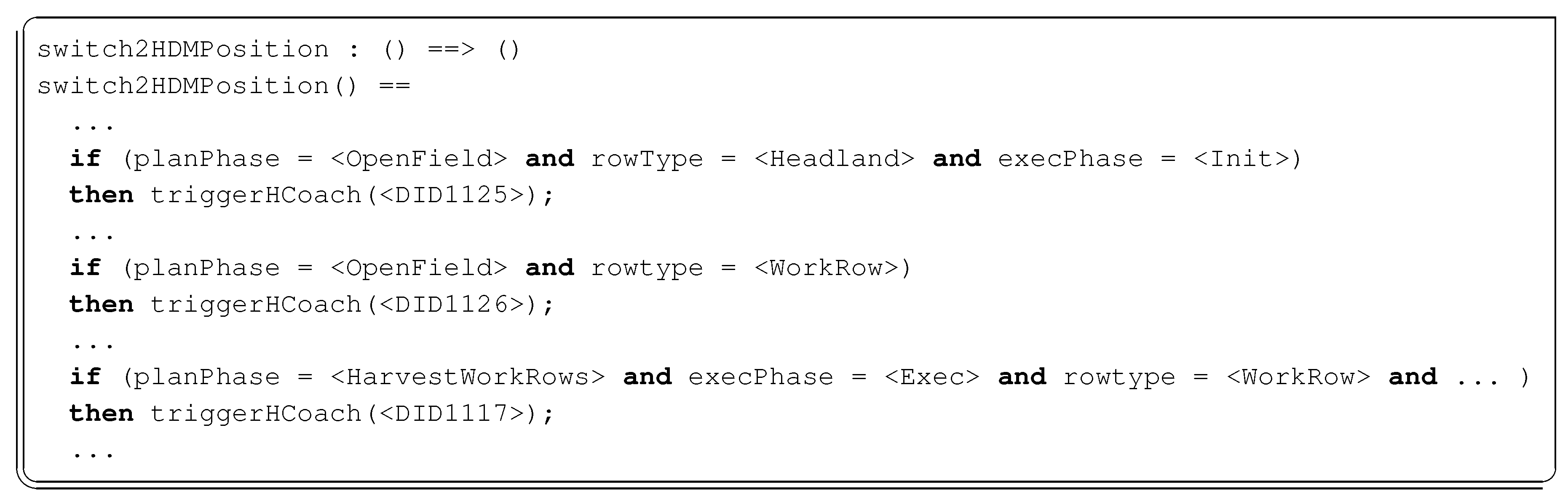
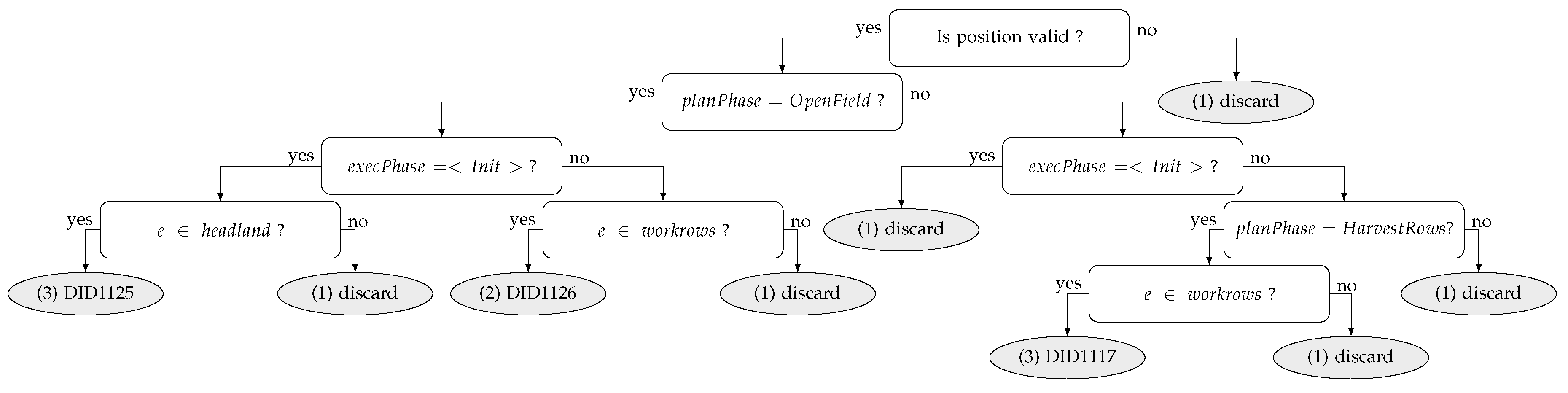
To classify the different position deviations we analyse if the position is valid, which kind of edge the vehicle is located at, and consult the harvest plan track automaton state. From the different possibilities, a decision tree is built to explore the possible deviation scenarios and to record the design choices prescribing whether to trigger or discard the issue of a new plan for each of the situations.
In
Figure 6 the decision tree that we use in our prototype to classify position deviations is shown. At each node there is a yes/no answer to a predicate on the decision parameters. At the root level, a decision is made on the validity of the deviating position. At the subsequent levels, the plan/execution phase and edge types are taken into account. Finally, at the leaf level, the deviation category is shown between parentheses, and the decision whether either to issue a new plan or not is given by either adding a unique id for the deviation (e.g., DID1125), or adding discard, respectively.
By following the graphical depiction in
Figure 6 the answer sequence: triple yes, no leads to the discard node on the left bottom corner of the figure. Such path encodes our design decision regarding manoeuvring outside of the field at the harvest process start. The number in parentheses in the tree node records that our decision was that such configuration constitutes a Category 1 deviation, so the decision to be issued is to discard it. The choices shown are heuristically driven and for the purpose of testing the HCA. It must be mentioned that a thorough analysis of the different scenarios is yet to be made.
As an example for the basis of the decision mentioned in the previous paragraph, consider a scenario where the harvesting operation has just started, and the vehicles have not yet reported any valid position neither a position in a headland or work row edge. For instance, the vehicle reports positions in a connecting edge. The position reported may be different from the plan because of the need to manoeuvre around other machinery blocking the driver way to the entrance of the field. We considered this a Category 1 deviation that is safe to ignore, for the route to follow is the same and the new plan would be the identical.
Although our work is abstract and serves as a mock-up of the desired solution, the future refinements of the exposed concepts are simple, and extensions to the transitions of the automaton and decision tree are the reasonable next steps. For instance, the accommodation of already existing sensor data (e.g., combine cutting header position/grain intake) which was not available during our project may increase the robustness of the deviation triage system, therefore minimising user interaction and false positives.
5. Yield Deviations
Another source of deviations is the discrepancy between the expected/planned level of grain inside the combine bins and the actual value as read by the bin sensor technology. These deviations occur due to the natural variance in the distribution of grain in the field (different field areas produce different amounts of grain due to various reasons) and are compounded with field’s yield forecast accuracy.
Our approach assumes one has statistical know-how on the yield map distribution for a field, and we assume a mapping “Litres of yield” which can be used to compute the expected addition of grain to the bin level after harvesting an edge in the field. Therefore, in case L, if a harvester reports a position , then the HLS assumes the bin count is the value at the entry of edge e plus 980 L. At each control loop, the HLS incrementally updates the estimated bin load level and compares it to the level reported using a sensor in the vehicles. Yet again, the sensor technology precision is inaccurate, thus we need a richer criterion beyond the difference of those values .
The decision when to trigger a deviation between the expected bin level and the actual bin load demands the computation of tolerated discrepancies between such numbers. Such tolerance must be defined taking into account two opposite criteria: the need to minimise replanning events and the need to make sure a re-plan is triggered in a timely fashion and the harvest process performance is not penalised by the deviation.
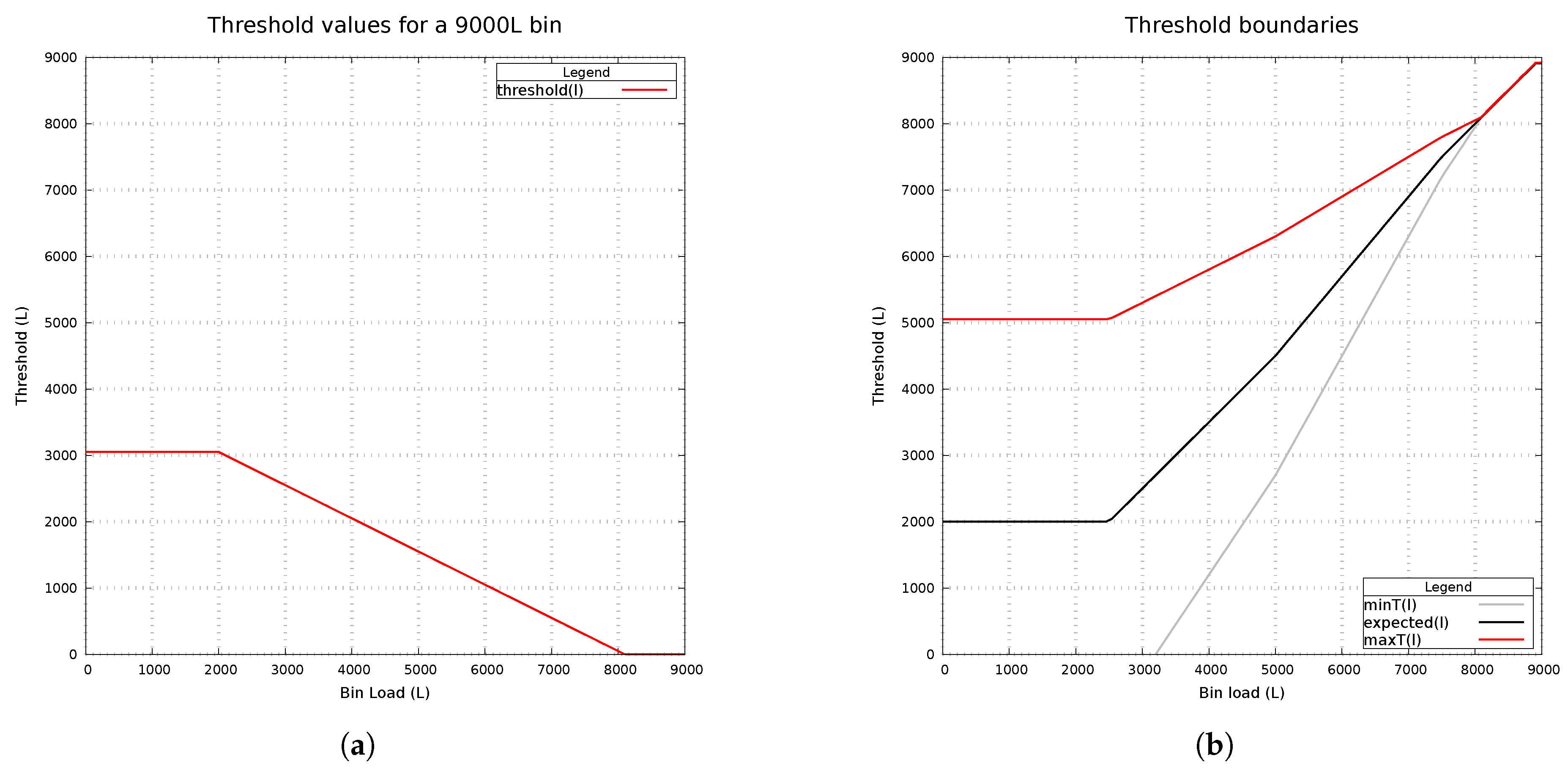
For that, we compute a dynamic threshold value for each load level. The threshold formula is displayed in (
3). The threshold depends on the capacity of the combine in litres (L) and the value of the sensor measured load
l. The fractional coefficients are tuneable, and we decided to use 90% of the bin capacity, for we assume that is the maximum value for the sensor, and we choose 50% of the remaining capacity as a practical tolerance value.
Given that the combine we used in this project has a bin capable of holding 9000 L, an amount of
of the capacity ensures 900 L as a safety buffer. (Note that in the case of a typical bin filling of 18 L/s that would allow the operator to be circa one minute late before overloading.) Also for our case study we assumed the bin sensor maximal reading value was 90%. As shown in the
Figure 7a, allowing a tolerance of half the remaining capacity translates into a wide tolerance while the bin is empty and a narrower tolerance as the bin becomes full.
The graphs express the dependency of the different threshold values in litres in terms of the load level expected to be present in the bin. We used a combine model with 9000 L bin capacity as an example, and as the bin sensor reports a level of 2000 L for all the values below 2000 L we observed the constant 3000 L threshold value. As the bin load increases, the allowed tolerance decreases.
Having a value for the threshold at each instant, the harvest deviation monitor needs only to check whether the difference between the expected load at that time and the effective load in the bin as read by the sensor is above or equal to the threshold:
To make sense of the Boolean predicate defined in (
4), one may observe the boundary lines plotted in
Figure 7b providing both the lower and upper thresholds for each load level. The graph plots a possible scenario of expected bin filling and the corresponding minimal and maximal thresholds for deviation for our combine model with 9000 L bin capacity. For the first 2000 L a deviation is triggered only if the plan expects a load above 5000 L. As the bin load reading increases, the tolerated deviations diminish according to our formula. For a 6000 L reading, the deviation is triggered in case the bin was expected to be below about 4500 L, or by the plan it was expected to be above about 7000 L.
Although not the scope of this work, one should emphasise how the planning of unloads can take into account the deviations threshold. For our case study, as depicted in
Figure 7b is worthless to plan unloads when the bin level is expected to be above 8100 L as the precision needed between expected load and real load cannot be achieved.
7. Results
The harvest coach architecture addition to the HLS prototype was tested in several experiments in the field. The usage of real world conditions involves many resources (e.g., combine, consumables, licensed operator, …), so during the project several experiments were performed beyond the guidance system operation tests. For instance, network checking, data-gathering checks, equipment manoeuvring, …The guidance system tests consisted in performing the expected harvest process with a combine machine in a farming field.
The field (in Foulum, Denmark) is a research farming testing field, and the tests were performed with the absence of farming crop both because our prototypes maturity was not ready to deal with the full conditions of a typical harvesting process, and that was not relevant for the project purposes. The absence of yield was the only difference to the real conditions, and that prevented testing the yield deviations developed and reported in
Section 5 in the field tests. Therefore, the HCA architecture was tested in the field with position deviations case-studies arising from the work in
Section 4 and
Section 6.
Regarding the joint operation of the HLS, HDM, and HC, we report on the results of three tests as shown in
Table 1. All the components prototype realisations of the system described in
Section 2 were in place and working under standard conditions. The HLS system provided guidance to the operator in the field and position deviations were monitored and triggered during the process. As no crop was present we decided to not perform tests in regards to yield deviations.
In a first test, which we term “initial” in
Table 1, we performed the first system integration test where the in lab matured prototypes are tested in real scenarios for the first time. During the execution we found several issues with both the HLS and the HC prototypes and the test was aborted due to severe faults.
In a second test, which we call “intermediate” in
Table 1, the correction to the issues found in the initial test were put to test. A big change to the HC was the introduction of a dialog interaction in the thin clients component described in
Section 2. The dialog informs the operator in case a deviation is triggered and the operator is asked whether he accepts the decision or not.
In a last test, which we term “final” test in
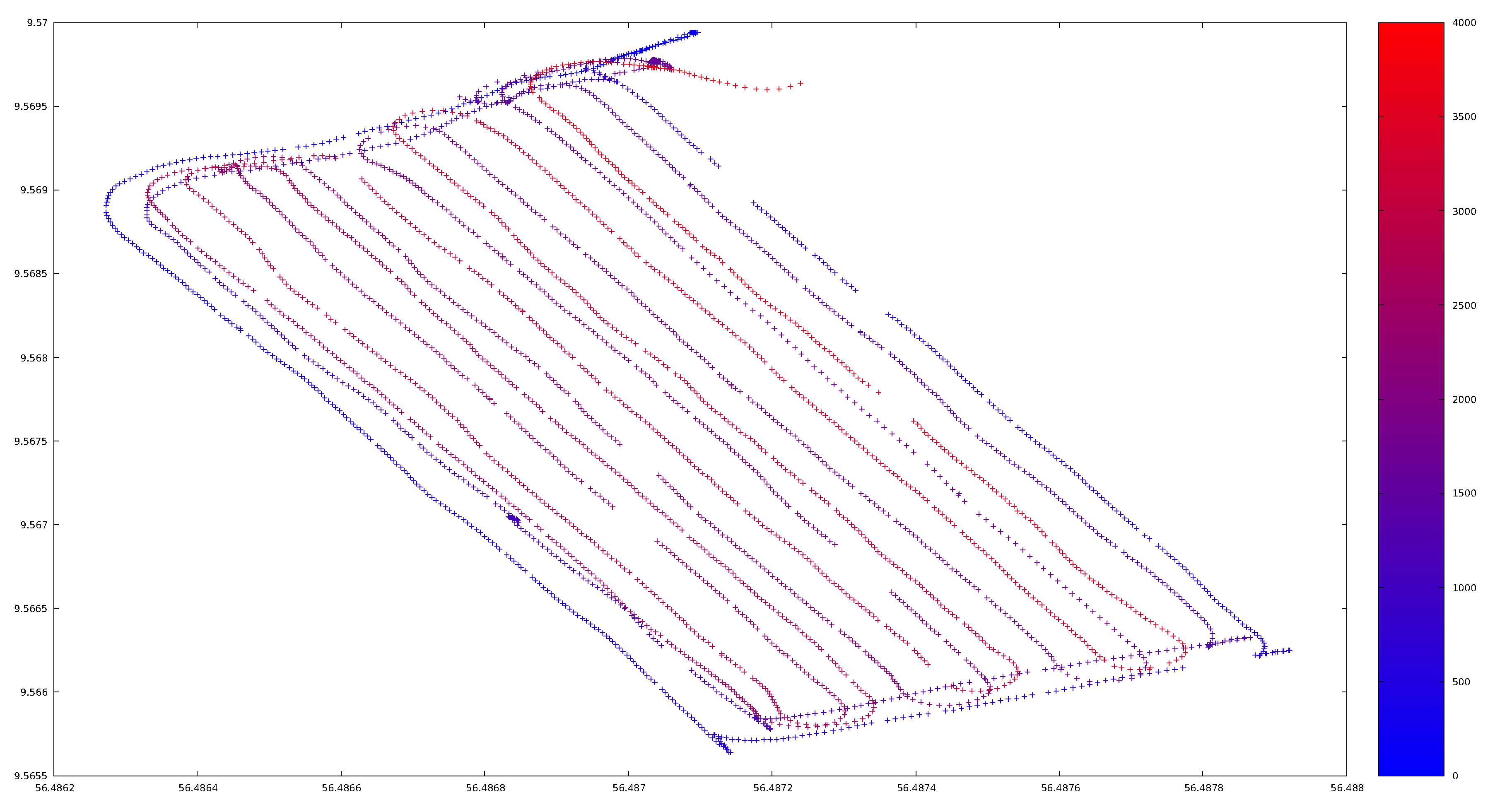
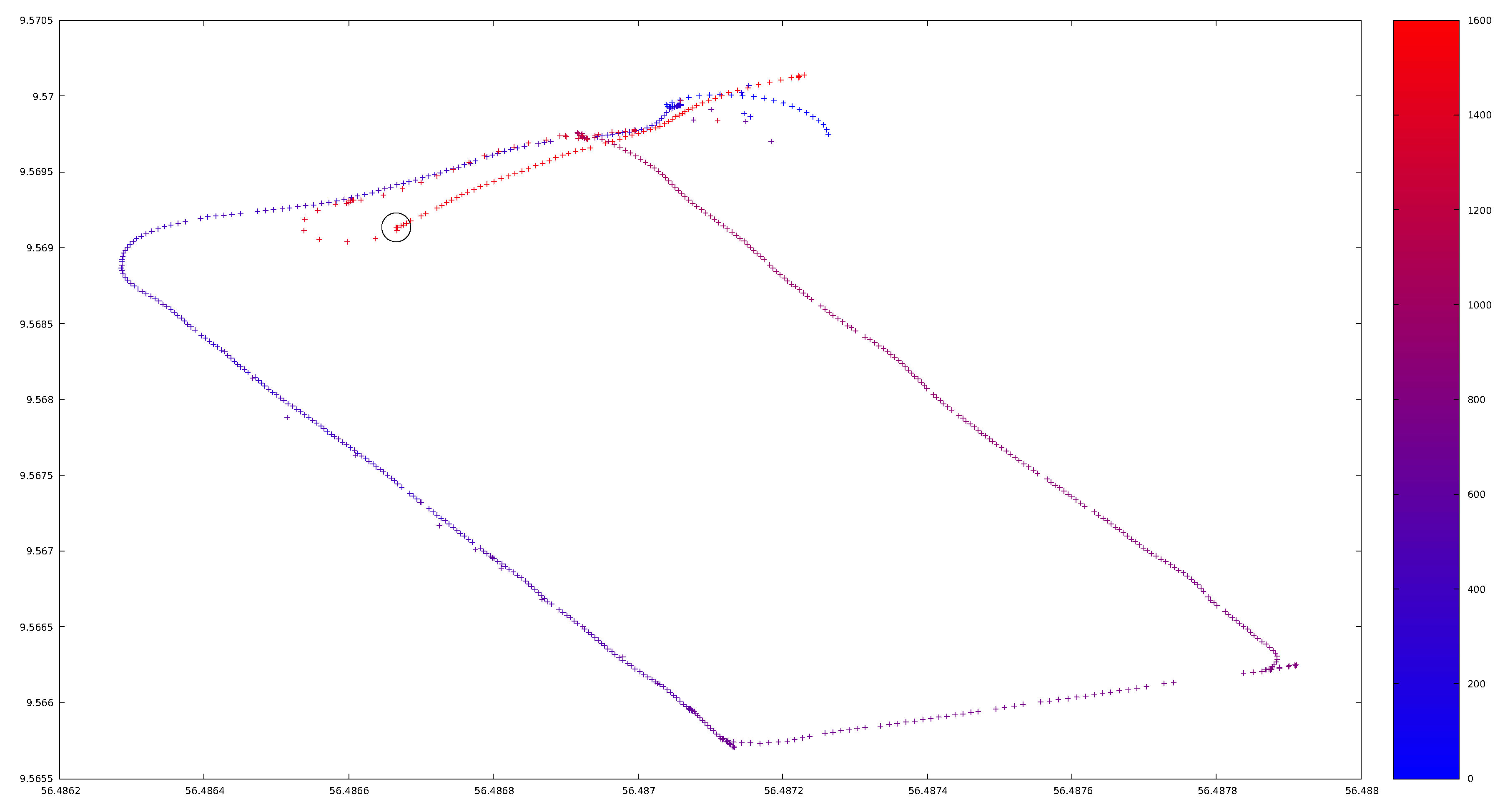
Table 1, all system components prototypes were working in standard conditions and served as an in field demonstration of the research project results. In a first go, the system was used and no Category 2 and 3 position deviations were introduced. The driver followed the plan as expected and positioning deviations of Category 1 appeared (as shown in the bottom right corner of
Figure 9 where a curve negotiation involved back and forward manoeuvring) and lead to no deviation being triggered. After completing the harvest process successfully, we introduced restarted our prototypes and the process, and forced a Category 2 position deviation, a wrong transition from the headland to the work rows with id
DID1126 in
Figure 6, and the HCA triggered it as depicted in
Figure 10.
We measured the number of deviations triggered by the HC in the late stage tests in the end of the project as reported in
Table 1. From that data we obtain an average of circa 1 deviation per hour triggered which points to) an acceptable performance of such an interactive system.
During the preparation of the field tests we observed slight discrepancies between the routes display in the maps of the different components, which later was confirmed to be due to an arithmetic precision problem in one of the geolocation libraries used, and the problem was solved by using another library providing higher accuracy.
During the “initial” and previous prototype component standalone tests, the driving operators provided valuable feedback in terms of GUI presentation and in the need of implementing a dialog ensuring the last decision on replanning belongs to the field operators. The solutions were readily deployed and are easy to solve in our test scenario with only one vehicle, yet in a scenario with multiple operators the problem may be more difficult to tackle.
Another curious finding was the observation of discontinuities of the reported positions (evident in the blanks in
Figure 9), the losses in messages, and out-of order message received at some points. Such high-critical subjects need thorough investigation in the future. Although critical, at the time of writing, it is still unclear what were the causes/reasons for such observations.