1. Introduction
Research related to graph theory and network analysis in the field of social science [
1] pioneered the development of social network analysis (SNA) methodologies. Graph theory provides the conceptual constructs, methods, and techniques in graph analysis. The SNA methodologies combine graph theory with the application of analytical techniques and visualization tools developed specifically for the analysis of social networks and other networks [
2]. The methodologies and techniques of criminal network analysis (CNA) are mainly adopted and adapted from SNA analytical models and metrics [
3]. Some commercial social networks, such as Facebook and recommender systems, introduce potential friends based on an SNA link prediction technique [
4].
Criminal networks, in particular, exhibit a relatively high propensity to have hidden or missing links because of the covert and stealthy nature of criminal activities [
3]. This characteristic of criminal networks is often due to incomplete, incorrect, and inconsistent captured data, either caused by deliberate deception on the part of criminals or unintentional human error by law enforcement personnel. Therefore, the common practise and techniques of predicting potential links between nodes within most social networks have become highly relevant and critical in the discovery of missing or hidden links within criminal networks.
Social network analysis metrics used in link prediction may be derived from either structural or content-related measures of a network. The typical structural and content-based measures are neighbourhood-based metrics, Katz-based metrics, and random walk-based metrics. The neighbourhood-based measures include the common neighbour, Jaccard index, and Adamic-Adar index [
5]. Deep reinforcement learning (DRL) refers to the machine learning technique of incorporating deep neural networks into the framework of reinforcement learning (RL) to achieve a general artificial intelligence capable of self-learning [
6]. Deep neural network or deep learning is one of the fields of machine learning methods based on the representation learning of structural patterns from a large dataset in contrast to predefined task algorithms. Representation learning can be supervised, semi-supervised, or unsupervised [
7,
8,
9]. Reinforcement learning is a technique in machine learning where programs, known as agents, interact with familiar or new environments in which the agents continuously adapt and learn based on points awarded upon completion of a task. The points awarded are labelled as rewards or punishments if positive or negative, respectively [
9]. This approach is different from the usual supervised machine learning approach as it does not rely on the use of training datasets [
6].
The design of an RL agent involves defining the policy learning and value learning functions. Policy learning relates to the modelling of the domain rules into the agent algorithm that maximizes the rewards from each action, while value learning relates to the modelling of the agent algorithm that maximizes the expected future returns of an action by generalizing from the values aggregated from all prior iterations of states and action pairs [
9]. Both policy and value learning functions can be trained using neural networks, which then form the policy and value networks of the RL agent, respectively.
One of the challenges of incorporating RL in the development of a hidden link prediction and reconstruction model is identifying suitable features of the dataset to train the value network to perform the task of function approximation [
10]. Function approximation is a method of supervised learning, the application of which can be found in the fields of machine learning, artificial neural networks, pattern recognition, and statistical learning [
11,
12]. The value network is designed to provide weights to the edges of the network dataset based on the probability of hidden links being an edge calculated using link prediction metrics. For the purpose of this research, RL and neural network techniques are leveraged upon to provide a DRL approach in the construction of the function approximator [
6]. The value network function approximator will identify the node pairs with the highest probability of having missing or hidden links to initiate a tree search in a network traversal.
Problem Definition
Supervised machine learning models usually require large datasets for training to achieve an optimum level of predictive performance. The significance of using a large dataset to assess the predictive performance of link prediction models has been demonstrated by Emrah Budur et al. [
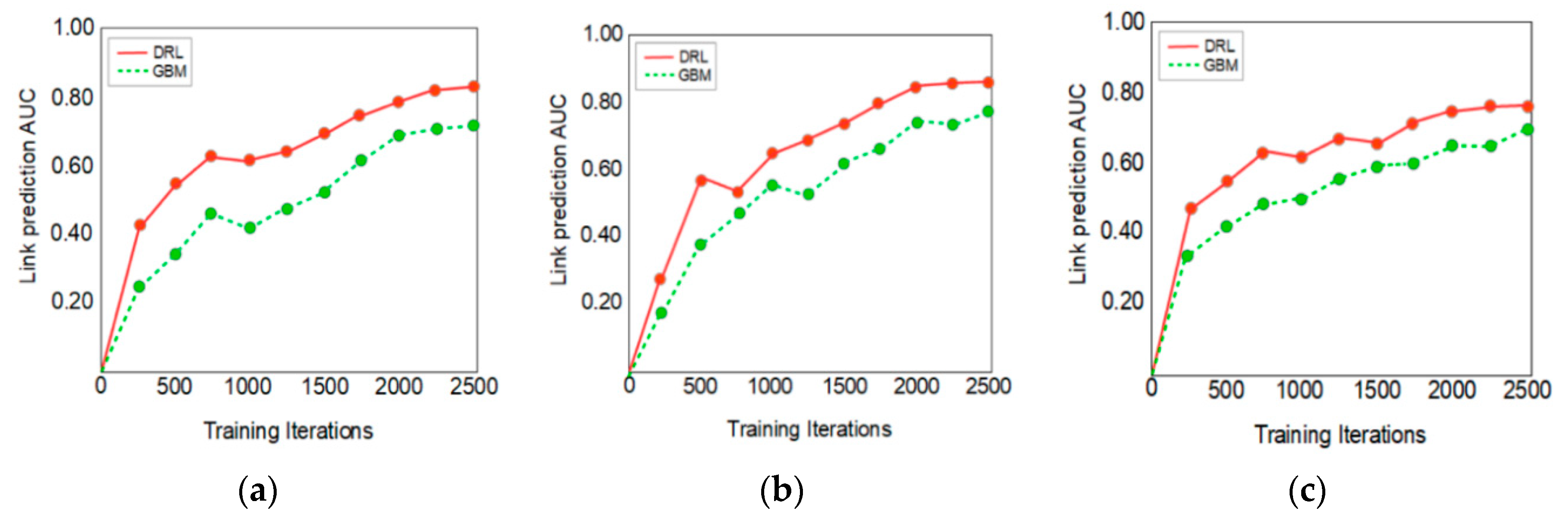
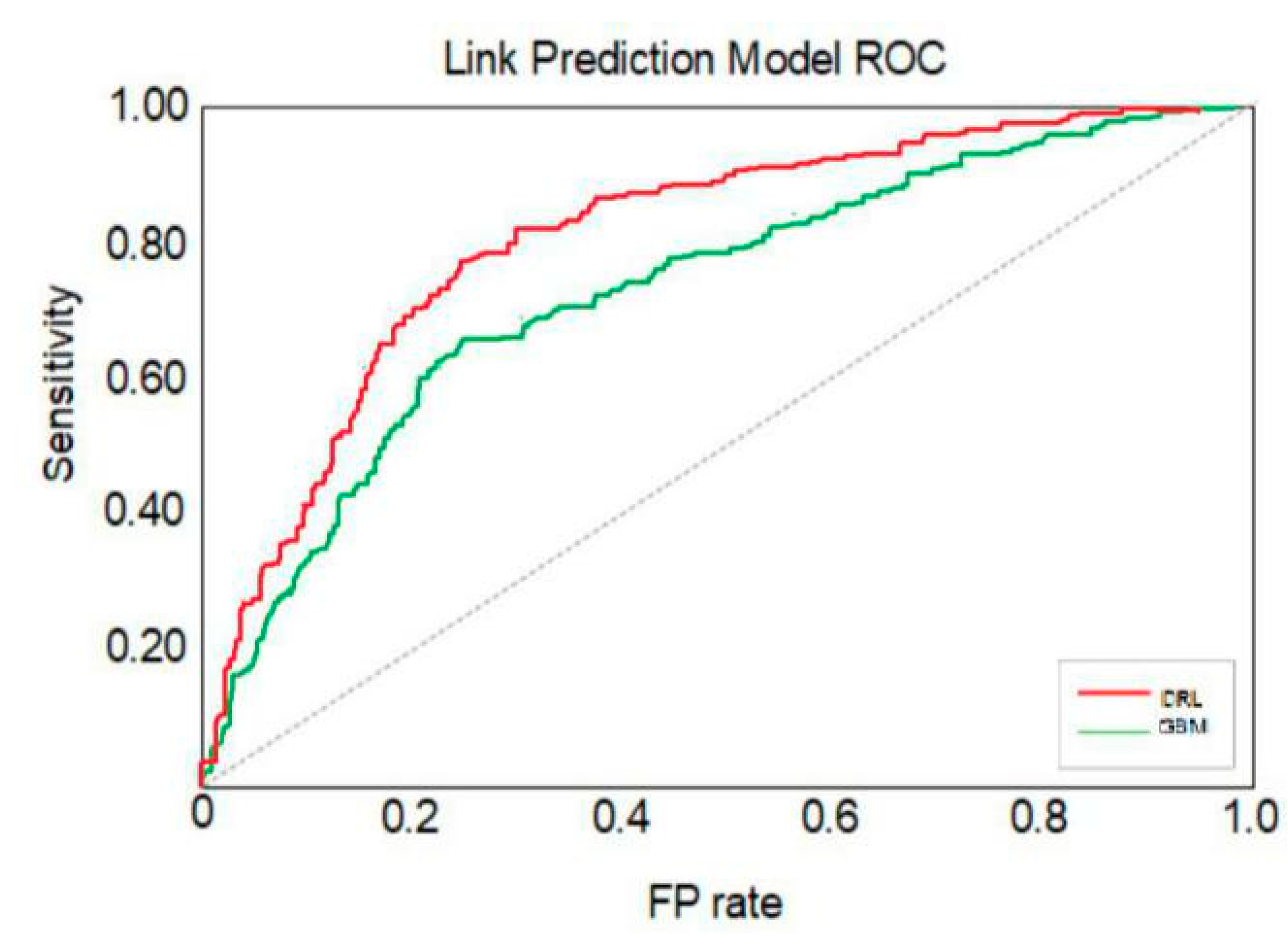
13] using the supervised learning technique known as the gradient boosting machine (GBM). The primary objective of this current research is to develop a criminal network link prediction and reconstruction model that can be trained on a relatively smaller dataset using the DRL technique without any significant deterioration in the predictive performance. The performance of the criminal networks link prediction model depends on the efficiency of the algorithms developed for both the deep learning and RL in the DRL technique.
In this research, the performance of the DRL technique is benchmarked against the performance of a conventional GBM model, which has been investigated by Emrah Budur et al. [
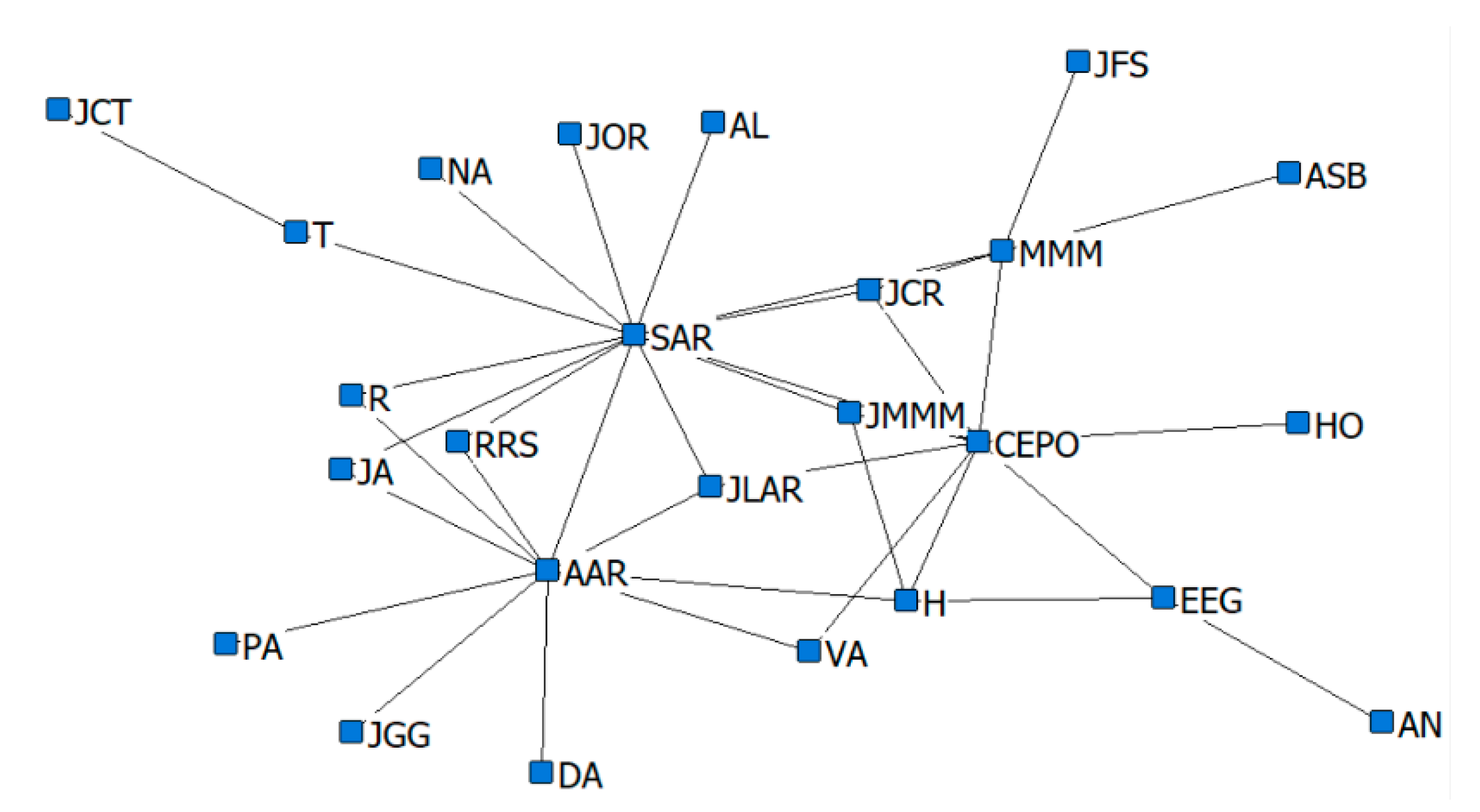
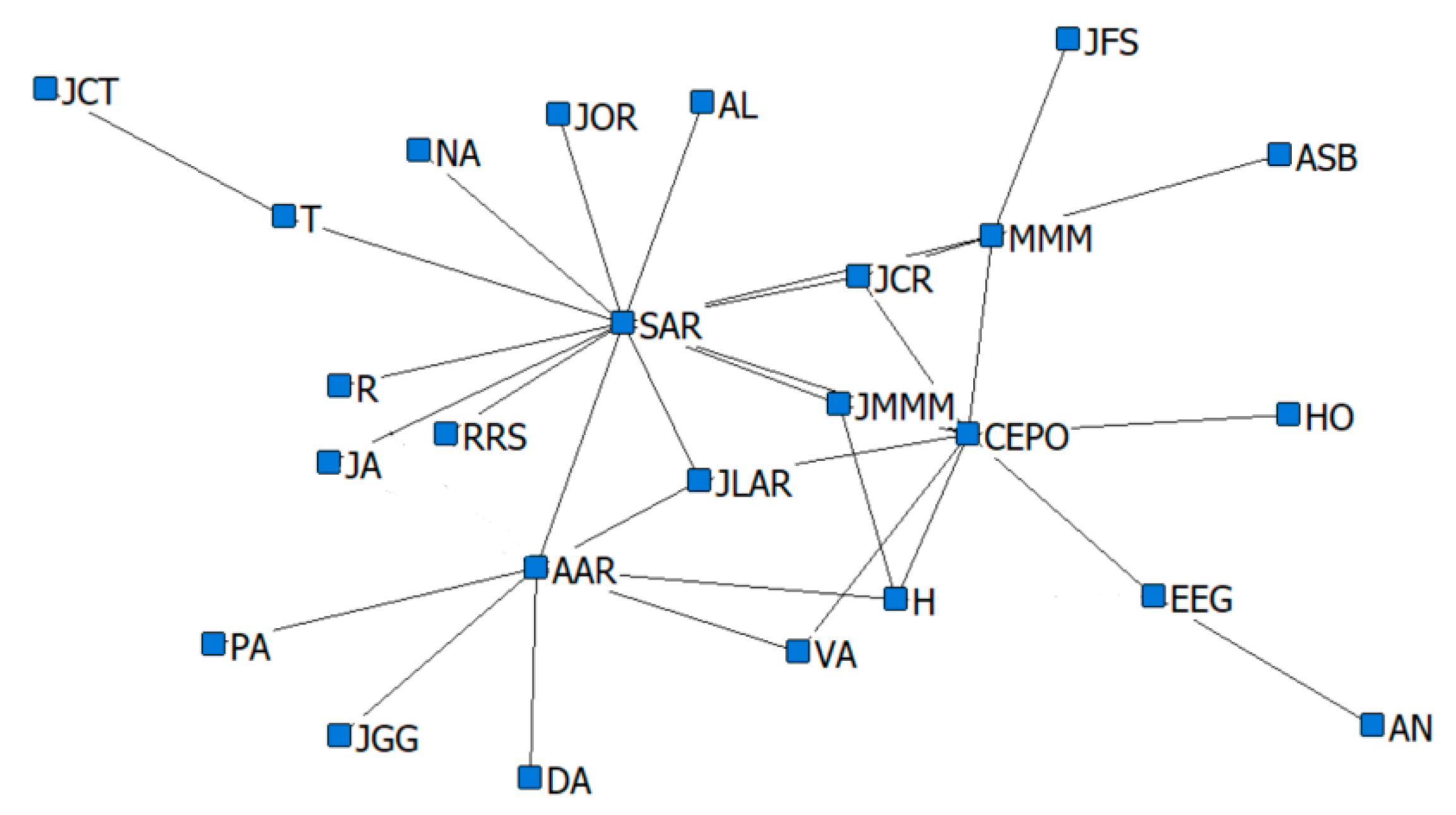
13], in the domain of criminal networks link prediction. The respective performances of the hidden link prediction models based on GBM and DRL are evaluated using the accuracy metrics of area under the curve (AUC) and the confusion matrix. The criminal network dataset used for this research is based on the UCINET cocaine smuggling dataset, which contains a dichotomous adjacency matrix of drug users in Hartford [
5]. The relatively small dataset used in this research is intended to exhibit that a DRL model with an acceptable predictive performance can be constructed, compared with a conventional supervised learning model such as GBM, which strongly depends on the availability of a large dataset.
2. Related Work
Emrah Budur et al. [
13] conducted research on link prediction of criminal networks with the application of SNA models and metrics based on machine learning techniques. They examined the machine learning techniques using the GBM supervised learning method to enhance the performance of hidden link prediction in a large dataset. An experiment was conducted with statistical models and probability link prediction metrics derived from the sampling of the criminal network dataset to assess the performance of the supervised link prediction model constructed by the GBM algorithm. The sample size used in the research consists of approximately 1.5 million nodes and four million undirected edges, which represent a significantly larger dataset size compared to sample sizes used in other research papers. The larger sample size used was expected to better represent the real characteristics of criminal networks. The use of a large size of sample dataset also demonstrated that the applied under-sampling technique improved the accuracy of the sampling method adopted in this research, as collaborated by the high performance of the trained link prediction model, indicated by the computed AUC metric. The AUC metric of a machine learning model indicates the predictive accuracy of the model and has a value that lies between 0 and 1, where a higher value indicates a better predictive accuracy.
Furthermore, the survey of research papers has provided considerable assistance in the feature selection from the criminal networks dataset and identification of a few models of link prediction metrics [
13] (i.e.,
Table 1), which were ensembled to improve the training of the GBM link prediction model. The research conducted by Emrah Budur et al. has contributed to the link prediction model in the identification of the mathematical machine language models, and the applied link prediction metrics are relevant and provide supportive evidence to the research methodology and trajectory of the current research work. The authors also stated that the lack of temporal data and information on suitable weights provided to the edges of criminal network datasets may have caused some restrictions in the effectiveness of the SNA and link prediction modelling. The significantly large size of the criminal network sample dataset used in the research, compared to the other research papers surveyed [
14], was also analysed, and analytical metrics that are more accurate in profiling the real characteristics of criminal networks were provided.
The research methodology, however, did have some limitations, considering that criminal network analysis is a critical and specialized area in law enforcement. Therefore, because of the absence of the engagement of experts from the domain of law enforcement and criminal intelligence analysis, the accuracy of the supervised machine learning technique applied in the link prediction model constructed from the reconstruction of the corrupted criminal network dataset cannot be ascertained conclusively.
Bellemare et al. [
15] investigated the optimisation of DRL algorithms using modern computing hardware specifications, combining central processing units (CPUs) and graphics processing units (GPUs), specifically NVIDIA DGX-1. They adapted both policy gradient and Q-learning algorithms in machine learning models, leveraging on parallel, synchronous, and asynchronous computing techniques. In their paper, two deep RL algorithm techniques are identified: the policy gradient method, which is trained on on-policy samples and the Q-value learning method, which involves off-policy training, an example of which is Deep Q-Networks (Mnih et al., 2015) [
16], trained using a GPU.
In the work of Bellemare et al., the two methods were combined in an experimentation under the same framework for scaling. While most of the experimentation conducted was based on synchronous, asynchronous, and parallel computing techniques using GPU, the initial baseline performance simulation of the RL algorithm was performed on multiple CPU cores. The experiments were conducted in the Atari-2600 domain to study the scaling characteristics of highly parallelised RL with three objectives: to determine the efficiency of the synchronized sampling engine and the speed that it can achieve; to confirm if the policy gradient and Q-learning algorithms can be adapted to learn based on parallel simulation without diminishing the learning performance; and to verify that large-batch training and/or asynchronous methods can improve optimisation without worsening the sample complexity. Although this paper introduced a unified framework to apply parallel computing with deep RL to achieve efficient feature learning mainly based on the use of hardware accelerators, the framework is relevant to a range of algorithms, including policy-gradient and Q-value learning methods. The experiments conducted demonstrated the ability of leading algorithms to learn a range of Atari games running in parallel computation without the loss of sample complexity and at unprecedented clock times.
Thomas Anthony et al. [
17] incorporated imitation learning methods with RL algorithms in the context of the game of Hex to improve the performance of the RL algorithms. The research was conducted in reference to the seminal research work on DRL by D. Silver et al. [
18] in the development of a program capable of playing the game of Go, named AlphaGo, in the field of artificial general intelligence. David Silver et al. made a significant breakthrough in their research on DRL [
19], where the program they developed, AlphaGo Zero, was, through DRL, capable of entirely mastering the ancient strategic game of Go by self-play. The program managed to attain a superhuman performance by defeating the top grandmasters of the game from South Korea and China. The AlphaGo program was successfully built using a trailblazing DRL technique of incorporating a neural network and RL. AlphaGo initially uses a neural net that is only coded with the basic rules of the game of Go. It then simulates millions of self-played games against various versions of itself. The knowledge gained from this self-play is then fed back to the neural network to recalibrate the hyper-parameters. The recalibrated neural network is then used to improve the efficiency of the Monte Carlo tree search (MCTS) algorithm by serving as a function approximator. The performance of AlphaGo Zero is thus increased minimally in each iteration. However, through millions of self-play experience in a day, the program could simulate the accumulation of decades of human knowledge of Go and performed like a top-level grandmaster in only three days.
While knowledge in the fields of both the neural network and RL was already known before the development of AlphaGo Zero, the key to the leap in the research by David Silver et al. was due to the novel design of the algorithm and vast improvement in the GPU parallel computing power. The development of the DRL technique first involves the configuration of a neural network to predict the best move in a given position and then to fine-tune this neural network with RL through self-play with different versions of the program. This neural network, which constitutes the policy network of AlphaGo, was found to be capable of beating the most advanced pure-play MCTS Go programs 85% of the time. This was a very significant breakthrough compared to the 10% that was previously achieved.
The research was then continued to enhance the performance by incorporating MCTS into the policy network. However, the policy network performed too slowly in the evaluation of each move branching from the millions of possible outcomes in the simulation of the game roll outs computed with MCTS. Therefore, a second value network was trained using the data generated through self-play; this could evaluate the outcomes faster, i.e., the roll-out network. The value network could evaluate a position faster based on the estimated probability of the game being won from a specific position. The combined policy network is only used once to obtain an estimate on an initial move with the highest winning probability. The faster roll-out policy network is then executed to traverse quickly using MCTS, through the many possible branches of moves needed to reach a decisive outcome of the game. This technique improves the selection of the initial move for a search algorithm in a simulation rather than via random selection and then leverages on the fast MCTS algorithm to complete the roll-out of each simulation. The key reason MCTS works efficiently for the game of Go is that it removes the difficult necessity of coding human-defined evaluation algorithms for specific patterns of positions in the game. As a result, the AlphaGo algorithm comprises a value network that is capable of predicting moves with the highest winning probability, which is then evaluated via simulation roll-outs using the MCTS policy network. The combination of the neural networks resulted in a huge leap in performance compared to the individual performance of each neural network. To optimize the AlphaGo performance, the program was then deployed using eight GPUs for the neural network parallel computing. The search threads of MCTS were executed on 48 CPUs.
Deep learning techniques based on a neural network have always been dependent on big data for accurate representation learning [
20]. Therefore, David Silver et al. have significantly contributed to the advancement of general artificial intelligence [
18], as was demonstrated by the AlphaGo performance. AlphaGo simulates the cognitive intuition of humans with the DRL algorithm, which automates the self-learning process by generating data simulated through self-play. Therefore, this DRL technique has removed the need for complex domain-related patterns to be programmed by humans and opened up possibilities of application in other domains where the lack of domain data is a limiting factor in training supervised or unsupervised machine learning.
Chen et al. explored an ensemble technique by integrating a few RL algorithms into an agent to enhance the learning efficiency and performance of the DRL technique [
21]. However, the experiment was conducted in a controlled environment that did not utilize a real world dataset, and the DRL models designed were not for the domain of a social or criminal network.
Therefore, one of the purposes of the current research paper is to close the gap in the development of a hidden or missing link prediction model for a criminal network based on SNA metrics by leveraging on DRL techniques. The DRL techniques that have been investigated by David et al. [
18] and found capable of being trained with relatively smaller datasets with self-simulation are relevant to the characteristics of a criminal network that has a large number of missing or hidden edges [
3].
5. Materials and Methods
The deep reinforcement learning technique involves incorporating machine learning techniques of deep learning (multi-layered neural network) and RL. Therefore, the performance of DRL for link prediction of criminal networks depends on a few factors and is evaluated based on the formulation of the SNA metrics (
Table 1) and DRL techniques.
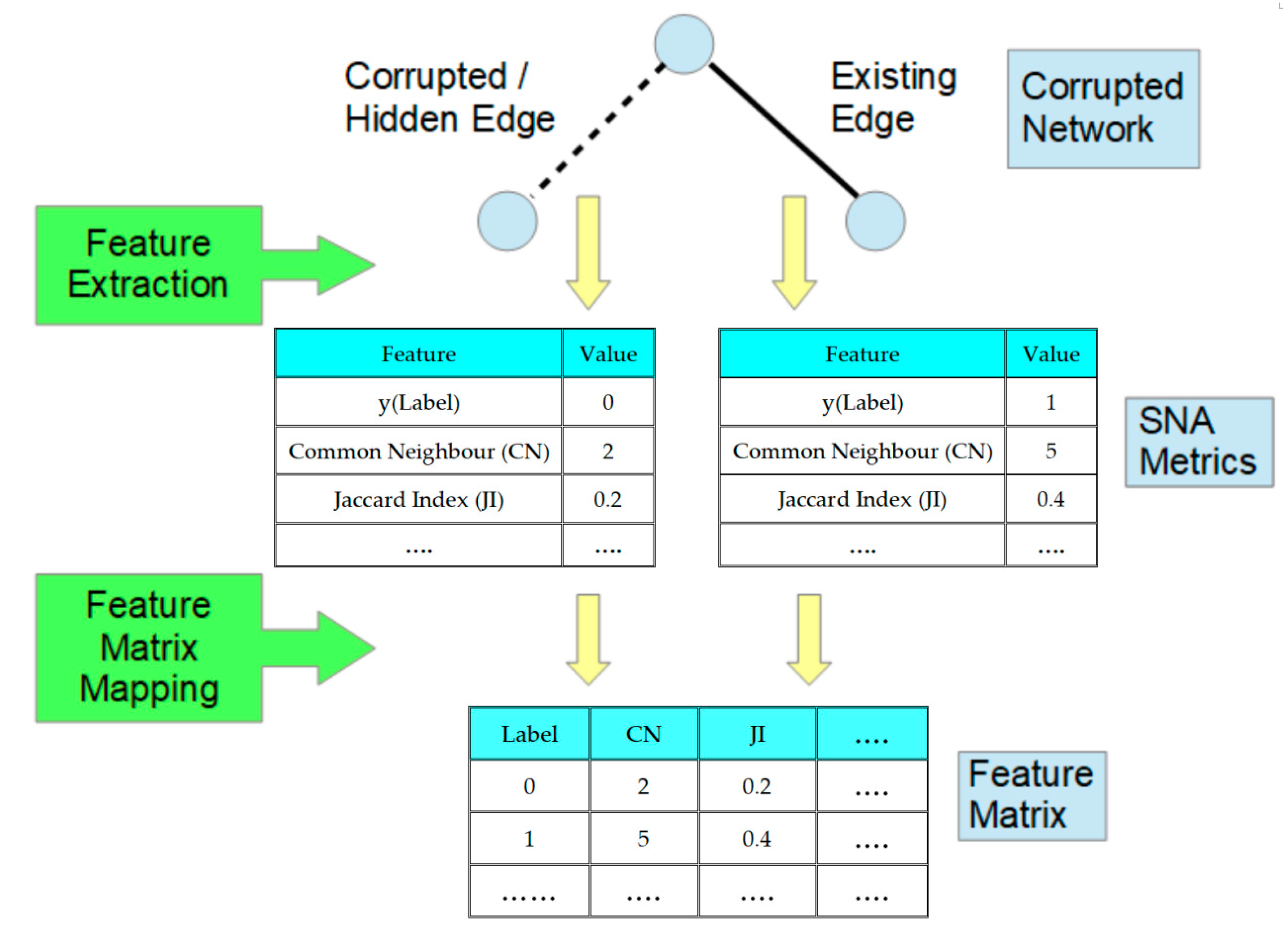
The prediction of the probability of the presence or absence of hidden links between nodes within a criminal network is formulated with a supervised learning technique as a binary classification problem. The development of the link prediction model for criminal networks in this research involves mapping a criminal network structure into a matrix of features for each pair of nodes derived from the metrics of SNA models. The metrics selected to populate the feature matrix consist of the common SNA metrics from neighbourhood-based, Katz-based, and random walk-based measures [
13]. Therefore, for every pair of nodes, an array of feature metrics is created as a data record. These data records are used for training purposes in supervised machine learning as a binary classification of positive-negative pairs of nodes. The pair of nodes where an edge exists is labelled as positive, and the pair where the edge is non-existent is labelled as negative.
During the training phase, the link prediction algorithm will generate a dataset where each data record with multiple features represents either a pair of nodes with a link between them or a pair of nodes without a link between them. The multiple features consist of the SNA link prediction metrics applicable to the pair of nodes. As a result of the construction of the training model from the data, the class label is indicative of the existence or absence of a link between the nodes. In the testing phase, every sample pair of nodes used is converted into a record with multiple features from which binary classification of the existence of an edge will be predicted by the model.
A deep neural network will be utilized as a function approximator to take the initial corrupted network structure, S0, as an input and output a vector of probabilities of edges. These probabilities of edges are derived based on the SNA metrics for each node, and the probability of hidden links is estimated from the initial network structure, S0.
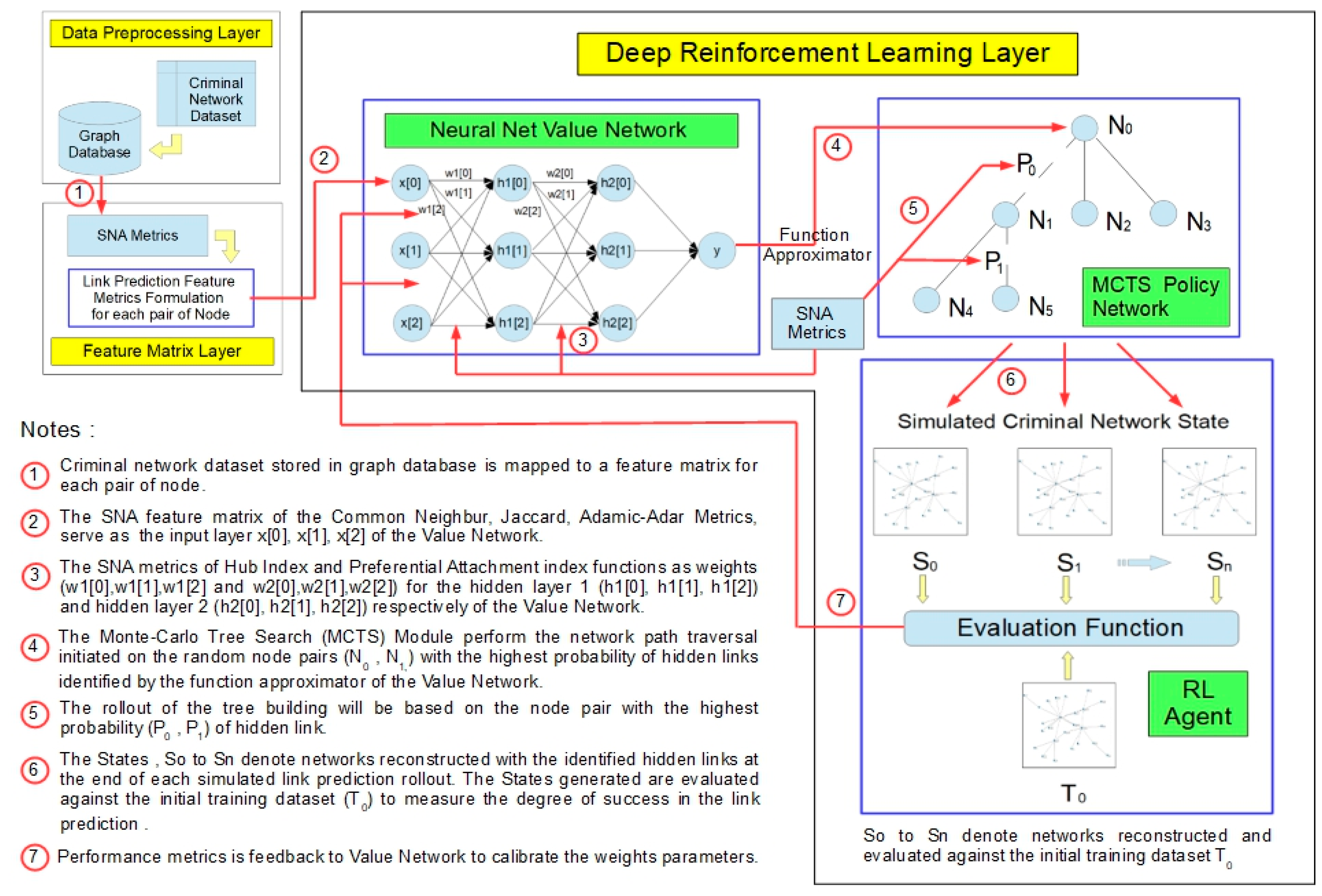
The neural network learns the probabilities of the hidden edges and value estimates based entirely on RL by self-simulation based on SNA metrics scoring. These values are then used to guide the network traversal search. The proposed criminal network reconstruction model (
Figure 1) uses a general-purpose MCTS algorithm (
Figure 1). Each search consists of a series of simulated reconstruction of self-scoring edges that traverse a tree from a root leaf. Each simulation proceeds by selecting, in each network structure, S, a hidden edge of high probability and high value according to the current neural network.
The search returns a vector representing a probability distribution over edges. The parameters of the value network are trained based on the dataset generated through self-simulation by RL, which is initially initialised by random parameters. The MCTS search function is based on SNA metrics with the highest probability approximated during a tree-search algorithm of the value network. The network structure simulations are repeated in the algorithm in order to derive an estimate of the value of states. The tree search will then be expanded further, traversing through the network with a higher probability of hidden edges. The explored edge with the highest probability is then identified.
In every simulation of the tree search, the probable hidden edges between nodes based on the tree search policy network will first be generated while the network path is being traversed. Second, in the roll-out phase, when the simulation reaches the end of the traversal of the network structure based on the default policy, the result obtained will then be used to adjust the estimates of the value of each pair of nodes derived during the first phase while the network is being traversed. Every traversal between nodes during the tree search represents a possible state of the network structure. The root node of the tree search represents the current state, and each child node represents an instance of the state from the current state as a result of a single probable hidden edge. The probable hidden edge identified from state S1 to S2 represents an action taken in order to reach S2 from S1. The number of states, N, will be generated through self-simulation until an acceptable AUC score is achieved.
Simulated network structures are constructed by selecting edges based on SNA metrics scoring. At the end of each simulation run, the reconstructed network structure is compared to the non-corrupted network structure derived from the original dataset. The hyper-parameters of the policy network are then adjusted to minimize the error between the predicted and actual missing edges. During this process, the similarity of the policy values compared to the search probabilities will be maximized. The parameters are then specifically adjusted by gradient descent based on a loss function. The loss function is aggregated over the mean-squared error and cross-entropy losses accordingly. The parameters that have been updated will then be used in the next iteration of the reconstruction of edges through self-simulation (
Figure 1).
The value network (
Figure 1) was constructed with two hidden layers of the neural net, utilizing the preferential attachment index and Hub index to evaluate the probability distribution of the nodes and edges from which the tree search function commences its search.
The RL policy network (
Figure 1) will compute the scoring based on the link prediction metrics of common neighbours, the Jaccard index, and the Adamic-Adar index to simulate link prediction at each state of the network. The scores achieved by each state of the network based on the RL policy network are then applied to train the value network of the model by adjusting the parameters to enhance the model performance.
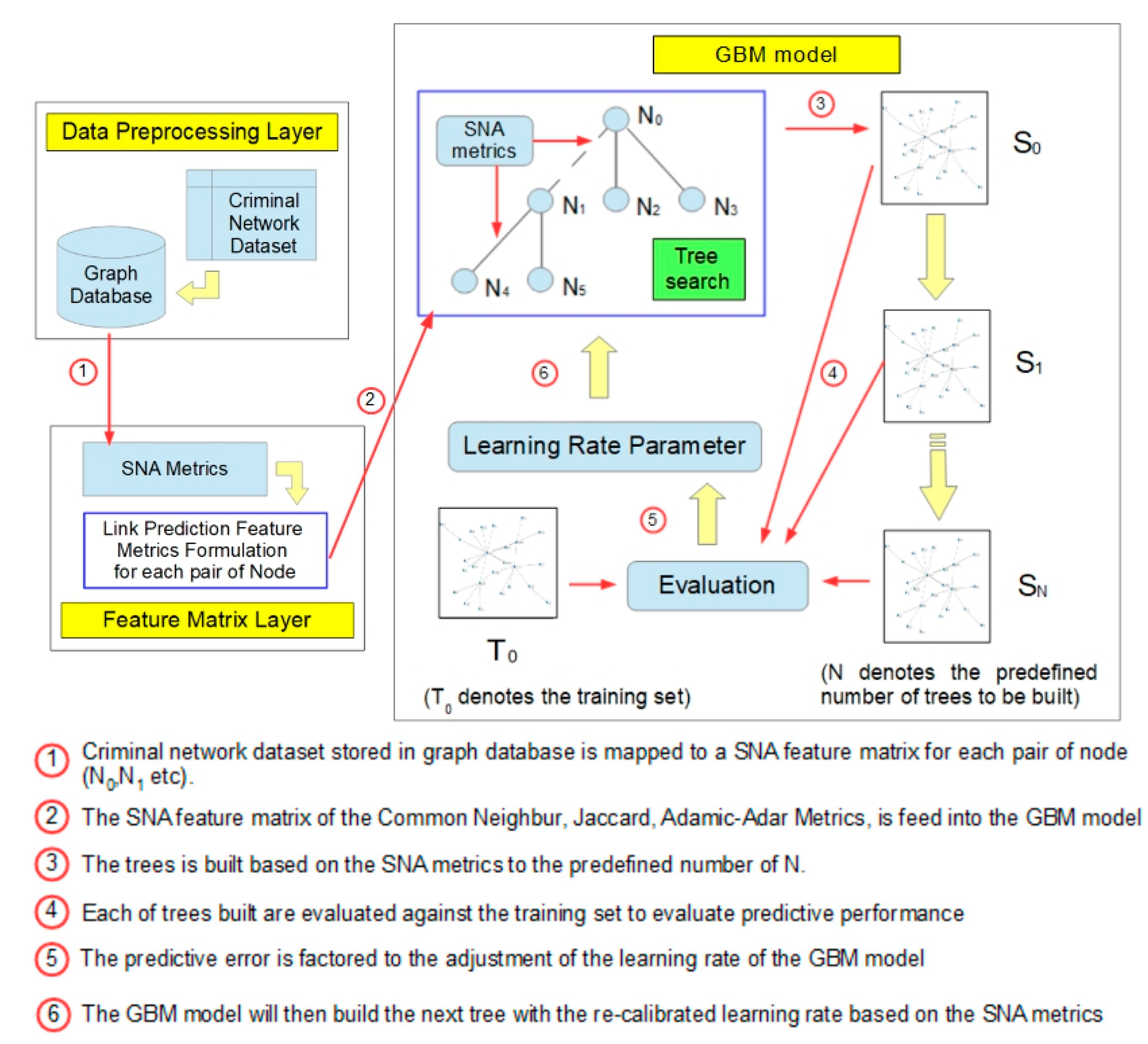
The GBM is a supervised machine learning model that utilizes a decision tree algorithm and improves (boosts) the learning performance by gradually reducing the prediction error from the prior iteration of the decision tree. The GBM model was constructed for the purpose of criminal networks link prediction based on SNA metrics (
Figure 2) [
13]. The performance of the DRL link prediction model is then evaluated by comparing it against the GBM model.