The Use of an Artificial Neural Network to Process Hydrographic Big Data during Surface Modeling †
Abstract
1. Introduction
2. Methods
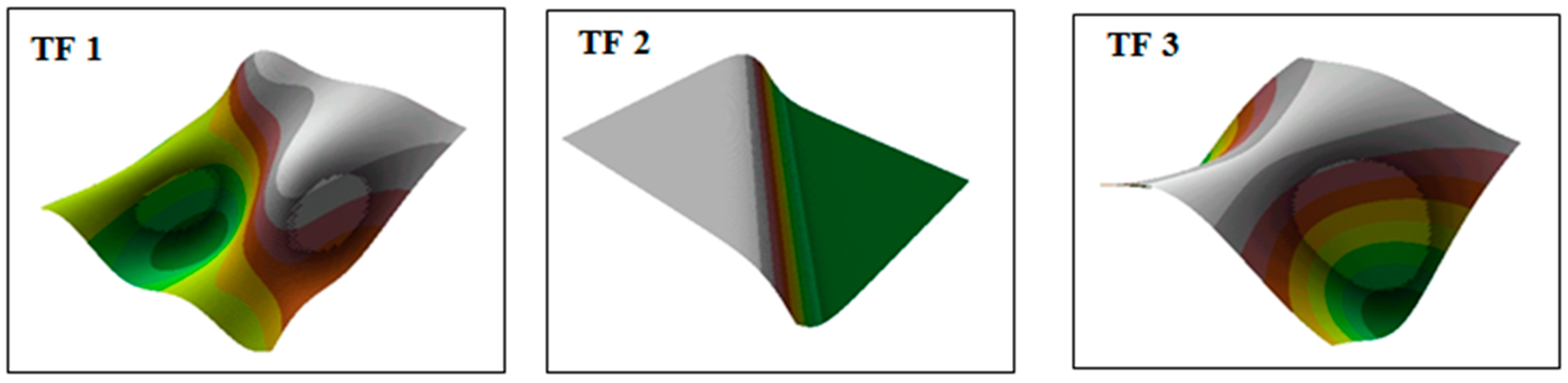
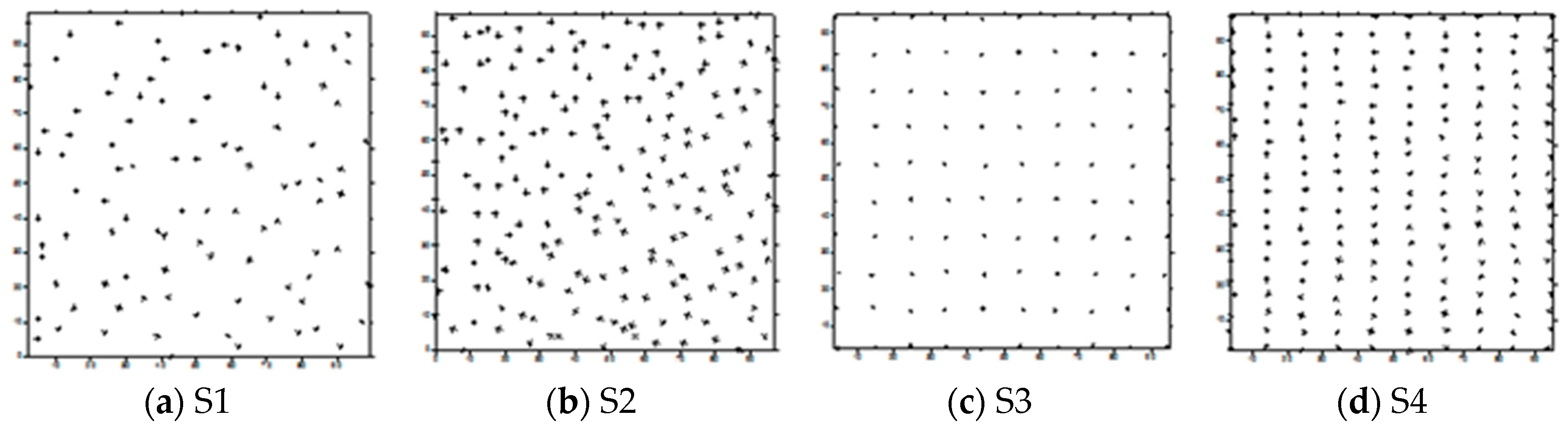
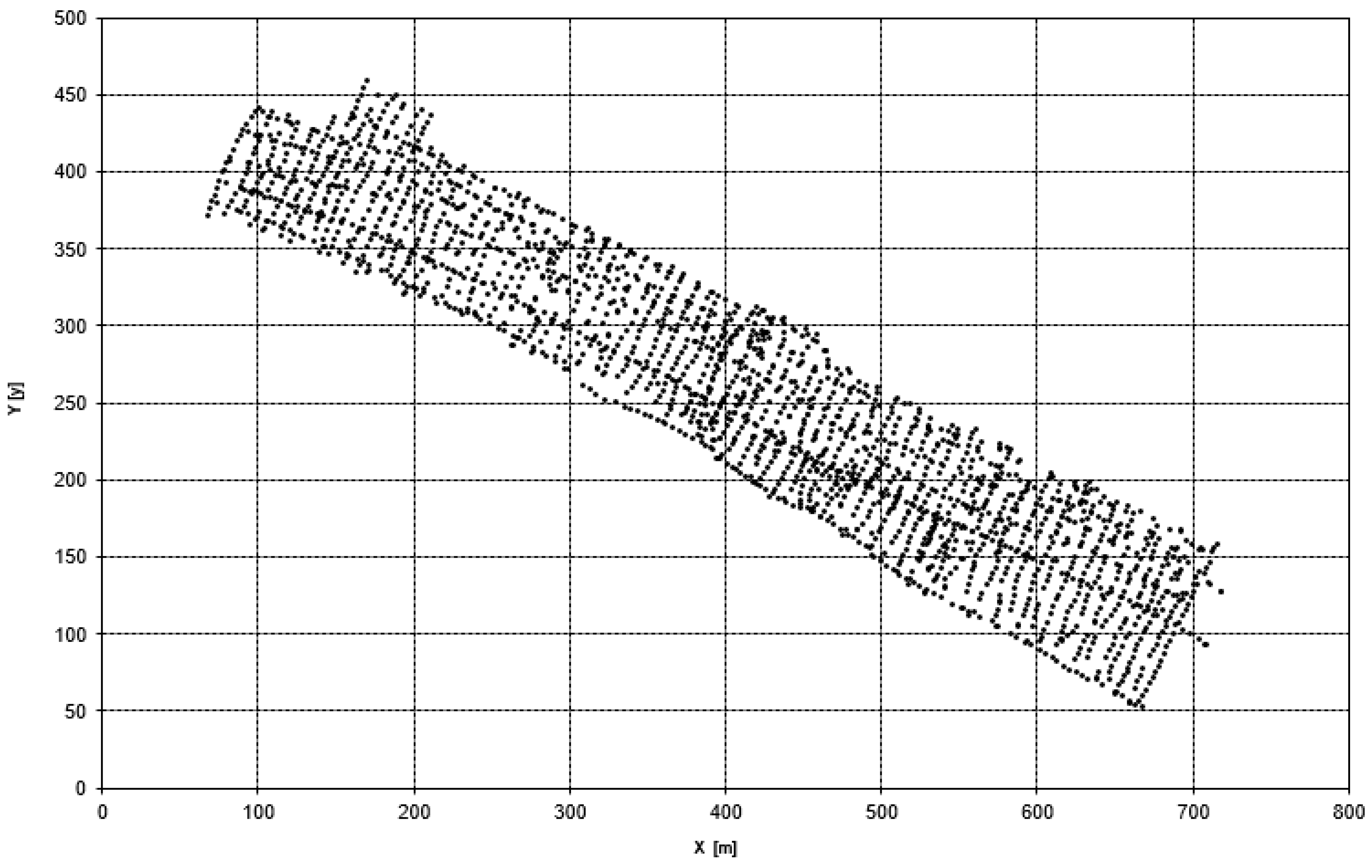
2.1. Surfaces Used During the Tests
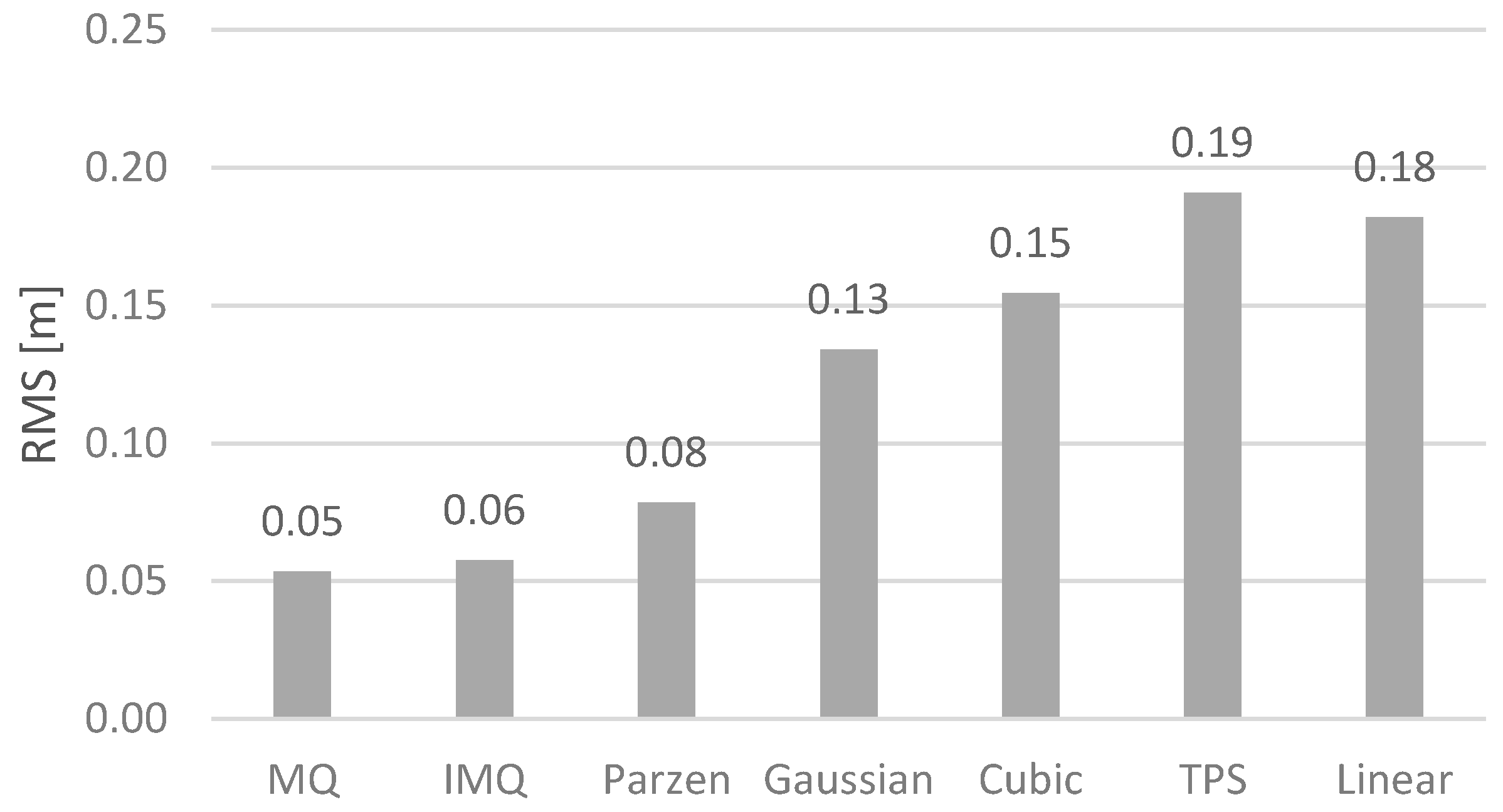
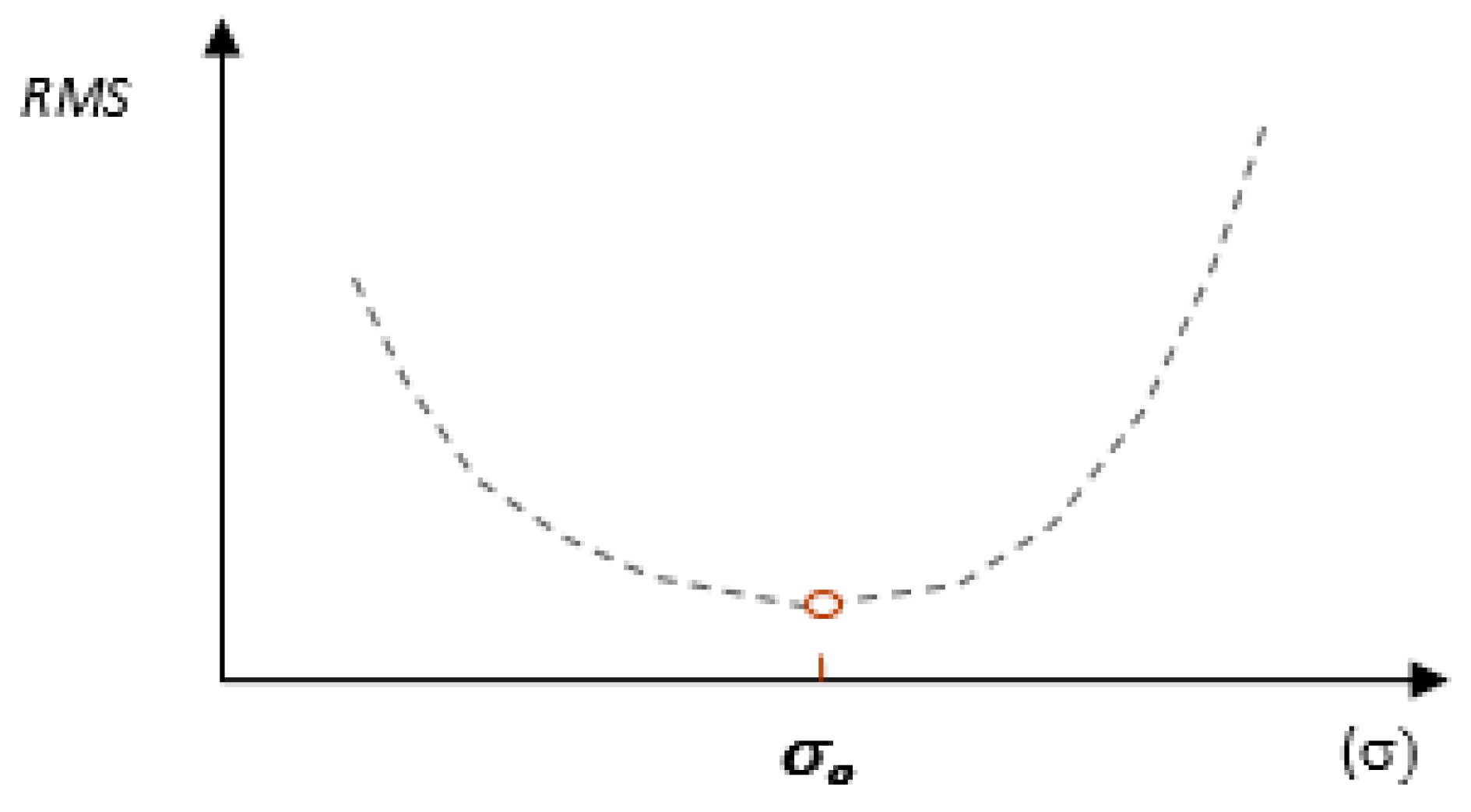
2.2. RBF Network Optimization for Geodata Interpolation
2.3. Neural Network Optimization for Geodata Reduction
3. Results and Discussion
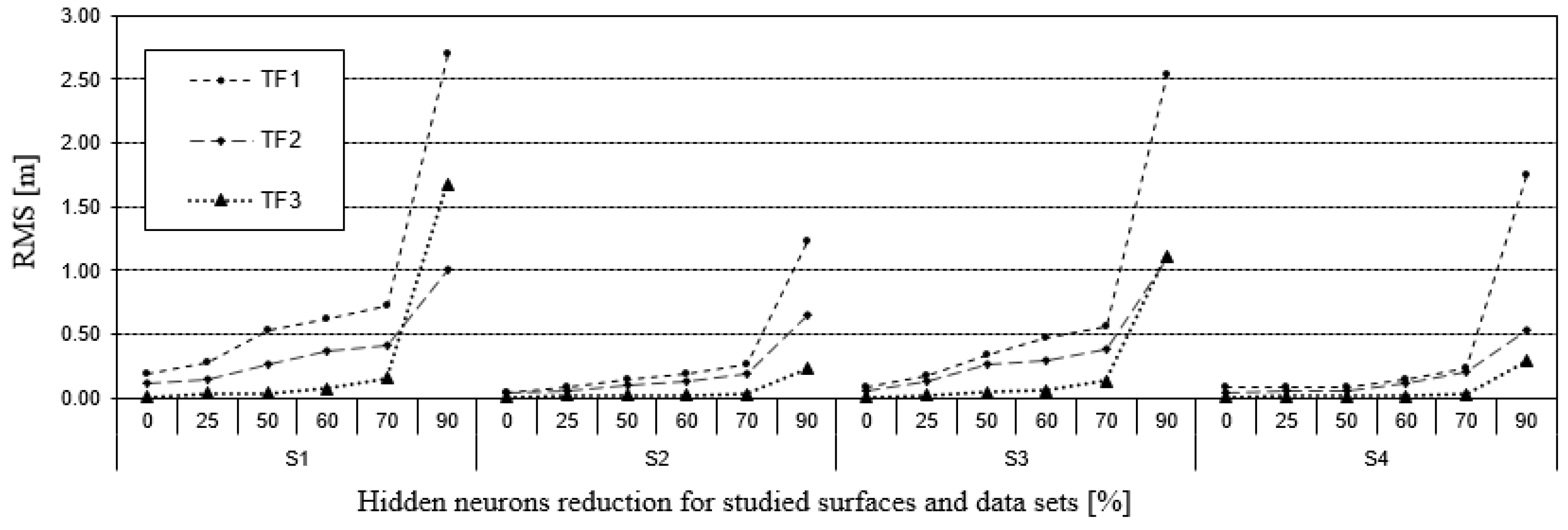
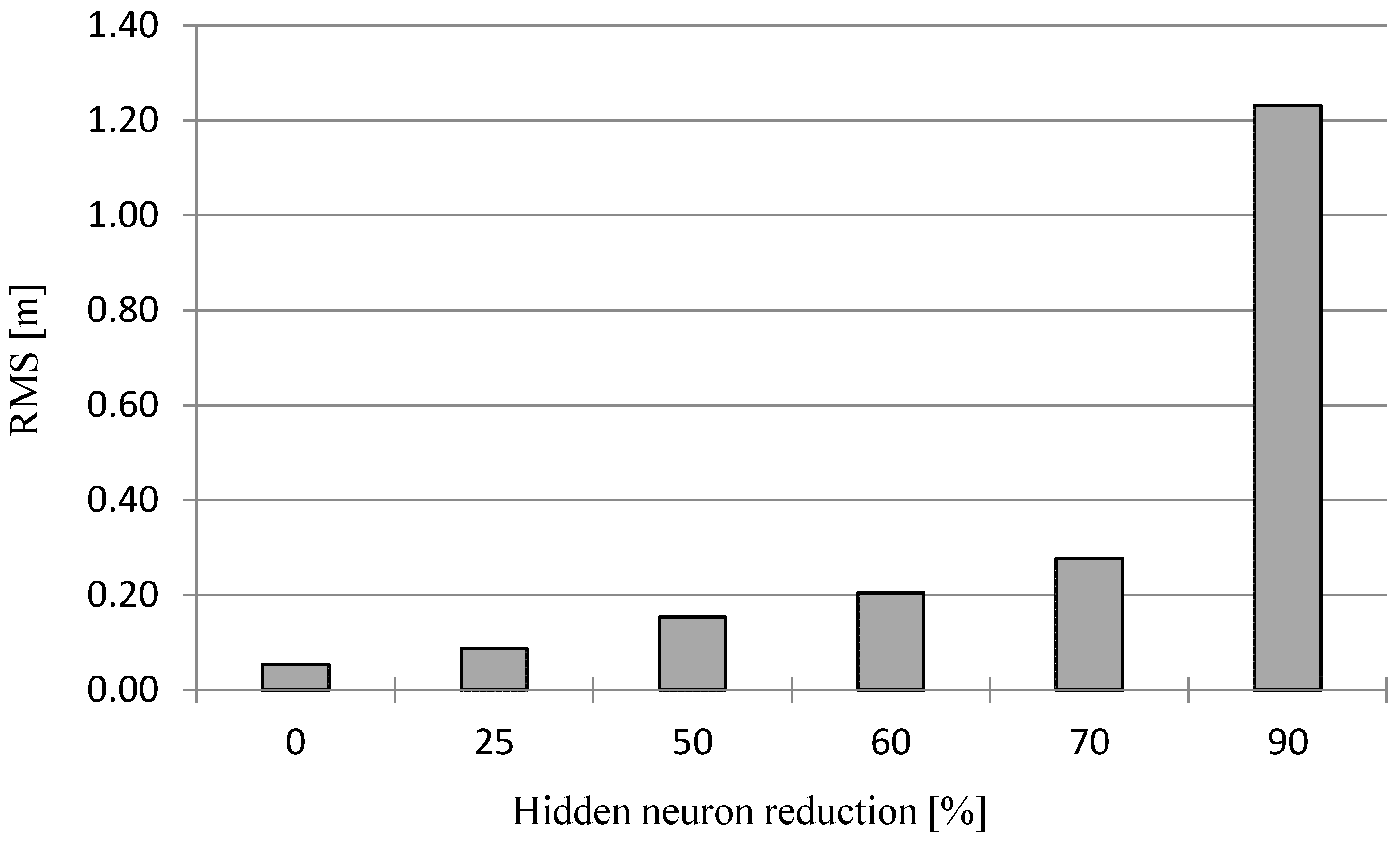
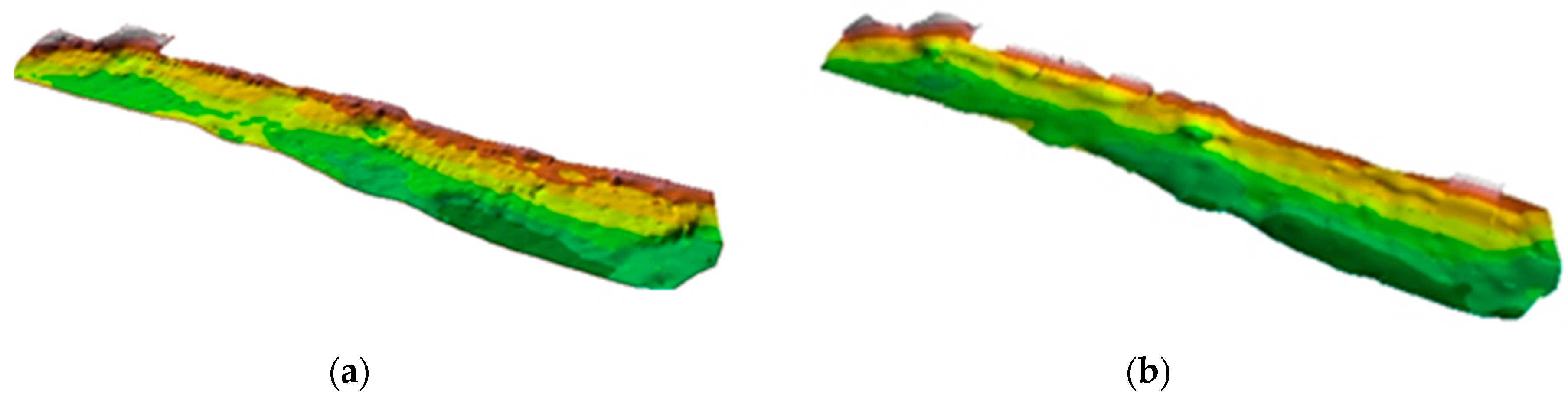
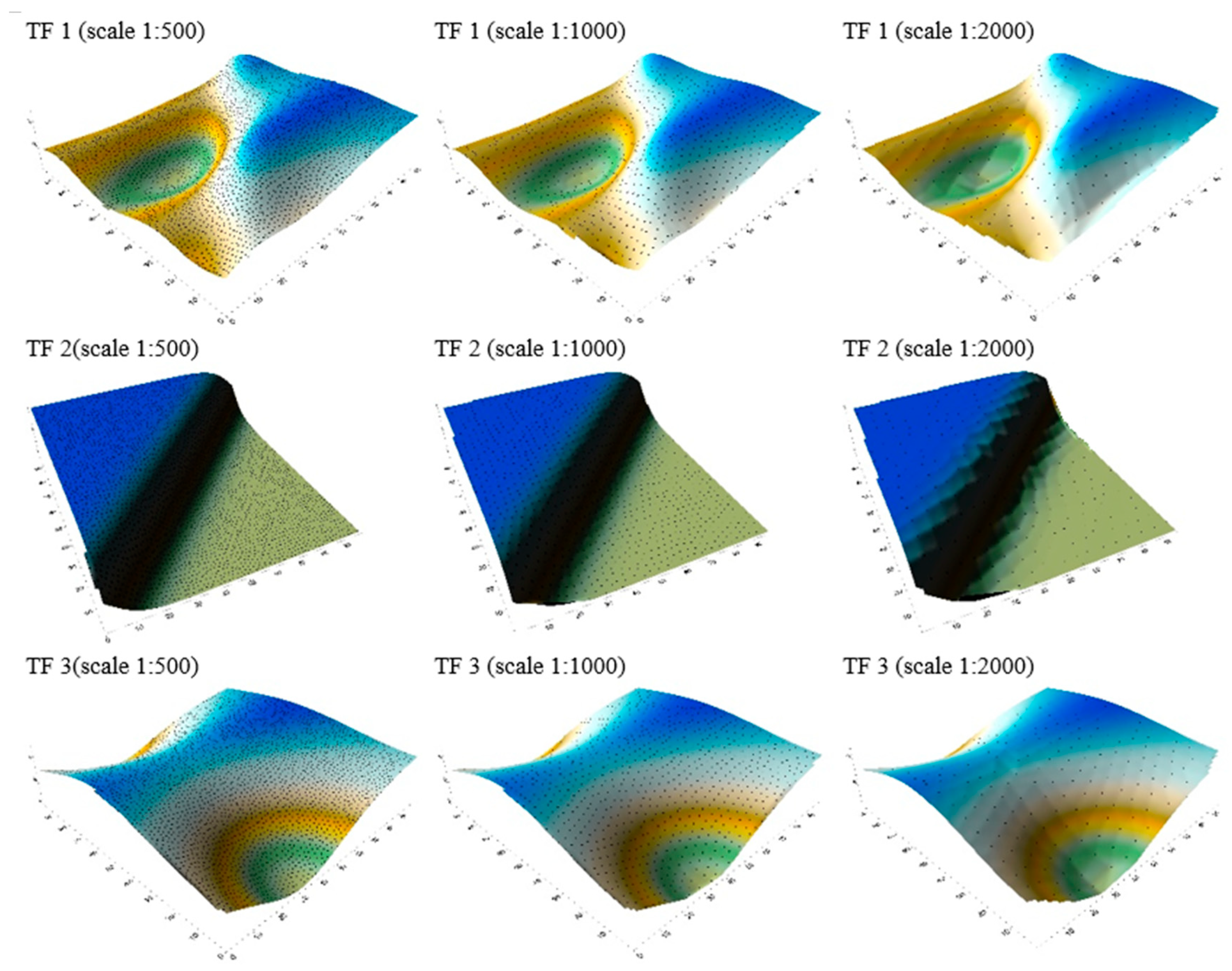
3.1. Interpolation of Bathymetric Data
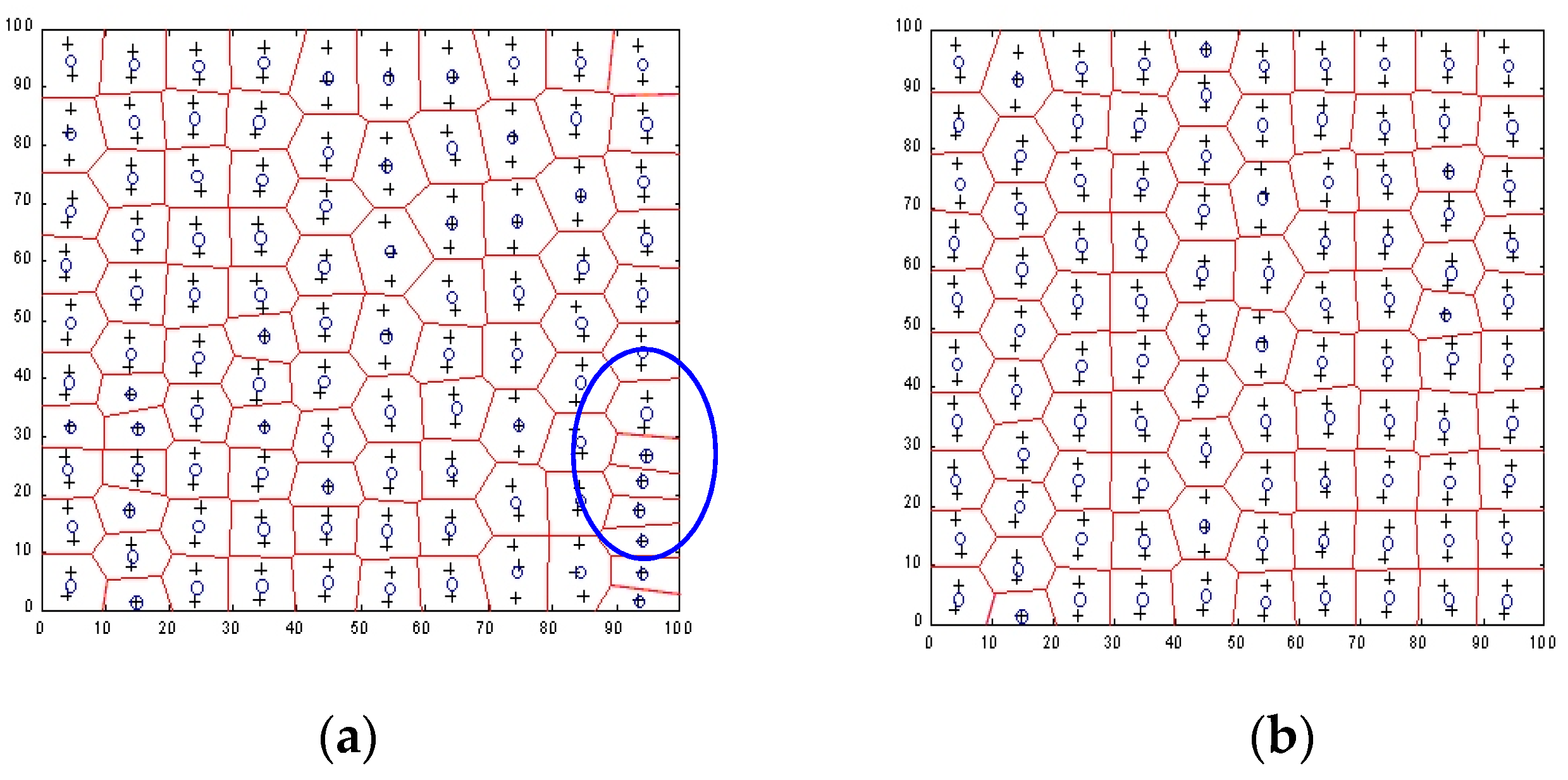
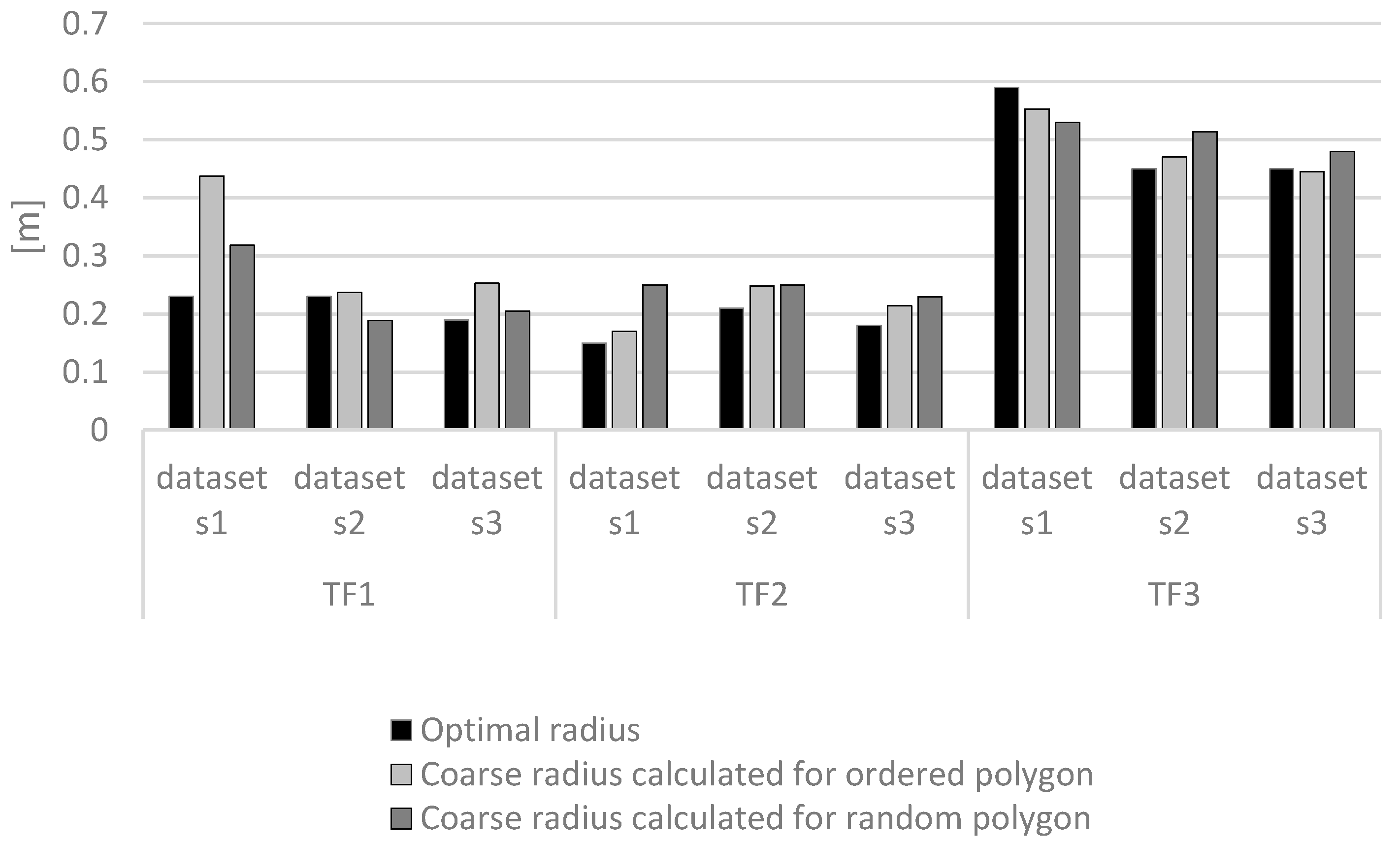
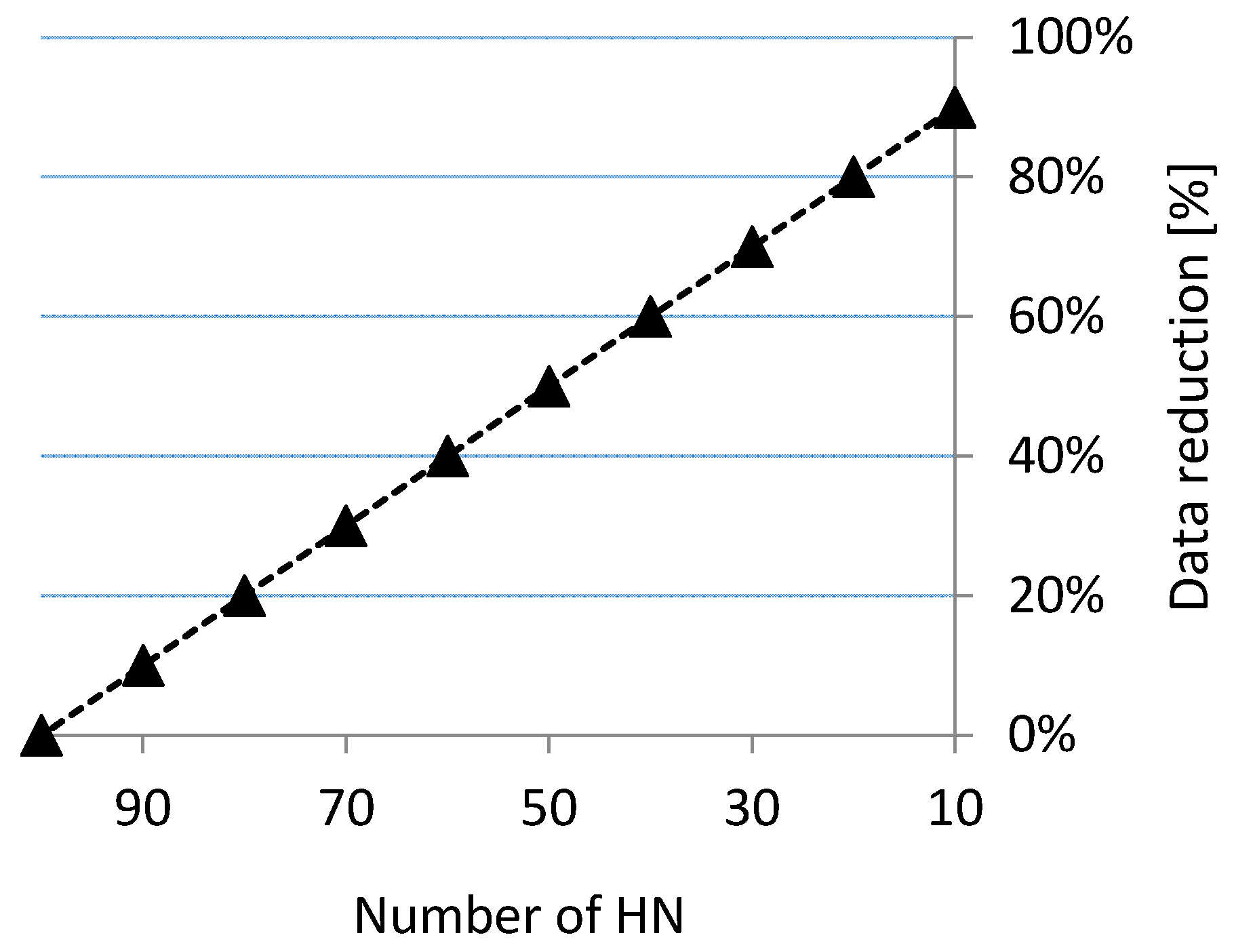
3.2. Reduction of Bathymetric Data
- for scale 1:500—4036 points XYZ (minimum depth 0.55 m and maximum depth 10.79 m);
- for scale 1:1000—1306 points XYZ (minimum depth 0.55 m and maximum depth 10.65 m);
- for scale 1:2000—497 points XYZ (minimum depth 0.55 m and maximum depth 10.56 m).
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Franke, R. Scattered data interpolation: Test of some methods. Math. Comput. 1982, 38, 181–200. [Google Scholar] [CrossRef]
- Maleika, W.; Palczynski, M.; Frejlichowski, D. Interpolation methods and the accuracy of bathymetric seabed models based on multibeam echosounder data. In Lecture Notes in Computer Science, Proceedings of the 4th International Scientific Asian Conference on Intelligent Information and Database Systems (ACIIDS), Kaohsiung, Taiwan, 19–21 March 2012; Pan, J.S., Chen, S.M., Nguyen, N.T., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7198, pp. 466–475. [Google Scholar] [CrossRef]
- Smith, M.; Goodchild, M.; Longley, P. Geospatial Analysis—A Comprehensive Guide to Principles, Techniques and Software Tools, 3rd ed.; Troubador Ltd.: Leicester, UK, 2009. [Google Scholar]
- Lainiotis, D.G.; Plataniotis, K.N. Neural network estimators: Application to ship position estimation. In Proceedings of the 1994 IEEE International Conference on Neural Networks (ICNN’94), Orlando, FL, USA, 28 June–2 July 1994; Volume 7, pp. 4710–4717. [Google Scholar] [CrossRef]
- Kazimierski, W. Proposal of neural approach to maritime radar and automatic identification system tracks association. IET Radar Sonar Navig. 2017, 11, 729–735. [Google Scholar] [CrossRef]
- Kogut, T.; Niemeyer, J.; Bujakiewicz, A. Neural networks for the generation of sea bed models using airborne lidar bathymetry data. Geod. Cartogr. 2016, 65, 41–53. [Google Scholar] [CrossRef]
- Stateczny, A. The Neural Method of Sea Bottom Shape Modelling for the Spatial Maritime Information System. In Maritime Engineering and Ports II. Book Series: Water Studies Series; Brebbia, C.A., Olivella, J., Eds.; Wit Press: Barcelona, Spain, 2000; Volume 9, pp. 251–259. [Google Scholar] [CrossRef]
- Lubczonek, J.; Wlodarczyk-Sielicka, M. The Use of an Artificial Neural Network for a Sea Bottom Modelling. In Information and Software Technologies. ICIST 2018. Communications in Computer and Information Science; Damaševičius, R., Vasiljevienė, G., Eds.; Springer: Cham, Switzerland, 2018; Volume 920. [Google Scholar] [CrossRef]
- Holland, M.; Hoggarth, A.; Nicholson, J. Hydrographic proccesing considerations in the “Big Data” age: An overview of technology trends in ocean and coastal surveys. Earth Environ. Sci. 2016, 34, 1–8. [Google Scholar]
- Fan, J.; Han, F.; Liu, H. Challenges of big data analysis. Natl. Sci. Rev. 2014, 1, 293–314. [Google Scholar] [CrossRef] [PubMed]
- Carlson, R.E.; Foley, T.A. Radial Basis Interpolation Methods on Track Data; No. UCRL-JC-1074238; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1991. [CrossRef]
- Franke, R.; Nielson, G. Smooth interpolation of large sets of scattered data. Int. J. Numer. Methods Eng. 1980, 15, 1691–1704. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Haykin, S. Neural Networks a Comprehensive Foundation; Macmillan College Publishing Company: New York, NY, USA, 1994. [Google Scholar]
- Masters, T. Practical Network Recipes in C++; Academic Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Kansa, E.J.; Carlson, R.E. Improved accuracy of multiquadric interpolation using variable shape parameter. Comput. Math. Appl. 1992, 24, 99–120. [Google Scholar] [CrossRef]
- Tarwater, A.E. A Parameter Study of Hardy’s Multiquadric Method for Scattered Data Interpolation; Technical Report: UCRL-53670; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1985.
- Lubczonek, J. Hybrid neural model of the sea bottom surface. In 7th International Conference on Artificial Intelligence and Soft Computing—ICAISC, Zakopane, Poland, 7–11 June 2004; Rutkowski, L., Siekmann, J., Tadeusiewicz, R., Zadeh, L.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar] [CrossRef]
- Ossowski, S. Neural Networks in Terms of Algorithmic; Scientific and Technical Publishers: Warsaw, Poland, 1996. (In Polish) [Google Scholar]
- Lubczonek, J.; Stateczny, A. Concept of neural model of the sea bottom surface. In Advances in Soft Computing, Proceedings of the Sixth International, Conference on Neural Network and Soft Computing, Zakopane, Poland, 11–15 June 2002; Rutkowski, L., Kacprzyk, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 861–866. [Google Scholar] [CrossRef]
- Wlodarczyk-Sielicka, M.; Stateczny, A. General Concept of Reduction Process for Big Data Obtained by Interferometric Methods. In Proceedings of the 18th International Radar Symposium (IRS 2017), Prague, Czech Republic, 28–30 June 2017; ISBN 978-3-7369-9343-3. [Google Scholar] [CrossRef]
- Wlodarczyk-Sielicka, M. Importance of neighborhood parameters during clustering of bathymetric data using neural network. In ICIST 2016, Communications in Computer and Information Science 639: Information and Software Technologies, Druskininkai, Lithuania, 13–15 October 2016; Dregvaite, G., Damasevicius, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 441–452. [Google Scholar] [CrossRef]
- Stateczny, A.; Wlodarczyk-Sielicka, M. Self-organizing artificial neural networks into hydrographic big data reduction process. In 2014 Joint Rough Set Symposium, Lecture Notes in Artificial Intelligence Granada, Madrid, Spain, 9–13 July 2014; Kryszkiewicz, M., Cornelis, C., Ciucci, D., Medina-Moreno, J., Motoda, H., Raś, Z.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2914; pp. 335–342. ISBN 0302-9743. [Google Scholar] [CrossRef]
- Wlodarczyk-Sielicka, M.; Stateczny, A. Selection of som parameters for the needs of clusterisation of data obtained by interferometric methods. In Proceedings of the 16th International Radar Symposium (IRS), Dresden, Germany, 24–26 June 2015; pp. 1129–1134. [Google Scholar] [CrossRef]
- Wlodarczyk-Sielicka, M.; Lubczonek, J.; Stateczny, A. Comparison of selected clustering algorithms of raw data obtained by interferometric methods using artificial neural networks. In Proceedings of the 17th International Radar Symposium (IRS), Krakow, Poland, 10–12 May 2016. [Google Scholar] [CrossRef]
- Wlodarczyk-Sielicka, M.; Stateczny, A. Fragmentation of hydrographic big data into subsets during reduction process. In Proceedings of the 2017 Baltic Geodetic Congress (Geomatics), Gdansk University of Technology, Gdansk, Poland, 22–25 June 2017. [Google Scholar] [CrossRef]
- Wlodarczyk-Sielicka, M.; Stateczny, A. Clustering bathymetric data for electronic navigational charts. J. Navig. 2016, 69, 1143–1153. [Google Scholar] [CrossRef]


| Radial Network | |
|---|---|
| Number of input, hidden, and output layers | 1 |
| Number of neurons in input layer/transfer function type | 2/linear |
| Number of neurons in output layer/transfer function type | 1/linear |
| Number of neurons in hidden layer/transfer function type | various/multiquadric |
| Training set pre-processing method | Min-Max normalization |
| Training algorithm | k-means with neuron fatigue mechanism |
| Min Depth [m] | Max Depth [m] | Mean Depth [m] | Max Error [m] | Mean Error [m] | |
|---|---|---|---|---|---|
| TF1, scale 1:500 | 5.00 | 29.73 | 14.92 | 0.5932 | 0.0118 |
| TF1, scale 1:1000 | 5.00 | 29.55 | 14.69 | 1.9475 | 0.0330 |
| TF1, scale 1:2000 | 5.00 | 29.56 | 14.27 | 3.2506 | 0.1370 |
| TF2, scale 1:500 | 4.52 | 15.11 | 9.71 | 0.3575 | 0.0058 |
| TF2, scale 1:1000 | 4.52 | 15.11 | 9.60 | 1.3723 | 0.0134 |
| TF2, scale 1:2000 | 4.52 | 15.11 | 9.37 | 2.5310 | 0.0473 |
| TF3, scale 1:500 | 4.88 | 30.27 | 12.13 | 0.7603 | 0.0061 |
| TF3, scale 1:1000 | 4.88 | 30.15 | 11.88 | 1.3959 | 0.0135 |
| TF3, scale 1:2000 | 4.88 | 29.44 | 11.55 | 1.5159 | 0.0499 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wlodarczyk-Sielicka, M.; Lubczonek, J. The Use of an Artificial Neural Network to Process Hydrographic Big Data during Surface Modeling. Computers 2019, 8, 26. https://doi.org/10.3390/computers8010026
Wlodarczyk-Sielicka M, Lubczonek J. The Use of an Artificial Neural Network to Process Hydrographic Big Data during Surface Modeling. Computers. 2019; 8(1):26. https://doi.org/10.3390/computers8010026
Chicago/Turabian StyleWlodarczyk-Sielicka, Marta, and Jacek Lubczonek. 2019. "The Use of an Artificial Neural Network to Process Hydrographic Big Data during Surface Modeling" Computers 8, no. 1: 26. https://doi.org/10.3390/computers8010026
APA StyleWlodarczyk-Sielicka, M., & Lubczonek, J. (2019). The Use of an Artificial Neural Network to Process Hydrographic Big Data during Surface Modeling. Computers, 8(1), 26. https://doi.org/10.3390/computers8010026






