Neural Network-Based Formula for the Buckling Load Prediction of I-Section Cellular Steel Beams
Abstract
1. Introduction
2. Data Generation
2.1. FE Modeling
2.2. Parametric Analysis
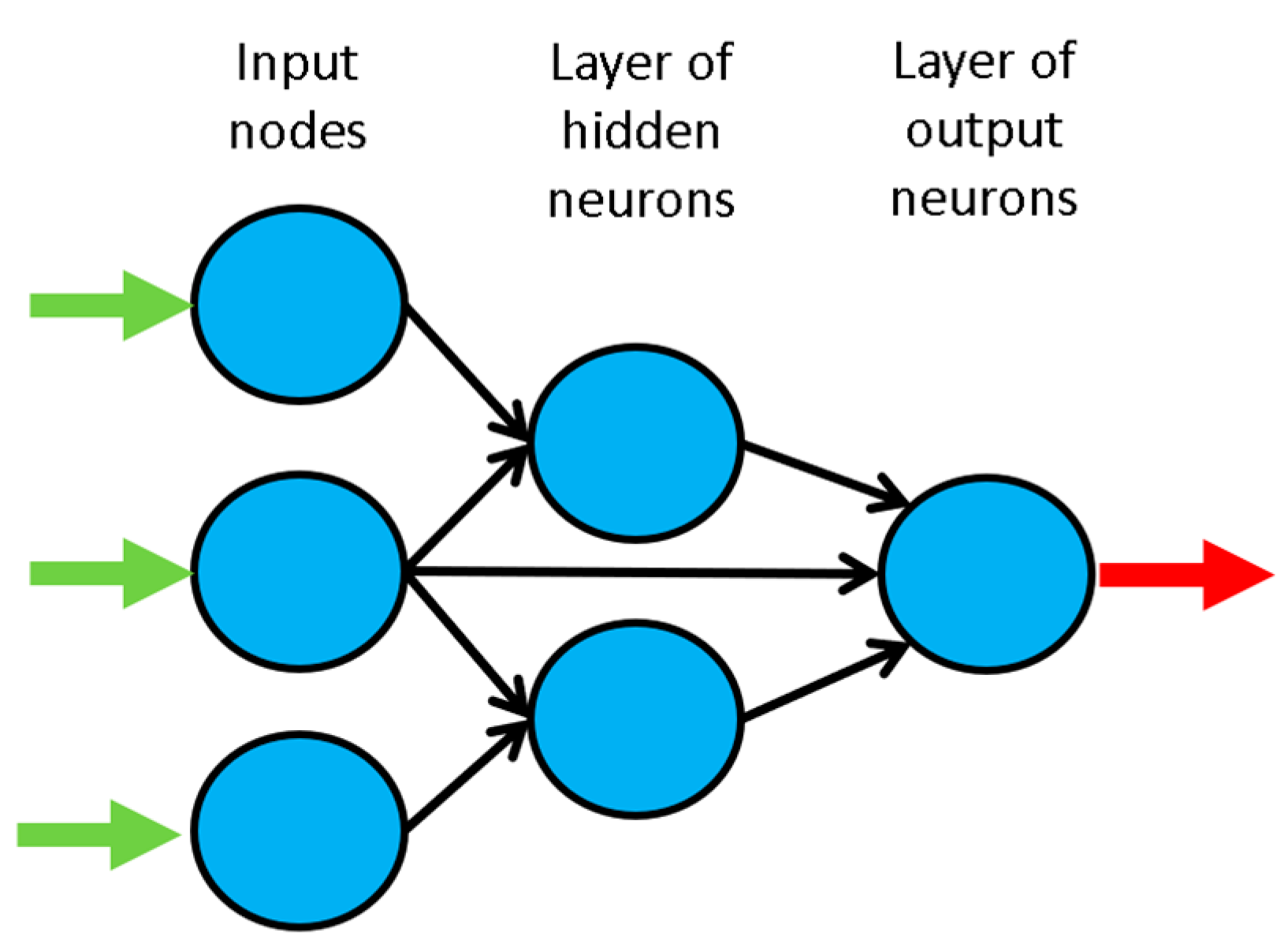
3. Artificial Neural Networks
3.1. Introduction
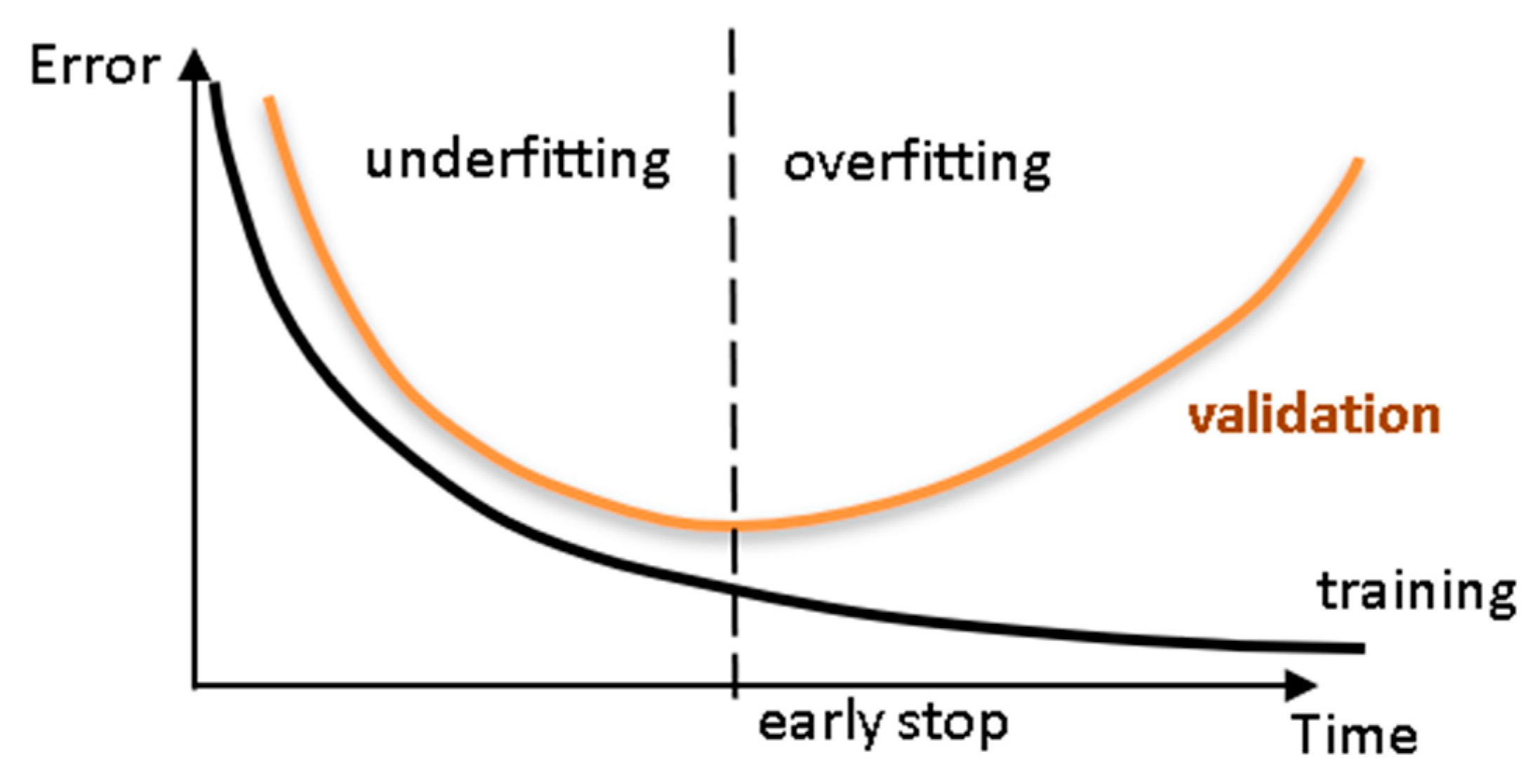
3.2. Learning
3.3. Implemented ANN features
3.3.1. Qualitative Variable Representation (Feature 1)
3.3.2. Dimensional Analysis (Feature 2)
3.3.3. Input Dimensionality Reduction (Feature 3)
Linear Correlation
Auto-Encoder
Orthogonal and Sparse Random Projections
3.3.4. Training, Validation and Testing Datasets (Feature 4)
- For each variable q (row) in the complete input dataset, compute its minimum and maximum values.
- Select all patterns (if some) from the learning dataset where each variable takes either its minimum or maximum value. Those patterns must be included in the training dataset, regardless what pt is. However, if the number of patterns ‘does not reach’ pt, one should add the missing amount, providing those patterns are the ones having more variables taking extreme (minimum or maximum) values.
- In order to select the validation patterns, randomly select pv/(pv + ptt) of those patterns not belonging to the previously defined training dataset. The remainder defines the testing dataset.
3.3.5. Input Normalization (Feature 5)
Linear Max Abs
Linear [0, 1] and [−1, 1]
Nonlinear
Linear Mean Std
3.3.6. Output Transfer Functions (Feature 6)
Logistic
Hyperbolic Tang
Bilinear
Identity
3.3.7. Output Normalization (Feature 7)
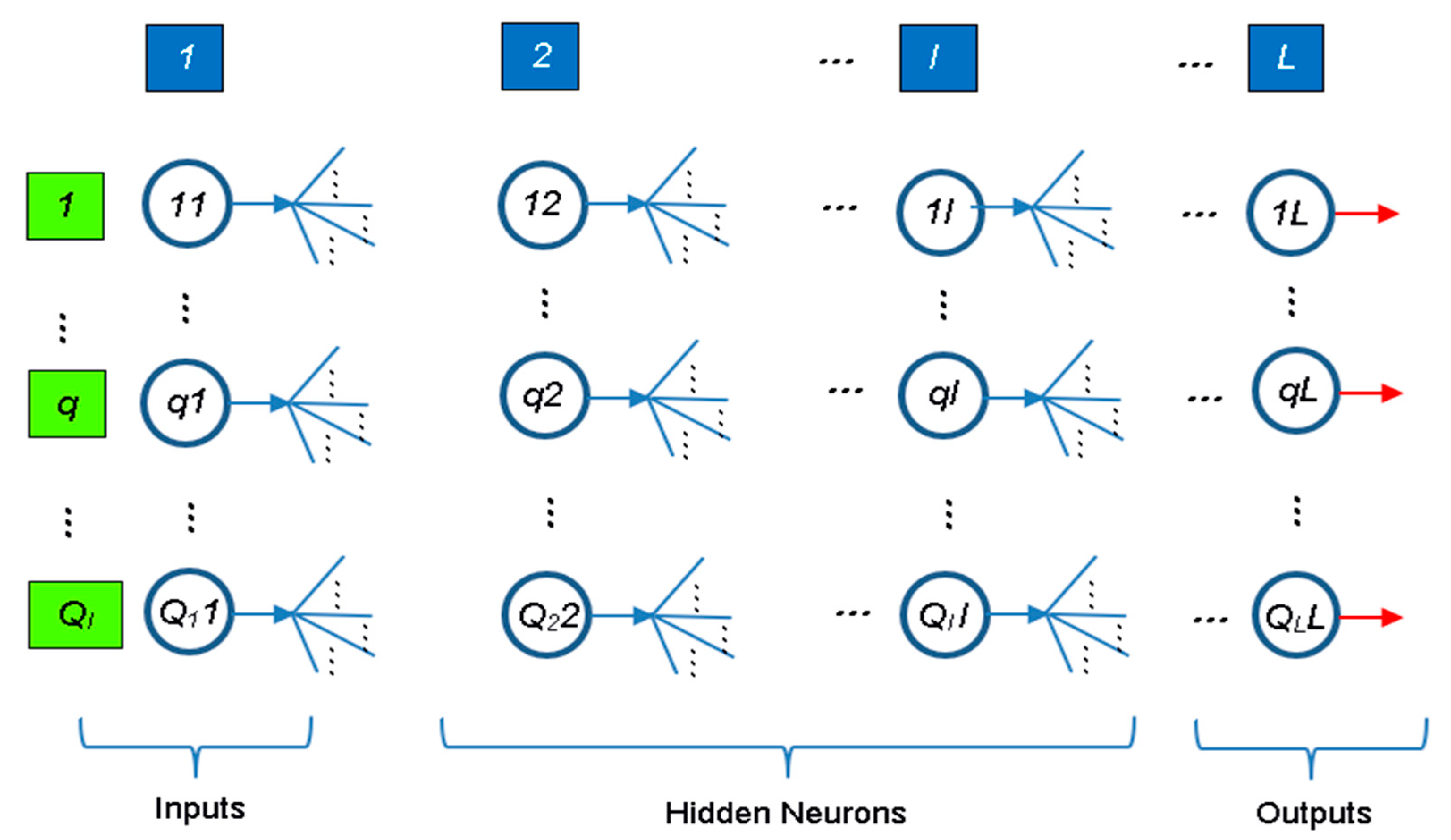
3.3.8. Network Architecture (Feature 8)
Multi-Layer Perceptron Network (MLPN)
Radial-Basis Function Network (RBFN)
3.3.9. Hidden Nodes (Feature 9)
3.3.10. Connectivity (Feature 10)
3.3.11. Hidden Transfer Functions (Feature 11)
Identity-Logistic
Bipolar
Positive Saturating Linear
Sinusoid
Radial Basis Functions (RBF)
3.3.12. Parameter Initialization (Feature 12)
Midpoint, Rands, Randnc, Randnr, Randsmall
Rand [−lim, lim]
SVD
Mini-Batch SVD
3.3.13. Learning Algorithm (Feature 13)
Back-Propagation (BP, BPA), Levenberg-Marquardt (LM)
- (i)
- Learning Rate = 0.01/cs0.5, being cs the chunk size, as defined in Section 3.3.15.
- (ii)
- Minimum performance gradient = 0.
Extreme Learning Machine (ELM, mb ELM, I-ELM, CI-ELM)
3.3.14. Performance Improvement (Feature 14)
3.3.15. Training Mode (Feature 15)
3.4. Network Performance Assessment
3.4.1. Maximum Error
3.4.2. Percentage of Errors > 3%
3.4.3. Performance
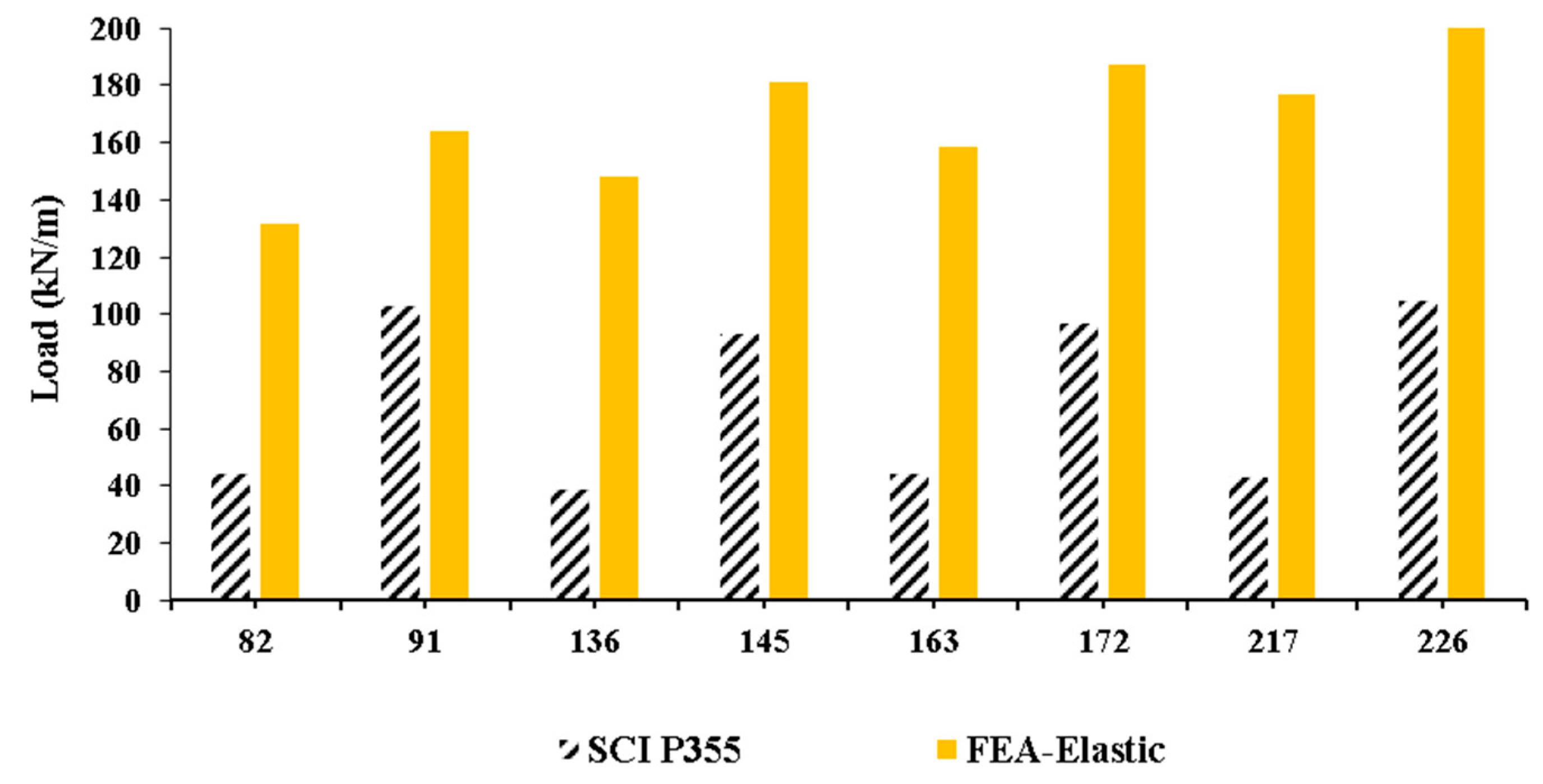
3.5. Software Validation
3.6. Parametric Analysis Results
3.7. Proposed ANN-Based Model
3.7.1. Input Data Preprocessing
Dimensional Analysis and Dimensionality Reduction
Input Normalization
3.7.2. ANN-Based Analytical Model
3.7.3. Output Data Postprocessing
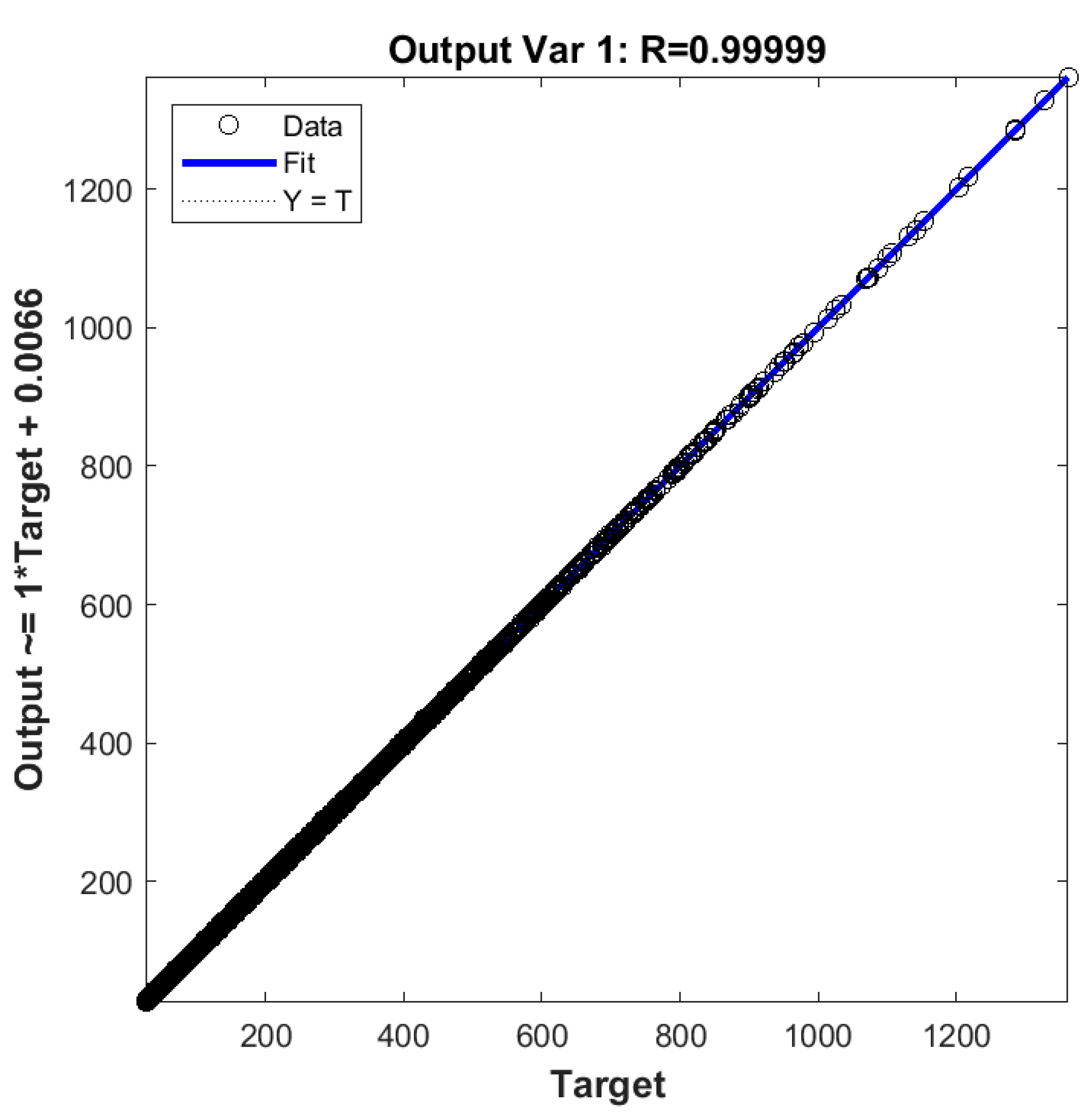
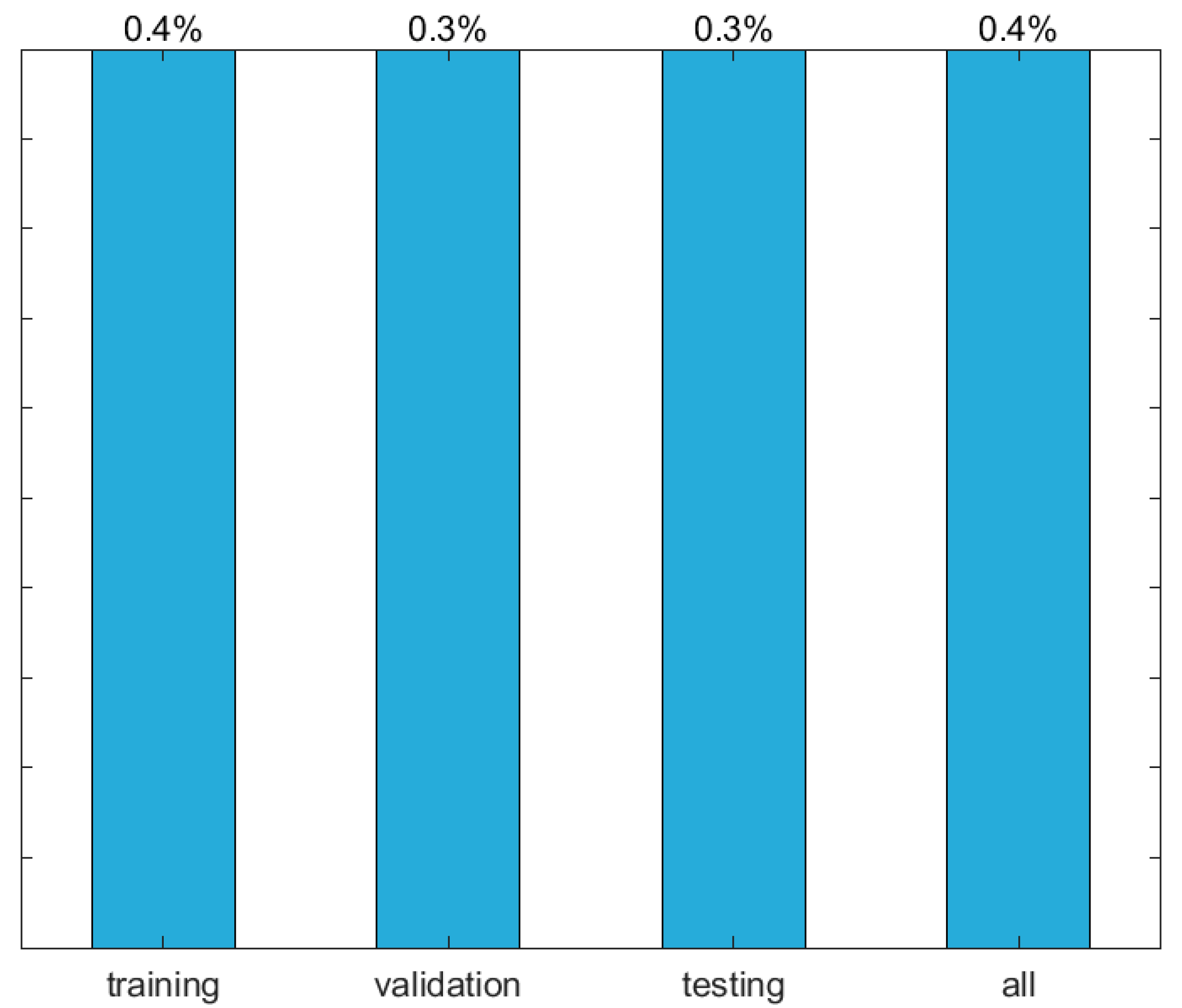
3.7.4. Performance Results
4. Design Considerations
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tsavdaridis, K.D. Structural Performance of Perforated Steel Beams with Novel Web Openings and with Partial Concrete Encasement. Ph.D. Thesis, City University of London, London, UK, 2010. [Google Scholar]
- Morkhade, S.G.; Gupta, L.M. An experimental and parametric study on steel beams with web openings. Int. J. Adv. Struct. Eng. 2015, 7, 249–260. [Google Scholar] [CrossRef]
- Akrami, V.; Erfani, S. Review and assessment of design methodologies for perforated steel beams. J. Struct. Eng. 2016, 142, 1–14. [Google Scholar] [CrossRef]
- Uenoya, M.; Redwood, R.G. Buckling of webs with openings. Comput. Struct. 1978, 9, 191–199. [Google Scholar] [CrossRef]
- Lucas, W.K.; Darwin, D. Steel and Composite Beams with Web Openings; The American Iron and Steel Institute: City of Wichita, KS, USA, 1990. [Google Scholar]
- Darwin, D. Steel and Composite Beams with Web Opening; Steel Design Guide Series 2; American Institute of Steel Construction (AISC): Chicago, IL, USA, 1990. [Google Scholar]
- SEI/ASCE. Specifications for Structural Steel Beams with Openings; SEI/ASCE 23-97; ASCE: Reston, VA, USA, 1998. [Google Scholar]
- Ward, J.K. Design of Composite and Non-Composite Cellular Beams SCI P100; Steel Construction Institute: Berkshire, UK, 1990. [Google Scholar]
- Chung, K.F.; Lui, T.C.H.; Ko, A.C.H. Investigation on vierendeel mechanism in steel beams with circular web openings. J. Constr. Steel Res. 2001, 57, 467–490. [Google Scholar] [CrossRef]
- Chung, K.F.; Liu, C.H.; Ko, A.C.H. Steel beams with large web openings of various shapes and sizes: An empirical design method using a generalized moment-shear interaction curve. J. Constr. Steel Res. 2003, 59, 1177–1200. [Google Scholar] [CrossRef]
- Tsavdaridis, K.D.; D’Mello, C. Finite Element Investigation of Perforated Beams with Different Web Opening Configurations. In Proceedings of the 6th International Conference on Advances is Steel Structures (ICASS 2009), Hong Kong, China, 16–18 December 2009; pp. 213–220. [Google Scholar]
- Tsavdaridis, K.D.; D’Mello, C. Web buckling study of the behaviour and strength of perforated steel beams with different novel web opening shapes. J. Constr. Steel Res. 2011, 67, 1605–1620. [Google Scholar] [CrossRef]
- Tsavdaridis, K.D.; D’Mello, C. Vierendeel bending study of perforated steel beams with various novel web opening shapes through non-linear finite element analyses. J. Struct. Eng. 2012, 138, 1214–1230. [Google Scholar] [CrossRef]
- Tsavdaridis, K.D.; Kingman, J.J.; Toropov, V.V. Application of Structural Topology Optimisation to Perforated Steel Beams. Comput. Struct. 2015, 158, 108–123. [Google Scholar] [CrossRef]
- Lawson, R.M.; Hicks, S.J. Design of Composite Beams with Large Openings SCI P355; Steel Construction Institute: Berkshire, UK, 2011. [Google Scholar]
- Lawson, R.M. Design for Openings in the Webs of Composite Beams SCI P068; Steel Construction Institute: Berkshire, UK, 1987. [Google Scholar]
- Verweij, J.G. Cellular Beam-Columns in Portal Frame Structures. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2010. [Google Scholar]
- Gholizadeh, S.; Pirmoz, A.; Attarnejad, R. Assessment of load carrying capacity of castellated steel beams by neural networks. J. Constr. Steel Res. 2011, 67, 770–779. [Google Scholar] [CrossRef]
- Sharifi, Y.; Tohidi, S. Lateral-torsional buckling capacity assessment of web opening steel girders by artificial neural networks—Elastic investigation. Front. Struct. Civ. Eng. 2014, 8, 167–177. [Google Scholar] [CrossRef]
- Tohidi, S.; Sharifi, Y. Inelastic lateral-torsional buckling capacity of corroded web opening steel beams using artificial neural networks. IES J. Part A Civ. Struct. Eng. 2014, 8, 24–40. [Google Scholar] [CrossRef]
- Tohidi, S.; Sharifi, Y. Load-carrying capacity of locally corroded steel plate girder ends using artificial neural network. Thin-Walled Struct. 2016, 100, 48–61. [Google Scholar] [CrossRef]
- Asteris, P.G.; Kolovos, K.G.; Douvika, M.G.; Roinos, K. Prediction of self-compacting concrete strength using artificial neural networks. Eur. J. Environ. Civ. Eng. 2016, 20 (Suppl. 1), S102–S122. [Google Scholar] [CrossRef]
- Cascardi, A.; Micelli, F.; Aiello, M.A. An Artificial Neural Networks model for the prediction of the compressive strength of FRP-confined concrete circular columns. Eng. Struct. 2017, 140, 199–208. [Google Scholar] [CrossRef]
- Marović, I.; Androjić, I.; Jajac, N.; Hanák, T. Urban Road Infrastructure Maintenance Planning with Application of Neural Networks. Complexity 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Wong, E.W.C.; Choi, H.S.; Kim, D.K.; Hashim, F.M. Development of ANN Model for the Prediction of VIV Fatigue Damage of Top-tensioned Riser. MATEC Web Conf. 2018, 203, 1013. [Google Scholar] [CrossRef]
- Dassault Systèmes. ABAQUS 6.11, Abaqus/CAE User’s Manual; Dassault Systemes: Vélizy-Villacoublay, France, 2011. [Google Scholar]
- Dassault Systèmes Simulia Corp. ABAQUS CAE (2017); Software; Dassault Systèmes Simulia Corp.: Vélizy-Villacoublay, France, 2017. [Google Scholar]
- Surtees, J.O.; Lui, Z. Report of Loading Tests on Cellform Beams; Research Report; University of Leeds: Leeds, UK, 1995. [Google Scholar]
- Rajana, K. Advanced Computational Parametric Study of the Linear Elastic and Non-Linear Post Buckling Behaviour of Non-Composite Cellular Steel Beams. Master’s Thesis, University of Leeds, Leeds, UK, 2018. [Google Scholar] [CrossRef]
- El-Sawhy, K.L.; Sweedan, A.M.I.; Martini, M.I. Moment gradient factor of cellular steel beams under inelastic flexure. J. Constr. Steel Res. 2014, 98, 20–34. [Google Scholar] [CrossRef]
- Developer. Dataset ANN [Data Set]. Zenodo. 2018. Available online: http://doi.org/10.5281/zenodo.1486181 (accessed on 29 November 2018).
- Hertzmann, A.; Fleet, D. Machine Learning and Data Mining; Lecture Notes CSC 411/D11; Computer Science Department, University of Toronto: Toronto, ON, Canada, 2012. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Hern, A. Google Says Machine Learning Is the Future. So I Tried It Myself. Available online: www.theguardian.com/technology/2016/jun/28/all (accessed on 2 November 2016).
- Prieto, A.; Prieto, B.; Ortigosa, E.M.; Ros, E.; Pelayo, F.; Ortega, J.; Rojas, I. Neural networks: An overview of early research, current frameworks and new challenges. Neurocomputing 2016, 214, 242–268. [Google Scholar] [CrossRef]
- Wilamowski, B.M.; Irwin, J.D. The Industrial Electronics Handbook: Intelligent Systems; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Flood, I. Towards the next generation of artificial neural networks for civil engineering. Adv. Eng. Inform. 2008, 228, 4–14. [Google Scholar] [CrossRef]
- Haykin, S.S. Neural Networks and Learning Machines; Prentice Hall/Pearson: New York, NY, USA, 2009. [Google Scholar]
- The Mathworks, Inc. MATLAB R2017a, User’s Guide; The Mathworks, Inc.: Natick, MA, USA, 2017. [Google Scholar]
- Bhaskar, R.; Nigam, A. Qualitative physics using dimensional analysis. Artif. Intell. 1990, 45, 111–173. [Google Scholar] [CrossRef]
- Kasun, L.L.C.; Yang, Y.; Huang, G.-B.; Zhang, Z. Dimension reduction with extreme learning machine. IEEE Trans. Image Process. 2016, 25, 3906–3918. [Google Scholar] [CrossRef] [PubMed]
- Lachtermacher, G.; Fuller, J.D. Backpropagation in time-series forecasting. J. Forecast. 1995, 14, 381–393. [Google Scholar] [CrossRef]
- Pu, Y.; Mesbahi, E. Application of artificial neural networks to evaluation of ultimate strength of steel panels. Eng. Struct. 2006, 28, 1190–1196. [Google Scholar] [CrossRef]
- Flood, I.; Kartam, N. Neural Networks in Civil Engineering: I-Principals and Understanding. J. Comput. Civ. Eng. 1994, 8, 131–148. [Google Scholar] [CrossRef]
- Mukherjee, A.; Deshpande, J.M.; Anmala, J. Prediction of buckling load of columns using artificial neural networks. J. Struct. Eng. 1996, 122, 1385–1387. [Google Scholar] [CrossRef]
- Wilamowski, B.M. Neural Network Architectures and Learning algorithms. IEEE Ind. Electron. Mag. 2009, 3, 56–63. [Google Scholar] [CrossRef]
- Xie, T.; Yu, H.; Wilamowski, B. Comparison between traditional neural networks and radial basis function networks. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics (ISIE), Gdansk University of Technology Gdansk, Gdansk, Poland, 27–30 June 2011; pp. 1194–1199. [Google Scholar]
- Aymerich, F.; Serra, M. Prediction of fatigue strength of composite laminates by means of neural networks. Key Eng. Mater. 1998, 144, 231–240. [Google Scholar] [CrossRef]
- Rafiq, M.; Bugmann, G.; Easterbrook, D. Neural network design for engineering applications. Comput. Struct. 2001, 79, 1541–1552. [Google Scholar] [CrossRef]
- Xu, S.; Chen, L. Novel approach for determining the optimal number of hidden layer neurons for FNN’s and its application in data mining. In Proceedings of the International Conference on Information Technology and Applications (ICITA), Cairns, Australia, 23–26 June 2008; pp. 683–686. [Google Scholar]
- Gunaratnam, D.J.; Gero, J.S. Effect of representation on the performance of neural networks in structural engineering applications. Comput.-Aided Civ. Infrastruct. Eng. 1994, 9, 97–108. [Google Scholar] [CrossRef]
- Lefik, M.; Schrefler, B.A. Artificial neural network as an incremental non-linear constitutive model for a finite element code. Comput. Methods Appl. Mech. Eng. 2003, 192, 3265–3283. [Google Scholar] [CrossRef]
- Bai, Z.; Huang, G.; Wang, D.; Wang, H.; Westover, M. Sparse extreme learning machine for classification. IEEE Trans. Cybern. 2014, 44, 1858–1870. [Google Scholar] [CrossRef] [PubMed]
- Schwenker, F.; Kestler, H.; Palm, G. Three learning phases for radial-basis-function networks. Neural Netw. 2001, 14, 439–458. [Google Scholar] [CrossRef]
- Waszczyszyn, Z. Neural Networks in the Analysis and Design of Structures; CISM Courses and Lectures No. 404; Springer: Wien, Austria; New York, NY, USA, 1999. [Google Scholar]
- Deng, W.-Y.; Bai, Z.; Huang, G.-B.; Zheng, Q.-H. A fast SVD-Hidden-nodes based extreme learning machine for large-scale data Analytics. Neural Netw. 2016, 77, 14–28. [Google Scholar] [CrossRef]
- Wilamowski, B.M. How to not get frustrated with neural networks. In Proceedings of the 2011 IEEE International Conference on Industrial Technology (ICIT), Auburn University, Auburn, AL, USA, 14–16 March 2011. [Google Scholar]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Liang, N.; Huang, G.; Saratchandran, P.; Sundararajan, N. A fast and accurate online Sequential learning algorithm for Feedforward networks. IEEE Trans. Neural Netw. 2006, 17, 1411–1423. [Google Scholar] [CrossRef]
- Huang, G.; Chen, L.; Siew, C. Universal approximation using incremental constructive feedforward networks with random hidden nodes. IEEE Trans. Neural Netw. 2006, 17, 879–892. [Google Scholar] [CrossRef]
- Huang, G.-B.; Chen, L. Convex incremental extreme learning machine. Neurocomputing 2007, 70, 3056–3062. [Google Scholar] [CrossRef]
- Beyer, W.; Liebscher, M.; Beer, M.; Graf, W. Neural Network Based Response Surface Methods—A Comparative Study. In Proceedings of the 5th German LS-DYNA Forum, Ulm, Germany, 12–13 October 2006; pp. 29–38. [Google Scholar]
- Wilson, D.R.; Martinez, T.R. The general inefficiency of batch training for gradient descent learning. Neural Netw. 2003, 16, 1429–1451. [Google Scholar] [CrossRef]
- The Researcher. ANNSoftwareValidation-Report.pdf. 2018. Available online: https://www.researchgate.net/profile/Abambres_M/project/Applied-Artificial-Intelligence/attachment/5aff6a82b53d2f63c3ccbaa0/AS:627790747541504@1526688386824/download/ANN+Software+Validation+-+Report.pdf?context=ProjectUpdatesLog (accessed on 29 November 2018).
- Developer. W and b Arrays [Data Set]. Zenodo. 2018. Available online: http://doi.org/10.5281/zenodo.1486268 (accessed on 29 November 2018).
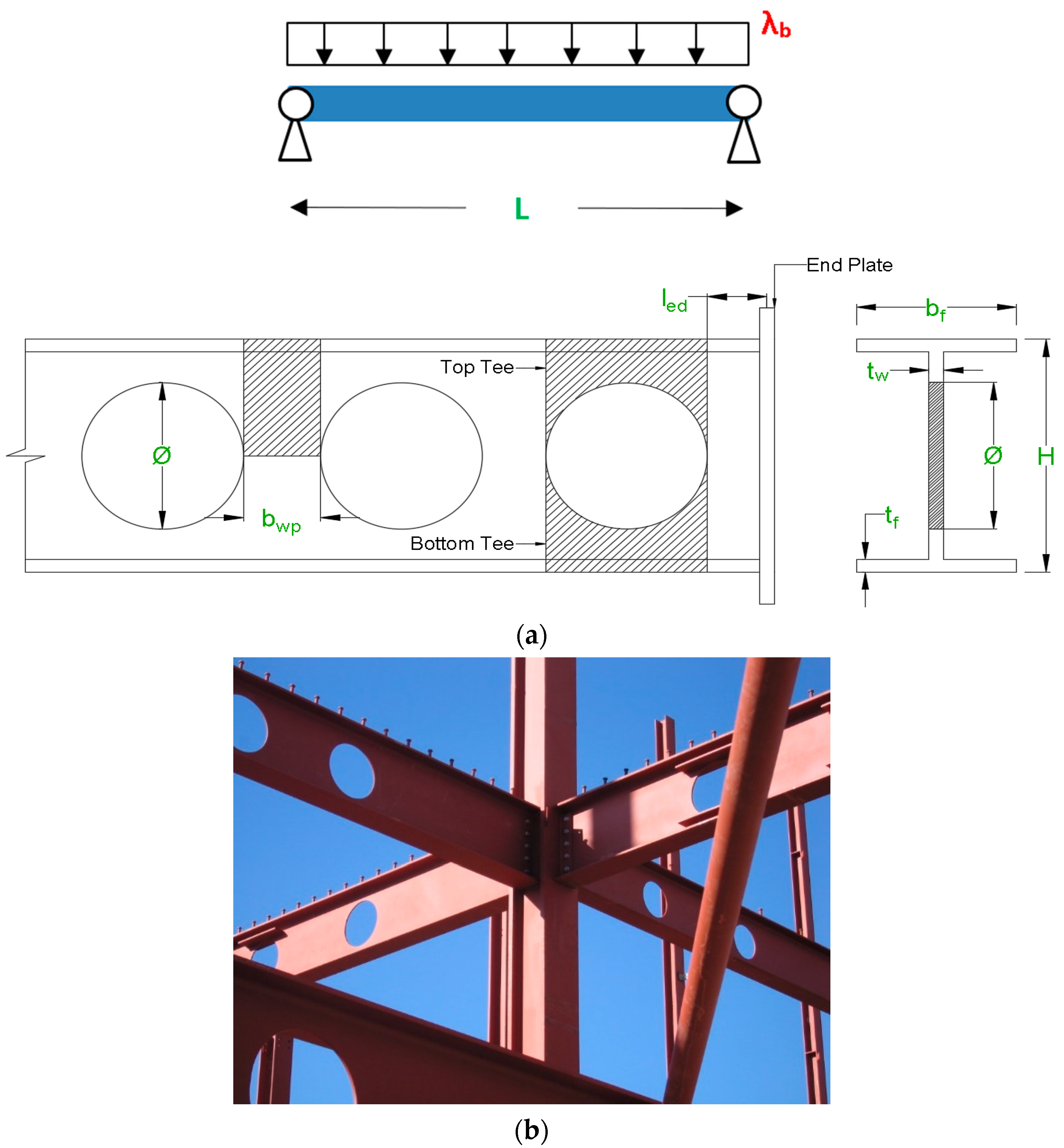
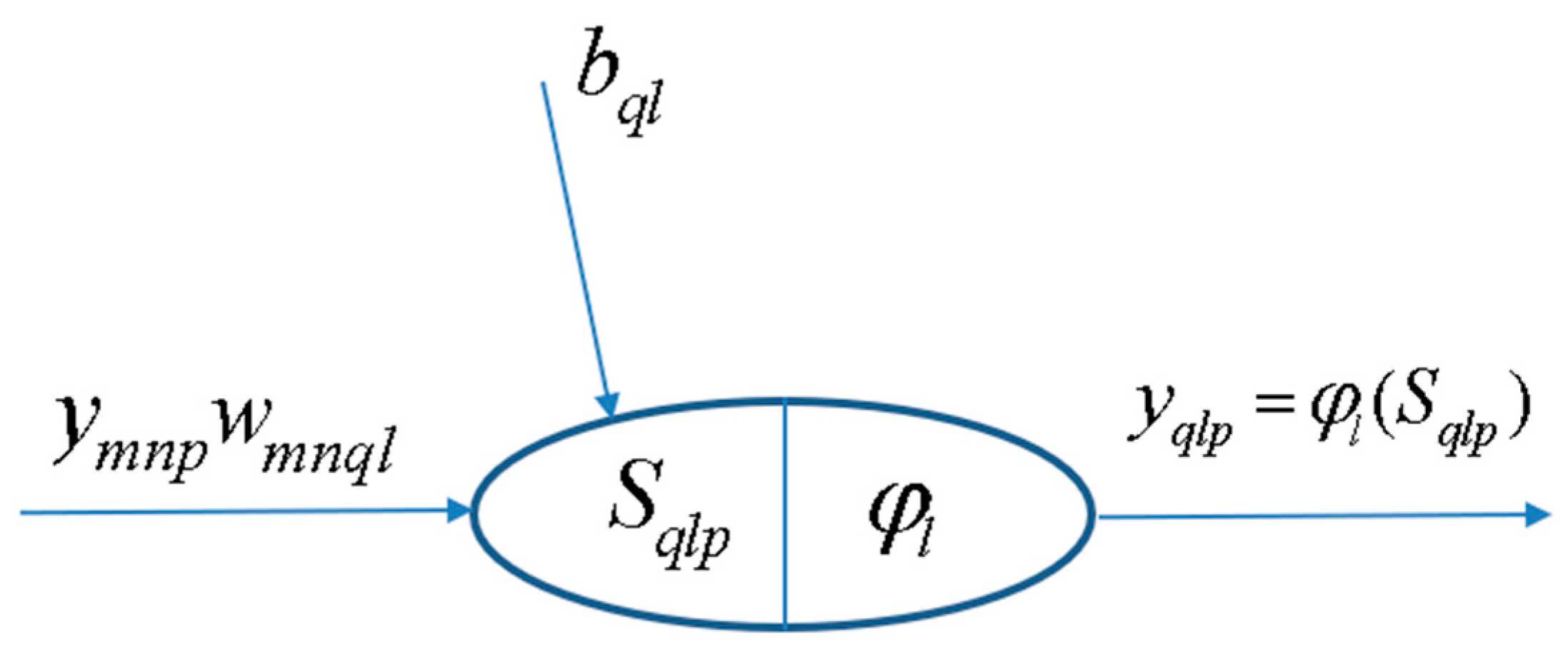
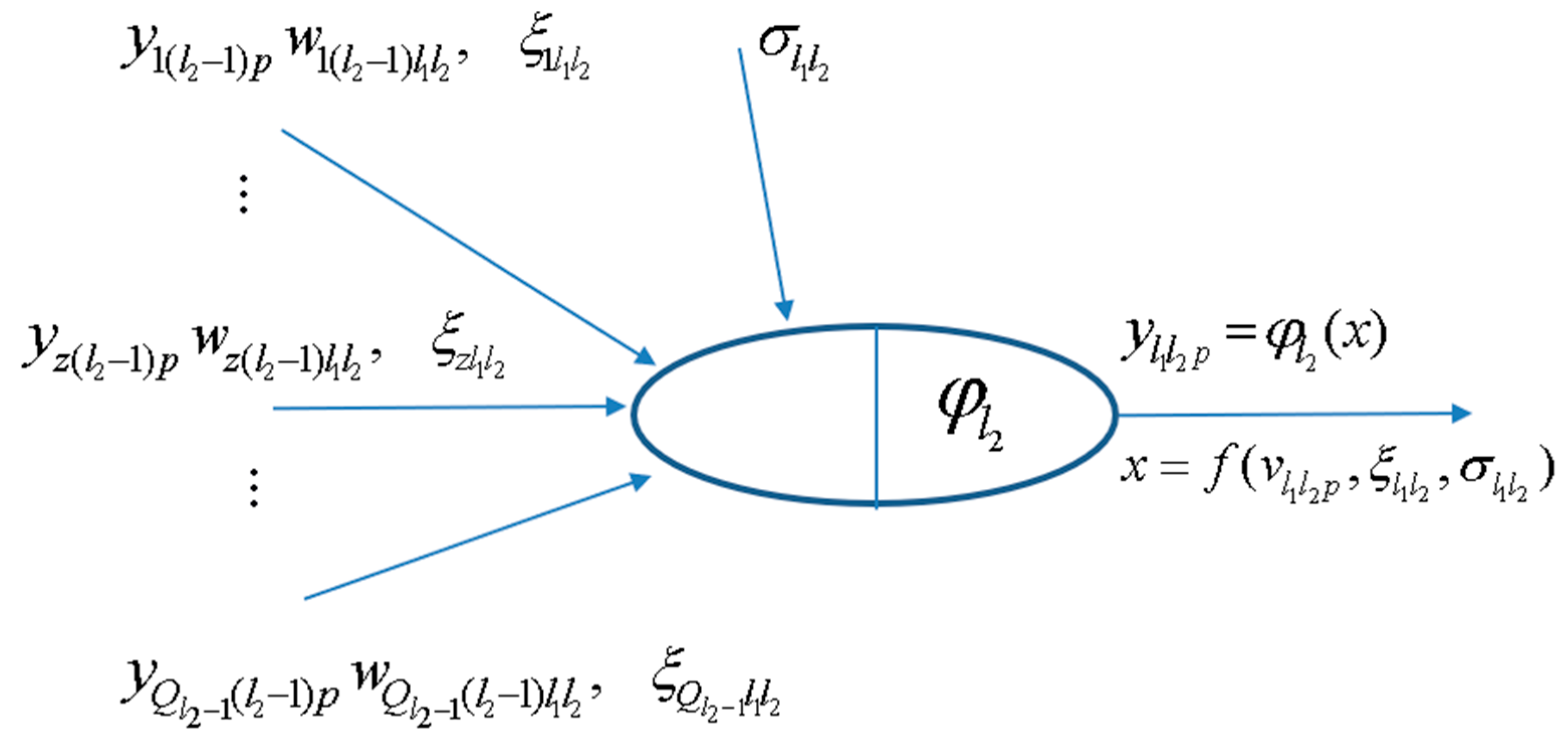
| Inputs Variables—Figure 1a | ANN Node No. | Possible Values | |||||
|---|---|---|---|---|---|---|---|
| Beam’s length | L (m) | 1 | 4 | 5 | 6 | 7 | 8 |
| Opening-support end distance | led (mm) | 2 | 135 values in [12, 718] | ||||
| Opening diameter | Φ (mm) | 3 | H/1.25 | H/1.5 | H/1.7 | - | - |
| Web-post width | bwp (mm) | 4 | Φ/10 | Φ/3.45 | Φ/2.04 | - | - |
| Section height | H (mm) | 5 | 700 | 560 | 420 | - | - |
| Web thickness | tw (mm) | 6 | 15 | 12 | 9 | - | - |
| Flange width | bf (mm) | 7 | 270 | 216 | 162 | - | - |
| Flange thickness | tf (mm) | 8 | 25 | 20 | 15 | - | - |
| Target/Output Variable | |||||||
| Elastic Buckling Load | λb (kN/m) | ||||||
| FEATURE METHOD | F1 | F2 | F3 | F4 | F5 |
|---|---|---|---|---|---|
| Qualitative Var Representation | Dimensional Analysis | Input Dimensionality Reduction | % Train-Valid-Test | Input Normalization | |
| 1 | Boolean vectors | Yes | Linear correlation | 80-10-10 | Linear max abs |
| 2 | Eq spaced in [0, 1] | No | Auto-encoder | 70-15-15 | Linear [0, 1] |
| 3 | - | - | - | 60-20-20 | Linear [−1, 1] |
| 4 | - | - | Ortho rand proj. | 50-25-25 | Nonlinear |
| 5 | - | - | Sparse rand proj. | - | Lin mean std |
| 6 | - | - | No | - | No |
| FEATURE METHOD | F6 | F7 | F8 | F9 | F10 |
|---|---|---|---|---|---|
| Output Transfer | Output Normalization | Net Architecture | Hidden Layers | Connectivity | |
| 1 | Logistic | Lin [a, b] = 0.7 [φmin, φmax] | MLPN | 1 HL | Adjacent layers |
| 2 | - | Lin [a, b] = 0.6 [φmin, φmax] | RBFN | 2 HL | Adj layers + in-out |
| 3 | Hyperbolic tang | Lin [a, b] = 0.5 [φmin, φmax] | - | 3 HL | Fully-connected |
| 4 | - | Linear mean std | - | - | - |
| 5 | Bilinear | No | - | - | - |
| 6 | Compet | - | - | - | - |
| 7 | Identity | - | - | - | - |
| FEATURE METHOD | F11 | F12 | F13 | F14 | F15 |
|---|---|---|---|---|---|
| Hidden Transfer | Parameter Initialization | Learning Algorithm | Performance Improvement | Training Mode | |
| 1 | Logistic | Midpoint (W) + Rands (b) | BP | NNC | Batch |
| 2 | Identity-logistic | Rands | BPA | - | Mini-Batch |
| 3 | Hyperbolic tang | Randnc (W) + Rands (b) | LM | - | Online |
| 4 | Bipolar | Randnr (W) + Rands (b) | ELM | - | - |
| 5 | Bilinear | Randsmall | mb ELM | - | - |
| 6 | Positive sat linear | Rand [−Δ, Δ] | I-ELM | - | - |
| 7 | Sinusoid | SVD | CI-ELM | - | - |
| 8 | Thin-plate spline | MB SVD | - | - | - |
| 9 | Gaussian | - | - | - | - |
| 10 | Multiquadratic | - | - | - | - |
| 11 | Radbas | - | - | - | - |
| SA | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 6 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 3 | 2 | 3 | 1 | 3 |
| 2 | 1 | 2 | 6 | 2 | 1 | 7 | 1 | 1 | 1 | 1 | 3 | 2 | 5 | 1 | 3 |
| 3 | 1 | 2 | 6 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 3 | 2 | 3 | 1 | 3 |
| 4 | 1 | 2 | 6 | 2 | 1 | 1 | 2 | 1 | 1 | 1 | 3 | 2 | 3 | 1 | 3 |
| 5 | 1 | 2 | 6 | 3 | 1 | 1 | 3 | 1 | 1 | 1 | 3 | 2 | 3 | 1 | 3 |
| 6 | 1 | 2 | 6 | 2 | 1 | 7 | 4 | 1 | 1 | 1 | 3 | 2 | 3 | 1 | 3 |
| 7 | 1 | 2 | 6 | 3 | 1 | 7 | 5 | 1 | 1 | 1 | 3 | 2 | 3 | 1 | 3 |
| 8 | 1 | 2 | 6 | 3 | 1 | 7 | 5 | 1 | 1 | 1 | 1 | 5 | 3 | 1 | 3 |
| 9 | 1 | 2 | 6 | 3 | 1 | 7 | 5 | 1 | 3 | 3 | 1 | 5 | 3 | 1 | 3 |
| SA | ANN | ||||
| Max Error (%) | Performance All Data (%) | Errors > 3% (%) | Total Hidden Nodes | Running Time/Data Point (s) | |
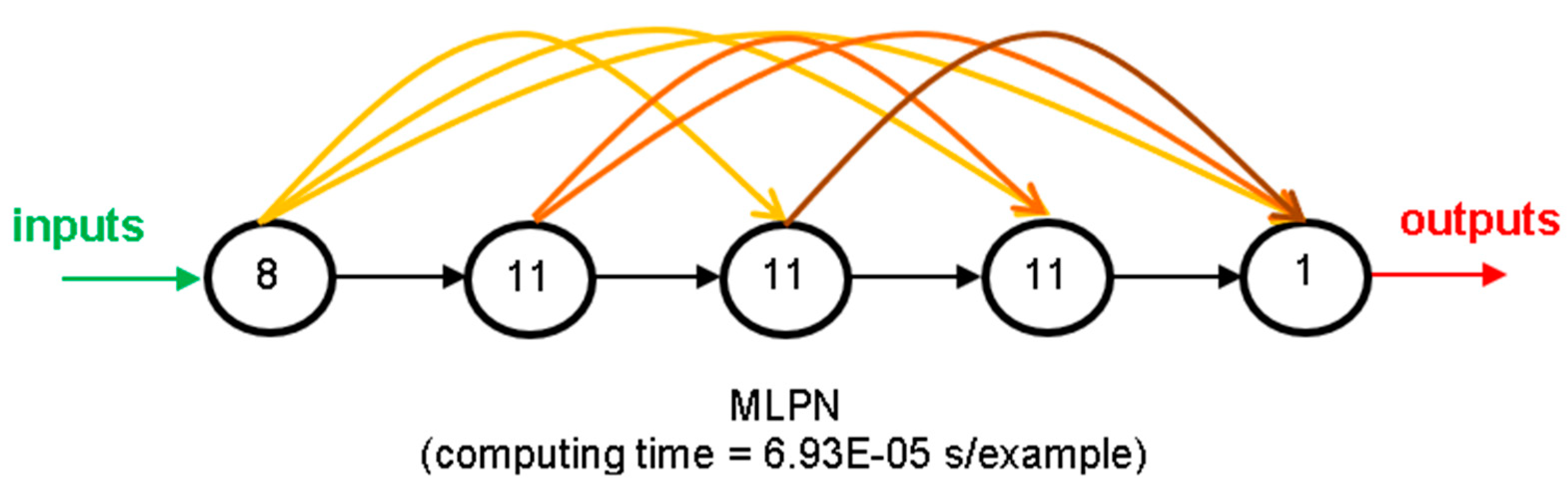
| 1 | 7.5 | 0.7 | 1.8 | 32 | 7.33 × 10−5 |
| 2 | 201.0 | 5.7 | 54.9 | 365 | 7.06 × 10−5 |
| 3 | 8.2 | 0.7 | 1.2 | 32 | 8.49 × 10−5 |
| 4 | 8.5 | 0.7 | 1.3 | 32 | 7.67 × 10−5 |
| 5 | 6.8 | 0.7 | 1.8 | 32 | 6.86 × 10−5 |
| 6 | 7.2 | 0.7 | 1.6 | 32 | 7.57 × 10−5 |
| 7 | 28.9 | 1.5 | 13.2 | 29 | 6.82 × 10−5 |
| 8 | 8.2 | 0.9 | 3.4 | 29 | 6.70 × 10−5 |
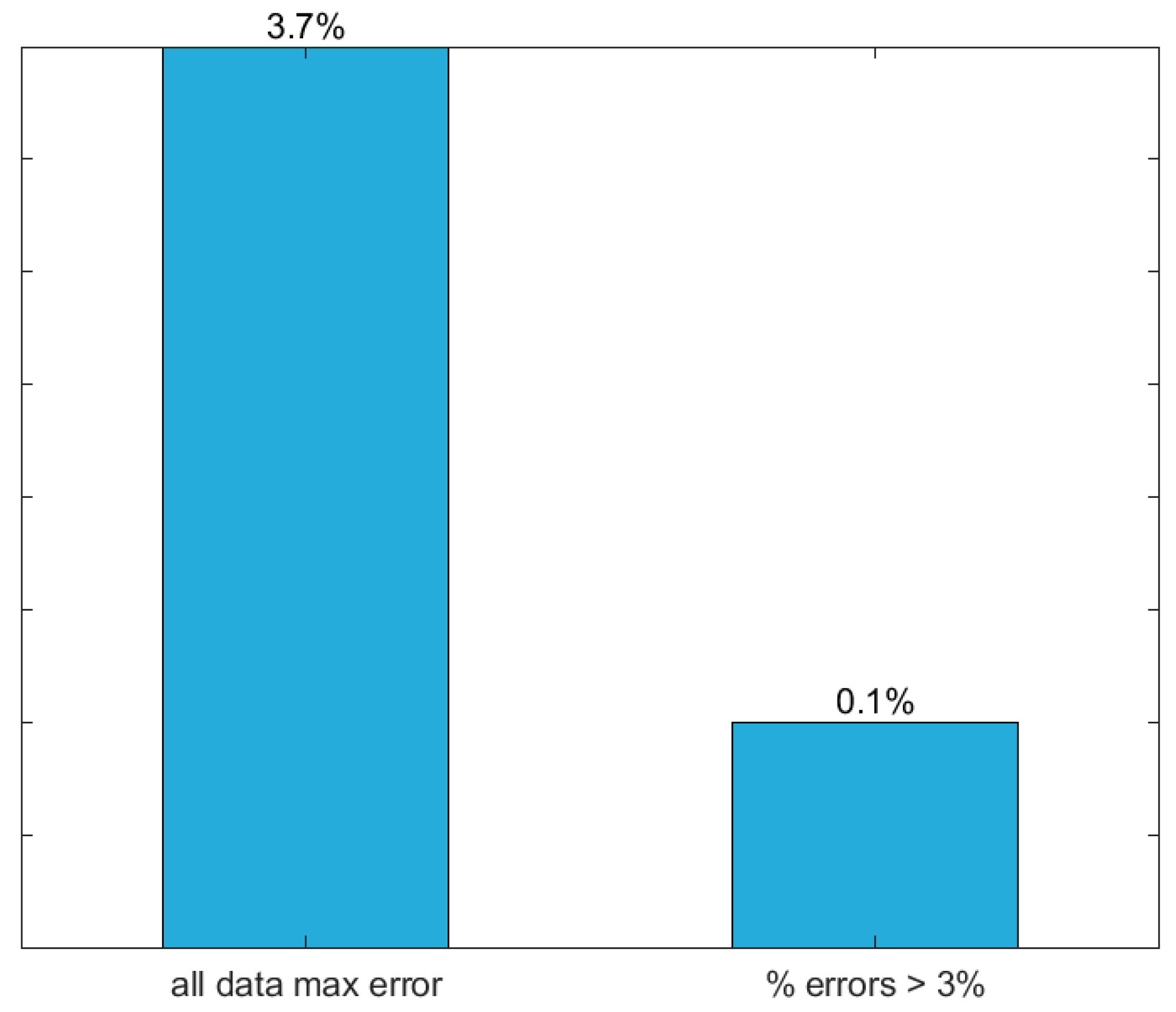
| 9 | 3.7 | 0.4 | 0.1 | 33 | 6.93 × 10−5 |
| SA | NNC | ||||
| Max Error (%) | Performance All Data (%) | Errors > 3% (%) | Total Hidden Nodes | Running Time/Data Point (s) | |
| 1 | - | - | - | - | - |
| 2 | 180.0 | 5.2 | 51.4 | 365 | 8.16 × 10−5 |
| 3 | - | - | - | - | - |
| 4 | 8.6 | 0.6 | 0.9 | 32 | 7.83 × 10−5 |
| 5 | - | - | - | - | - |
| 6 | 2.6 | 0.3 | 0.0 | 32 | 8.34 × 10−5 |
| 7 | 9.5 | 0.9 | 3.9 | 29 | 6.93 × 10−5 |
| 8 | 7.0 | 0.7 | 1.9 | 29 | 6.80 × 10−5 |
| 9 | - | - | - | - | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abambres, M.; Rajana, K.; Tsavdaridis, K.D.; Ribeiro, T.P. Neural Network-Based Formula for the Buckling Load Prediction of I-Section Cellular Steel Beams. Computers 2019, 8, 2. https://doi.org/10.3390/computers8010002
Abambres M, Rajana K, Tsavdaridis KD, Ribeiro TP. Neural Network-Based Formula for the Buckling Load Prediction of I-Section Cellular Steel Beams. Computers. 2019; 8(1):2. https://doi.org/10.3390/computers8010002
Chicago/Turabian StyleAbambres, Miguel, Komal Rajana, Konstantinos Daniel Tsavdaridis, and Tiago Pinto Ribeiro. 2019. "Neural Network-Based Formula for the Buckling Load Prediction of I-Section Cellular Steel Beams" Computers 8, no. 1: 2. https://doi.org/10.3390/computers8010002
APA StyleAbambres, M., Rajana, K., Tsavdaridis, K. D., & Ribeiro, T. P. (2019). Neural Network-Based Formula for the Buckling Load Prediction of I-Section Cellular Steel Beams. Computers, 8(1), 2. https://doi.org/10.3390/computers8010002







