Automatic Correction of Arabic Dyslexic Text
Abstract
:1. Introduction
2. Related Work
2.1. Arabic Spelling Correction
2.2. Dyslexia Spelling Correction
2.3. Commercial Tools
2.4. Differences from Previous Studies
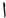 ’ [43]. Secondly, the system used in this study is based on various approaches, combining a statistical approach by using the PPM language model and edit operations to generate possible alternatives for each error (a candidates’ list). The correct alternative for each misspelled word is then selected automatically using the compression codelength of the sentence. The codelength is the number of bits required to encode the text using the compression algorithm.
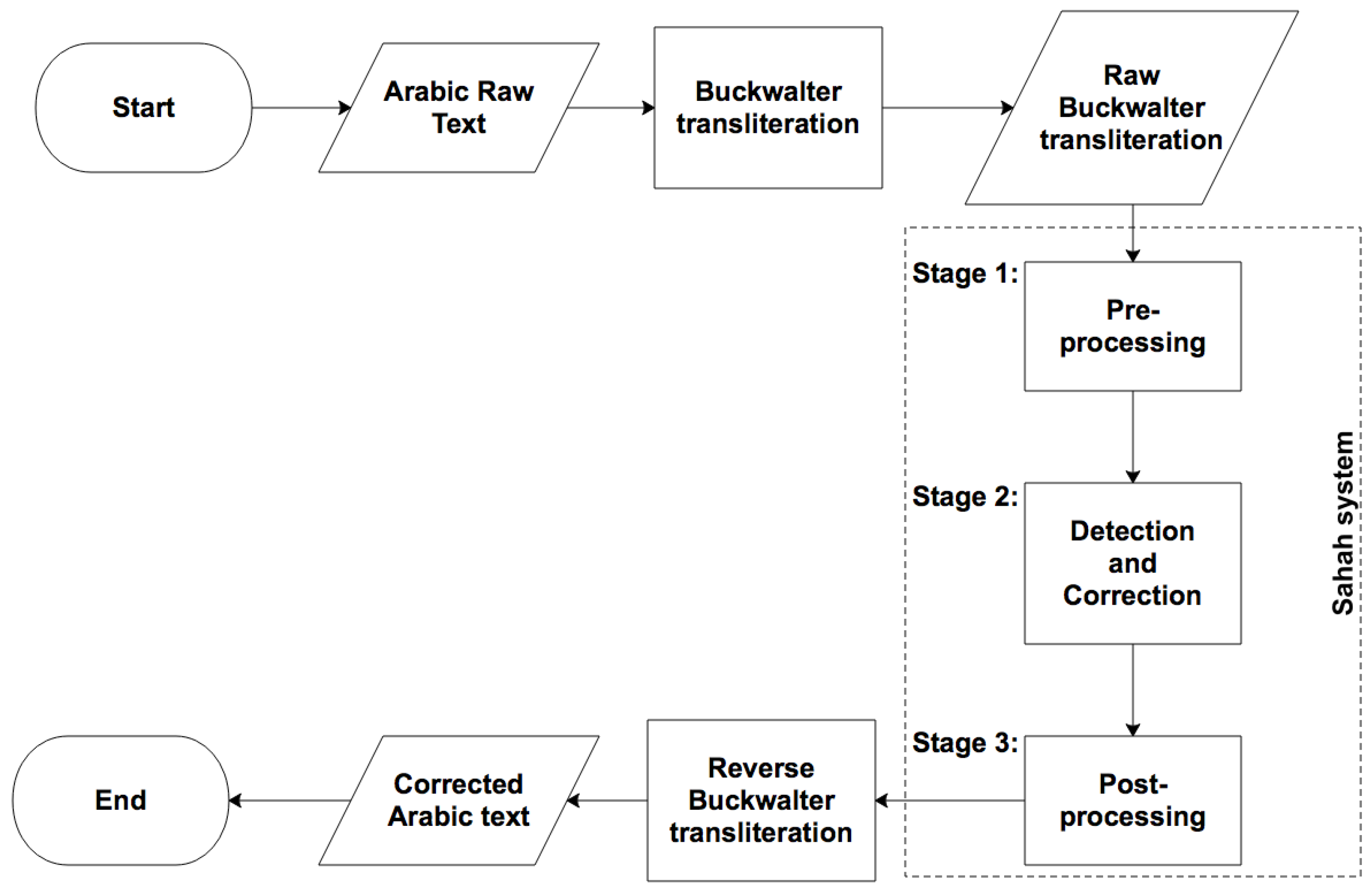
’ [43]. Secondly, the system used in this study is based on various approaches, combining a statistical approach by using the PPM language model and edit operations to generate possible alternatives for each error (a candidates’ list). The correct alternative for each misspelled word is then selected automatically using the compression codelength of the sentence. The codelength is the number of bits required to encode the text using the compression algorithm.3. The Sahah System for the Automatic Spelling Correction of Dyslexic Arabic Text
3.1. Pre-Processing Stage
| Arabic | اا | آآ | إإ | ءء | ئئ | ىى | ةة |
| Buckwalter | AA | || | << | ’’ | }} | YY | pp |
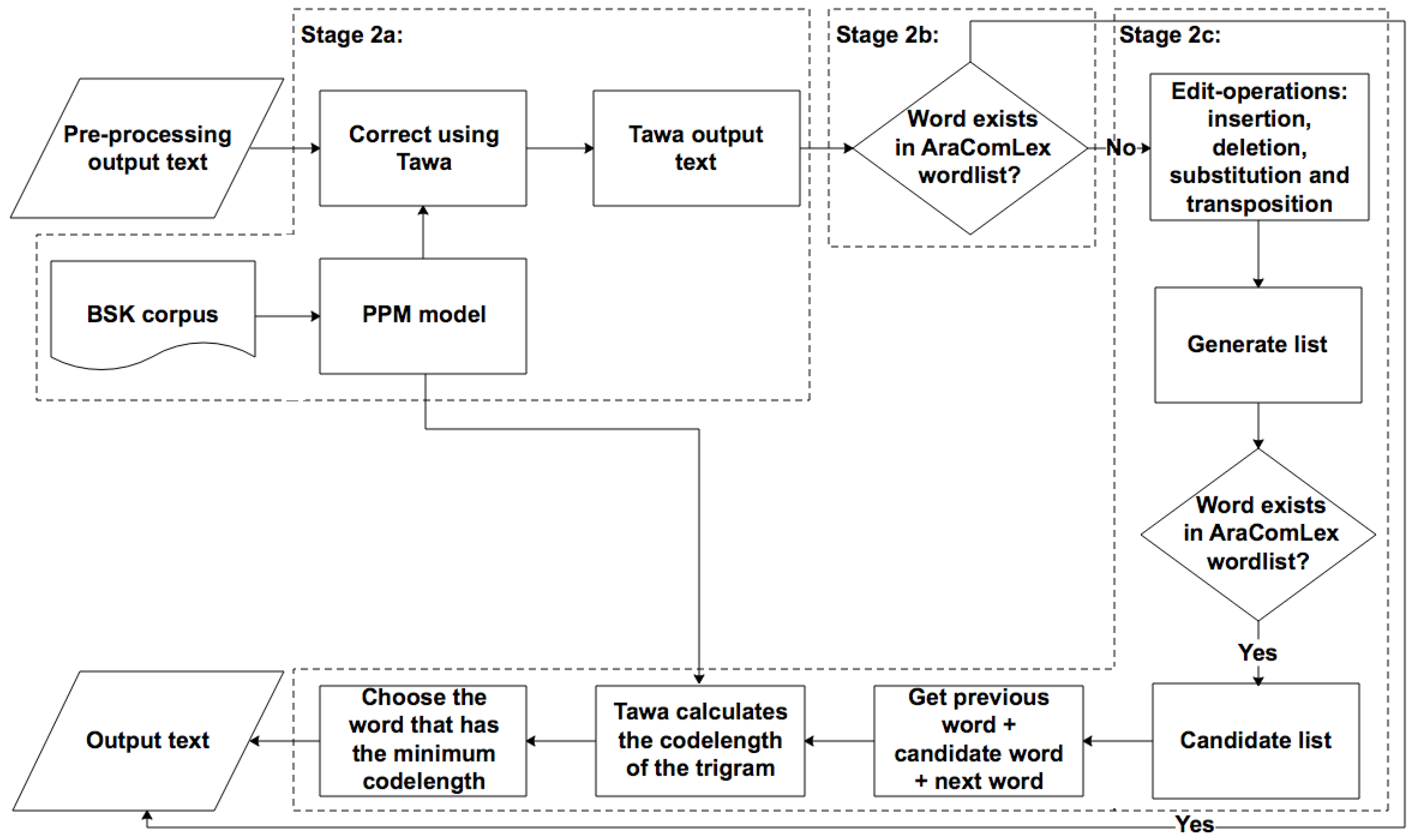
3.2. Error Detection and Correction Stage
3.2.1. Sub-Stage 2a: Statistical Stage
3.2.2. Sub-Stage 2b: Error Detection
3.2.3. Sub-Stage 2c: Edit Operation
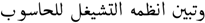 ” [B: “wtbyn AnZmh Alt$ygl llHAswb”], following Sub-stage 2a, which corrected the second word “وتبين أنظمة التشيغل للحاسوب” [B: “wtbyn >nZmp Alt$ygl llHAswb”], there was still an error in the third word “التشيغل” [B: “Alt$ygl|”], which was transposed under the common category. Table 7 shows the candidate list for the error word “التشيغل” [B: “Alt$ygl”]:
” [B: “wtbyn AnZmh Alt$ygl llHAswb”], following Sub-stage 2a, which corrected the second word “وتبين أنظمة التشيغل للحاسوب” [B: “wtbyn >nZmp Alt$ygl llHAswb”], there was still an error in the third word “التشيغل” [B: “Alt$ygl|”], which was transposed under the common category. Table 7 shows the candidate list for the error word “التشيغل” [B: “Alt$ygl”]:3.3. Post-Processing Stage
3.4. Evaluation
3.4.1. Evaluation Methodology
- Corrected case: The error is detected and replaced with the intended word (Case I).
- Incorrect alternative case: The error is detected and replaced with an incorrect alternative (Case II).
- Missed case: The error is not detected, and therefore, the system does not correct it (Case III).
- Skipped case: The word that is spelt correctly is accepted (Case IV).
- False alarm case: A word that is spelt correctly is changed (Case V).
- Case I: thei→they.
- Case II: leving→leaving.
- Case III: onle→onle.
- Case IV: were→were.
- Case V: land→island.
- True Positive (): This implies that a spelling error has successfully been detected.
- False Negative (): This implies that a spelling error has not been detected.
- False Positive (): This implies that a correctly-spelled word was detected as being a misspelled word.
- True Negative (): This implies that a correctly-spelled word was detected as being a correct word.
- True Positive (): This implies that a spelling error was successfully corrected.
- False Negative (): This implies that a spelling error was not corrected.
- False Positive (): This implies that a correctly-spelled word was changed.
- True Negative (): This implies that a correctly-spelled word was not changed.
3.4.2. Experimental Results
- Type I: The Sahah system in some cases could not detect an error if the word used matched with a word in the dictionary. Furthermore, it could not detect errors falling under the word boundary error category, for example the use of “لي عقولهم” [B: “ly Eqwlhm”] instead of “لعقولهم” [E: “To their minds” B: “lyEqwlhm”] where both words are valid. One solution is to check by pair instead of tokens. However, it is worth noting that none of the widely-used word processing software, Microsoft Office 2013 and Ayaspell 3.0 used in OpenOffice or the Farasa tool referred to above can detect this type of error.
- Type II: If more than one letter in the word is deleted or added, it makes the word hard to correct. In such cases, the Sahah system inserted an alternative word. For example, instead of the erroneous word “التر” [B: “Altr”], which is missing three letters, the Sahah system substituted “البر” [B: “Albr”] when the intended word was “التربية” [B: “Altrbyp”]. When the erroneous word contained more than three types of errors, the Sahah system could easily detect the error, but could not correct it, for example “اليلاملاي” [B: “AlylAmlAy”], which was used instead of “الإملائية” [B: “Al<mlA}yp”], which contained five errors that were detected by the Sahah system, which then exchanged it with the incorrect alternative “الئلام لأي” [B: “Al}lAm l>y”].
- Type II: An incorrect alternative occurred when the wrong candidates were chosen on the basis of the codelength of the trigram according to the statistical language model. For example, for “الصوص” [E: “The thieves” B: “AlSwS”], the candidates’ list included “اللصوص” [E: “The thieves” B: “AllSwS”] (94.727 bits) and “الصوت” [E: “The voice” B: “AlSwt”] (89.462 bits). The candidate list contained the intended word, but the smallest codelength was for [B: “AlSwt”], which is an incorrect alternative in this case.
- Type II: Addition words, deletion words or incorrect synonyms written for a word during dictation time such as “البيت” [E: “Home” B: “Albyet”] instead of “المنزل” [E: “House” B: “Almnzel”] fall outside the scope of this study as they are not contains errors and very rare in the BDAC corpus.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- International Dyslexia Association. Definition of Dyslexia; International Dyslexia Association: Baltimore, MD, USA, 2002. [Google Scholar]
- Nasen. Supporting Pupils with Specific Learning Difficulties (Dyslexia) in Secondary Schools; PDF file; Nasen: Tamworth, UK, 2015. [Google Scholar]
- Kuwait Dyslexia Association. A Survey Study of Dyslexia in Kuwait; Kuwait Dyslexia Association: Kuwait City, Kuwait, 2002. [Google Scholar]
- Elbeheri, G.; Everatt, J.; Al Malki, M. The incidence of dyslexia among young offenders in Kuwait. Dyslexia 2009, 15, 86–104. [Google Scholar] [CrossRef] [PubMed]
- Aboudan, R.; Eapen, V.; Bayshak, M.; Al-Mansouri, M.; Al-Shamsi, M. Dyslexia in the United Arab Emirates university—A study of prevalence in English and Arabic. Int. J. Engl. Linguist. 2011, 1, 64. [Google Scholar] [CrossRef]
- Goodwin, V.; Thomson, B. Dyslexia Toolkit: A Resource for Students and Their Tutors; The Open University Press: Milton Keynes, UK, 2007. [Google Scholar]
- Washburn, E.K.; Binks-Cantrell, E.S.; Joshi, R.M. What do preservice teachers from the USA and the UK know about dyslexia? Dyslexia 2014, 20, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Al Rowais, F.; Wald, M.; Wills, G. An Arabic framework for dyslexia training tools. In Proceedings of the 1st International Conference on Technology for Helping People with Special Needs (ICTHP-2013), Riyadh, Saudi Arabia, 18–19 February 2013; pp. 63–68. [Google Scholar]
- Abu-Rabia, S.; Taha, H. Reading and spelling error analysis of native Arabic dyslexic readers. Read. Writ. 2004, 17, 651–690. [Google Scholar] [CrossRef]
- Burhan, H.; Al-Salahat, M.M.; Al-Shradgeh, M.T.; Alali, W.A. Degree of Common Misspellings of Students with Learning Disabilities. Int. Interdiscip. J. Educ. 2014, 3, 1–11. [Google Scholar]
- Alamri, M.M.; Teahan, W.J. A New Error Annotation for Dyslexic texts in Arabic. In Proceedings of the Third Arabic Natural Language Processing Workshop, Valencia, Spain, 3–4 April 2017; pp. 72–78. [Google Scholar]
- Ali, M. Learning Difficulties Between Skills and Disorders, 1st ed.; DaR SaFa: Amman, Jordan, 2011. [Google Scholar]
- Rello, L.; Ballesteros, M.; Bigham, J.P. A spellchecker for dyslexia. In Proceedings of the 17th International ACM SIGACCESS Conference on Computers & Accessibility, Lisbon, Portugal, 26–28 October 2015; pp. 39–47. [Google Scholar]
- Graham, S.; Harris, K.R.; Larsen, L. Prevention and intervention of writing difficulties for students with learning disabilities. Learn. Disabil. Res. Pract. 2001, 16, 74–84. [Google Scholar] [CrossRef]
- Hiscox, L.; Leonavičiūtė, E.; Humby, T. The effects of automatic spelling correction software on understanding and comprehension in compensated dyslexia: Improved recall following dictation. Dyslexia 2014, 20, 208–224. [Google Scholar] [CrossRef] [PubMed]
- Liensberger, C. Context Sensitive Auto-Correction. U.S. Patent 20140067371A1, 22 December 2015. [Google Scholar]
- Douglas, S. The Intelligent Spell Checker. Blog, 17 December 2015. [Google Scholar]
- Berninger, V.W.; Nielsen, K.H.; Abbott, R.D.; Wijsman, E.; Raskind, W. Writing problems in developmental dyslexia: Under-recognized and under-treated. J. Sch. Psychol. 2008, 46, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Berninger, V.W.; Wolf, B.J. Dyslexia, Dysgraphia, OWL LD, and Dyscalculia; Brookes Publishing: Baltimore, MD, USA, 2016; p. 227. [Google Scholar]
- MacArthur, C.A.; Graham, S.; Haynes, J.B.; DeLaPaz, S. Spelling checkers and students with learning disabilities: Performance comparisons and impact on spelling. J. Spec. Educ. 1996, 30, 35–57. [Google Scholar] [CrossRef]
- Montgomery, D.J.; Karlan, G.R.; Coutinho, M. The effectiveness of word processor spellchecker programs to produce target words for misspellings generated by students with learning disabilities. J. Spec. Educ. Technol. 2001, 16, 27–42. [Google Scholar] [CrossRef]
- Leahy, M. Spelling, Spelling-Checkers and Dyslexia. In Proceedings of the CESI Conference, St. Patrick’s College, Dublin, Ireland, January 2002. [Google Scholar]
- Damerau, F.J. A technique for computer detection and correction of spelling errors. Commun. ACM 1964, 7, 171–176. [Google Scholar] [CrossRef]
- Kernighan, M.D.; Church, K.W.; Gale, W.A. A spelling correction program based on a noisy channel model. In Proceedings of the 13th Conference on Computational Linguistics, Helsinki, Finland, 20–25 August 1990; Volume 2, pp. 205–210. [Google Scholar]
- Church, K.W.; Gale, W.A. Probability scoring for spelling correction. Stat. Comput. 1991, 1, 93–103. [Google Scholar] [CrossRef]
- Kukich, K. Techniques for automatically correcting words in text. ACM Comput. Surv. (CSUR) 1992, 24, 377–439. [Google Scholar] [CrossRef]
- Brill, E.; Moore, R.C. An improved error model for noisy channel spelling correction. In Proceedings of the 38th Annual Meeting on Association for Computational Linguistics, Hong Kong, China, 3–6 October 2000; pp. 286–293. [Google Scholar]
- Peterson, J.L. Computer programs for detecting and correcting spelling errors. Commun. ACM 1980, 23, 676–687. [Google Scholar] [CrossRef]
- Attia, M.; Pecina, P.; Samih, Y.; Shaalan, K.; Genabith, J. Improved spelling error detection and correction for Arabic. In Proceedings of the COLING 2012 Posters, Bombay, India, 8–15 December 2012; pp. 103–112. [Google Scholar]
- Shaalan, K.F.; Magdy, M.; Fahmy, A. Analysis and feedback of erroneous Arabic verbs. Nat. Lang. Eng. 2013, 21, 271–323. [Google Scholar] [CrossRef]
- Mars, M. Toward a Robust Spell Checker for Arabic Text. In Proceedings of the International Conference on Computational Science and Its Applications, Beijing, China, 4–7 July 2016; pp. 312–322. [Google Scholar]
- AlShenaifi, N.; AlNefie, R.; Al-Yahya, M.; Al-Khalifa, H. Arib QALB-2015 Shared Task: A Hybrid Cascade Model for Arabic Spelling Error Detection and Correction. In Proceedings of the Second Workshop on Arabic Natural Language Processing, Beijing, China, 30 July 2015; pp. 127–132. [Google Scholar]
- Zerrouki, T.; Alhawiti, K.; Balla, A. Autocorrection of Arabic common errors for large text corpus. In Proceedings of the EMNLP Workshop on Arabic Natural Language Processing (ANLP), Doha, Qatar, 25 October 2014; pp. 127–131. [Google Scholar]
- Mubarak, H.; Darwish, K. Automatic correction of Arabic text: A cascaded approach. In Proceedings of the EMNLP 2014 Workshop on Arabic Natural Language Processing (ANLP), Doha, Qatar, 25 October 2014; pp. 132–136. [Google Scholar]
- Alkanhal, M.I.; Al-Badrashiny, M.A.; Alghamdi, M.M.; Al-Qabbany, A.O. Automatic stochastic Arabic spelling correction with emphasis on space insertions and deletions. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 2111–2122. [Google Scholar] [CrossRef]
- Zaghouani, W.; Zerrouki, T.; Balla, A. SAHSOH QALB-2015 Shared Task: A Rule-Based Correction Method of Common Arabic Native and Non-Native Speakers Errors. In Proceedings of the Second Workshop on Arabic Natural Language Processing, Beijing, China, 30 July 2015; pp. 155–160. [Google Scholar]
- Nawar, M.; Ragheb, M. Fast and robust Arabic error correction system. In Proceedings of the EMNLP 2014 Workshop on Arabic Natural Language Processing (ANLP), Doha, Qatar, 25 October 2014; pp. 143–147. [Google Scholar]
- Nawar, M.; Ragheb, M. CUFE QALB-2015 Shared Task: Arabic Error Correction System. In Proceedings of the Second Workshop on Arabic Natural Language Processing, Beijing, China, 30 July 2015; pp. 133–137. [Google Scholar]
- Mubarak, H.; Darwish, K.; Abdelali, A. QCRI QALB-2015 Shared Task: Correction of Arabic Text for Native and Non-Native Speakers’ Errors. In Proceedings of the Second Workshop on Arabic Natural Language Processing, Beijing, China, 30 July 2015; pp. 150–154. [Google Scholar]
- Shaalan, K.F.; Attia, M.; Pecina, P.; Samih, Y.; van Genabith, J. Arabic Word Generation and Modelling for Spell Checking. In Proceedings of the LREC, Istanbul, Turkey, 21–27 May 2012; pp. 719–725. [Google Scholar]
- Noaman, H.M.; Sarhan, S.S.; Rashwan, M. Automatic Arabic spelling errors detection and correction based on confusion matrix-noisy channel hybrid system. Egypt. Comput. Sci. J. 2016, 40, 54–64. [Google Scholar]
- Pedler, J. Computer Correction of Real-Word Spelling Errors in Dyslexic Text. Ph.D. Thesis, Birkbeck College, University of London, London, UK, 2007. [Google Scholar]
- Alamri, M.M.; Teahan, W.J. Towards a New Arabic Corpus of Dyslexic Texts. In Proceedings of the 2nd Workshop on Arabic Corpora and Processing Tools Theme: Social Media, Portorož, Slovenia, 27 May 2016; pp. 11–15. [Google Scholar]
- Teahan, W.J. A Compression-Based Toolkit for Modelling and Processing Natural Language Text. Information 2018, 9, 294. [Google Scholar] [CrossRef]
- Al-Wabil, A.; Meldah, E.; Al-Suwaidan, A.; AlZahrani, A. Designing Educational Games for Children with Specific Learning Difficulties: Insights from Involving Children and Practitioners. In Proceedings of the Fifth International Multi-Conference on Computing in the Global Information Technology (ICCGI), Valencia, Spain, 20–25 September 2010; pp. 195–198. [Google Scholar]
- Al-Edaily, A.; Al-Wabil, A.; Al-Ohali, Y. Dyslexia Explorer: A Screening System for Learning Difficulties in the Arabic Language Using Eye Tracking. In Human Factors in Computing and Informatics; Springer: Berlin/Heidelberg, Germany, 2013; pp. 831–834. [Google Scholar]
- El Kah, A.; Lakhouaja, A. Developing effective educative games for Arabic children primarily dyslexics. In Education and Information Technologies; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–20. [Google Scholar]
- Coleman, C.; Gregg, N.; McLain, L.; Bellair, L.W. A comparison of spelling performance across young adults with and without dyslexia. Assess. Effect. Interv. 2008. [Google Scholar] [CrossRef]
- Fischer, F.W.; Shankweiler, D.; Liberman, I.Y. Spelling proficiency and sensitivity to word structure. J. Mem. Lang. 1985, 24, 423–441. [Google Scholar] [CrossRef]
- Moats, L.C. Spelling error interpretation: Beyond the phonetic/dysphonetic dichotomy. Ann. Dyslexia 1993, 43, 174–185. [Google Scholar] [CrossRef] [PubMed]
- Larkey, L.S.; Ballesteros, L.; Connell, M.E. Improving stemming for Arabic information retrieval: Light stemming and co-occurrence analysis. In Proceedings of the 25th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Tampere, Finland, 11–15 August 2002; pp. 275–282. [Google Scholar]
- Hassan, Y.; Aly, M.; Atiya, A. Arabic spelling correction using supervised learning. arXiv, 2014; arXiv:1409.8309. [Google Scholar]
- Cleary, J.; Witten, I. Data compression using adaptive coding and partial string matching. IEEE Trans. Commun. 1984, 32, 396–402. [Google Scholar] [CrossRef]
- Teahan, W.J. Text classification and segmentation using minimum cross-entropy. Content-Based Multimed. Inf. Access 2000, 2, 943–961. [Google Scholar]
- Teahan, W.J.; Inglis, S.; Cleary, J.G.; Holmes, G. Correcting English text using PPM models. In Proceedings of the IEEE Data Compression Conference, Snowbird, UT, USA, 30 March–1 April 1998; pp. 289–298. [Google Scholar]
- Teahan, W.J. Modelling English Text. Ph.D. Thesis, University of Waikato, Hillcrest, New Zealand, 1998. [Google Scholar]
- Alhawiti, K.M. Adaptive Models of Arabic Text. Ph.D. Thesis, The School of Computer Science, Bangor University, Bangor, UK, 2014. [Google Scholar]
- Alkahtani, S. Building and Verifying Parallel Corpora Between Arabic and English. Ph.D. Thesis, The School of Computer Science, Bangor University, Bangor, UK, 2015. [Google Scholar]
- Alrabiah, M.; Al-Salman, A.; Atwell, E. The design and construction of the 50 million words KSUCCA. In Proceedings of the WACL2 Second Workshop on Arabic Corpus Linguistics, Lancaster, UK, 22–26 July 2013; pp. 5–8. [Google Scholar]
- Al-kazaz, N.R.; Irvine, S.A.; Teahan, W.J. An automatic cryptanalysis of simple substitution ciphers using compression. Inf. Secur. J. Glob. Perspect. 2018, 27, 57–75. [Google Scholar] [CrossRef]
- Viterbi, A. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Trans. Inf. Theory 1967, 13, 260–269. [Google Scholar] [CrossRef]
- Norvig, P. Natural language corpus data. In Beautiful Data; O’Reilly Media: Sebastopol, CA, USA, 2009; pp. 234–239. [Google Scholar]
| Arabic | Buckwalter | Arabic | Buckwalter | ||
|---|---|---|---|---|---|
| Prefixes | لل | ll | Suffixes | تما | tmA |
| ف | f | ها | hA | ||
| ك | k | وا | wA | ||
| ل | l | نا | nA | ||
| ا | A | تا | tA | ||
| كا | kA | تي | ty | ||
| ال | Al | ن | n | ||
| با | bA | ه | h | ||
| إل | <l | ت | t | ||
| فا | fA | ي | y | ||
| بي | by | ة | p |
| Error | Intended Word | After Pre-Processing |
|---|---|---|
| الممملك [B: “Almmmlk”] | الملك [E: “The king” B: “Almlk”] | المملك [B: “Almmlk”] |
| سماايه [B: “smAAyh”] | سمائه [E: “His sky” B: “smA}h”] | سمايه [B: “smAyh”] |
| اللصوره [B: “AllSwrh”] | الصورة [E: “The picture” B: “AlSwrp”] | اللصوره [B: “AllSwrh”] |
| Statistical | Detection → Edit Operation | |
| Order 1 | وتبين أنظمة التشيغل للحاسوب [B: “wtbyn <nZmp Alt$ygl llHAswb”] | وتبين أنظمة التشغيل للحاسوب [B: “wtbyn <nZmp Alt$gyl llHAswb”] |
| Detection → Edit Operation | Statistical | |
| Order 2 | وتبين نظمه التشغيل للحاسوب [B: “wtbyn nZmh Alt$gyl llHAswb”] | وتبين نظمه التشغيل للحاسوب [B: “wtbyn nZmh Alt$gyl llHAswb”] |
| Sub-Stage | Sub-Stage | Detection | Correction | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 2a | 2c | Rec. | Prec. | F1 | Acc. | Rec. | Prec. | F1 | Acc. |
| WUE | WUE | 76 | 94 | 84 | 88 | 42 | 90 | 57 | 75 |
| WUE | UE | 76 | 94 | 84 | 88 | 40 | 89 | 56 | 74 |
| أا | ظض |
| إا | ضظ |
| ىا | ؤو |
| اى | اٌن |
| ءأ | اٍن |
| ئي | اًن |
| تة | ن  |
| ةت | ن 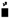 |
| هة | ن  |
| ةه | و 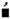 |
| واو | ي  |
| Confusion | Codelength |
|---|---|
| ‘ا’ [B: ‘A’] ‘إ’ [B: ‘<’] | إحمد [B: “<Hmd”] = 70.697 bits |
| ‘ا’ [B: ‘A’] ‘ى’ [B: ‘Y’] | ىحمد [B: “YHmd”] = 75.513 bits |
| ‘ا’ [B: ‘A’] ‘إ’ [B: ‘>’] | أحمد [B: “>Hmd”] = 61.424 bits |
| Candidate Word | Candidate Trigram | Codelength (Bits) |
|---|---|---|
| “التشغيل” [B: “Alt$gyl”] | “أنظمة التشغيل للحاسوب” [B: “>nZmp Alt$gyl llHAswb”] | 100.821 |
| “التشاغل” [B: “Alt$Agl”] | “أنظمة التشاغل للحاسوب” [B: “>nZmp Alt$Agl llHAswb”] | 106.453 |
| Cases | Total |
|---|---|
| Case I + Case II | 50 + 4 = 54 |
| Case III | 6 |
| Case IV | 20 |
| Case V | 23 |
| Rec. = 90%, Prec. = 70%, F1 = 79%, Acc. = 72% | |
| Cases | Total |
|---|---|
| Case I | 50 |
| Case V | 23 |
| Case II + Case III | 6 + 4 = 10 |
| Case IV | 20 |
| Rec. = 83%, Prec. = 68%, F1 = 75%, Acc. = 68% | |
| Rec. | Prec. | F1 | Acc. | |
|---|---|---|---|---|
| Detection | 54 | 93 | 68 | 84 |
| Correction | 29 | 88 | 44 | 77 |
| Rec. | Prec. | F1 | Acc. | |
|---|---|---|---|---|
| Detection | 75 | 94 | 83 | 91 |
| Correction | 43 | 89 | 58 | 81 |
| Spellchecker Tool | Rec. | Prec. | F1 | Acc. |
|---|---|---|---|---|
| MS word | 47 | 98 | 64 | 83 |
| Open Office Ayaspell | 53 | 98 | 69 | 85 |
| Sahah | 75 | 94 | 83 | 91 |
| Tool | Rec. | Prec. | F1 | Acc. |
|---|---|---|---|---|
| Farasa | 23 | 84 | 36 | 75 |
| Sahah | 43 | 89 | 58 | 81 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alamri, M.M.; Teahan, W.J. Automatic Correction of Arabic Dyslexic Text. Computers 2019, 8, 19. https://doi.org/10.3390/computers8010019
Alamri MM, Teahan WJ. Automatic Correction of Arabic Dyslexic Text. Computers. 2019; 8(1):19. https://doi.org/10.3390/computers8010019
Chicago/Turabian StyleAlamri, Maha M., and William J. Teahan. 2019. "Automatic Correction of Arabic Dyslexic Text" Computers 8, no. 1: 19. https://doi.org/10.3390/computers8010019
APA StyleAlamri, M. M., & Teahan, W. J. (2019). Automatic Correction of Arabic Dyslexic Text. Computers, 8(1), 19. https://doi.org/10.3390/computers8010019





