1. Introduction
Board games provide a popular pathway for using computer vision (CV) to support human-robot interaction research. The well-defined and fixed game rules allow us to simplify computer vision problems significantly by taking advantage of domain knowledge, making board games attractive for initial efforts into scene recognition and understanding. Chess is often used by researchers because of its reasonably high state-space complexity; in 1950, Claude Shannon [
1] first estimated the game-tree complexity of chess to be
; more than the number of atoms in the observable universe. This complexity makes “solving” chess a non-trivial problem that is challenging for both humans and computers.
Creating a robot that plays chess against humans requires three main subsystems to be developed: perception of the chess board and the current piece configuration, computation of the next game move, and actuation of the robot arm to manipulate the pieces on the board. In this paper, we present a project to use the Baxter humanoid robot developed by Rethink Robotics, as shown in
Figure 1, to play chess with minimal configuration in unstructured environments. A key goal was to play without controlled lighting conditions, without fixed board positions, and without needing to modify the chess board or pieces, which are shortcomings faced by other chess robot systems. Playing robustly without human intervention was also a key consideration. A driving motivation was to make Baxter play chess in the same way and under the same conditions as a human, without having to artificially modify the environment to suit the robot.
Using high-level open source tools, the computation and actuation problems were largely satisfied quickly. The main contribution of this paper is the use of cameras as the sensing mechanism for the development of a complete robotic chess playing system. This relies on the development of a computer vision algorithm for perceiving the chess board and the current board state. We extend our previous work [
2] by presenting two algorithmic contributions: a dynamic approach to using the Hough line transform for image segmentation, and a hybrid edge and morphology-based approach for object/occupancy detection. We also present more complete results with an experiment showing the robustness of this approach under varying lighting conditions. This research is unique when compared to existing chess robots which rely on specially designed chess boards, rather than perceiving and playing chess like humans do. In addition, research in this area also improves chess-related computer vision techniques as well as supporting human-robotics interaction research in related areas such as medical assistive robots and small-scale manipulation.
This paper is structured as follows;
Section 2 describes related works and highlights the differences between our implementation and existing chess-related research.
Section 3 discusses the computer vision algorithm, with the two key contributions highlighted in
Section 4 and
Section 5.
Section 6 briefly presents the chess engine and mechatronics subsystems, and
Section 7 explains how the subsystems are connected.
Section 8 presents results that demonstrate the robustness of the implementation, and
Section 9 discusses some areas for future work and concludes.
2. Related Works
Existing efforts in developing chess-playing robots generally greatly simplify the challenges of creating a holistic perceive-compute-actuate system by applying significant constraints. The most common is the use of a Digital Game Technology (DGT) board, which uses sensors physically embedded in the board and the pieces to report the current square location of each piece to a computer, thus removing any need for external perception. Examples of this include Chesska from Russia and the KUKA Monstr from Germany, which competed in a “World Championship for Robot Chess” [
3]. However, DGT boards are not only expensive but far less common than standard non-digital chess sets, immediately restricting the generality of the chess robot.
In cases where computer vision is used for perception, common simplifications include using non-standard colours (such as pink and green) to help the camera differentiate between the board squares and pieces [
4], and mounting the camera directly above the board to reduce perspective distortion [
5,
6]. CVChess [
7] uses Harris corner detection and heatmaps to detect the board and piece movements at acute camera angles from a laptop webcam, but requires manual move triggering and is susceptible to errors with an inability to recover. Neufeld and Hall [
8] propose a probabilistic matching algorithm based on image masks to detect and classify the pieces and their current positions, although with lower accuracy than our method. Tam, Lay, and Levy [
9] use a combination of Hough line transforms and domain knowledge to segment squares from populated chessboards in a similar approach to ours, although no piece detection is implemented. Bennett and Lasenby [
10] present a feature detector that identifies chess board vertices in a robust way, although again this method only finds chess boards and does not identify occupancy or pieces. Czyzewski [
11] describes a three-step system that finds, then analyses, and then refines the chess board segmentation from different angles using neural networks, but only a draft of the algorithm has been released and more tests need to be conducted to verify the reliability and robustness of this approach.
One of the common simplifications used by hobbyists for the mechatronics subsystem is to use an XY linear slide system, mounted on top of the board so that a gripper can easily and consistently move to a square and pick up or put down a piece. However, this requires a fixed board position, and can sometimes occlude the board from a human player, while also making the board much less portable. Most implementations require that the board be in a fixed position so that the physical location of each square (and therefore each piece) is known to the robot beforehand [
5]; this is also common with DGTs.
Gambit [
12] is the closest implementation to ours in terms of functionality, with a stated goal of achieving as much generality as possible. It is an autonomous system that uses an infrared depth camera in conjunction with a secondary camera to perceive the board and a custom 6-DoF robot arm for actuation. However, there are still significant differences in the approaches, such as Gambit’s use of SVMs to learn the piece types, and using two cameras to include depth information instead of just one camera. Our implementation takes a simpler approach to the perception problem, with similar overall results. Some other similar implementations include [
13,
14], but these papers do not report accuracy rates, speed, or other results.
3. Computer Vision Subsystems
Perhaps the most challenging part of creating a chess robot is giving the robot the ability to “see” the board. Baxter has a camera built into the arm, underneath the end effector as shown in
Figure 1. This provides a 1280 × 800 widescreen image with a 16:10 aspect ratio, although some of the image is obscured by the end effector, leaving roughly 1280 × 500 of the image usable. The sub-problems to be solved are shown in
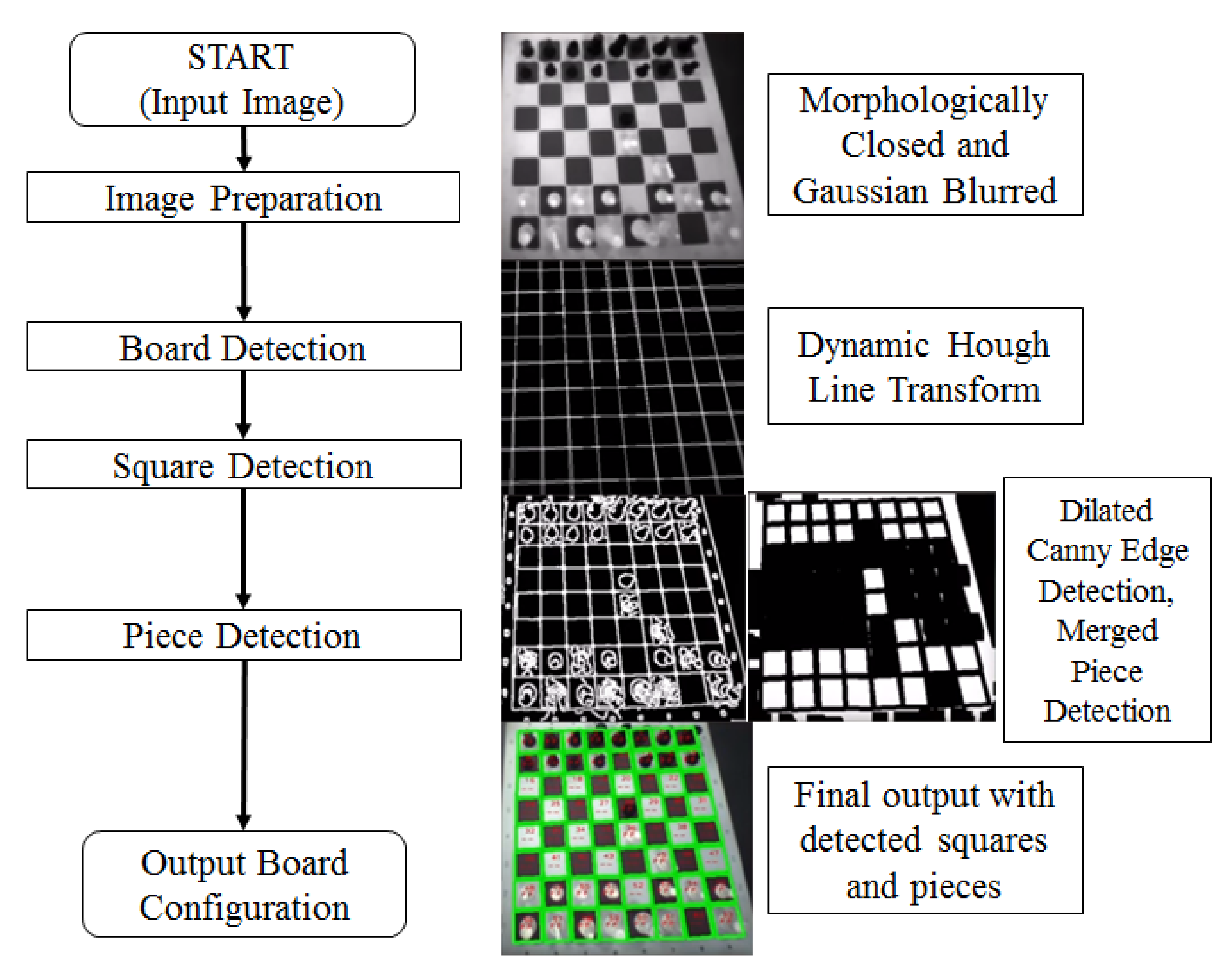
Figure 2: finding the chessboard from the wider image (board detection), segmenting the image into the individual squares on that chessboard (square detection), and finding the pieces on those squares (piece detection). At each step of the algorithm, if it is not successful (e.g., no board is detected) then the algorithm exits and waits for the next frame.
To assist with the development of the computer vision algorithms, we used OpenCV [
15], an open source image processing library. This not only helps with the development time, but also allows us to take advantage of efficient, optimised code. In order to obtain consistent and stable images, the arm (and therefore the camera) moves to a fixed position above the play area in order to perceive the current state of the chess board. We wanted to ensure that the CV algorithm can operate without the camera being directly above the board (i.e., that it can deal with some amount of perspective distortion), so the camera is positioned at a 0.4 radian angle from the perpendicular to the table. The desired output of the CV subsystem is the current position of all the pieces on the board, and the coordinates of a move if there is one.
Figure 3 shows a diagrammatic representation of the CV algorithm.
Firstly, image preparation or pre-processing is conducted. Conversion to greyscale reduces the amount of information for each pixel to reduce computation time and complexity, and greyscale information is sufficient for this task. Gaussian blurring reduces the amount of noise in the image by smoothing out the pixel intensities so that sharp changes in intensity are dampened. This is done by filtering the image with a 5 × 5 Gaussian kernel. The Otsu threshold is then calculated; this allows the algorithm to respond dynamically to lighting changes in-between images by recalculating the optimal threshold used for thresholding and edge detection purposes.
Board detection is relatively simple, as we are effectively looking for a large square in the image, as shown in
Figure 4. Canny edge detection [
16] is used to identify the boundaries of the objects, using hysteresis to produce more consistent edges than the Sobel or Prewitt operators. Dilation is a morphological operation that expands the edges found by the edge detection by a certain number of pixels, so that we can fill in any holes in those edges, creating continuous contours. Square contours can then be identified by iterating through all of the contours found and isolating those with four edges, at approximately right angles to each other, with approximately equal length and width. Some tolerance is allowed for each of these measures, which accounts for cases where perspective distortion may make the board seem slightly trapezoidal rather than exactly square. The largest square identified in the image, above a set minimum size or threshold, is designated the chessboard. If no chessboard is found, then the image is rejected and the subsystem should await the next image. If another object is incorrectly identified as the chessboard, then the image will fail later on in the algorithm during square or piece detection and still be rejected.
We slice the original wide image so that only the chessboard is present in the image in order to reduce the amount of processing required in later stages. The orientation of the chessboard relative to the camera is also calculated by determining the angles that the four chessboard edges make to the x and y-axes of the image. This allows us to account for cases where the board is not exactly parallel to the camera (and therefore the robot), which is very likely if the board is not fixed in position, as seen in
Figure 5. Our measurements indicate that the orientation can deviate by up to 10 degrees away from the perpendicular before the algorithm no longer detects the square shape of the chess board.
The algorithm then begins square detection, which segments the image into the 64 squares on the chess board. Contrast limited adaptive histogram equalization (CLAHE) is used to boost the differences in intensity throughout the image. This is to reduce the likelihood of white pieces on white squares or black pieces on black squares becoming indistinguishable. Local adaptive equalization helps avoid unwanted information loss that is often encountered in global histogram based contrasting, especially in situations where the lighting is not consistent across an image. We apply Gaussian blurring again to further filter out noise that sometimes arises from contrasting, and Canny edge detection and dilation are executed to produce stronger edges for the squares and pieces.
As the camera is not directly above the board, some of the square boundaries can be occluded by the pieces on the board. Additionally, perspective distortion can cause some of the square edges to not be exactly parallel/perpendicular to the x- and y-axes of the image. We developed an iterative and segmenting algorithm based on the Hough line transform that deals with these issues, explained in more detail in
Section 4. The dynamic Hough line transform outputs a series of lines that correspond to the edges of the squares on the chessboard; we also constrain the selection of lines to those that are roughly parallel to the x and y-axes of the board as identified earlier, spurious lines that cannot possibly be the edges of the squares (e.g., going diagonally across the board) are removed.
We use the same approach as in the board detection section to detect the square contours. Domain-specific knowledge is used to ensure that there are 64 (8 × 8) squares detected. If there are fewer than 64 squares, we reject the image. If there are more than 64 squares, then the smallest squares are removed as they usually originate from noise at the edges of the board. Occasionally, lighting can cause parts of the image to become saturated, making detection of the correct square edges difficult, and the image becoming rejected. However, usually the saturation only lasts for one or two frames, and the algorithm successfully processes a later frame. The OpenCV implementation of contour detection does not guarantee any particular order, so we use the centroids of each square to sort them into order from left-to-right, top-to-bottom. Masks are then created for each square to build an 8 × 8 occupancy grid.
For piece detection, we process the chessboard image in two different ways and merge the outputs. The strategy is to identify the edges of the chess pieces and use that information to determine which squares have pieces in them and which squares do not, which we call occupancy. This process is discussed in more detail in
Section 5. A differential image approach is taken, where the occupancy of each frame is compared to the previous frame to see which pieces have moved. This approach uses the assumption that the board is initially set up in a known configuration, in our case with the pieces set up correctly for the beginning of a match. There are three types of piece movements to check: a piece has moved to a previously unoccupied position, a piece has taken another piece and therefore moved to a previously occupied position, or two pieces have moved to previously unoccupied positions and castling has occurred. The algorithm does not check for the legality of moves; this is handled by the chess engine subsystem describe in
Section 6. From this analysis, an origin square and a destination square (both from 0 to 63, starting at the top left, incrementing left-to-right and top-to-bottom) can be determined and reported to the chess engine subsystem.
4. Dynamic Hough Line Transform
The Hough Transform [
17] is a useful algorithm for extracting shapes from images, although originally it was used to identify lines. Importantly, the lines can be detected even if there are holes in the line or some distortion in the image, which is useful in our case where many of the lines are occluded by pieces. The transform returns a set of lines, each represented by their parametric
(perpendicular distance from the origin) and
(angle from the horizontal axis measured counter-clockwise) values. The Hough line transform identifies points in the image, and then uses a voting mechanism to identify lines, with more votes indicating more points of that line found in the image and therefore the stronger likelihood of that line being real. This is the approach used for segmentation in [
9], which uses domain knowledge specific to chess to improve the accuracy of the algorithm, but requiring careful tuning for each set of environmental conditions as optimal threshold changes. The OpenCV implementation of the transform accepts a vote threshold as an input, which can be used to filter out lines with low votes that are either very short or generated from noise.
In our approach we use what we call a dynamic Hough line transform; we call this transform “dynamic” because in our approach we segment the image and apply transforms with different vote thresholds in order to create the most usable set of lines, and iteratively try different vote thresholds until our square detection succeeds (or gives up and exits). This approach accounts for the fact that the body of the robot can create a shadow over the chessboard, making squares further away from Baxter lighter than squares closer to Baxter. It also partially accounts for some perspective distortion, and recognises that lines that are closer to Baxter (at the bottom of the image) are typically longer and therefore we should use a higher vote threshold than parts of the image further away. This perspective distortion worsens as the angle of the camera view becomes more acute. Additionally, if there are pieces on the board in their initial positions, then the Hough line transform can mistake the line of pieces as a chess square edge, which should be filtered out. By dynamically determining the vote thresholds, we have fewer unwanted lines in the output, as shown in
Figure 6.
Using this approach has further applications in scenarios where it is difficult to calibrate cameras, such as on mobile robots. It allows shapes to be found even when perspective distortion alters the true shape of the object. While it is more computationally expensive than the standard transform (due to the iterative nature of testing the vote thresholds), the algorithm could be modified to use online learning and optimisation to learn the appropriate thresholds to avoid computing them again for each frame.
5. Occupancy Detection
In order to determine where the chess pieces are on the board, we use an edge-based approach to determine occupancy of the squares. While [
12] detects the type of the individual pieces (i.e., knight, rook, king), we found that this requires either a close camera or a high resolution camera in order to collect enough detail to discriminate between the pieces. It is actually possible to know which piece is being moved by keeping track of the move history, with the assumption that the game starts with pieces in their initial positions. Our strategy is based on differential comparison, where we remember the previous board state, compare it to the new board state, and use that to determine which move has been made (and therefore what the piece type was). We also aimed for a more computationally light algorithm without complicated deep learning.
We use two approaches to edge detection and merge the results. Firstly, we use the output of the Canny edge detection in the square detection step of the algorithm and morphologically close the edges, which we will call Method A. Morphological closing is a dilation operation followed by an erosion operation, which fills in any space between the edges. This process fills in the square if there are piece edges in the square, removing any requirement of the piece being perfectly in the centre of the square. This provides a good indication of where the pieces are, but is occasionally susceptible to misinterpreting small shadows on empty squares (especially white squares) as pieces. Secondly, we try to reduce the impact of shadows by using morphological edge detection. This applies morphological closing to the contrasted image before applying Canny edge detection and dilation, which we will call Method B. This process essentially blurs out smaller shadows by suppressing smaller edges and enhancing sharper edges. However, this can misinterpret changes in lighting across the board as new edges, for example when a light is shone across half of the board. This can cause the algorithm to incorrectly report pieces where there is actually just a lighting gradient.
Both approaches tend to over-report, i.e., find pieces where there are not any, as shown in
Figure 7. To counter this, we simply element-wise AND the output of both methods, so that both methods must agree for us to accept that there is a piece in a particular square. This method is more resistant to small shadows created by the pieces, while also avoiding misinterpretation of lighting gradients across the board, thus improving the accuracy of piece detection significantly, as described in the results section. This approach can still fail where there are larger/longer shadows, created by external light sources at low angles, but in our testing the method is generally robust under standard or natural lighting conditions. Using this approach has further applications in scenarios where the occupancy of spaces needs to be determined in uncontrolled environments, such as pick-and-place operations or scientific experiments.
We then determine the average intensity of each square in the occupancy grid, comparing it to an empirically determined threshold to determine if there is a piece present or not. A parameter sweep in increments of 10 was conducted to find a suitable value. Under standard lighting conditions, a threshold value of 70 out of 255 was suitable, and achieved the results shown in
Section 8.2. We also take the intensity of the centroid of the square from the original image to determine whether the piece is white or black based on another preset threshold.
6. Chess Engine and Mechatronics Subsystems
As the computer vision algorithm is the main focus of this paper, we give a light description of the chess engine and mechatronics subsystems to aid the reader in understanding how we tested the algorithm in realistic conditions. Rather than redevelop these subsystems from scratch, we use the open source chess engine Stockfish and the inverse kinematics solver IKFast as the core of the computation and actuation subsystems. Stockfish is one of the strongest chess engines in the world, currently ranked first in the Computer Chess Rating List (CCRL). It uses the Universal Chess Interface (UCI) protocol, which accepts as an input two algebraic notations, indicating the origin and destination squares of the last move. The engine also keeps track of the board configuration to recognise special cases, such as piece capture and castling. At the beginning of the game, we ask the user to select a difficulty level, which corresponds to the search depth that the engine uses. We use PyStockfish, an open-source wrapper that makes it easier to integrate Stockfish into our script since our code was developed in Python. We also use Chessnut, a Python open-source chess board modelling framework. This library verifies individual moves to check if they are legal; illegal moves could result from either erroneous analysis by the CV subsystem or by human interference. If an illegal move is detected, then we inform the user and request that they resolve the situation before Baxter plays his move. Once the origin and destination square numbers are provided by the CV subsystem, they are converted to their algebraic equivalents (from a1 to h8), verified by Chessnut, and then passed to Stockfish. Once Stockfish provides the next move, we convert the origin and destination squares for the next piece to cardinal square numbers in x–y co-ordinate space, and pass this to the mechatronics subsystem for actuation.
The Baxter arm has seven degrees of freedom as shown in
Figure 8, which is a non-trivial kinematics problem to solve. IKFast is used to greatly simplify this challenge, by allowing us to simply input the desired end effector co-ordinates relative to the centre of Baxter’s torso. Unlike many other implementations (as discussed in
Section 2), we do not need the board to be in a fixed position. During normal or energetic gameplay, the board can move slightly when touched by a human player, so the robot should dynamically recalculate the co-ordinates of the square positions before each move. This can be done based on the camera image, although some manual configuration at system initialisation is required so that the application knows how the pixels in the image correspond to physical distances.
As Baxter is designed to be safely used around humans without safety cages, the joints are compliant, meaning that the torques at each joint are constantly measured and the arm stops moving if it detects that the torque is not what it should be, for example if it hits an obstructing object, such as a human. However, this creates two significant problems for our application. Firstly, this makes the movement of the robot arm very slow in comparison to other robots, which is a limitation of the platform due to internal torque limitations. Secondly, the accuracy of the arm is not always perfect, as the compliant joints allow some deviation from the equilibrium position. To counteract this, we implemented intermediary waypoints between the initial position and the desired endpoint, which instructs the arm to make a series of smaller movements, reducing overshooting. This improved accuracy comes at the cost of even slower movement, but is required to ensure that Baxter plays chess robustly with minimal actuation error when the board is not in a fixed position. This could be improved through the use of better kinematics modelling, and could be made more natural through programming-by-demonstration [
18].
To assist with the accuracy of the square co-ordinates, a calibration sequence at system initialization gives the mechatronics subsystem the co-ordinates for the bottom left square. From this position, taking into account the orientation of the board provided by the CV subsystem, the end effector co-ordinates are calculated for each square on the board using a pre-configured square size. Given the origin and destination squares, the mechatronics subsystem then picks and places the piece. Baxter’s arm has an electric two-finger attachment that closes and opens to pick up and release the chess pieces as shown in
Figure 1 and
Figure 8. If a piece is already at the desired destination, then the move is capturing a piece, so the mechatronics subsystem first removes the captured piece and places it in a box beside the board before moving the capturing piece. The system also checks if the move from the chess engine is a castling move; if so, Baxter moves the second piece as well.
7. Overall System Control
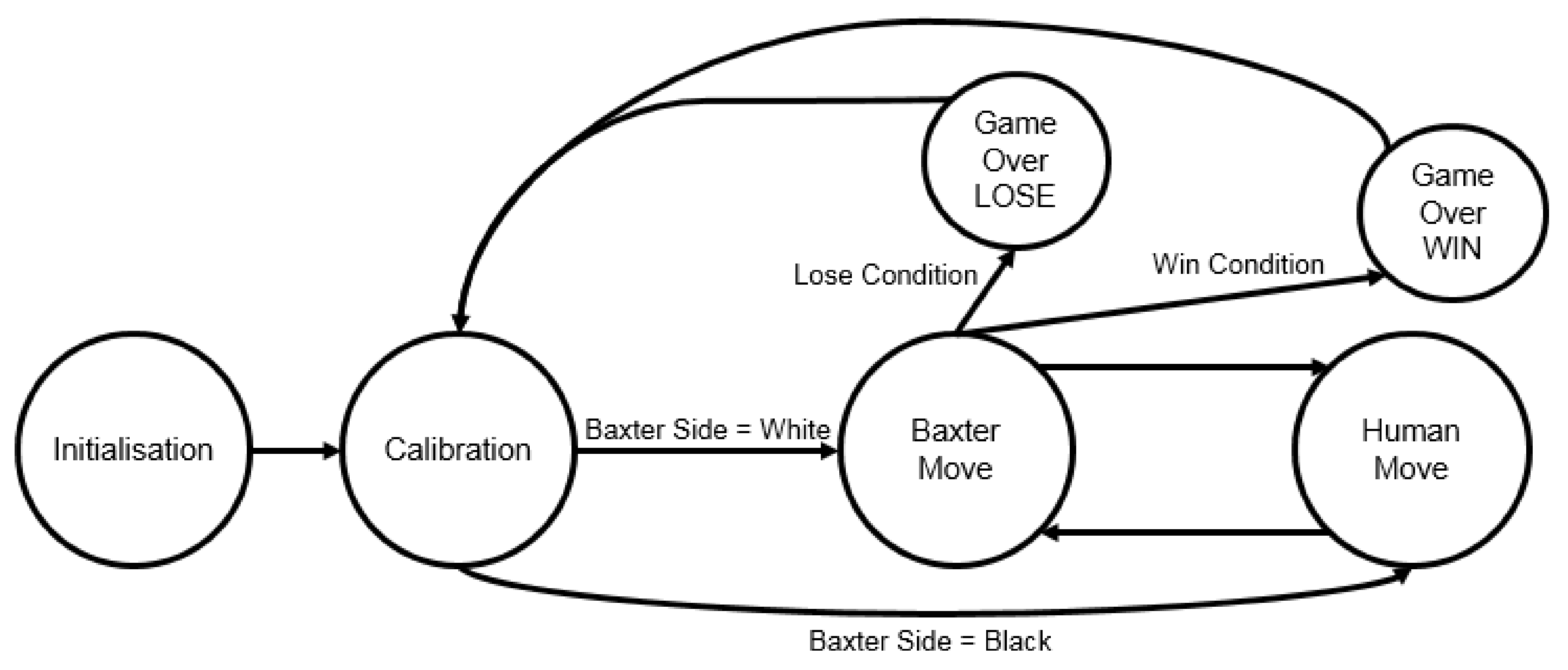
The system software is developed in Ubuntu using Python for scripting and ROS for communication with the robot and its peripherals. A finite state machine approach, shown in
Figure 9, is used to manage the different actions that Baxter takes in various circumstances. In the initial state, Baxter and its peripherals are set up. This includes moving the arms to neutral locations, configuring the correct cameras to be open and streaming, and loading the images to be shown on the screen (i.e., Baxter’s face). In the calibration state, we detect the current lighting conditions to set parameters in the CV subsystem, the user selects a difficulty level for the chess engine, and the mechatronics subsystem is calibrated as described in
Section 6 to help improve the accuracy of the positioning. Based on the brightness of the pieces closest to Baxter, the CV subsystem determines if Baxter is playing as white or black, and then transitions to the appropriate state.
If it is Baxter’s move, we move through a compute-actuate-perceive cycle, where the chess engine decides what the next move should be, the mechatronics subsystem executes that move, and then the CV subsystem verifies that the move was made correctly. If it has made a mistake, then the system asks for human intervention, although this is rare. The chess engine also determines if a checkmate has occurred; if so, then Baxter transitions to the appropriate game over state for winning or losing, otherwise it transitions to the human’s move state.
If it is the human’s move, then the arm moves to an observation position, and Baxter indicates to the human that it is their turn by nodding the head and changing his facial expression. If the human user takes too long, after awhile the image on Baxter’s screen changes so that it appears that Baxter is bored and asleep because it has been waiting for too long. Meanwhile, the CV subsystem continuously processes the frames arriving from the camera to determine if a move has been made. Unlike many other implementations (see
Section 2), no manual move triggering is required as the CV subsystem rejects images where no valid chessboard is found, such as when a hand is obscuring the board because it is moving a piece. No move is sent to the chess engine if no change in board configuration has been detected. When a move has been detected, Chessnut verifies the validity of the move (if it is illegal, Baxter displays a message asking the human to verify their move), and then the system transitions back to the Baxter move state.
To help Baxter appear more responsive, the robot responds differently depending on if it wins or loses to represent emotion [
19,
20]. When Baxter wins, the arms move to a neutral position, a happy expression is displayed on the screen, and the background behind Baxter’s face flashes different colours to indicate celebration; when he loses, Baxter crosses his arms and displays an upset facial expression on the screen to indicate disappointment and sadness.
8. Results
In this section, we will present the results in terms of the chess robot’s performance against humans, quantitative analysis of the CV algorithm, and some qualitative comments about the overall timing and errors.
8.1. Playing Chess Against Humans
Stockfish is a very strong chess engine, so the average person is not able to beat it since we use a minimum search depth of 6 (most humans only plan two or three moves ahead). As we have not tested Baxter against any Grandmasters, in over 50 complete games, no human has beaten Baxter at chess yet. We did not conduct a formal survey, but the main response from most human players was that they enjoyed playing against a humanoid robot, in particular highlighting the changes in facial expressions. They liked that the robot seemed to be responsive to the human moves, and that the camera placement was sufficiently high enough and out of the way that it did not obstruct the human player’s vision when trying to see the pieces on the board.
8.2. Analysis of Computer Vision Algorithm(s)
We took a sample of 500 frames from Baxter’s camera, with variations in the chess board orientation, chess board position, piece positions, external lighting intensity, and external lighting orientation. Of those, only about 270 frames were suitable for further analysis, because in many of the frames the camera was saturated, making it impossible to distinguish between edges or between white squares and white pieces, even to a human looking at the image. Most of this saturation would be temporary, so when running our algorithm in the real-world, it would simply reject these images and wait for a more suitable frame. In this test set, only 76 samples were taken in what could be considered “normal” lighting conditions; all other samples involved the use of a lamp to create extreme lighting conditions in order to challenge the CV algorithm, as shown in
Figure 10. This was done by moving the lamp to different positions and angles around the board to create bright (saturation) and dark (shadow) areas around the board. In a real-world scenario, it is unlikely that the lighting source would be so close to the board or at such an acute angle. For this experiment, all of the parameter and threshold values were held constant for all cases, even though changing some of these values could improve the accuracy under more adverse lighting situations.
The first observation from
Table 1 is that the board and square detection have relatively high accuracies, meaning that they generally succeed at identifying where the board is from the wider image and identifying where the squares are based on the Dynamic Hough line transform. The second observation is that the hybrid piece detection method is superior to method A or method B alone. Additionally, under normal lighting conditions, the hybrid piece detection method is very accurate, making it a robust implementation suitable for a human-facing chess robot.
It should also be noted that even in situations where the piece detection fails to identify the piece positions correctly, for example when external lighting creates a strong shadow edge on a white square, generally this does not cause any actual errors in the performance of the chess robot. This is because we use Chessnut for validating the legality of moves, and generally if the piece detection is erroneous then the move that the CV subsystem suggests is illegal. After implementing Chessnut, in our testing we have never encountered a situation where an illegal move is given to Stockfish unless a human has intentionally made an illegal move. In situations where the algorithm seems to be irrecoverable from an illegal move (or cheating on the part of the human), a message is displayed asking for human intervention to correct the last move.
8.3. Timing and Errors
We make the observation that Baxter plays chess with different timing requirements to human players. When humans play at a high level, the perception time for detecting and analysing a move is very short, the computation time of deciding the next move is comparatively long, and the actuation time of moving a piece is very short. For Baxter, this is exactly the opposite; running on a 1.9 GHz i5 processor, the CV subsystem can only process a few frames per second (faster if the algorithm does not find a chess board or squares), and the chess engine subsystem returns a move in a few seconds or less (depending on the difficulty level/search depth). However, actuating the piece can take a significant amount of time, about 45–90 s, depending on if Baxter needs to move one piece or two (such as during piece capture or castling). This can give the impression that Baxter is a very slow player, particularly at the beginning of the game when a human player usually executes well-known opening sequences from memory without much computation. However, as the game progresses and becomes more complex, human players slow down as they consider the different options and consequences of their moves, so Baxter can outpace them since its move time remains roughly the same throughout the game. If speed of play is an important factor, then our approach could be applied to an alternative camera/robot arm arrangement if necessary.
The mechatronics subsystem does occasionally knock over other pieces as it actuates; this should be considered in the context that even humans sometimes knock the pieces over during vigorous matches of chess. Baxter unfortunately cannot detect fallen pieces or know how to pick them up and re-orient them as this is a difficult challenge, so human intervention is currently required, but some fault tolerance could be developed as part of future work.
9. Future Work and Conclusions
As part of a broader chess robot system, a robust computer vision algorithm has been developed for analyzing chess boards and their current game states with fewer restrictions than other robot chess approaches. We developed a complete robotic system, incorporating computer vision, chess engine, and mechatronics subsystems to deliver an engaging experience for human chess players. With our focus on robustness and flexibility, Baxter can play with a standard chess board instead of an expensive DGT board, with a wide variety of board colours, using a camera that does not obstruct the player’s field of view by being fixed directly above the board, and with variation in the board position and orientation, as well as an ability to deal with varying lighting conditions.
In our computer vision algorithm, the most robust components are the board detection and square detection, but the accuracy of the piece detection could potentially still be improved. The problem of ignoring or removing shadows from an image, particularly small shadows that may move as lighting conditions change, remains challenging but in our experiments we show that our algorithms are sufficiently accurate to deliver reliable performance. An alternative area of exploration is the use of external/extrinsic calibration [
21] to transform the image to a birds-eye view, which might help with line and piece detection, but might also cause saturation effects to have a larger impact.
Developing more fault tolerance could be useful for further chess robot research, especially if it allows Baxter’s arm to move faster. To this end, better modelling of the chess pieces, such as the use of SVMs in [
8] or the use of 3D modeling [
22], could be used to tell the difference between a knocked over piece and two or three pieces in adjacent squares, and also put the correct pieces back onto the correct squares. There has also been recent interest in developing stronger chess engines like AlphaZero [
23], although since Stockfish is already stronger than most human players, the real-world effect would be essentially negligible.
In conclusion, our implementation of a chess-playing robot is robust, and is a useful case study for further human-robot interaction research with Baxter, as well as improving upon existing computer vision approaches towards analysing chess games, with two algorithmic developments presented for dealing with challenging unconstrained scenarios.