New Residue Number System Scaler for the Three-Moduli Set {2ⁿ⁺¹ − 1, 2ⁿ, 2ⁿ − 1}

Abstract

This work proposes the first scaler designed specifically for the three-moduli set $M_1=\{2^{n+1}-1,2^n,2^n-1\}$. Hence, there is no other functionally similar scaler to compare the proposed scaler with. However, when compared with the latest published scalers for a different moduli set, $M_2=\{2^n+1,2^n,2^n-1\}$, the proposed scaler has a better area and power performance, while it requires a longer time delay. As demonstrated in earlier publications, replacing the $(2^n+1)$ channel in the $M_2$ moduli set by the $(2^{n+1}-1)$ channel, to form the $M_1$ moduli set, considerably improves the overall time performance of residue-based multiply–accumulate arithmetic units.

1. Introduction

The residue number system (RNS) is a non-weighted number system representation. Numbers are represented using a set of relatively prime positive integers, referred to as moduli [1,2]. Specific arithmetic operations, such as addition, subtraction, and multiplication, are carried with respect to each modulus independently from other moduli. This feature allows parallel processing on all channels without having a carry propagating across different channels. Therefore, the RNS is used in applications that depend on the aforementioned operations, such as digital signal processing and cryptography [1,2,3,4,5]. However, division is considered a difficult RNS operation [6].

Scaling is an important operation needed whenever the results of computations carried out on each data set exceed specific allowable ranges within a RNS-based processor. The work that has been published so far regarding scaling the RNS deals either with moduli sets of general form or with the traditional set. The main scalers that deal specifically with the traditional moduli set $M_2=\{2^n+1,2^n,2^n-1\}$ are presented in [7,8,9,10,11,12,13]. Those that are most efficient in terms of different metrics are presented in [12,13].

Although it provides a dynamic range similar to that of the traditional set, the moduli set $M_1=\{2^{n+1}-1,2^n,2^n-1\}$ has no $(2^n+1)$ modulus. Compared to modulo $(2^{n+1}-1)$ multipliers, modulo $(2^n+1)$ multipliers require additional significant area, time delay, and power [14,15,16,17]. Expressed in terms of the gate-equivalent count and delay (which are technology-independent indicators), the modulo $(2^n+1)$ multiplier has 15–35% more gate equivalents and 10–15% more delay than the modulo $(2^{n+1}-1)$ multiplier [14].

These conclusions have also been supported experimentally in terms of integrated circuit area, time delay, and power consumption for values of n extending from 32 to 64 bits [17]. Additionally, in a very recent publication [18], circuit layout experiments on the moduli set $\{2^n+1,2^n,2^n-1\}$ over the range of $(3\le n\le 22)$ showed that the modulus $(2^n+1)$ increases the area and latency of a RNS-based arithmetic structure when compared with modulo $2^n$ and $(2^n-1)$ structures. A circuit layout of a Multiplier and an Accumulator (a single MAC structure) proved that the $(2^n+1)$ channel requires on average an 18.9–35.6% increase in area and a 21.9–45.2% increase in delay as compared with the $2^n$ and $(2^n-1)$ MACs [18]. Therefore, the $(2^n+1)$ channel leads to a serious latency imbalance across a RNS-based processor that uses the popular three-moduli set. This imbalance increases progressively when designing a multi-MAC RNS-based processor [18]. The delay avoided by excluding modulo $(2^n+1)$ arithmetic components such as adders and multipliers and replacing them with modulo $(2^{n+1}-1)$ components is considerably large, as demonstrated in [14,17,18]. Hence, using a $(2^n+1)$-free moduli set such as $M_1$ substantially improves the overall time performance of a RNS-based processor. To the best of the author’s knowledge, the scaler presented here is the first proposed in the literature to deal with $M_1$.

2. The Proposed Scaler

2.1. Decoding Analysis

For a three-moduli set, the Chinese remainder theorem (CRT), which is used to convert the RNS value to its weighted equivalent, is defined by the following [1]:

$$X={\left|\sum _{i=1}^3{\widehat{m}}_i{\left|{\widehat{m}}_i^{-1}\right|}_{m_i}{R}_i\right|}_M,$$

(1)

where

• $m_1=2^{n+1}-1$, $m_2=2^n$, and $m_3=2^n-1$;
• ${\widehat{m}}_1=m_2{m}_3=2^n(2^n-1)$, ${\widehat{m}}_2=m_1{m}_3=(2^{n+1}-1)(2^n-1)$, and ${\widehat{m}}_3=m_1{m}_2=2^n(2^{n+1}-1)$;
• ${\left|{\widehat{m}}_1^{-1}\right|}_{m_1}={\left|-4\right|}_{m_1}$, ${\left|{\widehat{m}}_2^{-1}\right|}_{m_2}=1$, and ${\left|{\widehat{m}}_3^{-1}\right|}_{m_3}=1$;
• M is the dynamic range given by $M=m_1{m}_2{m}_3$;
• X is an integer such that $X\in [0,M)$, with the binary value of X represented using $(3n+1)$ bits;
• the RNS representation of X is $X=(R_1,R_2,R_3)$, where $i=1,2, \mathrm{and} 3$, $R_i={\left|X\right|}_{m_i}$ (the least non-negative remainder when dividing X by $m_i$).

Substituting the above values into Equation (1) leads to

$$\begin{array}{c}\hfill \begin{array}{cc}X=\hfill & {\left|(-4)2^n(2^n-1)R_1+(2^{n+1}-1)(2^n-1)R_2+2^n(2^{n+1}-1)R_3\right|}_{{}_M}.\hfill \end{array}\end{array}$$

(2)

Using the notation $⌊.⌋$ to refer to the floor value of (.), X can be expressed as in [1]: $X=⌊\frac{X}{2^n}⌋2^n+{\left|X\right|}_{2^n}$. Because X is represented in $(3n+1)$ binary bits, the value ${\left|X\right|}_{2^n}$ represents the least-significant n bits of X. Moreover, the value $⌊\frac{X}{2^n}⌋$, which represents the most-significant $(2n+1)$ bits of X, is the scaled value of X, where the scaling factor is $2^n$. The floor value of $\frac{X}{2^n}$ is considered because the RNS represents only integer values [1].

The corresponding RNS digits of the scaled value $⌊\frac{X}{2^n}⌋$ are given by $(R_{1s},R_{2s},R_{3s})$, where

$$\begin{array}{c}\hfill \begin{array}{cc}{R}_{is}=\hfill & {\left|⌊\frac{X}{2^n}⌋\right|}_{m_i}.\hfill \end{array}\end{array}$$

(3)

Equation (2) is rewritten as follows [1]:

$$\begin{array}{c}\hfill \begin{array}{cc}X=\hfill & (-4)2^n(2^n-1)R_1+(2^{n+1}-1)(2^n-1)R_2+2^n(2^{n+1}-1)R_3-MI,\hfill \end{array}\end{array}$$

(4)

where I is the number of integer multiples of M in the summation of the right-hand side (RHS) of Equation (2).

To evaluate $⌊\frac{X}{2^n}⌋$, the floor value of dividing Equation (4) by $2^n$ produces

$$\begin{array}{c}\hfill \begin{array}{cc}⌊\frac{X}{2^n}⌋=\hfill & (-4)(2^n-1)R_1+\left(2^{n+1}-3\right)R_2+\left(2^{n+1}-1\right)R_3-m_1{m}_{3}I,\hfill \end{array}\end{array}$$

(5)

where the fractional part $\frac{R_2}{2^n}$ is dropped in Equation (5) when taking the floor value because $R_2<2^n$; hence, $⌊\frac{R_2}{2^n}⌋=0$.

Applying modulus $m_1{m}_3$ to Equation (5) produces

$$\begin{array}{c}\hfill \begin{array}{cc}⌊\frac{X}{2^n}⌋=\hfill & {\left|(-4)(2^n-1)R_1+\left(2^{n+1}-3\right)R_2+\left(2^{n+1}-1\right)R_3\right|}_{{}_{m_1{m}_3}}.\hfill \end{array}\end{array}$$

(6)

Observing that ${\left|{\left|(.)\right|}_{{}_{m_1{m}_3}}\right|}_{{}_{m_1}}={\left|(.)\right|}_{{}_{m_1}}$ [1], then applying modulus $m_1$ to Equation (6) results in

$$\begin{array}{c}\hfill \begin{array}{cc}{R}_{1s}\hfill & ={\left|-4(2^n-1)R_1+\left(m_1-2\right)R_2+m_1{R}_3\right|}_{{}_{m_1}}\hfill \\ & ={\left|-2(m_1-1)R_1-2R_2\right|}_{{}_{m_1}}={\left|(-2)(-1)R_1-2R_2\right|}_{{}_{m_1}}\hfill \\ & ={\left|2(R_1-R_2)\right|}_{m_1}.\hfill \end{array}\end{array}$$

(7)

Recalling that $m_3=(2^n-1)$, the three terms on the RHS of Equation (6) can be rewritten as follows: $(-4)(2^n-1)R_1=-4m_3{R}_1$, $(2^{n+1}-3)R_2=(2m_3-1)R_2$, and $(2^{n+1}-1)R_3=(2m_3+1)R_3$.

Substituting the last three expressions into Equation (6) leads to

$$\begin{array}{c}\hfill \begin{array}{cc}⌊\frac{X}{2^n}⌋=\hfill & {\left|-4m_3{R}_1+(2m_3-1)R_2+(2m_3+1)R_3\right|}_{{}_{m_1{m}_3}}.\hfill \end{array}\end{array}$$

(8)

Rearranging the terms in Equation (8) produces

$$\begin{array}{c}\hfill \begin{array}{cc}⌊\frac{X}{2^n}⌋=\hfill & {\left|{\left|m_3(-4R_1+2R_2+2R_3)\right|}_{{}_{m_1{m}_3}}{\left.+\left(R_3-R_2\right)\right|}_{{}_{m_1{m}_3}}\right|}_{{}_{m_1{m}_3}}.\hfill \end{array}\end{array}$$

(9)

Using the identity ${\left|m_3(.)\right|}_{{}_{m_1{m}_3}}=m_3{\left|(.)\right|}_{{}_{m_1}}$ [1], the term given by ${\left|m_3(-4R_1+2R_2+2R_3)\right|}_{{}_{m_1{m}_3}}$ on the RHS of Equation (9) can be rewritten as $m_3{\left|-4R_1+2R_2+2R_3\right|}_{{}_{m_1}}$.

Substituting the last expression into Equation (9) leads to

$$\begin{array}{c}\hfill \begin{array}{cc}⌊\frac{X}{2^n}⌋=\hfill & {\left|m_3{\left|(-4R_1+2R_2+2R_3)\right|}_{{}_{m_1}}+\left(R_3-R_2\right)\right|}_{{}_{m_1{m}_3}}.\hfill \end{array}\end{array}$$

(10)

Recalling the identity ${\left|{\left|(.)\right|}_{{}_{m_1{m}_3}}\right|}_{{}_{m_3}}={\left|(.)\right|}_{{}_{m_3}}$ [1], then applying modulus $m_3$ to Equation (10) deletes the term $m_3{\left|(-4R_1+2R_2+2R_3)\right|}_{{}_{m_1}}$, which is an integer multiple of $m_3$. This produces

$$\begin{array}{c}\hfill \begin{array}{cc}{R}_{3s}\hfill & ={\left|R_3-R_2\right|}_{m_3}.\hfill \end{array}\end{array}$$

(11)

Defining A and v to be

$$\begin{array}{c}\hfill A={\left|-4R_1+2R_2+2R_3\right|}_{{}_{m_1}},\end{array}$$

(12)

$$v=\left\{\begin{array}{cc}1,\hfill & \mathrm{if} ((A=0)\wedge (R_3<R_2)),\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(13)

where ∧ denotes a logical AND operation, then Equation (10) can be rewritten as

$$\begin{array}{c}\hfill \begin{array}{cc}⌊\frac{X}{2^n}⌋=\hfill & {\left|m_{3}A+(R_3-R_2)\right|}_{{}_{m_1{m}_3}}.\hfill \end{array}\end{array}$$

(14)

This allows the rewriting of Equation (14) as

$$⌊\frac{X}{2^n}⌋=\left\{\begin{array}{cc}{\left|R_3-R_2\right|}_{{}_{m_1{m}_3}},\hfill & \mathrm{if} v=1,\hfill \\ m_{3}A+R_3-R_2,\hfill & \mathrm{if} v=0.\hfill \end{array}\right.$$

(15)

Equivalently, Equation (15) can be rewritten as

$$⌊\frac{X}{2^n}⌋=\left\{\begin{array}{cc}{R}_3-R_2+m_1{m}_3,\hfill & \mathrm{if} v=1,\hfill \\ m_{3}A+R_3-R_2,\hfill & \mathrm{if} v=0.\hfill \end{array}\right.$$

(16)

Recalling that $R_{2s}={\left|⌊\frac{X}{2^n}⌋\right|}_{{}_{2^n}}$, $A=0$ if $v=1$, and ${\left|m_1{m}_3\right|}_{{}_{2^n}}=1$, then applying modulus $2^n$ to Equation (16) produces

$$R_{2s}=\left\{\begin{array}{cc}{\left|{\left|R_3-R_2\right|}_{2^n}-{\left|A\right|}_{{}_{2^n}}+1\right|}_{{}_{2^n}},\hfill & \mathrm{if} v=1,\hfill \\ {\left|{\left|R_3-R_2\right|}_{2^n}-{\left|A\right|}_{{}_{2^n}}\right|}_{{}_{2^n}},\hfill & \mathrm{if} v=0.\hfill \end{array}\right.$$

(17)

Equivalently, Equation (17) is rewritten as

$$\begin{array}{c}{R}_{2s}={\left|{\left|R_3-R_2\right|}_{2^n}-{\left|A\right|}_{{}_{2^n}}+v\right|}_{{}_{2^n}}.\hfill \end{array}$$

(18)

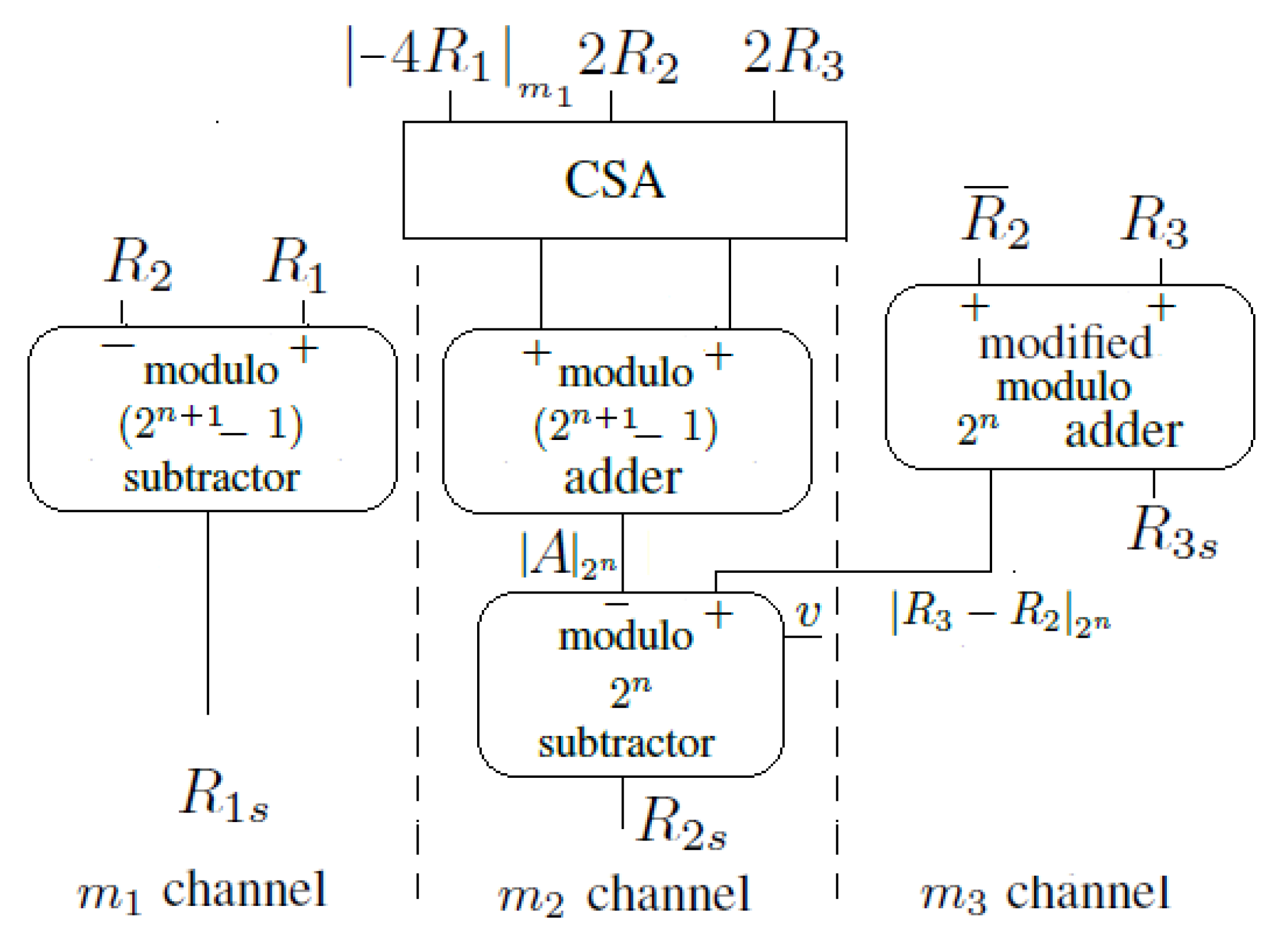
2.2. Hardware Implementation

The proposed hardware implementation of the CRT-based $2^n$ scaler of the moduli set $\{2^{n+1}-1,2^n,2^n-1\}$ is shown in Figure 1. The carry-save adder (CSA) of Figure 1 consists of $(n+1)$ full adders operating in parallel. The modulo $(2^{n+1}-1)$ adder, modulo $(2^{n+1}-1)$ subtractor, and modulo $2^n$ subtractor are described thoroughly in [19]. The modified $2^n$ modulo adder is described in the last paragraph of this section.

It is important to mention the modulo $(2^p-1)$ properties, where p is a positive integer [1]. The first property states that ${\left|2^{k}a\right|}_{(2^p-1)}$ is performed by rotating the binary representation of a to the left k-bits, where a and k are positive integers and $a<(2^p-1)$. The second property states that ${\left|-a\right|}_{(2^p-1)}$ is performed by obtaining the 1’s complement of a. Therefore, the value of ${\left|-4R_1\right|}_{m_1}$, applied to the CSA of Figure 1, is computed by rotating the binary representation of $R_1$ 2 bits to the left and then taking the 1’s complement of the rotated value. Assuming the binary representation of $R_1$ is given by $R_1=r_{1\left(n\right)}{r}_{1(n-1)}\cdots r_{1\left(1\right)}{r}_{1\left(0\right)}$, then ${\left|-4R_1\right|}_{m_1}={\overline{r}}_{1(n-2)}{\overline{r}}_{1(n-3)}\cdots {\overline{r}}_{1\left(1\right)}{\overline{r}}_{1\left(0\right)}{\overline{r}}_{1\left(n\right)}{\overline{r}}_{1(n-1)}$, where the overline $\overline{(.)}$ denotes the complement of the bit $(.)$. However, in the $m_1$ channel of Figure 1, $R_{1s}$ is obtained by rotating the output of the modulo $(2^{n+1}-1)$ adder 1 bit to the left.

The modified $2^n$ modulo adder in the $m_3$ channel is a binary adder that adds $R_3$ to ${\overline{R}}_2$. The modified adder is built as follows: The output of the parallel prefix structure of the adder is directed into two different and parallel tracks. In the first track, a 1 is added as an input carry to the output of the parallel prefix structure to produce ${\left|R_3+{\overline{R}}_2+1\right|}_{2^n}={\left|R_3-R_2\right|}_{2^n}$. In the second track, the output carry, $c_{{}_{out}}$, of the parallel prefix structure is reinserted and added as an input carry to produce $R_{3s}$ (i.e., ${\left|R_3-R_2\right|}_{(2^n-1)}={\left|R_3+{\overline{R}}_2\right|}_{(2^n-1)}={\left|R_3+{\overline{R}}_2+c_{{}_{out}}\right|}_{2^n}=R_{3s}$ [14]). A few additional gates (not shown in Figure 1) are used to verify if the condition v is true. The result of this verification is inserted as an input carry to the modulo $2^n$ subtractor in the $m_2$ channel. This input carry bit is injected into the least-significant prefix operator [19,20].

3. Comparison and VLSI Realization

There is no scaler published in the literature for the moduli set $\{2^{n+1}-1,2^n,2^n-1\}$. The new proposed scaler was compared with the most recent and efficient published scaler of the traditional moduli set $\{2^n+1,2^n,2^n-1\}$ [12,13]. The unit-gate model was used as a basis for theoretical comparison [14]. All two-input monotonic gates had an area of 1 unit and a delay of 1 unit. The XOR (Exclusive OR) and XNOR (Exclusive NOR) gates had an area of 2 units and a delay of 2 units. However, the inverters were ignored. The full adder had an area of 7 units and a delay of 4 units, while the half adder had an area of 3 units and a delay of 2 units. The $(2^p-1)$ modular adder has an area and delay of $\left(3p\lceil {log}_{{}_2}p\rceil +5p\right)$ and $\left(2\lceil {log}_{{}_2}p\rceil +3\right)$, respectively [19,20]. The area and delay of a $2^p$ binary adder are $\left(\frac{3}{2}\lceil {log}_{{}_2}p\rceil +5p\right)$ and $\left(2\lceil {log}_{{}_2}p\rceil +3\right)$, respectively [19,20]. The modified modulo $2^n$ adder has an area and delay of $\left(\frac{3}{2}p\lceil {log}_{{}_2}p\rceil +12p\right)$ and $\left(2\lceil {log}_{{}_2}p\rceil +5\right)$, respectively [19]. However, the area and delay of the $(2^p+1)$ modular adder are $\left(4.5p\lceil {log}_{{}_2}p\rceil +0.5p+6\right)$ and $\left(2\lceil {log}_{{}_2}p\rceil +3\right)$, respectively [20].

Table 1. Hardware and time requirements of the scaler proposed in this paper for $M_1=\{2^{n+1}-1,2^n,2^n-1\}$ and of the scalers proposed in [12,13] for $M_2=\{2^n+1,2^n,2^n-1\}$.

Channel	Proposed ${}^{★}$		[12] ${}^{★★}$		[13] ${}^{★★}$
	Area	Delay	Area	Delay	Area	Delay
${(2^{n+1}-1)}^{★}$	$3n\lceil {log}_{{}_2}n\rceil$	$2\lceil {log}_{{}_2}n\rceil$	$4.5n\lceil {log}_{{}_2}n\rceil$	$2\lceil {log}_{{}_2}n\rceil$	$4.5n\lceil {log}_{{}_2}n\rceil$	$2\lceil {log}_{{}_2}n\rceil$
${(2^n+1)}^{★★}$	$+5n+5$	+3	$+7.5n+6$	+7	$+3.5n+6$	+5
	$+3\lceil {log}_{{}_2}n\rceil$
$2^n$	$4.5n\lceil {log}_{{}_2}n\rceil$	$4\lceil {log}_{{}_2}n\rceil$	$3n\lceil {log}_{{}_2}n\rceil$	$2\lceil {log}_{{}_2}n\rceil$	$3n\lceil {log}_{{}_2}n\rceil$	$2\lceil {log}_{{}_2}n\rceil$
	$+20n+5$	$+10$	$+26n$	$+13$	$+23n$	$+9$
	$+3\lceil {log}_{{}_2}n\rceil$
$2^n-1$	$1.5n\lceil {log}_{{}_2}n\rceil$	$2\lceil {log}_{{}_2}n\rceil$	$3n\lceil {log}_{{}_2}n\rceil$	$2\lceil {log}_{{}_2}n\rceil$	$3n\lceil {log}_{{}_2}n\rceil$	$2\lceil {log}_{{}_2}n\rceil$
	$+12n$	$+5$	$+5n$	$+3$	$+5n$	$+3$
Total	$9n\lceil {log}_{{}_2}n\rceil$	$4\lceil {log}_{{}_2}n\rceil$	$10.5n\lceil {log}_{{}_2}n\rceil$	$2\lceil {log}_{{}_2}n\rceil$	$10.5n\lceil {log}_{{}_2}n\rceil$	$2\lceil {log}_{{}_2}n\rceil$
	$+37n+10$	$+10$	$+38.5n+6$	$+13$	$+31.5n+12$	$+9$
	$+6\lceil {log}_{{}_2}n\rceil$

lists the area and time delay requirements of the proposed scaler and those in [12,13].

To obtain a more precise estimation of the area, delay, and power for the three designs under consideration, all the structures were modeled in Verilog HDL(Hardware Description Language) for values of $n=6,12,18,24,$ and 30. Synopsys Design Compiler (G-2012.06) was used to synthesize the designs and map them into 65 nm Synopsys DesignWare Digital Logic Libraries. The “place-and-route” phase was performed using the Synopsys IC Compiler. The Synopsys Power Compiler was also used to estimate the power consumed. Moreover, the Synopsys Simulator was used to verify the correctness of the design functionality. The results are shown in

Table 2. VLSI (Very Large Scale Integration) implementation results of the proposed scaler of the moduli set ${\{2^{n+1}-1,2^n,2^n-1\}}^{★}$ and the scalers of [12,13] of the moduli set ${\{2^n+1,2^n,2^n-1\}}^{★★}$.

Scaler		Area	Delay	Power
	n	($\mathsf{\mu }$m${}^2$)	(ps)	($\mathsf{\mu }$W)
Proposed ${}^{★}$	6	1769.4	626.3	61.5
	12	3706.6	723.7	90.1
	18	5928.1	875.1	120.6
	24	7056.2	902.9	143.4
	30	8097.9	925.6	160.7
[12] ${}^{★★}$	6	2084.1	575.4	67.9
	12	4210.6	662.3	102.5
	18	6747.9	776.5	140.4
	24	7883.4	797.8	160.7
	30	9419.2	809.3	183.1
[13] ${}^{★★}$	6	1892.1	555.7	65.2
	12	3988.0	633.5	96.5
	18	6241.0	757.9	129.3
	24	7389.4	782.7	152.4
	30	8675.2	803.6	169.8

. The relative differences between the three designs (i.e., the proposed scaler [12,13]) are listed in

Table 3. Relative performance of the proposed scaler compared with [12,13].

Proposed Scaler		Area	Delay	Power
Compared with:	n	Reduction (%)	Reduction (%)	Reduction (%)
[12]	6	15.1	−8.8	9.4
	12	12.0	−9.3	12.1
	18	12.1	−12.7	14.1
	24	10.5	−13.2	10.8
	30	14.0	−14.4	12.2
[13]	6	6.5	−12.7	5.7
	12	7.1	−14.2	6.6
	18	5.0	−15.5	6.7
	24	4.5	−15.4	5.9
	30	6.7	−15.2	5.4

. Compared to the scaler of [12], Table 3 indicates that, on average, the proposed scaler had a area and power reduced by $12.7\%$ and $11.7\%$, respectively. The proposed scaler had, on average, an increased time delay of $11.7\%$. Compared to the scaler of [13], Table 3 shows that the proposed scaler required a slightly smaller area and power, by $5.9\%$ and $6.1\%$, respectively. However, it required an average time delay increase of $14.6\%$. Nevertheless, as mentioned in Section 1, avoiding the $(2^n+1)$ MAC unit and replacing it with the $(2^{n+1}-1)$ MAC unit saves a very significant processing time [18].

4. Conclusions

This paper proposes the first scaler for the moduli set $\{2^{n+1}-1,2^n,2^n-1\}$. When compared with the most recent and efficient scalers of the traditional three-moduli set $\{2^n+1,2^n,2^n-1\}$, the proposed scaler is proven to have an area- and power-efficient structure. However, the scalers of the traditional moduli set $\{2^n+1,2^n,2^n-1\}$ are more-time-efficient structures at the expense of having the modulo $(2^n+1)$ channel. Replacing the $(2^n+1)$ channel by the $(2^{n+1}-1)$ channel makes the proposed moduli set a faster alternative for RNS-based applications.