A New Strategy for Energy Saving in Spectrum-Sliced Elastic Optical Networks ^†

Abstract

In this paper, we propose a new approach for energy saving in Elastic Optical Networks (EONs) under physical impairments based on MILP solving instances. First, we seek to maximize the attended traffic on the network whereas the blocking probability is maintained below a defined limit. Hence, the next step is to minimize the power consumption on the network. The proposed MILP-based algorithm models the RMLSA problem and considers transponders, optical cross-connects (OXCs), and optical amplifiers as the physical components with influence on network optimization. The results show that our approach offers, on average, a reduction of up to 7.7% of the power consumed on the four moderate networks analyzed.

1. Introduction

WDM (Wavelength Division Multiplexing) transmission systems emerged in the late 70s to deal with the mismatch between the capacity of the transmission/reception of electrical transceivers (on the order of a few gigabits per second—Gbps) and the available bandwidth in optical fibers (of the order of a few terahertz—THz) [1]. Due to its simplicity and low cost, WDM technology was immediately used in peer-to-peer systems, first-generation optical networks (for example, SONET and SDH networks), and subsequently, in optical networks with wavelength routing (WRN), packet switching (OPS), or burst switching (OBS) [1,2].

Wavelength routing networks arose as a development of peer-to-peer when routing functions were introduced in the photonic domain. The success of these networks was such that today there are already many of them deployed and interconnected [1]. OPS and OBS networks use the time domain to share network resources, and thus, achieve statistical multiplexing gains. Consequently, OPS and OBS achieve improved spectrum utilization when compared with WRN networks. However, OPS networks are still seen as networks for the long-term as the technologies necessary for its implementation are still in the maturing stage, while OBS networks, although they have been released commercially, have not found success in the marketplace. WRN networks are still the most viable solution, currently used to transport large amounts of information over long distances and, therefore, much of the research in optical networks is still directed to them. In addition to the time domain, explored in the OPS and OBS technology, the spectral domain can be naturally operated to achieve greater flexibility and granularity transmission efficiency for WRN networks. The current optical communication systems use signals with On-Off Keying encoding (OOK), where 0 and 1 bits are encoded respectively by the presence and absence of light [1]. Despite its simplicity to be generated and detected, this encoding has a low spectral efficiency which limits the capacity utilization of optical fibers. To illustrate this fact, it is sufficient to note that a WDM commercial system with 10 Gbps channels allocated to a band of 50 GHz has a spectral efficiency of only 0.2 bps/Hz (10 Gbps/50 GHz); whereas the Shannon theorem states that this efficiency could reach levels of 7 bps/Hz [1] in optical systems.

According to Reference [1], so that the efficiency of optical systems approach this theoretical limit, it becomes necessary to use more sophisticated ways of using the available spectrum. One solution would be the use of advanced modulation formats and digital equalization in the electrical field, as these provide much higher spectral efficiencies than OOK systems. Some studies advanced in this direction [1], however, the insistence on the rigid spectral granularity of WDM systems makes it excessively difficult to maintain an efficient spectrum allocation for optical networks. This is because it is difficult to match the network resources and bandwidth necessary to meet the reporting requirements in an optical network with a hard spectrum. It is easy to see that in a system with different transmission rates, there is no single spectral spacing that is great for all data rates and the distances involved. These requirements suggest that optical networks are more flexible in relation to the data rate, more nimble, reconfigurable, and efficient on the allocation of resources.

Given this limitation due to the rigidity of the WDM grid, several recent studies [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] evaluated the use of optical network architectures that occupy the bandwidth in a more flexible, efficient, and scalable way, such as Spectrum-Sliced Elastic Optical Path Networks (SLICE), or simply Elastic Optical Networks (EONs) [18].

In this context, this paper proposes a new algorithm based on subsequent optimizations—through a new modified MILP (Mixed Integer Linear Programming) formula—to reduce the power consumption of an Elastic Optical Network—during its plan—while maintaining the blocking probability below a predefined threshold.

The following Sections are organized as follows. Section 2 presents the basic characteristics of Elastic Optical Networks. Section 3 provides an overview of the characteristics of the analyzed problem. Section 4 presents the basic optimization model used as a reference. In Section 5, the proposed power consumption model is presented. A modified formulation is introduced in Section 6. Section 7 presents the MILP-based algorithm and the simulations and results are discussed in Section 8. Finally, the conclusions are presented in Section 9, followed by references.

2. Elastic Optical Networks

SLICE networks use the O-OFDM modulation technology, allowing the allocation of optical channels with variable bandwidth through the use of appropriate optical tunable filters and routers. The essential idea is to not use a fixed grid of wavelengths (thus termed gridless). In addition, they must possess management and network elements capable of providing flexible bandwidth to the optical paths such that they can be allocated to any bandwidth, and can expand and contract freely according to the traffic volume and user requests.

These novel networks were introduced in Reference [18] and are also known in the literature as networks without a gridded, adaptive, spectrum-flexible, elastic optical paths, or simply Elastic Optical Networks (EONs). In them, the fiber spectrum is treated as a continuing resource, allowing greater compression and efficiency in the use of it. Basically, the optical path can be allocated to any continuous frequency range and must be separated from other optical paths by a guard band called Filter Guard Band (FGB). Wavelength-Selective Switches (WSS) and variable bandwidth optical filters are used for switching and filtering the flexible bandwidths [19]. Thus, along with the route, a sufficient amount of spectrum must be allocated for the creation of an optical path with appropriate transmission capacity. Finally, transmitters and receivers need to also be adapted to the flexibility of the spectrum usage available on the EON architecture.

3. Problem Characterization

Currently, some references in the literature emphasize the importance of energy efficiency in the operation of elastic optical networks, like References [20,21,22,23,24,25,26]. However, none of them evaluate the consumption of the network that is subject to adaptive modulation and the simultaneously spontaneous emission noise.

3.1. Adaptive-Modulation

Several authors have shown that adaptive-modulation provides considerable savings of elastic optical network resources [27,28,29] when considering the signal range and link distance to be traveled. However, the first to assess the real impact of the different modulation formats in the planning of the network was Reference [30]. They considered, besides the adaptive-modulation, the effect of spontaneous emission noise generated by the span between optical amplifiers.

Table 1. The modulations characteristics.

Modulation Format	Spectral Efficiency (bps/Hz)	Spectral Capacity (Gbps)
BPSK	1	12.5
QPSK	2	25
8-QAM	3	37.5
16-QAM	4	50
32-QAM	5	62.5
64-QAM	6	75

exemplifies the characteristics (spectral efficiency and data rate) of the six types of OFDM modulation.

The lower the spectral efficiency of the modulation, the larger the range and the lower the data rate. Thus, the necessary bandwidth for transmission will be major. It characterizes the trade-off between range and spectrum usage.

3.2. Amplified Spontaneous Emission Noise

In Reference [30], a MILP formulation, which considers the effect of amplified spontaneous emission noise (ASE noise) generated by the optical span between amplifiers, is presented. It is assumed that the performance of transmission systems are limited by two factors: (I) The accumulation of amplified spontaneous emission noise when a signal propagates through a link; and (II) the maximum finite power available for each channel, represented by the maximum threshold of the total noise emitted.

3.3. Power Consumption

In this paper, the concepts of adaptive modulation and spontaneous emission noise are integrated into the concept of power consumed by the EON elements in a new MILP formulation, which will be described in Section 6.

4. Optimization Model (RMLSA)

While performing a network planning with an emphasis on resource optimization, a SLICE network with multiple modulation formats provides a trade-off between the range of the optical path, the modulation format, and the number of slots demanded on the network. An appropriate model to quantify this trade-off was presented in Reference [30] which we will call “traditional MILP” for comparison purposes. Additionally, a model to measure the total power consumed on the network, described below, will be added to the traditional MILP.

5. Power Consumption Model

The power consumption model proposed in this paper considers amplifiers, transceivers, and optical cross-connects (OXCs) as components of the physical layer with the greatest influence on the optimization, as in Reference [23,24,25]. In this context, the total power consumed by the optical layer is given by the following:

$${\mathrm{PC}}_{\mathrm{total}}={\mathrm{PC}}_{\mathrm{OFDM}}+{\mathrm{PC}}_{\mathrm{OXC}}+{\mathrm{PC}}_{\mathrm{AMP}}$$

(1)

The power consumed by the transceivers (${\mathrm{PC}}_{\mathrm{OFDM}}$) is given by the following equation [24]:

$${\mathrm{PC}}_{\mathrm{OFDM}}=1.683\mathrm{\times }\mathrm{TR}+91.333\left[\mathrm{W}\right],$$

(2)

where $\mathrm{TR}$ is the transceiver transmission rate for the used modulation. The power consumed by the optical cross-connects (${\mathrm{PC}}_{\mathrm{OXC}}$) is given by [23] the following:

$${\mathrm{PC}}_{\mathrm{OXC}}=\mathrm{N}\times 85+\mathsf{\alpha }\times 100+150\left[\mathrm{W}\right],$$

(3)

where $\mathrm{N}$ is the physical degree of the OXC node (the number of connected fibers to the node) and α is the virtual degree of the OXC (the number of channels that can be inserted/deleted). Finally, the power consumed by each amplifier (${\mathrm{PC}}_{\mathrm{AMP}}$) is 30 W for each direction of the flow in the fiber [24]. Using these equations, it is possible to measure the total power consumed in the network while maximizing the amount of served traffic on the network.

6. Modified Formulation

Once the primary objective of the traditional formulation, which is to get the highest value for the attended demand (max($C_a$)), that is, to reduce to the maximum the blocking probability ($P_{block}$), is achieved, the next step is to minimize the power consumed in the network using that data as the input to the model. For this, it will be introduced as a new model, which we will call the “modified MILP”, described below.

6.1. Notation

• i and j denote the originating and terminating nodes, respectively, of a variable bandwidth (in terms of slots) lightpath.
• m and n denote the endpoints of a physical link in the network.
• z denotes the modulation format.

6.2. Given

• N: the number of nodes in the network.
• Λ^ij: the traffic matrix element, which denotes the traffic intensity (in bps) demanded from the source node i to the destination node j.
• d_mn: the physical topology, which represents the distance of the fiber interconnecting node m to n.
• MS: the capacity of each fiber. The maximum number of slots per link.
• GC: the filter guard band, which is the minimum spectrum width between wavebands (in terms of the number of slots).
• Ω: Slot width, which informs the slot width in Hz.
• E(z)max: the limit of the total cumulative spontaneous emission noise on a signal with “z” modulation format.
• l: the length of the fiber span between two amplifiers.
• f(l): the spontaneous emission noise produced by an amplifier to compensate a span with length l.
• ε_z: the spectral efficiency (bps/Hz) for “z” modulation format.
• K: a larger number to be used to make some integer variables.
• $P{C}_{{OXC}_m}$: the power consumed by OXC_m.
• $PC$_amp: the power consumed by each optical amplifier.
• N_amp: the number of amplifiers on the network.
• $G{f}_{mn}$: the binary variable used to account the degree of the node.
• $N_m$: the physical degree of node m (number of connected fibers to the node).
• α: the virtual degree of OXC (number of channels that can be inserted/deleted).
• The blocking probability:

  $${\mathrm{P}}_{\mathrm{block}}=1-\left(\max \left({\mathrm{C}}_{\mathrm{a}}\right)/{\mathrm{C}}_{\mathrm{r}}\right),$$

  (4)

  where max(${\mathrm{C}}_{\mathrm{a}}$) is the attended demand (Gbps) obtained by running the traditional MILP and ${\mathrm{C}}_{\mathrm{r}}$ is the total requested demand (Gbps) on the network.

6.3. Variables

• Lightpath bandwidth b_ijz: the bandwidth in terms of the number of slots of an elastic lightpath from node i to node j with “z” modulation format.
• Physical topology route ${\mathrm{P}}_{\mathrm{mn}}^{\mathrm{ijz}}$: the amount of bandwidth that the lightpath from node i to node j with “z” modulation format uses in fiber link m-n.
• f(i,j,z): the total cumulative spontaneous emission noise of a lightpath from node i to node j with the “z” modulation format.
• A binary variable ${\mathrm{A}}_{\mathrm{mn}}^{\mathrm{ijz}}$ to indicate whether the lightpath from node i to node j with “z” modulation format passes through a link m − n. ${\mathrm{A}}_{\mathrm{mn}}^{\mathrm{ijz}}$ equals 1 if ${\mathrm{P}}_{\mathrm{mn}}^{\mathrm{ijz}}$ > 0 and equals 0 if ${\mathrm{P}}_{\mathrm{mn}}^{\mathrm{ijz}}$ = 0.
• M_ijz: a binary variable to indicate which of the “z” modulation formats was used on the lightpath from node i to node j.
• TR_ijz: the transmission rate of the transceiver which sends the optical path (i,j) with modulation “z”.
• ${\mathrm{PC}}_{{\mathrm{OFDM}}_{\mathrm{ijz}}}$: the power consumed by each transceiver BV (Bandwidth Variable).
• $PC$_total: the total power consumed.

6.4. Modified MILP Formulation

Minimize:

$${\mathrm{PC}}_{\mathrm{total}}={\displaystyle \sum }_{\mathrm{m}}{\mathrm{PC}}_{{\mathrm{OXC}}_{\mathrm{m}}}+{\displaystyle \sum }_{\mathrm{ij}}\left[{\displaystyle \sum }_{\mathrm{z}}{\mathrm{PC}}_{{\mathrm{OFDM}}_{\mathrm{ijz}}}\right]+{\mathrm{N}}_{\mathrm{amp}}\times {\mathrm{PC}}_{\mathrm{amp}}$$

(5)

Subject to:

$${{\displaystyle \sum }}_{\mathrm{n}}{\mathrm{P}}_{\mathrm{mn}}^{\mathrm{ijz}}-{{\displaystyle \sum }}_{\mathrm{n}}{\mathrm{P}}_{\mathrm{nm}}^{\mathrm{ijz}}=\{-\begin{array}{cc}{\mathrm{b}}_{\mathrm{ijz}}& \mathrm{if}\mathrm{m}=\mathrm{i}\\ {\mathrm{b}}_{\mathrm{ijz}}& \mathrm{if}\mathrm{m}=\mathrm{j}\\ 0& \mathrm{if}\mathrm{m}\ne \mathrm{i},\mathrm{j}\end{array}\forall \mathrm{m},\mathrm{i},\mathrm{j},\mathrm{z}$$

(6)

$${{\displaystyle \sum }}_{\mathrm{ij}}({\mathrm{P}}_{\mathrm{mn}}^{\mathrm{ijz}}+\mathrm{FGB}\times {\mathrm{A}}_{\mathrm{mn}}^{\mathrm{ijz}})\le \mathrm{MS}\forall \mathrm{m},\mathrm{n},\mathrm{z}$$

(7)

$${\mathrm{A}}_{\mathrm{mn}}^{\mathrm{ijz}}\ge {\mathrm{P}}_{\mathrm{mn}}^{\mathrm{ijz}}/\mathrm{M}\forall \mathrm{i},\mathrm{j},\mathrm{m},\mathrm{n},\mathrm{z}$$

(8)

$${\mathrm{M}}_{\mathrm{ijz}}\ge {\mathrm{b}}_{\mathrm{ijz}}/\mathrm{M}\forall \mathrm{i},\mathrm{j},\mathrm{z}$$

(9)

$${{\displaystyle \sum }}_{\mathrm{z}}{\mathrm{M}}_{\mathrm{ijz}}\le 1\forall \mathrm{i},\mathrm{j}$$

(10)

$${\mathrm{b}}_{\mathrm{ijz}}\ge {\mathrm{M}}_{\mathrm{ijz}}\times {Ʌ}_{\mathrm{ij}}\times (1/{\mathsf{\epsilon }}_{\mathrm{z}})\times (1/\mathsf{\Omega })\forall \mathrm{i},\mathrm{j},\mathrm{z}$$

(11)

$${{\displaystyle \sum }}_{\mathrm{mn}}[({\mathrm{A}}_{\mathrm{mn}}^{\mathrm{ijz}}\times {\mathrm{d}}_{\mathrm{mn}})/\mathrm{l}]\times \mathrm{f}\left(\mathrm{l}\right)=\mathrm{f}\left(\mathrm{i},\mathrm{j},\mathrm{z}\right)\forall \mathrm{i},\mathrm{j},\mathrm{z}$$

(12)

$$\mathrm{f}\left(\mathrm{i},\mathrm{j},\mathrm{z}\right)\le \mathrm{E}\left(\mathrm{z}\right)\max \forall \mathrm{i},\mathrm{j},\mathrm{z}$$

(13)

$${\mathrm{PC}}_{{\mathrm{OXC}}_{\mathrm{m}}}={\mathrm{N}}_{\mathrm{m}}\times 85+\mathsf{\alpha }\times 100+150\left[\mathrm{W}\right]\forall \mathrm{m}$$

(14)

$${\mathrm{Gf}}_{\mathrm{mn}}=\{\begin{array}{cc}1,\hfill & \hfill {\mathrm{D}}_{\mathrm{mn}}>0\\ 0,\hfill & \hfill \mathrm{else}\end{array}\forall \mathrm{m},\mathrm{n}$$

(15)

$${\mathrm{N}}_{\mathrm{m}}={\displaystyle \sum }_{\mathrm{n}}{\mathrm{Gf}}_{\mathrm{mn}}\forall \mathrm{m}$$

(16)

$${\mathrm{PC}}_{{\mathrm{OFDM}}_{\mathrm{ijz}}}=1.683\times {\mathrm{TR}}_{\mathrm{ijz}}+{\mathrm{M}}_{\mathrm{ijz}}\times 91.333\left[\mathrm{W}\right]$$

(17)

$${\mathrm{TR}}_{\mathrm{ijz}}={\mathrm{M}}_{\mathrm{ijz}}\times {\mathsf{\epsilon }}_{\mathrm{z}}\times \mathsf{\Omega }\forall \mathrm{i},\mathrm{j},\mathrm{z}$$

(18)

$${\mathrm{PC}}_{\mathrm{amp}}=30\left[\mathrm{W}\right]$$

(19)

$${\mathrm{N}}_{\mathrm{amp}}={\displaystyle \sum }_{\mathrm{mn}}{\mathrm{d}}_{\mathrm{mn}}/{\mathrm{l}}_{\mathrm{amp}}$$

(20)

7. MILP-Based Algorithm

In this Section, an algorithm (Algorithm 1) is presented for solving various optimization goals using the MILP formulations previously presented in the subsequent steps (min MS, max Ca, min P_total), where MS is the maximum number of sub-carriers in a physical network link.

Algorithm 1: The MILP-based algorithm

Step 1: Run the traditional MILP to find the value of [min MS] having Pblock_limit as a parameter; Step 2: Set an MS values vector in which the elements are greater than [min MS] to meet Pblock_limit defined in the previous step; Step 3: Run the traditional MILP to find the value of the objective function [max Ca] and the value of PCtraditional for the vector of values chosen, MS; Step 4: With the value of [max Ca], we run the modified MILP to find the value of the new objective function [min PCmodified] for the same set of the values of MS; Step 5: Stop and show PCtraditional, PCmodified, ΔPC = [PCtraditional − PCmodified], and ΔPCperc = [ΔPC/PCtraditional].

In Steps 1 and 2, the vector of the MS values to be considered in view of the predefined maximum blocking probability (P_{block_limit}) is defined. Step 3 obtains the max Ca value—to be used as a parameter in Step 4—and the amount of power consumed by the traditional MILP (PC_traditional). In Step 4, the value of the power consumed with the modified MILP (PC_modified) is obtained. Finally, in Step 5 the absolute power savings (ΔPC) and the power savings percentage (ΔPC_perc) on the network is calculated.

8. Simulations and Results

The simulations were made in small networks (6NET) and large networks (NSFNET, ARPANET, Brazilian and COST239) using the AMPL programming language under the IBM simulation platform ILOP CPLEX Optimization Studio v.12.5, with an Intel Core processor I5-3230M (2.60 GHz), 4 G RAM, and a Windows 10 operational system, (64-bit). They were limited to 5 min to prevent high simulation times on large networks. The results are presented below.

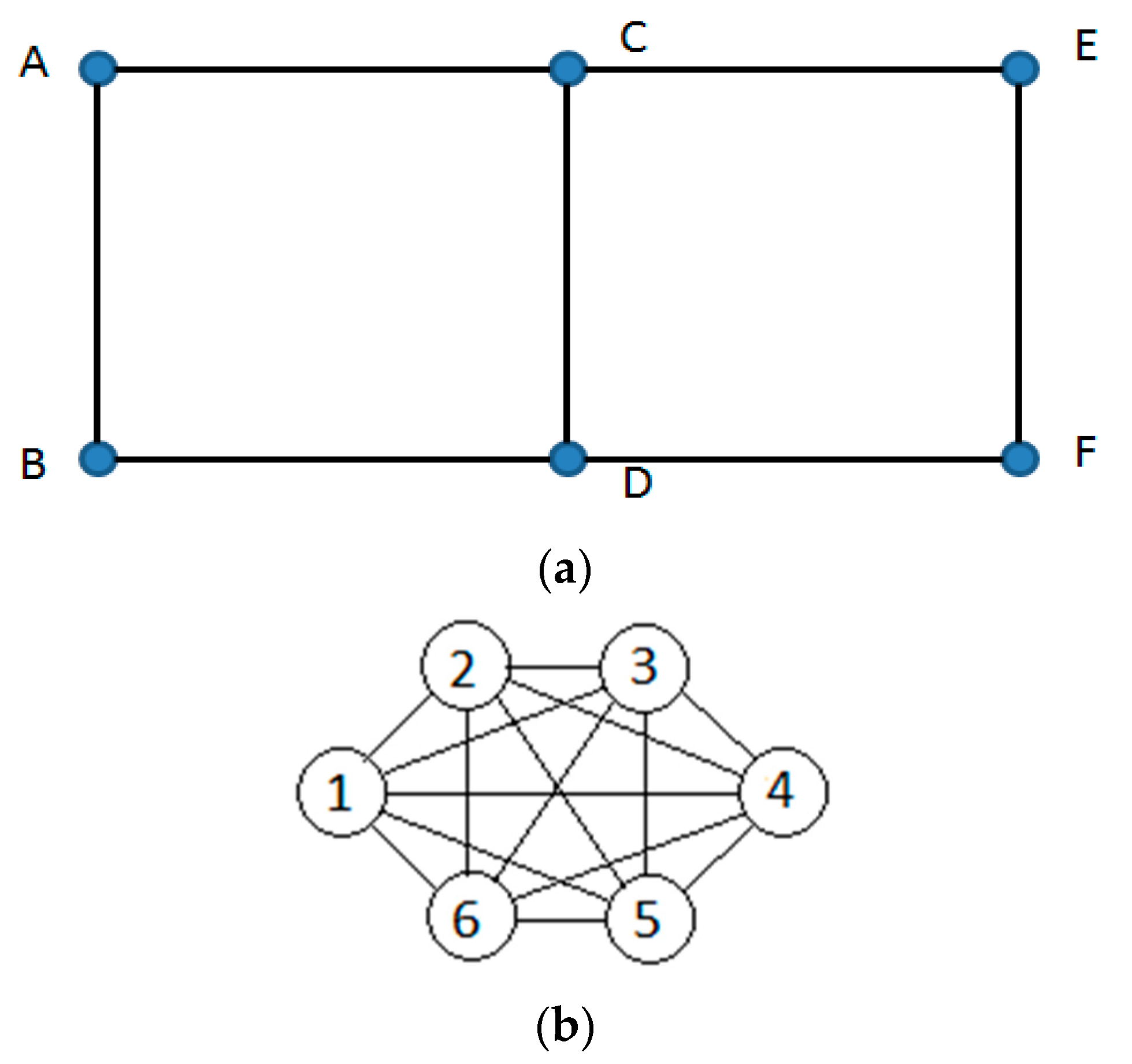
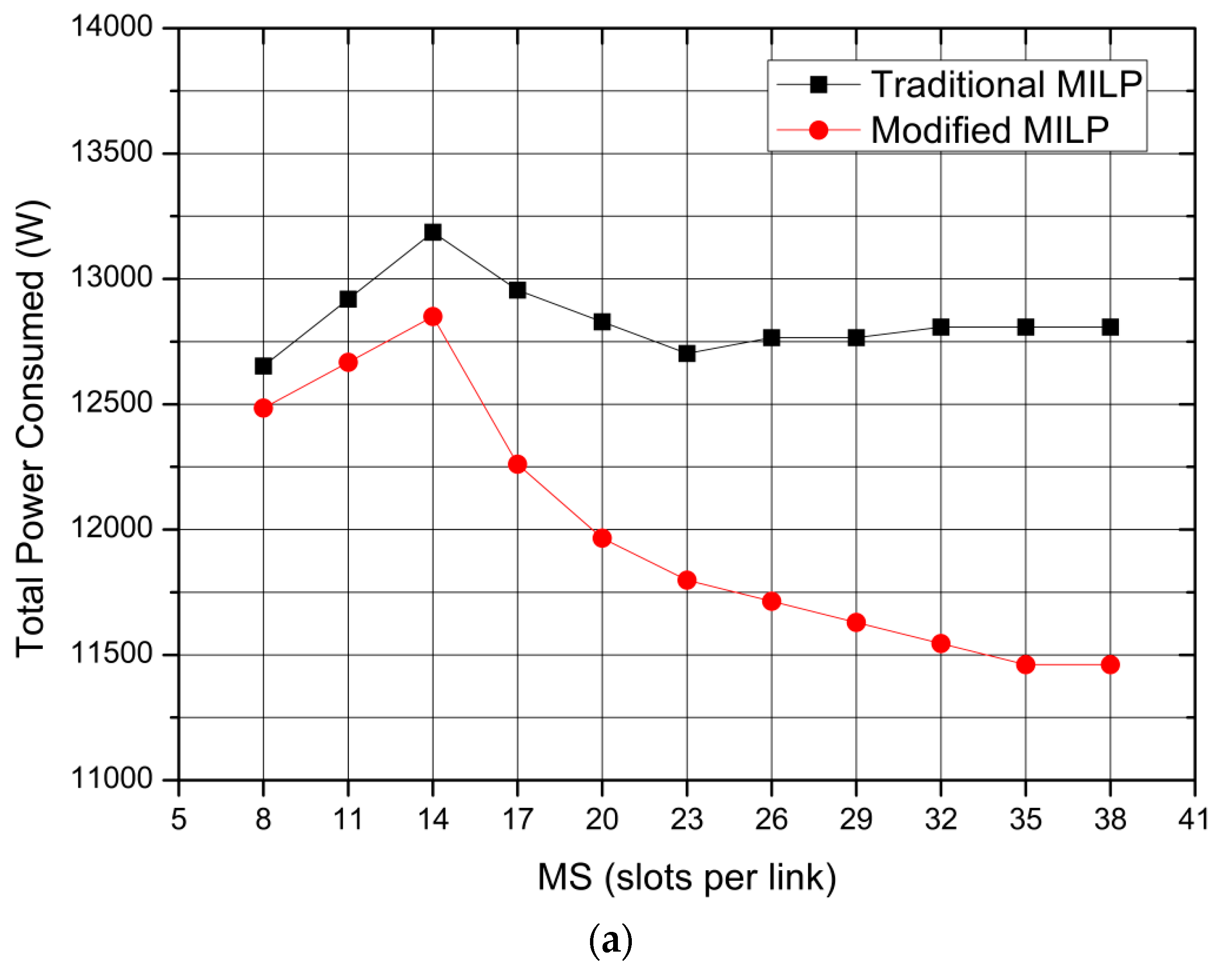
8.1. Small Network (6NET)

To evaluate the effectiveness of the proposed problem, we used two physical topologies, shown in Figure 1 below.

It is assumed that there is a pair of bidirectional fibers on each link and a distance of 1000 km between nodes. The guard band is FGB = 1 slot and the spectral width of the slot is Ω = 12.5 GHz. The requested traffic demand is uniform and equals 100 Gbps for each pair source–destination. The distance between amplifiers is l = 100 km with normalized spontaneous emission noise, f(l) = 1 (noise unit). Three different modulation formats were used (M₁ = BPSK, M₂ = QPSK and M₃ = 16-QAM) with spectral efficiencies ε₁ = 1, ε₂ = 2 and ε₃ = 4 (bps/Hz), where the noise threshold for each modulation is E(1)_max = 40, and E(2)_max = 30, and E(3)_max = 20 (noise units). The virtual degree of OXC (α) was considered to be equal to 3.

Figure 2 shows the total power consumed in the function of the number of slots per link in two different scenarios: with traditional MILP, disregarding the minimization of power, and the modified MILP. For 6NET, the maximum blocking probability was defined at 20%, resulting in the restriction of MS as being ≥ 7. Thus, the demand satisfied according to the capacity of the links is maintained above the blocking threshold due to the sequencing of the proposed algorithm. It is important to emphasize that, as the MS increases, the blocking probability decreases to become zero in MS = 13 for 6NET (this point we shall call MS_zero). It can be seen in Figure 2a that, from this point, the power consumed in the network tends to decrease due to the relaxation of the restriction related to the fiber capacity arising from the increase in MS. For 6MESH, the maximum blocking probability was defined at 0% with MS ≥ 2. The results for this network are shown in Figure 2b.

With this new approach for 6NET, the network power saving gets to be of the order of 1.3 KW at the points where MS ≥ 35, which represents a percentage saving of 10.5%. The average saving for the defined MS vector is 6.6%. Already for 6MESH, 1 KW is saved with MS ≥ 35, which results in a 5.3% saving and, for the defined vector, a 6.83% average saving. These prove the efficiency of the proposed modified MILP formulation for small networks.

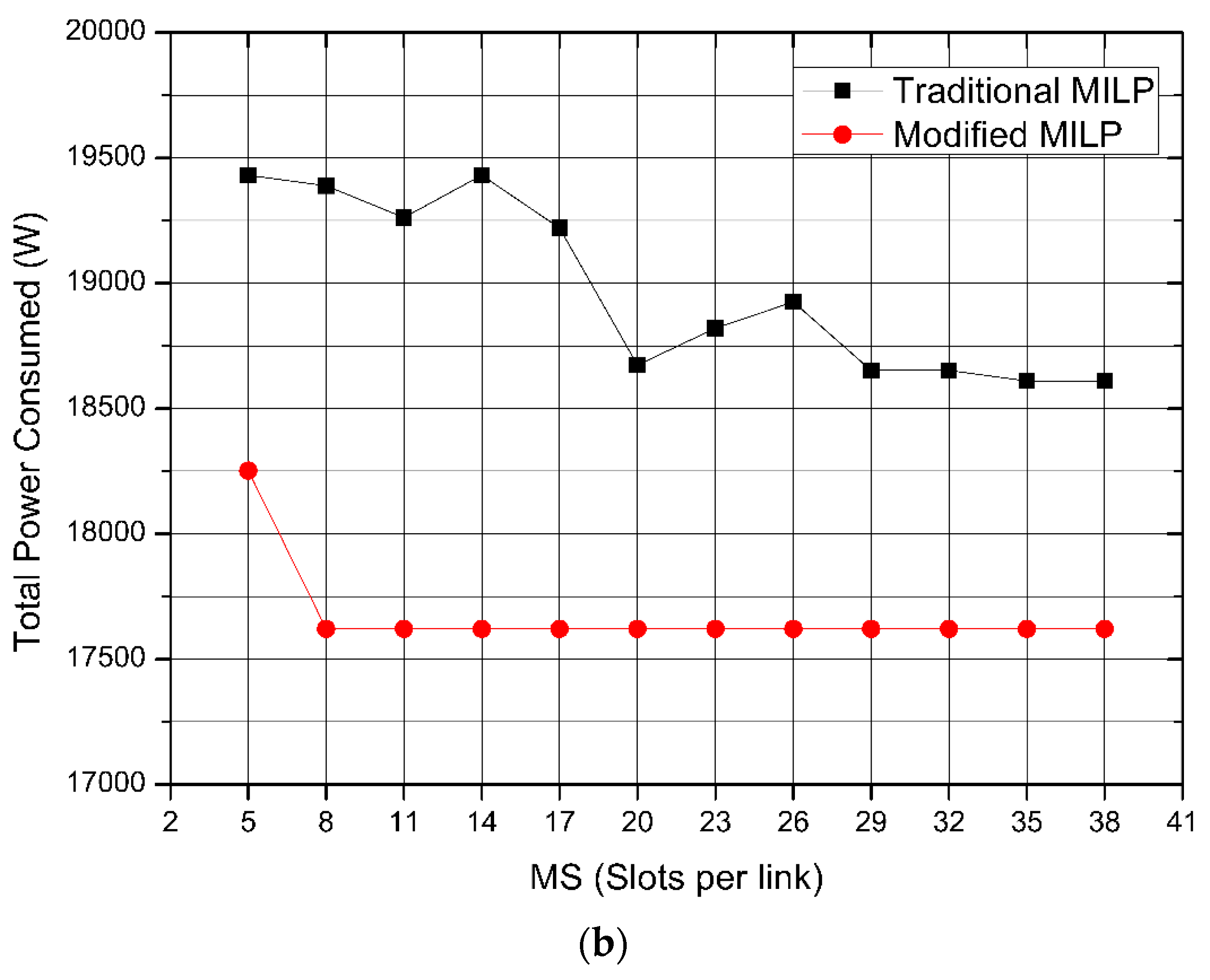
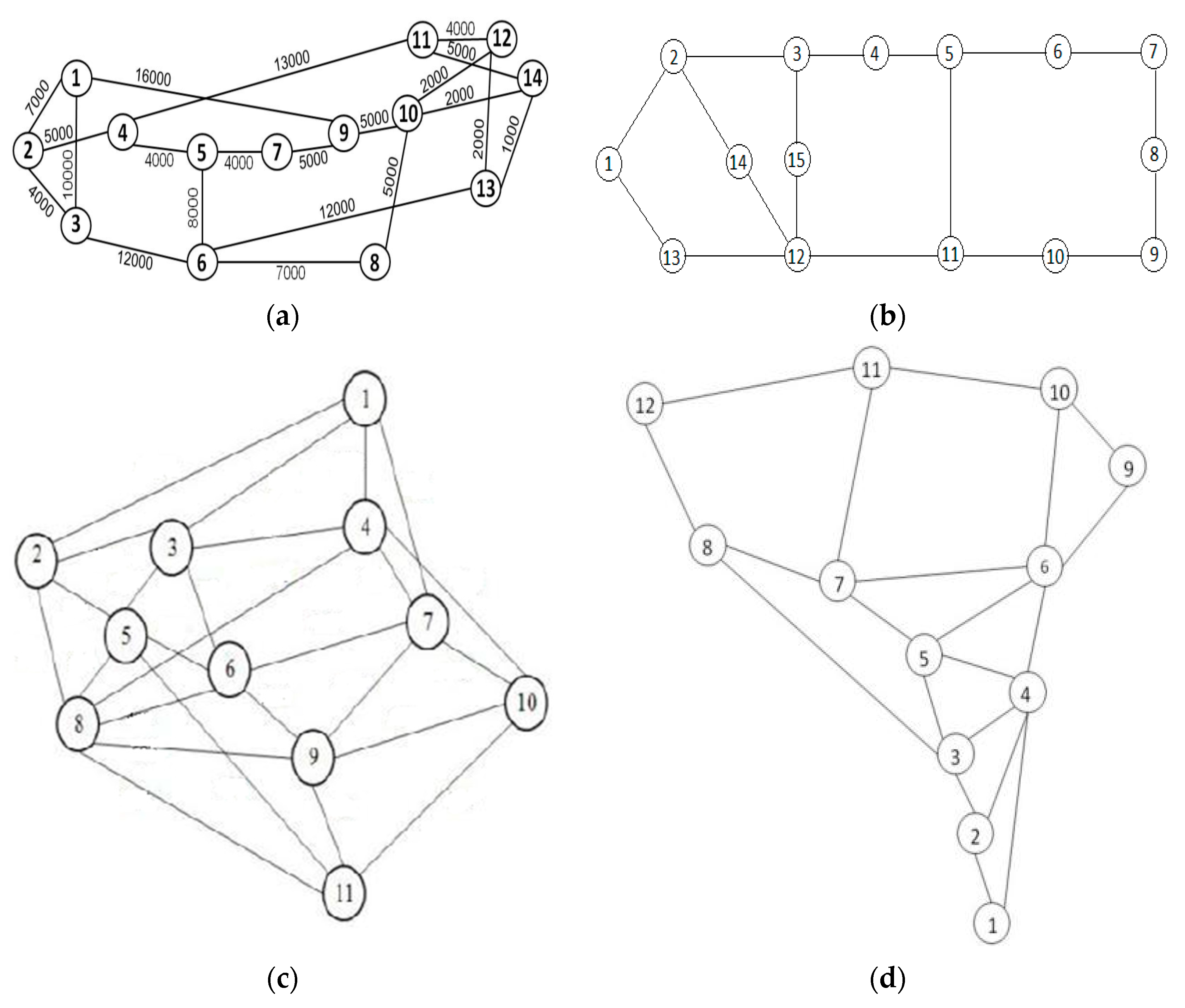
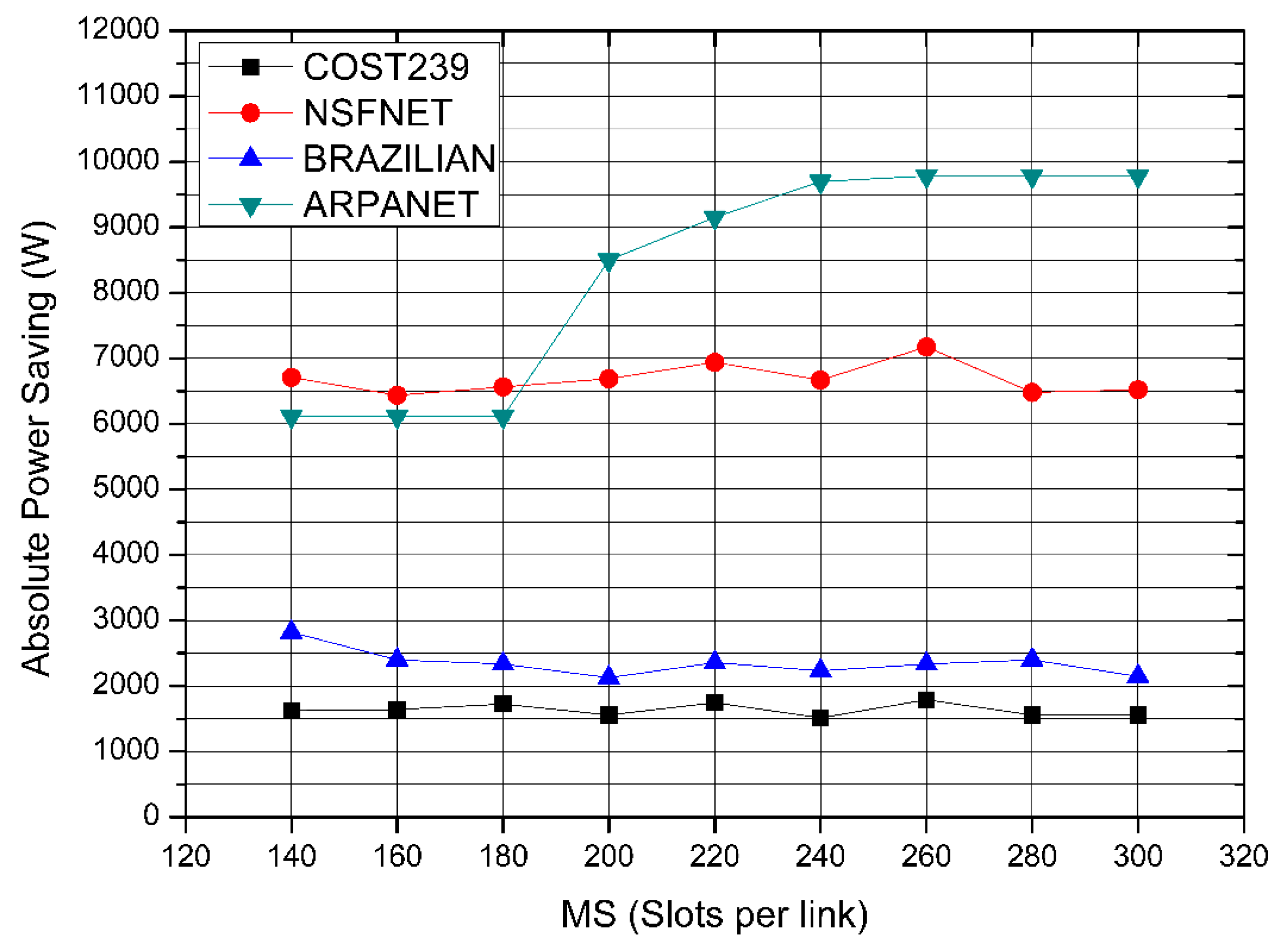
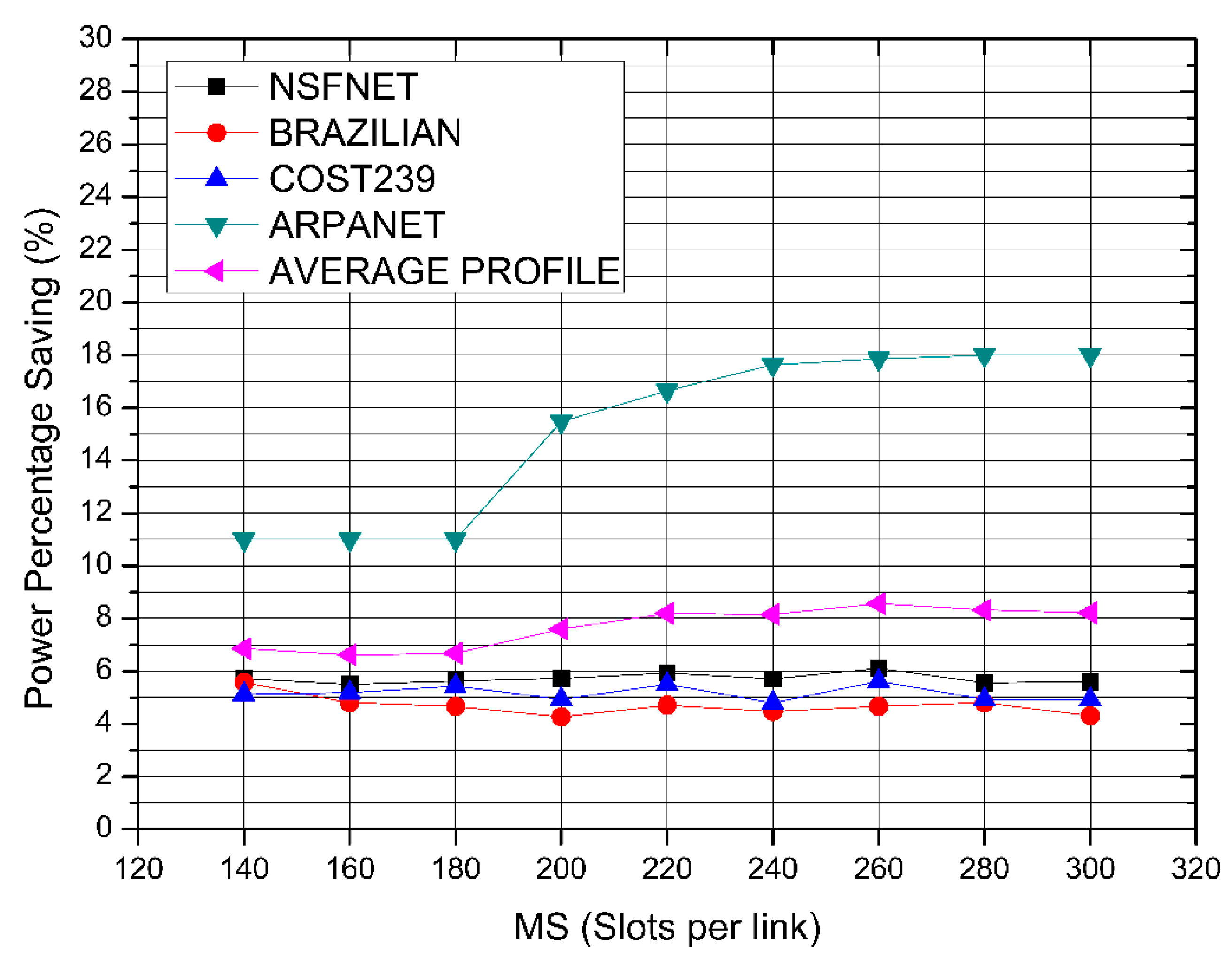
8.2. Moderate Sized Networks

In this Section, the results of the simulations in the four hypothetical moderate networks are presented (Figure 3).

For NSFNET, the noise limits are E(1)_max = 800, E(2)_max = 600, and E(3)_max = 300 (noise units) and the traffic demand, shown in

Table 2. The traffic demand for the NSFNET network (Gbps).

Node	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1		100	100	100	100	100	200	200	100	200	50	200	100	200
2	200		50	100	200	200	200	100	50	200	200	100	200	50
3	200	100		200	200	50	100	200	200	200	100	50	200	200
4	100	200	50		200	100	200	200	50	100	200	200	200	100
5	50	200	200	100		200	50	200	100	200	200	50	100	200
6	200	200	100	50	200		200	100	200	50	200	100	200	200
7	50	100	200	200	200	100		50	200	200	100	200	50	200
8	100	200	200	50	100	200	200		200	100	50	200	200	100
9	200	50	200	100	200	200	50	100		200	200	200	100	50
10	200	200	100	200	50	200	100	200	200		50	100	200	200
11	200	100	50	200	200	100	200	50	200	100		200	200	50
12	100	200	200	200	100	50	200	200	100	200	50		200	100
13	200	200	50	100	200	200	200	100	50	200	200	100		200
14	50	200	100	200	200	50	100	200	200	200	100	50	200

, is the same as that defined in Reference [30].

Already for ARPANET, the noise limits are E(1)_max = 1200, E(2)_max = 800, and E(3)_max = 400 (noise units). The length of the links (d_mn) is uniform and equals 1000 km and the traffic demand for each source-destination pair was defined randomly between 50 and 200 Gbps. For COST239, the noise limits are E(1)_max = 20, E(2)_max = 10, and E(3)_max = 5 (noise units). The length of the links (d_mn) are non-uniform, as shown in

Table 3. The length of the links on COST239 (km).

Node	1	2	3	4	5	6	7	8	9	10	11
1		1300	700	300			700
2	1300		500		300			400
3	700	500		600	200	300
4	300		600				300	1000		600	.
5		300	200			200		300			900
6			300		200		700	400	300
7	700			300		700			500	300
8		400		1000	300	400			600		800
9						300	500	600		700	300
10				600			300		700		800
11					900			800	300	800

and the traffic demand for each source–destination pair was defined randomly between 100 and 300 Gbps. For the BRAZILIAN network, the noise limits are E(1)_max = 80, E(2)_max = 40, and E(3)_max = 20 (noise units). The length of the links (d_mn) is uniform and equal 2000 km, and the required demand for each source–destination pair was defined randomly between 50 and 300 Gbps. Other parameters, for now unspecified, are the same as those used for the small networks in the previous Section.

Maximum blocking probability was set to 0%, that is, that all requests must be met, resulting in MS_NSFNET ≥ MS_NSFNETzero = 60, MS_ARPANET ≥ MS_ARPANETzero = 111, MS_BRASILEIRA ≥ MS_{BRASILEIRAzero} = 105, and MS_COST239 ≥ MS_COST239zero = 51. For a joint analysis, the vector MS = (140–300) for the four networks was defined. Thus, Figure 4 shows the absolute power savings according to the number of slots per link for these networks.

Figure 5 already shows the power savings percentage according to the number of slots per link for each network separately and together through the average profile.

With the implementation of the MILP-based algorithm, the maximum power savings on each network is up to the order of 9.8 KW (ARPANET), 7.2 KW (NSFNET), 2.8 KW (Brazilian), and 1.8 KW (COST239) at the points where MS = 260, 260, 140, and 260, representing a savings percentage of 17.8%, 6.1%, 5.6%, and 5.6%, respectively. Through the average profile, it can be seen that the average percentage savings for the four networks together was 7.7%, proving the efficiency of the proposed modified MILP formulation for moderately sized networks.

Note that if the maximum blocking probability was set to 40%, for example, implying MS_NSFNET ≥ 19, MS_ARPANET ≥ 32, MS_BRASILEIRA ≥ 28, and MS_COST239 ≥ 17, this case was not analyzed due to the impossibility of the MILP to solve the problem within the simulation time limit (5 min).

9. Conclusions

This paper presented a new modified MILP formulation and a sequential algorithm which aims to minimize the total power consumed by the components of an elastic optical network under adaptive modulation and physical layer constraints while maintaining the blocking probability below a predefined threshold.

The objectives of the proposed algorithm were reached and the simulations have proved the efficiency of the modified MILP model. Compared to the traditional one, it provides a maximum power percentage saving of 10.5% and an average power percentage saving of 6.6% in a small network (6NET), which means 1.3 KW and 0.8 KW, respectively. For moderately sized networks, it obtained a maximum power savings of 17.8% and an average savings of 7.7%, which represents 9.8 KW and 4.8 KW, respectively.

It was concluded that the total power consumed was reduced due to the better fit of modulations by the modified formulation, once it optimizes the traffic distribution over the network in terms of efficiency. This approach contributes to the sustainability of the network since it requires fewer resources for its operation. Thus, it brings out the concept of green elastic optical networks (Green EONs), a recent theme that is only slightly explored in the literature. Its focus is on a sustainable and the as harmless as possible operation towards the environment.

For larger networks, the proposed formulation is not feasible since the complexity of the MILP increases rapidly. In this context, new heuristics/meta-heuristics and hybrid-algorithms should be developed in future works.