Induction Motor Parameter Identification Using a Gravitational Search Algorithm

Abstract

The efficient use of electrical energy is a topic that has attracted attention for its environmental consequences. On the other hand, induction motors represent the main component in most industries. They consume the highest energy percentages in industrial facilities. This energy consumption depends on the operation conditions of the induction motor imposed by its internal parameters. Since the internal parameters of an induction motor are not directly measurable, an identification process must be conducted to obtain them. In the identification process, the parameter estimation is transformed into a multidimensional optimization problem where the internal parameters of the induction motor are considered as decision variables. Under this approach, the complexity of the optimization problem tends to produce multimodal error surfaces for which their cost functions are significantly difficult to minimize. Several algorithms based on evolutionary computation principles have been successfully applied to identify the optimal parameters of induction motors. However, most of them maintain an important limitation: They frequently obtain sub-optimal solutions as a result of an improper equilibrium between exploitation and exploration in their search strategies. This paper presents an algorithm for the optimal parameter identification of induction motors. To determine the parameters, the proposed method uses a recent evolutionary method called the gravitational search algorithm (GSA). Different from most of the existent evolutionary algorithms, the GSA presents a better performance in multimodal problems, avoiding critical flaws such as the premature convergence to sub-optimal solutions. Numerical simulations have been conducted on several models to show the effectiveness of the proposed scheme.

1. Introduction

The environmental consequences that overconsumption of electrical energy entails has recently attracted the attention in different fields of engineering. Therefore, the improvement of machinery and elements that have high electrical energy consumption levels has become an important task today [1].

Induction motors present several benefits such as their ruggedness, low price, cheap maintenance, and easy operation [2]. However, more than half of the electric energy consumed by industrial facilities is due to the use of induction motors. With the massive use of induction motors, electrical energy consumption has increased exponentially over the years. This fact has generated the need to improve their efficiency, which mainly depends on their internal parameters. The parameter estimation of induction motors represents a complex task due to its non-linearity. As a consequence, different alternatives have been proposed in the literature. Some examples include that proposed by Waters and Willoughby [3], where the parameter are estimated from the knowledge of certain variables, such as stator resistance and the leakage reactance, that proposed by Ansuj [4], where the identification is based on a sensitivity analysis, and that proposed by De Kock [5], where the estimation is conducted through an output error technique.

As an alternative to such techniques, the problem of parameter estimation in induction motors has also been addressed via evolutionary methods. In general, they have demonstrated, under several circumstances, to deliver better results than those based on deterministic approaches in terms of accuracy and robustness [6]. Some examples of these approaches used in the identification of parameters in induction motors involve methods, such as genetic algorithms (GAs) [7], particle swarm optimization (PSO) [8,9], artificial immune system (AIS) [10], the bacterial foraging algorithm (BFA) [11], the shuffled frog-leaping algorithm [12], a hybrid of GAs and PSO [13], and multiple-global-best guided artificial bee colony (ABC) [14]. Although these algorithms present interesting results, they have an important limitation: They frequently obtain sub-optimal solutions as a consequence of the limited balance between exploration and exploitation in their search strategies.

On the other hand, the gravitational search algorithm (GSA) [15] is a recent evolutionary computation algorithm which was inspired by the physical phenomenon of the gravity. In the GSA, its evolutionary operators are built considering gravitation principles. Different from most of the existent evolutionary algorithms, the GSA presents a better performance in multimodal problems, avoiding critical flaws such as the premature convergence to sub-optimal solutions [16,17]. Such characteristics have motivated its use to solve an extensive variety of engineering applications such as energy [18], image processing [6] and machine learning [19].

This paper presents an algorithm for the optimal parameter identification of induction motors. To determine the parameters, the proposed method uses a GSA. A comparison with state-of-the-art methods such as ABC [20], differential evolution (DE) [21], and PSO [22] on different induction models has been incorporated to demonstrate the performance of the proposed approach. Conclusions of the experimental comparison are validated through statistical tests that properly support the discussion.

The sections of this paper are organized as follows: Section 2 describes the GSA method. In Section 3, the identification problem is exposed. In Section 4, the experimental results are presented. Finally, in Section 5, the conclusions are stated.

2. Gravitational Search Algorithm

The GSA was proposed by Rashedi [15] in 2009, inspired by the laws of gravity. Different from most of the existent evolutionary algorithms, the GSA presents a better performance in multimodal problems, avoiding critical flaws such as the premature convergence to sub-optimal solutions [13,14]. In the GSA, candidate solutions emulate masses which attract each other through operators that mimic the gravitational force. Under the GSA, the mass (quality) of each candidate solution is assigned according to its corresponding fitness value. The GSA has been designed to find the global solution of a nonlinear optimization problem with box constraints in the form:

$$\begin{gathered} \text{minimize} f(x), x=(x^1,\dots ,x^d)\in {\text{ℝ}}^d, \\ \text{subject to} x\in X \end{gathered}$$

(1)

where $f:{\text{ℝ}}^d\to \text{ℝ}$ is a nonlinear function, whereas $X=\left\{x\in {\text{ℝ}}^d|l_h\le x^h\le u_h,h=1,\dots ,d\right\}$ is a bounded feasible space, constrained by the lower ($l_h$) and upper ($u_h$) limits. To solve the problem formulated in Equation (1), the GSA utilizes a population of N candidate solutions. Each mass (or candidate solution) represents a d-dimensional vector $x_i(t)=(x_i^1,\dots ,x_i^d) \left(i\in 1\dots ,N\right)$, where each dimension corresponds to a decision variable of the optimization problem at hand.

In the GSA, at a time t, the force acting from a mass i to a mass j of the h variable $\left(h\in 1\dots ,d\right)$ is defined as follows:

$$F_{ij}^h(t)=G(t)\frac{M{p}_i(t)\times M{a}_j(t)}{R_{ij}(t)+\epsilon }(x_j^h(t)-x_i^h(t))$$

(2)

where $M{a}_j$ is the active gravitational mass related to solution j, $M{p}_i$ symbolizes the passive gravitational mass of solution i, $G(t)$ is the gravitational constant at time t, $\epsilon$ is a small constant, and $R_{ij}$ is the Euclidian distance between the i-th and j-th individuals. In the GSA, G(t) is a function which is modified during the evolution process. The idea behind this modification is to adjust the balance between exploration and exploitation through the alteration of the attraction forces among solutions.

The total force acting over a candidate solution i is defined by the following model:

$$F_i^h(t)={\displaystyle \sum _{j=1,j\ne i}^N{F}_{ij}^h(t)}$$

(3)

Then, the acceleration of the candidate solution i at time t is computed as follows:

$$a_i^h(t)=\frac{F_i^h(t)}{M{n}_i(t)}$$

(4)

where $M{n}_i$ represents the inertial mass of the candidate solution i. Under such conditions, the new position of each candidate solution i is calculated as follows:

$$\begin{array}{l}{x}_i^h(t+1)=x_i^h(t)+v_i^h(t+1)\\ v_i^h(t+1)=\text{rand}()\cdot v_i^h(t)+a_i^h(t)\end{array}$$

(5)

At each iteration, the gravitational and inertia masses of each particle are evaluated in terms of its fitness function. Therefore, the gravitational and inertia masses are updated by the following equations:

$$M{a}_i=M{p}_i=M_{ii}=M_i$$

(6)

$$m_i(t)=\frac{f(x_i(t))-\mathrm{worst}(t)}{\text{best}(t)-\mathrm{worst}(t)}$$

(7)

$$M_i(t)=\frac{m_i(t)}{{\displaystyle {\sum }_{j=1}^N{m}_j(t)}}$$

(8)

where $f(\cdot )$ represents the objective function whose final result exhibits the fitness value. On the other hand, best(t) and worst(t) symbolizes the best and worst fitness values found at time t in the complete population. Algorithm 1 illustrates the pseudo code of the GSA method.

Algorithm 1. Gravitational search algorithm (GSA) pseudo code.

Random Initialization of the population

Find the best and worst solutions in the initial population

while (stop criteria)

for i = 1:N (for all elements)

update $G(t), best(t), worst(t)$ and $M_i(t)$ for $i=1,\mathrm{2..},N$

calculate the mass of individual $M_i(t)$

calculate the gravitational constant $G(t)$

calculate acceleration $a_i^h(t)$

update the velocity and positions of each individual $v_i^h, x_i^h$

end for

Find the best individual

end while

Display the best individual as the solution

3. Identification Problem Formulation

The parameters of an induction motor are not directly measurable. Because of this, they are commonly estimated by identification methods. Under such approaches, the behavior of an induction motor is modeled by equivalent nonlinear circuits. Depending on the accuracy, there are two different circuit models [10]: the approximate circuit model and the exact circuit model. In general, they allow the adequate relation of the motor parameters for their estimation.

In the identification process, the parameter estimation is transformed into a multidimensional optimization problem where the internal parameters of the induction motor are considered as decision variables. Therefore, the objective is to minimize the error between the estimated and the manufacturer data, adjusting the parameters of the equivalent circuit. Under this approach, the complexity of the produced formulations tends to produce multimodal error surfaces for which their cost functions are significantly difficult to minimize.

3.1. Approximate Circuit Model

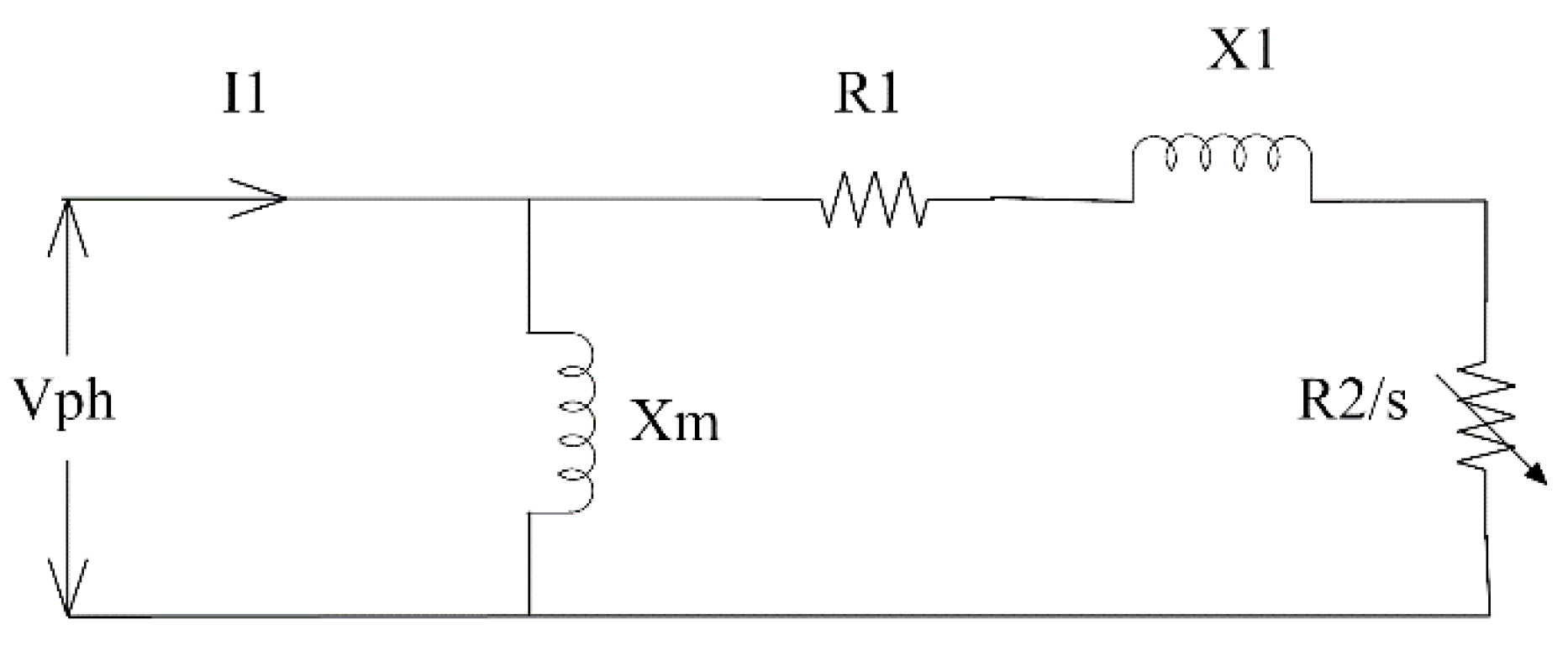
The approximate circuit model does not consider the magnetizing reactance and rotor reactance in its structure; hence, its accuracy is less than the exact circuit model. The approximate circuit model uses the manufacturer data starting torque ($T_{lr}$), maximum torque ($T_{\max }$), and full load torque $\left(T_{fl}\right)$ to determine the stator resistance ($R_1$), rotor resistance ($R_2$), stator leakage reactance $\left(X_1\right)$, and motor slip (s). Figure 1 illustrates the approximate circuit model. Under the approximate circuit model, the identification task can be formulated as the following optimization problem:

$$\begin{gathered} \text{minimize} J_A(x), x=(R_1,R_2,X_1,s)\in {\text{ℝ}}^4, \\ \text{subject to} 0\le R_1\le 1, 0\le R_2\le 1, 0\le X_1\le 10, 0\le s\le 1 \end{gathered}$$

(9)

where

$$\begin{gathered} J_A(x)={(f_1(x))}^2+{(f_2(x))}^2+{(f_3(x))}^2 \\ {f}_1(x)=\frac{\frac{K_t{R}_2}{s\left[{\left(R_1+\raisebox{1ex}{$R_2$}\!\left/ \!\raisebox{-1ex}{$s$}\right.\right)}^2+X_1^2\right]}-T_{fl}}{T_{fl}} \\ {f}_2(x)=\frac{\frac{K_t{R}_2}{{\left(R_1+R_2\right)}^2+X_1^2}-T_{lr}}{T_{lr}} \\ {f}_3(x)=\frac{\frac{K_t}{2\left[R_1+\sqrt{R_1^2+X_1^2}\right]}-T_{\max }}{T_{\max }} \\ {K}_t=\frac{3V_{ph}^2}{{\omega }_s} \end{gathered}$$

(10)

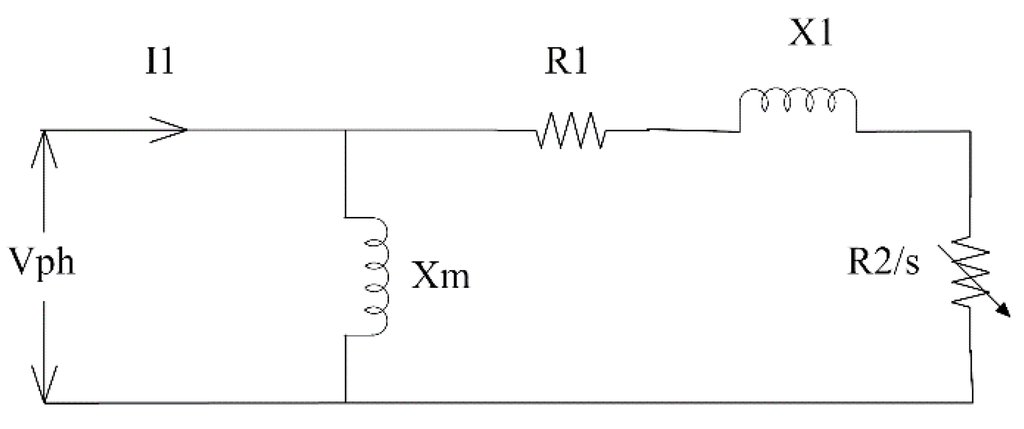
Figure 1. Approximate circuit model.

3.2. Exact Circuit Model

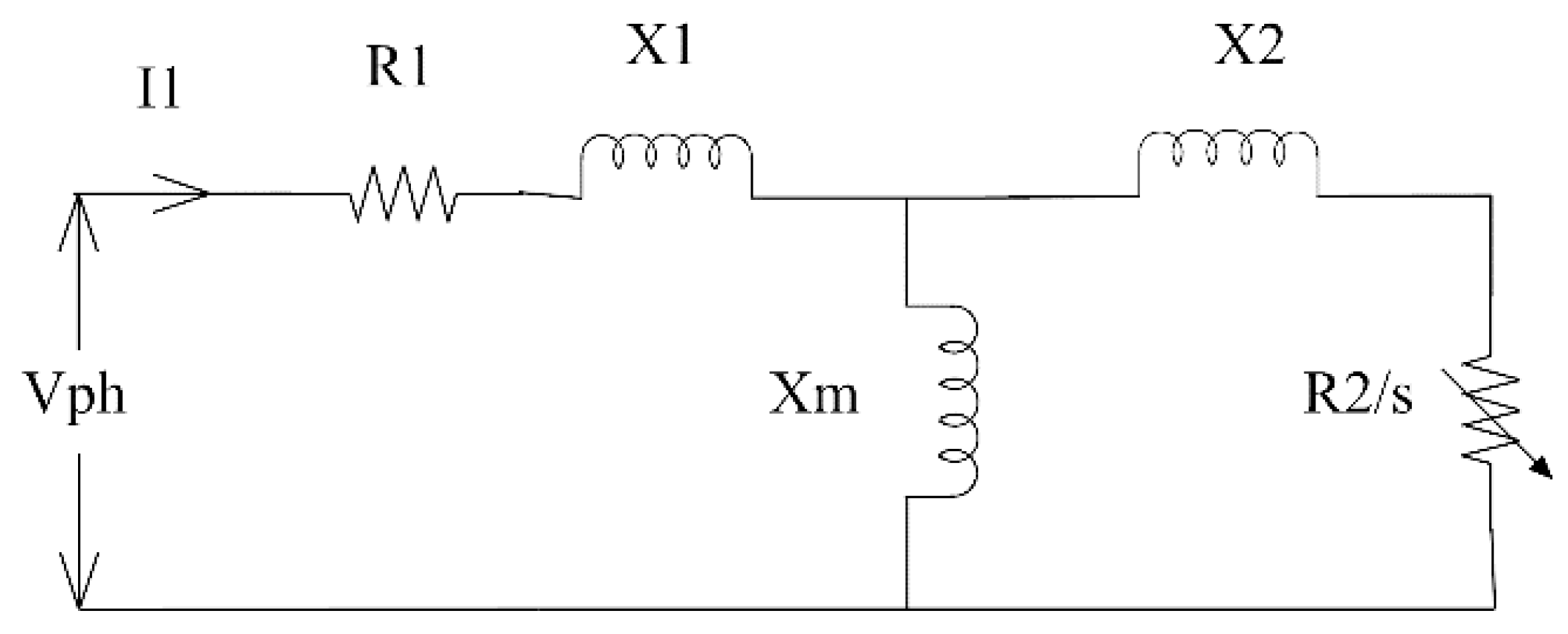
Different from the approximate circuit model, in the exact circuit model, the effects of the magnetizing reactance and rotor reactance are considered in the computation. In this model, the stator resistance ($R_1$), rotor resistance ($R_2$), stator leakage inductance $\left(X_1\right)$, rotor leakage reactance $\left(X_2\right)$, magnetizing leakage reactance $\left(X_m\right)$, and motor slip (s) are calculated to determine the maximum torque ($T_{\max }$), full load torque $\left(T_{fl}\right)$, starting torque ($T_{str}$), and full load power factor (pf). Figure 2 shows the exact circuit model. Under the exact circuit model, the identification task can be formulated as the following optimization problem:

$$\begin{gathered} \text{minimize} J_E(x), x=(R_1,R_2,X_1,X_2,X_m,s)\in {\text{ℝ}}^6, \\ \text{subject to} 0\le R_1\le 1, 0\le R_2\le 1, 0\le X_1\le 1, 0\le X_2\le 1, 0\le X_m\le 10, 0\le s\le 1 \end{gathered}$$

(11)

where

$$\begin{gathered} J_E(x)={(f_1(x))}^2+{(f_2(x))}^2+{(f_3(x))}^2+{(f_4(x))}^2 \\ {f}_1(x)=\frac{\frac{K_t{R}_2}{s\left[{\left(R_{th}+\raisebox{1ex}{$R_2$}\!\left/ \!\raisebox{-1ex}{$s$}\right.\right)}^2+X^2\right]}-T_{fl}}{T_{fl}}, f_2(x)=\frac{\frac{K_t{R}_2}{{\left(R_{th}+R_2\right)}^2+X^2}-T_{str}}{T_{str}} \\ {f}_3(x)=\frac{\frac{K_t}{2\left[R_{th}+\sqrt{R_{th}^2+X^2}\right]}-T_{\max }}{T_{\max }(mf)}, f_4(x)=\frac{\cos \left({\tan }^{-1}\left(\frac{X}{R_{th}+\raisebox{1ex}{$R_2$}\!\left/ \!\raisebox{-1ex}{$s$}\right.}\right)\right)-pf}{pf} \\ {R}_{th}=\frac{R_1{X}_m}{X_1+X_m}, V_{th}=\frac{V_{ph}{X}_m}{X_1+X_m}, X_{th}=\frac{X_1{X}_m}{X_1+X_m}, K_t=\frac{3V_{th}^2}{{\omega }_s}, X=X_2+X_{th} \end{gathered}$$

(12)

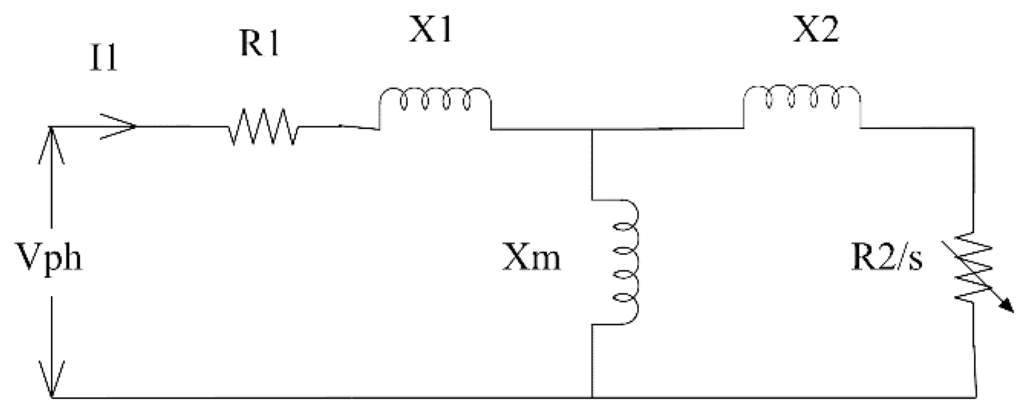
Figure 2. Exact circuit model.

In the minimization of Equation (11), it is also necessary to meet an additional condition, the values of the calculated parameters must fulfill the following restriction:

$$\frac{p_{fl}-(I_1^2{R}_1+I_2^2{R}_2+P_{rot})}{p_{fl}}={\eta }_{fl}$$

(13)

where $p_{fl}$ and $P_{rot}$ represents the rated power and rotational losses, respectively. Furthermore, ${\eta }_{fl}$ symbolizes the efficiency provided by the manufacturer. With this restriction, the calculated efficiency is forced to be equal to the manufacturer efficiency, maintaining a balance between both. In general, the parameters $p_{fl}$ and $P_{rot}$ are calculated through two experimental tests known as No-load-test and Blocked-rotor-test [23,24]. However, in order to maintain compatibility with similar works reported in the literature, they were obtained from references [11,12,13].

4. Experimental Results

In this paper, the GSA is used to determine the optimal parameters of two induction motors considering the approximate circuit model ($J_A$) and exact circuit model ($J_E$). Table 1 presents the technical characteristics of both motors used in the experiments. The proposed method is also evaluated in comparison with other similar approaches based on evolutionary algorithms. In the experiments, we have applied the GSA estimator to the parameter identification of both induction motors, whereas its results are compared to those produced by ABC [20], DE [21], and PSO [22]. The parameter settings of all compared algorithms are obtained from their own referenced papers. The parameter setting for each algorithm in the comparison is described as follows:

1-

PSO, parameters $c_1=2, c_2=2$ and weights factors were set $w_{\max }=0.9,$ and $w_{\min }=0.4$ [22].

2-

ABC, the parameters implemented were provided by [20], limit = 100.

3-

DE, in accordance with [21] the parameters were set $p_c=0.5$ and $f=0.5$.

4-

GSA, the parameter were set according to [15].

Table 1. Manufacturer data of the motors used in the experiments.

	Motor 1	Motor 2
Power (HP)	5	40
Voltage (V)	400	400
Current (A)	8	45
Frequency (Hz)	50	50
No. Poles	4	4
Full load slip (s)	0.07	0.09
Starting torque ($T_{str}$)	15	260
Max. Torque ($T_{\max }$)	42	370
Stator current	22	180
Full load torque ($T_{fl}$)	25	190

The experimental results are divided into three sub-sections. In the first Section 4.1, the performance of the proposed algorithm is evaluated with regard to its own tuning parameters (sensibility analysis). In Section 4.2, an overall performance of the proposed method in comparison with similar approaches is provided. Finally, in Section 4.3, the results are statistically analyzed and validated by using the Wilcoxon test.

4.1. Performance Evaluation with Regard to Its Own Tuning Parameters

In the GSA, the parameters $G_0$ and $\alpha$ affect mainly its expected performance [R]. In this sub-section, the behavior of the GSA over the motor parameter estimation problem is analyzed considering different setting parameters.

During the test, each parameter $G_0$ and $\alpha$ is set to a default value such as $G_0=100$ and $\alpha =20$. In the analysis, when one of the two parameters is evaluated, the other parameter remain fixed to the default value. To minimize the stochastic effect of the algorithm, each benchmark function is executed independently 30 times. As a termination criteria, the maximum number of iterations is considered, which has been set to 3000. In all simulations, the population size N has been configured to 25 individuals.

In the first stage, the behavior of the proposed algorithm is analyzed considering different values for $G_0$. In the analysis, the values of $G_0$ are varied from 80 to 120, whereas the values of $\alpha$ remains fixed at 10 and 30, respectively. In the simulation, the proposed method is executed independently 30 times for each value of $G_0$. The results obtained for the parameter combination of $G_0$ and $\alpha$ are shown in Table 2. Such values represent the minimum, maximum, standard deviation, and mean values of $J_E$ (exact circuit model), considering the characteristics of Motor 1. The best results are marked in boldface. From Table 2, we can conclude that the proposed GSA with $G_0=100$ maintains the best performance.

Table 2. Experimental results obtained by the proposed algorithm using different values of $G_0$.

	$\begin{array}{l}{\mathit{G}}_{\mathbf{0}}\mathbf{=}\mathbf{80}\\ \mathit{\alpha }\mathbf{=}\mathbf{20}\end{array}$	$\begin{array}{l}{\mathit{G}}_{\mathbf{0}}\mathbf{=}\mathbf{90}\\ \mathit{\alpha }\mathbf{=}\mathbf{20}\end{array}$	$\begin{array}{l}{\mathit{G}}_{\mathbf{0}}\mathbf{=}\mathbf{100}\\ \mathit{\alpha }\mathbf{=}\mathbf{20}\end{array}$	$\begin{array}{l}{\mathit{G}}_{\mathbf{0}}\mathbf{=}\mathbf{110}\\ \mathit{\alpha }\mathbf{=}\mathbf{20}\end{array}$	$\begin{array}{l}{\mathit{G}}_{\mathbf{0}}\mathbf{=}\mathbf{120}\\ \mathit{\alpha }\mathbf{=}\mathbf{20}\end{array}$
Min	0.0044	0.0036	0.0032	0.0036	0.0033
Max	0.0119	0.0103	0.0032	0.0082	0.0088
Std	0.0016	0.0013	0.0000	0.0012	0.0014
Mean	0.0052	0.0040	0.0032	0.0042	0.0039

Then, in the second stage, the performance of the proposed algorithm is evaluated considering different values for $\alpha$. In the experiment, the values of $\alpha$ are varied from 10 to 30 whereas the value of $G_0$ remains fixed to 100. The statistical results obtained by the GSA using different values of $\alpha$ are presented in Table 3. Such values represent the minimum, maximum, standard deviation, and mean values of $J_E$ (exact circuit model), considering the characteristics of Motor 2. The best results are marked in boldface. From Table 3, it is evident that the proposed algorithm with $\alpha =20$ outperforms the other parameter configurations.

Table 3. Experimental results obtained by the proposed algorithm using different values of $\alpha$.

	$\begin{array}{l}{\mathit{G}}_{\mathbf{0}}\mathbf{=}\mathbf{100}\\ \mathit{\alpha }\mathbf{=}\mathbf{10}\end{array}$	$\begin{array}{l}{\mathit{G}}_{\mathbf{0}}\mathbf{=}\mathbf{100}\\ \mathit{\alpha }\mathbf{=}\mathbf{15}\end{array}$	$\begin{array}{l}{\mathit{G}}_{\mathbf{0}}\mathbf{=}\mathbf{100}\\ \mathit{\alpha }\mathbf{=}\mathbf{20}\end{array}$	$\begin{array}{l}{\mathit{G}}_{\mathbf{0}}\mathbf{=}\mathbf{100}\\ \mathit{\alpha }\mathbf{=}\mathbf{25}\end{array}$	$\begin{array}{l}{\mathit{G}}_{\mathbf{0}}\mathbf{=}\mathbf{100}\\ \mathit{\alpha }\mathbf{=}\mathbf{30}\end{array}$
Min	0.0093	0.0093	0.0071	0.0093	0.0092
Max	0.0730	0.0433	0.0209	0.0435	0.0493
Std	0.0147	0.0085	0.0043	0.0094	0.0109
Mean	0.0235	0.0164	0.0094	0.0191	0.0215

In general, the experimental results in Table 2 and Table 3 suggest that a proper combination of different parameter values can improve the performance of the proposed method and the quality of the solutions. From the experiment, it can be concluded that the best parameter set is composed of the following values: $G_0=100$ and $\alpha =20$. Once they have been determined experimentally, they are kept for all test functions through the following experiments.

4.2. Induction Motor Parameter Identification

In this experiment, the performance of the proposed GSA method is compared with DE, ABC, and PSO, considering the parameter estimation of both circuit models. In the test, all algorithms are operated with a population of 25 individuals (N = 25). The maximum iteration number for all methods has been set to 3000. This stop criterion has been selected to maintain compatibility to similar works reported in the literature [20,21,22]. All the experimental results presented in this section consider the analysis of 35 independent executions of each algorithm. Thus, the values of $J_A$ (approximate model), deviation standard, and mean obtained by each algorithm for Motor 1 are reported in Table 4, whereas the results produced by Motor 2 are shown in Table 5. On the other hand, the values of $J_E$ (exact model) for Motor 1 and Motor 2 are exhibited in Table 6 and Table 7, respectively. The best results in all tables are marked in boldface.

Table 4. Results of $J_A$, considering Motor 1.

	GSA	DE	ABC	PSO
Min	3.4768×10−22	1.9687×10−15	2.5701×10−5	1.07474×10−4
Max	1.6715×10−20	0.0043	0.0126	0.0253
Mean	5.4439×10−21	1.5408×10−4	0.0030	0.0075
Std	4.1473×10−21	7.3369×10−4	0.0024	0.0075

Table 5. Results of $J_A$, considering Motor 2.

	GSA	DE	ABC	PSO
Min	3.7189×10−20	1.1369×10−13	3.6127×10−4	0.0016
Max	1.4020×10−18	0.0067	0.0251	0.0829
Mean	5.3373×10−19	4.5700×10−4	0.0078	0.0161
Std	3.8914×10−19	0.0013	0.0055	0.0165

Table 6. Results of $J_E$, considering Motor 1.

	GSA	DE	ABC	PSO
Min	0.0032	0.0172	0.0172	0.0174
Max	0.0032	0.0288	0.0477	0.0629
Mean	0.0032	0.0192	0.0231	0.0330
Std	0.0000	0.0035	0.0103	0.0629

Table 7. Results of $J_E$, considering Motor 2.

	GSA	DE	ABC	PSO
Min	0.0071	0.0091	0.0180	0.0072
Max	0.0209	0.0305	0.2720	0.6721
Mean	0.0094	0.0190	0.0791	0.0369
Std	0.0043	0.0057	0.0572	0.1108

According to the results from Table 4, Table 5, Table 6 and Table 7, the proposed approach provides a better performance than DE, ABC, and PSO in all tests. These differences are directly related to the better trade-off between exploration and exploitation of the GSA method.

Once the motor parameters of all algorithms were estimated, their estimations were compared with the ideal starting torque ($T_{str}$), maximum torque ($T_{\max }$), and full load torque $\left(T_{fl}\right)$ values provided by the manufacturer in Table 1. The main objective of this comparison is to evaluate the accuracy of each approach with regard to the actual motor parameters. Table 8 and Table 9 present the experimental results of J_A for Motors 1 and 2, respectively. On the other hand, Table 10 and Table 11 exhibit the comparative results of $J_E$ for Motors 1 and 2, respectively. The best results in all tables are marked in boldface.

Table 8. Comparison of GSA, DE, ABC, and PSO with manufacturer data, $J_A$, for Motor 1.

	True val	GSA	Error%	DE	Error%	ABC	Error%	PSO	Error%
Tst	15	15.00	0	14.9803	−0.131	14.3800	−4.133	15.4496	2.9973
Tmax	42	42.00	0	42.0568	0.135	40.5726	−3.398	39.6603	−5.570
Tfl	25	25.00	0	24.9608	−0.156	25.0480	0.192	25.7955	3.182

Table 9. Comparison of GSA, DE, ABC, and PSO with manufacturer data, $J_A$, for Motor 2.

	True val	GSA	Error%	DE	Error%	ABC	Error%	PSO	Error%
Tst	260	260.00	0	258.4709	−0.588	260.6362	0.2446	288.9052	11.117
Tmax	370	370.00	0	372.7692	0.7484	375.0662	1.3692	343.5384	−7.151
Tfl	190	190.00	0	189.0508	−0.499	204.1499	7.447	196.1172	3.2195

Table 10. Comparison of GSA, DE, ABC, and PSO with manufacturer data, $J_E$, for Motor 1.

	True val	GSA	Error%	DE	Error%	ABC	Error%	PSO	Error%
Tst	15	14.9470	−0.353	15.4089	2.726	16.4193	9.462	15.6462	4.308
Tmax	42	42.00	0	42.00	0	42.00	0	42.00	0
Tfl	25	25.0660	0.264	26.0829	4.3316	25.3395	1.358	26.6197	6.4788

Table 11. Comparison of GSA, DE, ABC, and PSO with manufacturer data, $J_E$, for Motor 2.

	True val	GSA	Error%	DE	Error%	ABC	Error%	PSO	Error%
Tst	260	258.1583	−0.708	262.0565	0.7909	246.2137	−5.302	281.8977	8.4221
Tmax	370	370.00	0	370.00	0	370.00	0	370.00	0
Tfl	190	189.8841	−0.061	192.2916	1.2061	207.9139	9.428	166.6764	−12.27

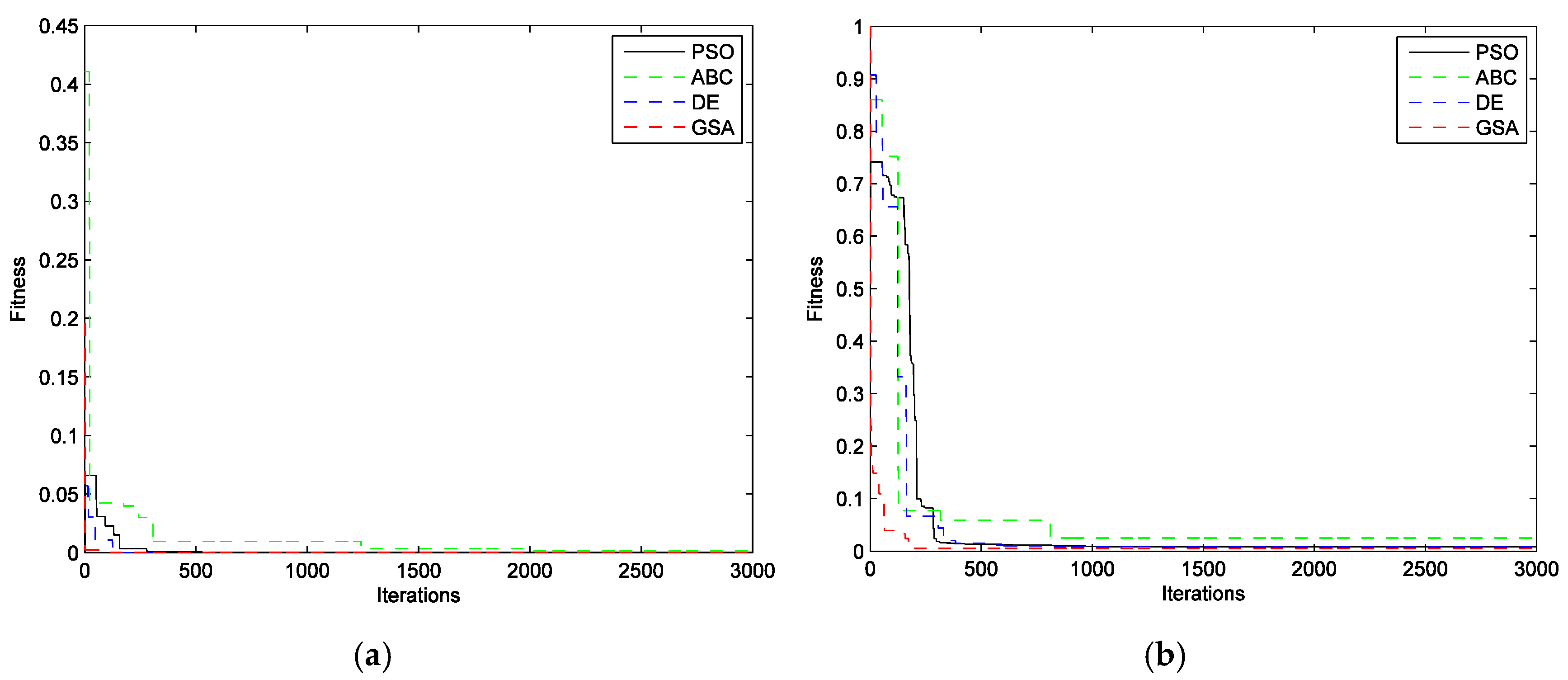
Since the convergence rate of evolutionary algorithms is an important characteristic to assess their performance for solving the optimization problems, the convergence of all algorithms facing functions $J_A$ and $J_E$ is compared in Figure 3a,b. The remarkable convergence rate of the proposed algorithm can be observed in both figures. According to these figures, it tends to find the global optimum faster than other algorithms.

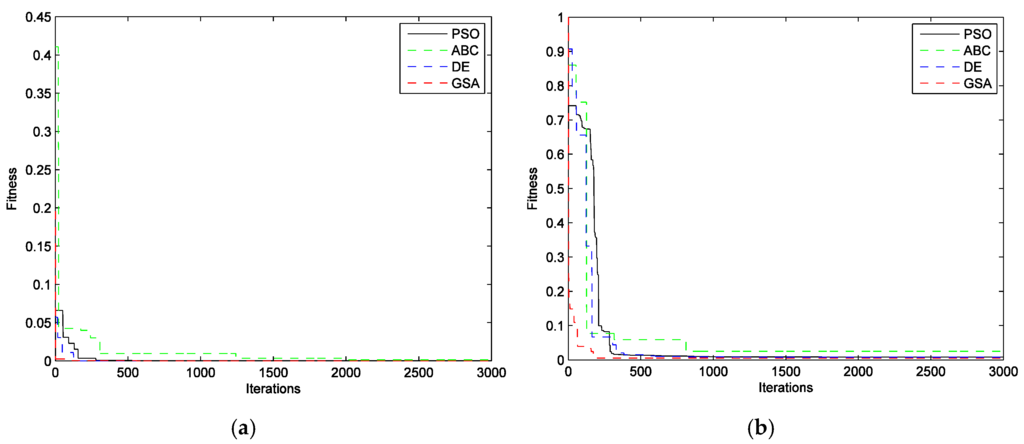
Figure 3. Convergence evolution through iterations: (a) Model 1 ($J_A$); (b) Model 2 ($J_E$).

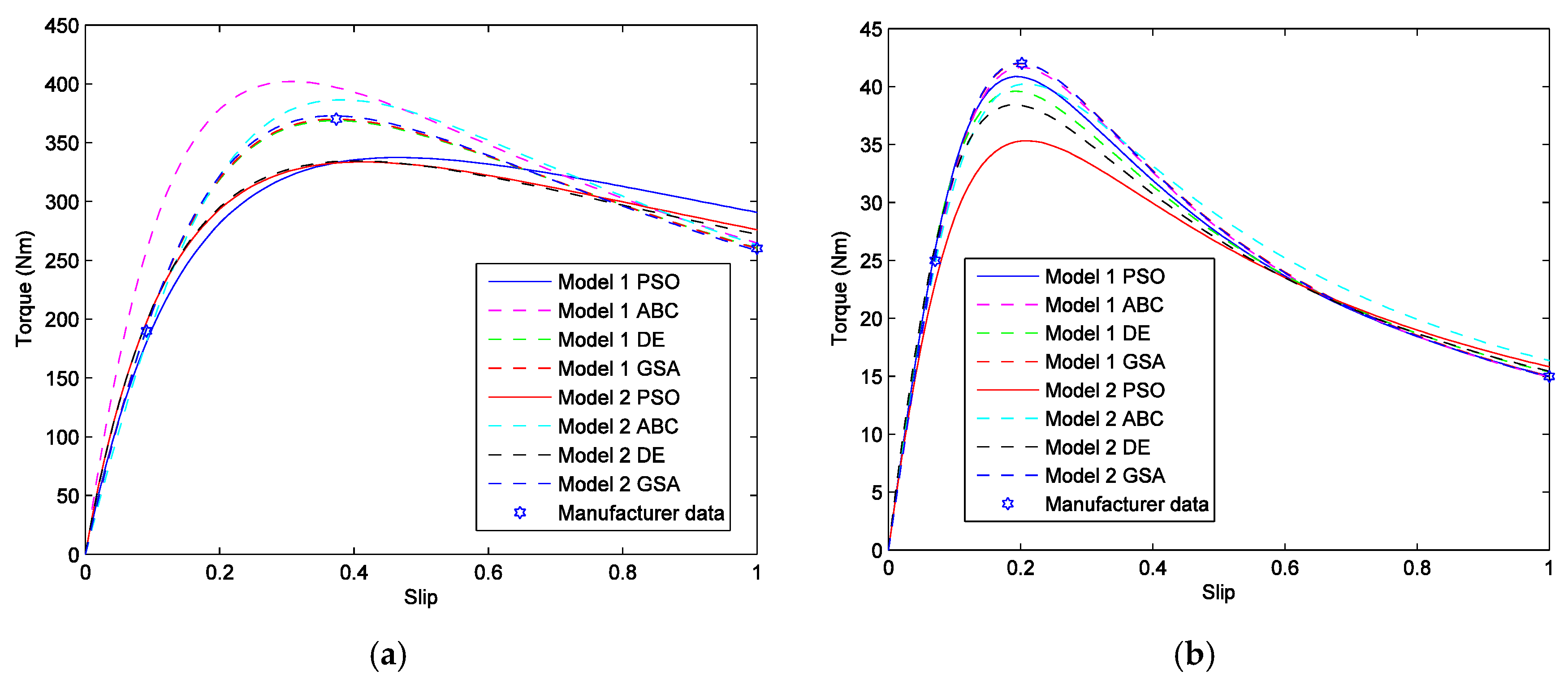
Finally, Figure 4 shows graphically the relation of the slip vs. torque for both models ($J_A$ and $J_E$) and for both Motors (1 and 2).

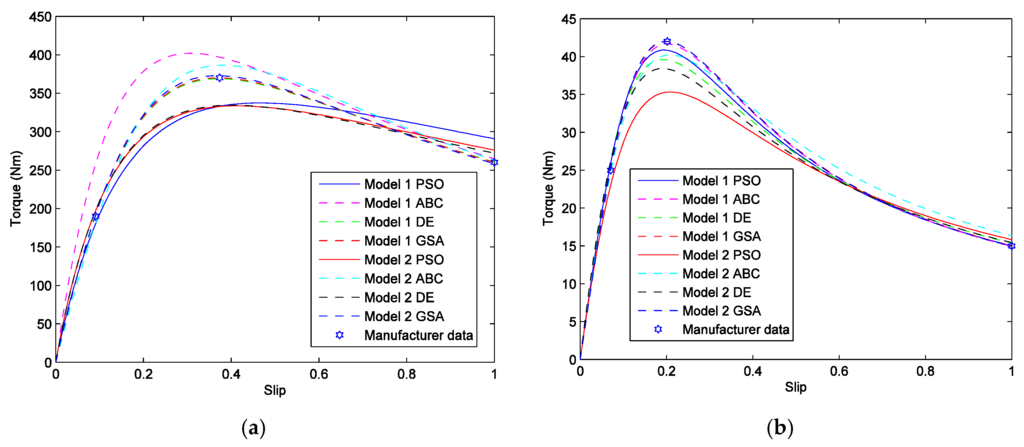
Figure 4. Curve slip vs. torque via PSO, ABC, DE, and GSA considering Model 1 ($J_A$), Model 2 ($J_E$), (a) Motor 1, and (b) Motor 2.

4.3. Statistical Analysis

To statistically analyze the results, a non-parametric test known as Wilcoxon analysis [25] was conducted. It permits the evaluation of the differences between two related methods. The test is performed in a 5% significance level over the mean fitness values of $J_A$ and $J_E$, considering Motors 1 and 2. Table 12 reports the p-values generated by Wilcoxon analysis for the pair-wise comparison among the algorithms. Under such conditions, three groups are produced: GSA vs. DE, GSA vs. ABC, and GSA vs. PSO. In the Wilcoxon test, it is assumed as a null hypothesis that there is no significant difference between the two algorithms. On the other hand, it is considered as an alternative hypothesis that there is a significant difference between both approaches. An inspection of Table 12 demonstrates that all p-values in the Table 12 are less than 0.05 (5% significance level). This fact provides strong evidence against the null hypothesis, indicating that the proposed method statistically presents better results than the other algorithms.

Table 12. p-values produced by Wilcoxon test comparing GSA vs. DE, GSA vs. ABC, and GSA vs. PSO over the mean fitness values of $J_A$ and $J_B$ considering the Motors 1 and 2 from Table 4, Table 5, Table 6 and Table 7.

GSA vs.	DE	ABC	PSO
$J_A$, Motor 1	6.545500588914223×10−13	6.545500588914223×10−13	6.545500588914223×10−13
$J_A$, Motor 2	0.009117078811112	0.036545600995029	0.004643055264741
$J_E$, Motor 1	6.545500588914223×10−13	6.545500588914223×10−13	6.545500588914223×10−13
$J_E$, Motor 2	1.612798082388261×10−9	9.465531545379272×10−13	3.483016312301559×10−8

5. Conclusions

In this paper, an algorithm for the optimal parameter identification of induction motors has been presented. In the proposed method, the parameter estimation process is transformed into a multidimensional optimization problem where the internal parameters of the induction motor are considered as decision variables. Under this approach, the complexity of the optimization problem tends to produce multimodal error surfaces for which their cost functions are significantly difficult to minimize. To determine the parameters, the proposed method uses a relatively recent evolutionary method called the gravitational search algorithm (GSA). Different from most of the existent evolutionary algorithms, the GSA presents a better performance in multimodal problems, avoiding critical flaws such as the premature convergence to sub-optimal solutions.

To illustrate the proficiency and robustness of the proposed approach, the GSA estimator has been experimentally evaluated considering two different motor models. To assess the performance of the proposed algorithm, it has been compared to other similar evolutionary approaches such as differential evolution (DE), ABC, and PSO. The experiments, statistically validated, have demonstrated that the proposed method outperforms the other techniques in most experiments in terms of solution quality.