An Adaptive Steganographic Method for Reversible Information Embedding in X-Ray Images

Abstract

The rapid digitalisation of the medical field has heightened concerns over protecting patients’ personal information during the transmission of medical images. This study introduces a method for securely transmitting X-ray images that contain embedded patient data. The proposed steganographic approach ensures that the original image remains intact while the embedded data is securely hidden, a critical requirement in medical contexts. To guarantee reversibility, the Interpolation Near Pixels method was utilised, recognised as one of the most effective techniques within reversible data hiding (RDH) frameworks. Additionally, the method integrates a statistical property preservation technique, enhancing the scheme’s alignment with ideal steganographic characteristics. Specifically, the “forest fire” algorithm partitions the image into interconnected regions, where statistical analyses of low-order bits are performed, followed by arithmetic decoding to achieve a desired distribution. This process successfully maintains the original statistical features of the image. The effectiveness of the proposed method was validated through stegoanalysis on real-world medical images from previous studies. The results revealed high robustness, with minimal distortion of stegocontainers, as evidenced by high PSNR values ranging between 52 and 81 dB.

1. Introduction

The scientific discipline of steganography emerged long ago, with a focus on enhancing the reliability and security of methods for transmitting hidden information in seemingly innocuous containers. Containers are defined as text files, executable programs, images, audio files, and graphs [1]. A container that contains concealed information is referred to as a stegocontainer. A substantial proportion of the field of steganography is dedicated to the analysis of digital images [2,3].

Presently, the safeguarding of medical images during their transmission over the network constitutes a pressing undertaking. The utilisation of Reverse Data Hiding (RDH) steganography within the medical domain ensures the optimal protection of confidential information. This technology facilitates the embedding of data into images, with the capability of complete restoration of the original image following the extraction of hidden data. This is of particular significance in the field of medicine, where the accuracy and integrity of data for patient diagnosis and treatment is paramount. Furthermore, the use of RDH steganography has the potential to enhance the confidentiality and security of patient records (EPRs), thereby providing an additional layer of protection.

Thus, in [4], a strategy for reversible data implementation for ehealth applications is proposed. The authors propose a methodology for dividing the image into 2 × 2 pixel blocks, and calculating the average point value to use when embedding by rearranging the pixel values. However, the authors claim a peak signal-to-noise ratio (PSNR) value of 40 dB, which is not a strong indicator.

The work [5] also raises the issue of the safety of patient data during the work of doctors in real time. The authors propose the utilisation of Least Significant Bit (LSB) steganography, a cryptographic method that enhances data protection. The findings of this study indicate the potential for enhancing steganographic methodologies employed for the covert embedding of patient data, with the objective of augmenting the confidentiality of such information during its transmission.

The study [6] also examines the issue of the security of medical images containing personal information about patients on the Internet of Medical Things (IoMT). The authors delineate the issue of prevailing medical image steganography methods that do not ensure data integrity. The present paper puts forward a steganographic approach based on image data prediction and the construction of reversible embedding in medical images.

In [7], several RDH algorithms were presented, which were divided into six categories: extension-based RDH, histogram shift-based RDH, code division multiplexing-based RDH, compression-based RDH, contrast enhancement with RDH, and RDH in the encrypted domain. Furthermore, the authors concluded that reversible data hiding has wider applications in medical imaging and secure communications.

In [8], the authors proposed a new approach for applying image interpolation and achieved superior PSNR index values for the obtained LSB method in comparison with known steganographic systems of this type.

A common approach to developing RDH steganographic systems for images involves the application of interpolation techniques [9,10] to enhance the payload of the container while preserving the visual quality.

The foundation for this research was laid back in [11], which addressed the information-theoretical approach to building stegosystems that are close to ideal. This approach is employed to enhance the interpolation-based RDH steganographic system, as this aspect has not been addressed in the extant research of other authors. The development of an adaptive method for estimating the statistical properties of a container has been undertaken for this purpose. The methodology to be employed involves the selection of areas in the image using the “forest fire” method [12].

Subsequently, the original image is subjected to interpolation, with the added pixels being utilised for the purpose of embedding hidden information. This process is informed by the statistics of the least significant bits, with consideration given to the area under consideration. In order to obtain a sequence with a given distribution, it is advisable to use an arithmetic decoder to recover the embedded information, that is to say, the corresponding arithmetic encoder. The developed method can be readily implemented in practice for most graphic data formats using nondistorting compression methods and can be applied to medical images. In order to evaluate the developed system, in addition to the quality indicators of containers that are utilised in the majority of studies on similar topics, a visual distortion assessment method and a dual statistics method obtained from spatial correlations in images [13] are applied. This will facilitate a more comprehensive evaluation of the stegosystem’s efficacy, leading to the identification of its deficiencies and the identification of additional methods to enhance its resistance to steganalysis.

The resilience of a stegosystem is contingent upon the ability of an intruder to discern hidden messages being transmitted under the cover of containers, and to decipher these messages, even when observing the information exchange between the sender and the receiver. The hypothesis is that if the distribution of the low-order bits of the container is taken into account, the output will be a stegocontainer in which the original distribution image is preserved. This will increase the robustness of the RDH method. The adaptability of the method is such that the consideration of the distribution of the low-order bits does not take place for the whole image at once; rather, it takes into account certain regions of the image.

The present paper [14] describes one of the effective RDH schemes based on histogram shifting of prediction errors. The authors propose a methodology for the division of the image into 4 × 4 pixel blocks, with a prediction process being performed on each block. This process is purported to preserve high image quality after embedding. The mean embedding capacity was found to be 0.77 bits per pixel, and the quality of the presented images was estimated to be 50 dB, a figure that surpasses that of other contemporary RDH methods. The authors of this work have demonstrated adaptability to the statistical properties of the image using the proposed method.

Histogram Shifting-based RDH [15] is one of the classical approaches to reversible data hiding based on modification of histogram differences in images. The method uses statistical features of differences of neighbouring pixels in an image to find ‘peaks’ in the histogram, which are then used for secure information embedding.

Difference Expansion-based RDH [16] is a reversible data hiding method based on the Difference Expansion (DE) technique. The method allows embedding information into a digital image in such a way that the original image can be accurately reconstructed without loss after data extraction. The approach is to calculate the differences in brightness values of pairs of neighbouring pixels, which are then expanded to create a “space” for the embedded data. The proposed algorithm demonstrates good image quality after embedding (high PSNR) and can be applied in areas where content integrity is important, such as medical imaging and forensic applications.

The paper [17] investigates the effectiveness of LSB steganography method for hiding medical information in images. The method consists in replacing the least significant bits of image pixels with the hidden data, which allows the unobtrusive transfer of information without significant loss of image quality. The authors demonstrate that this approach provides sufficiently high image quality after embedding (PSNR ~40–45 dB) and can be applied in resource-limited systems, e.g., in telemedicine.

In [18], a hybrid method combining Hide Behind Corner (HBC) and Reversible Data Hiding (RDH) is described. In this method, data is hidden in the “corners” of the image. This increases the level of concealment and enables the original image to be accurately reconstructed.

A gap in the extant literature pertains to the inadequacy of prevailing steganographic methodologies of this nature (RDH methods) in terms of their adaptability and resilience to statistical stegoanalysis. The majority of approaches under consideration emphasise the improvement of the embedding capacity through the exploitation of prediction error; however, they do not focus on the problem of preserving the statistical properties of the image in its original form. It is evident that researchers have not provided the results of visual analyses of the resulting bins. It is submitted that such a simple study could easily and clearly demonstrate the results obtained.

Adaptive steganographic methods refer to the development and research of steganographic methods for protecting medical data by reversible embedding of information in X-ray images. The following research questions have been posited:

• How can personal data be securely embedded and transmitted within medical images without compromising their diagnostic accuracy?
• What strategies can be employed to enhance the robustness of steganographic techniques in medical imaging applications?

In order to address the aforementioned questions, the objective was to develop a steganographic method that would allow personal data to be securely embedded in a medical image. The proposed method should be adaptive, that is, it should take into account the statistical properties of the container image to enhance the security of the transmission of embedded personal data. A notable gap in the existing literature pertains to the inadequacy of contemporary steganographic methods (RDH methods) in effectively countering statistical stegoanalysis.

The basis of this research question is the increasing digitalisation of healthcare and the resulting risks of personal data leakage and breach of medical confidentiality. Moreover, the potential for fraudulent insurance claims resulting from tampering with medical records is a salient concern. The developed method has the potential to be utilised in the protection of electronic medical records and data transmission in the context of telemedicine, as it ensures the integrity of the original data following the extraction of hidden information.

2. Materials and Methods

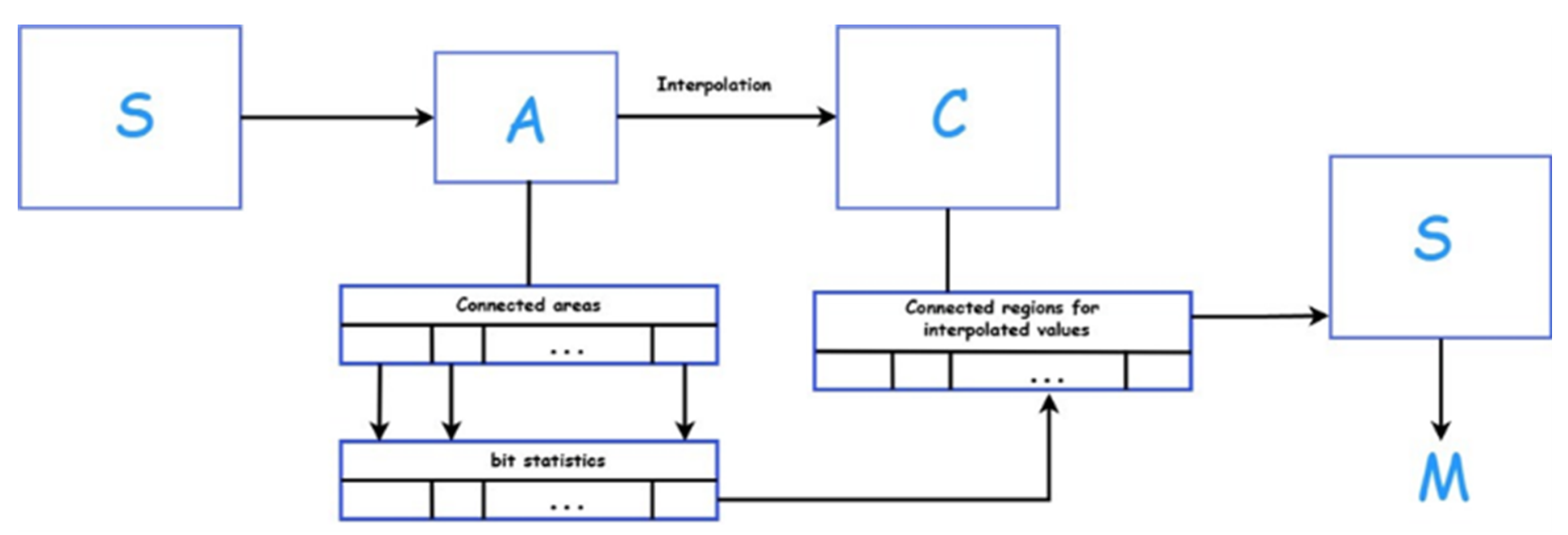
2.1. General Scheme of the Proposed Stegosystem

The following discussion will consider the algorithm of the proposed stegosystem in general terms. The sender’s initial data are designated as message M and the original container A. The message constitutes a pseudorandom bit sequence, the function of which is to encrypt information intended for storage in a container. The original container is an 8-bit grayscale BMP image (in this case, 256 × 256 pixels), representing the informational value during transmission. In the present studies, 1000 images from the BOSSBase v1.01 database [19] containing PGM files with a resolution of 512 × 512 pixels were utilised to establish the test set of containers. The images contained within the database were converted to the BMP format by employing standard tools to create a set of source images. These images were then resized to 256 × 256 pixels, which was the size of the set of original containers.

In the first step of the algorithm, the connected areas are determined in container A, for each of which the least significant bit statistics of this container are collected. A connected area of an image here refers to an area where all points have the same attribute value, and where there is a continuous path of points in this area between any two points. In the stegosystem presented in this work, areas were identified using the “forest fire” method based on falling within specific brightness value ranges. Thus, a large number of sets of image areas and their distributions are formed.

In the second step, an interpolation algorithm is applied to the original container A, resulting in a cover container C with a resolution of 512 × 512 pixels, containing the original container’s points and interpolated values.

In the third step, similar area identification is performed for the interpolated values of cover container C. The least significant bit statistics of the corresponding area of the original container A are used for each area to transform message M into code with a given probability distribution. The corresponding code is recorded in the least significant bits by the areas of cover container C, resulting in the creation of stegocontainer S with the embedded message (see Figure 1).

where A—original container (medical image; in the example it is an 8-bit bmp. image in shades of grey, representing information value in transmission).

C—cover container obtained by interpolation of container A.

S—stegocontainer obtained from container-cover C by adding hidden information.

M—hidden message (personal data represented as a pseudorandom bit sequence).

To extract the message from S, the original container A is restored, and the least significant bit statistics are determined by the identified areas in the same manner as during embedding. Then, A is interpolated again to obtain container C without the embedded message for the error-free determination of the corresponding areas in S. Then, using the obtained probability distribution of the least significant bits by areas of container A, message M is recovered from the code located in the areas of S (see Figure 2).

2.2. Interpolation Method

In the proposed stegosystem, any image interpolation algorithm can be used as a basis. The criterion for selecting the algorithm is the PSNR indicator. In this study, the INP interpolation algorithm [12] was used. The values of the points with coordinates i and j of the cover container C from the original image A with dimensions of mn pixels are calculated using Formula (1):

$$C(i,j)=\left\{\begin{array}{cc}{\displaystyle \frac{A(i-1,j)+A(i+1,j)}{2}},\hfill & \mathrm{if}i=2m+1,j=2n\hfill \\ {\displaystyle \frac{A(i,j-1)+A(i,j+1)}{2}},\hfill & \mathrm{if}i=2m,j=2n+1\hfill \\ {\displaystyle \frac{C(i-1,j)+C(i,j-1)}{2}},\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(1)

An example of computing interpolated values on a fragment of a given image A is shown in Figure 3. The values of the container C obtained using Formula (1) are highlighted in grey.

In this case, the white cells represent sample luminance values from container A (the medical image), while the grey cells indicate the interpolated values introduced in container C (the cover container).

2.3. Evaluation of the Least Significant Bit Statistics

There is a statistical dependency of the least significant bits (LSBs) on other elements of the container. This dependency is violated if independent data are written to the LSBs. In [20], an adaptive statistical model was proposed to estimate the probability distribution of LSBs in a container. Using frequency entropy estimation, the most significant context elements closely related to LSBs were identified. The training part used half of the container image, which was highlighted in the checkerboard pattern. However, in the current work, we use an interpolation method to separate the training part of the image, which imposes certain conditions on the context formation, as every second row does not contain training data for collecting statistics. The original image A is used as a training matrix for forming statistics and is then interpolated.

The probabilities are estimated using the pixels of the original image adaptively to each specific area. The state space for probability estimation is determined by considering the frequency entropy: the smaller the entropy value, the closer the statistical model is to the real source. The optimal context consists of the LSBs of the previous and next pixels as well as the second, third, and fourth LSBs of the current pixel. Note that the previous and next pixels in container C refer to the matrix of the original image A, so they remain unchanged when embedding information, and their LSBs can be used when restoring the statistics. The bits used in the current pixel also remain unchanged and are used when restoring statistics, as the information is written to the LSBs of the interpolated values of pixel matrix C.

2.4. Method for Obtaining a Given Distribution

The most efficient approximate solution to the coding problem, which transforms an encrypted message into a bit stream with a given distribution, is arithmetic decoding [21]. The arithmetic decoder is given the required zero and one probability distributions for each next output symbol, according to which it reproduces this symbol, considering the encrypted message as a code previously constructed by the corresponding arithmetic encoder. To restore the encrypted message from its code, an arithmetic encoder was applied, which received the same probability distributions as the decoder. To evaluate the LSB statistics and embed information considering these statistics, following the schemes in Figure 1 and Figure 2, the container A, whose pixels are the “training” part of the container C during embedding and the container S during message extraction, is used.

2.5. Method for Identifying Connected Areas in the Image

Previously, a method for dividing an image into connected areas based on brightness was used in similar experiments. The entire image was divided into 16 areas according to the specified brightness range. However, this approach allows the gathering of pixels into one area, which could be located in different parts of the image, distorting the container’s statistical properties in some cases.

In this work, a stack algorithm for tracing connected areas by the “forest fire” method [22] is used. The forest fire method in image processing is an algorithm used to split an image into connected regions. This method got its name due to the analogy of the spread of fire in a forest. The “fire” starts from one point and spreads to neighbouring pixels with similar characteristics. In the context of image processing, this approach is used to analyse the image structure and highlight areas with similar brightness or colour values. As a result of using this method, the image is divided into many disjointed connected regions, each of which is characterised by similar pixel brightness values.

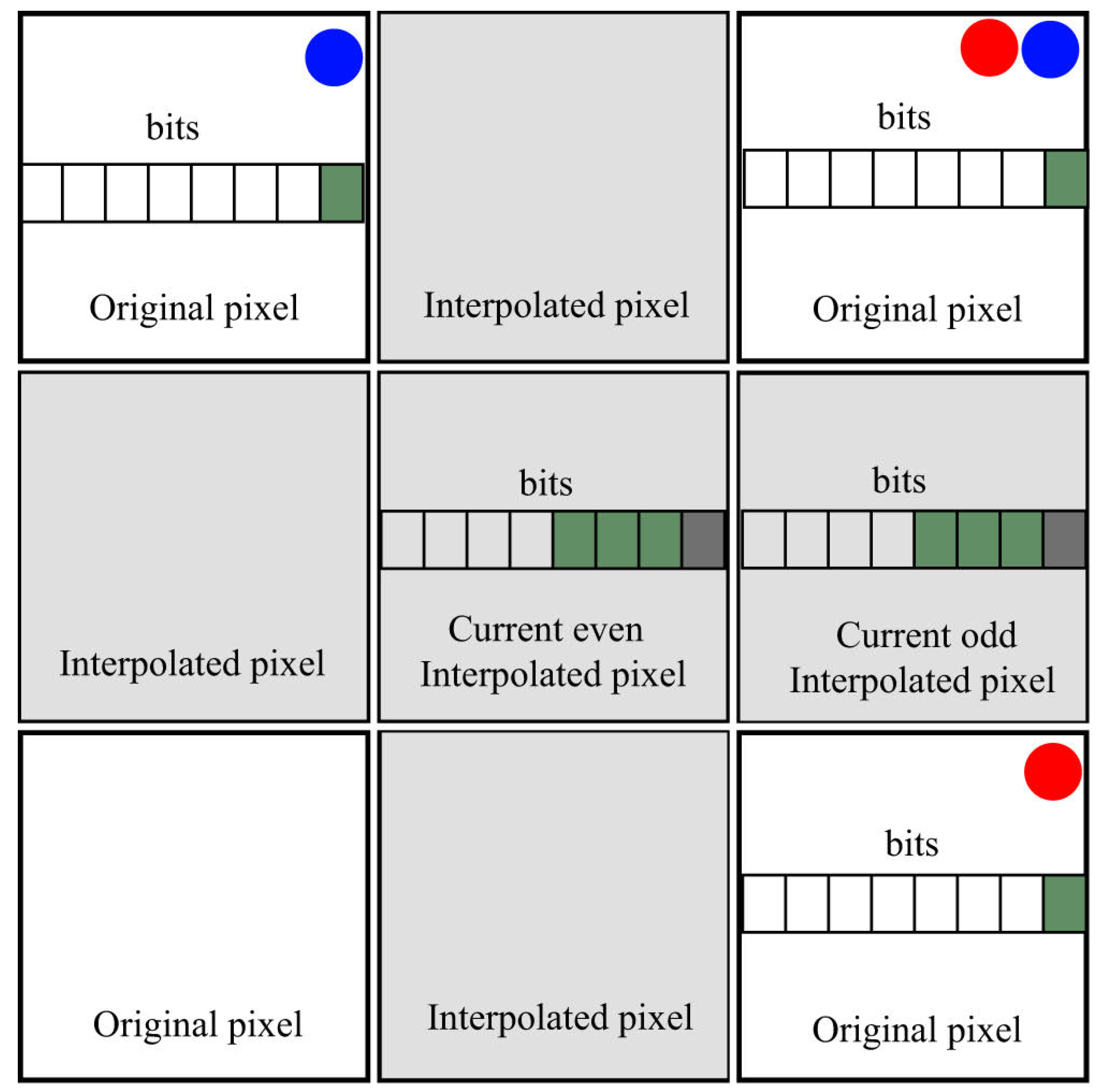
The subsequent image illustrates a context that was methodically selected on the basis of frequency entropy calculation and adapted to the interpolation method employed: The state space for probability estimation was determined by searching for the most significant elements of the context that were most statistically related to the least significant bits. As illustrated in the figure, the grey cells denote pixels that have been added through interpolation, with the smaller cells within them illustrating the individual components that constitute a pixel. In the interpolated values, the bits shown in green, i.e., the first, second, and third, were taken as the context for collecting statistics. The dark grey cell in the figure denotes the zero bit, which is not utilised when collecting statistics due to the fact that information is written to it. The white squares represent the pixels of the original image, which remain constant, and the zero bit in them is highlighted in green. This is used to collect statistical properties for each area of the image. In the pixels of the original image, no information will be entered into the zero bit, so it is used in collecting statistics, unlike the zero bit in the interpolated pixels. Therefore, the optimal context in this algorithm consists of the least significant (zero) bits of the previous and subsequent pixels, as well as the first, second, and third least significant bits of the current pixel. It is imperative to note that the two pixels that precede and succeed the current pixel under consideration are invariably derived from the original image A (i.e., the original medical image). The pixels of image A are illustrated as white cells in the accompanying figure. In the context of the interpolation process, the pixels of an image are organised into groups based on their immediate neighbours. The pixels that fall within the boundaries of these groups are then used to calculate statistical values. The figure illustrates this concept by highlighting the pixels that are adjacent to the original image with a blue circle. In the case of odd pixels, it is necessary to take the pixels of the original image from the row above and below as the previous and next pixel, respectively. These pixels are highlighted in the figure by red circles (see Figure 4).

While increasing the number of ranges enables more accurate identification of homogeneous areas where context statistics are particularly predictable, too fine a division results in too few pixels falling into each range. This means that the algorithm cannot build a reliable statistical model for them. If the model is poorly constructed (due to there being too few pixels in the range), the resulting distribution of the least significant bits will not correspond to the true distribution, reducing resistance to steganography analysis. Therefore, we selected this parameter as the optimal solution, striking a balance between the method’s capacity and its resistance to steganography analysis. In this implementation, we also propose using a range of 16 to divide the areas, which has been empirically found to produce good results and be optimal. Other values are not practical. Reducing the number of ranges means that too many pixels will fall into each region. Pixels with very different visual content will be mixed and the statistics will be averaged and less accurate, which reduces the robustness of the method.

It is noted that at any range value, there will inevitably be some small areas that will not allow the formation of statistics, and during embedding, will have a rather random LSB distribution. Simultaneously, large areas during information embedding are closest to the true LSB probability distribution.

2.6. Methods of Steganalysis

The first condition that all steganographic programs fulfill is that the distortions introduced into the container when embedding a message should be invisible to the human eye. Thus, even with 100% filling, that is, replacing all LSBs of the image matrix, we usually do not see distortions, especially if there is no original file for comparison. However, LSB replacement can be easily detected using a simple visual steganalysis method. To achieve this, the pixel values of container are transformed according to rule (2):

$$S^{\prime }(i,j)=\left\{\begin{array}{cc}255,\hfill & \mathrm{if}S(i,j)=1\hfill \\ 0,\hfill & \mathrm{if}S(i,j)=0\hfill \end{array}\right.$$

(2)

where i, j are the indices of the current pixel.

Next, a visual assessment method was used to compare the general contours in the images before and after transformation. Thus, with LSB replacement, we will observe random noise, and with preserved LSB correlations, the general contours of the image will be determined.

In this study, the RS analysis method (Regular–Singular) was also used to evaluate the steganographic resistance of the developed method. The essence of the analysis is to search for spatial correlations in the container, which is divided into connected pixel groups for which a real smoothness function is then determined (3):

$$f\left(G\right)=\sum _{i=1}^n\left|x_{i+1}-x_i\right|$$

(3)

where G is a set of n groups $x_1$…$x_n$ connected to the pixel groups in the container. The larger the value of this function, the noisier the group G. Reversible noise is then added to the groups, increasing the smoothness function in empty containers and amplifying the value spikes in filled containers [23]. Based on the results, the groups were divided into regular and singular groups and their quantitative characteristics were calculated, based on which a graph was constructed. The output is the estimated length of the embedded information in the container (L). The RS method may indicate a small non-zero message length owing to random deviations even for an empty container; when $L\ge 5$, the RS analysis classifies the container as filled.

In steganography, the task of classifying containers is reduced to choosing one of two hypotheses: $H_0$—the container is empty, and $H_1$—the container contains embedded information. However, any stego algorithm can mistakenly classify the containers. Therefore, it is customary to separate errors into two types: a type I error occurs when the steganalyst chooses hypothesis $H_1$ for an empty container (false positive) and a type II error occurs when hypothesis $H_0$ is chosen for a filled container (miss). Therefore, it is necessary to determine the proportion of false positives for a test set of empty containers before testing the method for the presence of embedded information using an algorithm.

To evaluate the quality of filled containers in steganography, the PSNR indicator was used (4):

$$PSNR=10·{log}_{10}\left({\displaystyle \frac{{255}^2}{ϵ}}\right)$$

(4)

where

• $ϵ={\displaystyle \frac{1}{MN}}{\sum }_{i=0}^M{\sum }_{j=0}^N{\left(S(i,j)-I(i,j)\right)}^2$ is the distortion;
• M and N are the height and width of the image, respectively.

The higher the PSNR value, the fewer are the discrepancies between the compared images.

Our method makes changes based on global brightness statistics and local context. However, since SRM analyses depend on pixels at a variety of distances and directions, our algorithm is not designed to preserve these complex, multilevel relationships unchanged. The changes made will appear as statistical noise, which the SRM model successfully captures. Additionally, sharp boundaries between brightness ranges can create subtle statistical anomalies that will become apparent to the high-dimensional SRM model. As with deep learning-based detectors, a neural network trained on examples of the work of our algorithm can learn to recognise it. However, analysing a single image with SRM, or especially a complex CNN, requires a significant amount of time and computing resources. A clinic or diagnostic centre may receive thousands of studies per day and performing deep steganography analysis on each image would place a significant computational burden on the system, resulting in delays to doctors receiving results.

The data used to evaluate the results of the proposed method were taken from the international database of images for research in the field of steganography (BOSS base). We supplemented the dataset with an additional 100 images taken at random from the NIH chest X-ray database: https://www.kaggle.com/datasets/nih-chest-xrays/sample/versions/1 (accessed on 12 August 2025). For the study, these images were converted to BMP format and reduced to 256 × 256 pixels.

3. Results

Consequently, a program was formulated that implemented the proposed new steganographic scheme for data embedding and extraction in raster images. In order to evaluate the characteristics of the method, experiments were conducted on 1000 images. The source code is available on GitHub: https://github.com/KaterinaMerzlyakova/Reversible-steganographic-system-for-the-transmission-of-personal-medical-data (accessed on 12 August 2025). (see Appendix A).

We provide the pseudocode above. We also provide performance metrics.

• Time complexity: $O\left(n^2\right)$ for an $n\times n$ image.
• Memory: $O\left(n^2\right)$ for image storage.
• Processing speed: ∼10⁴–10⁵ pixels per second on the CPU.

These experiments demonstrated that the average embedding capacity of the proposed steganographic algorithm was 0.6 bits per pixel. The visual analysis method demonstrated that certain correlations of the least significant bits (LSBs) were noticeably preserved in the filled container, whereas the containers themselves did not differ visually before and after embedding. For the purpose of comparison, another RDH (Reversible Data Hiding) steganographic scheme was considered and implemented. This scheme was proposed by other authors and was based on interpolation [24]. In this scheme, the process of embedding was executed exclusively within the LSBs of the image, with the objective of facilitating a more precise comparative analysis of the outcomes with those obtained through the method that was developed in the present study. Figure 5 shows examples of containers before and after embedding using the method developed in this study, as well as the LSB values following formula (2) for the source image and for containers filled by the two methods for comparison. Stegocontainer S was filled using the method we developed, and stegocontainer $S2$ was filled using the high-payload lossless steganography [20] method. The size of the presented containers was 512 × 512. From the provided data, it is noticeable that the LSB statistics tend toward a random distribution when the containers are filled using the conventional RDH method, whereas the proposed method shows areas that retain the LSB distribution.

The following discussion will involve visual analysis of the containers. The Source’ column represents the original container (the original medical image corresponding to container A in Figure 1), and the Stegocontainer $S^{\prime }$ column represents the filled container (corresponding to container S in Figure 1). In the Source’ column, the distribution of the low-order bits corresponding to the container from the ‘Source’ column is evident. The column entitled Stegocontainer’ also demonstrates the distribution of low-order bits; however, it does so for the stegocontainer that contains embedded data in the maximum possible amount for this container (0.6 bits per pixel). Upon observation of this distribution and subsequent comparison with the original distribution prior to embedding, it becomes evident that the visual characteristics of the original distribution of low-order bits of the original container are largely retained. This outcome is anticipated, as the methodology employed by the present study incorporates the statistical properties of the low-order bits. For the purpose of comparison, the column entitled Stegocontainer $S{2}^{\prime }$ presents the distribution of the low-order bits of the container that were filled by an alternative method, which did not take statistics into account. It is evident that the RDH method, when not accounting for the statistics of low-order bits, fails to preserve the image of the distribution. This is indicative of a filled container, which is readily discernible through statistical stegoanalysis. The rightmost column of this table demonstrates how the LSB distribution is distorted in all methods that do not consider the distribution of the low-order bits.

Thus, our method demonstrates high image quality after embedding the data, which is confirmed by the experimentally obtained values of the structural similarity (SSIM) and Pearson Correlation Coefficient (PCC) metrics. These results indicate a good structural similarity between the original and modified images, as well as a high degree of linear correlation between their pixel values.

A comparative analysis with the method presented in [25] demonstrated that both approaches utilize enhanced LSB embedding strategies and offer a high degree of invisibility. In the aforementioned paper, the authors achieved SSIM values ranging from 0.9956 to 0.998 and PCC values exceeding 0.999, which also serves as an indication of the high quality of the modified image. However, in contrast to the method that utilizes two stego images, our approach does not necessitate the transfer of multiple containers, thereby mitigating the risk of information loss and streamlining the data extraction process. It is noteworthy that both approaches offer the advantage of reversibility, a quality that renders them suitable to apply in the domain of medical image processing (see

Table 1. Results for SSIM and PCC.

Container	SSIM	PCC
	0.999938	0.999937
	0.999972	0.999972
	0.999943	0.999943

for a detailed comparison).

A comparison was also made with the method described in [26], which employs deep learning for the purpose of predictive analytics in the field of reversible steganography. In the aforementioned paper, the authors employ neural network architectures for the purpose of predicting pixel values. This approach enables efficient data embedding in the prediction error, thereby minimising distortions. The range of PSNR values obtained is from 50 to 70 dB, and the SSIM values are close to 1, which corresponds to very high image quality after embedding.

However, in contrast to this approach, the methodology developed in this study does not necessitate the training of a model, thereby facilitating its implementation and rendering it applicable in real time, particularly in environments characterised by resource constraints. In the context of telemedicine, for instance, this aspect assumes particular significance. It was also determined that the deep learning-based method is more susceptible to analysis if the prediction model becomes known to an attacker.

It is evident that the proposed methodology combines high image quality, which is comparable to state-of-the-art AI-based methods, while providing high resistance to detection and full reversibility. This renders it promising for application in medical systems.

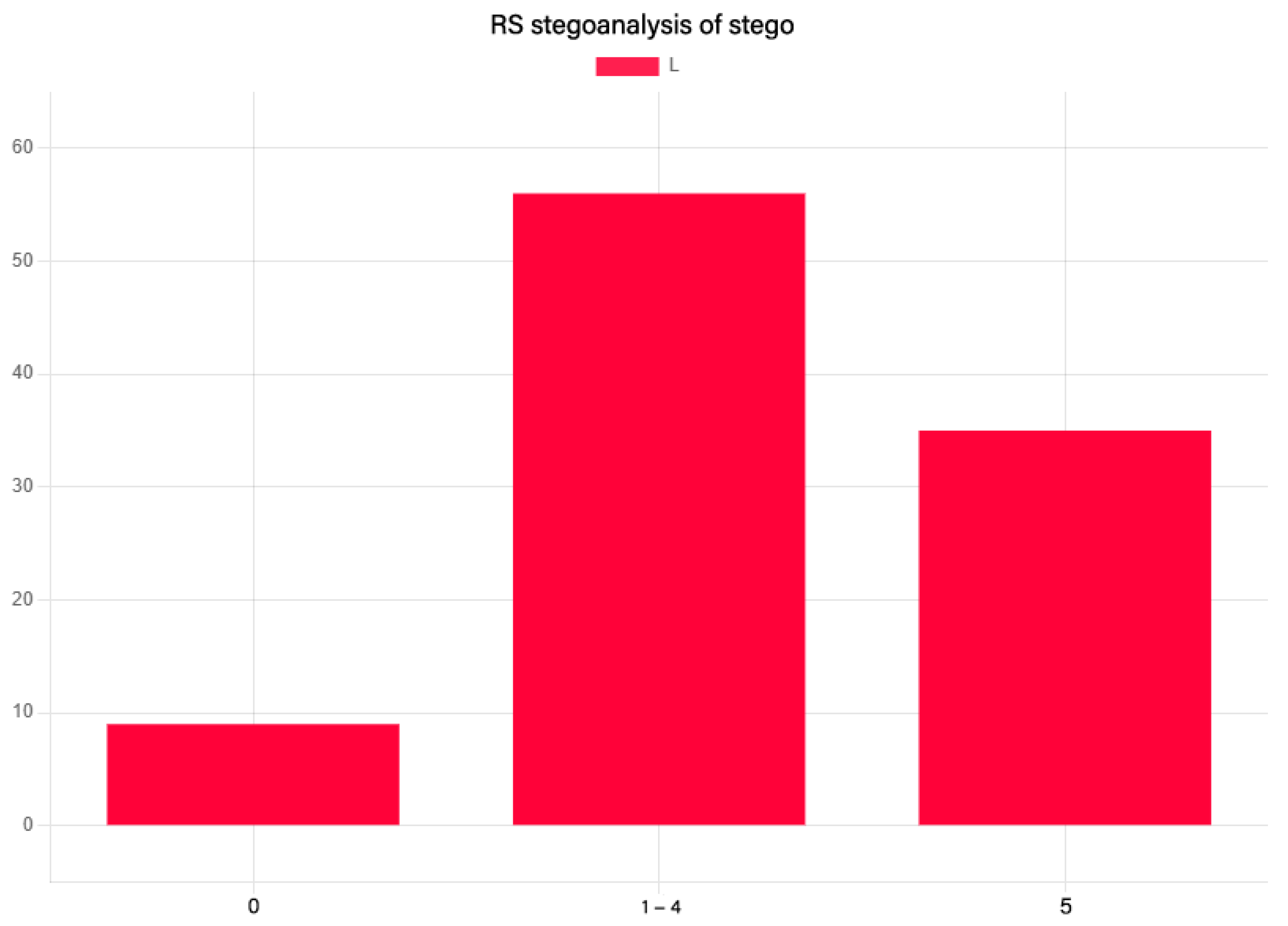
The RS analysis method on a set of 1000 empty source containers with a size of 512 × 512 showed a type I error of 27%. For the corresponding containers filled with the developed method, the percentage of files classified as filled was 35%, indicating that 8% revealed stegocontainers. These results suggest a good resistance of the method to this type of steganalysis.

Visualisation of the results of RS steganalysis on a set of 1000 images: this diagram (see Figure 6) demonstrates the result of RS steganalysis on empty images. The Y-axis shows the number of files from a set of 1000 images, indicated as a percentage. The RS steganalysis result is presented as an L value indicating the length of the detected embedded data.

In the source of the authors of this method of steganalysis, it is assumed that stegulation was found at $L\ge 5$. The value of L from 1 to 4 is marginal and can be considered as an error in determining the decomposition. Thus, this diagram shows that the error of the first kind in the RS steganalysis on this set of containers was 27%.

Accordingly, the following diagram (see Figure 7) shows the result of RS steganalysis on filled containers using the developed method with an average capacity of 0.6 bits per pixel.

In this instance, the proportion of detected files increased by 8%, which is a commendable outcome. It should be noted, however, that RS steganalysis detects LSB embedding in 100% of cases if container statistics are not taken into account.

The PSNR values for the test container samples filled using the two methods are listed in

Table 2. Comparison of the proposed method with other RDH algorithms.

Method	Container (bpp)	PSNR (dB)
Our method	0.4–0.9	52–81
High Payload Lossless Steganography [24]	≈0.5	≈60
Histogram Shifting-based RDH [15]	0.4–0.7	50–60
Difference Expansion-based RDH [16]	0.5–1.0	55–65
Pixel Class Interpolation [10]	0.4–0.9	>60
Reversible Data Hiding Using Pixel Intensity Classes [8]	Up to 1.0	>65
Efficiency of LSB Steganography on Medical Information [17]	0.5–1.0	40–45
Image Steganography Using HBC and RDH Technique [18]	0.4–0.6	>50
Advancing Reversible LSB Steganography: Addressing Imperfections and Embracing Pioneering Techniques for Enhanced Security is an improved method for reversible LSB steganography using a cryptographic key and randomly distributes changes across two copies of an image	2	>52
Deep Learning for Predictive Analytics in Reversible Steganography uses deep learning to predict pixel values to efficiently and reversibly embed data into images with minimal distortion	0.6	55–70

. These PSNR values indicate the fairly good quality of the obtained stegocontainers and exceed the results of methods based on interpolation without using statistics [9,10,20], where the embedding capacity was 0.4–0.9 bits per pixel.

With an average capacity of 0.6 bpp, it is possible to embed extensive patient data into a single typical X-ray image. Moreover, this leaves a significant margin. This means that multiple embeddings will not be required, which minimises risks.

The proposed adaptive steganographic method provides high-quality medical images due to the use of interpolation for data embedding into the low-order bits of the image without changing the original pixels, which guarantees reversibility and preserves the diagnostic value of images. Also, in order to comprehensively evaluate the model performance of the proposed method, a comparison of image (steganographic) quality metrics with several known reversible data embedding algorithms, including those applied to medical images, was performed. The following methods were chosen as comparison objects:

• High Payload Lossless Steganography [24]—a state-of-the-art method using image interpolation;
• Histogram Shifting-based RDH [15]—one of the classical approaches for reversible data hiding based on modifying the histogram of differences in images;
• Difference Expansion-based RDH [10]—a method of reversible data hiding based on the technique of expanding differences of neighbouring pixels;
• Pixel Class Interpolation [10], a steganography method based on image interpolation, in which the image enlarged by interpolation is used to embed data into new pixels;
• Reversible Data Hiding Using Pixel Intensity Classes [8]—a method of reversible data hiding based on image interpolation taking into account pixel intensity classes;
• Efficiency of LSB Steganography on Medical Information [17], a method based on using the least significant bit to hide medical information in X-rays and other medical images;
• Image Steganography Using HBC and RDH Technique [18] is a hybrid method combining Hide Behind Corner (HBC) and Reversible Data Hiding (RDH).

The results are presented in Table 2. The comparison metrics included peak signal-to-noise ratio (PSNR) and embedding capacity (bpp) as the most representative available characteristics of steganographic methods.

The blue line shows the average trend of the dependence, obtained by constructing a linear regression model based on the experimental data. This curve shows how the average capacity changes as the PSNR level changes. The observed decrease from left to right indicates negative dependence: as PSNR increases, i.e., as image quality improves, the embedding capacity decreases systematically. This corresponds to theoretical expectations for most steganographic algorithms.

The light blue band around the regression line is a 95% confidence interval showing the range within which the true dependence of capacity on PSNR is highly likely to be found. Its narrow, continuous shape, which does not intersect with the horizontal axis, indicates the statistical significance and stability of the identified feedback: as image quality (PSNR) increases, the embedding capacity decreases.

The average embedding capacity was 0.7327 bpp, with a 95% confidence interval of [0.7312, 0.7342]. This indicates that the method is highly stable and provides a reliable estimate of the mean for a sample of 100 images.

Therefore, despite the chest X-ray dataset’s slightly different data, the method produces excellent results with high PSNR (>52 dB) and good embedding capacity (around 0.73 bpp), making it effective for steganographic applications.

Thus, despite a slight decrease in embedding capacity, our method provides higher quality stegocontainers, which is also confirmed by the results of Table 1 and stegoanalysis.

The method has been enhanced by the incorporation of statistical analysis of low-order bits, facilitating the establishment of a steganographic system that exhibits characteristics reminiscent of optimal stegosystems. In order to achieve this objective, the lower bits of the container have been contemplated in a variety of contexts, which have been formed by the higher bits. The estimation of statistics was constructed using the Krichevski–Trofimov formula, as outlined in the approach previously outlined (5):

$$P(0\mid X)={\displaystyle \frac{2n_{x,0}+1}{2(n_{x,0}+n_{x,1})+2}},P(1\mid X)=1-P(0\mid X)$$

(5)

Here $n_x{,}_0$, $n_x{,}_1$ are counters of occurrence of values 0 and 1 in the context X. More details of this approach, which we apply in the proposed steganographic method, are given in [17].

Given a confidence level of 0.95, the true probability of success in the general population is calculated within the confidence interval $I=(P_1,P_2)$, where

$$P_1,P_2=P^{*}\pm t·\sqrt{{\displaystyle \frac{(1-P^{*})·P^{*}}{N}}}$$

(6)

Here, $P^{*}$ is the probability of success in N trials. During the experiment, the test set contained 1000 files, but the RS analysis revealed a Type I error in 27% of these files. Excluding these containers, we are left with N = 730 experiments. In this case, success is defined as the probability of "skipping" stegocontainers using the RS analysis method. This equates to a probability of 0.92%, since only 8% of the 730 selected images were classified as filled containers. Student’s t-criterion is t = 1.96 with a confidence level of y = 0.95. These calculations are valid when the number of experiments is large enough, i.e., when the following conditions are met:

$$N(1-P)>4,NP>4$$

(7)

In our case, these conditions are met; therefore, the confidence interval for experiments on a set of 512 × 512 pixel images is $I\_\left(RS\right)=(0.90031,0.93968)$. In experiments conducted on a sample of 100 radiograph images, the method demonstrated a consistently high capacity of 0.73 bpp on average.

The average volume of embedded data (approximately 24 KB per image) is sufficient to accommodate extensive medical information (e.g., a patient’s complete electronic patient record (EPR)). The capacity depends only weakly on the image content (all bpp values are close to the average), which confirms the effectiveness of the adaptive algorithm. The results are shown in the graph below (see Figure 8):

4. Discussion

The novelty of the proposed steganographic system is predicated on the utilisation of a method which takes into account the statistics of the low-order bits in RDH steganography. The previously mentioned method of taking the statistics of the low-order bits into account is applied in combination with the forest fire method in determining the connected regions of the image. This results in a robust steganographic scheme, one of the significant applications of which is considered in the field of digitalisation in medicine.

The method for embedding information into images that has been developed enhances the resistance to steganalysis by preserving LSB correlations. This steganographic scheme has been developed for the purpose of concealing patients’ personal data in medical images without compromising the integrity of the content. The proposed steganographic scheme demonstrates a superior PSNR in comparison to other ste ganographic schemes that employ interpolation methods in RDH, thereby signifying the superiority of the proposed scheme in terms of image quality.

In the context of comparative analyses of RDH methodologies, the prevailing contemporary studies employ two criteria: the embedding capacity of the embedding method and the PSNR container quality score. The result of the method capacity is hereby presented, which is found to be between $0.4$ and 0.7 bits per pixel. The variation in capacity is attributable to the nature of the container, which is an image that is partitioned into coherent regions depending on its content. A considerable number of studies have specified the capacity of RDH methods as ranging from $0.3$ to $1.6$ bits per pixel. However, it is important to note that as the capacity of these methods increases, the quality of the obtained stego-image decreases, and the methods become less resistant to stegoanalysis. Consequently, the capacity index of the developed method is not the primary index for comparison, but is provided for general informational purposes. A more informative metric is the PSNR index, which, in our method, is high based on the generally accepted value of 45 dB. Of greater significance is the comparative visual analysis of the distribution of the lower bits and the stegoanalysis of the filled bins. The incorporation of these criteria has introduced a novel dimension to the study of RDH methods.

The study was conducted on a set of 512 × 512 pixel grey BMP images. This method can be readily extended to colour images. However, the image size of more than 512 × 512 pixels is undesirable due to the linear complexity of the method. The utilisation of small medical images in telemedicine does not constitute a significant limitation of the method.

In such studies, the most significant indicator is the PSNR value, which ranges from 45–60 dB for all similar RDH methods. It has been demonstrated that the mean value of the developed method exceeds 60 dB. A PSNR value of more than 45 dB is generally considered adequate, thus rendering a comparison of this indicator on different sets of files redundant. In the present study, we have introduced several innovations, including the analysis of containers using visual comparison of the distribution of low-order bits, which is a more visual comparison method, and also conducted a study of a large set of stegocontainers using the RS steganalysis method, which has been overlooked in such works.

In conclusion, the SSIM and PCC metrics demonstrated that the modified images retained a high degree of structural similarity and exhibited a strong linear correlation with the original images, confirming the effectiveness of the proposed approach.

The proposed algorithm can be applied not only to LSBs but also to higher-order bits, with the probability distribution being evaluated in the same way. Concurrently, some distortion in the LSB statistics of the stegocontainer is to be anticipated, owing to the unavoidable existence of diminutive connected areas that are not conducive to the collection of statistics. It is therefore proposed that the algorithm be adapted further by the use of small connected areas for embedding, in conjunction with other stegometric methods.

5. Conclusions

In conclusion, the SSIM and PCC metrics demonstrated that the modified images retained a high degree of structural similarity and exhibited a strong linear correlation with the original images, confirming the effectiveness of the proposed approach. The proposed algorithm can be applied not only to LSBs but also to higher-order bits, with the probability distribution being evaluated in the same way. Concurrently, some distortion in the LSB statistics of the stegocontainer is to be anticipated, owing to the unavoidable existence of diminutive connected areas that are not conducive to the collection of statistics. It is therefore proposed that the algorithm be adapted further by the use of small connected areas for embedding, in conjunction with other stegometric methods.