Model Drift in Deployed Machine Learning Models for Predicting Learning Success
Abstract
1. Introduction
2. Materials and Methods
2.1. Educational Data and Corresponding Predictive Models
2.1.1. Digital Profile Dataset and the LSSp Model
- Demographic data: age, gender, citizenship status (domestic or international);
- General education data: type of funding, admission and social benefits, field of study, school/faculty, level of degree program (Bachelor’s, Specialist, or Master’s), type of study plan (general or individual), current year of study, and current semester (spring or fall);
- Relocation history: number of transfers between academic programs, academic leaves, academic dismissals, and reinstatements; reasons for the three most recent academic dismissals, reasons for the most recent academic leave and the most recent transfer; types of relocation in the current semester (if applicable);
- Student grade book data: final course grades from the three most recent semesters (both before and after retakes), number of exams taken, number of retakes, and number of academic debts.
2.1.2. Digital Footprint Dataset and the LSSc Model
- Active clicks—interactions with reading materials and viewing the course elements;
- Effective clicks—interactions with the e-course that change its content, e.g., submitting assignments, test attempts, etc.
- The overall score in the gradebook of the e-course at a given moment in time;
- The course-specific performance forecasts made by the Model for Forecasting Learning Success in Mastering a Course (LSC Model) [40].
- Assessing e-courses (in which course grades changed at least once for one of the subscribed users last week).
- Frequently visited e-courses (which were accessed by their subscribers at least 50 times last week).
- Week of semester, semester (spring or fall), year of study;
- Number of e-courses a student is subscribed to (total/for assessing/for frequently visited courses);
- Average grades (for all/assessing/frequently visited courses);
- Number of active clicks and number of effective clicks (for all/assessing/frequently visited courses);
- Averages of the forecasts made by the LSSc model (across all e-courses/assessing/frequently visited).
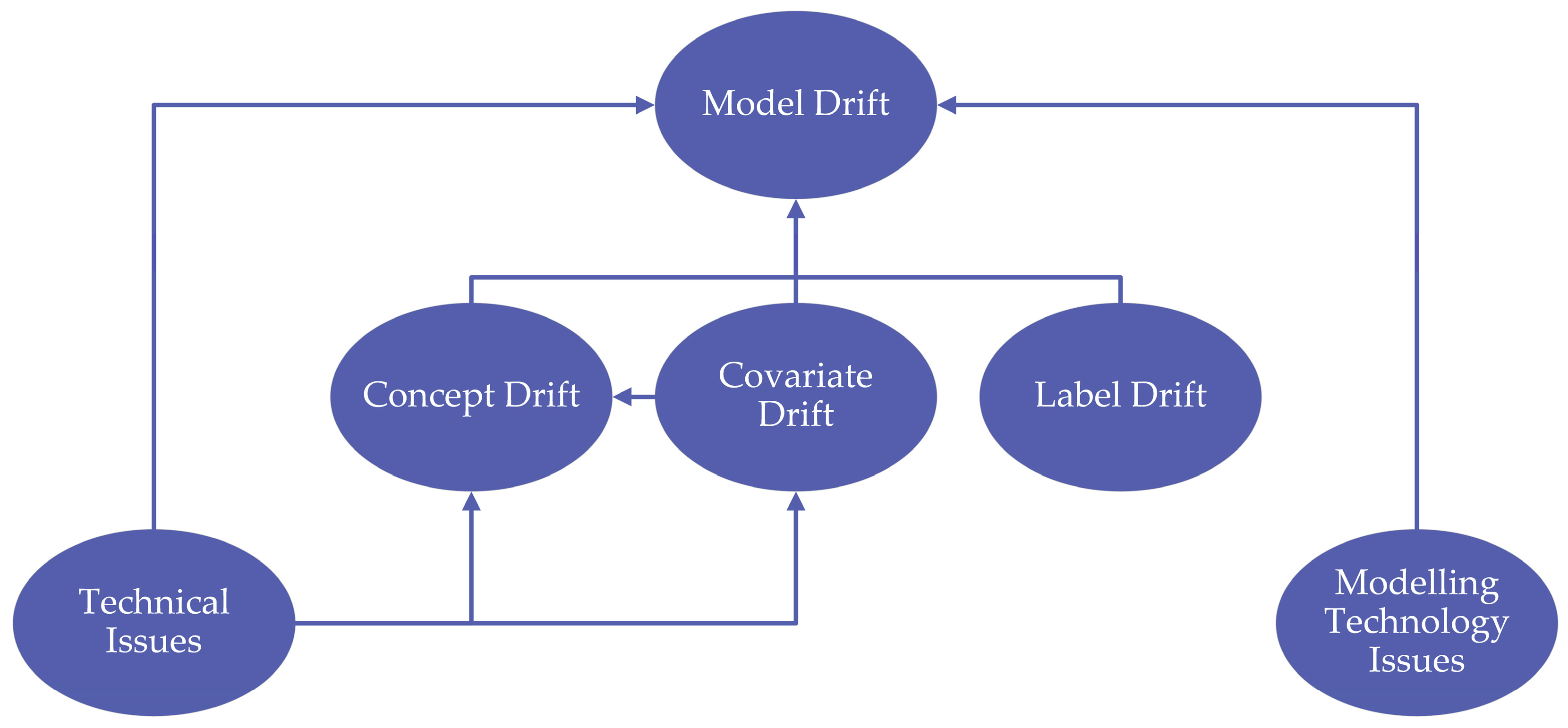
2.2. Data Drift and Model Degradation
- Covariate drift—changes in the distribution of features Pt(X1, …, Xn) ≠ Pt+T(X1, …, Xn);
- Label drift—changes in the distribution of the target variable Pt(Y) ≠ Pt+T(Y);
- Concept drift—changes in the relationships between features and the target: Pt(Y | X1, …, Xn) ≠ Pt+T(Y | X1, …, Xn).
2.3. Methods for Model Drift Detection
- PSI—to evaluate drift in univariate marginal and conditional distributions of educational features;
- Classifier-Based Drift Detector—to assess changes in the multivariate structure of student data;
- SHAP—to analyze model degradation in terms of performance metrics.
2.3.1. PSI
2.3.2. Classifier-Based Drift Detectors
2.3.3. SHAP Loss
- Define a practically meaningful effect size (prac_effect).
- For each predictor X, using the samples SHAP losstrain(X) and SHAP lossnew(X), the following steps can be performed:
- (a)
- Perform a power analysis to determine an appropriate significance level α;
- (b)
- Using t-test, compare the means of SHAP losstrain(X) and SHAP lossnew(X);
- (c)
- Calculate the observed effect size (Cohen’s d);
- (d)
- Conclude that data drift is present for predictor X if the difference in SHAP loss is statistically significant and Cohen’s d ≥ prac_effect.
3. Results
3.1. Data Drift in the Digital Profile Dataset
3.2. Model Degradation of the LSSp Model
- Extend the training dataset by adding all academic semesters up to the target year. For example, to make predictions for 2023, the model is trained on data from 2018 to 2022; for predictions in 2024, the training data includes the years from 2018 to 2023.
- Restrict training dataset to the previous academic year only.
3.3. Data Drift in the Digital Footprint Dataset
- All PSI values for feature distributions between 2022 and 2023 were below 0.1, indicating no significant data drift.
- For the 2023–2024 comparison, the feature “Year of study” exhibited a substantial drift with PSI = 0.5. Two other features, “Average grade for assessing e-courses (min–max scaled)” with PSI = 0.123 and “Average grade for all e-courses (min–max scaled)” with PSI = 0.124 showed moderate drift. For all other features PSI values were below 0.1.
- A comparison between 2022 and 2024 revealed that half of the features demonstrated drift that was moderate to significant. A new feature exhibiting substantial drift was “Number of active clicks for assessing e-courses” (PSI = 0.252), which had previously been stable. The moderate drift with PSI in the range from 0.1 to 0.25 was detected for the following features: “Number of effective clicks for frequently visited e-courses”, “Average forecast of model LSC for assessing/frequently visited/all e-courses”, “Number of active/effective clicks”, “Number of all/assessing e-courses”, “Average grade for assessing e-courses (min–max scaled)”, and “Average grade for all e-courses (min–max scaled)”.
- All conditional distributions of features given at_risk = 1 were stable between 2022 and 2023 (PSI < 0.1).
- Conditional distributions given at_risk = 0 remained within the range of insignificant change between 2023 and 2024 with PSI < 0.1, except for the feature “Year of study”, which exhibited substantial drift (PSI = 0.575).
- A significant drift in the conditional distribution given at_risk = 1 between 2023 and 2024 was also observed for “Year of study” (PSI = 0.411). Moderate drift was found for “Average forecast of model LSC for assessing/frequently visited/all e-courses”, “Average grade for assessing e-courses (min–max scaled)”, and “Average grade for all e-courses (min–max scaled)”.
- Out of the 30 Digital Footprint features compared between 2022 and 2024, only 10 remained within the threshold for insignificant drift (PSI < 0.1) for both conditional distributions given at_risk = 0 and at_risk = 1. These included “Average grade for all/assessing/frequently visited e-courses”, “Number of frequently visited courses”, and their min–max scaled variants.
- The distributions can be considered stable in the short term, particularly during the fall semesters. The results show only minor drift between the years 2022 and 2023, and between 2023 and 2024.
- In the long term, data drift tends to accumulate, leading to the emergence of moderate to significant drift across several features.
- The analysis of conditional distributions demonstrated that data drift depends on learner groups as defined by the target variable. For students without academic debts, moderate changes in activity on the e-learning platform “e-Courses” were observed, with more pronounced variations during spring semesters.
3.4. Model Degradation of the LSSc Models
- Fall 2023: recall = 0.58; weighted F-score = 0.695;
- Fall 2024: recall = 0.689; weighted F-score = 0.748;
- Spring 2023: recall = 0.741, weighted F-score = 0.757.
- Retraining the LSSc-spring and LSSc-fall models on 2022 data using the full set of predictors but with a more conservative set of hyperparameters;
- Sequentially removing predictors from the models—starting from the top of Table A3—that showed the most pronounced SHAP loss drift in 2023, followed by retraining on 2022 data;
- Combining both approaches: applying a more conservative set of hyperparameters and removing predictors with the most significant SHAP loss drift in 2023.
- Model complexity was controlled through regularization parameters: max_depth, min_child_weight, reg_alpha, reg_lambda, and gamma.
- Robustness to noise was enhanced by using non-default values for subsample and colsample_bytree.
- Predictors that exhibited the most significant SHAP loss drift in 2023 compared with 2022 were excluded from the models. After modification, both the LSSc-fall and the LSSc-spring models include only nine predictors.
4. Discussion
4.1. Data Stability
4.2. Mitigating Model Drift Caused by Modeling Technology Issues
- Adaptive selection of models based on “aging” metrics.Instead of selecting a single machine learning model, it can be useful to consider a diverse portfolio of models. For example, in our study, alongside XGBoost, we could have also included k-Nearest Neighbors, Random Forest, and regularized logistic regression—despite their lower performance on the 2018–2021 test set.The idea is to initially deploy the best-performing model in the forecasting system while continuing to generate forecasts using the remaining models in parallel. After several periods of deployment on new data, evaluate each model’s performance and rate of degradation—e.g., via relative model error, as described in [36]. Based on both performance and “aging” metrics, a data-driven decision can then be made regarding which model to adopt for the forecasting service in the next academic term.
- Stress testing during model training.It can be beneficial to incorporate stress tests during the model training phase to identify which types of models are most robust to noise and data perturbations. An example of the adoption of such an approach can be found in [59].
4.3. Pipelines for Monitoring and Refinement of the Deployed Models
- Assess predictive performance of all models from the portfolio on new data and compute aging metrics.
- In cases of significant model degradation, conduct SHAP loss analysis, using the procedure described in Section 2.3.3 to evaluate the extent and the nature of model drift.
- Retrain all models of the portfolio using different strategies for incorporating most recent data, as described in Section 3.2. Additionally, explore retraining variants that exclude features showing the most significant SHAP loss drift.
- From the set of retrained models, select the one with the best performance and the lowest aging metric to deploy in the forecasting system for the upcoming semester.
- If retrained models still underperform, consider deeper modifications like feature engineering, prioritizing interpretable features. This improves transparency in academic success predictions for staff involved in student guidance.
4.4. Detection of Biased Subgroups for Predictive Models
4.5. Limitation of the Study and Future Research Directions
5. Conclusions
- We proposed a methodology for the comprehensive analysis of learning performance prediction models under data drift, incorporating the following techniques: calculating PSI, training and analyzing Classifier-Based Drift Detector models, and testing hypotheses about SHAP loss value shifts. This allows the evaluation of concept drift, covariate drift, and label drift, as well as the overall model degradation.
- We found that educational data of different types could exhibit varying degrees of data drift. Specifically, Digital Profile data in our study demonstrated only a minor covariate shift, and the academic success prediction model based on these data showed slight performance degradation. At the same time, Digital Footprint data from the online course platform changed significantly over time. This was revealed both through covariate shift detection methods and SHAP loss drift analysis. The corresponding predictive model demonstrated a substantial degree of model drift. However, the observed improvements in recall for the LSSc model suggest that LMS-derived behavioral features can enhance the detection of at-risk students if data quality is sufficient. Improving the pedagogical design and standardization of e-courses could significantly enhance the predictive power and stability of LMS-based features.
- We explored and tested several model drift mitigating strategies: using conservative hyperparameters, retraining the model including more recent data, and excluding features with large SHAP loss drift. While we managed to successfully mitigate the degradation of the predictive model based on Digital Profile data, we did not achieve a significant improvement in prediction performance on new data for the model based on Digital Footprint data. It is likely that the most effective strategy for mitigating model degradation in our case may be the development and application of criteria for selecting electronic courses, whose Digital Footprint data will be used for prediction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GPA | Grade Point Average |
| FI | Feature Importance |
| HEI | Higher Educational Institution |
| LA | Learning Analytics |
| LMS | Learning Management System |
| ML | Machine Learning |
| Model LSC | Model for Forecasting Learning Success in Mastering a Course |
| Model LSSc | Model for Forecasting Learning Success in Completing the Semester Based on Current Educational History |
| Model LSSp | Model for Forecasting Learning Success in Completing the Semester Based on Previous Educational History |
| PSI | Population Stability Index |
| RF | Random Forest |
| RF-Drift Detector | Random Forest based drift detector model |
| SHAP | SHapley Additive exPlanations |
| SHAP Loss | SHAP values computed with respect to the model’s loss |
| SibFU | Siberian Federal University |
Appendix A
| Feature | Source | Description | Type | Update Frequency |
|---|---|---|---|---|
| At risk (target variable) | Grade book | Whether a student failed at least one exam in the current semester | Categorical | Dynamic (once a week) |
| Age | Student profile | Student’s age | Numerical | Dynamic (once a week) |
| Sex | Student profile | Gender | Categorical | Static |
| International student status | Student profile | Indicator of foreign citizenship or international enrollment | Categorical | Static |
| Social benefits status | Student profile | Whether the student is eligible for state benefits | Categorical | Static |
| School | Student profile | Faculty within the university | Categorical | Dynamic (once a week) |
| Year of study | Student profile | Current year of study | Categorical | Dynamic (once a year) |
| Current semester (term) | Student profile | Current semester of study | Categorical | Dynamic (once a semester) |
| Study mode | Student profile | Full-time, part-time, or distance | Categorical | Static |
| Funding type | Student profile | Enrollment category: state-funded, tuition-paying, or targeted training | Categorical | Dynamic (once a week) |
| Level of academic program | Student profile | Degree level: Bachelor’s, Specialist, or Master’s program | Categorical | Dynamic (once a week) |
| Field of study category | Student profile | Broad academic domain: humanities, technical, natural sciences, social sciences, etc. | Categorical | Dynamic (once a week) |
| Individual study plan | Student profile | Indicator of non-standard/personalized curriculum | Categorical | Dynamic (once a year) |
| Amount of academic leave | Administrative records | Total amount of academic leave taken since enrollment | Numerical | Dynamic (once a week) |
| Reason for the last academic leave | Administrative records | Primary justification for the most recent academic leave | Categorical | Dynamic (once a week) |
| Number of transfers | Administrative records | Total number of transfers to other degree programs within the university since enrollment | Numerical | Dynamic (once a week) |
| Reason for the last transfer | Administrative records | Stated reason for the most recent transfer to another degree program | Categorical | Dynamic (once a week) |
| Number of academic dismissals | Administrative records | Total number of prior academic dismissals from the university | Numerical | Dynamic (once a week) |
| Reason for the last academic dismissal | Administrative records | Official reason for the most recent dismissal | Categorical | Dynamic (once a week) |
| GPA in the current semester | Grade book | Grade point average across all courses in the current semester, before retakes | Numerical | Dynamic (once a semester) |
| Number of courses in the current semester | Grade book | Total number of courses enrolled in this semester | Numerical | Dynamic (once a semester) |
| Number of pass/fail exams in current semester | Grade book | Number of courses in the current semester evaluated through pass/fail exams | Numerical | Dynamic (once a semester) |
| Number of graded exams in current semester | Grade book | Number of courses evaluated by formal graded examinations | Numerical | Dynamic (once a semester) |
| Number of academic debts in the current semester | Grade book | Total number of failed exams (both graded and pass/fail) by the current date | Numerical | Dynamic (once a week) |
| Number of academic debts for pass/fail exams in the current semester | Grade book | Number of failed pass/fail exams | Numerical | Dynamic (once a week) |
| Number of first retakes in the current semester | Grade book | Number of completed initial retake attempts for examinations | Numerical | Dynamic (once a week) |
| Number of academic debts for graded exams after first retakes | Grade book | Count of unsuccessfully retaken graded exams (after first retakes) | Numerical | Dynamic (once a week) |
| GPA after first retakes (current semester) | Grade book | GPA recalculated after the results of the first retakes are included | Numerical | Dynamic (once a week) |
| Number of academic debts for pass/fail exams after first retakes | Grade book | Count of unsuccessfully retaken pass/fail exams (after the first retake) | Numerical | Dynamic (once a week) |
| Number of second retakes in the current semester | Grade book | Number of completed second retake attempts for examinations | Numerical | Dynamic (once a week) |
| Number of academic debts for graded exams after second retakes | Grade book | Count of unsuccessfully retaken graded exams (after second retakes) | Numerical | Dynamic (once a week) |
| GPA after second retakes (current semester) | Grade book | Final GPA after all second retakes’ results are recorded | Numerical | Dynamic (once a semester) |
| Number of academic debts for pass/fail exams after second retakes | Grade book | Count of unsuccessfully retaken pass/fail exams (after second retakes) | Numerical | Dynamic (once a semester) |
| GPA in the previous semester | Grade book | GPA in the immediately preceding semester, before retakes | Numerical | Dynamic (once a semester) |
| Number of courses in previous semester | Grade book | Total number of courses enrolled in the previous semester | Numerical | Dynamic (once a semester) |
| Number of pass/fail exams in previous semester | Grade book | Total number of pass/fail exams in the previous semester | Numerical | Dynamic (once a semester) |
| Number of graded exams in the previous semester | Grade book | Number of courses evaluated by graded examinations in the previous semester | Numerical | Dynamic (once a semester) |
| Number of academic debts in the previous semester | Grade book | Total number of failed exams from previous semester (not yet retaken) | Numerical | Dynamic (once a semester) |
| Number of academic debts for pass/fail exams in the previous semester | Grade book | Total number of failed pass/fail exams from previous semester (not yet retaken) | Numerical | Dynamic (once a semester) |
| Number of first retakes in the previous semester | Grade book | Number of completed initial retake attempts for exams of the previous semester | Numerical | Dynamic (once a semester) |
| Number of academic debts for graded exams after first retakes (in the previous semester) | Grade book | Number of failed graded exams from previous semester (after first retakes passed) | Numerical | Dynamic (once a semester) |
| GPA after first retakes (previous semester) | Grade book | GPA in the previous semester after including results of first retakes | Numerical | Dynamic (once a semester) |
| Number of academic debts for pass/fail exams after first retakes (previous semester) | Grade book | Number of failed pass/fail exams from previous semester (after first retakes passed) | Numerical | Dynamic (once a semester) |
| Number of second retakes in the previous semester | Grade book | Number of second retake attempts for exams of the previous semester | Numerical | Dynamic (once a semester) |
| Number of academic debts for graded exams after second retake (previous semester) | Grade book | Number of failed graded exams from previous semester (after second retakes passed) | Numerical | Dynamic (once a semester) |
| GPA after second retakes (previous semester) | Grade book | GPA in the previous semester after including results of second retakes | Numerical | Dynamic (once a semester) |
| Number of academic debts for pass/fail exams after second retakes (previous semester) | Grade book | Number of failed pass/fail exams from previous semester (after second retakes passed) | Numerical | Dynamic (once a semester) |
| GPA from two semesters prior | Grade book | GPA in the semester before the previous one, before retakes | Numerical | Dynamic (once a semester) |
| Number of courses from two semesters prior | Grade book | Number of courses enrolled from two semesters prior | Numerical | Dynamic (once a semester) |
| Number of pass/fail exams from two semesters prior | Grade book | Total number of pass/fail exams from two semesters prior | Numerical | Dynamic (once a semester) |
| Number of graded exams from two semesters prior | Grade book | Number of courses evaluated by graded examinations from two semesters prior | Numerical | Dynamic (once a semester) |
| Number of academic debts two semesters prior | Grade book | Total number of failed exams from two semesters prior (not yet retaken) | Numerical | Dynamic (once a semester) |
| Number of academic debts for pass/fail exams two semesters prior | Grade book | Number of failed pass/fail exams from two semesters prior (not yet retaken) | Numerical | Dynamic (once a semester) |
| Number of first retakes from two semesters prior | Grade book | Number of completed initial retake attempts for exams from two semesters prior | Numerical | Dynamic (once a semester) |
| Number of academic debts for graded exams after first retake (two semesters prior) | Grade book | Number of failed graded exams from two semesters prior (after first retakes passed) | Numerical | Dynamic (once a semester) |
| GPA after first retakes (two semesters prior) | Grade book | GPA from two semesters prior after including results of first retakes | Numerical | Dynamic (once a semester) |
| Number of academic debts for pass/fail exams after first retakes (two semesters prior) | Grade book | Number of failed pass/fail exams from two semesters prior (after first retakes passed) | Numerical | Dynamic (once a semester) |
| Number of second retakes two semesters prior | Grade book | Number of second retake attempts for exams from two semesters prior | Numerical | Dynamic (once a semester) |
| Number of academic debts for graded exams after second retakes (two semesters prior) | Grade book | Number of failed graded exams from two semesters prior (after second retakes passed) | Numerical | Dynamic (once a semester) |
| GPA after second retakes (two semesters prior) | Grade book | GPA from two semesters prior after including results of second retakes | Numerical | Dynamic (once a semester) |
| Number of academic debts for pass/fail exams after second retake (two semesters prior) | Grade book | Number of failed pass/fail exams from two semesters prior (after second retakes passed) | Numerical | Dynamic (once a semester) |
| GPA from three semesters prior | Grade book | GPA from three semesters prior (before retakes) | Numerical | Dynamic (once a year) |
| Number of courses from three semesters prior | Grade book | Number of courses enrolled from two semesters prior | Numerical | Dynamic (once a year) |
| Number of pass/fail exams from three semesters prior | Grade book | Total number of pass/fail exams from three semesters prior | Numerical | Dynamic (once a year) |
| Number of graded exams from three semesters prior | Grade book | Number of courses evaluated by graded examinations from three semesters prior | Numerical | Dynamic (once a year) |
| Number of academic debts from three semesters prior | Grade book | Total number of failed exams from three semesters prior (not yet retaken) | Numerical | Dynamic (once a year) |
| Number of academic debts for pass/fail exams from three semesters prior | Grade book | Number of failed pass/fail exams from three semesters prior (not yet retaken) | Numerical | Dynamic (once a year) |
| Number of first retakes from three semesters prior | Grade book | Number of completed initial retake attempts for exams from three semesters prior | Numerical | Dynamic (once a year) |
| Number of academic debts for graded exams after first retakes (three semesters prior) | Grade book | Number of failed graded exams from three semesters prior (after first retakes passed) | Numerical | Dynamic (once a year) |
| GPA after first retakes (three semesters prior) | Grade book | GPA from three semesters prior after including results of first retakes | Numerical | Dynamic (once a year) |
| Number of academic debts for pass/fail exams after first retakes (three semesters prior) | Grade book | Number of failed pass/fail exams from three semesters prior (after first retakes passed) | Numerical | Dynamic (once a year) |
| Number of second retakes from three semesters prior | Grade book | Number of second retake attempts for exams from three semesters prior | Numerical | Dynamic (once a year) |
| Number of academic debts for graded exams after second retakes (three semesters prior) | Grade book | Number of failed graded exams from three semesters prior (after second retakes passed) | Numerical | Dynamic (once a year) |
| GPA after second retakes (three semesters prior) | Grade book | GPA from three semesters prior after including results of second retakes | Numerical | Dynamic (once a year) |
| Number of academic debts for pass/fail exams after second retakes (three semesters prior) | Grade book | Number of failed pass/fail exams from three semesters prior (after second retakes passed) | Numerical | Dynamic (once a year) |
| Feature | Source | Description | Type | Update Frequency |
|---|---|---|---|---|
| At risk (target variable) | Grade book | Whether a student failed at least one exam in the current semester | Categorical | Dynamic (once a week) |
| Prediction proba LSSp | Derived | Predicted probability of being “at risk” from the LSSp model | Numerical | Dynamic (once a week) |
| Week | LMS Moodle | Current academic week of the semester | Categorical | Dynamic (once a week) |
| Year of study | Student profile | Current year of study | Categorical | Dynamic (once a year) |
| Total number of e-courses | LMS Moodle | Total number of electronic courses the student is enrolled in the current semester | Numerical | Dynamic (once a week) |
| Number of assessing e-courses | Derived | Number of assessing e-courses the student is enrolled in | Numerical | Dynamic (once a week) |
| Number of frequently visited e-courses | Derived | Number frequently visited e-courses the student is enrolled in | Numerical | Dynamic (once a week) |
| Number of active clicks | LMS Moodle | Total count of user interactions | Numerical | Dynamic (once a week) |
| Number of active clicks for assessing e-courses | LMS Moodle | Active clicks in assessing e-courses | Numerical | Dynamic (once a week) |
| Number of active clicks for frequently visited e-courses | LMS Moodle | Active clicks in frequently visited e-courses | Numerical | Dynamic (once a week) |
| Number of effective clicks | LMS Moodle | Count of meaningful interactions indicating engagement | Numerical | Dynamic (once a week) |
| Number of effective clicks for assessing e-courses | LMS Moodle | Effective clicks in assessing e-courses | Numerical | Dynamic (once a week) |
| Number of effective clicks for frequently visited e-courses | LMS Moodle | Effective clicks in frequently visited e-courses | Numerical | Dynamic (once a week) |
| Average grade for all e-courses | LMS Moodle | Mean grade across all e-courses the student is enrolled in | Numerical | Dynamic (once a week) |
| Average grade for assessing e-courses | LMS Moodle | Mean grade in assessing e-courses | Numerical | Dynamic (once a week) |
| Average grade for frequently visited e-courses | LMS Moodle | Mean grade in frequently visited e-courses) | Numerical | Dynamic (once a week) |
| Average grade for all e-courses (z-scaled) | Derived | Z-standardized average grade by group across all e-courses | Numerical | Dynamic (once a week) |
| Average grade for all e-courses (min–max scaled) | Derived | Min–max normalized by group average grade across all e-courses | Numerical | Dynamic (once a week) |
| Average grade for assessing e-courses (z-scaled) | Derived | Z-standardized by group average grade in assessing e-courses | Numerical | Dynamic (once a week) |
| Average grade for assessing e-courses (min–max scaled) | Derived | Min–max normalized by group average grade in assessing e-courses | Numerical | Dynamic (once a week) |
| Number of active clicks (z-scaled) | Derived | Active clicks standardized by group | Numerical | Dynamic (once a week) |
| Number of active clicks (min–max scaled) | Derived | Active clicks normalized using the group’s maximum and minimum counts | Numerical | Dynamic (once a week) |
| Number of active clicks for assessing e-courses (z-scaled) | Derived | Z-standardized active clicks in assessing e-courses | Numerical | Dynamic (once a week) |
| Number of active clicks for assessing e-courses (min–max scaled) | Derived | Min–max normalized active clicks in assessing e-courses | Numerical | Dynamic (once a week) |
| Number of effective clicks (z-scaled) | Derived | Z-standardized effective clicks | Numerical | Dynamic (once a week) |
| Number of effective clicks (min–max scaled) | Derived | Min–max normalized effective clicks | Numerical | Dynamic (once a week) |
| Number of effective clicks for assessing e-courses (z-scaled) | Derived | Z-standardized effective clicks in assessing e-courses | Numerical | Dynamic (once a week) |
| Number of effective clicks for assessing e-courses (min–max scaled) | Derived | Min–max normalized effective clicks in assessing e-courses | Numerical | Dynamic (once a week) |
| Average forecast of model LSC for all e-courses | Derived | Mathematical expectation of grade for all courses calculated in the LSC model | Numerical | Dynamic (once a week) |
| Average forecast of model LSC for assessing e-courses | Derived | Mathematical expectation of grade for assessing e-courses calculated in the LSC model | Numerical | Dynamic (once a week) |
| Average forecast of model LSC for frequently visited e-courses | Derived | Mathematical expectation of grade for frequently visited e-courses calculated in the LSC model | Numerical | Dynamic (once a week) |
| Downtime | LMS Moodle | Total duration of inactivity in the LMS (in weeks) | Numerical | Dynamic (once a week) |
| LSSc-Fall Model | LSSc-Spring Model | ||||
|---|---|---|---|---|---|
| Feature | Maximum Cohen’s d | Feature Importance | Feature | Maximum Cohen’s d | Feature Importance |
| Cohen’s d ≥ 0.4 | |||||
| Week | 0.43 | 0.022 | Average grade for all e-courses | 0.41 | 0.032 |
| Total number of e-courses | 0.42 | 0.037 | |||
| 0.3 ≤ Cohen’s d < 0.4 | |||||
| Number of active clicks (z-scaled) | 0.35 | 0.035 | Average grade for assessing e-courses | 0.39 | 0.029 |
| Average forecast of model LSC for assessing e-courses | 0.34 | 0.027 | Average forecast of model LSC for frequently visited e-courses | 0.37 | 0.023 |
| Number of effective clicks for assessing e-courses (z-scaled) | 0.34 | 0.019 | |||
| Number of active clicks for assessing e-courses (z-scaled) | 0.36 | 0.023 | |||
| Number of assessing e-courses | 0.31 | 0.039 | Total number of e-courses | 0.35 | 0.034 |
| Average grade for assessing e-courses (z-scaled) | 0.31 | 0.023 | Average forecast of model LSC for all e-courses | 0.34 | 0.027 |
| Average grade for all e-courses (min–max scaled) | 0.31 | 0.024 | Average grade for frequently visited e-courses | 0.34 | 0.030 |
| Number of frequently visited e-courses | 0.3 | 0.031 | Number of effective clicks (min–max scaled) | 0.32 | 0.030 |
| Year of study_2 | 0.32 | 0.036 | |||
| Number of effective clicks (z-scaled) | 0.32 | 0.028 | |||
| Average forecast of model LSC for assessing e-courses | 0.31 | 0.025 | |||
| Average grade for assessing e-courses (z-scaled) | 0.3 | 0.021 | |||
| Number of active clicks for assessing e-courses (min–max scaled) | 0.3 | 0.021 | |||
| 0.2 ≤ Cohen’s d < 0.3 | |||||
| Average grade for assessing e-courses | 0.29 | 0.023 | Number of frequently visited e-courses | 0.29 | 0.029 |
| Number of active clicks (min–max scaled) | 0.29 | 0.025 | |||
| Number of active clicks (min–max scaled) | 0.28 | 0.025 | |||
| Number of active clicks | 0.29 | 0.025 | |||
| Average grade for assessing e-courses (min–max scaled) | 0.26 | 0.026 | |||
| Number of effective clicks | 0.29 | 0.028 | |||
| Average grade for all e-courses | 0.28 | 0.027 | Number of effective clicks | 0.26 | 0.034 |
| Number of effective clicks (z-scaled) | 0.27 | 0.029 | Average grade for all e-courses (z-scaled) | 0.26 | 0.028 |
| Average grade for all e-courses (min–max scaled) | 0.26 | 0.026 | |||
| Number of active clicks for assessing e-courses | 0.27 | 0.020 | |||
| Number of effective clicks for assessing e-courses (min–max scaled) | 0.25 | 0.021 | |||
| Number of active clicks for frequently visited e-courses | 0.27 | 0.018 | |||
| Number of active clicks for assessing e-courses | 0.25 | 0.020 | |||
| Average grade for all e-courses (z-scaled) | 0.27 | 0.023 | |||
| Number of assessing e-courses | 0.24 | 0.034 | |||
| Number of effective clicks for frequently visited e-courses | 0.23 | 0.018 | |||
| Year of study_2 | 0.26 | 0.054 | |||
| Average forecast of model LSC for all e-courses | 0.26 | 0.023 | |||
| Number of effective clicks for assessing e-courses (z-scaled) | 0.23 | 0.021 | |||
| Number of active clicks for assessing e-courses (min–max scaled) | 0.26 | 0.025 | |||
| Number of active clicks (z-scaled) | 0.21 | 0.026 | |||
| Average grade for frequently visited e-courses | 0.26 | 0.022 | |||
| Average forecast of model LSC for frequently visited e-courses | 0.25 | 0.022 | |||
| Number of effective clicks for assessing e-courses (min–max scaled) | 0.25 | 0.019 | |||
| Number of effective clicks (min–max scaled) | 0.24 | 0.025 | |||
| Number of effective clicks for assessing e-courses | 0.23 | 0.019 | |||
| Average grade for assessing e-courses (min–max scaled) | 0.22 | 0.020 | |||
| Number of active clicks for assessing e-courses (z-scaled) | 0.21 | 0.021 | |||
| Cohen’s d ≤ 0.2 | |||||
| Number of effective clicks for frequently visited e-courses | 0.17 | 0.017 | Number of active clicks | 0.19 | 0.024 |
| Number of active clicks for frequently visited e-courses | 0.18 | 0.017 | |||
| Downtime | 0.16 | 0.020 | |||
| Year of study_4 | 0.13 | 0.032 | |||
| Week | 0.18 | 0.017 | |||
| Number of effective clicks for assessing e-courses | 0.17 | 0.026 | |||
| Year of study_3 | 0.10 | 0.039 | |||
| Prediction_proba_LSSp | 0.08 | 0.095 | Year of study_4 | 0.09 | 0.029 |
| Year of study_5 | 0.08 | 0.05 | |||
| Prediction_proba_LSSp | 0.07 | 0.132 | |||
| Year of study_5 | 0.05 | 0.037 | |||
References
- Alkhnbashi, O.S.; Mohammad, R.; Bamasoud, D.M. Education in transition: Adapting and thriving in a post-COVID world. Systems 2024, 12, 402. [Google Scholar] [CrossRef]
- Alsabban, A.; Yaqub, R.M.S.; Rehman, A.; Yaqub, M.Z. Adapting the Higher Education through E-Learning Mechanisms—A Post COVID-19 Perspective. Open J. Bus. Manag. 2024, 12, 2381–2401. [Google Scholar] [CrossRef]
- Guppy, N.; Verpoorten, D.; Boud, D.; Lin, L.; Tai, J.; Bartolic, S. The post-COVID-19 future of digital learning in higher education: Views from educators, students, and other professionals in six countries. Br. J. Educ. Technol. 2022, 53, 1750–1765. [Google Scholar] [CrossRef]
- Stecuła, K.; Wolniak, R. Influence of COVID-19 pandemic on dissemination of innovative e-learning tools in higher education in Poland. J. Open Innov. Technol. Mark. Complex. 2022, 8, 89. [Google Scholar] [CrossRef]
- Gligorea, I.; Cioca, M.; Oancea, R.; Gorski, A.-T.; Gorski, H.; Tudorache, P. Adaptive Learning Using Artificial Intelligence in e-Learning: A Literature Review. Educ. Sci. 2023, 13, 1216. [Google Scholar] [CrossRef]
- Hakimi, M.; Katebzadah, S.; Fazil, A.W. Comprehensive insights into e-learning in contemporary education: Analyzing trends, challenges, and best practices. J. Educ. Teach. Learn. 2024, 6, 86–105. [Google Scholar] [CrossRef]
- Omodan, B.I. Redefining university infrastructure for the 21st century: An interplay between physical assets and digital evolution. J. Infrastruct. Policy Dev. 2024, 8, 3468. [Google Scholar] [CrossRef]
- Mitrofanova, Y.S.; Tukshumskaya, A.V.; Burenina, V.I.; Ivanova, E.V.; Popova, T.N. Integration of Smart Universities in the Region as a Basis for Development of Educational Information Infrastructure; Smart Education and e-Learning 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 407–416. [Google Scholar] [CrossRef]
- Vishnu, S.; Tengli, M.B.; Ramadas, S.; Sathyan, A.R.; Bhatt, A. Correction: Bridging the Divide: Assessing Digital Infrastructure for Higher Education Online Learning. TechTrends 2024, 68, 1117. [Google Scholar] [CrossRef]
- Alyahyan, E.; Düştegör, D. Predicting academic success in higher education: Literature review and best practices. Int. J. Educ. Technol. High. Educ. 2020, 17, 3. [Google Scholar] [CrossRef]
- Gaftandzhieva, S.; Doneva, R. Data Analytics to Improve and Optimize University Processes. In Proceedings of the 14th annual International Conference of Education, Online Conference, 8–9 November 2021; pp. 6236–6245. [Google Scholar] [CrossRef]
- Kustitskaya, T.A.; Esin, R.V.; Kytmanov, A.A.; Zykova, T.V. Designing an Education Database in a Higher Education Institution for the Data-Driven Management of the Educational Process. Educ. Sci. 2023, 13, 947. [Google Scholar] [CrossRef]
- Gil, P.D.; da Cruz Martins, S.; Moro, S.; Costa, J.M. A data-driven approach to predict first-year students’ academic success in higher education institutions. Educ. Inf. Technol. 2021, 26, 2165–2190. [Google Scholar] [CrossRef]
- Kaspi, S.; Venkatraman, S. Data-driven decision-making (DDDM) for higher education assessments: A case study. Systems 2023, 11, 306. [Google Scholar] [CrossRef]
- Alston, G.L.; Lane, D.; Wright, N.J. The methodology for the early identification of students at risk for failure in a professional degree program. Curr. Pharm. Teach. Learn. 2014, 6, 798–806. [Google Scholar] [CrossRef]
- Rabelo, A.M.; Zárate, L.E. A model for predicting dropout of higher education students. Data Sci. Manag. 2025, 8, 72–85. [Google Scholar] [CrossRef]
- Alhazmi, E.; Sheneamer, A. Early predicting of students performance in higher education. IEEE Access 2023, 11, 27579–27589. [Google Scholar] [CrossRef]
- Azizah, Z.; Ohyama, T.; Zhao, X.; Ohkawa, Y.; Mitsuishi, T. Predicting at-risk students in the early stage of a blended learning course via machine learning using limited data. Comput. Educ. Artif. Intell. 2024, 7, 100261. [Google Scholar] [CrossRef]
- Pedro, E.d.M.; Leitão, J.; Alves, H. Students’ satisfaction and empowerment of a sustainable university campus. Environ. Dev. Sustain. 2025, 27, 1175–1198. [Google Scholar] [CrossRef]
- Esin, R.; Zykova, T.; Kustitskaya, T.; Kytmanov, A. Digital educational history as a component of the digital student’s profile in the context of education transformation. Perspekt. Nauk. Obraz.—Perspect. Sci. Educ. 2022, 59, 566–584. [Google Scholar] [CrossRef]
- Kukkar, A.; Mohana, R.; Sharma, A.; Nayyar, A. A novel methodology using RNN+ LSTM+ ML for predicting student’s academic performance. Educ. Inf. Technol. 2024, 29, 14365–14401. [Google Scholar] [CrossRef]
- Jovanović, J.; Gašević, D.; Dawson, S.; Pardo, A.; Mirriahi, N. Learning analytics to unveil learning strategies in a flipped classroom. Internet High. Educ. 2017, 33, 74–85. [Google Scholar] [CrossRef]
- Abdulkareem Shafiq, D.; Marjani, M.; Ahamed Ariyaluran Habeeb, R.; Asirvatham, D. Digital Footprints of Academic Success: An Empirical Analysis of Moodle Logs and Traditional Factors for Student Performance. Educ. Sci. 2025, 15, 304. [Google Scholar] [CrossRef]
- Delahoz-Dominguez, E.; Zuluaga, R.; Fontalvo-Herrera, T. Dataset of academic performance evolution for engineering students. Data Brief 2020, 30, 105537. [Google Scholar] [CrossRef] [PubMed]
- Farhood, H.; Joudah, I.; Beheshti, A.; Muller, S. Advancing student outcome predictions through generative adversarial networks. Comput. Educ. Artif. Intell. 2024, 7, 100293. [Google Scholar] [CrossRef]
- Pallathadka, H.; Wenda, A.; Ramirez-Asís, E.; Asís-López, M.; Flores-Albornoz, J.; Phasinam, K. Classification and prediction of student performance data using various machine learning algorithms. Mater. Today Proc. 2023, 80, 3782–3785. [Google Scholar] [CrossRef]
- Mohammad, A.S.; Al-Kaltakchi, M.T.S.; Alshehabi Al-Ani, J.; Chambers, J.A. Comprehensive Evaluations of Student Performance Estimation via Machine Learning. Mathematics 2023, 11, 3153. [Google Scholar] [CrossRef]
- Abdalkareem, M.; Min-Allah, N. Explainable Models for Predicting Academic Pathways for High School Students in Saudi Arabia. IEEE Access 2024, 12, 30604–30626. [Google Scholar] [CrossRef]
- Villar, A.; de Andrade, C.R.V. Supervised machine learning algorithms for predicting student dropout and academic success: A comparative study. Discov. Artif. Intell. 2024, 4, 2. [Google Scholar] [CrossRef]
- Bravo-Agapito, J.; Romero, S.J.; Pamplona, S. Early prediction of undergraduate Student’s academic performance in completely online learning: A five-year study. Comput. Hum. Behav. 2021, 115, 106595. [Google Scholar] [CrossRef]
- Leal, F.; Veloso, B.; Pereira, C.S.; Moreira, F.; Durão, N.; Silva, N.J. Interpretable Success Prediction in Higher Education Institutions Using Pedagogical Surveys. Sustainability 2022, 14, 13446. [Google Scholar] [CrossRef]
- Deho, O.B.; Liu, L.; Li, J.; Liu, J.; Zhan, C.; Joksimovic, S. When the past!= the future: Assessing the Impact of Dataset Drift on the Fairness of Learning Analytics Models. IEEE Trans. Learn. Technol. 2024, 17, 1007–1020. [Google Scholar] [CrossRef]
- Guo, L.L.; Pfohl, S.R.; Fries, J.; Posada, J.; Fleming, S.L.; Aftandilian, C.; Shah, N.; Sung, L. Systematic review of approaches to preserve machine learning performance in the presence of temporal dataset shift in clinical medicine. Appl. Clin. Inform. 2021, 12, 808–815. [Google Scholar] [CrossRef]
- Sahiner, B.; Chen, W.; Samala, R.K.; Petrick, N. Data drift in medical machine learning: Implications and potential remedies. Br. J. Radiol. 2023, 96, 20220878. [Google Scholar] [CrossRef]
- Vela, D.; Sharp, A.; Zhang, R.; Nguyen, T.; Hoang, A.; Pianykh, O.S. Temporal quality degradation in AI models. Sci. Rep. 2022, 12, 11654. [Google Scholar] [CrossRef]
- Nigenda, D.; Karnin, Z.; Zafar, M.B.; Ramesha, R.; Tan, A.; Donini, M.; Kenthapadi, K. Amazon sagemaker model monitor: A system for real-time insights into deployed machine learning models. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 3671–3681. [Google Scholar] [CrossRef]
- Santyev, E.A.; Zakharyin, K.N.; Shniperov, A.N.; Kurchenko, R.A.; Shefer, I.A.; Vainshtein, Y.V.; Somova, M.V.; Fedotova, I.M.; Noskov, M.V.; Kustitskaya, T.A.; et al. “Pythia” Academic Performance Prediction System. 2023. Available online: https://p.sfu-kras.ru/ (accessed on 19 August 2025).
- Somova, M.V. Methodological model of personalized educational process based on prediction of success in subject training. Mod. High Technol. 2023, 12-1, 165–170. (In Russian) [Google Scholar] [CrossRef]
- Kustitskaya, T.A.; Esin, R.V.; Vainshtein, Y.V.; Noskov, M.V. Hybrid Approach to Predicting Learning Success Based on Digital Educational History for Timely Identification of At-Risk Students. Educ. Sci. 2024, 14, 657. (In Russian) [Google Scholar] [CrossRef]
- Noskov, M.V.; Vaynshteyn, Y.V.; Somova, M.V.; Fedotova, I.M. Prognostic model for assessing the success of subject learning in conditions of digitalization of education. RUDN J. Informatiz. Educ. 2023, 20, 7–19. [Google Scholar] [CrossRef]
- Yıldırım, H. The multicollinearity effect on the performance of machine learning algorithms: Case examples in healthcare modelling. Acad. Platf. J. Eng. Smart Syst. 2024, 12, 68–80. [Google Scholar] [CrossRef]
- Lacson, R.; Eskian, M.; Licaros, A.; Kapoor, N.; Khorasani, R. Machine learning model drift: Predicting diagnostic imaging follow-up as a case example. J. Am. Coll. Radiol. 2022, 19, 1162–1169. [Google Scholar] [CrossRef] [PubMed]
- Bayram, F.; Ahmed, B.S.; Kassler, A. From concept drift to model degradation: An overview on performance-aware drift detectors. Knowl. Based Syst. 2022, 245, 108632. [Google Scholar] [CrossRef]
- Gama, J.; Medas, P.; Castillo, G.; Rodrigues, P. Learning with drift detection. In Advances in Artificial Intelligence–SBIA 2004: 17th Brazilian Symposium on Artificial Intelligence, Sao Luis, Maranhao, Brazil, 29 September–1 Ocotber, 2004; Proceedings 17; Springer: Berlin/Heidelberg, Germany, 2004; pp. 286–295. [Google Scholar] [CrossRef]
- Baena-Garcıa, M.; del Campo-Ávila, J.; Fidalgo, R.; Bifet, A.; Gavalda, R.; Morales-Bueno, R. Early drift detection method. In Proceedings of the Fourth International Workshop on Knowledge Discovery from Data Streams, Berlin, Germany, 18 September 2006; pp. 77–86. [Google Scholar]
- Bifet, A.; Gavalda, R. Learning from time-changing data with adaptive windowing. In Proceedings of the 2007 SIAM International Conference on Data Mining, Minneapolis, MN, USA, 26–28 April 2007; pp. 443–448. [Google Scholar] [CrossRef]
- Liu, A.; Lu, J.; Liu, F.; Zhang, G. Accumulating regional density dissimilarity for concept drift detection in data streams. Pattern Recognit. 2018, 76, 256–272. [Google Scholar] [CrossRef]
- Yurdakul, B. Statistical Properties of Population Stability Index; Western Michigan University: Kalamazoo, MI, USA, 2018. [Google Scholar]
- Kurian, J.F.; Allali, M. Detecting drifts in data streams using Kullback-Leibler (KL) divergence measure for data engineering applications. J. Data Inf. Manag. 2024, 6, 207–216. [Google Scholar] [CrossRef]
- Siddiqi, N. Credit Risk Scorecards: Developing and Implementing Intelligent Credit Scoring; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 3. [Google Scholar]
- Abdualrhman, M.A.A.; Padma, M. Deterministic concept drift detection in ensemble classifier based data stream classification process. Int. J. Grid High Perform. Comput. 2019, 11, 29–48. [Google Scholar] [CrossRef]
- Farid, D.M.; Zhang, L.; Hossain, A.; Rahman, C.M.; Strachan, R.; Sexton, G.; Dahal, K. An adaptive ensemble classifier for mining concept drifting data streams. Expert Syst. Appl. 2013, 40, 5895–5906. [Google Scholar] [CrossRef]
- Agrahari, S.; Singh, A.K. Concept drift detection in data stream mining: A literature review. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 9523–9540. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30. Available online: https://proceedings.neurips.cc/paper_files/paper/2017/file/8a20a8621978632d76c43dfd28b67767-Paper.pdf (accessed on 19 August 2025).
- Zheng, S.; van der Zon, S.B.; Pechenizkiy, M.; de Campos, C.P.; van Ipenburg, W.; de Harder, H.; Nederland, R. Labelless concept drift detection and explanation. In Proceedings of the NeurIPS 2019 Workshop on Robust AI in Financial Services: Data, Fairness, Explainability, Trustworthiness, and Privacy, Vancouver, BC, Canada, 13–14 December 2019; Available online: https://pure.tue.nl/ws/portalfiles/portal/142599201/Thesis_Final_version_Shihao_Zheng.pdf (accessed on 19 August 2025).
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Kustitskaya, T.A.; Esin, R.V. Monitoring data shift in the learning success forecasting model using Shapley values. Inform. Educ. 2025, 40, 57–68. [Google Scholar] [CrossRef]
- Sawilowsky, S.S. New effect size rules of thumb. J. Mod. Appl. Stat. Methods 2009, 8, 26. [Google Scholar] [CrossRef]
- Chuah, J.; Kruger, U.; Wang, G.; Yan, P.; Hahn, J. Framework for Testing Robustness of Machine Learning-Based Classifiers. J. Pers. Med. 2022, 12, 1314. [Google Scholar] [CrossRef]
- d’Eon, G.; d’Eon, J.; Wright, J.R.; Leyton-Brown, K. The spotlight: A general method for discovering systematic errors in deep learning models. In Proceedings of the 2022 ACM Conference on Fairness, Accountability, and Transparency, Seoul, Republic of Korea, 21–24 June 2022; pp. 1962–1981. [Google Scholar] [CrossRef]
- Pastor, E.; de Alfaro, L.; Baralis, E. Identifying biased subgroups in ranking and classification. arXiv 2021, arXiv:2108.07450. [Google Scholar] [CrossRef]

| Model | LSSc-Fall | LSSc-Spring |
|---|---|---|
| Number of predictors | 35 | 33 |
| Top 15 of important predictors and their feature importance score | Prediction_proba_LSSp (0.095) | Prediction_proba_LSSp (0.132) |
| Year of study_2 (0.054) | Year of study_5 (0.051) | |
| Year of study_3 (0.039) | Year of study_2 (0.036) | |
| Number of assessing courses (0.039) | Number of effective clicks (0.034) | |
| Year of study_6 (0.037) | Total number of e-courses (0.034) | |
| Year of study_5 (0.037) | Number of assessing e-courses (0.034) | |
| Total number of e-courses (0.037) | Year of study_3 (0.033) | |
| Number of active clicks (z-scaled) (0.035) | Average grade for all e-courses (0.032) | |
| Year of study_4 (0.032) | Average grade for all e-courses (min–max scaled) (0.030) | |
| Number of frequently visited e-courses (0.031) | Average grade for frequently visited e-courses (0.030) | |
| Number of effective clicks (z-scaled) (0.029) | Number of effective clicks (min–max scaled) (0.030) | |
| Number of effective clicks (0.028) | Year of study_4 (0.030) | |
| Average grade for all e-courses (0.027) | Average grade for assessing e-courses (0.029) | |
| Average of the forecasts made by model LSC (0.027) | Number of frequently visited e-courses (0.029) | |
| Number of active clicks in assessing e-courses (min–max scaled) (0.025) | Number of effective clicks (z-scaled) (0.028) | |
| Model hyperparameters with non-default values | learning_rate = 0.2 max_depth = 15 n_estimators = 500 reg_lambda = 0.5 | |
| Recall/weighted F-score on 5-fold cross validation | 0.991/0.990 | 0.993/0.994 |
| Academic Years | Precision | Recall | F1-Score |
|---|---|---|---|
| 2018–2021 | 0.79 | 0.88 | 0.84 |
| 2022 | 0.69 | 0.54 | 0.60 |
| 2023 | 0.79 | 0.76 | 0.77 |
| Data | Accuracy | Precision | Recall | Weighted F | |
|---|---|---|---|---|---|
| 1 | 2018–2021, validation set (Fall + Spring) | 0.780 | 0.764 | 0.662 | 0.741 |
| 2 | 2022 (Fall + Spring) | 0.756 | 0.703 | 0.640 | 0.689 |
| 3 | 2022, Fall | 0.727 | 0.639 | 0.627 | 0.637 |
| 4 | 2022, Spring | 0.784 | 0.772 | 0.652 | 0.745 |
| 5 | 2023 (Fall + Spring) | 0.756 | 0.718 | 0.663 | 0.706 |
| 6 | 2023, Fall | 0.720 | 0.667 | 0.624 | 0.658 |
| 7 | 2023, Spring | 0.792 | 0.770 | 0.701 | 0.755 |
| 8 | 2024, Fall | 0.785 | 0.718 | 0.680 | 0.710 |
| Model | LSSc-Fall | LSSc-Spring |
|---|---|---|
| Set of predictors after models’ refitting using strategy 3 | Prediction_proba_LSSp Number of effective clicks for assessing e-courses Number of active clicks for assessing e-courses (z-scaled) Number of effective clicks (min–max scaled) Downtime Year of study_3 Year of study_4 Year of study_5 Year of study_6 | Prediction_proba_LSSp Number of effective clicks for assessing e-courses (z-scaled) Number of active clicks for assessing e-courses Number of effective clicks for assessing courses (z-scaled) Number of active clicks Downtime Year of study_3 Year of study_4 Year of study_5 |
| Model hyperparameters with non-default values after models’ refitting using strategy 3 | learning_rate = 0.2, n_estimators = 300, reg_alpha = 10, reg_lambda= 10, gamma = 2, max_depth = 3, min_child_weight = 20, colsample_bytree = 0.75, subsample = 0.75 | |
| Averages of quality metrics on 5-fold cross validation for 2022 | ||
| Before refitting using strategy 3 | weighted F = 0.990 recall = 0.991 | weighted F = 0.994 recall = 0.993 |
| After refitting using strategy 3 | weighted F = 0.7706 recall = 0.7407 | weighted F = 0.8163 recall = 0.7916 |
| Averages of quality metrics for 2023 | ||
| Before refitting using strategy 3 | weighted F = 0.6946 recall = 0.5802 | weighted F = 0.7520 recall = 0.7368 |
| After refitting using strategy 3 | weighted F = 0.7112 recall = 0.6405 | weighted F = 0.7648 recall = 0.7686 |
| Averages of quality metrics for 2024 | ||
| Before refitting using strategy 3 | weighted F = 0.7477 recall = 0.6892 | — |
| After refitting using strategy 3 | weighted F = 0.7508 recall = 0.7371 | |
| Data | Average Weighted F-Score | |
|---|---|---|
| First-Year Students | Students of Second Year of Study and Above | |
| 2022, Fall | 0.519 | 0.716 |
| 2022, Spring | 0.748 | 0.743 |
| 2023, Fall | 0.558 | 0.742 |
| 2023, Spring | 0.779 | 0.737 |
| 2024, Fall | 0.604 | 0.763 |
| Data | Model LSSp Fitted on 2018–2021 | Model LSSp Refitted on Data from 2018 to 2021 to Previous Year | Model LSSp Refitted Only on Previous Year |
|---|---|---|---|
| Weighted F/Recall | Weighted F/Recall | Weighted F/Recall | |
| 2023, Fall | 0.658/0.624 | 0.655/0.611 | 0.678/0.600 |
| 2023, Spring | 0.755/0.701 | 0.752/0.704 | 0.754/0.714 |
| 2024, Fall | 0.710/0.680 | 0.712/0.680 | 0.720/0.701 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kustitskaya, T.A.; Esin, R.V.; Noskov, M.V. Model Drift in Deployed Machine Learning Models for Predicting Learning Success. Computers 2025, 14, 351. https://doi.org/10.3390/computers14090351
Kustitskaya TA, Esin RV, Noskov MV. Model Drift in Deployed Machine Learning Models for Predicting Learning Success. Computers. 2025; 14(9):351. https://doi.org/10.3390/computers14090351
Chicago/Turabian StyleKustitskaya, Tatiana A., Roman V. Esin, and Mikhail V. Noskov. 2025. "Model Drift in Deployed Machine Learning Models for Predicting Learning Success" Computers 14, no. 9: 351. https://doi.org/10.3390/computers14090351
APA StyleKustitskaya, T. A., Esin, R. V., & Noskov, M. V. (2025). Model Drift in Deployed Machine Learning Models for Predicting Learning Success. Computers, 14(9), 351. https://doi.org/10.3390/computers14090351







