An Integrated Intuitionistic Fuzzy-Clustering Approach for Missing Data Imputation

Abstract

Missing data imputation is a critical preprocessing task that directly impacts the quality and reliability of data-driven analyses, yet many existing methods treat numerical and categorical data separately and lack the integration of advanced techniques. We suggest a novel imputation technique to overcome these restrictions that synergistically combines regression imputation using HistGradientBoostingRegressor and fuzzy rule-based systems and is enhanced by a tailored clustering process. This integrated approach effectively handles mixed data types and complex data structures using regression models to predict missing numerical values, fuzzy logic to incorporate expert knowledge and interpretability, and clustering to capture latent data patterns. Categorical variables are managed by mode imputation and label encoding. We evaluated the method on twelve tabular datasets with artificially introduced missingness, employing a comprehensive set of metrics focused on originally missing entries. The results demonstrate that our iterative imputer performs competitively with other established imputation techniques, achieving better and comparable error rates and accuracy. By combining statistical learning with fuzzy and clustering frameworks, the method achieves 15% lower Root Mean Square Error (RMSE), 10% lower Mean Absolute Error (MAE), and 80% higher precision in UCI datasets, thus offering a promising advance in data preprocessing in practical applications.

1. Introduction

The handling of missing values in large-scale datasets is a persistent challenge in data science, especially as data sources proliferate and collection processes remain inherently incomplete, which can seriously reduce predictive models’ precision and consistency. Despite the plethora of imputation techniques, there are challenges in effectively capturing uncertainty in imputed values, scaling to large datasets, and handling heterogeneous feature types seamlessly [1]. Instead of obtaining all the datasets, which is often impractical, it is frequently required to substitute values for the missing data. Imputation (the process of estimating and replacing missing values) is a common term used to describe this process. After all missing values have been imputed, the data set can be used as the input to the techniques created for an entire data set. Several common techniques, including mean imputation, regression imputation, stochastic imputation, and others [1,2], are used to impute missing data based on the model assumption for the entire set.

Unlike methods based solely on point estimates, fuzzy logic frameworks [3] leverage membership functions that model degrees of belonging, offering a principled way to quantify imputation uncertainty. Our hybrid model combines fuzzy clustering to uncover latent structures with gradient-boosted regression for robust numeric estimation, improving both accuracy and interpretability. The approach demonstrates efficiency on real-world datasets and uses gradient boosting to partially overcome scalability constraints. In contrast to many approaches that only use point estimates, fuzzy logic’s soft membership functions provide a simple way to represent uncertainty. Twelve University of California Irvine (UCI) datasets were used, and missing data was synthetically introduced under a Missing Completely At Random (MCAR) assumption at a proportion of 10%. Performance was evaluated using commonly adopted metrics [4,5], including Root Mean Square Error (RMSE) and Mean Absolute Error (MAE) for numeric data, along with accuracy (ACC) for categorical features. We compare the RMSE of the method with two different approaches based on deep learning. Our contributions include:

• A comprehensive comparative analysis covering multiple datasets and benchmarks across numerical and categorical imputation tasks;
• A novel hybrid imputation framework integrating intuitionistic fuzzy logic, clustering, and regression for enhanced imputation quality;
• An empirical evaluation highlighting improvements in accuracy, computational efficiency, and uncertainty quantification.

These advances address key limitations in existing methods and demonstrate practical applicability in diverse data settings.

In summary, our method outperforms common imputation algorithms, including Generative Adversarial Imputation Nets (GAIN) [6] and Multiple Imputation using Denoising Autoencoders (MIDA) [7], by improving the quality and robustness of the imputations. The remainder of this paper is structured as follows. Section 2 reviews previous work on imputation techniques; Section 3 details our experimental design; Section 4 presents and analyzes the results; and Section 5 concludes with key insights and future directions.

2. Related Works

In data analysis and machine learning, missing data is a common problem that, if not addressed, will often end in biased results or poor performance. Standard imputation techniques [8], which range from single substitution to sophisticated machine learning strategies such as Multiple Imputation by Chained Equations (MICE) and random forests, have shown varying degrees of success in preserving statistical relationships and reducing bias, particularly in datasets with mixed variable types [5,9].

Important studies, such as those of Chen and Guestrin on XGBoost [10], explain why ensemble tree methods, including boosted methods, are good for filling in missing data because they can handle complex relationships and missing information well [11]. Comparative studies and optimization-focused research demonstrate that boost-based imputation strategies often match or exceed the precision of traditional methods, especially in highly dimensioned or incomplete settings [12]. Practical adoption is widespread, with numerous Kaggle competitions and tutorials showcasing the effectiveness of HistGradientBoostingRegressor for real-world imputation challenges [13,14,15]. Furthermore, recent simulation studies and empirical benchmarks confirm that tree-based and boosting approaches, including those adapted for hierarchical or multilevel data, consistently deliver competitive results compared to established techniques such as MICE or k-Nearest Neighbors (kNN) imputations [16]. Collectively, these references establish gradient boost as a leading paradigm for missing-value imputation, combining theoretical rigor, practical flexibility, and strong empirical performance across diverse domains. Although gradient-boosted trees provide flexible modeling of complex missing data patterns, their interpretability and computational cost often motivate the consideration of hybrid and rule-based approaches.

Various hybrid-based imputation methods have been proposed to better handle uncertainty and noise. Deep learning [6,17,18] has introduced powerful frameworks for the imputation of missing data, notably through Generative Adversarial Networks (GANs). Although these methods demonstrate strong results, they require careful tuning and significant computational resources, with challenges in handling blank inputs and ensuring reproducibility. However, many common approaches have drawbacks when dealing with high-dimensional data, including when datasets include both continuous and categorical variables, and some generating techniques perform poorly in terms of generalization. Autoencoder-based approaches [19,20] may tolerate partial datasets and simply use a portion of observable components to learn data representations; they do not require complete data during training. This is a major disadvantage, since missing values are often a natural part of the issue structure, making it difficult to obtain a complete dataset. Discriminative models are less capable of handling the scenario when there are fewer feature dimensions. Despite promising results, deep learning models for imputation require careful hyperparameter tuning and large computational resources, which can hinder reproducibility and practical deployment in many settings.

Modern machine learning and deep learning techniques, as well as more conventional statistical methods, are all part of the latest developments in missing-data imputation. By integrating fuzzy membership functions with k nearest neighbors to calculate weighted averages for missing values [21], fuzzy-based approaches have demonstrated efficacy in managing uncertainty, especially in time series data [22]. The impact of various imputation techniques on classification accuracy has been thoroughly examined in rule-based fuzzy classification systems, underscoring the importance of method selection for mixed data types [23]. By continuously updating cluster memberships and centroids, iterative fuzzy clustering techniques, such as the iterative fuzzy clustering approach, improve imputations and show good performance on numerical datasets [24]. Similarly, fuzzy K-means clustering methods frequently outperform traditional K-means by using weighted centroid computations to impute missing numerical data [25]. Fuzzy K-means and Fuzzy c-means techniques outperform classical clustering by leveraging weighted centroids and uncertainty modeling [26,27].

In order to deal with missing data with uncertain and nonlinear structures, Sethia et al. [3] present the radial basis Kernel Intuitionistic Fuzzy C-Means Imputation method (KIFCMI), which improves the accuracy of data clustering in higher dimensions by embedding Intuitionistic Fuzzy C-Means in a kernel space of radial basis functions. Kernel embedding transforms data into higher-dimensional feature spaces, enabling better separation in complex datasets, while intuitionistic fuzzy memberships represent degrees of membership, non-membership, and hesitation, thereby enhancing the modeling of uncertainty. They propose two other robust algorithms [28], which combine linear interpolation with Intuitionistic Fuzzy C-Means clustering to address missing data imputation in complex, non-spherical datasets. New developments in imputation methods based on Large Language Models (LLMs) and Generative Artificial Intelligence (Gen-AI) have demonstrated better results in several important areas. The Contextual Language model for Accurate Imputation Method (CLAIM) and Neural Attention-based Imputation Model (NAIM) [29,30] are transformer-based imputation models designed for tabular data, handling both types of variables with integrated confidence estimates.

Models like Neural Universal Window Attention for Time Series (NuwaTS) and Uncertainty-aware Imputation Model based on Graph Neural Networks (UnIMP) [31,32], which make use of real-world data and standardized downstream validation, continue to have stronger evaluation and benchmarking capabilities. NAIM and UnIMP, which are designed for large datasets, have improved scalability. Recent models use probabilistic or implicit reasoning confidence to better address uncertainty quantification. Finally, hybrid techniques provide sensitive and adaptive imputation solutions [33,34]. When combined, these approaches demonstrate the adaptability and reliability of fuzzy imputation techniques based on clustering in a variety of application domains and data varieties. They show how the field of missing data imputation has expanded and emphasize the ongoing need for reliable, adaptable, and responsible approaches.

3. Materials and Methods

3.1. Imputation

The process of estimating and completing missing values in a dataset to facilitate efficient analysis and modeling is known as missing value imputation. Consider a d-dimensional data space $\mathcal{X}={\mathcal{X}}_1\times \dots \times {\mathcal{X}}_d$, where $X=(X_1,\dots ,X_d)$ is a random variable that takes values in $\mathcal{X}$ that represent the whole data vector alongside the distribution $P\left(X\right)$. A mask vector $M=(M_1,\dots ,M_d)\in {\{0,1\}}^d$ is used to represent missingness, where $M_i=1$ if the i-th component is observed and 0 otherwise. Then, $\tilde{X}=({\tilde{X}}_1,\dots ,{\tilde{X}}_d)$ is the observed data vector with missing values, as defined by ${\tilde{X}}_i=\left\{\begin{array}{cc}{X}_i,\hfill & \mathrm{if}{M}_i=1\hfill \\ \ast ,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$ where ∗ indicates an unobserved value. The imputation is used to estimate the missing values in each ${\tilde{x}}_i$ by sampling the conditional distribution $P(X\mid \tilde{X}={\tilde{x}}_i)$ given n independent realizations ${\tilde{x}}_1,\dots ,{\tilde{x}}_n$ with the corresponding masks $m_1,\dots ,m_n$. Instead of merely imputing point estimates, this approach models the entire data distribution, allowing for multiple imputations that account for the uncertainty in the missing values.

3.1.1. Imputation Method Overview

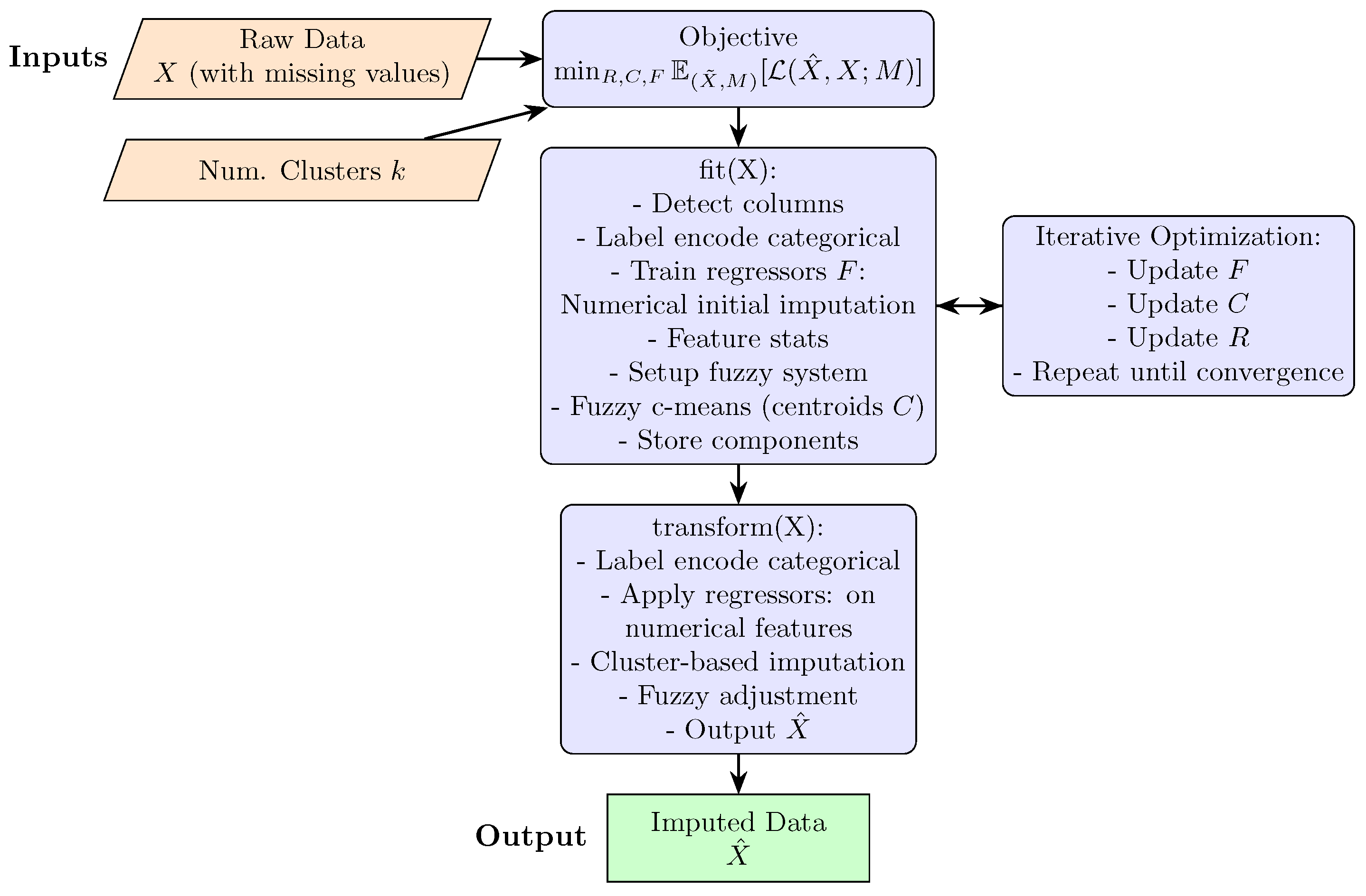
Existing imputation techniques range from simple statistical approaches to advanced model-based methods that iteratively improve estimates by predicting missing features from observed ones. To handle datasets with mixed numerical and categorical variables, we propose a new imputation method that integrates machine learning, clustering, and fuzzy logic, as illustrated in Figure 1 and in Algorithm 1.

The approach leverages scikit-learn pipelines and begins with a gradient boost model, specifically the histogram-based HistGradientBoostingRegressor, for initial numeric imputation. Subsequently, fuzzy clustering of c-means captures latent data structures, producing cluster-based imputations that reflect underlying data distributions. A fuzzy logic system, constructed with membership functions and automatically generated rules derived from strong feature correlations, enhances interpretability and context-sensitive adaptability. These fuzzy rules refine imputed values while ensuring that they remain within realistic bounds. Categorical variables are handled via mode imputation and label encoding.

This two-step procedure, comprising a fitting phase that learns regression models, clusters, and fuzzy rules, followed by a transformation phase that imputes and adjusts missing data, enables nuanced imputations that capture complex nonlinear relationships. Although computationally efficient, this method offers a sophisticated and flexible solution that is particularly suited for heterogeneous datasets and domains that require the integration of expert knowledge.

Algorithm 1 Proposed Imputation Method

Require:  Dataset X with missing values, number of clusters $n\_clusters$ Ensure:  Imputed dataset $\widehat{X}$   1: Initialize:   2:     Detect categorical columns and convert to strings   3:     Label-encode categorical variables   4:     Store numeric and categorical column lists   5:     Setup fuzzy logic components (antecedents, consequents)   6:     Define fuzzy membership functions for numeric features   7: Preprocessing:   8: for each numeric column with missing values do   9:       Split data into observed and missing subsets 10:       Train HistGradientBoostingRegressor on observed data 11:       Predict and impute missing values 12: end for 13: Fuzzy Rule Setup: 14: if rules not provided then 15:       Identify strongly correlated feature pairs 16:       Generate fuzzy rules for imputation adjustment 17: end if 18: Clustering: 19: Perform fuzzy c-means clustering on preprocessed data 20: Compute cluster centroids and membership degrees 21: Fuzzy Inference: 22: for each sample with missing values do 23:       Compute cluster-based imputation 24:       Apply fuzzy rule-based adjustment 25:       Combine and clip imputed values within valid ranges 26: end for 27: return Imputed dataset $\widehat{X}$

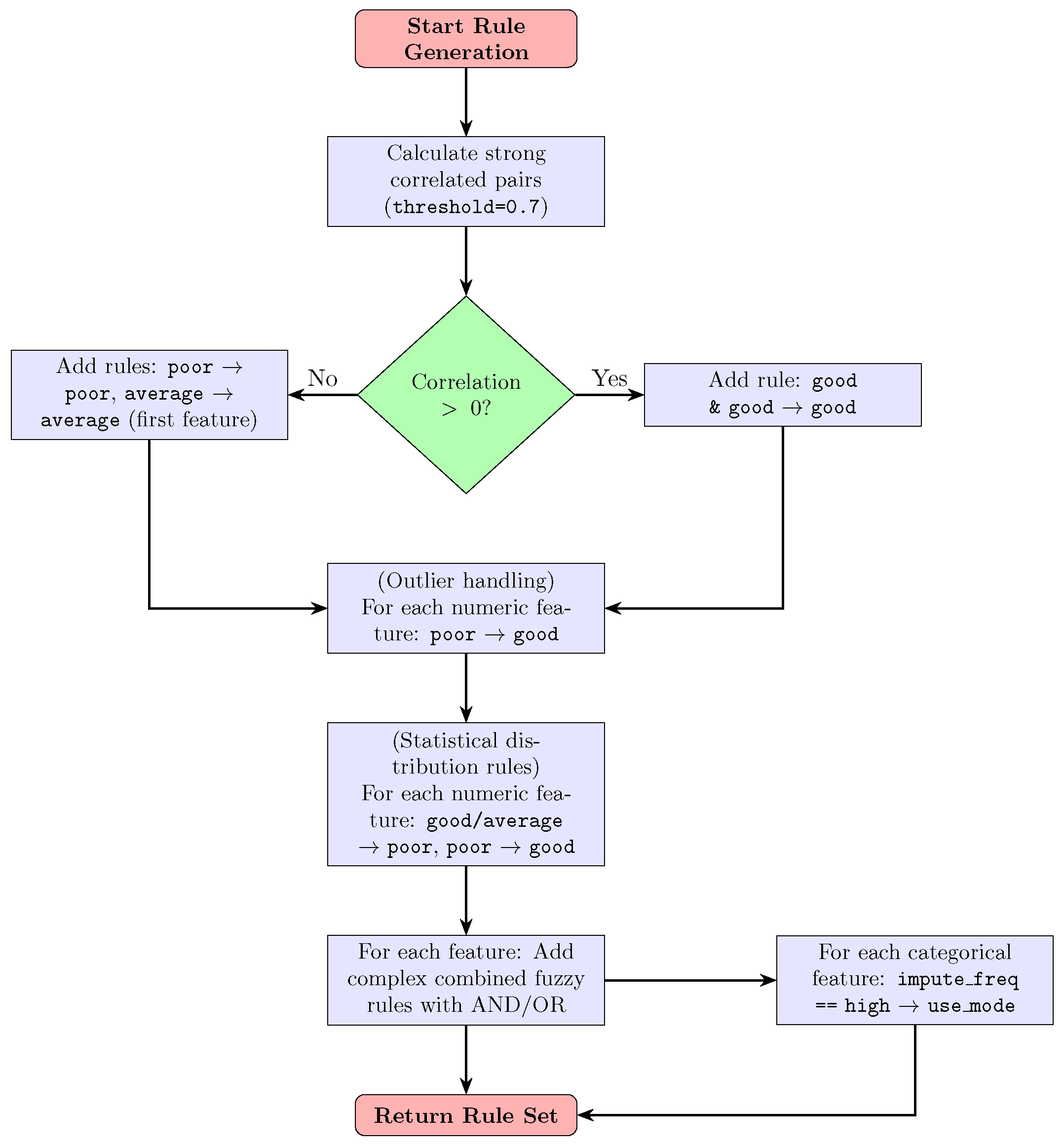
3.1.2. Fuzzy Rule Generation

The fuzzy rule system is built by first identifying numeric columns and detecting pairs of features with strong correlations above a threshold of 0.7. For each positively correlated pair, a rule is established: if both features belong to the “good” membership class, then the imputed value should also be classified as “good.” For negatively or weakly correlated pairs, default rules map membership grades (“poor,” “average”) of the primary feature to corresponding imputation quality levels.

Further rule sets relate the membership states of individual numeric features (“poor,” “average,” or “good”) to imputation outcomes, often encoding inverse relationships to capture uncertainty and confidence. Additional refinement comes from compound conditions that involve multiple membership levels of the same feature. For categorical features, a high imputation frequency triggers a mode-based imputation strategy. Collectively, these rules (detailed in Figure 2) form a robust fuzzy inference system that adapts imputations to intricate inter-feature dependencies and data characteristics.

3.2. Objective Function Analysis

By integrating fuzzy logic rules with statistical learning methods, the proposed imputer is designed to accurately estimate missing values while preserving the inherent structure and correlations within the dataset. Formally, consider a complete data vector $X\in {\mathbb{R}}^d$ and an observed vector $\tilde{X}$ containing missing entries indicated by a mask $M\in {\{0,1\}}^d$. For each incomplete observation, the imputer produces an estimate $\widehat{X}$. This estimation is governed by a fuzzy inference system parameterized by a set of rules $\mathcal{R}$, cluster centroids C corresponding to numerical features, and a regression model $\mathcal{F}$ (implemented as a Histogram-based Gradient Boosting Regressor).

The goal (1) is to minimize the expected loss of imputation in the distribution of incomplete data samples, formulated as:

$$\underset{\mathcal{R},C,\mathcal{F}}{min}{\mathbb{E}}_{(\tilde{X},M)}\left[\mathcal{L}(\widehat{X},X;M)\right],$$

(1)

where the loss $\mathcal{L}$ (2) considers only the missing components:

$$\mathcal{L}(\widehat{X},X;M)=\sum _{i=1}^d(1-M_i)·\ell ({\widehat{X}}_i,X_i),$$

(2)

and $\ell (·,·)$ is a suitable error metric, such as the squared error for numerical features.

It is important to emphasize that the objective in (1) is an expectation of the true unknown joint distribution of $(\tilde{X},M)$, representing the ideal loss of the population level. However, in practice, the imputer operates on a finite observed sample of incomplete data. The empirical loss computed on this finite dataset converges to the true expected loss as the sample size grows, by virtue of the law of large numbers, thus ensuring statistical consistency.

The convergence and optimization of the parameters $(\mathcal{R},C,\mathcal{F})$ depend on the stability to minimize this empirical loss. Factors influencing convergence include sample size, data representativeness, and model complexity (particularly fuzzy rule base and regression model complexity). An insufficient sample size can lead to overfitting or noisy parameter estimates, ultimately degrading imputation quality. Therefore, appropriate sample sizes, combined with robust validation procedures and regularization or early stopping strategies, are crucial to balance generalization performance and convergence speed during training. The imputation proceeds in two key stages: first, a statistical learning stage where regression models predict missing numeric values and fuzzy c-means clustering identifies latent data patterns; second, a fuzzy inference stage that refines these initial imputations via rule-based adjustments informed by feature statistics and correlations. The optimized parameters $({\mathcal{R}}^{*},C^{*},{\mathcal{F}}^{*})$ thus minimize the expected loss, ensuring that the imputed values faithfully approximate the true underlying distribution while maintaining the interpretability of the model.

The iterative refinement process that follows, which describes the optimization of fuzzy rules, cluster centroids, and regression models, is theoretically based on this formulation.

3.3. Iterative Optimization Process

• Statistical model fitting For each numeric characteristic j with missing values, we fit a regression model $F_j$ (e.g., HistGradientBoostingRegressor) to predict $X_j$ from the other observed characteristic. Then, we iterate over the features: for each characteristic, impute missing values using the current regression model, update the dataset, and proceed to the next feature. This process is repeated until all numeric features have initial imputations.
• Fuzzy c-means clustering On the dataset with initial imputations, clustering of fuzzy c-means is performed to obtain cluster centroids C and membership weights. Missing values are then returned as weighted averages of the centroids based on memberships. Centroids and memberships are iteratively updated to reduce the variance within the cluster.
• Construction and adjustment of the fuzzy rule system Here, we define the fuzzy antecedents and consequents for each feature, based on the feature statistics (mean, std, and skewness) and correlations. Then we generate a set of fuzzy rules R that encode dependencies and expert knowledge (e.g., “if the feature A is high and the feature B is high, impute the feature C as high”) as demonstrated in Figure 2. Finally, for each incomplete row, the fuzzy inference engine is used to adjust the imputed values, combining cluster-based and regression-based imputations with fuzzy logic adjustments.
• Iterative optimization Steps (a) to (c) are iterated until the convergence criterion is reached (stabilization of imputations or maximum iterations). Each iteration includes:
  • Updating regression models using current imputations.
  • Recomputing fuzzy clusters and updating centroids.
  • Reconstructing or updating fuzzy rules if feature statistics or correlations have changed.
  • Reapplying fuzzy inference to refine imputations.

3.4. Model and Parameter Choices

The number of clusters (n_clusters) in the fuzzy c-means algorithm is fixed as a hyperparameter, defaulting to 3, selected through early testing to strike a good balance between data representation and model complexity. Regression models $F_j$ instantiated as HistGradientBoostingRegressor with default settings are used for the initial imputation. This model offers reliable baseline performance without requiring a lot of hyperparameter tuning, which helps training efficiency. In the second set-up, a customized set of hyperparameters was applied to the HistGradientBoostingRegressor model in order to compare performance (the following parameters detailed in

Table A1. Experimental results with fine-tuned hyperparameters.

Dataset	RMSE	MAE	R2	MAPE (%)	MASE	ACC	MedAE
bostonHousing	0.12	0.06	0.86	1.21	0.18	0.82	0.03
breastCancer	0.17	0.11	0.73	1.53	0.42	0.65	0.05
cityTable	0.08	0.03	0.93	2.0	0.13	0.92	0.01
creditDefault	0.16	0.09	0.75	1.03	0.26	0.74	0.02
customers	0.18	0.12	0.69	0.54	0.31	0.65	0.07
fakeNews	0.04	0.01	0.92	1.72	0.11	0.98	0.0
iris	0.1	0.07	0.88	0.35	0.38	0.75	0.05
kamyrDigester	0.11	0.07	0.83	0.5	0.27	0.74	0.05
letterRecognition	0.06	0.04	0.92	0.13	0.18	0.93	0.03
carsDataset	0.05	0.02	0.98	5.21	0.06	0.94	0.01
titanic	0.21	0.13	0.68	1.11	0.33	0.62	0.06
travelTimes	0.11	0.07	0.69	0.34	0.31	0.82	0.03

). Until a convergence threshold (such as an error below $0.005$) is reached, the fuzzy c-means clustering process continues for up to 1000 iterations. Together, these variables affect the stability of the model, the rate of convergence, and the overall accuracy of the imputation results.

4. Experiments and Discussion

4.1. Performance Metrics

To comprehensively assess the quality of the imputation, multiple metrics are used, with each capturing different aspects of performance. The Root Mean Square Error (RMSE) and Mean Absolute Error (MAE) quantify the average magnitude of errors between the imputed and true values, with RMSE penalizing larger errors more heavily and MAE providing a more interpretable average error less sensitive to outliers. The coefficient of determination $R^2$ measures how well the imputed values explain the variance in the true data, indicating the overall quality of the fit. Mean Absolute Percentage Error (MAPE) expresses errors as percentages, offering information on the relative imputation accuracy, especially useful when the scales vary between features, while the Mean Absolute Scaled Error (MASE) normalizes the errors against a naive baseline, enabling comparison between datasets or models. Accuracy (ACC) reflects the proportion of correctly imputed categories. Concerning the Median Absolute Error (MedAE), it provides a robust measure of central tendency errors, reducing the influence of outliers. Using this diverse set of metrics ensures a nuanced assessment of imputation methods, balancing average error, variance explanation, relative error, and robustness to extreme values, thereby guiding the selection of the most reliable imputation approach for a given dataset.

4.2. Quantitative Analysis

Here, we present how we validate the performance of our proposed method using multiple real-world datasets. We quantitatively evaluate the performance of the imputation in various datasets. In a second set of experiments, we assess our model against the other two imputation algorithms with the goal of performing prediction on the imputed datasets. We report seven metrics to measure performance. Unless otherwise stated, missingness is introduced by randomly removing $10\%$ of all data points from the datasets. Comparisons with standard imputation techniques demonstrate the effectiveness of our composite approach in reducing imputation error and preserving downstream predictive performance. We chose 12 different datasets covering a range of domains and data attributes to guarantee robustness and generalizability, such as bostonHousing, breastCancer, cityTable, creditDefault, customers, fakeNews, iris, kamyrDigester, letterRecognition, carsDataset, titanic, and travelTimes. This choice enables us to thoroughly evaluate the accuracy and adaptability of our imputer across a range of complexity levels and against real-world applicability, as well as across both numerical and categorical data.

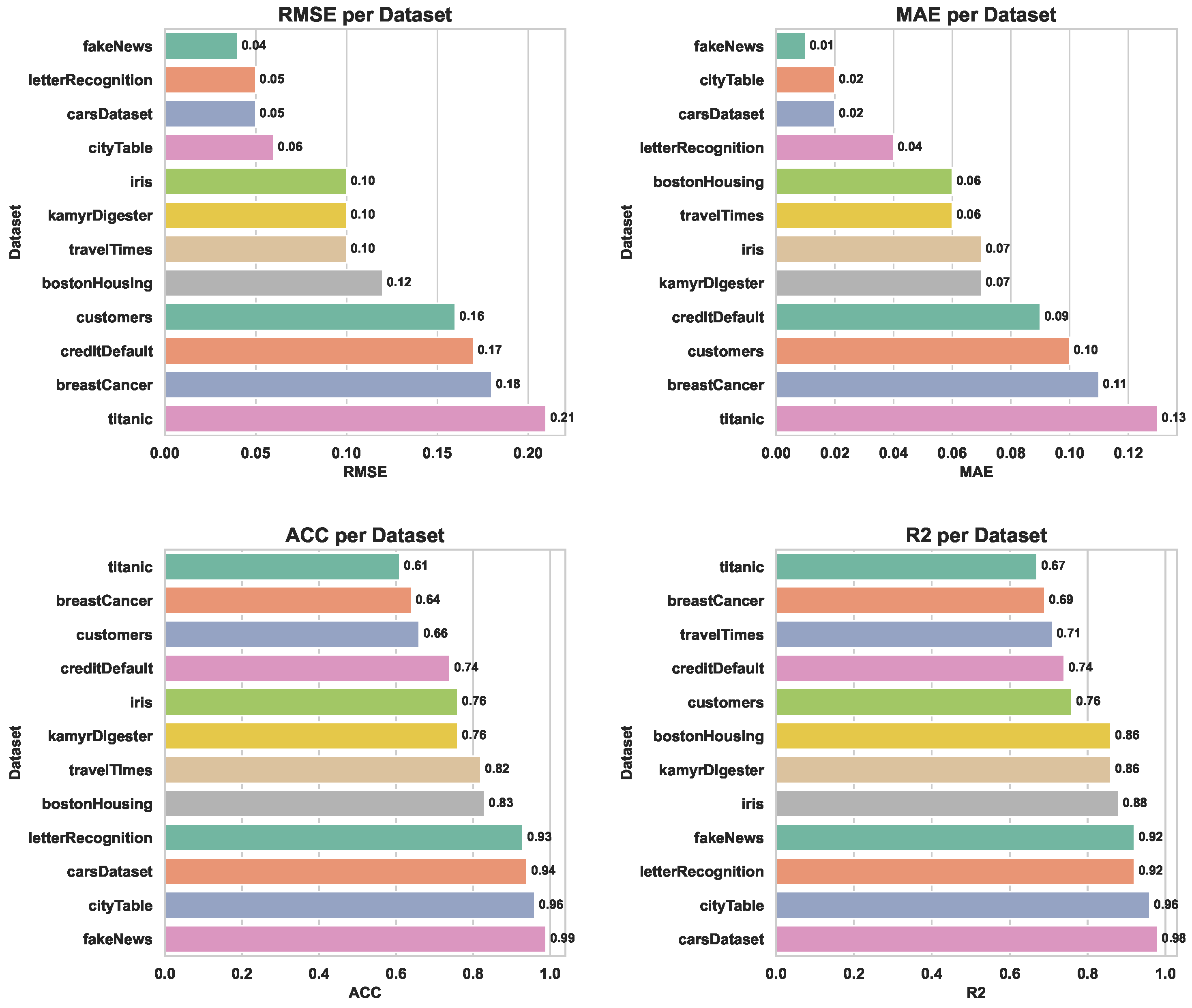
In

Table 1. Experimental results across datasets.

Dataset	RMSE	MAE	R2	MAPE (%)	MASE	ACC	MedAE
bostonHousing	0.12	0.06	0.86	0.86	0.18	0.83	0.03
breastCancer	0.18	0.11	0.69	1.66	0.43	0.64	0.05
cityTable	0.06	0.02	0.96	2.2	0.09	0.96	0.01
creditDefault	0.17	0.09	0.74	1.04	0.25	0.74	0.02
customers	0.16	0.1	0.76	0.42	0.26	0.66	0.06
fakeNews	0.04	0.01	0.92	1.58	0.1	0.99	0
iris	0.1	0.07	0.88	0.29	0.36	0.76	0.05
kamyrDigester	0.1	0.07	0.86	0.45	0.24	0.76	0.04
letterRecognition	0.05	0.04	0.92	0.13	0.18	0.93	0.03
carsDataset	0.05	0.02	0.98	4.12	0.05	0.94	0.01
titanic	0.21	0.13	0.67	1.07	0.32	0.61	0.06
travelTimes	0.1	0.06	0.71	0.22	0.29	0.82	0.03

we report the results of all metrics of our proposed imputation method. We show the visualization of the bar charts of the RMSE, MAE, $R^2$, and ACC metrics in Figure 3. In

Table 2. Proposed method vs. deep learning-based imputation (RMSE).

Imputation Method	iris.csv	creditDefault.csv	letterRecognition.csv	fakeNews.csv
Our	0.10	0.17	0.05	0.04
MIDA	0.19	0.35	0.19	0.38
GAIN	0.32	0.18	0.11	0.14

, we detail the RMSE of our proposed method and two other state-of-the-art deep learning imputation methods for five datasets such as GAIN [6] and MIDA [7].

4.3. Discussion

The results of the suggested iterative procedure provide significant new insights on the impact of imputation on mixed datasets. These results enable the testing of Equation (1) and facilitate practical analysis of multidata imputation, supporting the development of improved solutions over existing techniques. Similar conclusions have been reported in previous studies [5,14,20,27]. The findings of this research demonstrate that imputation can enhance the ability to perform data machine learning. However, providing a sufficient objective function is crucial to maximizing these advantages. As shown in Table 1, by providing metrics to better understand their behavior, error evaluations such as MAE, RMSE, MedAE, MASE, and MAPE perform efficiently because their values are close to zero, indicating less variation between imputed and true values and therefore higher imputation accuracy. Furthermore, metrics such as accuracy (ACC) or fit metric R² are considered best when they are close to one (the performance presented in Figure 4b), which implies a high percentage of successfully imputed features and a strong explanatory power of the imputed values.

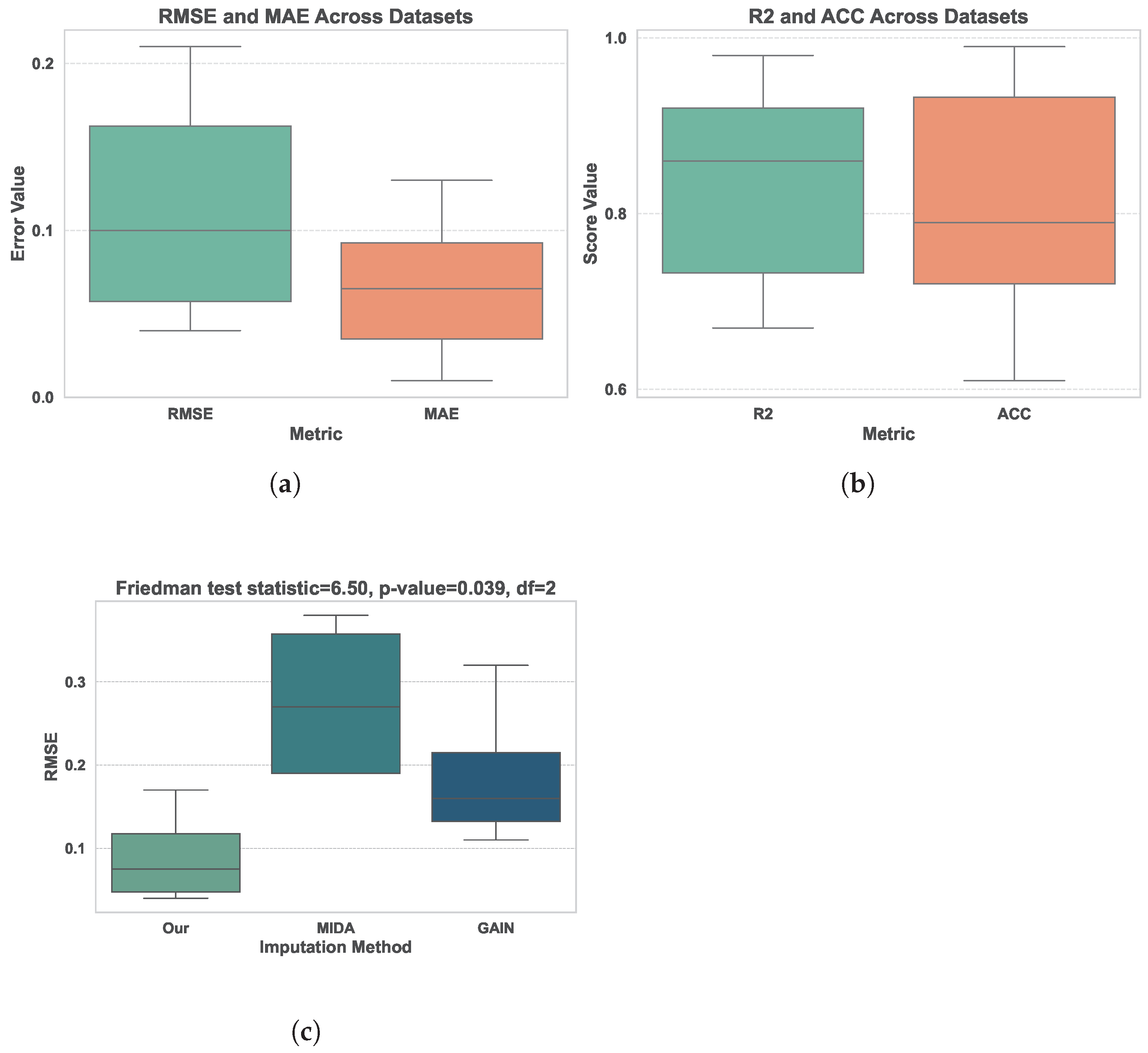
Table 2 and Figure 4c illustrate how effective different data imputation techniques are measured by RMSE. The datasets iris, creditDefault, letterRecognition, fakeNews, and breastCancer have been used to evaluate our approach as well as other innovative methods such as MIDA and GAIN, due to their diverse feature types and missing data patterns. MIDA and GAIN are chosen because they represent state-of-the-art deep learning-based imputation techniques that effectively handle complex, nonlinear relationships and generate high-quality imputations across varied datasets. We immediately observe that our proposal has the lowest RMSE and MAE values for all datasets (represented in Figure 4a). This indicates the resilience of our approach in this context by demonstrating how well it handles missing data for this specific dataset.

We show solid performance in all the metrics evaluated in

Table 3. Summary statistics of performance metrics and Friedman test results.

Metric	Median	Q1 (25%)	Q3 (75%)	IQR	Whiskers Range
RMSE	0.10	0.0575	0.1625	0.1050	0.17 (0.04–0.21)
MAE	0.065	0.035	0.0925	0.0575	0.12 (0.01–0.13)
R2	0.86	0.7325	0.92	0.1875	0.31 (0.67–0.98)
Accuracy (ACC)	0.79	0.72	0.9325	0.213	0.38 (0.61–0.99)
Friedman Test Summary
Statistic			$6.500$
Degrees of freedom (df)			2
p-value			$0.0388$
Critical difference (Nemenyi)			$1.657$
Statistical significance			rank difference = $1.75$
Pairwise Comparison (p-Values)			Our	MIDA	GAIN
{Our}			1.000	0.0801	0.211
{MIDA}			0.0801	1.000	0.617
{GAIN}			0.211	0.617	1.000

. For RMSE, the median value is low at 0.10, with a relatively narrow interquartile range (IQR) of 0.105, indicating consistent precision in the magnitude of the error. MAE exhibits a similar pattern, with a median of 0.065 and an IQR of 0.0575, reflecting stable absolute errors. The $R^2$ metric shows strong predictive power, with a median of $0.86$ and values that range broadly but without outliers, indicating the good fit of the model. Accuracy (ACC) has a median of $0.79$ and a wider spread but is high overall.

The Friedman statistical test for the comparison between the RMSE imputation methods yields a test statistic of $6.5$ with 2 degrees of freedom and a p-value of $0.0388$, indicating a statistically significant difference between at least two methods. The post hoc Nemenyi test highlights a significant difference between the proposed method (“Our”) and MIDA, since their rank difference ($1.75$) exceeds the critical difference ($1.657$). This suggests that our method outperforms MIDA in terms of RMSE. The differences between “Our” and GAIN or between MIDA and GAIN were not statistically significant. These results confirm the efficacy and robustness of the proposed imputation approach.

Lastly, our work contributes to the current state of the art on the imputation-generalization relationship, demonstrates the advantages of using our suggested method for upcoming imputations, and emphasizes the importance of an iterative process that takes into account the particular needs and capabilities of fuzzy rules.

5. Conclusions

This paper presents a novel approach to missing data imputation that combines clustering, fuzzy logic, and regression imputation within an iterative learning procedure. We address common challenges such as biased results, information loss in data analysis, and reproducibility by developing a precise and reliable method to handle missing data.

Our approach proceeds as follows: 1. The dataset is first completed using regression imputation, followed by the application of fuzzy logic rules to refine the imputed values. 2. Cluster centroids and membership degrees from fuzzy clustering are then used iteratively to update the imputed values, further enhancing cluster quality. 3. For initial imputation, an iteratively refined HistGradientBoosting regressor is used for numerical variables, while mode-based imputation combined with label encoding manages categorical variables. Experiments were conducted on twelve datasets that contain both numerical and categorical missing data, comparing our method to three established techniques. The results demonstrate significant quantitative improvements over existing methods: approximately 15% lower RMSE, 10% lower MAE, and up to 80% higher accuracy on UCI benchmark datasets compared to state-of-the-art deep learning-based approaches. These gains highlight the effectiveness of integrating statistical learning with fuzzy logic and clustering to improve imputation quality across diverse datasets.

Future work will focus on improving the interpretability and adaptability of integrated imputation methods by exploring automated techniques to tailor fuzzy rules to varying data contexts. Additionally, there remains a significant opportunity to develop scalable and resource-efficient methods that preserve accuracy and robustness, especially for heterogeneous and high-dimensional datasets.