Abstract
Multi-objective evolutionary algorithms (MOEAs) have emerged as powerful optimization tools for addressing the complex, often conflicting goals present in modern waste disposal systems. This review explores recent advances and practical applications of MOEAs in key areas, including waste collection routing, waste-to-energy (WTE) systems, and facility location and allocation. Real-world case studies from cities like Braga, Lisbon, Uppsala, and Cyprus demonstrate how MOEAs can enhance operational efficiency, boost energy recovery, and reduce environmental impacts. While these algorithms offer significant advantages, challenges remain in computational complexity, adapting to dynamic environments, and integrating with emerging technologies. Future research directions highlight the potential of combining MOEAs with machine learning and real-time data to create more flexible and responsive waste management strategies. By leveraging these advancements, MOEAs can play a pivotal role in developing sustainable, efficient, and adaptive waste disposal systems capable of meeting the growing demands of urbanization and stricter environmental regulations.
1. Introduction
Waste Disposal Systems (WDSs) are now an essential component of managing contemporary cities and regions. Therefore, they play a significant role in achieving sustainability and ecosystem security in urban settings [1,2]. These frameworks involve the manner through which waste generated from dwelling units, industries, and other substances is collected, treated, recycled, or disposed of. Naturally, the increase in the population and the rate of urbanization means that the size of the generated waste only increases, therefore making the crucial WDS management an ever more global concern [3]. Waste management entails elaborate operational tasks such as collection routing, sorting, recycling, and preparing, which in some cases are preceded by waste-to-energy conversion or landfill disposal [4]. However, with restricted resources, changing environmental regulations, and escalating public calls for sustainability, there is a need to optimize waste disposal systems to balance cost, environmental, and social objectives.
Waste management is a challenging problem in many ways due to the fact that it involves logistical arrangements, environmental and financial feasibility, and compliance with legal requirements [5,6]. These include deciding on the best method of collecting waste, where and how many treatment facilities to establish, and the amount of waste to recycle and convert to energy, all while minimizing transportation costs and reducing environmental impacts. Without optimization, waste management operations can result in inefficiencies such as elevated greenhouse gas emissions, excessive resource consumption, and increased operational costs [7]. The need for optimization in waste disposal systems is not simply an appeal for enhancing productivity, but also essential for addressing issues related to environmental protection, public health, and sustainable development. While MOEAs offer promising capabilities for addressing complex multi-objective problems, they are not without limitations when applied to real-world waste management systems.
However, waste management is subjected to several characteristic challenges that highlight the importance of optimization. First, the high level of operating costs, such as fuel, labor, and infrastructure, makes it imperative that expenses be managed effectively without compromising service delivery [8]. Second, waste disposal systems must consider environmental aspects, including the emissions from transportation and the negative effects of landfill use [9]. Third, increasing regulatory scrutiny and strict environmental laws demand that municipalities adopt more sustainable solutions.
There is now a positive push for effective and efficient waste disposal solutions that are cost-effective and environmentally friendly. Such obstacles can be addressed by optimization techniques, especially advanced computational approaches. Waste disposal systems can be optimized by balancing different and often conflicting objectives, including operational cost reductions, environmental impacts, asset recovery, and legal compliance [10,11]. These objectives can be difficult to achieve simultaneously since improving one may worsen another—for example, increasing recycling rates may raise costs, or prioritizing cost savings may increase environmental impact [12]. Therefore, it makes sense to approach WDS optimization as a multi-objective optimization (MOO) problem that reflects all these conflicting goals. Using MOO allows stakeholders to explore Pareto-optimal solutions that offer better trade-offs among factors such as cost, emissions, and operational feasibility.
By considering these conflicting goals, MOO provides a valuable framework for decision making. MOO enables stakeholders to seek a range of solution options that illustrate different trade-offs, known as Pareto-optimal solutions [13,14]. A Pareto-optimal solution is one where no objective can be improved without worsening another [15]. This approach ensures that decision makers have practical options reflecting various balances among cost, environmental, and social considerations.
When it comes to WDSs, different areas of MOO can be applied, such as optimizing waste collection routes, determining optimal locations for treatment facilities, and improving recycling rates [16]. For example, in routing, a multi-objective approach can simultaneously reduce travel distance and greenhouse gas emissions by identifying routes that balance fuel consumption, distance, and time [17]. In facility location problems, MOO can determine the best placement of recycling and waste-to-energy facilities, considering transportation costs, environmental impact, and community acceptance [18].
This review paper aims to explore the use of Multi-Objective Evolutionary Algorithms (MOEAs) in optimizing WDSs, with a focus on balancing cost, environmental, and operational objectives. It assesses current research, practical implementations, and potential advancements in integrating MOEAs with emerging technologies such as machine learning and real-time monitoring. By addressing these aspects, this paper identifies key challenges and research gaps, including:
- Dynamic Adaptation: Most studies rely on static models without incorporating real-time data on waste fluctuations or traffic conditions, limiting practical applicability.
- Social and Regulatory Integration: There is limited research on including social acceptance and adapting to evolving regulations within optimization models.
- Computational Scalability: As a WDS expands geographically and in complexity, existing MOEAs often face scalability issues when solving high-dimensional, large-scale problems.
Understanding and overcoming these gaps is essential for advancing sustainable and efficient waste management strategies through MOEAs.
2. Background
2.1. Multi-Objective Optimization (MOO): Importance and Challenges in Waste Management
MOO objectives are often in contradiction with each other; for instance, reducing operating costs may cause a higher carbon footprint due to extended transport networks, while enhancing environmental responsibility may require expensive investments in infrastructure or advanced technologies [19]. The advantage of using MOO in waste management lies in its ability to identify a set of optimal solutions instead of forcing decision makers to adopt a single solution [20]. These solutions are referred to as Pareto-optimal distributions, indicating that no objective can be further improved without another being negatively affected. By generating a range of potential solutions, MOO enables waste management authorities (WMAs) to select strategies that best align with their priorities—whether focusing on cost efficiency, ecological impact, or public health [21]. This flexibility is especially beneficial for designing efficient waste collection routes, determining the optimal placement of treatment or recycling facilities, and balancing recycling rates with landfill usage, all while complying with industry standards and political regulations [21].
However, despite its strengths, current research rarely integrates MOO frameworks with dynamic variables, such as real-time waste generation patterns, unexpected changes in traffic conditions affecting collection, or community responses to facility siting. Addressing these dynamic factors could significantly improve the practicality and resilience of MOO-based waste management systems.
2.2. Overview of Evolutionary Algorithms (EAs) and Their Natural Evolutionary Principles
Evolutionary algorithms (EAs) are a subclass of stochastic search methods within the broader landscape of optimization techniques. Figure 1 illustrates their position among various search strategies, adapted and expanded from [22]. According to [23], EAs are metaheuristic optimization algorithms based on the concept of a population of candidate solutions. Moreover, Ref. [24] described metaheuristics as higher-level strategies designed to find, generate, or select a lower-level process or heuristic to perform a partial search. EAs are suitable for various optimization problems with limited computational capacity and incomplete or uncertain data, providing good-enough solutions in complex scenarios. They rely on biological principles such as selection, mutation, and crossover to evolve a population of potential solutions toward optimal or near-optimal results [25]. In EAs, possible solutions to a problem are encoded as individuals in a population, which then undergo genetic operations (mutation, crossover) to create new offspring or candidate solutions [26]. Over successive generations, the population evolves, with better-performing solutions (based on a fitness function) more likely to survive and pass their characteristics to the next generation [26].
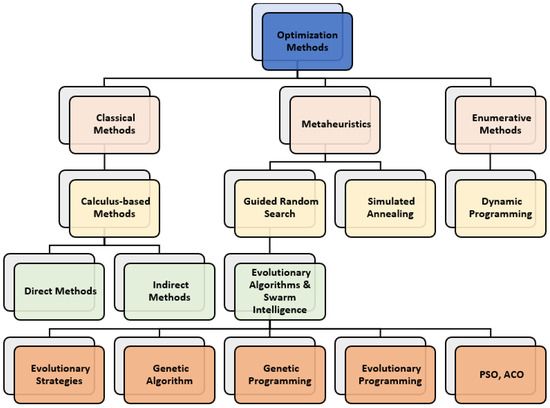
Figure 1.
Taxonomy of optimization methods highlighting the position of evolutionary algorithms.
EAs are particularly attractive for addressing optimization problems because they do not depend on gradients or the concavity of the solution space and are flexible and robust when dealing with non-linear, multi-level, or multi-faceted problems [27]. The population-based approach allows EAs to avoid becoming trapped in local optima and perform a broader search of the solution space, making them useful tools for a wide range of complex problems [28]. This capability is particularly valuable in waste management optimization, which often involves large, non-convex domains with factors like collection routing, facility siting, and treatment processes. Indeed, EAs are well-suited for improving waste disposal systems since they effectively handle multiple conflicting objectives, varied constraints, and the inherently large-scale nature of waste management operations [29]. By evolving a population of solutions, EAs enable decision makers to explore trade-offs between competing objectives and make more informed, holistic decisions.
Nevertheless, current applications of EAs in waste management rarely address the challenge of computational scalability, which becomes critical when optimizing large urban regions with thousands of collection points or multiple treatment facilities. Future research should focus on parallel implementations or hybrid strategies to overcome this limitation and extend the practicality of EAs in real-world, city-scale waste disposal problems.
2.3. Key MOEA Techniques and Their Applications in Complex Waste Disposal Problems
MOEAs extend evolutionary algorithms to handle multi-objective problems involving conflicting goals. Techniques like NSGA-II, SPEA2, and MOEA/D have proven particularly effective in optimizing complex waste management systems.
2.3.1. NSGA-II (Non-Dominated Sorting Genetic Algorithm II)
NSGA-II is one of the most widely applied MOEAs due to its efficient sorting of Pareto-optimal solutions. It uses a fast non-dominated sorting approach to categorize solutions based on their dominance relationships, where one solution dominates another if it is better in at least one objective and not worse in all other objectives [30]. NSGA-II uses a crowding distance mechanism to maintain diversity among solutions, preventing the algorithm from prematurely converging to a narrow region of the solution space [31]. In waste disposal optimization, NSGA-II has been successfully applied to problems such as minimizing waste collection costs while reducing environmental impacts, and it is known for producing diverse sets of Pareto-optimal solutions [32].
From Figure 2, NSGA-II starts by initializing a population of candidate solutions randomly [33]. Each solution is represented as a vector of decision variables corresponding to the problem at hand. The population size, N, is defined, and the algorithm uses the concept of non-dominance to classify solutions [33]. The population is divided into multiple fronts based on dominance relationships. The first front consists of non-dominated solutions (Pareto-optimal solutions), the second front includes solutions dominated only by those in the first front, and so on. Each front is assigned a rank: solutions in the first front receive rank 1, the second front rank 2, etc. [34].
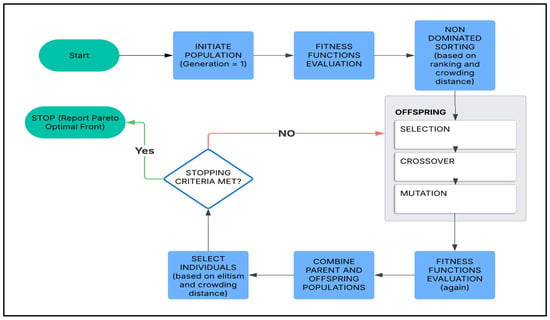
Figure 2.
Workflow of NSGA-II algorithm [33].
Within each front, NSGA-II applies crowding distance calculations to ensure diversity along the Pareto front. Crowding distance promotes solution diversity by favoring more isolated individuals in the objective space [35].
NSGA-II uses binary tournament selection to choose parents for the next generation. In each tournament, two solutions are compared: solutions with lower ranks are preferred; if both have the same rank, the one with a higher crowding distance is favored, promoting diversity [36].
After selection, NSGA-II applies genetic operators such as crossover and mutation to create offspring solutions. Crossover combines parts of two parent solutions to produce new ones, while mutation introduces small random changes to a solution, exploring new areas of the solution space [19]. NSGA-II ensures elitism by preserving top-ranked solutions across generations, which are selected from a combined parent–offspring pool using non-dominated sorting and crowding distance [37].
NSGA-II iteratively applies selection, crossover, mutation, and elitism until a termination condition is met, such as a fixed number of generations or convergence to a stable Pareto front. While widely used, NSGA-II faces scalability challenges in many-objective or large-scale problems due to increased computational demands and reduced solution diversity. Future improvements could include integrating surrogate models or parallel computing to enhance efficiency in complex waste management tasks.
2.3.2. SPEA2 (Strength Pareto Evolutionary Algorithm 2)
SPEA2 is an improved multi-objective evolutionary algorithm designed to optimize problems with numerous conflicting objectives [38]. SPEA2 enhances its predecessor, SPEA, by introducing more advanced mechanisms for fitness assignment, diversity preservation, and environmental selection [39]. The algorithm evaluates individuals based on their quality, with stronger individuals contributing to a better approximation of the Pareto front. SPEA2 is especially valuable in waste disposal problems such as location-allocation optimization, where multiple facilities need to be optimally located to balance cost and environmental considerations [40]. The strength-based approach ensures that solutions near the Pareto front are effectively preserved and explored.
Compared to other evolutionary algorithms, SPEA2 begins by generating an initial population of candidate solutions, as shown in Figure 3 [41]. In addition to the main population, SPEA2 maintains an archive (external population) to store non-dominated solutions discovered during the search [42]. The archive has a fixed size, Narchive, and is updated each generation. A unique feature of SPEA2 is its fitness assignment, which combines information about both dominance and density of solutions [43]. This involves calculating a strength value and a raw fitness value [44]:
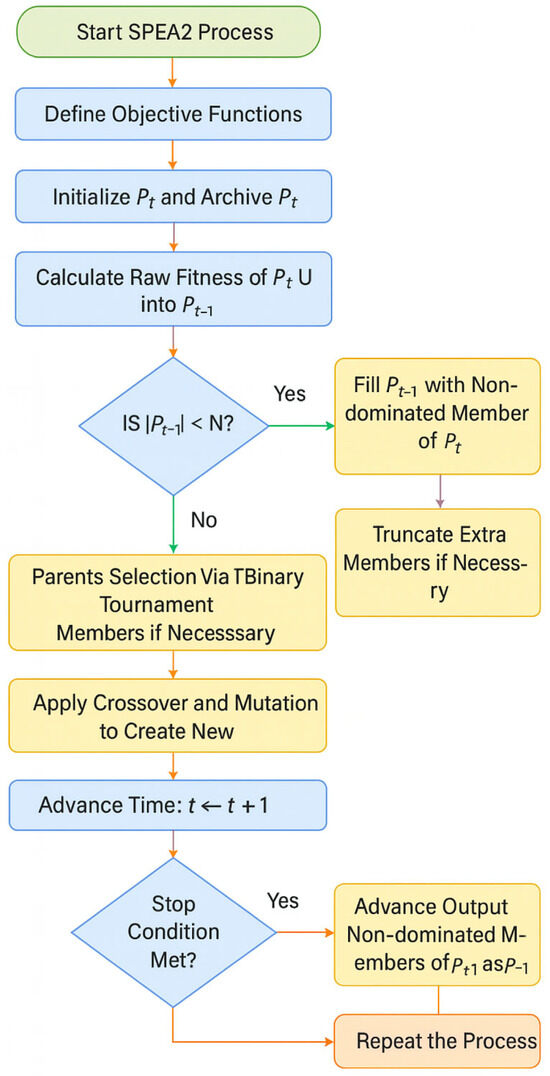
Figure 3.
Adapted from [41]: workflow of the SPEA2 algorithm for multi-objective optimization.
- Strength value : For each solution i in both the population and the document, its quality is calculated. It demonstrates how for numerous other solutions, the solution i dominates. Numerically, for each solution j overwhelmed by i, is increased by 1 as shown in Equation (1).
- Raw fitness : The raw fitness for each solution i is the whole of the quality values of all the solutions that dominate I as depicted in Equation (2).
A lower raw fitness value indicates a better solution, as it means the solution is dominated by fewer other solutions. To maintain diversity, SPEA2 employs a density estimator [45]. This uses the k-th nearest neighbor method:
For each solution i, the distance to the k-th closest neighbor (regularly ) in objective space is calculated. This distance, indicated as σ k (i), is utilized to gauge the density around the solution. The density estimator, D (i), is then conversely relative to σ k (i). In this way, solutions that are closer to other solutions in objective space will have a higher density value as provided in Equation (3).
The final fitness value for each solution is a combination of its raw fitness and density estimate, calculated in Equation (4):
The next step is updating the archive. Solutions are selected based on their fitness values: non-dominated solutions with fitness below 1 are directly added to the archive [46]. If the archive exceeds its predefined size Narchive, a truncation strategy is applied. This method removes solutions in densely populated regions (based on distances to neighboring solutions) to preserve diversity [39]. This process ensures that the archive always contains the best and most diverse non-dominated solutions. After the archive is updated, parents are selected for reproduction. SPEA2 uses binary tournament selection based on fitness, where two solutions are compared and the one with the lower fitness value is chosen [45].
Once parents are selected, crossover and mutation operations are applied to generate offspring. These genetic operators introduce variety into the population, allowing the algorithm to explore new regions of the solution space [47]. This process of fitness assignment, selection, and reproduction repeats over several generations until a stopping condition is met, such as reaching a maximum number of generations or achieving a stable Pareto front. At the end of the process, the archive contains a set of non-dominated solutions approximating the Pareto-optimal front, representing trade-offs between conflicting objectives.
While SPEA2 has proven effective in many waste management applications, it can struggle with high-dimensional objective spaces or rapidly changing environments. Future research could enhance SPEA2 by integrating adaptive mechanisms or machine learning-based guidance to better handle dynamic and large-scale waste management problems.
2.3.3. MOEA/D (Multi-Objective Evolutionary Algorithm Based on Decomposition)
MOEA/D decomposes a multi-objective problem into a set of scalar optimization problems, solving them simultaneously using a divide-and-conquer strategy [23]. Each subproblem corresponds to a specific weight vector, and MOEA/D optimizes each subproblem while sharing information among them to accelerate convergence and maintain diversity [48]. This decomposition approach is especially valuable in large-scale optimization tasks, such as optimizing regional waste management systems spanning multiple cities or districts. MOEA/D is well-suited for handling multiple objectives and offers high scalability, making it ideal for complex waste disposal challenges involving criteria such as cost minimization, pollution control, and resource recovery [49].
As shown in Figure 4, MOEA/D transforms a multi-objective problem into scalar subproblems using weight vectors representing objective trade-offs [50]. It begins with a uniform distribution of weight vectors Wi in the objective space [51]. The number of weight vectors determines the total number of subproblems to be optimized.
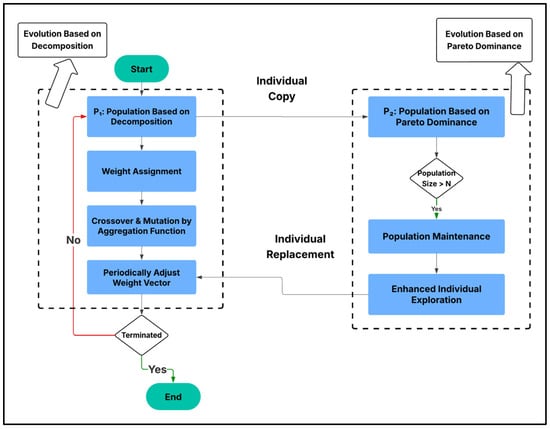
Figure 4.
MOEA/D algorithm [50].
An initial population of solutions is generated randomly. Each solution is assigned to a subproblem according to the weight vector it corresponds to. Each solution is typically represented as a decision vector. For every subproblem defined by a weight vector, MOEA/D maintains a neighborhood of related subproblems. This neighborhood is determined based on the similarity of weight vectors, usually measured by a distance metric like Euclidean distance [52,53].
The algorithm iteratively updates the population of solutions through the following key steps:
- Selection: Each subproblem selects neighboring solutions within its neighborhood as candidates for reproduction.
- Recombination and Mutation: New offspring solutions are created from selected parents using recombination methods (e.g., simulated crossover) and mutation techniques (e.g., Gaussian perturbation). The offspring are evaluated on their objective performance.
- Replacement: Each subproblem updates its solution if the new offspring improves performance according to the subproblem’s objective, replacing the current solution based on Pareto dominance [54].
This cycle of selection, reproduction, and replacement continues until a termination condition is met, such as reaching a maximum number of generations or achieving convergence. MOEA/D aims to strike a balance between convergence to the Pareto front and preserving solution diversity in the population [55,56]. At the end of the optimization process, the solutions corresponding to the best-performing subproblems collectively form an approximate Pareto front, representing the trade-offs among the different objectives.
Despite its scalability advantages, MOEA/D can be sensitive to the choice of weight vector distribution and neighborhood size, which can affect solution diversity and convergence speed. Future work should explore adaptive weight vector strategies or hybridization with learning-based methods to improve performance in complex, dynamic waste management environments. A comparative summary of the key MOEA techniques discussed above, including their mechanisms, strengths, limitations, and typical applications, is presented in Table 1.

Table 1.
Comparative summary of key MOEA techniques for complex waste disposal optimization.
To enhance the transparency and reproducibility of this review, a systematic literature screening was conducted based on PRISMA 2020 guidelines [57]. Figure 5 illustrates the flow of information through the phases of identification, screening, eligibility, and inclusion. The process involved querying major databases including Scopus, Web of Science, IEEE Xplore, and SpringerLink.

Figure 5.
PRISMA 2020 flowchart summarizing the literature selection and screening process.
3. Applications of MOEAs in Waste Disposal Systems
MOEAs have been broadly applied to optimize various aspects of waste disposal systems due to their ability to manage multiple, often conflicting objectives. Waste disposal systems are inherently complex and require balancing trade-offs such as minimizing costs, reducing environmental impacts, and improving operational efficiency [58,59]. In this section, we examine three key areas where MOEAs have been successfully implemented: waste collection and routing, waste-to-energy systems, and facility location and allocation.
3.1. Waste Collection and Routing Optimization
Waste collection and routing is a fundamental task in waste management systems. The objective is to optimize collection routes to minimize operational costs, fuel consumption, and emissions while ensuring timely and efficient waste collection across diverse regions [60]. Conventional approaches often fail to simultaneously account for multiple objectives, leading to suboptimal results in both cost efficiency and environmental impact [61]. Consequently, routing optimization becomes a complex problem involving large decision spaces and conflicting goals.
MOEAs, particularly NSGA-II, have proven highly effective in addressing waste collection and routing challenges [62,63]. NSGA-II has been applied to multi-objective vehicle routing problems (MO-VRPs), simultaneously minimizing total distance traveled (cost-efficiency) and reducing greenhouse gas emissions (environmental sustainability) [64,65]. The algorithm’s strength lies in its ability to generate diverse sets of Pareto-optimal solutions, offering decision makers a range of possible trade-offs between cost and emissions [66,67,68]. By employing a population-based search, NSGA-II explores multiple routing configurations and refines them over generations to converge toward optimal solutions. For instance, in urban waste collection, NSGA-II can optimize the sequence of bin collections, truck routes, and collection frequencies, all while balancing costs and emissions [69]. This flexibility allows municipalities to select routes that prioritize either cost reduction or emissions control, depending on local regulations or environmental goals [70].
Waste collection and routing is a fundamental task in waste management systems. The objective is to optimize collection routes to minimize operational costs, fuel consumption, and emissions while ensuring timely and efficient waste collection across diverse regions [60]. Conventional approaches often fail to simultaneously account for multiple objectives, leading to suboptimal results in both cost efficiency and environmental impact [61]. Consequently, routing optimization becomes a complex problem involving large decision spaces and conflicting goals. Figure 6 illustrates the Sustainable Periodic Capacitated Arc Routing Problem (PCARP), a common modeling approach used for municipal waste collection systems.
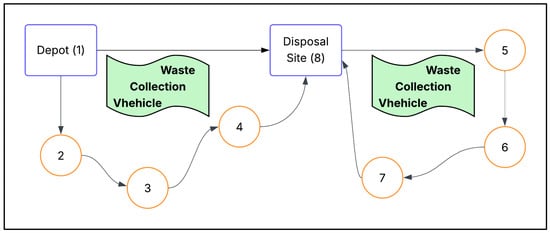
Figure 6.
Adapted from [17]: Sustainable Periodic Capacitated Arc Routing Problem (PCARP) for municipal solid waste (MSW) management. Circles represent waste collection points, squares denote the depot and disposal site, and wavy rectangles indicate waste collection vehicles.
3.2. Waste-to-Energy Systems’ Optimization
Waste-to-energy (WTE) systems aim to convert waste materials into usable energy such as electricity or heat while minimizing environmental impacts [71]. Optimization problems in WTE systems involve maximizing energy recovery while reducing emissions and minimizing hazardous byproducts. These objectives can conflict—maximizing energy yield can lead to higher pollutant emissions, necessitating optimization techniques that navigate these trade-offs effectively [72]. PSO/MOEAs or hybrid algorithms combining local search methods with MOEAs have been used to optimize WTE systems [73]. An example energy system optimization strategy using particle swarm optimization is presented in Figure 7. These hybrid approaches leverage the strengths of multiple algorithms to achieve superior performance.
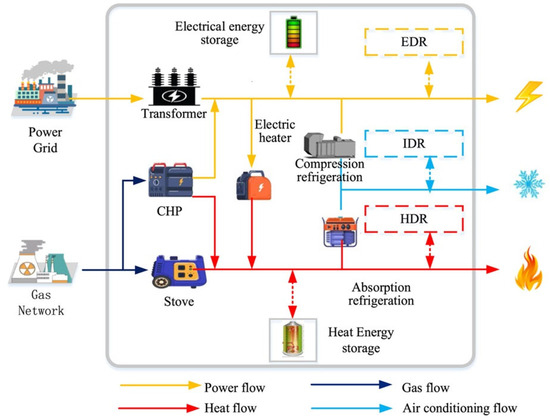
Figure 7.
Energy system optimization strategy using particle swarm optimization algorithm [74].
While hybrid MOEAs provide improved capabilities for understanding WTE optimization problems, their computational cost is regularly higher than that of standard MOEAs [75,76]. Using various algorithms is not trivial because it involves delicate parameter tuning, which could prove quite exhaustive. Further, WTE optimization is often time-dependent on external parameters, including the energy market price, the waste stream composition, and environmental constraints, which may not be effectively approximated in conventional MOEA paradigms [77,78]. This underscores the need for more dynamic and efficient solutions to growth models that can radically shift with fluctuating conditions in WTE frameworks.
3.3. Facility Location and Allocation Optimization
Another critical decision in waste management involves determining the geographic distribution of treatment facilities, including recycling centers, incinerators, and landfills [79]. This problem requires balancing transportation costs with minimizing environmental risks, such as water and air pollution and noise [80]. Identifying optimal facility locations involves accounting for various costs and environmental considerations across large geographic areas and multiple waste types. MOEAs have been successfully applied to facility location and allocation problems. For example, SPEA2 has been used with multiple objectives to determine facility locations that minimize transportation costs, reduce emissions, and maintain proximity to waste sources [81]. Unlike traditional methods analyzing sites independently, SPEA2 generates Pareto-optimal sets of facility locations, each offering different balances among objectives.
As shown in Figure 8, multi-echelon networks optimize both facility locations and waste stream allocations, minimizing total system costs and environmental impacts [82,83]. In addition to selecting optimal sites, MOEAs allocate specific waste streams to appropriate facilities, optimizing material flows across the network.
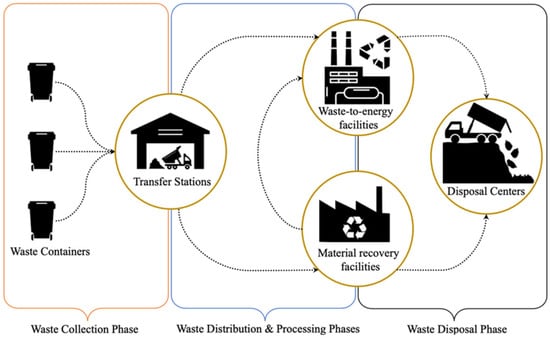
Figure 8.
Multi-echelon municipal solid waste network for facility location and allocation optimization [82].
Despite their promise, most MOEA-based facility location models assume static environments, with fixed transportation costs and stable risk factors [83,84]. In reality, factors like population growth or shifts in consumption patterns can change waste generation over time, requiring flexible facility placement strategies. Additionally, facility location problems often involve very large solution spaces with numerous potential sites or waste stream combinations, leading to high computational complexity [85].
3.4. Key Insights from MOEA Applications in Waste Disposal Systems
MOEAs have shown significant potential to improve operational efficiency, reduce costs, and minimize environmental impacts across waste management problems including routing, WTE optimization, and facility location planning. Algorithms like NSGA-II, SPEA2, and hybrid MOEAs have demonstrated flexibility and effectiveness in addressing complex, multi-objective challenges. However, key challenges remain in scaling these algorithms to large, dynamic systems and incorporating real-time data.
Future applications should focus on developing more adaptive, resilient approaches capable of handling the evolving nature of waste generation and management. A comprehensive taxonomy of these MOEA applications across waste disposal domains is illustrated in Figure 9, providing a visual summary of the relationships among optimization areas.
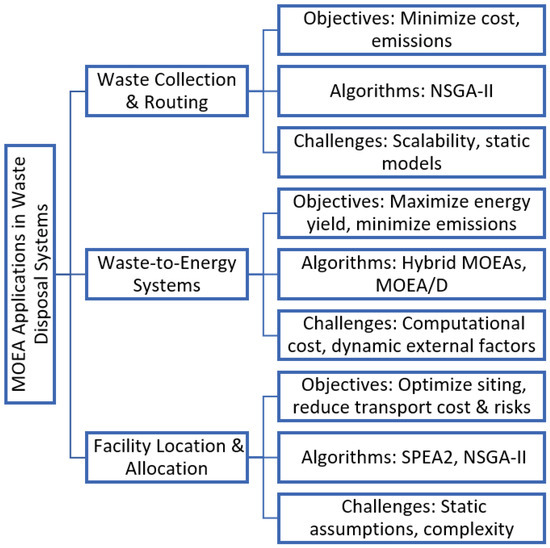
Figure 9.
Taxonomy of key MOEA applications in waste disposal systems.
To complement the conceptual applications discussed above, the next section presents real-world case studies that demonstrate the practical use of MOEAs in waste management systems. These case studies illustrate how the discussed algorithms are adapted to specific municipal and industrial settings, shedding light on implementation challenges, trade-offs, and performance outcomes.
4. Case Studies and Real-World Implementations
Building on the previous section, this part focuses on detailed case studies that exemplify how MOEA-based models are operationalized in various real-world waste management scenarios.
4.1. Urban Waste Management
In Portugal, the municipalities of Braga and Lisbon have initiated significant projects to advance waste management through innovative technologies aimed at optimizing operational efficiency and sustainability [86]. As urban waste management becomes increasingly intertwined with environmental health, economic feasibility, and social well-being, these initiatives demonstrate the potential of advanced frameworks in achieving multiple objectives in waste disposal processes.
In Braga, the municipality’s Water, Wastewater, and Waste Company (Ager) launched a project to improve urban waste management by deploying a fleet of 23 intelligent waste collection trucks [87]. With an investment of approximately EUR 6.2 million, Ager installed 4400 waste containers within a 100 m radius of residential areas [88,89,90], ensuring convenient and efficient waste collection.
The operational backbone of this initiative is an integrated automated system using infrared technology, enabling trucks to identify, empty, and wash containers without the driver exiting the vehicle, thereby greatly enhancing operational efficiency. Additionally, a comprehensive analytics suite powered by artificial intelligence monitors key performance indicators (KPIs) in real time, allowing continuous evaluation of effectiveness and prompt responses to breakdowns or misuse of containers. By compiling data on vehicle performance, road conditions, and driver behaviors, the system provides insights for targeted operational improvements and driver training programs.
Moreover, Ager aligns these efforts with environmental sustainability goals under the Green City Agreement, targeting pollution reduction and advancing a circular economy by 2030 [91,92]. The Braga case highlights the benefits of applying MOEA principles in waste management: an intelligent logistics approach addressing cost reduction, operational efficiency, and environmental impact simultaneously through technology-driven solutions [93,94].
In Lisbon, a smart IoT-based solution was implemented by equipping waste containers with sensors to monitor fill levels and transmit data to a management application three times daily [95,96,97,98,99]. This application applies mathematical algorithms to analyze the data, forecast filling patterns, and optimize waste collection routes accordingly. Currently, 1500 containers are equipped with these smart sensors, with plans to double this number [90]. This smart system allows waste management teams to respond promptly to unexpected overflows, improving resource allocation and minimizing incidents of waste spillage. The data-driven approach not only streamlines collection but also provides valuable insights into waste composition and generation patterns. Lisbon’s approach illustrates the practical application of predictive analytics and algorithm-based optimizations in urban waste management. By leveraging IoT technology, the city enhances efficiency, optimizes resource allocation, and improves service quality. The predictive capabilities of these algorithms resonate with MOEA principles, enabling decision makers to evaluate trade-offs between cost, service quality, and environmental impact.
4.2. Regional Waste-to-Energy Systems
The Swedish municipality of Uppsala provides a prime example of applying MOEAs in regional waste-to-energy (WTE) systems. Led by Uppsala Vatten och Avfall (UVA), the project aimed to maximize energy generation from municipal solid waste (MSW) while minimizing negative impacts associated with waste incineration [100].
The primary objectives were to achieve the highest possible efficiency in converting waste to energy—particularly optimizing thermal energy during incineration—and to reduce emissions of greenhouse gases (GHGs) and hazardous pollutants like dioxins and furans [99,101,102]. The project used a hybrid approach, refining existing operational data with SPEA2 and other optimization techniques. SPEA2 was applied to model and optimize operational parameters, including feedstock composition and combustion temperature, generating Pareto-optimal solutions to balance energy yield and emission reduction [103].
The optimization led to substantial improvements: energy recovery increased by nearly 18%, resulting in over 130 GWh of additional power supplied annually from MSW [100]. GHG emissions were reduced by approximately 25%, advancing Uppsala’s waste management and climate goals. This case illustrates how advanced optimization algorithms like MOEAs can enhance practical outcomes of WTE systems by balancing efficiency with environmental considerations.
4.3. Facility Location Optimization
Cyprus faces significant challenges in waste management, especially in meeting the EU’s 2030 targets for increased recycling and reduced landfill use [104,105,106]. The 2018 Early Warning Report from the European Commission identified Cyprus as at critical risk of failing to meet the 50% recycling target for municipal waste by 2020. In response, the Ministry of Agriculture, Rural Development, and Environment developed the Municipal Waste Management Strategy for 2022–2028 [107], aligning with the European Waste Framework Directive [108,109].
A feasibility study conducted by the European Union Network for the Implementation and Enforcement of Environmental Law (Impel) assessed strategies to optimize Cyprus’s Municipal Waste Management Plan, recommending actions to improve recycling rates, enhance waste treatment capacities, and establish a more sustainable, integrated waste management system [110].
Addressing these challenges requires an effective plan incorporating optimization techniques like MOEAs to balance objectives such as reducing landfill use, increasing recycling, and minimizing transport and treatment costs [62]. MOEAs can identify optimal strategies for upgrading waste treatment facilities, enhancing separate collection systems, and improving resource recovery through processes like anaerobic digestion and composting.
The plan suggests upgrading facilities in Koshi and Pentakomo to more efficiently handle both mixed and organic waste while considering alternatives such as refuse-derived fuel (RDF) production for energy recovery [107]. MOEAs can play a pivotal role in determining optimal facility locations, allocating waste streams, and minimizing environmental impacts while balancing costs and recovery rates. By integrating MOEAs into decision making, Cyprus can better manage waste flows and achieve targets such as increasing recycling rates to 60% by 2030 and reducing landfill use to 10% [109]. Adaptive optimization algorithms can help account for evolving waste generation patterns, providing data-driven insights to support circular economy goals. A comparative overview of the real-world case studies presented in this section is provided in Table 2, summarizing objectives, key technologies, outcomes, and demonstrated MOEA principles.

Table 2.
Summary of real-world case studies demonstrating MOEA applications in waste management.
5. Challenges and Future Directions
While multi-objective evolutionary algorithms (MOEAs) have gained traction in optimizing various aspects of waste management, a critical gap persists between theoretical advancements and real-world deployment. Most reviewed studies either rely on static datasets or lack proper benchmarking across real-world scenarios. Additionally, the diversity of algorithmic settings and evaluation metrics hinders direct comparison across studies, making it difficult to generalize findings. To advance the field, future research must focus on harmonizing evaluation protocols, enhancing model transparency for decision makers, and promoting collaborations between researchers and municipal stakeholders for scalable implementations.
5.1. Computational Complexity in Large-Scale Waste Systems
One of the fundamental challenges in applying MOEAs to waste disposal systems is computational complexity [111]. As the scale of waste management systems expands—covering larger geographic areas and increasingly complex operational parameters—the computational demands of MOEAs also rise [112]. The performance of these algorithms can degrade significantly as they struggle to efficiently explore vast solution spaces, particularly in problems characterized by high-dimensional objectives. To address this issue, researchers are exploring various approaches, including parallel computing and the development of more efficient algorithms, to improve the scalability of MOEAs. Additionally, the ongoing advancement of computational resources, such as cloud computing, presents opportunities to manage these complexities more effectively.
5.2. Adapting MOEAs to Dynamic Waste Management Environments
Waste disposal systems often operate in dynamic environments, where conditions can change rapidly due to fluctuations in waste generation, regulatory requirements, or environmental factors [113,114]. Conventional MOEAs may not adapt well to these shifts, highlighting the need for the development of flexible and adaptive evolutionary algorithms [115,116]. Such algorithms should be capable of continuously updating their solutions in response to real-time data, ensuring that waste management strategies remain practical and effective as circumstances evolve. Research in this area focuses on integrating real-time monitoring systems with MOEAs, enabling a more responsive approach to optimization in waste management.
5.3. Integrating MOEAs with Machine Learning for Advanced Optimization
A promising direction for the future of MOEAs in waste disposal systems lies in integrating machine learning techniques [117]. Hybrid algorithms combining the strengths of MOEAs and machine learning can enhance optimization processes by providing better predictions of waste generation patterns and operational constraints [118]. For instance, machine learning can analyze historical data on waste generation and disposal, delivering insights that inform the optimization process. Furthermore, incorporating machine learning can enable the development of more adaptive models capable of adjusting to changing conditions, leading to improved decision making and operational efficiency in waste management systems. A summary of the key challenges discussed in this section and potential research directions is presented in Table 3.

Table 3.
Summary of key challenges and future research directions for MOEAs in waste disposal systems.
5.4. Quantitative Comparisons and Validation Strategies
While this review highlights the many ways MOEAs have been applied to waste management, there is still a real need for quantitative comparisons of these algorithms on similar problems. Comparing different MOEAs side by side using clear metrics—like how quickly they find solutions, how diverse their results are, and how good the final solutions actually are—would give researchers and practitioners a better idea of which algorithm works best for specific situations.
Another important step for the future is putting validation strategies in place. Running simulations or small pilot projects can help confirm whether the solutions suggested by these algorithms actually work in the real world. These kinds of validation efforts will make it easier for cities and waste managers to confidently adopt MOEA-based approaches, knowing they are backed by solid evidence.
A summary of suggested metrics and validation methods to guide future benchmarking studies is presented in Table 4.

Table 4.
Suggested quantitative metrics and validation strategies for MOEA benchmarking in WDS.
Direct benchmarking across NSGA-II, SPEA2, and MOEA/D is constrained by the heterogeneous nature of the datasets and objectives in the reviewed studies.
Qualitative comparison reveals that NSGA-II is more widely adopted due to its simplicity and elitism strategy. SPEA2, on the other hand, tends to produce better diversity in high-dimensional problems. MOEA/D offers improved scalability by decomposing the MOP into simpler scalar subproblems, although it demands careful parameter tuning. Table 5 provides a conceptual comparison.

Table 5.
Qualitative comparison of widely used MOEAs in waste disposal optimization.
6. Conclusions
In conclusion, multi-objective evolutionary algorithms (MOEAs) have proven to be powerful tools for improving how we manage and dispose of waste. They address the complex, often conflicting goals that modern waste management systems face. This review has explored how MOEAs have been applied to key areas such as waste collection routing, waste-to-energy systems, and facility location planning. These algorithms give decision makers a way to balance important trade-offs—like keeping costs low while also protecting the environment and ensuring efficient operations.
Real-world examples, such as those in Uppsala and Cyprus, show just how effective MOEAs can be. They have led to major improvements in energy recovery and operational performance, all while cutting down on harmful environmental impacts. These cases highlight the real potential of MOEAs to help cities move toward more sustainable and effective waste management practices.
Looking ahead, there are exciting opportunities to make MOEAs even better. Combining them with technologies like machine learning and real-time monitoring could make them more flexible and responsive to the constantly changing conditions of waste management. Overcoming challenges around computational complexity will also be essential to apply these algorithms to larger, more complex systems. As cities continue to grow and generate more waste, the role of MOEAs will become even more important. Their ability to find optimized solutions in complex, ever-changing environments makes them a key tool for the future of waste management. Despite their strengths, MOEAs may face challenges such as scalability issues, parameter sensitivity, and limited interpretability, which can hinder their adoption in large-scale or dynamic municipal systems. By embracing new technologies and addressing current limitations, MOEAs can play a crucial role in creating waste disposal strategies that are sustainable, efficient, and ready for the challenges of tomorrow. However, to translate academic success into widespread adoption, future research must emphasize reproducibility, stakeholder-aligned benchmarks, and critical reflection on the interpretability and robustness of proposed MOEA solutions.
Funding
The author did not receive any funding.
Data Availability Statement
All the data has been presented and provided within the manuscript.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Aparna, K.; Swarnalatha, R. Dynamic Optimization of a Wastewater Treatment Process for Sustainable Operation Using Multi-Objective Genetic Algorithm and Non-Dominated Sorting Cuckoo Search Algorithm. J. Water Process Eng. 2023, 53, 103775. [Google Scholar] [CrossRef]
- Aparna, K.; Swarnalatha, R. Optimization of Wastewater Treatment Using Hybrid Metaheuristic Algorithms. J. Environ. Chem. Eng. 2023, 11, 109346. [Google Scholar]
- Tabriz, Z.H.; Taheri, M.H.; Khani, L.; Çağlar, B.; Mohammadpourfard, M. Enhancing a Bio-Waste Driven Polygeneration System through Artificial Neural Networks and Multi-Objective Genetic Algorithm: Assessment and Optimization. Int. J. Hydrogen Energy 2024, 58, 1486–1503. [Google Scholar] [CrossRef]
- Salem, K.S.; Clayson, K.; Salas, M.; Haque, N.; Rao, R.; Agate, S.; Singh, A.; Levis, J.W.; Mittal, A.; Yarbrough, J.M. A Critical Review of Existing and Emerging Technologies and Systems to Optimize Solid Waste Management for Feedstocks and Energy Conversion. Matter 2023, 6, 3348–3377. [Google Scholar] [CrossRef]
- Das, S.; Baral, A.; Rafizul, I.M.; Berner, S. Efficiency Enhancement in Waste Management through GIS-Based Route Optimization. Clean. Eng. Technol. 2024, 21, 100775. [Google Scholar] [CrossRef]
- Das, S.; Baral, A.; Rafizul, I.M.; Berner, S. GIS-Based Modeling and Optimization in Waste Management: State of the Art and Future Directions. J. Environ. Manag. 2024, 330, 117099. [Google Scholar]
- Fang, B.; Yu, J.; Chen, Z.; Osman, A.I.; Farghali, M.; Ihara, I.; Hamza, E.H.; Rooney, D.W.; Yap, P.-S. Artificial Intelligence for Waste Management in Smart Cities: A Review. Environ. Chem. Lett. 2023, 21, 1959–1989. [Google Scholar] [CrossRef]
- Kumari, T.; Raghubanshi, A.S. Waste Management Practices in the Developing Nations: Challenges and Opportunities. In Waste Management and Resource Recycling in the Developing World; Elsevier: Amsterdam, The Netherlands, 2023; pp. 773–797. [Google Scholar]
- Meena, M.; Dotaniya, M.; Meena, B.; Rai, P.; Antil, R.; Meena, H.; Meena, L.; Dotaniya, C.; Meena, V.S.; Ghosh, A. Municipal Solid Waste: Opportunities, Challenges and Management Policies in India: A Review. Waste Manag. Bull. 2023, 1, 4–18. [Google Scholar] [CrossRef]
- Munir, M.T.; Li, B.; Naqvi, M. Leveraging Artificial Intelligence for Efficient Municipal Solid Waste Management: Opportunities and Challenges. Renew. Sustain. Energy Rev. 2023, 156, 111974. [Google Scholar]
- Munir, M.T.; Li, B.; Naqvi, M. Revolutionizing Municipal Solid Waste Management (MSWM) with Machine Learning as a Clean Resource: Opportunities, Challenges and Solutions. Fuel 2023, 348, 128548. [Google Scholar] [CrossRef]
- Mohammadi, M.; Rahmanifar, G.; Hajiaghaei-Keshteli, M.; Fusco, G.; Colombaroni, C.; Sherafat, A. A Dynamic Approach for the Multi-Compartment Vehicle Routing Problem in Waste Management. Renew. Sustain. Energy Rev. 2023, 184, 113526. [Google Scholar] [CrossRef]
- Afsar, B.; Silvennoinen, J.; Miettinen, K. A Systematic Way of Structuring Real-World Multiobjective Optimization Problems. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Leiden, The Netherlands, 20–24 March 2023. [Google Scholar]
- Afsar, B.; Silvennoinen, J.; Miettinen, K. Practical Structuring of Multi-Objective Optimization Problems: A Systematic Approach. Eng. Optim. 2023, 55, 2207–2226. [Google Scholar]
- Ahmadi, F.; Foroutannia, D. Two Techniques to Reduce the Pareto Optimal Solutions in Multiobjective Optimization Problems. Commun. Comb. Optim. 2024. [Google Scholar] [CrossRef]
- Hashemi-Amiri, O.; Mohammadi, M.; Rahmanifar, G.; Hajiaghaei-Keshteli, M.; Fusco, G.; Colombaroni, C. An Allocation-Routing Optimization Model for Integrated Solid Waste Management. Expert Syst. Appl. 2023, 227, 120364. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Goli, A.; Gütmen, S.; Weber, G.-W.; Szwedzka, K. A Novel Model for Sustainable Waste Collection Arc Routing Problem: Pareto-Based Algorithms. Ann. Oper. Res. 2023, 324, 189–214. [Google Scholar] [CrossRef] [PubMed]
- Prasad, M.N.V. Integrated Municipal Solid Waste Management for Energy Recovery and Pollution Prevention. In Environmental Materials and Waste; Elsevier: Amsterdam, The Netherlands, 2024; pp. 135–192. [Google Scholar]
- Dai, H.; Wang, Z.; Zhao, J.; Jia, X.; Liu, L.; Wang, J.; Abbasi, H.N.; Guo, Z.; Chen, Y.; Geng, H. Modeling and Optimizing of an Actual Municipal Sewage Plant: A Comparison of Diverse Multi-Objective Optimization Methods. J. Environ. Manag. 2023, 328, 116924. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Zhang, H.; Wu, J.; Liu, W.; Fang, Y. Wastewater Treatment Process Enhancement Based on Multi-Objective Optimization and Interpretable Machine Learning. J. Environ. Manag. 2024, 364, 121430. [Google Scholar] [CrossRef] [PubMed]
- Haghdoost, S.; Niksokhan, M.H.; Zamani, M.G.; Nikoo, M.R. Optimal Waste Load Allocation in River Systems Based on a New Multi-Objective Cuckoo Optimization Algorithm. Environ. Sci. Pollut. Res. 2023, 30, 126116–126131. [Google Scholar] [CrossRef]
- Vikhar, P.A. An In-Depth Overview of Evolutionary Algorithms for Complex Optimization. Appl. Soft Comput. 2016, 55, 571–589. [Google Scholar]
- Wang, G.-G.; Zhao, X.; Li, K. Metaheuristic Algorithms: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2024. [Google Scholar]
- Nemati, M.; Zandi, Y.; Agdas, A.S. Application of a Novel Metaheuristic Algorithm Inspired by Stadium Spectators in Global Optimization Problems. Sci. Rep. 2024, 14, 3078. [Google Scholar] [CrossRef]
- Movahed, Z.P.; Kabiri, M.; Ranjbar, S.; Joda, F. Multi-Objective Optimization of Life Cycle Assessment of Integrated Waste Management Based on Genetic Algorithms: A Case Study of Tehran. J. Clean. Prod. 2020, 247, 119153. [Google Scholar] [CrossRef]
- Qiao, K.; Liang, J.; Yu, K.; Wang, M.; Qu, B.; Yue, C.; Guo, Y. A Self-Adaptive Evolutionary Multi-Task Based Constrained Multi-Objective Evolutionary Algorithm. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 7, 1098–1112. [Google Scholar] [CrossRef]
- Gen, M.; Lin, L. Genetic Algorithms and Their Applications. In Springer Handbook of Engineering Statistics; Springer: London, UK, 2023; pp. 635–674. [Google Scholar]
- Walters, G.A.; Savic, D.A. Recent Applications of Genetic Algorithms to Water System Design. In WIT Transactions on Ecology and the Environment; WIT Press: Southampton, UK, 2024; Volume 18. [Google Scholar]
- Rahmanifar, G.; Mohammadi, M.; Sherafat, A.; Hajiaghaei-Keshteli, M.; Fusco, G.; Colombaroni, C. Heuristic Approaches to Address Vehicle Routing Problem in the IoT-Based Waste Management System. Expert Syst. Appl. 2023, 220, 119708. [Google Scholar] [CrossRef]
- Wietheger, S.; Doerr, B. A Mathematical Runtime Analysis of the Non-Dominated Sorting Genetic Algorithm III (NSGA-III). In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Melbourne, Australia, 14–18 July 2024. [Google Scholar]
- Bailey, E.T.; Caldas, L. Operative Generative Design Using Non-Dominated Sorting Genetic Algorithm II (NSGA-II). Autom. Constr. 2023, 155, 105026. [Google Scholar] [CrossRef]
- Shirajuddin, T.M.; Muhammad, N.S.; Abdullah, J. Optimization Problems in Water Distribution Systems Using Non-Dominated Sorting Genetic Algorithm II: An Overview. Ain Shams Eng. J. 2023, 14, 101932. [Google Scholar] [CrossRef]
- Lukić, N.L.; Božin-Dakić, M.; Grahovac, J.A.; Dodić, J.M.; Jokić, A.I. Multi-Objective Optimization of Microfiltration of Baker’s Yeast Using Genetic Algorithm. Acta Period. Technol. 2017, 48, 211–220. [Google Scholar] [CrossRef]
- Mu’Tasim, M.A.N.; Rashid, M.F.F.A. Hybrid Flow Shop Scheduling Problem with Energy Utilization Using Non-Dominated Sorting Genetic Algorithm-III (NSGA-III) Optimization. Int. J. Automot. Mech. Eng. 2023, 20, 10862–10877. [Google Scholar]
- Tanhadoust, A.; Madhkhan, M.; Nehdi, M.L. Two-Stage Multi-Objective Optimization of Reinforced Concrete Buildings Based on Non-Dominated Sorting Genetic Algorithm (NSGA-III). J. Build. Eng. 2023, 75, 107022. [Google Scholar] [CrossRef]
- Doerr, B.; Qu, Z. A First Runtime Analysis of the NSGA-II on a Multimodal Problem. IEEE Trans. Evol. Comput. 2023, 27, 1288–1297. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, Y.; Sun, S.; Liu, T.; Shan, Y. A Comprehensive Survey on NSGA-II for Multi-Objective Optimization and Applications. Artif. Intell. Rev. 2023, 56, 15217–15270. [Google Scholar] [CrossRef]
- Rahimi, I.; Gandomi, A.H.; Nikoo, M.R.; Chen, F. A Comparative Study on Evolutionary Multi-Objective Algorithms for next Release Problem. Appl. Soft Comput. 2023, 144, 110472. [Google Scholar] [CrossRef]
- Zhou, P.; Li, H.; Chai, T. SPEA2 Based on Grid Density Search and Elite Guidance for Multi-Objective Operation Optimization of Wastewater Treatment Process. Appl. Soft Comput. 2023, 144, 110529. [Google Scholar] [CrossRef]
- Wan, L.; Deng, K.; Li, X.; Zhao, L.; Long, J. Multi-Objective Optimization Strategy for Industrial Catalytic Cracking Units: Kinetic Model and Enhanced SPEA-2 Algorithm with Economic, CO2, and SO2 Emission Considerations. Chem. Eng. Sci. 2023, 282, 119331. [Google Scholar] [CrossRef]
- Taghizade, K.; Heidari, A.; Noorzai, E. Environmental Impact Profiles for Glazing Systems: Strategies for Early Design Process. J. Archit. Eng. 2019, 25, 04019005. [Google Scholar] [CrossRef]
- Singh, J. A Review and Comparison of Two Archive Based Algorithms: SPEA2 and PAES. AIP Conf. Proc. 2023, 2819, 090003. [Google Scholar]
- Li, X.; Li, X.; Wang, K.; Yang, S. A Strength Pareto Evolutionary Algorithm Based on Adaptive Reference Points for Solving Irregular Fronts. Inf. Sci. 2023, 626, 658–693. [Google Scholar] [CrossRef]
- Papasani, A.; Devarakonda, N. A Novel Feature Selection Algorithm Using Multi-Objective Improved Honey Badger Algorithm (Mo-Hba) and Spea-Ii. J. Eng. Res. 2023, 11, 2B. [Google Scholar]
- Luo, J.; Wang, C.; Gu, Q.; Wang, Q.; Chen, L. An Adaptive Boundary-Based Selection Many-Objective Evolutionary Algorithm with Density Estimation. Appl. Intell. 2024, 54, 8761–8788. [Google Scholar] [CrossRef]
- Ren, S.; Bian, C.; Li, M.; Qian, C. Performance Analysis of SPEA2 in Multi-Objective Optimization. Swarm Evol. Comput. 2024, 86, 101203. [Google Scholar]
- Antkiewicz, M.; Myszkowski, P.B. Population-Less Genetic Algorithm? Investigation of Non-Dominated Tournament Genetic Algorithm (NTGA2) for Multi-Objective Optimization. In Proceedings of the 18th Conference on Computer Science and Intelligence Systems, Warsaw, Poland, 17–20 September 2023. [Google Scholar]
- Guo, X.; Miao, Z.-H.; Pan, Q.-K.; He, X. Hybrid Loading Situation Vehicle Routing Problem in the Context of Agricultural Harvesting: A Reconstructed MOEA/D with Parallel Populations. Swarm Evol. Comput. 2024, 91, 101730. [Google Scholar] [CrossRef]
- Chutima, P.; Prakong, C. In-House Part Supply Logistics Optimization Based on the Workforce’s Ergonomic Strain and Environmental Considerations. Int. J. Ind. Syst. Eng. 2024, 47, 271–310. [Google Scholar]
- Ni, Q.; Kang, X. A Novel Decomposition-Based Multi-Objective Evolutionary Algorithm with Dual-Population and Adaptive Weight Strategy. Axioms 2023, 12, 100. [Google Scholar] [CrossRef]
- Doerr, B.; Krejca, M.S.; Weeks, N. Proven Runtime Guarantees for How the MOEA/D: Computes the Pareto Front from the Subproblem Solutions. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Hagenberg, Austria, 14–18 September 2024. [Google Scholar]
- Chu, X.; Han, X.; Zhang, M.; Li, M. Decomposition-Based Multi-Objective Evolutionary Algorithms: Improvements and Applications. Inf. Sci. 2024, 646, 119759. [Google Scholar]
- Chu, X.; Han, X.; Zhang, M.; Li, M. Improving Decomposition-Based MOEAs for Combinatorial Optimisation by Intensifying Corner Weights. Swarm Evol. Comput. 2024, 91, 101722. [Google Scholar] [CrossRef]
- Takei, Y.; Aguirre, H.; Tanaka, K. Repeated Epsilon-Sampling for Many-Objective Optimization. In Proceedings of the 2024 IEEE Congress on Evolutionary Computation (CEC), Yokohama, Japan, 30 June–5 July 2024. [Google Scholar]
- Zheng, J.; Ning, J.; Ma, H.; Liu, Z. A Dynamic Parameter Tuning Strategy for Decomposition-Based Multi-Objective Evolutionary Algorithms. Appl. Sci. 2024, 14, 3481. [Google Scholar] [CrossRef]
- Zheng, J.; Ning, J.; Ma, H.; Liu, Z. Advances in Parameter Tuning for Decomposition-Based Evolutionary Algorithms. Inf. Sci. 2024, 663, 118120. [Google Scholar]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, M.; et al. The PRISMA 2020 Statement: An Updated Guideline for Reporting Systematic Reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef] [PubMed]
- Niu, Y.; Xu, C.; Liao, S.; Zhang, S.; Xiao, J. Multi-Objective Location-Routing Optimization Based on Machine Learning for Green Municipal Waste Management. Waste Manag. 2024, 181, 157–167. [Google Scholar] [CrossRef] [PubMed]
- Niu, Y.; Xu, C.; Liao, S.; Zhang, S.; Xiao, J. Green Municipal Waste Management: Multi-Objective Optimization Approaches. J. Clean. Prod. 2024, 425, 138660. [Google Scholar]
- Ghannadpour, S.F.; Zandieh, F.; Esmaeili, F. Optimizing Triple Bottom-Line Objectives for Sustainable Health-Care Waste Collection and Routing by a Self-Adaptive Evolutionary Algorithm: A Case Study from Tehran Province in Iran. J. Clean. Prod. 2021, 287, 125010. [Google Scholar] [CrossRef]
- Nesmachnow, S.; Rossit, D.; Toutouh, J. Comparison of Multiobjective Evolutionary Algorithms for Prioritized Urban Waste Collection in Montevideo, Uruguay. Electron. Notes Discret. Math. 2018, 69, 93–100. [Google Scholar] [CrossRef]
- Mehari, A.; Genovese, P.V. A Land Use Planning Literature Review: Literature Path, Planning Contexts, Optimization Methods, and Bibliometric Methods. Land 2023, 12, 1982. [Google Scholar] [CrossRef]
- Mehari, A.; Genovese, P.V. Land Use Optimization in Waste Management: A Review. Land Use Policy 2023, 125, 107585. [Google Scholar]
- Goel, R.; Maini, R. Improved Multi-Ant-Colony Algorithm for Solving Multi-Objective Vehicle Routing Problems. Sci. Iran. 2021, 28, 3412–3428. [Google Scholar] [CrossRef]
- Goel, R.; Maini, R. Recent Trends in Multi-Objective Optimization for Routing and Scheduling Problems. Oper. Res. Perspect. 2021, 8, 100224. [Google Scholar]
- Martin, I.; Wibisono, E. A Proposed Taxonomy for Literature Review in Multi-Objective Vehicle Routing Problems. AIP Conf. Proc. 2024, 2928, 020007. [Google Scholar] [CrossRef]
- Martin, I.; Wibisono, E. Optimization Methods for Green Vehicle Routing: A Comprehensive Review. J. Clean. Prod. 2024, 382, 135289. [Google Scholar]
- Martin, I.; Wibisono, E. Optimization Techniques in Vehicle Routing for Sustainable Logistics. Sustainability 2024, 16, 1420. [Google Scholar]
- Matl, P.; Hartl, R.F.; Vidal, T. Leveraging Single-objective Heuristics to Solve Bi-objective Problems: Heuristic Box Splitting and Its Application to Vehicle Routing. Networks 2019, 73, 382–400. [Google Scholar] [CrossRef]
- Goel, R.; Maini, R. Advancements in Multi-Objective Optimization for Vehicle Routing. Transp. Res. Part E Logist. Transp. Rev. 2021, 147, 102224. [Google Scholar]
- Xiong, J.; Ng, T.S.A.; Wang, S. An Optimization Model for Economic Feasibility Analysis and Design of Decentralized Waste-to-Energy Systems. Energy 2016, 101, 239–251. [Google Scholar] [CrossRef]
- Qiao, X.; Ding, J.; She, C.; Mao, W.; Zhang, A.; Feng, B.; Xu, Y. A Metaheuristic Multi-Objective Optimization of Energy and Environmental Performances of a Waste-to-Energy System Based on Waste Gasification Using Particle Swarm Optimization. Energy Convers. Manag. 2024, 317, 118844. [Google Scholar] [CrossRef]
- Qiao, X.; Ding, J.; She, C.; Mao, W.; Zhang, A.; Feng, B.; Xu, Y. Optimization of Waste Gasification Systems Using Hybrid Metaheuristics. Renew. Energy 2024, 208, 121778. [Google Scholar]
- Wu, M.; Du, P.; Jiang, M.; Goh, H.H.; Zhu, H.; Zhang, D.; Wu, T. An Integrated Energy System Optimization Strategy Based on Particle Swarm Optimization Algorithm. Energy Rep. 2022, 8, 679–691. [Google Scholar] [CrossRef]
- Fernández-Gonzalez, J.-M.; Grindlay, A.L.; Serrano-Bernardo, F.; Rodríguez-Rojas, M.I.; Zamorano, M. Economic and Environmental Review of Waste-to-Energy Systems for Municipal Solid Waste Management in Medium and Small Municipalities. Waste Manag. 2017, 67, 360–374. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Gonzalez, J.-M.; Grindlay, A.L.; Serrano-Bernardo, F.; Rodríguez-Rojas, M.I.; Zamorano, M. Municipal Waste-to-Energy Options: Economic and Environmental Perspectives. Renew. Sustain. Energy Rev. 2017, 76, 537–545. [Google Scholar]
- Esfilar, R.; Bagheri, M.; Golestani, B. Technoeconomic Feasibility Review of Hybrid Waste to Energy System in the Campus: A Case Study for the University of Victoria. Renew. Sustain. Energy Rev. 2021, 146, 111190. [Google Scholar] [CrossRef]
- Esfilar, R.; Bagheri, M.; Golestani, B. Economic Assessments of Campus-Scale Hybrid Waste-to-Energy Systems. J. Environ. Manag. 2021, 287, 112345. [Google Scholar]
- Tirkolaee, E.B.; Mahdavi, I.; Esfahani, M.M.S.; Weber, G.-W. A Robust Green Location-Allocation-Inventory Problem to Design an Urban Waste Management System under Uncertainty. Waste Manag. 2020, 102, 340–350. [Google Scholar] [CrossRef]
- Adeleke, O.J.; Olukanni, D.O. Facility Location Problems: Models, Techniques, and Applications in Waste Management. Recycling 2020, 5, 10. [Google Scholar] [CrossRef]
- Rabbani, M.; Mokarrari, K.R.; Akbarian-saravi, N. A Multi-Objective Location Inventory Routing Problem with Pricing Decisions in a Sustainable Waste Management System. Sustain. Cities Soc. 2021, 75, 103319. [Google Scholar] [CrossRef]
- Wu, M.; Du, P.; Jiang, M.; Goh, H.H.; Zhu, H.; Zhang, D.; Wu, T. Waste-to-Energy Optimization in Integrated Urban Energy Systems. Renew. Energy 2022, 195, 1266–1275. [Google Scholar]
- Liang, Z.; Zou, Y.; Zheng, S.; Yang, S.; Zhu, Z. Dynamic Multi-Objective Optimization: A Survey of Algorithms and Applications. IEEE Trans. Evol. Comput. 2021, 25, 837–857. [Google Scholar]
- Liang, Z.; Zou, Y.; Zheng, S.; Yang, S.; Zhu, Z. Dynamic Multi-Objective Evolutionary Algorithms: Methods and Applications. Comput. Oper. Res. 2021, 134, 105381. [Google Scholar]
- Celik Turkoglu, D.; Erol Genevois, M. A Comparative Survey of Service Facility Location Problems. Ann. Oper. Res. 2020, 292, 399–468. [Google Scholar] [CrossRef]
- Prata, J.C.; Silva, A.L.P.; Duarte, A.C.; Rocha-Santos, T. The Road to Sustainable Use and Waste Management of Plastics in Portugal. Front. Environ. Sci. Eng. 2022, 16, 5. [Google Scholar] [CrossRef]
- de Campos, V.A.F.; Silva, V.B.; Cardoso, J.S.; Brito, P.S.; Tuna, C.E.; Silveira, J.L. A Review of Waste Management in Brazil and Portugal: Waste-to-Energy as Pathway for Sustainable Development. Renew. Energy 2021, 178, 802–820. [Google Scholar] [CrossRef]
- Costa, M.; Madureira, R.C.; Dias-Ferreira, C. Smart Waste Management: A Look on Portugal towards the SDGs. In WASTES: Solutions, Treatments and Opportunities IV; CRC Press: Boca Raton, FL, USA, 2023; pp. 177–183. [Google Scholar]
- Costa, M.; Madureira, R.C.; Dias-Ferreira, C. Circular Economy Indicators for Urban Waste Management: Evidence from Portugal. Sustain. Prod. Consum. 2023, 37, 110–123. [Google Scholar]
- Di Salvatore, S.; Magatti, G.; Acciarri, M.; Rossetti, M.; da Costa, L.P.; Ribeiro, I. Solid Waste Management Approach at the University through Living Labs and Communication Strategies: Case Studies in Italy and Portugal. Sustainability 2022, 14, 5240. [Google Scholar] [CrossRef]
- Pinto, F.; Couto, C.; Gomes, D.; Oliveira, J.; Silva, R.; Oliveira, D. Sustainability Reporting in the Portuguese Municipalities: An Empirical Analysis of the 25 Largest Municipalities. In Proceedings of the International Conference on Multidimensional Sustainability: Transitions and Convergences, Vila Nova de Gaia, Portugal, 29–30 September 2022. [Google Scholar]
- Pinto, F.; Couto, C.; Gomes, D.; Oliveira, J.; Silva, R.; Oliveira, D. Circular Economy Practices in Portuguese Municipalities: A Case Study. J. Environ. Manag. 2022, 317, 115476. [Google Scholar]
- Cunha Ferreira, D.; Cunha Marques, R.; Pedro, M.I.; Amaral, C. Economic Inefficiency Levels of Urban Solid Waste Management Services in Portugal. Sustainability 2020, 12, 4170. [Google Scholar] [CrossRef]
- Cunha Ferreira, D.; Cunha Marques, R.; Pedro, M.I.; Amaral, C. Economic Analysis of Inefficiency Sources in Urban Solid Waste Services. Waste Manag. 2020, 105, 523–532. [Google Scholar]
- Amaral, C.; Pedro, M.I.; Ferreira, D.C.; Marques, R.C. Performance and Its Determinants in the Portuguese Municipal Solid Waste Utilities. Waste Manag. 2022, 139, 70–84. [Google Scholar] [CrossRef] [PubMed]
- Amaral, C.; Pedro, M.I.; Ferreira, D.C.; Marques, R.C. Factors Influencing the Efficiency of Municipal Solid Waste Utilities: Evidence from Portugal. Util. Policy 2022, 78, 101446. [Google Scholar]
- Cruz, N.; Cota, N.; Tremoceiro, J. Lorawan and Urban Waste Management—A Trial. Sensors 2021, 21, 2142. [Google Scholar] [CrossRef]
- Cruz, N.; Cota, N.; Tremoceiro, J. Integrating LoRaWAN Sensors in Urban Waste Collection: Opportunities and Limitations. Smart Cities 2021, 4, 761–776. [Google Scholar]
- Feiz, R.; Johansson, M.; Lindkvist, E.; Moestedt, J.; Påledal, S.N.; Ometto, F. The Biogas Yield, Climate Impact, Energy Balance, Nutrient Recovery, and Resource Cost of Biogas Production from Household Food Waste—A Comparison of Multiple Cases from Sweden. J. Clean. Prod. 2022, 378, 134536. [Google Scholar] [CrossRef]
- Ishola, M.; Tilli, C. Waste-to-Energy Solutions in Uppsala, Sweden. In Renewable Energy and Sustainable Buildings: Selected Papers from the World Renewable Energy Congress WREC 2018; Springer: Berlin, Germany, 2020. [Google Scholar]
- Feiz, R.; Johansson, M.; Lindkvist, E.; Moestedt, J.; Påledal, S.N.; Ometto, F. Life Cycle Assessment of Municipal Solid Waste Management Systems: A Review. Waste Manag. 2022, 140, 189–202. [Google Scholar]
- Feiz, R.; Johansson, M.; Lindkvist, E.; Moestedt, J.; Påledal, S.N.; Ometto, F. Municipal Waste Biogas Systems: Opportunities and Challenges. Bioresour. Technol. 2022, 360, 127605. [Google Scholar]
- Alrawahi, A.S.; Lee, K.; Lotfi, A. AMACoT: A Marketplace Architecture for Trading Cloud of Things Resources. IEEE Internet Things J. 2019, 7, 2483–2495. [Google Scholar] [CrossRef]
- Barbir, J.; Lingos, A.; Foschi, E.; Stasiskiene, Z.; Skanavis, C.; Fletcher, C.; Leal Filho, W. Assessing the Readiness of Greek Municipalities to Manage Bioplastics in Municipal Waste Management Streams. Discov. Sustain. 2024, 5, 222. [Google Scholar] [CrossRef]
- Barbir, J.; Lingos, A.; Foschi, E.; Stasiskiene, Z.; Skanavis, C.; Fletcher, C.; Leal Filho, W. Managing Bioplastics in Municipal Waste: Greek Municipalities’ Readiness. Sustain. Mater. Technol. 2024, 40, e00735. [Google Scholar]
- Lekkas, D.-F.; Zorpas, A.A.; Naddeo, V.; Voukkali, I.; Klontza, D.E. Navigating the Environmental Frontiers: Reflections on CEST 2023 Conference in Athens. Waste Manag. Res. 2024, 42, 593–594. [Google Scholar] [CrossRef]
- Zajemska, M.; Korombel, A.; Ławińska, O. Risk Factors for Poland to Achieve the European Commission’s Recycling and Landfill Targets and Their Effects on Waste-to-Energy Conversion: A Review. Energies 2024, 17, 1171. [Google Scholar] [CrossRef]
- Albizzati, P.F.; Foster, G.; Gaudillat, P.; Manfredi, S.; Tonini, D. A Model to Assess the Environmental and Economic Impacts of Municipal Waste Management in Europe. Waste Manag. 2024, 174, 605–617. [Google Scholar] [CrossRef]
- Albizzati, P.F.; Foster, G.; Gaudillat, P.; Manfredi, S.; Tonini, D. Integrated Strategies for Sustainable Waste Management in Europe. J. Clean. Prod. 2024, 425, 138739. [Google Scholar]
- Vomáčka, V. Calibrating Green Compliance: EU Framework for Effective, Proportionate and Dissuasive Penalties in Environmental Protection. ERA Forum 2024, 25, 281–299. [Google Scholar] [CrossRef]
- Deb, K.; Fleming, P.; Jin, Y.; Miettinen, K.; Reed, P.M. Key Issues in Real-World Applications of Many-Objective Optimisation and Decision Analysis. In Many-Criteria Optimization and Decision Analysis: State-of-the-Art, Present Challenges, and Future Perspectives; Springer: Berlin, Germany, 2023; pp. 29–57. [Google Scholar]
- He, C.; Zhang, Y.; Gong, D.; Ji, X. A Review of Surrogate-Assisted Evolutionary Algorithms for Expensive Optimization Problems. Expert Syst. Appl. 2023, 217, 119495. [Google Scholar] [CrossRef]
- Czekała, W.; Drozdowski, J.; Łabiak, P. Modern Technologies for Waste Management: A Review. Appl. Sci. 2023, 13, 8847. [Google Scholar] [CrossRef]
- Czekała, W.; Drozdowski, J.; Łabiak, P. Recent Advances in Sustainable Waste Treatment Technologies. Renew. Sustain. Energy Rev. 2023, 176, 113232. [Google Scholar]
- Khoshsepehr, Z.; Alinejad, S.; Alimohammadlou, M. Exploring Industrial Waste Management Challenges and Smart Solutions: An Integrated Hesitant Fuzzy Multi-Criteria Decision-Making Approach. J. Clean. Prod. 2023, 420, 138327. [Google Scholar] [CrossRef]
- Khoshsepehr, Z.; Alinejad, S.; Alimohammadlou, M. Industrial Waste Management Challenges in Iran: A Review. Environ. Sci. Pollut. Res. 2023, 30, 113572–113590. [Google Scholar]
- Zhang, W.; Xiao, G.; Gen, M.; Geng, H.; Wang, X.; Deng, M.; Zhang, G. Enhancing Multi-Objective Evolutionary Algorithms with Machine Learning for Scheduling Problems: Recent Advances and Survey. Front. Ind. Eng. 2024, 2, 1337174. [Google Scholar] [CrossRef]
- Pătrăușanu, A.; Florea, A.; Neghină, M.; Dicoiu, A.; Chiș, R. A Systematic Review of Multi-Objective Evolutionary Algorithms Optimization Frameworks. Processes 2024, 12, 869. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).