Abstract
This study evaluates machine learning-based methods for retrieving thin Arctic sea ice thickness (SIT) from L-band radiometry, using data from the European Space Agency’s (ESA) Soil Moisture and Ocean Salinity (SMOS) satellite. In addition to the operational ESA product, three alternative approaches are assessed: a Random Forest (RF) algorithm, a Convolutional Neural Network (CNN) that incorporates spatial coherence, and a Long Short-Term Memory (LSTM) neural network designed to capture temporal coherence. Validation against in situ data from the Beaufort Gyre Exploration Project (BGEP) moorings and the ESA SMOSice campaign demonstrates that the RF algorithm achieves robust performance comparable to the ESA product, despite its simplicity and lack of explicit spatial or temporal modeling. The CNN exhibits a tendency to overestimate SIT and shows higher dispersion, suggesting limited added value when spatial coherence is already present in the input data. The LSTM approach does not improve retrieval accuracy, likely due to the mismatch between satellite resolution and the temporal variability of sea ice conditions. These results highlight the importance of L-band sea ice emission modeling over increasing algorithm complexity and suggest that simpler, adaptable methods such as RF offer a promising foundation for future SIT retrieval efforts. The findings are relevant for refining current methods used with SMOS and for developing upcoming satellite missions, such as ESA’s Copernicus Imaging Microwave Radiometer (CIMR).
1. Introduction
Sea ice is a key component of the Earth system. Its extent undergoes annual periodicity and covers almost 7% of the Earth’s surface at its maximum extent in September, mainly at the poles. It has a crucial effect on climate change, as it participates in the so-called ice–albedo feedback loop [1]. Arctic sea ice has been significantly decreasing in recent decades [2], also suffering a shift to younger and thinner ice [3].
Since the launch of the first Earth Observation (EO) satellites in the early 1970s, passive microwave radiometers have been used to observe sea ice. The European Space Agency (ESA) mission Soil Moisture and Ocean Salinity (SMOS) [4,5], initiated in 2009, and NASA’s Advanced Microwave Scanning Radiometer (AMSR) series, which has operated on different satellites from 2002 to the present, as well as the Soil Moisture Active Passive (SMAP) [6] mission, launched in 2015, are key contributors. In particular, the focus of this study is on passive L-band radiometers such as SMOS, working at 1.4 GHz with a penetration depth of up to 1 m or even more in low-salinity sea ice.
Currently, two distinct algorithms for estimating Arctic thin sea ice thickness from SMOS measurements during the non-melting period (October to April) exist. The first, distributed by the European Space Agency (ESA), is a semi-empirical algorithm developed by the Alfred Wegener Institute (AWI) as described in [7,8]. However, a significant drawback is its inability to consider the presence of snow on top of sea ice. This limitation is critical due to the substantial impact of snow on emitted L-band radiation [9] and subsequent thickness retrieval processes. The second algorithm, from the University of Bremen (UB) and detailed in [10], adopts an empirical approach. Despite this, a notable limitation of the UB product is its restricted sensitivity, reaching only up to 0.5 m. While the UB product explicitly limits the sea ice thickness retrieval, the AWI product does not have a clearly defined upper limit, with sensitivity typically ranging between 0.5 and 1.5 m depending on sea ice conditions.
Other emerging methodologies include the use of Global Navigation Satellite System Reflectometry (GNSS-R), which, beyond its previous applications for retrieving various geophysical parameters, has also been explored for sea ice applications. Recent studies have shown its potential to detect sea ice and estimate its thickness, although these results have so far only been demonstrated in simulations [11,12]. Nevertheless, GNSS-R remains promising as a valuable complement to passive L-band measurements in the future.
Artificial intelligence (AI) holds the potential to transform the processing and analysis of Earth Observation (EO) data acquired through remote sensing. AI offers the capability to improve the analysis of these data, enhancing our ability to monitor and predict the evolution of many geophysical variables. Recent efforts to retrieve sea ice parameters from satellite observations using artificial intelligence have increasingly focused on applying machine learning techniques to passive microwave data. One of the earlier examples is found in [13], where a neural network was used to try to estimate snow depth over sea ice using AMSR2 and SMOS data. Similarly, ref. [14] applied two machine learning algorithms to retrieve sea ice thickness from a combination of TechDemoSat-1 (TDS-1) and SMOS observations. Ref. [15] developed an ensemble Convolutional Neural Network (CNN) to retrieve daily sea ice thickness from AMSR2 data. Likewise, ref. [16,17] used a combination of frequencies ranging from 1.4 to 36 GHz, applying AI-based methodologies to estimate and analyze sea ice thickness and volume trends. Beyond SMOS and AMSR2, ref. [18] used a neural network to retrieve sea ice thickness from FSSCat nanosatellite data [19]. Meanwhile, ref. [20,21] investigated machine learning approaches for sea ice sensing using data from a C-band Synthetic Aperture Radar (SAR) sensor like Sentinel-1.
An application of machine learning to Arctic sea ice thickness retrieval from SMOS observations was presented in [22]. That study employed two decision-tree-based algorithms—Random Forest (RF) and Gradient Boosting (GB)—within a supervised learning framework. These algorithms were trained on data derived from maps generated through model inversion. The results were promising, demonstrating good agreement with ESA’s sea ice thickness product and achieving improved validation against in situ datasets. Building on this foundation, the objective of this work is to assess the performance of deep learning methods in enhancing retrieval accuracy. Specifically, it extends the methodology by implementing a Convolutional Neural Network (CNN) and a Long Short-Term Memory (LSTM) neural network. These approaches represent significant advancements in data processing: the CNN leverages spatial coherence by treating input variables as maps, while the LSTM captures temporal coherence by utilizing sequential information from consecutive observations.
Since the training dataset is entirely derived from a physical emission model due to the lack of sufficient in situ data, the performance of the ML algorithms is ultimately constrained by the accuracy and assumptions of that model. Therefore, this study focuses on evaluating the ability of different architectures to learn and approximate its behavior. To assess their performance, the operational ESA sea ice thickness product is included as a baseline for comparison. Accordingly, the main contributions of this work are threefold: (1) a comparative evaluation of three ML architectures (RF, CNN, LSTM) for retrieving sea ice thickness from L-band radiometry; (2) an assessment of how these approximations perform on real-world satellite data; and (3) a benchmark comparison against the ESA product to highlight strengths and limitations relative to existing retrieval approaches.
The paper is organized as follows: Section 2 describes the various data sources used as input, the generation of the training dataset, and the datasets employed for validation. Section 3 outlines the different algorithmic approaches. The results of the assessment are presented in Section 4, followed by a discussion in Section 5. Finally, the conclusions of the study are summarized in Section 6.
2. Data Collection and Processing
This section describes the datasets used both as input variables for the proposed algorithms and as in situ observations for their validation. Additionally, it provides details on data preparation and the processing steps undertaken to generate the training dataset.
2.1. Input Datasets
The input variables consist of a combination of satellite-derived products and reanalysis model outputs, providing comprehensive coverage of Arctic sea ice conditions. The satellite datasets include the ESA’s SMOS sea ice thickness product, from which only the TB is extracted and used as input, and a sea ice surface temperature data product. Additionally, a reanalysis model provides the required information about sea ice and seawater properties. The final subsection explains how these variables are processed for use as input for the proposed methodology.
2.1.1. ESA SMOS Sea Ice Thickness Product
The SMOS satellite carries the Microwave Imaging Radiometer Aperture Synthesis (MIRAS) payload, which measures brightness temperatures in full polarization at L-band with incidence angles ranging from 0° to 65°, including all four Stokes parameters [23]. The instrument provides global coverage every three days and daily coverage in the polar regions. The hexagonal two-dimensional snapshots taken by the MIRAS instrument have a spatial dimension of approximately 1200 km across and can capture brightness temperature every 1.2 s, with spatial resolution varying from about 35 km at nadir view to over 50 km at higher incidence angles. Each snapshot measures one of the Stokes components in the antenna reference frame, including horizontally (TBH) and vertically (TBV) polarized brightness temperatures. The intensity is obtained by averaging the horizontally and vertically polarized brightness temperatures. Moreover, the brightness temperature (TB) intensity of the signal over sea ice remains relatively consistent regardless of the angle at which it is measured within the – range; therefore, it is computed as an average of this interval. The daily averaged brightness temperature intensity in the Arctic region is interpolated using a nearest neighbor algorithm and gridded onto the National Snow and Ice Data Center (NSIDC) polar stereographic projection with a grid resolution of 12.5 km.
The SMOS L3 Sea Ice Thickness product is produced by AWI and distributed by ESA, and provides information on sea ice thickness in the Arctic region from October to April, covering the period from 2010 to the present. It was first described in [7,8]. The sea ice thickness is determined using an iterative retrieval algorithm that incorporates a thermodynamic sea ice model and a three-layer radiative transfer model. The radiative transfer model calculates the emissivity of the sea ice layer and the underlying seawater, and brightness temperatures are derived from the emissivity and physical temperatures of the sea ice and seawater. The bulk ice temperature is estimated using a thermodynamic model, which utilizes the 2 m air temperature from atmospheric reanalysis data as an input parameter, while the bulk ice salinity is computed from an empirical relation described in [24]. The retrieval algorithm also accounts for variations in ice thickness within the SMOS spatial resolution by using a statistical thickness distribution function based on high-resolution ice thickness measurements from NASA’s Operation IceBridge (OIB) campaign.
In this work, the brightness temperature (TB) intensity maps measured by SMOS are taken from the ESA/AWI SMOS sea ice thickness product (https://earth.esa.int/eogateway/catalog/smos-l3-sea-ice-thickness, accessed on 24 July 2025) and used as input for the algorithms. Consequently, all processing details related to the TB, including the handling of the angular distribution of satellite measurements, are described in the product’s Algorithm Theoretical Basis Document (ATBD, [25]).
2.1.2. Surface Temperature Satellite Product
The Arctic Ocean-Sea and Ice Surface Temperature Reprocessed product [26], produced by the Danish Meteorological Institute (DMI) and distributed by the Copernicus Marine Service (CMEMS), provides information on Arctic sea and ice surface temperatures. These data are derived from reprocessed observations obtained through the Advanced Very-High-Resolution Radiometer (AVHRR), the Advanced Along Track Scanning Radiometers (AATSR), and the Sea and Land Surface Temperature Radiometer (SLSTR). These observations come from different sources, including the ESA Climate Change Initiative (CCI) project, the Copernicus Climate Change Service (C3S) project, and the Arctic & Antarctic Ice Surface Temperatures from Thermal Infrared Satellite Sensors (AASTI) dataset. The product provides a daily interpolated field at a resolution of 0.05 degrees, encompassing surface temperatures in the ocean, sea ice, and the marginal ice zone. The computation of surface temperature employs the optimal interpolation method, with the previous day’s value serving as the initial guess field.
In this work, a linear temperature gradient within the ice is assumed, as supported by findings in [27]. Consequently, the calculation of the bulk ice temperature () is determined by the following expression:
where is the surface temperature obtained from the satellite product, and is the seawater temperature, for which a typical value for the Arctic of −1.8 °C is assumed.
2.1.3. Arctic Ocean Physics Reanalysis Model
The Arctic Ocean Physics Reanalysis model, produced by the Nansen Environmental and Remote Sensing Center (NERSC) and distributed by CMEMS [28], provides physical variables derived from the reanalysis model TOPAZ (version 4b). This model assimilates a diverse set of observations, including sea level anomalies from satellite altimeters, sea surface temperature from the Operational Sea Surface Temperature and Sea Ice Analysis (OSTIA), in situ temperature and salinity data from hydrographic cruises and moorings, sea ice concentration from OSI-SAF, CS2SMOS ice thickness data, and sea surface salinity from the Barcelona Expert Center (BEC) utilizing SMOS satellite data.
In this work, the seawater salinity, sea ice thickness, and snow depth variables are obtained from this model. To compute the sea ice salinity, an empirical formula from [24] is used:
where is the seawater salinity and is the sea ice thickness in cm, both obtained from the Arctic Ocean Physics Reanalysis model. The growth rate coefficient, denoted as a, ranges between 0.35 and 0.5; , the salinity ratio of the bulk ice salinity at the end of the ice growth season, is also crucial for determining the empirical equation for the sea ice salinity. Ref. [24] proposes using a value of 0.5 for a and 0.13 for . However, ref. [29] suggests using 0.175 for instead of 0.13 after comparing Equation (2) with observed data in the Arctic.
Finally, the determination of the snow presence variable is based on a straightforward assumption: if the snow thickness variable derived from TOPAZ is positive, it is inferred that snow is present; conversely, if it is zero, snow is considered absent.
2.2. Training Dataset Generation Through Model-Based Simulation
Available data for the Arctic region are extremely limited. Due to the absence of a comprehensive dataset on thin sea ice thickness, it becomes necessary to create one through the use of sea ice emission modeling. The Burke emission model [30], incorporating the Vant formulation for ice permittivity [31], is employed in an inverted manner to generate realistic scenarios of Arctic sea ice thickness distributions. The goal is to replicate these situations as accurately as possible. All variables, i.e., the SMOS TB, the sea ice temperature and salinity, and the snow presence, are first regridded to the 12.5 km × 12.5 km NSIDC Polar Stereographic grid. This workflow for generating the training dataset is summarized in Figure 1. It is noteworthy that the sensitivity of brightness temperature to ice thickness in this frequency band is strongly influenced by ice conditions, specifically temperature and salinity. To avoid imposing an artificial training threshold, the maximum thickness that can be retrieved (the point at which brightness temperature saturation begins) is computed for each configuration of ice conditions. Subsequently, the thickness derived from the model inversion is compared to this maximum thickness. If the latter is smaller, the inverted solution is adjusted to match this maximum thickness.
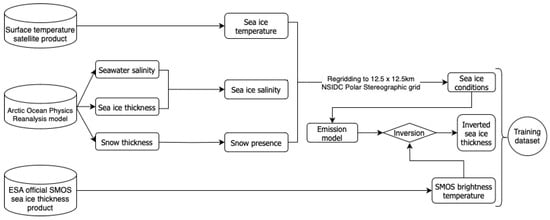
Figure 1.
Diagram of the methodology’s workflow. The variables extracted from different sources are input to invert an emission model and simulate the sea ice thickness distribution.
The accuracy of this model-based simulation fundamentally depends on the performance of the L-band sea ice emission modeling. However, it is currently not possible to quantify its precision due to the lack of Arctic-wide ground truth observations. The Burke model, originally developed for soil applications, has been widely adopted as an incoherent approach for simulating sea ice emission. Alternatively, a coherent approach could be considered [32], since coherence effects may arise when two or more interfaces exist within a plane-parallel medium, allowing an electromagnetic plane wave to interfere with its reflected counterpart [10]. Nevertheless, these effects are generally assumed to be averaged out over the satellite footprint, and to date, no significant influence has been confirmed. More complex radiative transfer models, such as the Snow Microwave Radiative Transfer model (SMRT, [33]), which account for internal scattering within the medium, are not necessary in this context, as such effects are negligible at L-band frequencies. The main source of uncertainty in modeling sea ice emission lies in the dielectric constant. As discussed in [27,34], the Vant formulation is comparable to theoretical models that treat sea ice as a mixture of pure ice and brine. The brine component, with its variable shapes and properties, plays a critical role in the emission process. However, there is still no consensus on which permittivity formulation is the most accurate, as it depends on the growth conditions of the sea ice, information that is not available during satellite-based sea ice thickness retrieval. Nonetheless, the combination of the Burke model with the Vant permittivity formulation appears to be a robust choice [34], capable of realistically reproducing the L-band emission of snow-covered sea ice across the Arctic.
Ultimately, the training dataset is composed of maps generated through the model-based simulation. All samples are extracted from model output maps covering two complete freeze-up seasons (15 October to 15 April in 2019–2020 and 2020–2021). Specifically, the initial dataset consisted of 366 Arctic-wide maps, containing a total of 199,385,088 valid pixels. After removing duplicates, the data were randomly shuffled. Furthermore, for each specific approach, the volume of training data was reduced through trial and error, in order to optimize both computational resources and model performance. The exact number of samples used in each case is provided in the corresponding subsections of Section 3. The dataset was not divided into separate training and testing subsets. This is because the performance is assessed exclusively using independent in situ measurements, as described in Section 2.3, and the corresponding results are presented in Section 4. No internal validation set was used, as the term “validation” here refers to this comparison with ground-truth datasets. The input and output variables of the training dataset are summarized in Table 1.

Table 1.
Description of input and output variables in the training dataset.
2.3. Validation Datasets
The in situ data used in the validation are based on measurements from moored sensors at two locations in the Arctic Ocean, along with data from a campaign conducted in the Barents Sea in 2014, which unexpectedly—for the time of the year—encountered thin sea ice.
2.3.1. BGEP Mooring Data
The Upward-Looking Sonar (ULS) mooring buoys within the Beaufort Gyre Exploration Project (BGEP) are specifically designed for measuring the sea ice draft, representing the portion of sea ice submerged underwater. Consequently, to derive the total thickness of sea ice, a conversion is necessary. Following the approach outlined in [35], an empirical factor of 1.136 is applied to the ice draft to obtain the total thickness. This coefficient was determined through an empirical analysis that included nearly 400 sea ice drillings conducted in the Fram Strait [36]. The BGEP ULS data, consisting of daily averages of sea ice thickness from three mooring instruments situated within the Beaufort Gyre, serve as one of the datasets for validating the methodology.
2.3.2. Barents 2014: ESA SMOSice Campaign
The ESA SMOSice campaign took place in March 2014 in the Barents Sea ice marginal zone, specifically on newly formed thin sea ice in the south-east of Svalbard. It includes measurements collected by a helicopter operating from RV Lance and the research aircraft Polar 5 [37]. Sea ice thickness was determined utilizing an electromagnetic induction system positioned at the bow of RV Lance (SEM), as well as another EM system towed beneath the helicopter (HEM). Furthermore, a Riegl VQ-580 laser scanner (ALS) mounted on the Polar 5 aircraft was used to measure the sea ice freeboard, which was later converted to sea ice thickness by assuming hydrostatic equilibrium. All these data have been regridded to the ESA SMOS sea ice thickness product 12.5 km grid using the arithmetic average calculated with GMT blockmean [38], courtesy of Dr. Lars Kaleschke.
3. Methodology
This study introduces approaches to sea ice thickness estimation that incorporate both spatial and temporal coherence into the modeling process. Spatial coherence is achieved by utilizing maps as input data, allowing the influence of neighboring pixels to be considered, while temporal coherence is addressed by including data from the previous day to enhance predictions of current conditions. The primary objective is to evaluate and determine the most effective approach among the proposed methods, leaving uncertainty computation as a focus for future work. In previous research [22], Random Forest (RF) and Gradient Boosting (GB) algorithms were trained using a pixel-by-pixel methodology. Although these models demonstrated strong agreement with ESA’s sea ice thickness product and showed improved correlation with reduced error when validated against in situ datasets, this approach inherently breaks the spatial and temporal continuity present in the original data. In reality, the data exhibit clear spatial and temporal dependencies, and failing to account for them may limit the physical consistency of the predictions. Therefore, this study addresses a necessary step: evaluating whether preserving spatial coherence (as with the CNN) or temporal continuity (as with the LSTM) leads to more physically meaningful and accurate sea ice thickness retrievals. For the three proposed approaches, the input variables are prepared as detailed in Section 2.2, with some specific modifications for each approach that are described below. It is important to note that although sea ice concentration (SIC) is indeed a major source of uncertainty in sea ice thickness retrievals from L-band radiometry, it is not explicitly included in this assessment, as the comparison is restricted to locations where the ESA product provides valid thickness values. This product assumes 100% SIC, justified by the fact that most ice-covered areas in winter have SIC > 90%, and that uncertainties in SIC products could introduce larger errors than the underestimation caused by assuming full ice cover [7,8]. Therefore, to ensure a fair comparison, no SIC correction is applied in this study.
Three different machine learning algorithms are evaluated, but they all rely on the same methodology and use the same input and output variables, which are described in Section 2.1 and summarized in Figure 1. Specifically, the four input variables are SMOS brightness temperature, sea ice temperature, sea ice salinity, and snow presence. The output variable is sea ice thickness, which, during the training phase, corresponds to the values derived from the inversion of the emission model, as detailed in Section 2.2.
3.1. Pixel-by-Pixel Approach: Random Forest and Gradient Boosting
Focusing on supervised learning, specifically within the realm of regression methods, the machine learning algorithms chosen for this task include Random Forest (RF, [39]) and Gradient Boosting (GB, [40]). These algorithms serve as more robust extensions of decision trees, sharing numerous similarities but diverging in their approaches to tree construction and combination. Both algorithms are configured with 50 estimators, a reasonable choice after experimenting with other options ranging from 10 to 1000. Following thorough testing, no further hyperparameters are fine-tuned as there is no discernible improvement in the results. Individual data points are extracted from comprehensive Arctic sea ice thickness distribution maps and fed into these algorithms for training. Therefore, this approach is named pixel-by-pixel, as training is performed considering individual values within the distribution. The training dataset is composed of 100,000 pixels extracted from the maps of each day, after removing the duplicates, from 15 October 2019 to 15 April 2020 and from 15 October 2020 to 15 April 2021. Both RF and GB algorithms provide similar results, but in this work, the RF is selected to be assessed with the other approaches. The use of a decision tree-based method enables an assessment of feature importance in determining the algorithm’s output. In this specific case, the feature importances are 94.13%, 4.33%, 1.11%, and 0.43% for SMOS TB, sea ice temperature, sea ice salinity, and snow presence, respectively. The TB is the dominant factor influencing the results, which aligns with its high variability compared to the other inputs. Sea ice salinity tends to stabilize around a value of 5 after the initial freeze-up [41], and snow presence exhibits limited variability, as a snow layer is present in almost all pixels. Nevertheless, the inclusion of snow presence remains crucial, as it has a clear impact on the measured TB [9].
3.2. Spatially Coherent Approach: Convolutional Neural Network
Convolutional Neural Networks (CNNs; [42]) are a class of deep learning neural networks primarily designed to process and analyze visual data. In this work, we aim to leverage their potential to deal with images and introducing spatial coherence into the algorithm. Sea ice pixels are not independent of their neighbors; similar conditions should lead to similar thickness distributions. All variables in the selected grid are arrays with dimensions of 896 × 608. The convolutional layers use 3 × 3 kernels with padding to preserve the dimensional integrity of the variables throughout the network architecture.
After hyperparameter tuning, the batch size was fixed at 64 with 200 training epochs. The optimal combination of layers and filters for each convolution is presented in Table 2. Each convolutional layer contains 6, 12, or 24 filters of size 3 × 3 applied to the input image. The ReLu activation function introduces non-linearity, and when combined with “same” padding, ensures that the spatial dimensions of the output feature maps remain identical to those of the input. Batch normalization is applied after each convolutional layer, normalizing the activations from the previous layer to help stabilize and accelerate the training process. The final convolutional layer contains a single filter of size 3 × 3. The linear activation function indicates that no activation function is applied to the output, making this layer perform essentially a linear transformation. The training dataset is conformed by 181 maps extracted from two periods: 15 October 2019 to 15 April 2020, and 15 October 2020 to 15 April 2021.

Table 2.
Layers of the Convolutional Neural Network (CNN) designed for the spatial-coherence approach.
3.3. Temporally Coherent Approach: Long Short-Term Memory Neural Networks
Despite the robust performance that can be achieved with the CNN by including its inherent spatial coherence, the temporal coherence should be explored. Therefore, the Long Short-Term Memory (LSTM; [43]) neural network structure is implemented. LSTMs are a specialized type of recurrent neural network (RNN) designed to effectively capture and learn temporal dependencies in sequential data by incorporating a memory cell. Intuitively, sea ice evolution has a clear temporal component; the present day prediction should be linked to previous day conditions. Therefore, for this approach, the dataset is shifted in order to predict the sea ice thickness distribution accounting for the previous day information. However, since the input for this approach is 1D, this methodology works pixel-by-pixel, so no spatial component is included.
The architecture consists of three LSTM layers, summarized in Table 3. All of these layers use a hyperbolic tangent activation function and a sigmoid recurrent activation function to control the flow of information through the cell state. The output of these layers is passed as a sequence to the next layer, except for the last layer, which returns only the final output of the sequence. A final dense layer with a single unit and a linear activation function is applied to produce the model’s prediction. After testing, the optimal batch size is set to 2, with 50 training epochs. The training dataset is the same as that described for the CNN algorithm: 181 maps from 2019 and 2020, but with the temporal shift as previously mentioned.

Table 3.
Layers of the Long Short-Term Memory (LSTM) neural network designed for the temporal-coherence approach.
4. Results
To evaluate the different approaches, validation using in situ data is performed. Specifically, we use the two datasets described in Section 2.3: the BGEP moorings and the ESA SMOSice campaign data are utilized. Furthermore, the ESA/AWI product described in Section 2.1.1 is also included in the assessment as a baseline. To ensure a fair assessment, all algorithm predictions exceeding 1 m are capped at exactly 1 m. The selected metrics are the correlation coefficient (R2), the mean absolute error (MAE), the standard deviation (Std Dev), and the overestimation and underestimation percentages. These percentages are calculated by identifying a value as overestimated or underestimated if it exceeds or falls short of the ground truth value by at least 25%.
To provide an initial visual assessment of each algorithm, Figure 2 presents Arctic-wide and Barents Sea-focused sea ice thickness maps produced by each algorithm. In these maps, the areas covered by the validation datasets are marked. All four approaches capture the broad spatial patterns of SIT, with thicker ice concentrated north of Greenland and the Canadian Arctic Archipelago, and thinner ice in the marginal zones. The ESA product shows relatively smooth gradients and generally higher SIT values in the marginal ice zone compared to the ML methods. The RF exhibits sharper spatial transitions and slightly noisier patterns, particularly near the ice edge. The CNN output appears more smooth than RF, yet preserves fine-scale spatial variability, especially in the Barents Sea. The LSTM model produces the most homogeneous fields, with reduced spatial detail, likely reflecting the influence of temporal averaging or memory in the algorithm’s architecture. Overall, the ESA, RF, and LSTM algorithms produce broadly similar sea ice thickness distributions, with local differences that become more evident upon closer inspection, such as in the Barents Sea region. In contrast, the CNN model tends to predict higher thickness values in several areas and shows limited sensitivity to the finer spatial structures associated with thinner ice. This characteristic can significantly affect the model’s performance, particularly given that the primary objective of the methodology is to retrieve thin sea ice thickness. Consequently, such behavior may also influence the outcomes of the validation process.
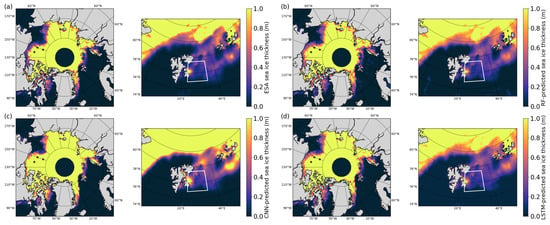
Figure 2.
Arctic-wide and Barents Sea-focused maps showing sea ice thickness estimates from each algorithm: ESA (a), RF (b), CNN (c), and LSTM (d). The Arctic-wide map corresponds to 1 December 2019, while the Barents Sea-focused map represents the average over the campaign period, conducted from 19 to 24 March 2014. Red stars indicate the locations of BGEP moorings in the Arctic-wide maps, while the Barents Sea maps highlight the ESA SMOSice campaign sampling area with a white perimeter.
Figure 3 shows the results of comparing the predictions given by the different algorithms, using the BGEP moorings dataset described in Section 2.3. The points are complemented by their respective density to depict the distribution of output values. However, since many data points correspond to 1 m after the imposed limitation, they are not included in the density computation to improve the visualization throughout the thickness range. The RF algorithm presents similar results to ESA, while the CNN tends to overestimate, and the LSTM shows more dispersion and underestimation, especially for thinner ice. The most homogeneous point-density distribution is presented by the RF, highlighting its robustness. The metrics are provided in Table 4, where the initially observed characteristics of each algorithm are confirmed. Although all approaches show similar error, correlation, and dispersion, it is clear that the CNN is overestimating, by approximately 10% more than the others. These results suggest that for this dataset, both the RF and ESA algorithms slightly outperform the others. Therefore, the spatially and temporally coherent approaches, represented by the CNN and LSTM algorithms, do not provide better capture of the sea ice evolution depicted by the BGEP moorings.
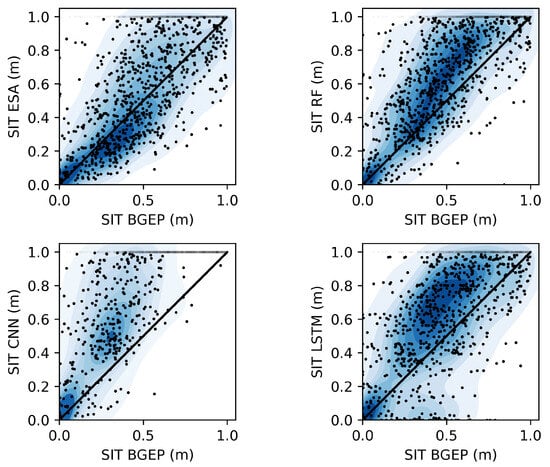
Figure 3.
Scatter and density plots of the validation of the algorithms (ESA, RF, CNN, and LSTM) using the BGEP moorings dataset.

Table 4.
Metrics of the validation of the algorithms (ESA, RF, CNN, and LSTM) using the BGEP moorings dataset.
The ESA SMOSice campaign provides a unique dataset that contains sufficient thin sea ice to perform validation. In fact, this dataset was used to validate the ESA SMOS sea ice thickness product described in Section 2.1.1. A similar assessment to that conducted for the BGEP moorings dataset is conducted, using the three sub-datasets that were collected: HEM, SEM, and ALS. Figure 4 shows the validation of the assessed algorithms against these in situ datasets. The different sub-datasets present distinct SIT distributions, allowing for a comprehensive assessment of the algorithm performance. For the HEM data, which cover a broader SIT range, the RF and CNN models show the best agreement with the reference measurements, followed closely by ESA, while the LSTM consistently underestimates SIT across the range. In the case of SEM, which measured very thin ice, none of the algorithms are capable of reproducing the observed values, since predictions are consistently too dispersed. For the ALS dataset, which includes thicker ice, all algorithms tend to underestimate SIT, although the CNN performs better, showing the least bias. It is remarkable that the LSTM shows negative thicknesses, which is physically unrealistic, but this is due to the inherent stochasticity of the algorithm’s architecture. Table 5 summarizes the validation performance of the four algorithms across the three datasets: HEM, SEM, and ALS. In the HEM dataset, the CNN achieved the highest R2 (0.51) and lowest MAE (0.30 m), while the ESA and RF models followed closely with comparable MAE values and moderately lower R2 scores. The LSTM performed similarly in terms of MAE but displayed a lower R2, indicating slightly less correlation with the observed data. For the SEM dataset, performance dropped across all algorithms, with R2 values remaining below 0.25, reflecting the increased difficulty in modeling this dataset. The CNN again had the highest R2 (0.23), but RF and ESA maintained lower MAE values, suggesting a better trade-off between error magnitude and model consistency. Regarding the ALS dataset, all models improved substantially, with the LSTM and RF showing stronger R2 values (0.59 and 0.57, respectively) and lower MAE (0.19–0.22 m), with the CNN and ESA being slightly worse.
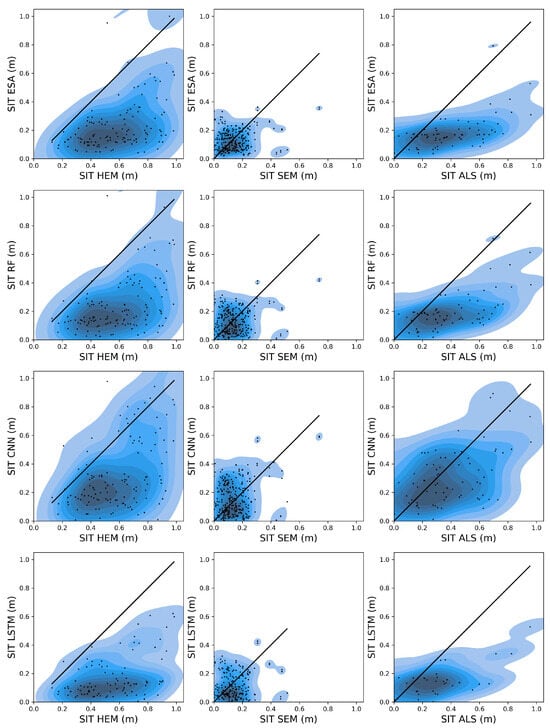
Figure 4.
Scatter and density plots of the validation of the algorithms (ESA, RF, CNN, and LSTM) using the ESA SMOSice campaign dataset.

Table 5.
Metrics of the validation of the algorithms (ESA, RF, CNN, and LSTM) using the ESA SMOSice campaign datasets, namely HEM, SEM, and ALS data.
5. Discussion
The results presented in Section 4 suggest that the two in situ datasets involved in the validation have some disparities regarding their thickness distributions. Therefore, a thorough analysis is required to avoid divergent conclusions.
Regarding the BGEP moorings dataset, Figure 5 shows the temporal evolution from the in situ mooring measurements and from the predictions of the algorithms. Here, the algorithm’s predictions are not limited to 1 m since no metric computation is involved, but they are graphically separated. It is also noteworthy that the unrealistic data jumps occur because only the BGEP-measured values from the initial growth phase (lower than 1 m) are considered for each period, i.e., from October to April of the following year, spanning from 2010 to 2021.
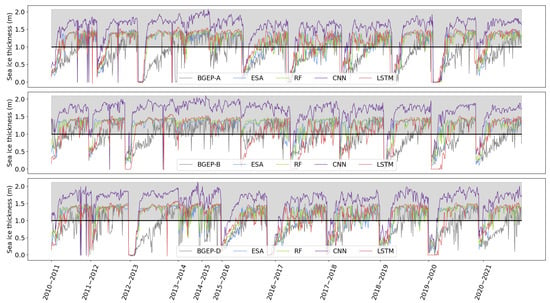
Figure 5.
Temporal evolution of the BGEP moorings (A, B, C) sea ice thickness from October 2010 to April 2021, alongside the algorithm’s prediction. The shaded part above the black solid line correspond to the values above 1 m that are not considered in the analysis.
From this representation, it is clear that the majority of the error occurs because the slow growth observed by the moored buoys is not successfully captured by any algorithm. Except for some specific periods, the algorithms rapidly transition from very thin to already grown ice. However, this effect is not unexpected because of the resolution disparities between the in situ and remote sensing observations. This can be explained by the fact that these buoys represent single points within one vast satellite pixel, so there can exist huge thickness variability within them. Furthermore, these moorings cannot be considered as stable platforms, since they are affected by physical processes such as ice drifting and ocean currents underneath. Despite all these drawbacks, and since the validation is performed equally for all the algorithms, one can say that the CNN is significantly overestimating, especially from 0.5 m onward. For the other approaches, both Figure 3 and Figure 5 show similar behavior for all of them.
The validation using the ESA SMOSice campaign dataset highlights a systematic underestimation of sea ice thickness (SIT), particularly in the thin ice regime, with varying levels of accuracy and bias across the assessed algorithms. It is important to note that all datasets were interpolated onto the SMOS grid, facilitating intercomparison among products. However, none of the algorithms could reproduce the SEM measurements, which suggests this dataset may have limited reliability, and results based on it should be interpreted with caution.
In general, ESA estimates exhibited lower dispersion and smaller errors, while the RF algorithm delivered a balanced performance across all datasets. The CNN showed higher correlation with in situ data but also slightly increased error and variability. The LSTM generally underperformed, although it yielded better results under more stable conditions, such as those represented by the ALS dataset.
The pixel-by-pixel approach of the RF algorithm performs comparably to that of ESA, showing similar validation metrics across all datasets. Both exhibit strong correlations and reasonable levels of error and dispersion, despite their relative simplicity in terms of algorithmic complexity, as neither explicitly incorporates spatial or temporal coherence. However, they differ in how sea ice emission is modeled. Although a detailed discussion of emission modeling is beyond the scope of this work, it is worth noting that the RF algorithm—and the overall methodology presented—can be readily adapted to any desired emission model. This flexibility stems from the fact that modifying the emission modeling would only require regenerating the training dataset using the new forward model. With the new dataset produced, the rest of the methodology would remain unchanged, underscoring its robustness and adaptability.
In contrast, the CNN tends to overestimate sea ice thickness across the validation datasets and shows the highest dispersion. This may be due to the fact that the input variables are already smooth and spatially coherent (see Figure 2 in [22]), which reduces the need for additional spatial modeling. This explains why the simpler pixel-wise methods perform well, as spatial coherence is already embedded in the inputs, making complex architectures like CNNs less advantageous in this context. Similarly, the temporally coherent approach of the LSTM does not appear to improve the estimation of sea ice thickness. One possible explanation is that local sea ice inhomogeneities evolve too rapidly to be captured at the resolution of satellite observations. Additionally, these small-scale variations are effectively averaged out, meaning that the temporal evolution of each pixel is smoother and can be captured by simpler models, reducing the need for complex temporal modeling techniques such as LSTMs.
Regarding the computational resources needed for each assessed algorithm, there are important differences among them. Starting with the ESA product, although no information is published, the description in [8] includes the simulation of a thermodynamic model, which can easily increase the computational requirements. Since the RF is a simple ML algorithm, the computation time is negligible, both for training and predicting. However, since the CNN and the LSTM are deep learning approaches, the computational resources are significantly increased. However, the procedures involved in the presented algorithms are in no way limiting for a hypothetical operational product. The order of magnitude of the time required for the training phase of the algorithms ranges from seconds for the RF, to hours for both the CNN and the LSTM. To perform predictions, the RF needs nanoseconds while the others need seconds. No specific metrics are provided since the computational resources are not an impediment, and thus, there is no need to include high performance computing metrics or similar information.
Finally, it is worth mentioning that aside from the algorithms presented here, similar variants have been tested within this study. Regarding the pixel-by-pixel approach, aside from the mentioned RF and GB, the widely-used XGBoost [44] was tested without achieving better results. For the spatially coherent approach, the U-Net structure [45] was also used as a variant of the standard CNN, but again no significant improvements were found. Moreover, a fourth approach was attempted for the sake of completeness, accounting for both the spatial and temporal coherence. This was carried out by using a 2D-CNNLSTM structure, combining the two already presented methods. However, despite the important increase in computational resources required for the training phase, the results were not better than those obtained by using the standard CNN or LSTM.
6. Conclusions
This study evaluates various approaches for retrieving thin sea ice thickness from L-band radiometry observations, including a machine learning framework, two deep learning algorithms, and the ESA official product as a baseline. The findings highlight that there is still significant potential to refine the current algorithms used for sea ice thickness retrieval from SMOS. These refinements are also critical for the upcoming ESA’s Copernicus Imaging Microwave Radiometer (CIMR) mission, which will expand observations to higher frequencies (up to 36.5 GHz) while retaining 1.4 GHz capabilities.
Overall, the ESA product has demonstrated robustness despite known limitations, while the novel methodologies show potential advantages, offering opportunities to optimize computational efficiency and improve the retrieval.
Among the assessed methods, the RF algorithm shows balanced performance, comparable to the ESA’s product in terms of correlation, error, and dispersion, despite being much simpler and not modeling spatial or temporal coherence explicitly. This performance, coupled with its flexibility in adapting to different emission models, underscores the robustness and adaptability of the RF approach. In contrast, the CNN tends to overestimate SIT and exhibits greater dispersion, suggesting that the spatial coherence already embedded in the input variables diminishes the added value of the CNN’s architectural complexity. Similarly, the LSTM algorithm does not significantly improve results, likely due to the rapid evolution and spatial averaging of sea ice conditions that make temporal coherence less impactful at the satellite scale.
Based on these findings, the assessment suggests that while the ESA SMOS sea ice thickness retrieval algorithm is still a valid approach, there is still potential for improvement. The proposed pixel-by-pixel approach, represented by the RF algorithm, shows robust performance and could serve as a solid foundation for future operational products. In comparison, the more complex structures such as the CNN and the LSTM do not offer clear advantages in this case. Therefore, future work should not focus exclusively on developing more complex methodologies, but also on improving the modeling of sea ice emission at L-band. This improvement could be directly applied to the presented method to further increase the accuracy of the sea ice thickness estimates.
Author Contributions
Conceptualization, F.H.-M., G.S.G., C.G. and M.J.E.; methodology, F.H.-M. and G.S.G.; software, F.H.-M.; validation, F.H.-M.; formal analysis, F.H.-M.; investigation, F.H.-M.; resources, F.H.-M., G.S.G., C.G. and M.J.E.; data curation, F.H.-M.; writing—original draft preparation, F.H.-M.; writing—review and editing, G.S.G., C.G. and M.J.E.; visualization, F.H.-M.; supervision, G.S.G., C.G. and M.J.E.; project administration, C.G. and M.J.E.; funding acquisition, C.G. and M.J.E. All authors have read and agreed to the published version of the manuscript.
Funding
This project is funded from the AEI with the ARCTIC-MON project (PID2021-125324OB-I00), and from a Doctorat Industrial (AGAUR), with expedient number 2023 DI 0007.
Data Availability Statement
The data supporting the conclusions of this article will be made available by the authors on request. These data were derived from the following resources available in the public domain: The production of SMOS sea ice thickness data was funded by the ESA project SMOS & CryoSat-2 Sea Ice Data Product Processing and Dissemination Service, and data from 15 October 2010 to 15 April 2021 were obtained from AWI. The BGEP data used in the validation were collected and made available by the Beaufort Gyre Exploration Program based at the Woods Hole Oceanographic Institution (https://www2.whoi.edu/site/beaufortgyre, accessed on 24 July 2025) in collaboration with researchers from Fisheries and Oceans Canada at the Institute of Ocean Sciences. Remote sensing data processing was executed at the Barcelona Expert Center on Remote Sensing (BEC-RS, https://bec.icm.csic.es, accessed on 24 July 2025) of the Institut de Ciències del Mar ICM-CSIC. The source codes are available for downloading at the following link: https://github.com/ferranhema/smos-mlsit (accessed on 24 July 2025).
Acknowledgments
This work is supported by the Spanish government through the “Severo Ochoa Centre of Excellence” accreditation (Grant CEX2024-001494-S funded by AEI 10.13039/501100011033). This work has been conducted in the framework of the PhD in Computer Science program of the Universitat Autònoma de Barcelona (UAB). This work is part of a Doctorat Industrial (AGAUR), with expedient number 2023 DI 0007.
Conflicts of Interest
Authors Ferran Hernández-Macià and Maria José Escorihuela are employed by isardSAT, S.L., Spain. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Budyko, M.I. The effect of solar radiation variations on the climate of the Earth. Tellus 1969, 21, 611–619. [Google Scholar] [CrossRef]
- Kwok, R. Arctic sea ice thickness, volume, and multiyear ice coverage: Losses and coupled variability (1958–2018). Environ. Res. Lett. 2018, 13, 105005. [Google Scholar] [CrossRef]
- Meredith, M.; Sommerkorn, M.; Cassotta, S.; Derksen, C.; Ekaykin, A.; Hollowed, A.; Kofinas, G.; Mackintosh, A.; Melbourne-Thomas, J.; Muelbert, M.; et al. Polar Regions. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2019; pp. 203–320. [Google Scholar] [CrossRef]
- Mecklenburg, S.; Wright, N.; Bouzina, C.; Delwart, S. Getting down to business-SMOS operations and products. ESA Bull. 2009, 137, 25–30. [Google Scholar]
- Kerr, Y.; Waldteufel, P.; Wigneron, J.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements of the global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Kaleschke, L.; Tian-Kunze, X.; Maaß, N.; Mäkynen, M.; Drusch, M. Sea ice thickness retrieval from SMOS brightness temperatures during the Arctic freeze-up period. Geophys. Res. Lett. 2012, 39, L05501. [Google Scholar] [CrossRef]
- Tian-Kunze, X.; Kaleschke, L.; Maaß, N.; Mäkynen, M.; Serra, N.; Drusch, M.; Krumpen, T. SMOS-derived thin sea ice thickness: Algorithm baseline, product specifications and initial verification. Cryosphere 2014, 8, 997–1018. [Google Scholar] [CrossRef]
- Maass, N.; Kaleschke, L.; Tian-Kunze, X.; Tonboe, R.T. Snow thickness retrieval from L-band brightness temperatures: A model comparison. Ann. Glaciol. 2015, 56, 9–17. [Google Scholar] [CrossRef]
- Huntemann, M.; Heygster, G.; Kaleschke, L.; Krumpen, T.; Mäkynen, M.; Drusch, M. Empirical sea ice thickness retrieval during the freeze-up period from SMOS high incident angle observations. Cryosphere 2014, 8, 439–451. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W. Spaceborne GNSS-R Sea Ice Detection Using Delay-Doppler Maps: First Results From the U.K. TechDemoSat-1 Mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4795–4801. [Google Scholar] [CrossRef]
- Wang, F.; Yang, D.; Zhang, B.; Yang, L. Can sea ice thickness be retrieved using GNSS-interferometric reflectometry? GPS Solut. 2022, 26, 128. [Google Scholar] [CrossRef]
- Braakmann-Folgmann, A.; Donlon, C. Estimating snow depth on Arctic sea ice using satellite microwave radiometry and a neural network. Cryosphere 2019, 13, 2421–2438. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W. Sea Ice Thickness Estimation From TechDemoSat-1 and Soil Moisture Ocean Salinity Data Using Machine Learning Methods. In Proceedings of the Global Oceans 2020: Singapore–U.S. Gulf Coast, Biloxi, MS, USA, 5–30 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Chi, J.; Kim, H.C. Retrieval of daily sea ice thickness from AMSR2 passive microwave data using ensemble convolutional neural networks. GIScience Remote Sens. 2021, 58, 812–830. [Google Scholar] [CrossRef]
- Soriot, C.; Prigent, C.; Jimenez, C.; Frappart, F. Arctic Sea Ice Thickness Estimation From Passive Microwave Satellite Observations Between 1.4 and 36 GHz. Earth Space Sci. 2023, 10, e2022EA002542. [Google Scholar] [CrossRef]
- Soriot, C.; Vancoppenolle, M.; Prigent, C.; Jimenez, C.; Frappart, F. Winter Arctic sea ice volume decline: Uncertainties reduced using passive microwave-based sea ice thickness. Sci. Rep. 2024, 14, 21000. [Google Scholar] [CrossRef]
- Herbert, C.; Munoz-Martin, J.F.; Llaveria, D.; Pablos, M.; Camps, A. Sea Ice Thickness Estimation Based on Regression Neural Networks Using L-Band Microwave Radiometry Data from the FSSCat Mission. Remote Sens. 2021, 13, 1366. [Google Scholar] [CrossRef]
- Camps, A.; Golkar, A.; Gutierrez, A.; de Azua, J.R.; Munoz-Martin, J.; Fernandez, L.; Diez, C.; Aguilella, A.; Briatore, S.; Akhtyamov, R.; et al. Fsscat, the 2017 Copernicus Masters’ “Esa Sentinel Small Satellite Challenge” Winner: A Federated Polar and Soil Moisture Tandem Mission Based on 6U Cubesats. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8285–8287. [Google Scholar] [CrossRef]
- Shamshiri, R.; Eide, E.; Høyland, K.V. Spatio-temporal distribution of sea-ice thickness using a machine learning approach with Google Earth Engine and Sentinel-1 GRD data. Remote Sens. Environ. 2022, 270, 112851. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, Z.; Li, W.; Tian, K.; Zhan, Z.; Shan, P.; Li, L. Sea Ice Type and Thickness Identification Based on Vibration Sensor Networks and Machine Learning. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar] [CrossRef]
- Hernández-Macià, F.; Gabarró, C.; Gomez, G.S.; Escorihuela, M.J. A Machine Learning Approach on SMOS Thin Sea Ice Thickness Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 10752–10758. [Google Scholar] [CrossRef]
- Kerr, Y.; Waldteufel, P.; Wigneron, J.P.; Martinuzzi, J.; Font, J.; Berger, M. Soil moisture retrieval from space: The Soil Moisture and Ocean Salinity (SMOS) mission. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1729–1735. [Google Scholar] [CrossRef]
- Ryvlin, A.I. Method of forecasting flexural strength of an ice cover. Probl. Arct. Antarct. 1974, 45, 79–86. [Google Scholar]
- Tian-Kunze, X.; Kaleschke, L.; Crapolicchio, R. SMOS L3 Sea Ice Thickness ATBD: Algorithm Theoretical Baseline Document; Technical Report; European Space Agency (ESA): Paris, France, 2021. [Google Scholar]
- Karagali, I.; Nielsen-Englyst, P.; Kolbe, W.M.; Høyer, J.L. Arctic Ocean-Sea and Ice Surface Temperature REPROCESSED. 2024. Available online: https://data.marine.copernicus.eu/product/SEAICE_ARC_PHY_CLIMATE_L4_MY_011_016/description (accessed on 24 July 2025).
- Huntemann, M. Thickness Retrieval and Emissivity Modeling of Thin Sea Ice at L-Band for SMOS Satellite Observations. Ph.D. Thesis, University of Bremen, Bremen, Germany, 2015. [Google Scholar]
- Ali, A.; Burud, A.; Williams, T.; Xie, J.; Yumruktepe, C.; Wakamatsu, T.; Melsom, A.; Bertino, L.; Gao, S. Arctic Ocean Physics Reanalysis. 2024. Available online: https://data.marine.copernicus.eu/product/ARCTIC_MULTIYEAR_PHY_002_003/description (accessed on 24 July 2025).
- Kovacs, A.; U.S. Army, Corps of Engineers; Cold Regions Research and Engineering Laboratory (U.S.). Sea Ice: Bulk Salinity Versus Ice Floe Thickness; Number Part 1 in CRREL Report; U.S. Army Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1996. [Google Scholar]
- Burke, W.; Schmugge, T.; Paris, J. Comparison of 2.8- and 21-cm microwave radiometer observations over soils with emission model calculations. J. Geophys. Res. 1979, 84, 287–294. [Google Scholar] [CrossRef]
- Vant, M.; Ramseier, R.; Makios, V. The complex-dielectric constant of sea ice at frequencies in the range 0.1–40 GHz. J. Appl. Phys. 1978, 49, 1264–1280. [Google Scholar] [CrossRef]
- Wilheit, T.T. Radiative Transfer in a Plane Stratified Dielectric. IEEE Trans. Geosci. Electron. 1978, 16, 138–143. [Google Scholar] [CrossRef]
- Picard, G.; Sandells, M.; Löwe, H. SMRT: An active–passive microwave radiative transfer model for snow with multiple microstructure and scattering formulations (v1.0). Geosci. Model Dev. 2018, 11, 2763–2788. [Google Scholar] [CrossRef]
- Hernández-Macià, F.; Gabarró, C.; Huntemann, M.; Naderpour, R.; Johnson, J.T.; Jezek, K.C. On sea ice emission modeling for MOSAiC’s L-band radiometric measurements. Ann. Glaciol. 2024, 65, e37. [Google Scholar] [CrossRef]
- Belter, H.J.; Krumpen, T.; Hendricks, S.; Hoelemann, J.; Janout, M.A.; Ricker, R.; Haas, C. Satellite-based sea ice thickness changes in the Laptev Sea from 2002 to 2017: Comparison to mooring observations. Cryosphere 2020, 14, 2189–2203. [Google Scholar] [CrossRef]
- Vinje, T.; Finnekåsa, Ø. The Ice Transport Through the Fram Strait; Norsk Polarinstitutt: Oslo, Norway; Tromsø, Norway, 1986. [Google Scholar]
- Kaleschke, L.; Tian-Kunze, X.; Maaß, N.; Beitsch, A.; Wernecke, A.; Miernecki, M.; Müller, G.; Fock, B.H.; Gierisch, A.M.; Schlünzen, K.H.; et al. SMOS sea ice product: Operational application and validation in the Barents Sea marginal ice zone. Remote Sens. Environ. 2016, 180, 264–273. [Google Scholar] [CrossRef]
- Wessel, P.; Luis, J.F.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.H.F.; Tian, D. The Generic Mapping Tools Version 6. Geochem. Geophys. Geosyst. 2019, 20, 5556–5564. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Nakawo, M.; Sinha, N.K. Growth Rate and Salinity Profile of First-Year Sea Ice in the High Arctic. J. Glaciol. 1981, 27, 315–330. [Google Scholar] [CrossRef]
- O’Shea, K.; Nash, R. An Introduction to Convolutional Neural Networks. arXiv 2015, arXiv:1511.08458. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).