Informing Disaster Recovery Through Predictive Relocation Modeling
Abstract
1. Introduction
2. Literature Review
2.1. Related Studies on Relocation Factors
2.2. Related Studies on Machine Learning Algorithm
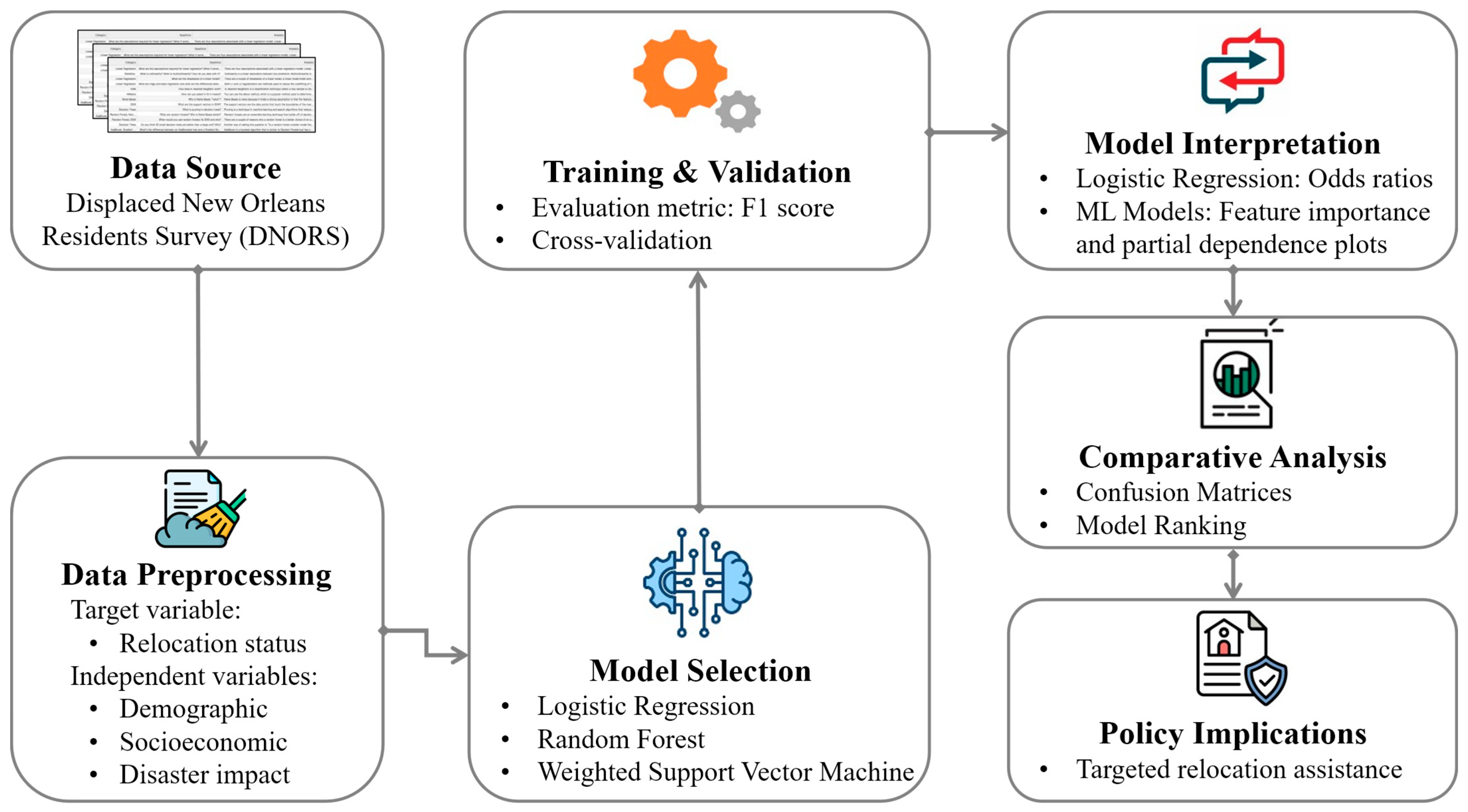
3. Methodology
3.1. Data Description
- Selection Bias: Individuals who were more difficult to locate or contact, such as those experiencing prolonged or multiple displacements, may be underrepresented in the sample.
- Non-Response Bias: Households that declined participation or could not be reached may differ systematically from respondents, potentially affecting the generalizability of the findings.
- Recall Bias: Given the retrospective nature of some survey questions, participants’ recollections of pre- and post-Katrina experiences may be subject to inaccuracies.
3.2. Models
3.2.1. Logistic Regression (LR)
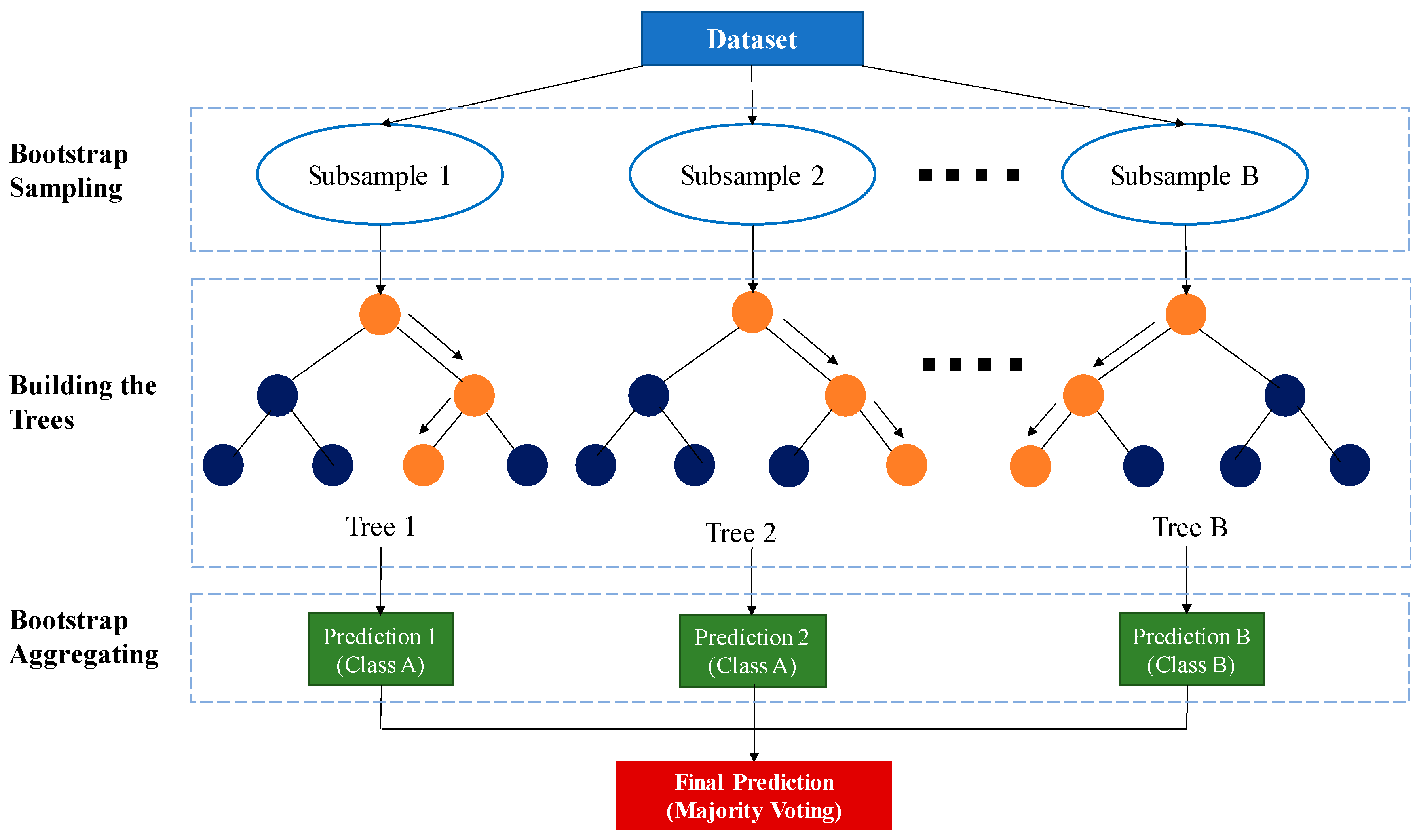
3.2.2. Random Forest (RF)
3.2.3. Weighted Support Vector Machine (WSVM)
4. Results
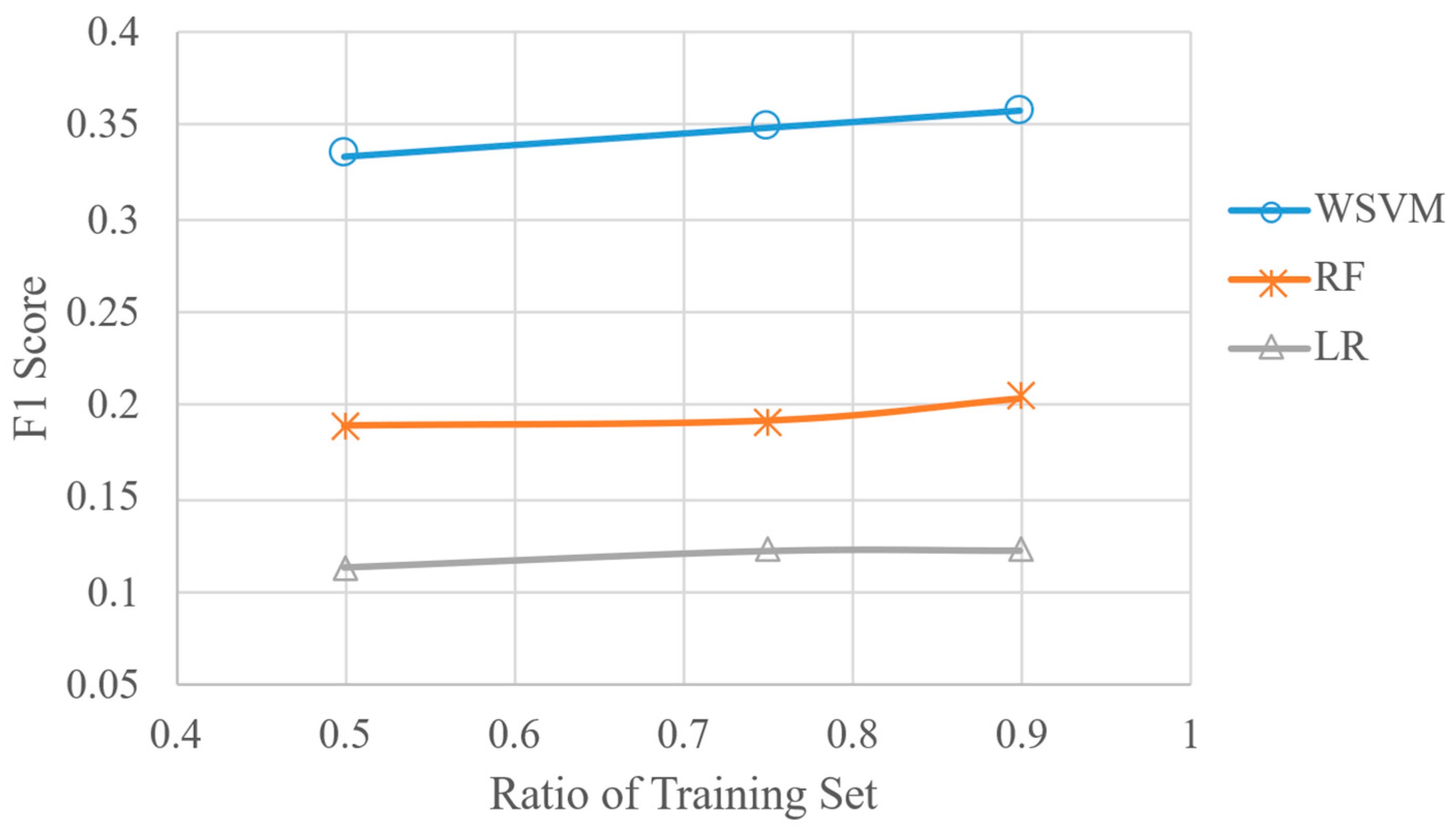
4.1. Metrics
4.2. Model Comparison
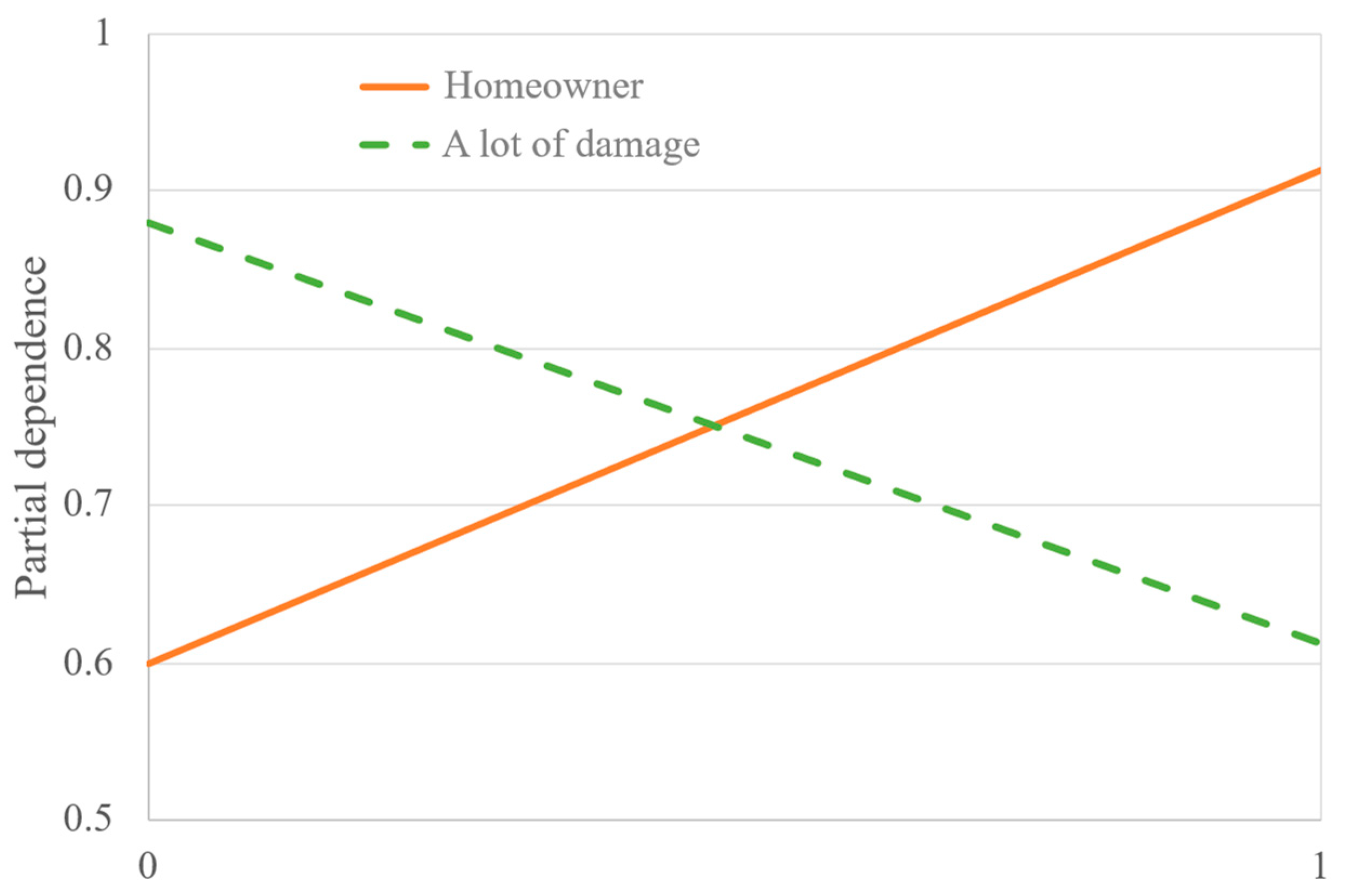
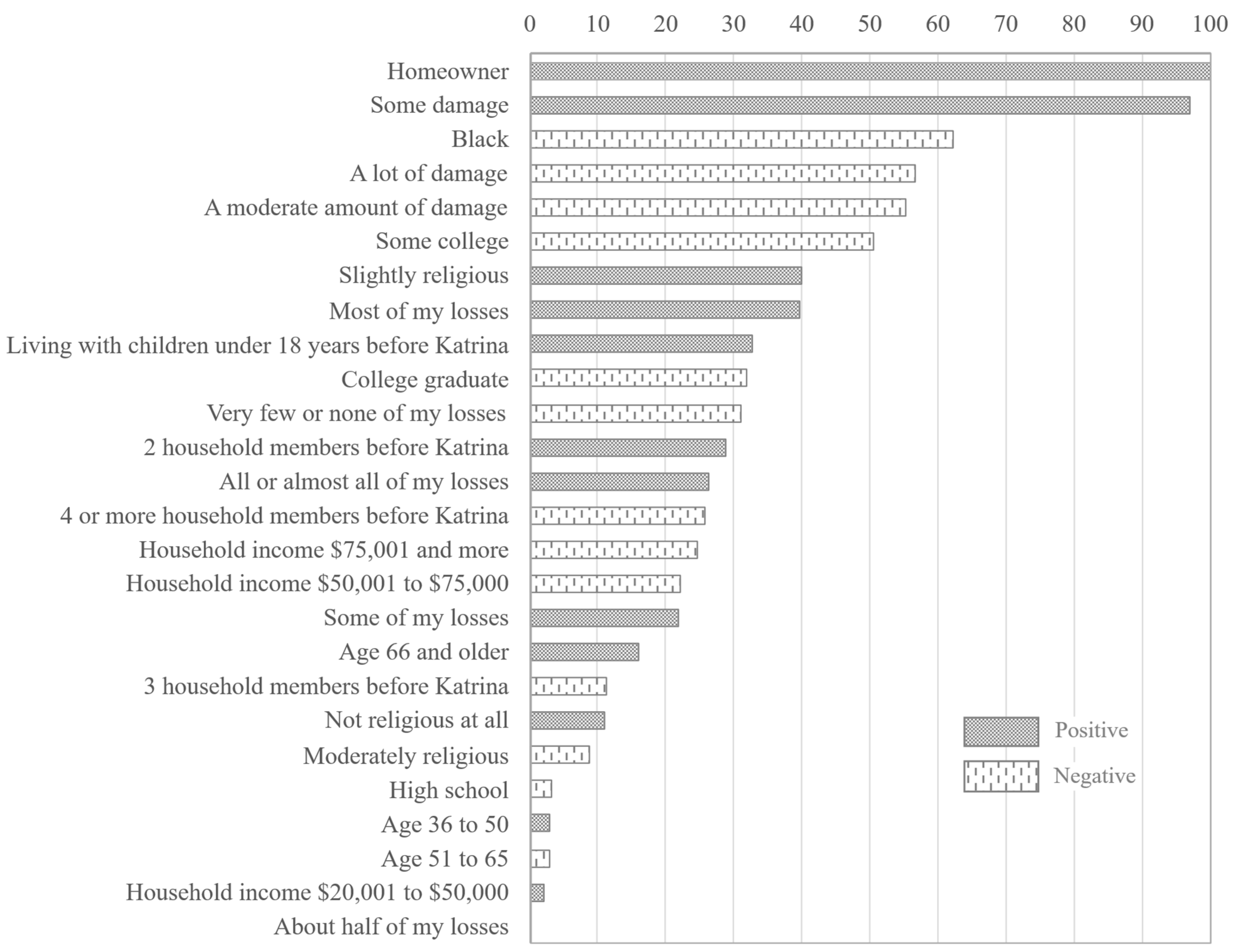
4.3. Variable Interpretation
5. Discussion
5.1. Interpretation of Findings
5.2. Limitations and Future Work
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weather-Related Disasters Are Increasing. Available online: https://www.economist.com/graphic-detail/2017/08/29/weather-related-disasters-are-increasing (accessed on 25 April 2025).
- Hill, C. 43% of U.S. Homes Are at High Risk of Natural Disaster. Available online: https://www.marketwatch.com/story/43-of-us-homes-are-at-high-risk-of-natural-disaster-2015-09-03 (accessed on 25 April 2025).
- Comerio, M. Disaster Hits Home: New Policy for Urban Housing Recovery, 1st ed.; University of California Press: Oakland, CA, USA, 1998; ISBN 978-0-520-20780-6. [Google Scholar]
- Hu, D.; Nejat, A. Role of Spatial Effect in Postdisaster Housing Recovery: Case Study of Hurricane Katrina. J. Infrastruct. Syst. 2021, 27, 05020009. [Google Scholar] [CrossRef]
- Mayer, J.; Moradi, S.; Nejat, A.; Ghosh, S.; Cong, Z.; Liang, D. Drivers of Post-Disaster Relocations: The Case of Moore and Hattiesburg Tornados. Int. J. Disaster Risk Reduct. 2020, 49, 101643. [Google Scholar] [CrossRef]
- Hu, D.; Yu, W.; Zhao, J.; Liu, W.; Han, F.; Yi, X. A Hierarchical Mixed Logit Model of Individuals’ Return Decisions after Hurricane Katrina. Int. J. Disaster Risk Reduct. 2019, 34, 443–447. [Google Scholar] [CrossRef]
- Morrice, S. Heartache and Hurricane Katrina: Recognising the Influence of Emotion in Post-Disaster Return Decisions. Area 2013, 45, 33–39. [Google Scholar] [CrossRef]
- Kytola, K.L.; Cherry, K.E.; Marks, L.D.; Hatch, T.G. When Neighborhoods Are Destroyed by Disaster: Relocate or Return and Rebuild? In Traumatic Stress and Long-Term Recovery: Coping with Disasters and Other Negative Life Events; Cherry, K.E., Ed.; Springer International Publishing: Cham, Switzerland, 2015; pp. 211–229. ISBN 978-3-319-18866-9. [Google Scholar]
- Hu, D.; Nejat, A.; Shankar, V. Random Parameter Model of Postdisaster Household Relocation. Nat. Hazards Rev. 2021, 22, 04021027. [Google Scholar] [CrossRef]
- Moradi, S.; Nejat, A.; Hu, D.; Ghosh, S. Perceived Neighborhood: Preferences versus Actualities. Int. J. Disaster Risk Reduct. 2020, 51, 101824. [Google Scholar] [CrossRef]
- Groen, J.A.; Polivka, A.E. Going Home after Hurricane Katrina: Determinants of Return Migration and Changes in Affected Areas. Demography 2010, 47, 821–844. [Google Scholar] [CrossRef]
- Finn, D.; Chandrasekhar, D. Influence of Household Recovery Capacity and Urgency on Post-Disaster Relocation. Available online: https://hazards.colorado.edu/quick-response-report/influence-of-household-recovery-capacity-and-urgency-on-post-disaster-relocation (accessed on 30 May 2025).
- Binder, S.B. Resilience and Postdisaster Relocation: A Study of New York’s Home Buyout Plan in the Wake of Hurricane Sandy. Ph.D. Thesis, University of Hawaii at Manoa, Waikiki, HI, USA, 2014. [Google Scholar]
- Fussell, E.; Sastry, N.; VanLandingham, M. Race, Socioeconomic Status, and Return Migration to New Orleans after Hurricane Katrina. Popul. Environ. 2010, 31, 20–42. [Google Scholar] [CrossRef]
- Elliott, J.R.; Pais, J. Race, Class, and Hurricane Katrina: Social Differences in Human Responses to Disaster. Soc. Sci. Res. 2006, 35, 295–321. [Google Scholar] [CrossRef]
- Weng, S.F.; Reps, J.; Kai, J.; Garibaldi, J.M.; Qureshi, N. Can Machine-Learning Improve Cardiovascular Risk Prediction Using Routine Clinical Data? PLoS ONE 2017, 12, e0174944. [Google Scholar] [CrossRef]
- Hamby, S.E.; Hirst, J.D. Prediction of Glycosylation Sites Using Random Forests. BMC Bioinform. 2008, 9, 500. [Google Scholar] [CrossRef] [PubMed]
- Bukvic, A.; Smith, A.; Zhang, A. Evaluating Drivers of Coastal Relocation in Hurricane Sandy Affected Communities. Int. J. Disaster Risk Reduct. 2015, 13, 215–228. [Google Scholar] [CrossRef]
- Jamali, M.; Nejat, A. Place Attachment and Disasters: Knowns and Unknowns. J. Emerg. Manag. 2016, 14, 349–364. [Google Scholar] [CrossRef]
- Xiao, Y.; Van Zandt, S. Building Community Resiliency: Spatial Links between Household and Business Post-Disaster Return. Urban Stud. 2012, 49, 2523–2542. [Google Scholar] [CrossRef]
- Najarian, L.M.; Goenjian, A.K.; Pelcovttz, D.; Mandel, F.; Najarian, B. Relocation after a Disaster: Posttraumatic Stress Disorder in Armenia after the Earthquake. J. Am. Acad. Child Adolesc. Psychiatry 1996, 35, 374–383. [Google Scholar] [CrossRef]
- Tierney, K.J. Businesses and Disasters: Vulnerability, Impacts, and Recovery. In Handbook of Disaster Research; Rodríguez, H., Quarantelli, E.L., Dynes, R.R., Eds.; Springer: New York, NY, USA, 2007; pp. 275–296. ISBN 978-0-387-32353-4. [Google Scholar]
- Lee, J.Y.; Van Zandt, S. Housing Tenure and Social Vulnerability to Disasters: A Review of the Evidence. J. Plan. Lit. 2019, 34, 156–170. [Google Scholar] [CrossRef]
- Peek, L.; Morrissey, B.; Marlatt, H. Disaster Hits Home: A Model of Displaced Family Adjustment After Hurricane Katrina. J. Fam. Issues 2011, 32, 1371–1396. [Google Scholar] [CrossRef]
- Binder, S.; Baker, C.; Barile, J. Rebuild or Relocate? Resilience and Postdisaster Decision-Making After Hurricane Sandy. Am. J. Community Psychol. 2015, 56, 180–196. [Google Scholar] [CrossRef]
- Marjanović, M.; Kovačević, M.; Bajat, B.; Voženílek, V. Landslide Susceptibility Assessment Using SVM Machine Learning Algorithm. Eng. Geol. 2011, 123, 225–234. [Google Scholar] [CrossRef]
- Ganggayah, M.D.; Taib, N.A.; Har, Y.C.; Lio, P.; Dhillon, S.K. Predicting Factors for Survival of Breast Cancer Patients Using Machine Learning Techniques. BMC Med. Inform. Decis. Mak. 2019, 19, 48. [Google Scholar] [CrossRef]
- Zhao, X.; Lovreglio, R.; Nilsson, D. Modelling and Interpreting Pre-Evacuation Decision-Making Using Machine Learning. Autom. Constr. 2020, 113, 103140. [Google Scholar] [CrossRef]
- Ganguly, K.K.; Nahar, N.; Hossain, B.M. A Machine Learning-Based Prediction and Analysis of Flood Affected Households: A Case Study of Floods in Bangladesh. Int. J. Disaster Risk Reduct. 2019, 34, 283–294. [Google Scholar] [CrossRef]
- Muchlinski, D.; Siroky, D.; He, J.; Kocher, M. Comparing Random Forest with Logistic Regression for Predicting Class-Imbalanced Civil War Onset Data. Polit. Anal. 2016, 24, 87–103. [Google Scholar] [CrossRef]
- Krstajic, D.; Buturovic, L.J.; Leahy, D.E.; Thomas, S. Cross-Validation Pitfalls When Selecting and Assessing Regression and Classification Models. J. Cheminform. 2014, 6, 10. [Google Scholar] [CrossRef] [PubMed]
- Pregibon, D. Logistic Regression Diagnostics. Ann. Stat. 1981, 9, 705–724. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Ferri, C.; Hernández-Orallo, J.; Modroiu, R. An Experimental Comparison of Performance Measures for Classification. Pattern Recognit. Lett. 2009, 30, 27–38. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Kim, J.; Oh, S. The Virtuous Circle in Disaster Recovery: Who Returns and Stays in Town after Disaster Evacuation? J. Risk Res. 2014, 17, 5. [Google Scholar] [CrossRef]
- Myers, C.A.; Slack, T.; Singelmann, J. Social Vulnerability and Migration in the Wake of Disaster: The Case of Hurricanes Katrina and Rita. Popul. Environ. 2008, 29, 271–291. [Google Scholar] [CrossRef]
- Huan, Y.; Song, L.; Khan, U.; Zhang, B. Stacking Ensemble of Machine Learning Methods for Landslide Susceptibility Mapping in Zhangjiajie City, Hunan Province, China. Environ. Earth Sci. 2022, 82, 35. [Google Scholar] [CrossRef]
- Zhang, B.; Tang, J.; Huan, Y.; Song, L.; Shah, S.Y.A.; Wang, L. Multi-Scale Convolutional Neural Networks (CNNs) for Landslide Inventory Mapping from Remote Sensing Imagery and Landslide Susceptibility Mapping (LSM). Geomat. Nat. Hazards Risk 2024, 15, 2383309. [Google Scholar] [CrossRef]
| Variable | N | Variable | N |
|---|---|---|---|
| Age | Education | ||
| 19 to 35 | 168 | Less than high school | 223 |
| 36 to 50 | 407 | High school | 302 |
| 51 to 65 | 473 | Some college | 312 |
| 66 and older | 256 | College graduate | 467 |
| Household income | Religion | ||
| 0 to USD 20,000 | 393 | Very religious | 493 |
| USD 20,001 to USD 50,000 | 477 | Moderately religious | 561 |
| USD 50,001 to USD 75,000 | 173 | Slightly religious | 152 |
| USD 75,001 and more | 261 | Not religious at all | 98 |
| Living with children under 18 years before Katrina | Number of pre-Katrina household members | ||
| Yes | 516 | 1 | 329 |
| No | 788 | 2 | 423 |
| Insurance coverage | 3 | 232 | |
| All or almost all of my losses | 143 | 4 or more | 320 |
| Most of my losses | 201 | Homeownership | |
| About half of my losses | 143 | Owner | 942 |
| Some of my losses | 294 | Renter | 362 |
| Very few or none of my losses | 189 | Housing damage | |
| No insurance | 334 | No damage | 56 |
| Race/Ethnicity | Some damage | 375 | |
| Black | 807 | A moderate amount of damage | 611 |
| White and others | 497 | A lot of damage | 262 |
| Variable | Odds Ratio |
|---|---|
| Black | 0.983 |
| Homeowner | 2.927 *** |
| Living with children under 18 years before Katrina | 1.131 |
| High school | 0.636 † |
| Some college | 0.423 ** |
| College graduate | 0.522 * |
| Moderately religious | 1.155 |
| Slightly religious | 2.873 ** |
| Not religious at all | 1.486 |
| All or almost all of my losses | 1.277 |
| Most of my losses | 1.500 |
| About half of my losses | 0.809 |
| Some of my losses | 1.195 |
| Very few or none of my losses | 0.747 |
| Some damage | 0.401 |
| A moderate amount of damage | 0.151 *** |
| A lot of damage | 0.122 ** |
| Age 36 to 50 | 1.035 |
| Age 51 to 65 | 0.927 |
| Age 66 and older | 0.835 |
| Household income USD 20,001 to USD 50,000 | 1.077 |
| Household income USD 50,001 to USD 75,000 | 0.635 † |
| Household income USD 75,001 and more | 0.945 |
| 2 household members before Katrina | 1.056 |
| 3 household members before Katrina | 0.733 |
| 4 or more household members before Katrina | 0.706 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, C.; Hu, D. Informing Disaster Recovery Through Predictive Relocation Modeling. Computers 2025, 14, 240. https://doi.org/10.3390/computers14060240
He C, Hu D. Informing Disaster Recovery Through Predictive Relocation Modeling. Computers. 2025; 14(6):240. https://doi.org/10.3390/computers14060240
Chicago/Turabian StyleHe, Chao, and Da Hu. 2025. "Informing Disaster Recovery Through Predictive Relocation Modeling" Computers 14, no. 6: 240. https://doi.org/10.3390/computers14060240
APA StyleHe, C., & Hu, D. (2025). Informing Disaster Recovery Through Predictive Relocation Modeling. Computers, 14(6), 240. https://doi.org/10.3390/computers14060240







