An xLSTM–XGBoost Ensemble Model for Forecasting Non-Stationary and Highly Volatile Gasoline Price
Abstract
1. Introduction
2. Related Work
- This study first uses the STL (Seasonal and Trend decomposition using Loess) decomposition method to divide the gasoline price time series into trend terms, periodic terms, and residual terms so as to model and predict subsequences with different characteristics separately.
- In the modeling stage, the xLSTM model is used for the period and trend terms to fully explore the long-term dependencies in the time series; the XGBoost model is used to model the residual term, and its powerful non-linear fitting ability is used to make a fine prediction of the residual error. Through this differentiated model selection and collaborative modeling strategy, the accuracy and robustness of the overall prediction are effectively improved.
- The prediction results of the three sub-models are reversely combined according to the STL decomposition logic to obtain the final prediction value of gasoline prices. In the experimental part, the proposed xLSTM–XGBoost combination model is compared with single models (such as LSTM, ARIMA, CNN, and ELM). The results show that the proposed combined model outperforms the existing mainstream methods in terms of prediction accuracy and error control and exhibits stronger adaptability and stability.
3. Hybrid Model Based on ARIMA–xLSTM–XGBoost
3.1. STL Decomposition Method
- Seasonal Extraction: In each round of iteration, the seasonal component is first extracted from the original series by removing the currently estimated trend term and residual term. Then, based on the Loess local regression algorithm, the data points at each periodic position (such as January, February, and December each year) are smoothed to obtain a new seasonal estimate. This process helps capture the periodic laws in the sequence while reducing the interference of trend changes.
- Trend Extraction and Smoothing: After removing the currently updated seasonal term from the sequence, a deseasonalized sequence is obtained. At this point, the Loess smoother is applied again to extract the long-term trend component. This trend estimate can flexibly adapt to nonlinear changes, enabling the model to handle complex trend structures.
- Remainder Calculation: The updated seasonal term and trend term are removed from the original sequence together to obtain the residual part. The residual mainly reflects the short-term random fluctuations or abnormal changes in the data and is a concentrated reflection of the prediction error and unexplainable factors. This step is particularly critical for subsequent outlier detection and model optimization.
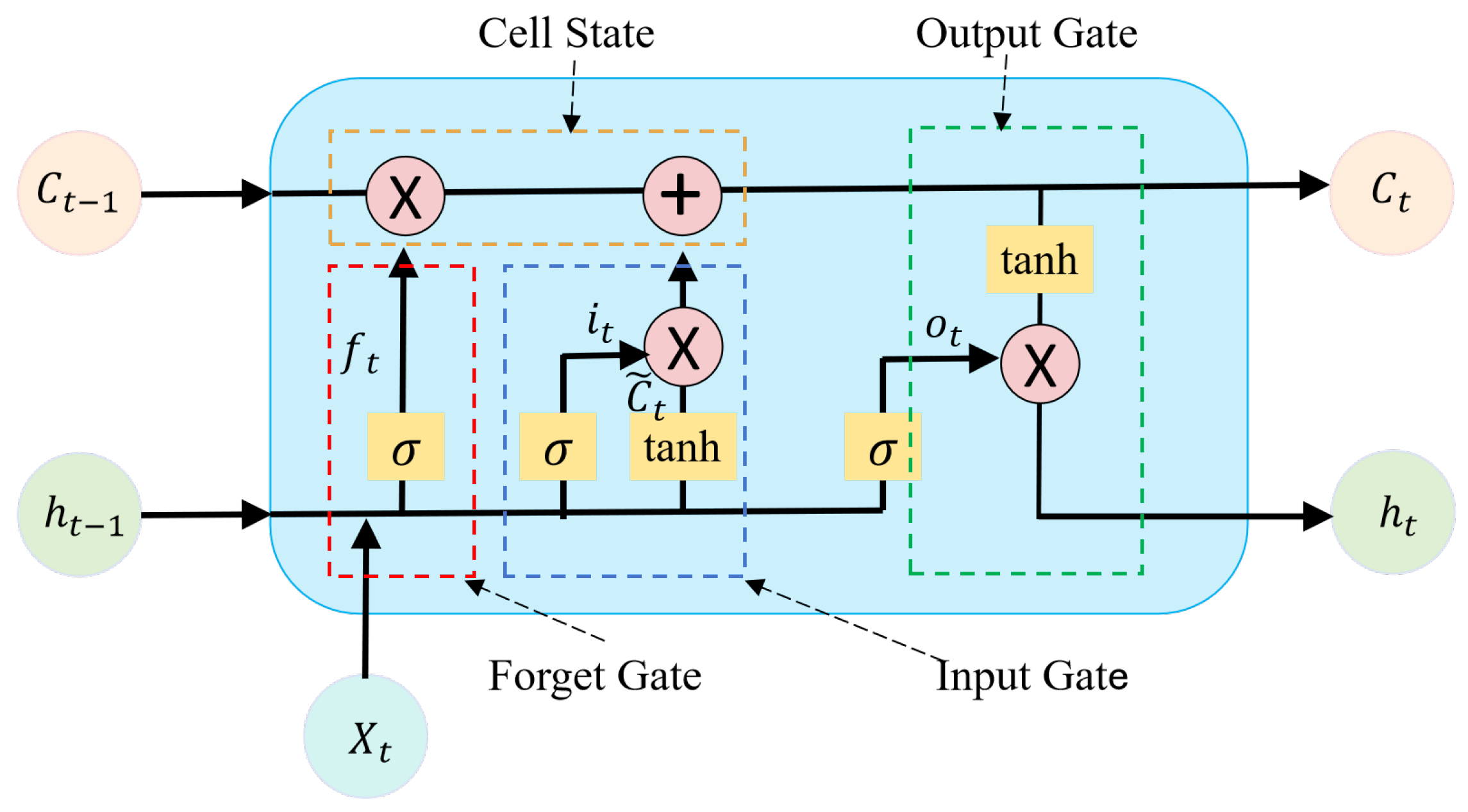
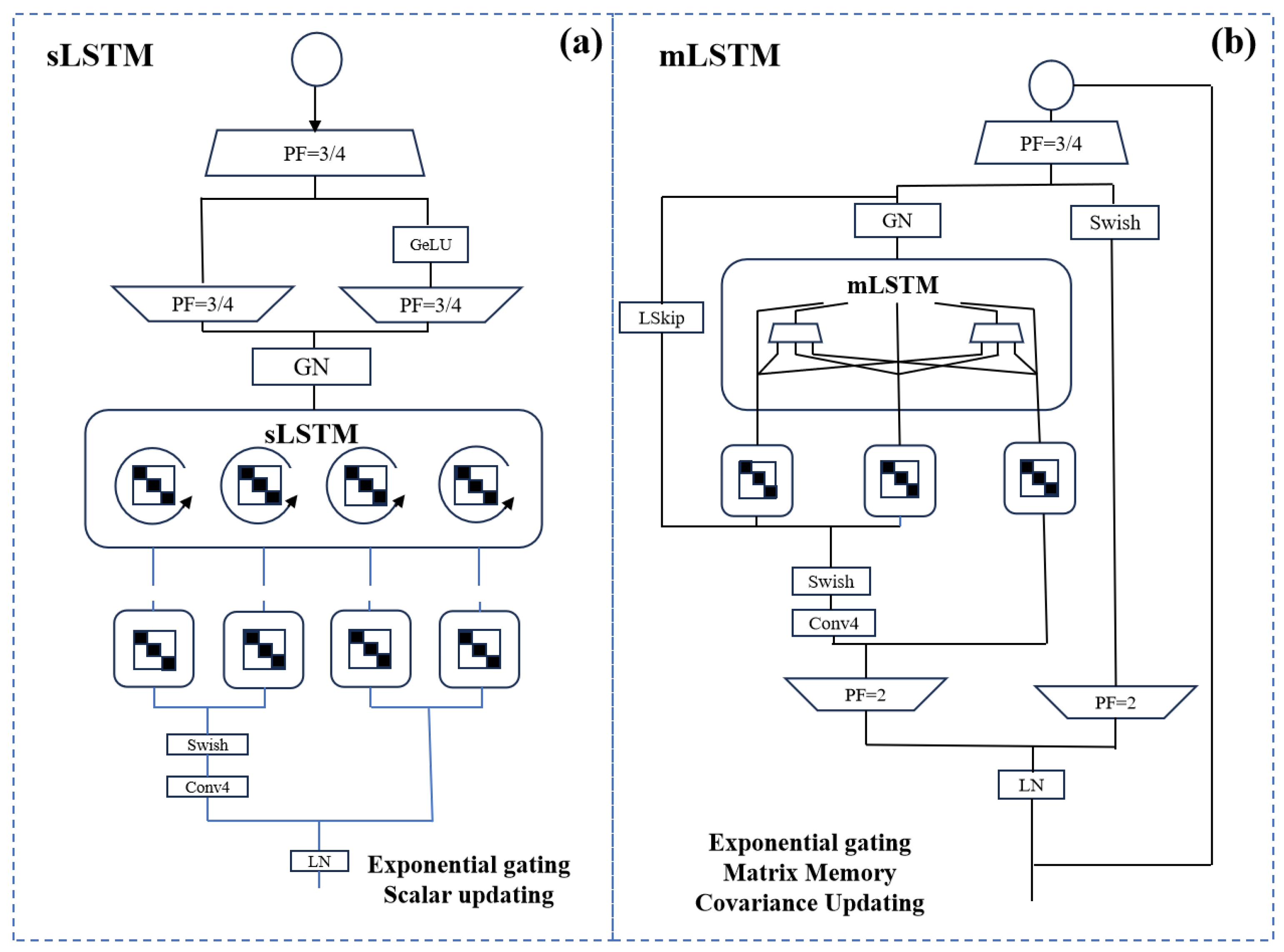
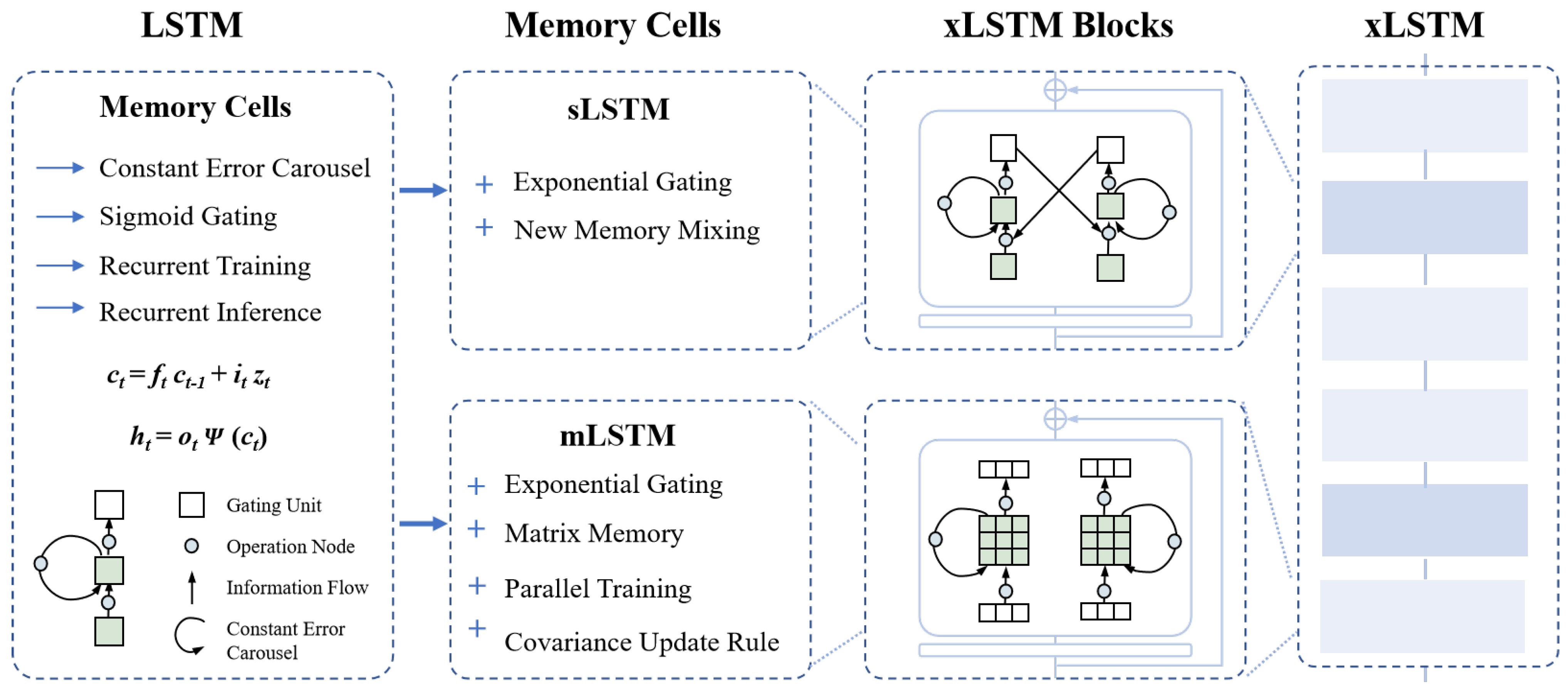
3.2. xLSTM Model
3.3. XGBoost Model
3.4. xLSTM–XGBoost Combined Model Prediction Process
3.5. Evaluation Metrics
4. Experimental Design and Results Analysis
4.1. STL Decomposition of Original Data
4.2. xLSTM Modeling of Trend and Seasonal Values
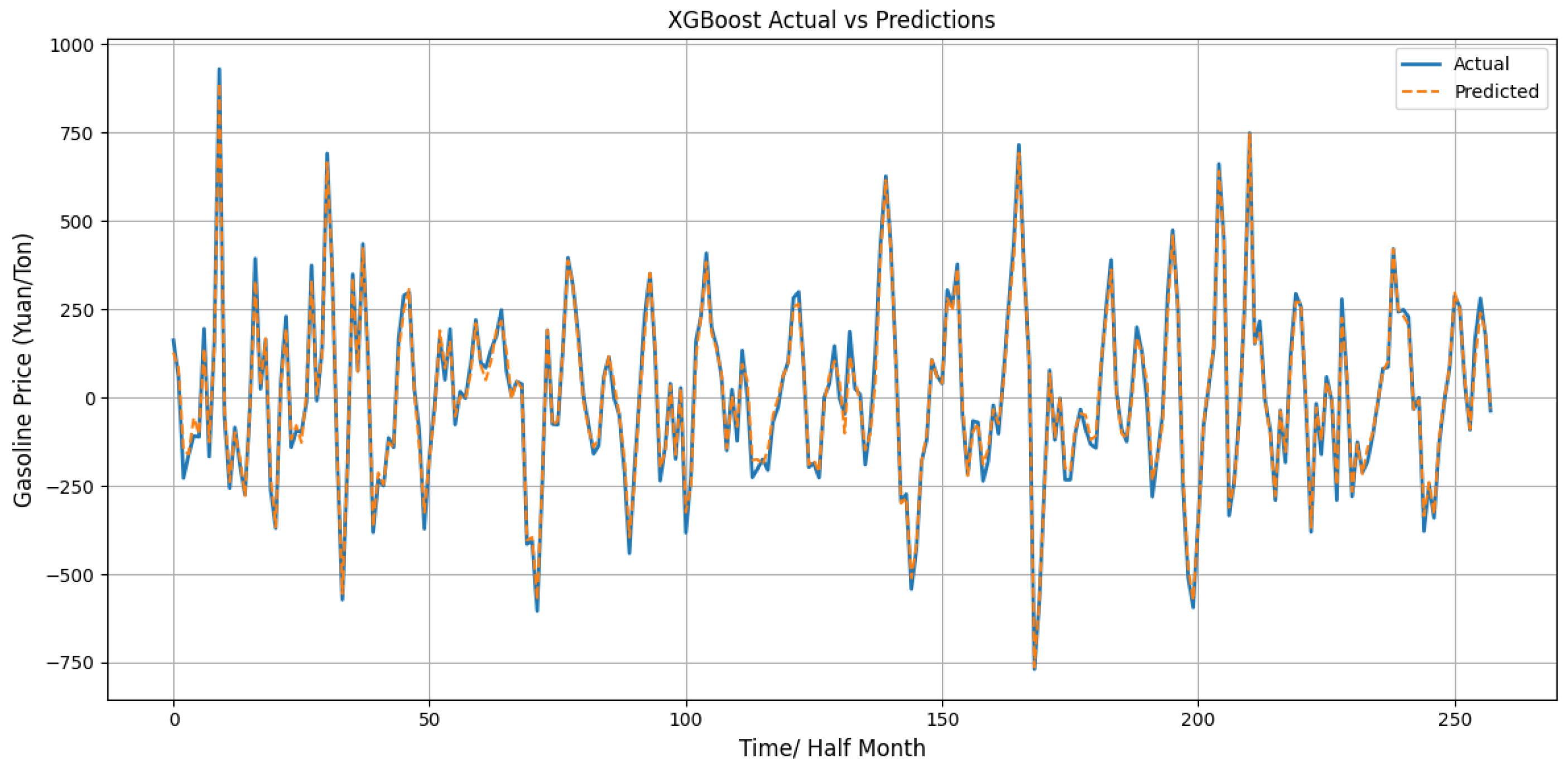
4.3. XGBoost Modeling of Residual Values
4.4. Analysis of Combined Model Prediction Results
4.5. Model Generalization Analysis
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hasanov, F.J.; Javid, M.; Mikayilov, J.I.; Shabaneh, R.; Darandary, A.; Alyamani, R. Macroeconomic and sectoral effects of natural gas price: Policy insights from a macroeconometric model. Energy Econ. 2025, 143, 108233. [Google Scholar] [CrossRef]
- Mao, Z.; Suzuki, S.; Nabae, H.; Miyagawa, S.; Suzumori, K.; Maeda, S. Machine learning-enhanced soft robotic system inspired by rectal functions to investigate fecal incontinence. Bio-Des. Manuf. 2025, 8, 482–494. [Google Scholar] [CrossRef]
- Mao, Z.; Kobayashi, R.; Nabae, H.; Suzumori, K. Multimodal strain sensing system for shape recognition of tensegrity structures by combining traditional regression and deep learning approaches. IEEE Robot. Autom. Lett. 2024, 9, 10050–10056. [Google Scholar] [CrossRef]
- Khanna, A.A.; Dubernet, I.; Jochem, P. Do car drivers respond differently to fuel price changes? Evidence from German household data. Transportation 2025, 52, 579–613. [Google Scholar] [CrossRef]
- Kamocsai, L.; Ormos, M. Modeling gasoline price volatility. Financ. Res. Lett. 2025, 73, 106657. [Google Scholar] [CrossRef]
- Safaei, N.; Zhou, C.; Safaei, B.; Masoud, A. Gasoline prices and their relationship to the number of fatal crashes on US roads. Transp. Eng. 2021, 4, 100053. [Google Scholar] [CrossRef]
- Mao, Z.; Bai, X.; Peng, Y.; Shen, Y. Design, modeling, and characteristics of ring-shaped robot actuated by functional fluid. J. Intell. Mater. Syst. Struct. 2024, 35, 1459–1470. [Google Scholar] [CrossRef]
- Montag, F.; Sagimuldina, A.; Schnitzer, M. Does Tax Policy Work When Consumers Have Imperfect Price Information? Theory and Evidence; Technical Report, CESifo Working Paper; The MIT Press: Cambridge, MA, USA, 2021. [Google Scholar]
- Indrakala, S. A study on mathematical methods for predicting accuracy of crude oil futures prices by multi grey Markov model. Malaya J. Mat. 2021, 9, 621–626. [Google Scholar] [CrossRef]
- Li, W.; Becker, D.M. Day-ahead electricity price prediction applying hybrid models of LSTM-based deep learning methods and feature selection algorithms under consideration of market coupling. Energy 2021, 237, 121543. [Google Scholar] [CrossRef]
- Noel, M. Do retail gasoline prices respond asymmetrically to cost shocks? The influence of Edgeworth Cycles. Rand J. Econ. 2009, 40, 582–595. [Google Scholar] [CrossRef]
- Yoon, S.; Park, M. Prediction of gasoline orders at gas stations in South Korea using VAE-based machine learning model to address data asymmetry. Appl. Sci. 2023, 13, 11124. [Google Scholar] [CrossRef]
- Eliwa, E.H.I.; El Koshiry, A.M.; Abd El-Hafeez, T.; Omar, A. Optimal gasoline price predictions: Leveraging the ANFIS regression model. Int. J. Intell. Syst. 2024, 2024, 8462056. [Google Scholar] [CrossRef]
- He, M.; Qian, X. Forecasting tourist arrivals using STL-XGBoost method. Tour. Econ. 2025, 13548166241313411. [Google Scholar] [CrossRef]
- Cardona, G.A.; Kamale, D.; Vasile, C.I. STL and wSTL control synthesis: A disjunction-centric mixed-integer linear programming approach. Nonlinear Anal. Hybrid Syst. 2025, 56, 101576. [Google Scholar] [CrossRef]
- Luo, S.; Lambert, N.; Liang, P.; Cirio, M. Quantum-classical decomposition of Gaussian quantum environments: A stochastic pseudomode model. PRX Quantum 2023, 4, 030316. [Google Scholar] [CrossRef]
- Singh, S.; Parmar, K.S.; Kumar, J.; Makkhan, S.J.S. Development of new hybrid model of discrete wavelet decomposition and autoregressive integrated moving average (ARIMA) models in application to one month forecast the casualties cases of COVID-19. Chaos Solitons Fractals 2020, 135, 109866. [Google Scholar] [CrossRef] [PubMed]
- Rehman, N.; Mandic, D.P. Multivariate empirical mode decomposition. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 1291–1302. [Google Scholar] [CrossRef]
- Peng, Y.; Yang, X.; Li, D.; Ma, Z.; Liu, Z.; Bai, X.; Mao, Z. Predicting flow status of a flexible rectifier using cognitive computing. Expert Syst. Appl. 2025, 264, 125878. [Google Scholar] [CrossRef]
- Peng, Y.; Sakai, Y.; Funabora, Y.; Yokoe, K.; Aoyama, T.; Doki, S. Funabot-Sleeve: A Wearable Device Employing McKibben Artificial Muscles for Haptic Sensation in the Forearm. IEEE Robot. Autom. Lett. 2025, 10, 1944–1951. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, X.; Rao, M.; Qin, Y.; Wang, Z.; Ji, Y. Explicit speed-integrated LSTM network for non-stationary gearbox vibration representation and fault detection under varying speed conditions. Reliab. Eng. Syst. Saf. 2025, 254, 110596. [Google Scholar] [CrossRef]
- Yuan, F.; Huang, X.; Zheng, L.; Wang, L.; Wang, Y.; Yan, X.; Gu, S.; Peng, Y. The evolution and optimization strategies of a PBFT consensus algorithm for consortium blockchains. Information 2025, 16, 268. [Google Scholar] [CrossRef]
- Wang, X.; Yu, H.; Kold, S.; Rahbek, O.; Bai, S. Wearable sensors for activity monitoring and motion control: A review. Biomim. Intell. Robot. 2023, 3, 100089. [Google Scholar] [CrossRef]
- Wen, X.; Wang, Y.; Zhu, Q.; Wu, J.; Xiong, R.; Xie, A. Design of recognition algorithm for multiclass digital display instrument based on convolution neural network. Biomim. Intell. Robot. 2023, 3, 100118. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Mariappan, Y.; Ramasamy, K.; Velusamy, D. An optimized deep learning based hybrid model for prediction of daily average global solar irradiance using CNN SLSTM architecture. Sci. Rep. 2025, 15, 10761. [Google Scholar] [CrossRef]
- Alharthi, M.; Mahmood, A. xlstmtime: Long-term time series forecasting with xlstm. AI 2024, 5, 1482–1495. [Google Scholar] [CrossRef]
- Schmied, T.; Adler, T.; Patil, V.; Beck, M.; Pöppel, K.; Brandstetter, J.; Klambauer, G.; Pascanu, R.; Hochreiter, S. A Large Recurrent Action Model: xLSTM enables Fast Inference for Robotics Tasks. arXiv 2024, arXiv:2410.22391. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhou, S.; Cheng, D.; Li, J.; Hua, Z. STDF: Joint Spatiotemporal Differences Based on xLSTM Dendritic Fusion Network for Remote Sensing Change Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 1–16. [Google Scholar] [CrossRef]
- Ni, J.; Chen, Y.; Tang, G.; Shi, J.; Cao, W.; Shi, P. Deep learning-based scene understanding for autonomous robots: A survey. Intell. Robot. 2023, 3, 374–401. [Google Scholar] [CrossRef]
- Mao, Z.; Suzuki, S.; Wiranata, A.; Zheng, Y.; Miyagawa, S. Bio-inspired circular soft actuators for simulating defecation process of human rectum. J. Artif. Organs 2025, 28, 252–261. [Google Scholar] [CrossRef]
- Shen, Z.; Jiang, Z.; Zhang, J.; Wu, J.; Zhu, Q. Learning-based robot assembly method for peg insertion tasks on inclined hole using time-series force information. Biomim. Intell. Robot. 2025, 5, 100209. [Google Scholar] [CrossRef]
- Pöppel, K.; Beck, M.; Spanring, M.; Auer, A.; Prudnikova, O.; Kopp, M.K.; Klambauer, G.; Brandstetter, J.; Hochreiter, S. xlstm: Extended long short-term memory. In Proceedings of the First Workshop on Long-Context Foundation Models@ ICML 2024, Vienna, Austria, 21–27 July 2024. [Google Scholar] [CrossRef]
- Kühne, N.L.; Østergaard, J.; Jensen, J.; Tan, Z.H. xLSTM-SENet: xLSTM for Single-Channel Speech Enhancement. arXiv 2025, arXiv:2501.06146. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Zhang, X.; Feng, H. Multi-scale Attention-based xLSTM for Rolling Bearing Fault diagnosis. Meas. Sci. Technol. 2025, 36, 066116. [Google Scholar] [CrossRef]
- He, H.; Liao, R.; Li, Y. MSAFNet: A novel approach to facial expression recognition in embodied AI systems. Intell. Robot. 2025, 5, 313–332. [Google Scholar] [CrossRef]
- Li, J.; Yang, S.X. Digital twins to embodied artificial intelligence: Review and perspective. Intell. Robot. 2025, 5, 202–227. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Dhaliwal, S.S.; Nahid, A.A.; Abbas, R. Effective intrusion detection system using XGBoost. Information 2018, 9, 149. [Google Scholar] [CrossRef]
- Li, J.; An, X.; Li, Q.; Wang, C.; Yu, H.; Zhou, X.; Geng, Y.a. Application of XGBoost algorithm in the optimization of pollutant concentration. Atmos. Res. 2022, 276, 106238. [Google Scholar] [CrossRef]
- Mavrogiorgos, K.; Kiourtis, A.; Mavrogiorgou, A.; Menychtas, A.; Kyriazis, D. Bias in Machine Learning: A Literature Review. Appl. Sci. 2024, 14, 8860. [Google Scholar] [CrossRef]






| Model | Full Name | Key Improvements | Suitable Scenarios | Advantages |
|---|---|---|---|---|
| LSTM | Long Short-Term Memory | Gating mechanism to suppress gradient vanishing | Sequence modeling, language models, time series | Stable and widely used |
| xLSTM | Extended LSTM | Additional context connections, deeper architecture | Long-range dependencies, complex contexts | Enhanced ability to model long-term dependencies |
| mLSTM | Multiplicative LSTM | Multiplicative interaction between input and hidden state | Language modeling, NLP | Stronger expressiveness and flexible information control |
| sLSTM | Structural/Spatial LSTM | Modeling structural or spatial dependencies (e.g., graphs) | GNNs, image and video analysis | Capable of handling dependencies in non-sequential data |
| Models | MAE | RMSE | |
|---|---|---|---|
| LSTM | 0.3443 | 0.4137 | 0.9168 |
| xLSTM | 0.0914 | 0.1118 | 0.9948 |
| sLSTM | 0.1092 | 0.1321 | 0.9929 |
| mLSTM | 0.1222 | 0.1468 | 0.9911 |
| Models | MAE | RMSE | Training Time (s) | |
|---|---|---|---|---|
| LSTM | 0.5644 | 0.6175 | 0.8041 | 35.2 |
| xLSTM | 0.3114 | 0.3906 | 0.9216 | 48.6 |
| sLSTM | 0.2506 | 0.3192 | 0.9476 | 45.9 |
| mLSTM | 0.2619 | 0.3293 | 0.9442 | 49.7 |
| ARIMA | 0.6396 | 0.7203 | 0.7283 | 6.3 |
| CNN | 0.4178 | 0.5231 | 0.1486 | 38.4 |
| ELM | 0.3130 | 0.4257 | 0.9154 | 12.5 |
| LSTM–XGBoost | 0.1949 | 0.2298 | 0.9782 | 59.8 |
| sLSTM–XGBoost | 0.1129 | 0.1389 | 0.9920 | 57.3 |
| mLSTM–XGBoost | 0.1279 | 0.1547 | 0.9901 | 61.2 |
| xLSTM–XGBoost | 0.0961 | 0.1184 | 0.9942 | 63.9 |
| Model | t-Test p (MAE) | t-Test p (RMSE) |
|---|---|---|
| LSTM | ||
| xLSTM | ||
| sLSTM | ||
| mLSTM | ||
| ARIMA | ||
| CNN | ||
| ELM | ||
| LSTM–xgboost | ||
| sLSTM–xgboost | ||
| mLSTM–xgboost |
| Models | MAE | RMSE | |
|---|---|---|---|
| LSTM–XGBoost | 0.5581 | 0.5827 | 0.8258 |
| sLSTM–XGBoost | 0.1275 | 0.1476 | 0.9889 |
| mLSTM–XGBoost | 0.1113 | 0.1297 | 0.9913 |
| xLSTM–XGBoost | 0.1091 | 0.1274 | 0.9917 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, F.; Huang, X.; Jiang, H.; Jiang, Y.; Zuo, Z.; Wang, L.; Wang, Y.; Gu, S.; Peng, Y. An xLSTM–XGBoost Ensemble Model for Forecasting Non-Stationary and Highly Volatile Gasoline Price. Computers 2025, 14, 256. https://doi.org/10.3390/computers14070256
Yuan F, Huang X, Jiang H, Jiang Y, Zuo Z, Wang L, Wang Y, Gu S, Peng Y. An xLSTM–XGBoost Ensemble Model for Forecasting Non-Stationary and Highly Volatile Gasoline Price. Computers. 2025; 14(7):256. https://doi.org/10.3390/computers14070256
Chicago/Turabian StyleYuan, Fujiang, Xia Huang, Hong Jiang, Yang Jiang, Zihao Zuo, Lusheng Wang, Yuxin Wang, Shaojie Gu, and Yanhong Peng. 2025. "An xLSTM–XGBoost Ensemble Model for Forecasting Non-Stationary and Highly Volatile Gasoline Price" Computers 14, no. 7: 256. https://doi.org/10.3390/computers14070256
APA StyleYuan, F., Huang, X., Jiang, H., Jiang, Y., Zuo, Z., Wang, L., Wang, Y., Gu, S., & Peng, Y. (2025). An xLSTM–XGBoost Ensemble Model for Forecasting Non-Stationary and Highly Volatile Gasoline Price. Computers, 14(7), 256. https://doi.org/10.3390/computers14070256








