Abstract
To address critical challenges in tiny object detection within remote sensing imagery, including resolution–semantic imbalance, inefficient feature fusion, and insufficient localization accuracy, this study proposes Hierarchical Feature Compensation You Only Look Once 11 (HFC-YOLO11), a lightweight detection model based on hierarchical feature compensation. Firstly, by reconstructing the feature pyramid architecture, we preserve the high-resolution P2 feature layer in shallow networks to enhance the fine-grained feature representation for tiny targets, while eliminating redundant P5 layers to reduce the computational complexity. In addition, a depth-aware differentiated module design strategy is proposed: GhostBottleneck modules are adopted in shallow layers to improve its feature reuse efficiency, while standard Bottleneck modules are maintained in deep layers to strengthen the semantic feature extraction. Furthermore, an Extended Intersection over Union loss function (EIoU) is developed, incorporating boundary alignment penalty terms and scale-adaptive weight mechanisms to optimize the sub-pixel-level localization accuracy. Experimental results on the AI-TOD and VisDrone2019 datasets demonstrate that the improved model achieves mAP50 improvements of 3.4% and 2.7%, respectively, compared to the baseline YOLO11s, while reducing its parameters by 27.4%. Ablation studies validate the balanced performance of the hierarchical feature compensation strategy in the preservation of resolution and computational efficiency. Visualization results confirm an enhanced robustness against complex background interference. HFC-YOLO11 exhibits superior accuracy and generalization capability in tiny object detection tasks, effectively meeting practical application requirements for tiny object recognition.
1. Introduction
With the continuous advancement in high-resolution remote sensing technology, the abundant image data acquired by unmanned aerial vehicles (UAVs) and satellite platforms has provided critical information support for smart city management, ecological conservation, and national security [1,2,3,4]. However, the precise detection of tiny objects (e.g., vehicle wreckage, unauthorized structures, and specific vegetation patches) remains a significant challenge in time-sensitive scenarios such as disaster emergency response, transportation infrastructure monitoring, and agricultural and forestry resource surveys. These targets typically occupy imaging areas of merely 10 to 30 pixels, exhibiting characteristics of a low signal-to-noise ratio, weak textural features, and a dense spatial distribution under complex background interference and variable lighting conditions [5,6,7]. Traditional detection methods relying on handcrafted features (e.g., HOG [8], SIFT [9]) and sliding window search strategies [10] face dual bottlenecks of an inadequate feature representation and low computational efficiency when processing remote sensing images with large-scale and multi-channel characteristics. Although deep learning techniques have significantly improved their detection accuracy through end-to-end feature learning, the existing models still suffer from resolution–semantic imbalance, inefficient multi-scale feature fusion, and cumulative sub-pixel localization errors in remote sensing small object detection tasks [11,12].
Current mainstream detection frameworks can be primarily classified into two technical paradigms, two-stage and single-stage detectors, both exhibiting inherent limitations in remote sensing small object detection. Representative two-stage detectors like Faster R-CNN [13] and its derivatives (Mask R-CNN [14], Cascade R-CNN [15], etc.) employ Region Proposal Networks (RPNs) to generate candidate regions, followed by refined feature extraction for high-precision detection. Although these methods demonstrate excellent performance in general object detection, their cascaded processing pipeline results in an elevated computational latency, making them unsuitable for UAV real-time inspection requirements. Single-stage detectors, exemplified by the YOLO series and RetinaNet, achieve efficient detection through fully convolutional architectures, yet their feature pyramid designs present specific limitations. The multi-scale prediction mechanism in YOLOv3/v4 implements information fusion through simple feature concatenation, leading to an insufficient interaction between shallow-level details and deep-level semantics [16]. While RetinaNet mitigates class imbalance through Focal Loss, its feature pyramid lacks dynamic modulation capabilities in cross-layer feature compensation [17].
In terms of feature enhancement for object detection models, Wang proposed to improve small object visibility through super-resolution reconstruction preprocessing, but the additional network branches double the end-to-end training complexity [18]. Zhang developed a Densely Connected Feature Pyramid Network (DC-FPN) to enhance the cross-layer information flow, though its increased parameter count compared to conventional FPN hinders lightweight deployment requirements [19]. Regarding loss function optimization, the CIoU loss proposed by Zheng improves small object localization accuracy by incorporating center distance and aspect ratio constraints compared with traditional IoU, yet its indirect optimization approach to edge alignment errors shows an insufficient sub-pixel deviation correction capability [20]. For optimization of its efficiency, Tang employed Neural Architecture Search (NAS) techniques to compress the model’s scale, but the automatically generated architectures exhibit poor generalization in remote sensing data domains [21].
To address the aforementioned challenges, this study proposes a Hierarchical Feature Compensation Network model (HFC-YOLO11) that enhances the detection capability for tiny remote sensing targets without significantly increasing the model’s complexity through the reconstruction of the feature pyramid architecture, design of a bidirectional dynamic compensation mechanism, and improvement of loss functions. The main contributions of this paper are as follows:
- Compared with traditional P3\P4\P5 layers, we add a P2 layer to extract finer features at high-resolution stages while removing the P5 layer, effectively reducing the model’s parameters and computational load. This modification improves small object detection’s accuracy through enhanced feature granularity;
- A depth-aware heterogeneous architecture is developed by implementing GhostBottleneck in shallow layers and Bottleneck in deep layers. This design achieves the dynamic balancing of computational resources: GhostBottleneck efficiently processes abundant basic features in shallow networks, reducing unnecessary computations, while Bottleneck thoroughly explores complex semantic features in deep networks to ensure accuracy of recognition;
- An EIoU loss function is proposed, which innovatively integrates direct boundary alignment penalty terms and scale-adaptive weighting mechanisms into the CIoU geometric constraint framework. This advancement explicitly optimizes the coordinate errors of all four bounding box edges, while dynamically amplifying the loss contributions of small targets based on their areas.
The remainder of this paper is organized as follows: Section 2 reviews related work. Section 3 provides detailed descriptions of the proposed model and its improvements. Section 4 presents comparative experiments, ablation studies, and visualizations of the results. Finally, Section 5 concludes this research.
2. Related Work
2.1. Single-Stage Detection Models
Current object detection methods are primarily categorized into multi-stage and single-stage paradigms. Multi-stage approaches, such as Faster R-CNN and Mask R-CNN, achieve high-precision detection through Region Proposal Networks (RPNs) and refined classification–regression pipelines. However, their cascaded workflows result in a low computational efficiency, failing to meet real-time requirements [22,23,24].
Single-stage detection frameworks, predominantly represented by the YOLO series, employ fully convolutional architectures for end-to-end detection inference, demonstrating significant advantages in computational efficiency and models’ lightweightness [25]. YOLOv1 pioneered object detection as a regression task, but its fully connected layers caused spatial information loss [26]. YOLOv2 introduced anchor mechanisms and batch normalization, yet a limited network depth constrained semantic feature extraction [27]. YOLOv3 adopted Darknet-53 and feature pyramids but suffered from inefficient cross-scale feature fusion [28]. YOLOv4 improved the computational efficiency via CSPDarknet53 and SPP-PANet modules, at the cost of lightweight potential [29]. YOLOv5 enhanced its engineering practicality with Mosaic data augmentation and adaptive anchors, though its Focus operation introduced noise risks [30]. YOLOv6 achieved hardware-level optimization through re-parameterizable designs but exhibited poor adaptability to dynamic scenes [31]. YOLOv7 strengthened its feature representation via ELAN networks, yet increased its complexity with multi-branch structures [32]. YOLOv8 improved occluded object detection using Transformer modules but required excessive GPU memory [33]. YOLOv9 proposed programmable gradient information mechanisms but slowed its training convergence [34]. YOLOv10 achieved NMS-free end-to-end training but relied on multi-modal data [35]. As the latest iteration in the Ultralytics YOLO series, YOLO11 enhances its feature extraction capabilities through an optimized backbone and neck architectures, improving its detection accuracy and performance in complex tasks [36].
Beyond the YOLO series, other single-stage detectors include SSD (Single Shot MultiBox Detector), which predicts objects directly via multi-scale feature maps but struggles with insufficient semantic information in shallow layers, degrading its small object detection [37]. RetinaNet addressed class imbalance via Focal Loss, yet its feature pyramid’s static weighting allocation limited its multi-scale adaptability [38]. EfficientDet optimized feature pyramids and scaling strategies through Neural Architecture Search (NAS), but its automated architectures showed poor generalization on remote sensing data. Meanwhile, its computational cost is high [39]. NanoDet achieved extreme lightweightness via depthwise separable convolutions and dynamic label assignment, at the expense of distinguishing densely distributed small targets [40]. Considering the low signal-to-noise ratios and dense distribution characteristics of tiny objects in remote sensing imagery, along with the trade-offs among the existing methods, this study selects the lightweight YOLO11 as the baseline model.
2.2. Loss Functions for Object Detection
Breakthroughs in object detection performance have been intrinsically linked to innovations in bounding box regression loss functions. From intuitive geometric overlap metrics to refined distribution-matching modeling, this research domain has evolved along a clear trajectory: enhancing the accuracy of localization, while balancing the inherent trade-offs between small object sensitivity and computational efficiency.
The Intersection over Union (IoU) metric, as a foundational similarity measure for bounding boxes, established scale invariance through area overlap calculations [41]. However, its inherent limitations include gradients vanishing in non-overlapping scenarios and the inability to capture geometric properties like center offset and aspect ratio differences. The Generalized IoU (GIoU) proposed by Rezatofighi [42] introduced a minimum enclosing box penalty mechanism to enable gradient propagation in non-overlapping regions, yet it revealed the limitations of geometric bounding box theory through performance degradation in highly overlapping scenarios and weak error responses for small objects. Zheng subsequently developed a DIoU-CIoU collaborative optimization framework: DIoU accelerates the model’s convergence via explicit constraints on the normalized center distance, while CIoU incorporates aspect ratio angular deviation penalties, transforming the bounding box regression from single overlap metrics to multi-dimensional geometric feature optimization [43,44]. Nevertheless, their indirect edge position constraints result in insufficient sub-pixel deviation correction capabilities, particularly prone to accumulation of errors in dense small object scenarios. For rotated object detection, the SIoU proposed by Gevorgyan [45] integrates orientation deviation into the loss function through angular cost terms to guide rotation-invariant feature learning, yet it introduces model complexity via additional parameters and risks optimization conflicts from coupled size constraints.
The inadequate small object sensitivity of traditional IoU-based methods has driven the exploration of paradigms beyond geometric overlap. The Normalized Wasserstein Distance (NWD) developed by Wang [46] enhances small object error responses through Gaussian distribution modeling and Wasserstein metrics, but it incurs directional information loss and elevated computational costs under distribution assumptions.
The existing methods face three challenges in balancing geometric sensitivity and computational efficiency. Indirect feature optimization fails to achieve explicit edge alignment control; distribution matching enhances small object sensitivity at the expense of boundary constraint strength and computational efficiency; and static weighting strategies cannot adapt to multi-scale dynamic optimization requirements. To address these limitations, this study proposes an EIoU loss that directly optimizes edge positions through coordinate errors of all four bounding box boundaries, combined with a target-scale-adaptive dynamic weighting mechanism. Inheriting the CIoU geometric constraint framework, our method achieves a synergistic improvement in pixel-level localization accuracy and small object sensitivity.
2.3. GhostNet and Cheap Operations
GhostNet, as a lightweight neural network architecture, achieves its core innovation through the efficient generation and utilization of feature maps, which reduces computational costs and parameter quantities while maintaining the model’s performance [47]. The concept of “cheap operations” in this context does not imply a low model quality but rather emphasizes a capability for high-efficiency feature extraction with low computational resource consumption.
Traditional convolutional neural networks typically require extensive convolution operations to generate rich feature maps during feature extraction, leading to a significant computational overhead and parameter redundancy. In contrast, GhostNet employs linear transformations on a small set of primitive feature maps to produce numerous “ghost” feature maps. These ghost features, combined with the original ones, collectively form a comprehensive feature representation. By leveraging the low computational complexity of linear transformations, GhostNet accomplishes feature map expansion at a minimal computational cost, thereby reducing the network’s overall computational burden and parameter count.
In shallow-layer networks where the network depth is limited, the computational capacity and feature extraction ability of each layer remain relatively constrained. While traditional deep networks rely on layer stacking to obtain complex feature representations, shallow networks with fewer layers may encounter an insufficient feature extraction or prohibitively high computational costs when using conventional convolution operations. GhostNet’s design principles inherently align with these characteristics of shallow architectures.
From the perspective of feature generation, shallow networks must extract representative features as efficiently as possible within limited layers. The Ghost module addresses this by generating ghost feature maps through linear transformations of primitive features, enabling the creation of sufficiently diverse feature representations at low computational costs in shallow networks. Furthermore, computational efficiency analysis reveals that replacing traditional convolution modules with Ghost modules in each layer of shallow networks can reduce the overall computational complexity of the network.
3. Proposed Model
3.1. YOLO11 Baseline Model
YOLO11, as the latest iteration in the Ultralytics YOLO series, employs optimized backbone and neck architectures to enhance its feature extraction capabilities, thereby improving its detection accuracy and performance in complex tasks [47]. Its streamlined architecture design and optimized training protocols achieve accelerated processing speeds, while maintaining a balance between precision and computational efficiency. This architectural innovation primarily manifests itself in three core components. The backbone network replaces conventional C2f structures with redesigned C3k2 modules, improving the parameter efficiency while preserving the feature extraction capacity. A novel Cross-Stage Partial Pyramid Spatial Attention (C2PSA) module is introduced after the SPPF layer, integrating pyramid spatial attention mechanisms with cross-stage partial connections. This design dynamically recalibrates multi-scale spatial features to address detection challenges in complex scenarios. The C2PSA module achieves global interaction modeling across feature subspaces through a coordinated multi-head self-attention architecture and enhanced feed-forward neural networks. Embedded residual connections optimize gradient flow characteristics during backpropagation, while preserving the fine-grained spatial information critical for target localization. The detection head incorporates depthwise separable convolutions that significantly reduce the computational overhead without compromising the representational power.
As illustrated in Figure 1, despite notable advancements in object detection, YOLO11 exhibits limitations in its small object detection performance. Increasing the model’s depth risks the feature loss of small targets or interference from background noise, necessitating the effective retention of small object feature information throughout the network.
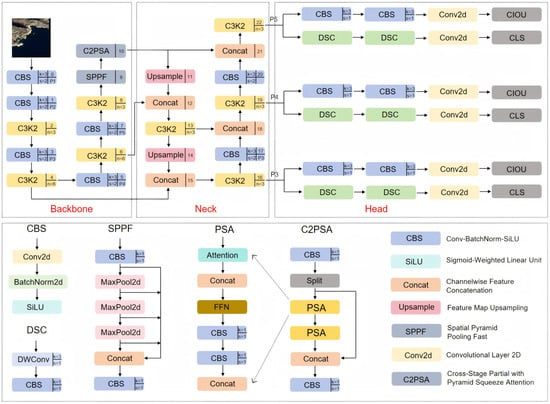
Figure 1.
Architectural diagram of the YOLO11 model.
When configured with C3k = false, the module employs standard Bottleneck layers, making it architecturally identical to the C2f module in YOLOv8 through preserved residual connections and feature fusion pathways. When activated with C3k = true, the implementation replaces the Bottleneck modules with a C3k module composed of multiple stacked Bottleneck modules with interleaved group convolutions. This parameter-controlled architecture enables flexible feature representation scaling. The detailed architectural configurations under different parameter settings are illustrated in Figure 2.
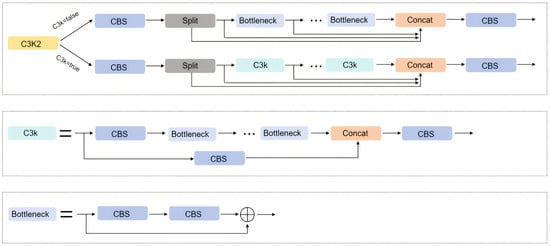
Figure 2.
Architectural diagram of the C3K2 model.
3.2. HFC-YOLO11 Architecture
To address the challenge of small object detection in remote sensing imagery, we propose a hierarchical optimization strategy based on feature pyramid reconstruction. Conventional detection networks tend to lose critical high-resolution details from shallow layers during deep feature abstraction, while the spatial sensitivity of high-level features with receptive fields significantly diminishes for small targets.
The proposed methodology fundamentally reconfigures the feature representation by preserving the P2 high-resolution feature layer in shallow networks to capture sub-pixel-level texture details, while eliminating the redundant P5 abstraction layer to suppress background noise interference. This dual-strategy optimization achieves synergistic improvements in detection accuracy and computational efficiency [48], formally designated as the High-Resolution Shallow (HRS) enhancement.
The core mechanism of the feature pyramid reconstruction lies in establishing a hierarchical feature selection framework. Through two sequential upsampling operations, the feature map resolution is progressively enhanced and subsequently fused with the original P2 features. Concurrent architectural adjustments optimize the inter-branch connectivity: the P2 branch channel dimension is configured at 128 to prioritize the preservation of spatial detail, while the P3 and P4 branches are set at 256 and 512 channels, respectively, to balance semantic abstraction.
As the foundational feature extractor, the P2 layer’s enhanced spatial resolution (1/4 input scale) effectively preserves the critical discriminative characteristics of micro-targets, including edge gradients and local contrast patterns. Conversely, the eliminated P5 layer exhibits two inherent limitations in small object detection: excessive receptive fields that submerge local details within global contextual noise and cumulative non-linear distortions in deep network layers that compromise the geometric fidelity of small targets.
To further enhance the model’s compactness while maintaining precision in detection, we implement a heterogeneous Bottleneck configuration. GhostBottleneck modules replace standard Bottleneck components in shallow C3k2 layers, while retaining the original Bottleneck modules in deep network layers to preserve high-level semantic representation. This stratified Bottleneck strategy synergistically reduces the model’s complexity.
A final performance optimization is accomplished through our proposed EIoU loss function. The comprehensive architectural configuration is illustrated in Figure 3.
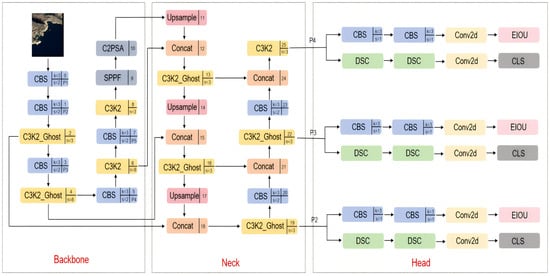
Figure 3.
Architectural diagram of the HFC-YOLO11 model.
3.3. GhostBottleneck Module
The GhostBottleneck module originates from the innovative design philosophy of GhostNet, with its core innovation lying in the fundamental optimization of convolutional operations [49]. Traditional convolutional layers exhibit substantial redundant computations during feature extraction, while GhostConv addresses this limitation through an efficient two-stage process, generating base feature maps via minimal essential convolutions, followed by linear combinations to produce supplementary feature representations. This approach inherently reduces the computational complexity, while maintaining features’ expressiveness. Specifically, GhostConv implements a dual-path architecture that synergizes base feature mapping with dynamically generated phantom features. The primary path executes sparse convolutional operations to capture critical feature patterns, while the secondary path applies lightweight linear transformations to expand the features’ diversity.
In the shallow-network stages of the YOLO11 model, input images retain large spatial dimensions and contain abundant foundational features. The conventional Bottleneck architecture induces excessive computational demands through its dense convolutional operations, resulting in resource inefficiency and a degradation in processing speed. The GhostBottleneck module addresses these limitations by integrating lightweight convolutional components (GhostConv and DWconv), which reduces the computational complexity and memory footprint. This architectural modification enables the rapid extraction of primary image features in shallow layers, establishing computationally efficient initial representations for subsequent feature processing and object detection. The generation of supplementary feature maps through linear combinations of base features enhances multi-scale feature utilization for small targets. Such a hierarchical feature enrichment improves the preliminary localization accuracy for micro-objects, while maintaining structural simplicity.
As the network depth increases, the feature map dimensions progressively contract, while the channel depth expands exponentially, necessitating the sophisticated processing of complex semantic information. The conventional convolutional layers in Bottleneck architectures demonstrate superior capability in capturing global inter-feature correlations through systematic feature transformation. The modified model architecture is illustrated in Figure 4.
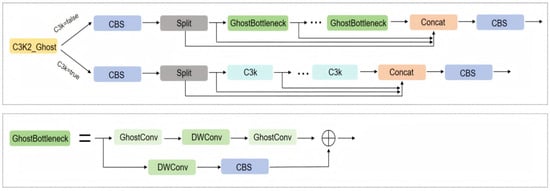
Figure 4.
Architectural diagram of the C3K3_Ghost model.
3.4. EIoU Loss Function
Let the predicted bounding box parameters be denoted as A = (x₁, y₁, w₁, h₁) and the ground truth bounding box parameters as B = (x₂, y₂, w₂, h₂), where (x, y) represent the centroid coordinates, and (w, h) specify the width and height dimensions, respectively.
The CIoU computation comprises three principal components, the Intersection-over-Union (IoU) metric, a centroid displacement penalty term, and an aspect ratio discrepancy penalty term, as formalized in Equation (1).
where IoU represents the Intersection over Union, ρ2 represents the squared Euclidean distance between centers, c2 represents the squared diagonal length of the minimum enclosing box, v represents the aspect ratio discrepancy term, and α represents the dynamic weighting coefficient.
In object detection tasks, the Intersection over Union (IoU) metric is utilized to quantify the spatial overlap between anchor boxes and ground truth boxes. The IoU is mathematically defined as the ratio of intersection area to union area, as formalized in Equation (2).
To quantify the centroid deviation between predicted and ground truth boxes, the squared Euclidean distance between centers (ρ2) is computed. The minimization of this metric constrains the predicted box to progressively converge toward the ground truth centroid, as formulated in Equation (3).
To normalize the centroid distance and the mitigate scale sensitivity, the squared diagonal length of the minimum enclosing box (c2) is computed, as formulated in Equations (4)–(6).
where width represents the computed x-axis dimension of the minimum enclosing box, and height represents the corresponding y-axis dimension.
To quantify the aspect ratio discrepancy between the predicted and ground truth boxes, the angular difference is projected onto the [0, 1] interval to achieve normalization. Simultaneously, the aspect ratio (w/h) is converted into angular representation to eliminate scale dependency. This process introduces the aspect ratio discrepancy term v, as formulated in Equation (7).
A dynamic weighting coefficient (α) is introduced to adaptively adjust the penalty weight according to the current IoU and aspect ratio discrepancy. When the IoU is low, α increases to emphasize the aspect ratio’s optimization; when the IoU is elevated, α decreases to prioritize centroid alignment, as mathematically defined in Equation (8).
where ε represents an infinitesimal constant to prevent division by zero.
The proposed EIoU loss function retains all the components of the original CIoU formulation, while incorporating a novel edge-alignment penalty term to directly optimize edge localization. This enhancement significantly improves the pixel-level localization accuracy for small targets. Furthermore, the loss contribution is adaptively scaled according to the target area, which amplifies edge displacement errors in small objects and enhances the model’s sensitivity. The complete mathematical formulation is presented in Equations (9) and (10).
where e1i represents the edge coordinates of the predicted bounding box, and e2i represents the corresponding edge coordinates of the ground truth bounding box; S is defined as the normalized area of the ground truth bounding box. As the target area S decreases, the weighting factor increases proportionally, thereby amplifying the contribution of edge displacement errors. The coefficient λ regulates the intensity of the edge penalty term.
Figure 5a shows a schematic diagram of the CIoU loss function, and Figure 5b shows a schematic diagram of the EIoU loss function. The triangle represents the midpoint of the prediction box and the bounding box.
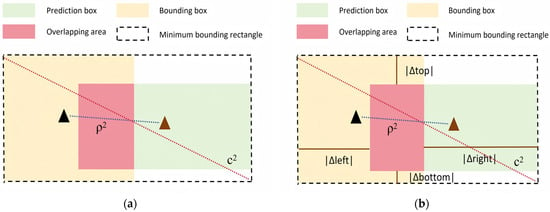
Figure 5.
(a) CIoU loss function; (b) EIoU loss function.
4. Experiments
4.1. Experimental Environment and Parameters
To systematically evaluate the performance advantages of the HFC-YOLO11 model in small remote sensing object detection tasks, we conducted a comprehensive validation using a benchmark remote sensing detection dataset. The experiments were implemented on the TensorFlow 2.12.0 deep learning framework, with the detailed hardware configurations and hyperparameter settings summarized in Table 1.

Table 1.
Experimental environment.
4.2. Experimental Datasets
4.2.1. AI-TOD Dataset
The AI-TOD dataset is a specialized benchmark designed for small object detection in aerial imagery, comprising 28,036 high-resolution aerial images with 700,621 annotated object instances across eight typical remote sensing categories (e.g., person, vehicle, ship) [50]. Its defining characteristic lies in the exceptionally small target dimensions—averaging merely 12.8 pixels (approximately 1/8 of the target size in conventional aerial detection datasets)—which poses substantial challenges to detection algorithms. The dataset is partitioned into training (11,214 images), validation (2804 images), and test (14,018 images) subsets. Figure 6 illustrates the statistical distribution of the training set.
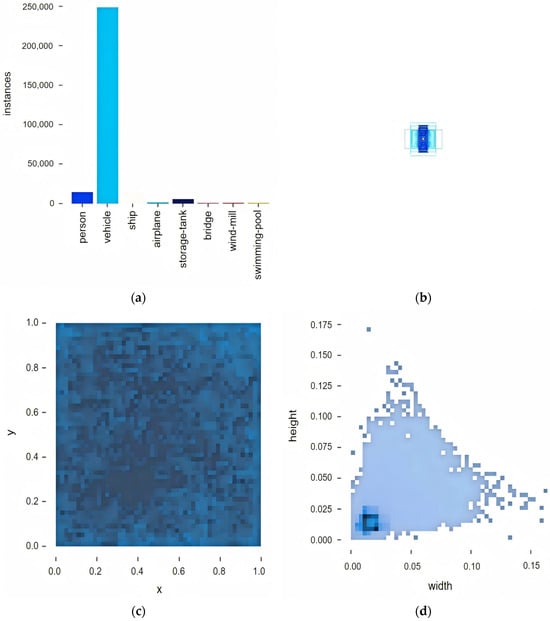
Figure 6.
Distribution of AI-TOD datasets. (a) visualizes that the class distribution histogram reveals a significant class imbalance, which critically challenges the model’s feature generalization capabilities; (b) visualizes the size-frequency distribution of the bounding boxes, showing that the majority of instances are predominantly composed of small-scale targets; (c) visualizes the spatial distribution of instance centroids through scatter plots, exhibiting a homogeneous distribution across the image domain, while revealing no spatial bias in the dataset; (d) quantifies the width-to-height ratio distribution of targets relative to image dimensions.
4.2.2. VisDrone2019 Dataset
The VisDrone2019 dataset represents a seminal open benchmark in UAV remote sensing, jointly established in 2019 by Tianjin University’s Machine Learning and Data Mining Laboratory and multiple research institutions [51]. Constructed through multi-platform UAV deployments across distinct geographical regions (including urban, suburban, and rural environments), this dataset comprehensively captures complex environmental characteristics under authentic remote sensing scenarios. It contains 8629 high-resolution static images (ranging from 960 × 540 to 4000 × 3000 pixels), partitioned into training (6471 images), validation (548 images), and test (1610 images) subsets. All the data underwent rigorous geospatial registration and radiometric calibration. Figure 7 presents the statistical profile of the training set.
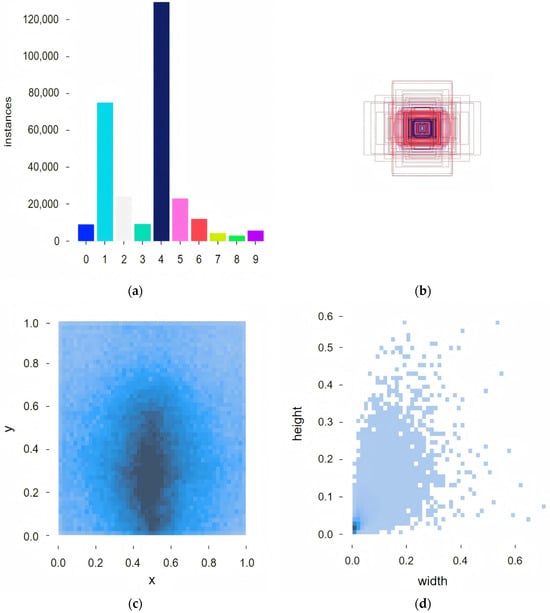
Figure 7.
Distribution of VisDrone datasets. (a) visualizes that the class distribution; (b) visualizes the size-frequency distribution; (c) visualizes the spatial distribution; (d) quantifies the width-to-height ratio distribution.
4.3. Evaluation Metrics
The experiment employs seven quantitative metrics to assess the model’s performance: precision (P), recall (R), F1-score, mAP50, mAP50-95, floating-point operations (FLOPs), and parameter count.
Precision quantifies the ratio of correctly identified positive instances to all predicted positives, reflecting the reliability of positive class predictions and the system’s robustness against false-positive interferences. Recall quantifies the proportion of true positives successfully retrieved from all actual positives, characterizing the model’s coverage capability for ground-truth positives. The F1-score, as the harmonic mean of precision and recall, is employed to balance their relative importance. This metric enables a balanced performance evaluation when models exhibit imbalanced metric distributions. mAP (mean average precision) quantifies the averaged detection accuracy across all object categories. The FLOPs quantifies computational complexity through floating-point operations, while parameter count enumerates all trainable parameters in the network architecture.
These metrics collectively measure the detection accuracy, operational efficiency, and computational complexity of models, providing a comprehensive quantitative assessment for algorithm improvements’ effectiveness. The mathematical formulations of these metrics are provided below.
In the formulations, TP (true positive) represents correctly identified positive instances, FP (false positive) represents negative samples erroneously classified as positive, and FN (false negative) represents positive instances either undetected or misclassified as negative. P(r) represents the precision–recall curve, AP represents the average precision for the i-th object category, and k represents the total number of target classes.
4.4. Experimental Results
To validate the effectiveness of the proposed architectural modifications, we implemented our improvements across three YOLO11 variants: YOLO11n, YOLO11s, and YOLO11m. The enhanced models were designated as HFC-YOLO11n, HFC-YOLO11s, and HFC-YOLO11m, respectively. Comparative experiments were conducted under identical training parameters and dataset conditions. Table 2 summarizes a quantitative comparison of the key performance metrics across these architectures.

Table 2.
Comparison of improvement strategies in YOLO11 series models on AI-TOD.
As evidenced in Table 2, our enhancement strategy yielded consistent accuracy improvements, while achieving a significant parameter reduction across all model scales. Based on the optimal balance between detection accuracy and architectural efficiency, HFC-YOLO11s was selected as the final proposed model in this study.
To further demonstrate the superiority of HFC-YOLO11s, we conducted comparative analyses against mainstream models with comparable parameter scales (YOLOv5su, YOLOv6s, YOLOv8s, YOLOv10s, and baseline YOLO11s) on the AI-TOD dataset. Table 3 summarizes the comparative performance metrics, revealing our model’s competitive advantages in both precision and computational efficiency over the established counterparts.

Table 3.
Comparison of performance between HFC-YOLO11s and other models on AI-TOD.
The experimental results demonstrate that HFC-YOLO11s outperforms comparable models across multiple metrics, including precision, pecall, F1-score, mAP50, and mAP50-95, while maintaining the smallest parameter count and low computational costs. Notably, compared to the baseline YOLO11s, our model achieves 3.4% and 2.0% improvements in mAP50 and mAP50-95, respectively, coupled with a 27.4% parameter reduction. When benchmarked against YOLOv8s, HFC-YOLO11s demonstrates superior detection accuracy (a 4.0% higher mAP50, 2.4% higher mAP50-95), while requiring only 61.7% of the parameters and 85.4% of the computational operations.
The HFC-YOLO11s model outperforms other YOLO models in detecting small remote sensing targets, while also possessing favorable lightweight characteristics, making it suitable for deployment on edge devices.
4.5. Visualization Analysis
To systematically evaluate the model enhancement’s effects, Figure 8 presents a comparative visualization between the baseline YOLO11s and our HFC-YOLO11s in small target detection across five representative scenarios. Each case study contains a tripartite visualization—source imagery (left), baseline detection results (middle), and enhanced model outputs (right)—with detection boxes colored through a dynamic color-coding scheme (green: confidence score > 0.5, blue: confidence score ≤ 0.5).

Figure 8.
Visual detection results of AI-TOD datasets. (a) a dim and complex scene; (b) a scene with numerous obstacles; (c) a road scenario; (d) an open area scene; (e) a maritime scene.
Figure 8a illustrates a dim and complex scene, where the improved model detects more small targets compared to the baseline model and exhibits higher confidence levels in its detections. Figure 8b illustrates a scene with numerous obstacles, where the improved model accurately identifies and detects the small targets within it. Figure 8c illustrates a road scenario; while the baseline model detected larger vehicles nearby, it overlooked many small vehicles in the distance, whereas the improved model performed better. Figure 8d illustrates an open area scene, where the baseline model incorrectly detected targets such as the goalposts as vehicles, while the improved model effectively distinguished between vehicles and other objects, reducing the probability of false positives. Figure 8e illustrates a maritime scene, where the improved model successfully detects a greater number of small targets.
4.6. Ablation Study
To quantify the contributions of the proposed modules (HRS, GhostBottleneck, and EIoU), this paper conducted systematic ablation experiments on the AI-TOD dataset. HRS modifies the architecture by preserving the P2 feature layer while removing the P5 layer. GhostBottleneck replaces the original Bottleneck modules in the shallow layers of YOLO11. EIoU replaces the default loss function.
Table 4 presents the impact of adding or removing components on the evaluation metrics, where checkmarks (√) indicates that the module is included, and crosses (×) indicates that the module is excluded.

Table 4.
Ablation experiments of the proposed HFC-YOLO11m on AI-TOD.
To systematically evaluate the effectiveness of the proposed modules, comprehensive ablation experiments were conducted on the AI-TOD dataset. The HRS module, which preserves the high-resolution P2 feature layer (160 × 160) while eliminating the P5 layer (20 × 20), demonstrated a 2.8 percentage point (pp) improvement in mAP50, alongside a 24.6% reduction in parameter count, albeit with a 24.9% increase in computational cost due to the elevated spatial resolution of the P2 features. To mitigate this computational overhead, the GhostBottleneck architecture was implemented in shallow network layers, achieving a 9.6% reduction in GFLOPs and a 3.6% decrease in parameters, while maintaining the baseline accuracy. Concurrently, the EIoU loss function enhanced localization precision by 1.1%, without incurring additional computational or parametric costs.
The integrated implementation of all three modules yielded optimal performance, a 3.4% mAP50, a 27.4% parameter reduction, and a controlled 12.9% computation increase, establishing an effective balance between accuracy in detection and model efficiency for small object recognition tasks.
4.7. Experiments on VisDrone Dataset
To comprehensively validate the cross-dataset generalization capability of the proposed HFC-YOLO11s model for small targets, we conducted comparative experiments on the VisDrone benchmark.
The visualization results are shown in Figure 9, where different instances are represented by detection boxes of varying colors. The left side displays the original image, the middle section presents the detection results from the baseline model, and the right side illustrates the outputs from the improved model. This effectively demonstrates the efficacy of the HFC-YOLO11s model, with detailed experimental comparison results provided in Table 5.

Figure 9.
Visual detection results of VisDrone datasets. (a) Daytime close-range scenarios; (b) Daytime long-distance scenario; (c) Nighttime occlusion scenario.

Table 5.
Comparison of performance between HFC-YOLO11s and other models on VisDrone.
Based on the performance on the VisDrone dataset, the YOLO11s model exhibits the highest accuracy compared to the other original YOLO models, while maintaining a relatively low number of parameters and computational load.
Furthermore, the HFC-YOLO11s model shows an improvement of 2.7% in mAP50 and 1.3% in mAP50-95 compared to the baseline model YOLO11s. This further confirms the effectiveness and generalization capability of the proposed model in detecting small targets.
The YOLO11 model features a comprehensive architecture with a detailed modular design. Through targeted modifications to the YOLO11 framework, this study validates the effectiveness of the proposed methodology in small object detection via a controlled experiment, ablation study, and transfer experiment. The enhanced model demonstrates improved detection accuracy for minute targets, while maintaining its lightweight characteristics, thereby providing a feasible direction for advancing precision in small object recognition. Furthermore, HFC-YOLO11 exhibits direct transferability to other datasets for training and detection tasks.
4.8. Analysis of Model Limitations
Although the HFC-YOLO11 model outperforms baseline models in overall detection accuracy, it exhibits suboptimal performance in scenarios involving extreme scale variations and densely clustered objects. As illustrated in Figure 10a, which depicts a densely clustered scenario, the model successfully detects a large number of targets; however, the quality and confidence scores of its predicted bounding boxes remain relatively low, indicating substantial room for improvement. Figure 10b demonstrates a multi-scale variation scenario containing both small-pixel pedestrians and large-pixel vehicles, along with partial occlusions. These challenges lead to a suboptimal detection performance, resulting in a significant number of missed detections.

Figure 10.
(a) Dense clustering scenarios; (b) extreme scale variation scenarios.
To address these limitations, future work will focus on designing a cluster-aware loss function and optimizing the multi-scale fusion architecture based on the current model framework. These enhancements aim to further improve the model’s detection performance and generalization capability across diverse scenarios.
5. Conclusions
To address the core challenges in small remote sensing object detection, including resolution–semantics imbalance, deep feature attenuation, and sub-pixel localization error accumulation, this paper proposes the Hierarchical Feature Compensation Network (HFC-YOLO11s).
Systematic experimentation and theoretical analysis demonstrate that our hierarchical optimization strategy, based on feature pyramid reconstruction, effectively mitigates the conflict between resolution and semantic preservation. By retaining the high-resolution P2 feature layer while removing redundant P5 layers, the model achieves a 32.8% to 36.2% improvement in mAP50 on the AI-TOD dataset, coupled with a 27.4% reduction in parameter count. Visualization results confirm enhanced edge feature extraction for tiny targets in complex backgrounds. This architecture balances computational efficiency and feature representation through a depth-aware module design. Shallow GhostBottleneck layers reduce the FLOPs by 9.6%, while preserved deep Bottleneck modules ensure semantic integrity. The proposed EIoU loss function further improves its precision in detection.
The adaptability of this model to extreme scale variations needs improvement. Future work will explore dynamic resolution adjustment mechanisms and model compression methods based on knowledge distillation to further enhance the algorithm’s capability for deployment on mobile devices. HFC-YOLO11s improves the accuracy of small target detection in remote sensing through a multidimensional collaborative optimization while maintaining lightweight characteristics, providing reliable technical support for practical applications such as drone emergency inspections and smart city management.
Author Contributions
Conceptualization, J.B. and W.Z.; methodology, J.B.; software, J.B.; validation, Z.N. and X.Y.; formal analysis, D.L.; investigation, W.Z.; resources, W.Z.; data curation, W.Z.; writing—original draft preparation, J.B.; writing—review and editing, Q.X.; visualization, J.B.; supervision, W.Z.; project administration, W.Z.; funding acquisition, W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Social Science Foundation, grant number 2023-SKJJ-B-107.
Data Availability Statement
The datasets presented in this study can be download here: https://github.com/jwwangchn/AI-TOD (accessed on 21 February 2025); https://github.com/VisDrone/VisDrone-Dataset (accessed on 10 March 2025); https://github.com/BaiBai2002/BAIBAI-HFC-YOLO11.git (accessed on 5 May 2025).
Acknowledgments
We thank the editors and reviewers for their hard work and valuable advice.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yao, F.; Liu, S.; Wang, D.; Geng, X.; Wang, C.; Jiang, N.; Wang, Y. Review on the development of multi- and hyperspectral remote sensing technology for exploration of copper-gold deposits. Ore Geol. Rev. 2023, 162, 105732. [Google Scholar] [CrossRef]
- Liu, S.; Du, K.; Zheng, Y.; Chen, J.; Du, P.; Tong, X. Remote sensing change detection technology in the era of artificial intelligence: Inheritance, development and challenges. Natl. Remote Sens. Bull. 2023, 27, 1975–1987. [Google Scholar] [CrossRef]
- Acharya, T.D.; Lee, D.H. Remote sensing and geospatial technologies for sustainable development: A review of applications. Sens. Mater. 2019, 31, 3931–3945. [Google Scholar] [CrossRef]
- Bi, S.; Lin, X.; Wu, Z.; Yang, S. Development technology of principle prototype of high-resolution quantum remote sensing imaging. Proc. SPIE 2018, 10540, 105400Q. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Z.; Qi, G.; Hu, G.; Zhu, Z.; Huang, X. Remote sensing micro-object detection under global and local attention mechanism. Remote Sens. 2024, 16, 644. [Google Scholar] [CrossRef]
- Wu, J.; Zhao, F.; Jin, Z. LEN-YOLO: A lightweight remote sensing small aircraft object detection model for satellite on-orbit detection. J. Real-Time Image Process 2024, 22, 25. [Google Scholar] [CrossRef]
- Hua, X.; Wang, X.; Rui, T. A fast self-attention cascaded network for object detection in large scene remote sensing images. Appl. Soft Comput. 2020, 94, 106495. [Google Scholar] [CrossRef]
- Molla, Y.K.; Mitiku, E.A. CNN-HOG-Based Hybrid Feature Mining for Classification of Coffee Bean Varieties Using Image Processing. Multimed. Tools Appl. 2025, 84, 749–764. [Google Scholar] [CrossRef]
- Qadir, I.; Iqbal, M.A.; Ashraf, S.; Akram, S. A Fusion of CNN and SIFT for Multicultural Facial Expression Recognition. Multimed. Tools Appl. 2025, 84. [Google Scholar] [CrossRef]
- Wang, Z.N.; He, D.; Zhao, M.J. Lane line detection and lane departure warning algorithm based on sliding window searching. Automot. Eng. 2023, 9, 15–20+28. [Google Scholar] [CrossRef]
- Guan, Q.; Liu, Y.; Chen, L.; Zhao, S.; Li, G. Aircraft detection and fine-grained recognition based on high-resolution remote sensing images. Electronics 2023, 12, 3146. [Google Scholar] [CrossRef]
- Guo, D.; Zhao, C.; Shuai, H.; Zhang, J.; Zhang, X. Enhancing sustainable traffic monitoring: Leveraging NanoSight–YOLO for precision detection of micro-vehicle targets in satellite imagery. Sustainability 2024, 16, 7539. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Gkioxari, G.; Dollar, P.; Girshick, R. Mask R-CNN. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 386–397. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.; Vasconcelos, N. Cascade R-CNN: High quality object detection and instance segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 1483–1498. [Google Scholar] [CrossRef]
- Jiang, P.; Ergu, D.; Liu, F.; Cai, Y.; Ma, B. A review of YOLO algorithm developments. Procedia Comput. Sci. 2022, 199, 1066–1073. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, Y. A steel surface defect detection method based on improved RetinaNet. Sci. Rep. 2025, 15, 6045. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Yan, J.; Cai, J.; Deng, J.; Qin, Q.; Cheng, Y. Super-resolution reconstruction of single image for latent features. Comput. Vis. Media 2024, 6, 1219–1239. [Google Scholar] [CrossRef]
- Zhang, K.; Teng, G.; Fan, T.; Li, C. FPN multi-scale object detection algorithm based on dense connectivity. Comput. Appl. Softw. 2020, 37, 165–171. [Google Scholar]
- Wang, A.; Liang, G.; Wang, X.; Song, Y. Application of the YOLOv6 combining CBAM and CIoU in forest fire and smoke detection. Forests 2023, 14, 2261. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, M.; Li, B.; Wang, Y.; Ouyang, W. NAS-PED: Neural architecture search for pedestrian detection. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 1800–1817. [Google Scholar] [CrossRef] [PubMed]
- Su, W.; Jing, D. DDL R-CNN: Dynamic direction learning R-CNN for rotated object detection. Algorithms 2025, 18, 21. [Google Scholar] [CrossRef]
- Li, F.; Sun, T.; Dong, P.; Wang, Q.; Li, Y.; Sun, C. MSF-CSPNet: A specially designed backbone network for Faster R-CNN. IEEE Access 2024, 12, 52390–52399. [Google Scholar] [CrossRef]
- Yuan, M.; Meng, H.; Wu, J.; Cai, S. Global recurrent Mask R-CNN: Marine ship instance segmentation. Comput. Graph. 2025, 126, 104112. [Google Scholar] [CrossRef]
- Shao, Y.; Zhang, D.; Chu, H.; Zhang, X.; Rao, Y. A review of YOLO object detection based on deep learning. J. Electron. Inf. Technol. 2022, 44, 3697–3708. [Google Scholar] [CrossRef]
- Wang, Z.; Li, F.; Zheng, X.; Nong, H.; Zeng, B.; Yang, W. Detection of cassava stem based on deep convolutional neural network. J. Agric. Mech. Res. 2023, 45, 144–148. [Google Scholar] [CrossRef]
- Sang, J.; Wu, Z.; Guo, P.; Hu, H.; Xiang, H.; Zhang, Q.; Cai, B. An improved YOLOv2 for vehicle detection. Sensors 2018, 18, 4272. [Google Scholar] [CrossRef]
- Xu, F.; Huang, L.; Gao, X.; Yu, T.; Zhang, L. Research on YOLOv3 model compression strategy for UAV deployment. Cogn. Robot. 2024, 4, 8–18. [Google Scholar] [CrossRef]
- Nguyen, D.; Nguyen, D.; Le, M.; Nguyen, Q. FPGA-SoC implementation of YOLOv4 for flying-object detection. J. Real-Time Image Process 2024, 21, 63. [Google Scholar] [CrossRef]
- Li, Y.; Shi, X.; Xu, X.; Zhang, H.; Yang, F. Yolov5s-PSG: Improved Yolov5s-based helmet recognition in complex scenes. IEEE Access 2025, 13, 34915–34924. [Google Scholar] [CrossRef]
- Li, N.; Wang, M.; Yang, G.; Li, B.; Yuan, B.; Xu, S. DENS-YOLOv6: A small object detection model for garbage detection on water surface. Multimed. Tools Appl. 2024, 83, 55751–55771. [Google Scholar] [CrossRef]
- Qin, Z.; Chen, D.; Wang, H. MCA-YOLOv7: An improved UAV target detection algorithm based on YOLOv7. IEEE Access 2024, 12, 42642–42650. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Z.; Wang, K.; Huang, W.; Li, P. OBC-YOLOv8: An improved road damage detection model based on YOLOv8. PeerJ Comput. Sci. 2025, 11, e2593. [Google Scholar] [CrossRef] [PubMed]
- Geng, X.; Han, X.; Cao, X.; Su, Y.; Shu, D. YOLOV9-CBM: An improved fire detection algorithm based on YOLOV9. IEEE Access 2025, 13, 19612–19623. [Google Scholar] [CrossRef]
- Sun, H.; Yao, G.; Zhu, S.; Zhang, L.; Xu, H.; Kong, J. SOD-YOLOv10: Small object detection in remote sensing images based on YOLOv10. IEEE Geosci. Remote Sens. Lett. 2025, 22. [Google Scholar] [CrossRef]
- Xuan, Y.; Zhang, X.; Li, C.; Wang, H.; Mu, C. LAM-YOLOv11 for UAV transmission line inspection: Overcoming environmental challenges with enhanced detection efficiency. Multimed. Syst. 2025, 31. [Google Scholar] [CrossRef]
- Wang, H.; Qian, H.; Feng, S.; Wang, W. L-SSD: Lightweight SSD target detection based on depth-separable convolution. J. Real-Time Image Process 2024, 21, 33. [Google Scholar] [CrossRef]
- Wu, J.; Fan, X.; Sun, Y.; Gui, W. Ghost-RetinaNet: Fast shadow detection method for photovoltaic panels based on improved RetinaNet. CMES-Comput. Model. Eng. Sci. 2023, 134, 1305–1321. [Google Scholar] [CrossRef]
- Li, X.; Liu, F.; Han, B.; Wu, Z. MEDMCN: A novel multi-modal EfficientDet with multi-scale CapsNet for object detection. J. Supercomput. 2024, 80, 1–28. [Google Scholar] [CrossRef]
- Liu, F.; Li, Y. SAR remote sensing image ship detection method NanoDet based on visual saliency. J. Radars. 2021, 10, 885. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Rezatofighi, H.; Tsoi, N.; Gwak, J.; Sadeghian, A.; Reid, I.; Savarese, S. Generalized intersection over union: A metric and a loss for bounding box regression. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Zheng, Z.; Wang, P.; Liu, W.; Li, J.; Ye, R.; Ren, D. Distance-IoU loss: Faster and better learning for bounding box regression. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Zheng, Z.; Wang, P.; Ren, D.; Liu, W.; Ye, R.; Hu, Q.; Zuo, W. Enhancing geometric factors in model learning and inference for object detection and instance segmentation. IEEE Trans. Cybern. 2022, 52, 8574–8586. [Google Scholar] [CrossRef] [PubMed]
- Gevorgyan, Z. SIoU Loss: More Powerful Learning for Bounding Box Regression. arXiv 2022, arXiv:2205.12740. [Google Scholar]
- Wang, J.; Xu, C.; Yang, W.; Yu, L. A Normalized Gaussian Wasserstein Distance for Tiny Object Detection. arXiv 2022, arXiv:2110.13389. [Google Scholar]
- Gao, Y.; Xin, Y.; Yang, H.; Wang, Y. A lightweight anti-unmanned aerial vehicle detection method based on improved YOLOv11. Drones 2024, 9, 11. [Google Scholar] [CrossRef]
- Wang, Z.; Su, Y.; Kang, F.; Wang, L.; Lin, Y.; Wu, Q.; Li, H.; Cai, Z. PC-YOLO11s: A lightweight and effective feature extraction method for small target image detection. Sensors 2025, 25, 348. [Google Scholar] [CrossRef]
- Han, K.; Wang, Y.; Tian, Q.; Guo, J.; Xu, C.; Xu, C. GhostNet: More features from cheap operations. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Haroon, M.; Shahzad, M.; Fraz, M.M. Multisized object detection using spaceborne optical imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3032–3046. [Google Scholar] [CrossRef]
- Du, D.; Zhu, P.; Wen, L.; Bian, X.; Lin, H.; Hu, Q.; Peng, T.; Zheng, J.; Wang, X.; Zhang, Y.; et al. VisDrone-DET2019: The vision meets drone object detection in image challenge results. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops (ICCVW), Seoul, Republic of Korea, 27–28 October 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).