Fine-Tuning Network Slicing in 5G: Unveiling Mathematical Equations for Precision Classification
Abstract
1. Introduction
- Is it possible to obtain highly accurate SEs using the GPSC that can be used to determine the network slice class type with high classification accuracy?
- Does the oversampling technique have any influence on the accuracy of obtained SEs?
- Can the RHVS method be used to find the optimal combination of GPSC hyperparameters with which mathematical equations could be obtained with high classification accuracy?
- Using 5FCV, is it possible to obtain highly accurate and robust SEs for the detection of network slicing type?
- Can a combination of all the best SEs for each class applied on an initial imbalanced dataset achieve the same or similar classification accuracy as those SEs achieve on balanced dataset variations?
2. Materials and Methods
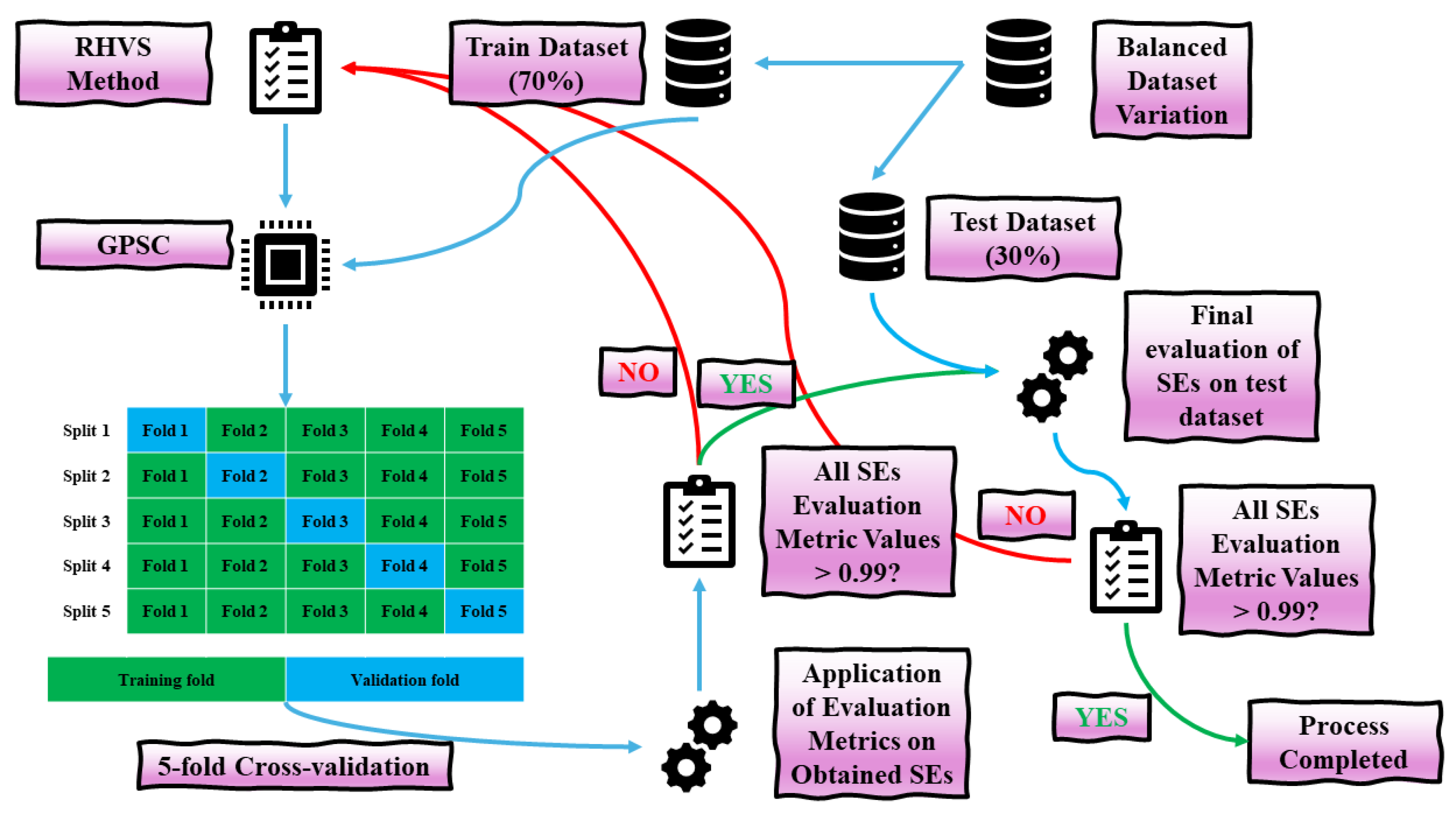
2.1. Research Methodology
- Initial Dataset Investigation—the initial dataset is examined, with non-integer-type variables being converted to integer types using Label Encoding. A correlation analysis is performed to explore the relationships between variables. The number of classes in the dataset is determined, along with the number of samples in each class.
- Dataset Oversampling—given the imbalanced nature of the dataset, different oversampling techniques are applied to balance the dataset, creating several variations of balanced datasets.
- GPSC + RHVS + 5-fold CV—the GPSC method is applied to each variation of the balanced dataset. The RHVS technique is used to identify the optimal combination of GPSC hyperparameters, resulting in symbolic expressions with high classification accuracy. The GPSC is trained using 5-fold cross-validation on each balanced dataset variation.
- Evaluation of Best Symbolic Expressions on the Initial Dataset—the best symbolic expressions from each class are combined and evaluated on the original dataset to assess whether high classification accuracy can be achieved.
2.2. Dataset Description
- Use Case—types of use cases include Smartphone, Industry 4.0, Smart City and Home, AR/VR/Gaming, IoT Devices, Healthcare, Public Safety, and Smart Transportation.
- LTE/5G Category—it refers to the specific generation or technology level of the network that is being utilized for a particular network slice. The LTE categories are in the 1–16 range, which defines different network capabilities and maximum data rates for LTE devices. Higher categories generally indicate more advanced technologies and higher performance. The 5G categories are in the 1–22 range and are defined for 5G devices and networks. Similar to LTE, the higher categories represent more advanced features and higher performance in terms of data rates, modulation schemes, and other capabilities.
- Technology Supported—this provides information about the underlying communication technologies associated with each network slice.
- Day—the day of the week on which the data were collected.
- Time—the hours of the day at which the data were collected.
- GBR—this stands for Guaranteed Bit Rate, and it is a key parameter in network slicing. The GBR is the minimum data transfer rate that is assured to a network slice for a particular service or application. GBR ensures that a certain amount of network resources, typically bandwidth, is reserved exclusively for the use of specific network slices, even during periods of network congestion. This reservation guarantees a minimum level of performance for applications that require a consistent and reliable data transfer rate.
- Packet Loss Rate—the value of packets that did not reach their destination within the network slice.
- Packet Delay—this refers to the delay experienced by data packets as they traverse the network.
- Slice Type—Mobile Broadband (eMBB), Ultra-Reliable Low-Latency Communication (URLLC), Massive Machine Type Communication (mMTC).
- –
- eMBB—high-bandwidth and high-velocity data transmission; it facilitates activities such as high-definition video streaming, online gaming, and immersive media experiences.
- –
- URLLC—accentuating highly dependable and low-latency connections, it caters to critical applications such as autonomous vehicles, industrial automation, and remote surgery.
- –
- mMTC—concentrating on supporting an extensive multitude of interconnected devices, it enables efficient communication between Internet of Things (IoT) devices, smart cities, and sensor networks.
- The first strategy maintains the original target variable but applies oversampling techniques to generate balanced versions of the dataset. The one-versus-rest (OvR) approach is then used during training, allowing the GPSC to treat each class individually.
- The second strategy converts the multiclass target into three separate binary classification problems. For instance, when training for class_0, all its instances are labeled as 1, while instances of *class_1* and class_2 are labeled as 0. This conversion is repeated for each class, resulting in three dedicated binary datasets—each focusing on one class versus the rest.
2.3. Oversampling Techniques
2.3.1. KMeansSMOTE
- KMeansSMOTE addresses class overlap and is useful for noisy datasets.
- It generates synthetic instances within clusters, contributing to better generalization.
- It enhances model robustness in complex data distributions, where traditional SMOTE might fail.
- The method requires tuning additional parameters, such as the number of clusters in the KMeans algorithm. Poor selection of the number of clusters can impact the quality of the synthetic instances.
- The computational complexity is higher than that of traditional SMOTE due to the clustering step, which could be a challenge with large datasets or in resource-constrained environments.
2.3.2. SMOTE
- It effectively balances the dataset by increasing the representation of the minority class, which can lead to improved classification performance.
- SMOTE mitigates model bias toward the majority class and reduces the risk of overfitting by avoiding simple duplication of minority class samples.
- The method promotes better generalization by introducing variability into the training data through synthetic sampling.
- It may be less effective in datasets with high noise levels or significant class overlap, where generated samples might introduce ambiguity and degrade model performance.
- The effectiveness of SMOTE is highly dependent on the choice of the k parameter (number of nearest neighbors). An inappropriate k value may produce synthetic samples that do not accurately reflect the underlying data distribution, necessitating careful parameter tuning.
2.3.3. Random Oversampling
- Simplicity: Random Oversampling is easy to implement and requires minimal parameter tuning.
- Computational Efficiency: it is a straightforward and computationally efficient technique, especially when the class imbalance is not extreme.
- Prevention of Model Bias: by duplicating instances of the minority class, it helps prevent bias towards the majority class, ensuring a more equitable representation.
- Risk of Overfitting: Duplicating instances without regard for their characteristics can lead to overfitting the minority class. The model might learn redundant patterns that do not generalize well to unseen data.
- Lack of Diversity: Since only existing instances are duplicated, this method does not introduce any diversity into the dataset. This may limit the model’s ability to generalize to new data, especially in cases of severe imbalance.
2.3.4. Datasets Obtained from Application of Oversampling Techniques
2.4. Genetic Programming Symbolic Classifier
- Define the initial boundary values of each hyperparameter;
- Test each GPSC hyperparameter boundary value to see if the GPSC will successfully execute;
- If needed, adjust the boundaries of each GPSC hyperparameter before applying it in research.
- PopSize—this defines the size of the population that will be evolved by the GPSC algorithm.
- GenNum—this specifies the number of generations used to evolve the population. This serves as one of the termination criteria, meaning that the GPSC will stop once the specified number of generations is reached.
- InitTreeDepth—this sets the depth range for the initial population trees. In the GPSC, each symbolic expression is represented as a tree, with the root node being a mathematical function. The tree is constructed from the root to the deepest leaf node, which can contain mathematical functions, input variables, or constants. The initial trees are generated using the ramped half-and-half method: half of the population is created using the full method (trees of maximum depth), while the other half uses the grow method (trees of variable shape). The “ramped” aspect refers to selecting tree depths from a defined range. For example, a range of (5, 18) creates initial trees with depths between 5 and 18.
- TournamentSize—this determines the number of population members randomly selected to participate in tournament selection. The member with the lowest fitness value generally wins, but the tree length (i.e., complexity) is also considered through the parsimony pressure method (controlled by ParsimonyCoeff). This helps avoid selecting overly complex solutions. Genetic operations such as crossover or mutation are then applied to the tournament winners.
- Crossover—this specifies the probability of applying the crossover operation. This operation requires two selected individuals (tournament winners). A random subtree is selected from each, and the subtree from the second individual replaces the one in the first to generate a new individual for the next generation.
- SubtreeMute—this defines the probability of performing subtree mutation. This operation selects a random subtree in a single individual and replaces it with a newly generated subtree using available functions, variables, and constants.
- PointMute—this specifies the probability of applying point mutation. This operation randomly selects nodes within an individual and modifies them: constants are replaced with new constants, variables with other variables, and functions with others requiring the same number of input arguments.
- HoistMute—this sets the probability of hoist mutation. A random subtree is selected from the individual, and a random node within that subtree replaces the entire subtree, creating a new individual for the next generation.
- ConstRange—this defines the range of constant values used when constructing initial trees and during mutation operations.
- StoppingCrit—this sets a minimum fitness threshold as a termination criterion. If a population member’s fitness drops below this predefined value, the GPSC execution is terminated early. The fitness function in the GPSC is computed as follows:
- The training set samples (values of input variables) are used to compute the output of the population member.
- This output is used in the Sigmoid function as the input to compute the output i.e., to determine the class (0 or 1). The Sigmoid function can be written as:where x is the output generated by the population member.
- The output of the Sigmoid function is used as the input alongside the real output from the dataset to compute the LogLoss value. The LogLoss formula can be written as:where N is the number of dataset samples, y is the true label (0 or 1), and p is the predicted probability that the sample belongs to Class 1.
- MinSize—this indicates the minimum fraction of the training set to be used in evaluating individuals. A value slightly less than 1 enables the estimation of out-of-bag (OOB) fitness. OOB samples are those excluded from an individual’s training subset and are used to estimate generalization performance without requiring a separate validation set.
- ParsimonyCoeff—the coefficient used in the parsimony pressure method to prevent bloat, a phenomenon where individuals grow excessively large without fitness improvement. Large individuals have their fitness penalized proportionally to their size, making them less likely to win tournament selection. This prevents prolonged execution times and memory exhaustion errors. The adjusted fitness f is computed as:where f is the original fitness, L is the size (length) of the individual, and is the parsimony coefficient.
2.5. Evaluation Metrics
2.6. Training/Testing Procedure
- Each balanced dataset variation, on which the GPSC was applied, was split into training and testing subsets with a 70:30 ratio, where 70% of the data were used for training and the remaining 30% were reserved for testing.
- After the initial dataset split, the RHVS method was invoked, randomly selecting GPSC hyperparameter values from predefined boundaries. These hyperparameters were then used in the GPSC, which was trained using 5-fold cross-validation.
- Following 5-fold cross-validation, five symbolic expressions were obtained as the GPSC was trained on each fold. For these five symbolic expressions, the mean evaluation metric values (ACC, AUC, precision, recall, and F1-score) were calculated, along with their standard deviation ().
- If the mean evaluation metrics exceeded 0.99, the process moved to the testing phase, where the symbolic expressions were tested on the remaining 30% of the dataset. If the mean evaluation metrics were below 0.99, the process was restarted with a new random selection of GPSC hyperparameters using the RHVS method.
- During the testing phase, the testing dataset was applied to the five symbolic expressions, and the mean evaluation metrics were recalculated from both the training and testing phases. If all evaluation metrics exceeded 0.99, the process was completed. If not, the process was repeated, starting with a new random selection of hyperparameters.
3. Results
3.1. The Results Obtained on the Balanced Dataset Variations
3.2. Evaluation of All Symbolic Expressions on Initial Dataset
4. Discussion
- For class_0, the lowest average depth and length were observed in the SMOTE Class 0 dataset, while the highest values were seen in the Random Oversampling Class 0 dataset.
- For class_1, SEs from the SMOTE Class 1 dataset exhibited the lowest depth and length, while the highest values came from the Random Oversampling Class 1 dataset.
- For class_2, SEs from the SMOTE Class 2 dataset had the lowest values, and those from KMeansSMOTE Class 2 had the highest.
5. Conclusions
- The GPSC method can be used to obtain symbolic expressions (SEs) with high classification performance, i.e., to determine the network slice class with high accuracy.
- Oversampling techniques generated balanced dataset variations, which were used in the GPSC to obtain SEs with high classification performance. This shows that oversampling techniques have a significant impact on generating SEs with high classification accuracy.
- The RHVS method proved to be a valuable tool in the GPSC for finding the optimal combination of hyperparameter values, leading to SEs that achieved high classification performance.
- Unlike the classic train/test procedure, 5-fold cross-validation (5FCV) proved to be an effective approach for generating a large number of highly accurate SEs. Using the classic train/test procedure in GPSC resulted in only one SE with high classification accuracy, provided that optimal hyperparameter values were defined. In contrast, 5FCV produced five different SEs with high classification accuracy, offering a more reliable estimate of model performance, reducing the impact of data variability, mitigating overfitting or underfitting risks, and providing a more robust assessment of generalization capabilities.
- Combining the best sets of SEs for each class, obtained from oversampled datasets, and applying them to the initial imbalanced dataset proved to be a good approach. This method achieved the same classification accuracy as that obtained on the balanced dataset variations.
- The use of various oversampling techniques generated multiple versions of the balanced dataset, providing a solid foundation for the application of the GPSC algorithm.
- The RHVS method in the GPSC identified the optimal combination of hyperparameter values, achieving high classification accuracy in the obtained SEs. This approach is faster compared to traditional grid search, especially given the large number of hyperparameters in the GPSC.
- The 5FCV process in the GPSC generated a large number of highly accurate SEs, leading to a more robust model, preventing overfitting and underfitting, offering a more reliable estimate of model performance, and reducing the impact of data variability.
- The combination of the best SEs for each class and their application on the imbalanced dataset proved to be effective, as the same classification accuracy was achieved as on the balanced dataset variations.
- The RHVS method can be time-consuming when searching for the optimal combination of GPSC hyperparameter values. Each randomly selected combination of hyperparameters must be applied in the GPSC to obtain SEs and evaluate whether they generate highly accurate SEs.
- Although 5FCV is a superior training method compared to the classical train/test approach, applying the GPSC algorithm to this procedure significantly increases the time required to obtain all five SEs (one SE per subset).
- Further investigation of GPSC hyperparameters: Future work should explore whether similar classification accuracy can be achieved by lowering the predefined maximum number of generations or increasing the stopping criteria value. Additionally, reducing the population size should be examined to determine if the same classification performance can be achieved with lower diversity in the GPSC population.
- Exploration of advanced hyperparameter tuning techniques: future work could investigate more sophisticated hyperparameter tuning methods beyond random selections, such as Bayesian optimization or evolutionary algorithms (e.g., Genetic Algorithm, Particle Swarm Optimization), to potentially enhance the efficiency and effectiveness of hyperparameter optimization.
- Further investigation of oversampling or inclusion of undersampling techniques: Future work could explore whether other oversampling techniques could be applied to the dataset. Since the initial dataset contains a large number of samples, we could investigate whether undersampling techniques could be used to balance the class samples.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Modification of Mathematical Functions Used in GPSC
Appendix B. How to Use Obtained SEs
- The dataset input variables are used to calculate the output of obtained SEs.
- Use the output of obtained SEs as input in the Sigmoid function to determine the class value 0 or 1.
References
- Debbabi, F.; Jmal, R.; Chaari Fourati, L. 5G network slicing: Fundamental concepts, architectures, algorithmics, projects practices, and open issues. Concurr. Comput. Pract. Exp. 2021, 33, e6352. [Google Scholar] [CrossRef]
- Belaid, M.O.N. 5G-Based Grid Protection, Automation, and Control: Investigation, Design, and Implementation. Ph.D. Thesis, Université Gustave Eiffel, Champs-sur-Marne, France, 2023. [Google Scholar]
- Afolabi, I.; Taleb, T.; Samdanis, K.; Ksentini, A.; Flinck, H. Network slicing and softwarization: A survey on principles, enabling technologies, and solutions. IEEE Commun. Surv. Tutorials 2018, 20, 2429–2453. [Google Scholar] [CrossRef]
- Khan, L.U.; Yaqoob, I.; Tran, N.H.; Han, Z.; Hong, C.S. Network slicing: Recent advances, taxonomy, requirements, and open research challenges. IEEE Access 2020, 8, 36009–36028. [Google Scholar] [CrossRef]
- Santos, J.; Wauters, T.; Volckaert, B.; De Turck, F. Towards low-latency service delivery in a continuum of virtual resources: State-of-the-art and research directions. IEEE Commun. Surv. Tutorials 2021, 23, 2557–2589. [Google Scholar] [CrossRef]
- Babbar, H.; Rani, S.; AlZubi, A.A.; Singh, A.; Nasser, N.; Ali, A. Role of network slicing in software defined networking for 5G: Use cases and future directions. IEEE Wirel. Commun. 2022, 29, 112–118. [Google Scholar] [CrossRef]
- Arzo, S.T. Towards Network Automation: A Multi-Agent Based Intelligent Networking System. Ph.D. Thesis, Università degli Studi di Trento, Trento, Italy, 2021. [Google Scholar]
- Chowdhury, S.; Dey, P.; Joel-Edgar, S.; Bhattacharya, S.; Rodriguez-Espindola, O.; Abadie, A.; Truong, L. Unlocking the value of artificial intelligence in human resource management through AI capability framework. Hum. Resour. Manag. Rev. 2023, 33, 100899. [Google Scholar] [CrossRef]
- Papa, A.; Jano, A.; Ayvaşık, S.; Ayan, O.; Gürsu, H.M.; Kellerer, W. User-based quality of service aware multi-cell radio access network slicing. IEEE Trans. Netw. Serv. Manag. 2021, 19, 756–768. [Google Scholar] [CrossRef]
- Bega, D.; Gramaglia, M.; Garcia-Saavedra, A.; Fiore, M.; Banchs, A.; Costa-Perez, X. Network slicing meets artificial intelligence: An AI-based framework for slice management. IEEE Commun. Mag. 2020, 58, 32–38. [Google Scholar] [CrossRef]
- Camargo, J.S.; Coronado, E.; Ramirez, W.; Camps, D.; Deutsch, S.S.; Pérez-Romero, J.; Antonopoulos, A.; Trullols-Cruces, O.; Gonzalez-Diaz, S.; Otura, B.; et al. Dynamic slicing reconfiguration for virtualized 5G networks using ML forecasting of computing capacity. Comput. Netw. 2023, 236, 110001. [Google Scholar] [CrossRef]
- Mahmood, M.R.; Matin, M.A.; Sarigiannidis, P.; Goudos, S.K. A comprehensive review on artificial intelligence/machine learning algorithms for empowering the future IoT toward 6G era. IEEE Access 2022, 10, 87535–87562. [Google Scholar] [CrossRef]
- Wu, W.; Zhou, C.; Li, M.; Wu, H.; Zhou, H.; Zhang, N.; Shen, X.S.; Zhuang, W. AI-native network slicing for 6G networks. IEEE Wirel. Commun. 2022, 29, 96–103. [Google Scholar] [CrossRef]
- Alsharif, M.H.; Jahid, A.; Kannadasan, R.; Kim, M.K. Unleashing the potential of sixth generation (6G) wireless networks in smart energy grid management: A comprehensive review. Energy Rep. 2024, 11, 1376–1398. [Google Scholar] [CrossRef]
- Malkoc, M.; Kholidy, H.A. 5G Network Slicing: Analysis of Multiple Machine Learning Classifiers. arXiv 2023, arXiv:2310.01747. [Google Scholar]
- Thantharate, A.; Paropkari, R.; Walunj, V.; Beard, C. DeepSlice: A deep learning approach towards an efficient and reliable network slicing in 5G networks. In Proceedings of the 2019 IEEE 10th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 10–12 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 762–767. [Google Scholar]
- Kuadey, N.A.E.; Maale, G.T.; Kwantwi, T.; Sun, G.; Liu, G. DeepSecure: Detection of distributed denial of service attacks on 5G network slicing—Deep learning approach. IEEE Wirel. Commun. Lett. 2021, 11, 488–492. [Google Scholar] [CrossRef]
- Venkatapathy, S.; Srinivasan, T.; Jo, H.G.; Ra, I.H. An E2E Network Slicing Framework for Slice Creation and Deployment Using Machine Learning. Sensors 2023, 23, 9608. [Google Scholar] [CrossRef]
- Dangi, R.; Lalwani, P. An Efficient Network Slice Allocation in 5G Network Based on Machine Learning. In Proceedings of the 2022 IEEE International Conference on Current Development in Engineering and Technology (CCET), Bhopal, India, 23–24 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Sedgwick, P. Pearson’s correlation coefficient. BMJ 2012, 345. [Google Scholar] [CrossRef]
- Singh, K.; Upadhyaya, S. Outlier detection: Applications and techniques. Int. J. Comput. Sci. Issues (IJCSI) 2012, 9, 307. [Google Scholar]
- Last, F.; Douzas, G.; Bacao, F. Oversampling for imbalanced learning based on k-means and smote. arXiv 2017, arXiv:1711.00837. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Mohammed, R.; Rawashdeh, J.; Abdullah, M. Machine learning with oversampling and undersampling techniques: Overview study and experimental results. In Proceedings of the 2020 11th International Conference on Information and Communication Systems (ICICS), Irbid, Jordan, 7–9 April 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 243–248. [Google Scholar]
- Espejo, P.G.; Ventura, S.; Herrera, F. A survey on the application of genetic programming to classification. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2009, 40, 121–144. [Google Scholar] [CrossRef]
- Sokolova, M.; Japkowicz, N.; Szpakowicz, S. Beyond accuracy, F-score and ROC: A family of discriminant measures for performance evaluation. In Proceedings of the Australasian Joint Conference on Artificial Intelligence, Hobart, Australia, 4–8 December 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1015–1021. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2001. [Google Scholar]




| Reference | AI Methods | Classification Performance |
|---|---|---|
| [15] | LR, LDM, KNN, DTC, RFC, SVC, GNB | ACC = 1.0 |
| [16] | DeepSlice (DNN) | ACC = 0.95 |
| [17] | DeepSecure (LSTM) | ACC = 0.98798 |
| [18] | k-NN, NB, SVC, RFC, MLP | ACC = 0.98 Precision = 0.98 Recall = 0.98 F1-Score = 0.98 |
| [19] | SVC, RFC, DTC, and ANN | ACC = 0.9446 Precision = 0.9425 Recall = 0.9361 F1-score = 0.9288 |
| Use Case | Technology Supported | Day | GBR | Slice Type | |||||
|---|---|---|---|---|---|---|---|---|---|
| Original Value | Numeric Value | Original Value | Numeric Value | Original Value | Numeric Value | Original Value | Numeric Value | Original Value | Numeric Value |
| AR/VR/Gaming | 0 | IoT (LTE-M, NB-IoT) | 0 | Monday | 0 | GBR | 0 | URLLC | 0 |
| Healthcare | 1 | LTE/5G | 1 | Tuesday | 1 | Non-GBR | 1 | eMBB | 1 |
| Industry 4.0 | 2 | — | — | Wednesday | 2 | — | — | mMTC | 2 |
| IoT Devices | 3 | — | — | Thursday | 3 | — | — | — | — |
| Public Safety | 4 | — | — | Friday | 4 | — | — | — | — |
| Smart City and Home | 5 | — | — | Saturday | 5 | — | — | — | — |
| Smart Transportation | 6 | — | — | Sunday | 6 | — | — | — | — |
| Smartphone | 7 | — | — | — | — | — | — | — | — |
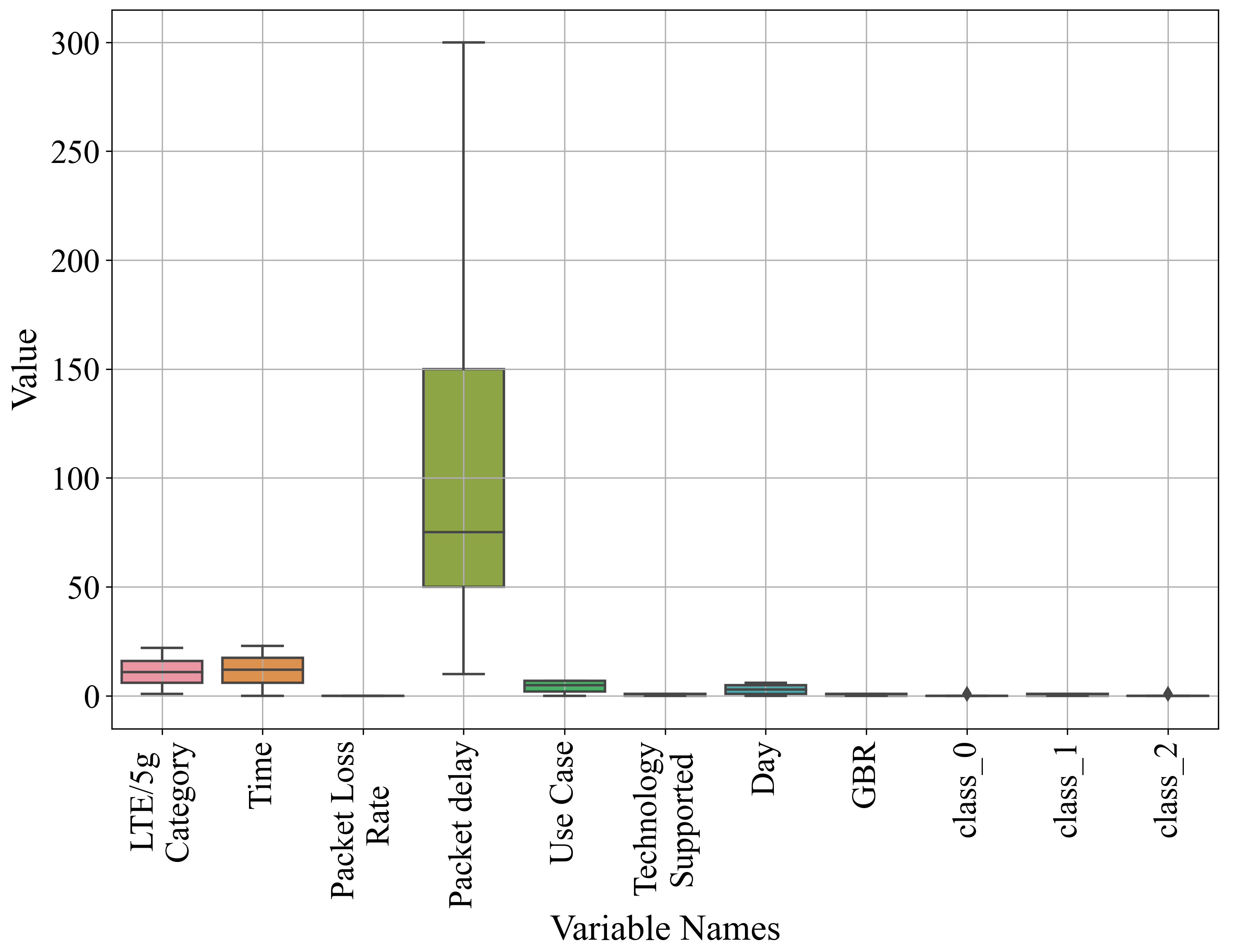
| Variable Name | Count | Mean | Std | Min | Max | GPSC Variable Representation | Variable Type |
|---|---|---|---|---|---|---|---|
| LTE/5G Category | 63,167 | 10.96 | 6.06 | 1 | 22 | Input variables | |
| Time | 11.50 | 6.92 | 0 | 23 | |||
| Packet Loss Rate | 0.003091 | 0.004 | 0.01 | ||||
| Packet Delay | 114.30 | 106.32 | 10 | 300 | |||
| Use Case | 4.61 | 2.56 | 0 | 7 | |||
| Technology Supported | 0.531907 | 0.49 | 0 | 1 | |||
| Day | 3 | 2 | 0 | 6 | |||
| GBR | 0.55 | 0.49 | 0 | 1 | |||
| class_0 | 0.23 | 0.42 | 0 | 1 | Output variable | ||
| class_1 | 0.53 | 0.49 | 0 | 1 | Output variable | ||
| class_2 | 0.23 | 0.42 | 0 | 1 | Output variable |
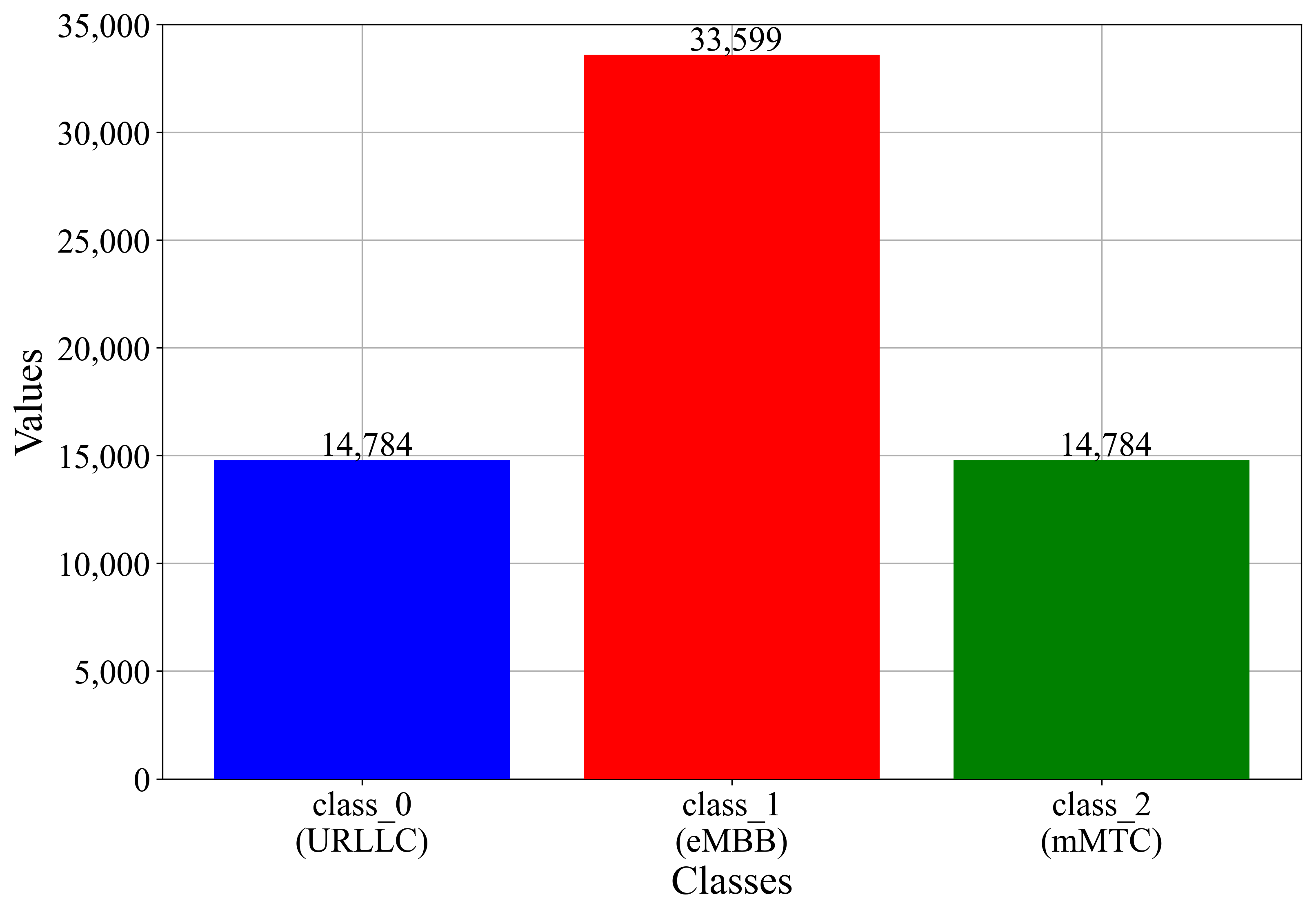
| Dataset Name | Samples Belong to the Class | Samples Do Not Belong to the Class |
|---|---|---|
| Initial dataset class_0 | 14,784 | 48,383 |
| Initial dataset class_1 | 33,599 | 29,568 |
| Initial dataset class_2 | 14,784 | 48,383 |
| Dataset Name | Belong to Class (Label 1) | Do Not Belong to Class (Label 0) | Total Samples Number |
|---|---|---|---|
| Initial dataset Class 0 | 14,784 | 48,383 | 63,167 |
| Initial dataset Class 1 | 29,568 | 33,599 | 63,167 |
| Initial dataset Class 2 | 14,784 | 48,383 | 63,167 |
| KMeansSMOTE Class 0 | 48,383 | 48,383 | 96,766 |
| Random Oversampling Class 0 | 48,383 | 48,383 | 96,766 |
| SMOTE Class 0 | 48,383 | 48,383 | 96,766 |
| KMeansSMOTE Class 1 | 33,599 | 33,601 | 67,200 |
| Random Oversampling Class 1 | 33,599 | 33,599 | 67,198 |
| SMOTE Class 1 | 33,599 | 33,599 | 67,198 |
| KMeansSMOTE Class 2 | 48,385 | 48,383 | 96,768 |
| Random Oversampling Class 2 | 48,383 | 48,383 | 96,766 |
| SMOTE Class 2 | 48,383 | 48,383 | 96,766 |
| Hyperparameter Name | Lower Boundary | Upper Boundary |
|---|---|---|
| PopSize | 1000 | 2000 |
| GenNum | 200 | 300 |
| InitTreeDepth | 3 | 18 |
| TournamentSize | 100 | 500 |
| Crossover | 0.001 | 1 |
| SubtreeMute | 0.001 | 1 |
| PointMute | 0.001 | 1 |
| HoistMute | 0.001 | 1 |
| ConstRange | −1,000,000 | 1,000,000 |
| StoppingCrit | ||
| MinSize | 0.99 | 1 |
| ParsimonyCoeff |
| Dataset | PopSize, GenNum, TournamentSize, InitTreeDepth, Crossover, SubtreeMute, PointMute, HoistMute, StoppingCrit, MaxSamples, ConstRange, ParsimonyCoeff |
|---|---|
| KMeansSMOTE Class 0 | 1635, 250, 481, (4, 12), 0.0087, 0.975, 0.011, 0.0036, 0.000925, 0.997, (−301,700.69, 942,674.18), |
| Random Oversampling Class 0 | 1661, 209, 141, (7, 17), 0.003, 0.95, 0.021, 0.019, 0.000129, 0.995, (−596,786.6, 272,352.52), |
| SMOTE Class 0 | 1801, 286, 429, (6, 12), 0.039, 0.956, 0.0019, 0.0027, 0.00032, 0.99, (−178,629.2, 152,684.75), |
| KMeansSMOTE Class 1 | 1009, 253, 168, (7, 13), 0.012, 0.954, 0.014, 0.018, , 0.992, (−961,606.57, 916,549.35), |
| Random Oversampling Class 1 | 1232, 226, 435, (7, 12), 0.021, 0.954, 0.019, 0.0041, 0.000441, 0.995, (−191,244.26, 675,108.15), |
| SMOTE Class 1 | 1570, 228, 249, (3, 12), 0.01, 0.961, 0.013, 0.0148, , 0.997, (−448,676.52, 295,584.56), |
| KMeansSMOTE Class 2 | 1145, 202, 397, (4, 14), 0.0017, 0.959, 0.033, 0.0044, 0.000398, 0.993, (−495,217.82, 691,481.82), |
| Random Oversampling Class 2 | 1786, 267, 250, (7, 12), 0.0094, 0.95, 0.0071, 0.03, , 0.99, (−987,687.37, 676,238.71), |
| SMOTE Class 2 | 1504, 262, 345, (6, 14), 0.001, 0.96, 0.034, 0.0028, 0.00054, 0.997, (−200,908.45, 851,092.06), |
| Dataset | SE1 | SE2 | SE3 | SE4 | SE5 | Average | |
|---|---|---|---|---|---|---|---|
| KMeansSMOTE Class 0 | Depth | 4 | 12 | 21 | 5 | 8 | 10 |
| Length | 8 | 57 | 54 | 21 | 25 | 33 | |
| Random Oversampling Class 0 | Depth | 13 | 13 | 10 | 10 | 6 | 10.4 |
| Length | 26 | 179 | 26 | 71 | 11 | 62.2 | |
| SMOTE Class 0 | Depth | 3 | 3 | 11 | 10 | 7 | 6.8 |
| Length | 8 | 5 | 32 | 41 | 55 | 28.2 | |
| KMeansSMOTE Class 1 | Dept | 12 | 9 | 3 | 13 | 5 | 8.4 |
| Length | 60 | 24 | 8 | 29 | 13 | 26.8 | |
| Random Oversampling Class 1 | Dept | 17 | 2 | 14 | 22 | 7 | 12.4 |
| Length | 142 | 7 | 31 | 90 | 54 | 64.8 | |
| SMOTE Class 1 | Dept | 8 | 2 | 5 | 5 | 4 | 4.8 |
| Length | 11 | 6 | 12 | 13 | 20 | 12.4 | |
| KMeansSMOTE Class 2 | Dept | 26 | 12 | 15 | 13 | 9 | 15 |
| Length | 78 | 77 | 80 | 79 | 42 | 71.2 | |
| Random Oversampling Class 2 | Dept | 5 | 16 | 9 | 9 | 26 | 13 |
| Length | 11 | 81 | 64 | 45 | 113 | 62.8 | |
| SMOTE Class 2 | Dept | 10 | 9 | 11 | 11 | 15 | 11.2 |
| Length | 44 | 40 | 56 | 25 | 65 | 46 |
| Evaluation Metric | Initial Dataset Class_0 | Initial Dataset Class_1 | Initial Dataset Class_2 |
|---|---|---|---|
| 1.0 | 1.0 | 1.0 | |
| 1.0 | 1.0 | 1.0 | |
| 1.0 | 1.0 | 1.0 | |
| 1.0 | 1.0 | 1.0 | |
| - | 1.0 | 1.0 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anđelić, N.; Baressi Šegota, S.; Mrzljak, V. Fine-Tuning Network Slicing in 5G: Unveiling Mathematical Equations for Precision Classification. Computers 2025, 14, 159. https://doi.org/10.3390/computers14050159
Anđelić N, Baressi Šegota S, Mrzljak V. Fine-Tuning Network Slicing in 5G: Unveiling Mathematical Equations for Precision Classification. Computers. 2025; 14(5):159. https://doi.org/10.3390/computers14050159
Chicago/Turabian StyleAnđelić, Nikola, Sandi Baressi Šegota, and Vedran Mrzljak. 2025. "Fine-Tuning Network Slicing in 5G: Unveiling Mathematical Equations for Precision Classification" Computers 14, no. 5: 159. https://doi.org/10.3390/computers14050159
APA StyleAnđelić, N., Baressi Šegota, S., & Mrzljak, V. (2025). Fine-Tuning Network Slicing in 5G: Unveiling Mathematical Equations for Precision Classification. Computers, 14(5), 159. https://doi.org/10.3390/computers14050159









