Optimal Selection of Sampling Rates and Mother Wavelet for an Algorithm to Classify Power Quality Disturbances
Abstract
1. Introduction
2. Discrete Wavelet Transform
3. Support Vector Machine
- Linear:
- Polynomial:
- Sigmoid:
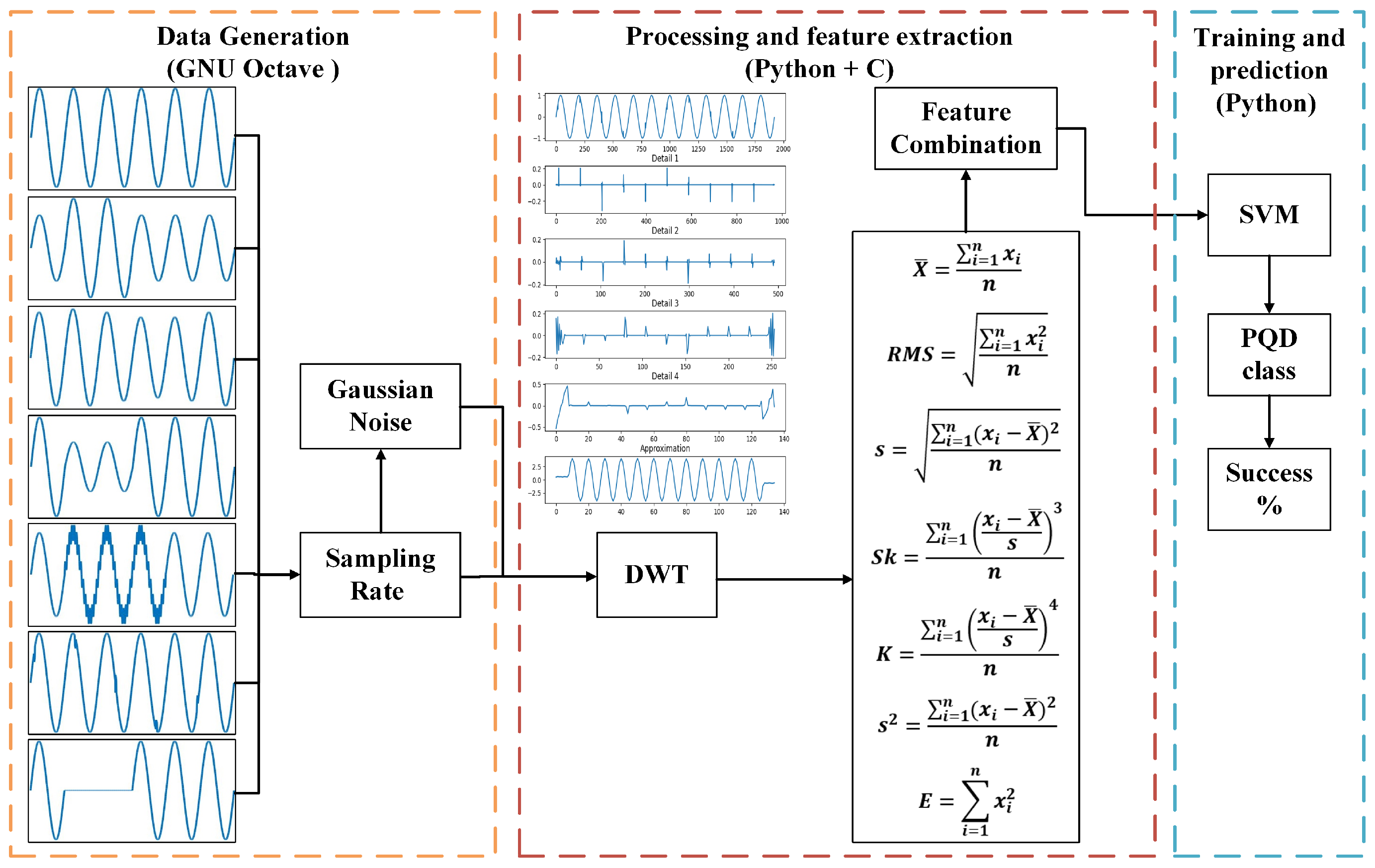
4. Materials and Methods
4.1. Data Generation
4.2. Processing and Feature Extraction
4.3. Training and Prediction
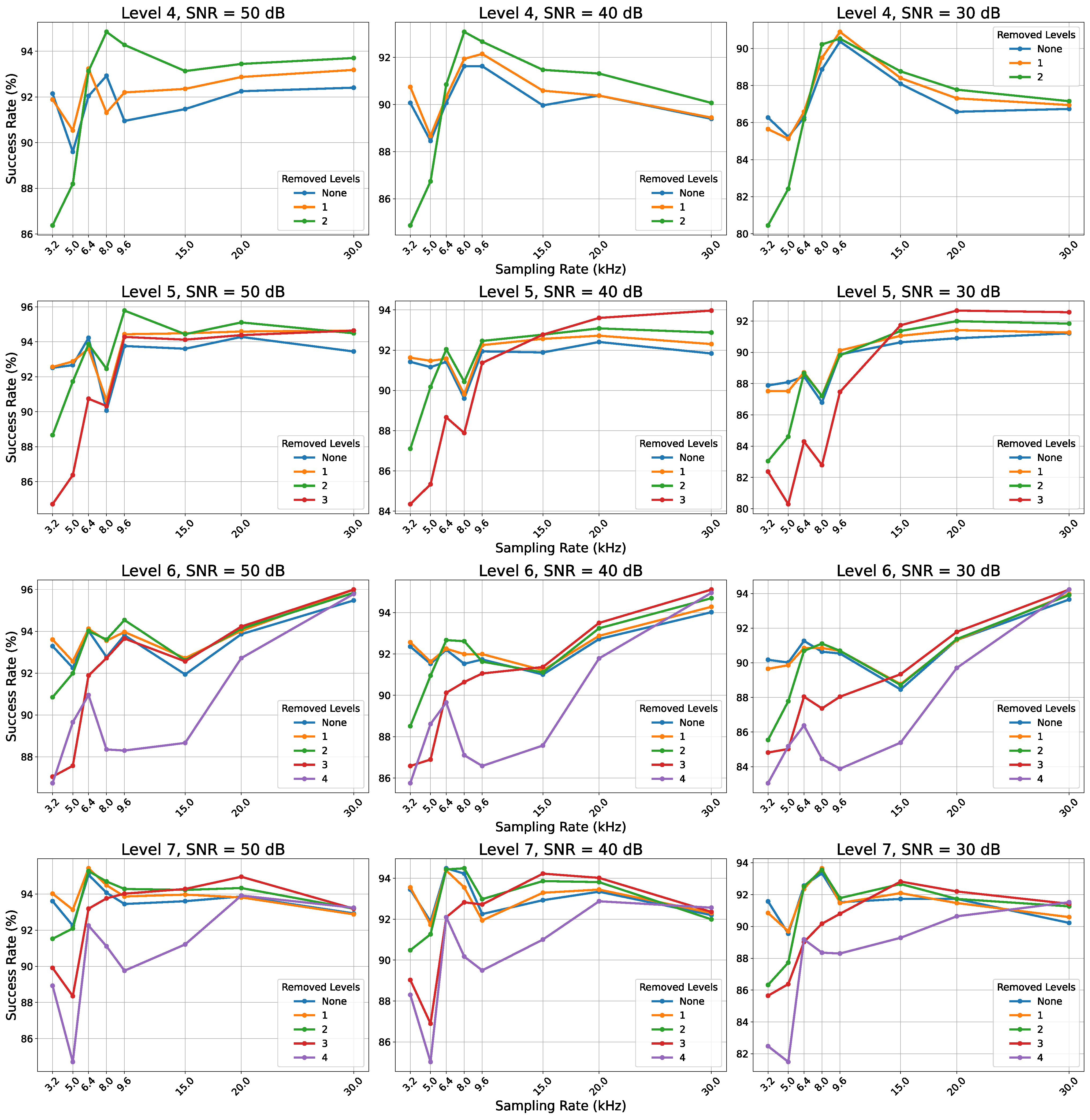
5. Results
6. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PQ | Power Quality |
| PQD | Power Quality Disturbance |
| FFT | Fast Fourier Transform |
| DWT | Discrete Wavelet Transform |
| ST | Stockwell Transform |
| TTT | Time-Time Transform |
| DT | Decision Tree |
| SVM | Support Vector Machine |
| RFC | Random Forest Classifier |
| ELM | Modular Probabilistic Neural Network |
| STFT | Short-Time Fourier Transform |
| LSTM | Long Short-Term Memory |
| OAA | One-Against-All |
| OAO | One-Against-One |
| SNR | Signal-to-Noise Ratio |
| Sampling Rate | |
| WGN | White Gaussian Noise |
| GAN | Generative Adversarial Network |
| WT | Wavelet Transform |
References
- Thiyagarajan, V.; Subramaniam, N.P. Wavelet approach and support vector networks based power quality events recognition and categorisation. In Proceedings of the 2016 International Conference on Signal Processing, Communication, Power and Embedded System (SCOPES), Paralakhemundi, India, 3–5 October 2016; pp. 1667–1671. [Google Scholar] [CrossRef]
- Mishra, S.; Mallick, R.; Gadanayak, D.A.; Nayak, P.; Sharma, R.; Panda, G.; Al-Numay, M.; Siano, P. Real Time Intelligent Detection of PQ Disturbances With Variational Mode Energy Features and Hybrid Optimized Light GBM Classifier. IEEE Access 2024, 12, 47155–47172. [Google Scholar] [CrossRef]
- Suganthi, S.T.; Vinayagam, A.; Veerasamy, V.; Deepa, A.; Abouhawwash, M.; Thirumeni, M. Detection and classification of multiple power quality disturbances in Microgrid network using probabilistic based intelligent classifier. Sustain. Energy Technol. Assess. 2021, 47, 101470. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G.; Khan, B.; Mahla, R.; Alhelou, H.H. Recognition of Complex Power Quality Disturbances Using S-Transform Based Ruled Decision Tree. IEEE Access 2020, 8, 173530–173547. [Google Scholar] [CrossRef]
- Markovska, M.; Taskovski, D.; Kokolanski, Z.; Dimchev, V.; Velkovski, B. Real-Time Implementation of Optimized Power Quality Events Classifier. IEEE Trans. Ind. Appl. 2020, 56, 3431–3442. [Google Scholar] [CrossRef]
- Enshaee, A.; Enshaee, P. A New S-Transform-Based Method for Identification of Power Quality Disturbances. Arab. J. Sci. Eng. 2018, 43, 2817–2832. [Google Scholar] [CrossRef]
- Samanta, I.S.; Rout, P.K.; Mishra, S. An optimal extreme learning-based classification method for power quality events using fractional Fourier transform. Neural Comput. Appl. 2021, 33, 4979–4995. [Google Scholar] [CrossRef]
- Rahul. Multiple power quality events recognition and classification based on adaptive Eigen-based type-2 fuzzy logic algorithm. Iran J. Comput. Sci. 2022, 5, 55–68. [Google Scholar] [CrossRef]
- Samanta, I.S.; Rout, P.K.; Mishra, S. Power Quality Events Recognition Using S-Transform and Wild Goat Optimization-Based Extreme Learning Machine. Arab. J. Sci. Eng. 2020, 45, 1855–1870. [Google Scholar] [CrossRef]
- Motlagh, S.; Akbari Foroud, A. Power quality disturbances recognition using adaptive chirp mode pursuit and grasshopper optimized Support Vector Machines. Measurement 2021, 168, 108461. [Google Scholar] [CrossRef]
- Khokhar, S.; Zin, A.M.; Mokhtar, A.; Bhayo, M.; Naderipour, A. Automatic classification of single and hybrid power quality disturbances using Wavelet Transform and Modular Probabilistic Neural Network. In Proceedings of the 2015 IEEE Conference on Energy Conversion (CENCON), Johor Bahru, Malaysia, 19–20 October 2015; pp. 457–462. [Google Scholar] [CrossRef]
- Jian, X.; Wang, X. A novel semi-supervised method for classification of power quality disturbance using generative adversarial network. J. Intell. Fuzzy Syst. 2021, 40, 3875–3885. [Google Scholar] [CrossRef]
- Chiam, D.H.; Lim, K.H.; Law, K.H. LSTM power quality disturbance classification with wavelets and attention mechanism. Electr. Eng. 2023, 105, 259–266. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, D.; Zhou, Y. Ensemble deep learning for automated classification of power quality disturbances signals. Electr. Power Syst. Res. 2022, 213, 108695. [Google Scholar] [CrossRef]
- Khetarpal, P.; Nagpal, N.; Siano, P.; Al-Numay, M. Power quality disturbance signal segmentation and classification based on modified BI-LSTM with double attention mechanism. IET Gener. Transm. Distrib. 2024, 18, 50–62. [Google Scholar] [CrossRef]
- Eisenmann, A.; Streubel, T.; Rudion, K. PQ classification by way of parallel computing—A sensitivity analysis for a real-time LSTM approach using waveform and RMS data. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, J.; Tang, Q.; Ma, J.; Qiu, W. FFNet: An automated identification framework for complex power quality disturbances. Electr. Power Syst. Res. 2022, 208, 107866. [Google Scholar] [CrossRef]
- Achlerkar, P.D.; Samantaray, S.R.; Sabarimalai Manikandan, M. Variational Mode Decomposition and Decision Tree Based Detection and Classification of Power Quality Disturbances in Grid-Connected Distributed Generation System. IEEE Trans. Smart Grid 2018, 9, 3122–3132. [Google Scholar] [CrossRef]
- Karasu, S.; Saraç, Z. Investigation of power quality disturbances by using 2D discrete orthonormal S-transform, machine learning and multi-objective evolutionary algorithms. Swarm Evol. Comput. 2019, 44, 1060–1072. [Google Scholar] [CrossRef]
- Grossmann, A.; Morlet, J. Decomposition of Hardy Functions into Square Integrable Wavelets of Constant Shape. SIAM J. Math. Anal. 1984, 15, 723–736. [Google Scholar] [CrossRef]
- Erişti, H.; Demir, Y. Automatic classification of power quality events and disturbances using wavelet transform and Support Vector Machines. IET Gener. Transm. Distrib. 2012, 6, 968–976. [Google Scholar] [CrossRef]
- Nieto, N.; Orozco, D.M. El uso de la transformada Wavelet discreta en la reconstrucción de señales senosoidales. Sci. Tech. 2008, 1, 381–386. [Google Scholar]
- Mallat, S. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Lester, M. Introducción a Wavelets, Buenos Aires, Argentina, 2006. 20 February. Available online: https://users.exa.unicen.edu.ar/catedras/escuelapav/cursos/wavelets.htm (accessed on 1 February 2025).
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Thirumala, K.; Pal, S.; Jain, T.; Umarikar, A.C. A classification method for multiple power quality disturbances using EWT based adaptive filtering and multiclass SVM. Neurocomputing 2019, 334, 265–274. [Google Scholar] [CrossRef]
- Rodrigues Junior, W.L.; Borges, F.A.S.; Veloso, A.F.d.S.; Rabêlo, R.d.A.L.; Rodrigues, J.J.P.C. Low voltage smart meter for monitoring of power quality disturbances applied in Smart Grid. Measurement 2019, 147, 106890. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics), 1st ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Panigrahi, R.R.; Mishra, M.; Nayak, J.; Shanmuganathan, V.; Naik, B.; Jung, Y.A. A power quality detection and classification algorithm based on FDST and hyper-parameter tuned light-GBM using memetic firefly algorithm. Measurement 2022, 187, 110260. [Google Scholar] [CrossRef]
- IEEE Std 1159-2009; IEEE Recommended Practice for Monitoring Electric Power Quality, (Revision of IEEE Std 1159-1995). Institute of Electrical and Electronics Engineers: New York, NY, USA, 2009; pp. 1–94. [CrossRef]
- Lee, G.R.; Gommers, R.; Waselewski, F.; Wohlfahrt, K.; Leary, A. PyWavelets: A Python package for wavelet analysis. J. Open Source Softw. 2019, 4, 1237. [Google Scholar] [CrossRef]
- Medina-Molina, J.A.; Arzate-Rueda, B.; Reyes-Archundia, E.; Gutiérrez-Gnecchi, J.A.; Olivares-Rojas, J.C.; Rodríguez-Herrejón, J.A.; Guerrero-Rodríguez, N.F. Execution time comparison of algorithms to classify power quality disturbances in single board computers. In Proceedings of the 2024 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 1–2 November 2024; Volume 8, pp. 1–6. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]


| Name | Class | Mathematical Model | Parameters |
|---|---|---|---|
| Normal | C1 | ||
| Sag | C2 | ||
| Transient Oscillation | C3 | ||
| Swell | C4 | ||
| Flicker | C5 | ||
| Interruption | C6 | ||
| Notch | C7 | ||
| Feature | Equation | Feature | Equation |
|---|---|---|---|
| Mean (1) | Root Mean Square (2) | ||
| Standard Deviation (3) | Symmetry (4) | ||
| Kurtosis (5) | Variance (6) | ||
| Energy (7) |
| (kHz) | DWT Level | Levels Removed | Noise Level (SNR) | Comb. | Success % | DWT Level | Levels Removed | Noise Level (SNR) | Comb. | Success % |
|---|---|---|---|---|---|---|---|---|---|---|
| 3.2 | 5 | - | - | 1, 3, 4, 5, 6 | 97.44 | 7 | 1 | 50 | 2, 4, 5, 6 | 94.02 |
| 5 | 6 | - | - | 1, 2, 3, 4, 5, 6 | 96.18 | 7 | 1 | 50 | 1, 3, 5, 6 | 93.14 |
| 6.4 | 6 | - | - | 3, 4, 5, 6 | 98.95 | 7 | 1 | 50 | 1, 2, 3, 4, 5, 6 | 95.42 |
| 8 | 7 | - | - | 1, 2, 3, 4, 5, 6 | 97.49 | 4 | 2 | 50 | 3, 5, 6 | 94.85 |
| 9.6 | 5 | - | - | 1, 5, 6 | 99.90 | 5 | 2 | 50 | 3, 5, 6 | 95.79 |
| 15 | 7 | - | - | 1, 3, 4, 5, 6 | 97.39 | 5 | 1 | 50 | 1, 3, 4, 5, 6 | 94.49 |
| 20 | 7 | - | - | 1, 2, 3, 5, 6 | 97.04 | 5 | 2 | 50 | 3, 4, 5, 6 | 95.11 |
| 30 | 7 | - | - | 4, 5, 6 | 97.54 | 6 | 1 | 50 | 3, 5, 6 | 96.00 |
| 3.2 | 7 | - | 30 | 3, 4, 5, 6 | 91.58 | 7 | 1 | 40 | 1, 2, 4, 5, 6 | 93.55 |
| 5 | 6 | - | 30 | 2, 4, 5, 6 | 90.02 | 7 | - | 40 | 2, 3, 4, 5, 6 | 91.89 |
| 6.4 | 7 | - | 30 | 1, 2, 3, 5, 6 | 92.56 | 7 | - | 40 | 1, 2, 3, 4, 5, 6 | 94.49 |
| 8 | 7 | 1 | 30 | 1, 2, 3, 5, 6 | 93.66 | 7 | 2 | 40 | 1, 3, 5, 6 | 94.49 |
| 9.6 | 7 | 2 | 30 | 1, 2, 4, 5, 6 | 91.78 | 7 | 2 | 40 | 3, 4, 5, 6 | 92.98 |
| 15 | 7 | 3 | 30 | 1, 4, 5, 6 | 92.82 | 7 | 3 | 40 | 1, 2, 4, 5, 6 | 94.23 |
| 20 | 5 | 3 | 30 | 1, 3, 5, 6 | 92.67 | 7 | 3 | 40 | 1, 3, 5, 6 | 94.02 |
| 30 | 6 | 3 | 30 | 1, 2, 3, 4, 5, 6 | 94.23 | 6 | 3 | 40 | 3, 4, 5, 6 | 95.11 |
| (kHz) | SNR | Mother Wavelet | DWT Level | Levels Removed | Comb. | Success Rate | Run-Time (s) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AVG | C1 | C2 | C3 | C4 | C5 | C6 | C7 | |||||||
| 3.2 | - | dmey | 5 | - | 1, 3, 4, 5, 6 | 97.4 | 94.7 | 96.7 | 99.7 | 98.6 | 100 | 91.8 | 100 | 239 |
| 5 | - | db28 | 6 | - | 1, 2, 3, 4, 5, 6 | 96.2 | 93.1 | 93.9 | 100 | 97.6 | 100 | 88.4 | 99.7 | 277 |
| 6.4 | - | dmey | 6 | - | 3, 4, 5, 6 | 98.9 | 100 | 97.5 | 100 | 100 | 100 | 95 | 99.7 | 294 |
| 8 | - | bior4.4 | 7 | - | 1, 2, 3, 4, 5, 6 | 98.3 | 95.1 | 96.5 | 99.7 | 100 | 100 | 96.8 | 100 | 212 |
| 9.6 | - | dmey | 5 | - | 1, 5, 6 | 99.9 | 100 | 100 | 100 | 100 | 100 | 99.6 | 99.7 | 323 |
| 15 | - | dmey | 7 | - | 1, 3, 4, 5, 6 | 97.4 | 93.7 | 96.2 | 99.7 | 100 | 100 | 91.5 | 100 | 445 |
| 20 | - | dmey | 7 | - | 1, 2, 3, 5, 6 | 97 | 91.6 | 97.3 | 100 | 100 | 99.3 | 90.8 | 100 | 527 |
| 30 | - | db28 | 7 | - | 4, 5, 6 | 99.6 | 98.6 | 100 | 100 | 100 | 100 | 98.8 | 99.7 | 661 |
| 3.2 | 50 | bior4.4 | 7 | 1 | 2, 4, 5, 6 | 94.3 | 80.6 | 94.7 | 100 | 97.9 | 100 | 90.3 | 100 | 314 |
| 5 | rbio3.1 | 7 | 1 | 1, 3, 5, 6 | 93.9 | 82.3 | 97.3 | 100 | 99.3 | 97.7 | 85.7 | 99.3 | 306 | |
| 6.4 | dmey | 7 | 1 | 1, 2, 3, 4, 5, 6 | 95.4 | 84.8 | 96.7 | 100 | 97.9 | 100 | 90.6 | 100 | 544 | |
| 8 | dmey | 4 | 2 | 3, 5, 6 | 94.9 | 86.9 | 97 | 100 | 97.2 | 96.9 | 88.3 | 100 | 387 | |
| 9.6 | dmey | 5 | 2 | 3, 5, 6 | 95.8 | 86.7 | 97.5 | 100 | 99.3 | 99.2 | 89.9 | 100 | 401 | |
| 15 | dmey | 5 | 1 | 1, 3, 4, 5, 6 | 94.5 | 83.7 | 95.4 | 100 | 97.5 | 98.8 | 88.8 | 100 | 477 | |
| 20 | dmey | 5 | 2 | 3, 4, 5, 6 | 95.1 | 86.8 | 98.3 | 100 | 97.9 | 96.2 | 89.1 | 100 | 399 | |
| 30 | dmey | 6 | 1 | 3, 5, 6 | 96 | 88.4 | 97.2 | 100 | 98 | 98.5 | 91.4 | 100 | 482 | |
| 3.2 | 40 | dmey | 7 | 1 | 1, 2, 4, 5, 6 | 93.6 | 76.6 | 95.4 | 100 | 99.6 | 98.5 | 90.7 | 100 | 566 |
| 5 | rbio3.1 | 7 | - | 2, 3, 4, 5, 6 | 93.2 | 80.1 | 97.2 | 100 | 99.3 | 96.3 | 85.7 | 99.3 | 435 | |
| 6.4 | db28 | 7 | - | 1, 2, 3, 4, 5, 6 | 94.7 | 83.4 | 95 | 100 | 98.6 | 100 | 88.6 | 100 | 698 | |
| 8 | rbio3.1 | 7 | 2 | 1, 3, 5, 6 | 95.4 | 86.8 | 96.6 | 100 | 97.4 | 99.6 | 89.5 | 99.6 | 233 | |
| 9.6 | dmey | 7 | 2 | 3, 4, 5, 6 | 93 | 85 | 92.2 | 100 | 91.8 | 97 | 86.8 | 99.6 | 477 | |
| 15 | dmey | 7 | 3 | 1, 2, 4, 5, 6 | 94.2 | 81.2 | 96 | 100 | 98.9 | 100 | 87.6 | 100 | 448 | |
| 20 | dmey | 7 | 3 | 1, 3, 5, 6 | 94 | 82.6 | 96.4 | 100 | 98.2 | 98.5 | 86.3 | 100 | 449 | |
| 30 | dmey | 6 | 3 | 3, 4, 5, 6 | 95.1 | 84 | 98.7 | 100 | 98.2 | 99.2 | 88.9 | 100 | 384 | |
| 3.2 | 30 | db4 | 7 | - | 3, 4, 5, 6 | 91.9 | 76.4 | 91.2 | 100 | 97.8 | 97 | 86.1 | 100 | 443 |
| 5 | rbio3.1 | 6 | - | 2, 4, 5, 6 | 93 | 79.8 | 96.4 | 100 | 97.9 | 98.1 | 86.4 | 97.4 | 429 | |
| 6.4 | rbio3.1 | 7 | - | 1, 2, 3, 5, 6 | 93.7 | 79.9 | 99.5 | 100 | 97.9 | 99.2 | 86.4 | 98.5 | 434 | |
| 8 | rbio3.1 | 7 | 1 | 1, 2, 3, 5, 6 | 94.6 | 84.4 | 95 | 100 | 97.6 | 99.2 | 88.5 | 99.6 | 300 | |
| 9.6 | bior4.4 | 7 | 2 | 1, 2, 4, 5, 6 | 93.2 | 79.8 | 91.2 | 99.6 | 97.1 | 99.2 | 89.6 | 99.3 | 256 | |
| 15 | dmey | 7 | 3 | 1, 4, 5, 6 | 92.8 | 78.3 | 92.1 | 100 | 98.6 | 98.9 | 86.5 | 99.6 | 439 | |
| 20 | db4 | 5 | 3 | 1, 3, 5, 6 | 93.9 | 86.8 | 94.1 | 100 | 95.3 | 96.6 | 86.7 | 100 | 146 | |
| 30 | bior4.4 | 6 | 3 | 1, 2, 3, 4, 5, 6 | 95.2 | 86.4 | 97.9 | 100 | 99.3 | 97.7 | 88.2 | 99.6 | 208 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medina-Molina, J.A.; Reyes-Archundia, E.; Gutiérrez-Gnecchi, J.A.; Rodríguez-Herrejón, J.A.; Chávez-Báez, M.V.; Olivares-Rojas, J.C.; Guerrero-Rodríguez, N.F. Optimal Selection of Sampling Rates and Mother Wavelet for an Algorithm to Classify Power Quality Disturbances. Computers 2025, 14, 138. https://doi.org/10.3390/computers14040138
Medina-Molina JA, Reyes-Archundia E, Gutiérrez-Gnecchi JA, Rodríguez-Herrejón JA, Chávez-Báez MV, Olivares-Rojas JC, Guerrero-Rodríguez NF. Optimal Selection of Sampling Rates and Mother Wavelet for an Algorithm to Classify Power Quality Disturbances. Computers. 2025; 14(4):138. https://doi.org/10.3390/computers14040138
Chicago/Turabian StyleMedina-Molina, Jonatan A., Enrique Reyes-Archundia, José A. Gutiérrez-Gnecchi, Javier A. Rodríguez-Herrejón, Marco V. Chávez-Báez, Juan C. Olivares-Rojas, and Néstor F. Guerrero-Rodríguez. 2025. "Optimal Selection of Sampling Rates and Mother Wavelet for an Algorithm to Classify Power Quality Disturbances" Computers 14, no. 4: 138. https://doi.org/10.3390/computers14040138
APA StyleMedina-Molina, J. A., Reyes-Archundia, E., Gutiérrez-Gnecchi, J. A., Rodríguez-Herrejón, J. A., Chávez-Báez, M. V., Olivares-Rojas, J. C., & Guerrero-Rodríguez, N. F. (2025). Optimal Selection of Sampling Rates and Mother Wavelet for an Algorithm to Classify Power Quality Disturbances. Computers, 14(4), 138. https://doi.org/10.3390/computers14040138










