Quantum Testing of Recommender Algorithms on GPU-Based Quantum Simulators

Abstract

This study explores the application of quantum computing in asset management, focusing on the use of the Quantum Approximate Optimization Algorithm (QAOA) to solve specific classes of financial asset recommendation problems. While quantum computing holds promise for combinatorial optimization tasks, its application to portfolio management faces significant challenges in scalability for practical implementations. In this work, we model the problem using a graph representation where nodes represent investors, and edges reflect significant similarities in asset choices. We test the proposed method using quantum simulators, including cuQuantum, Cirq-GPU, and Cirq with IonQ, and compare the performance of quantum optimization against classical brute-force methods. Our results suggest that quantum algorithms may offer computational advantages for certain use cases, though classical heuristics also provide competitive performance for smaller datasets. This study contributes to the ongoing investigation into the potential of quantum computing for real-time financial decision-making, providing insights into both its applicability and limitations in asset management for larger and more complex investor datasets.

1. Introduction

Making effective financial asset recommendations is a fundamental challenge in portfolio management. The objective is to classify investors based on their investment profiles and portfolio allocations, and then recommend suitable assets. Traditional methods, such as statistical clustering and factor models, face scalability issues and struggle to capture the often complex, nonlinear relationships between investors and assets [1,2]. These classical approaches also fail to address the dynamic nature of continuously updating financial data, which demands more sophisticated techniques.

The Max-Cut algorithm presents a compelling solution, as it partitions a graph to maximize a function of the edges between the two sets, naturally aligning with the task of grouping investors based on investment profiles and portfolio allocations [3,4]. This approach has shown great promise in graph partitioning, providing better segmentation of complex datasets as compared to more traditional approaches [5]. The Max-Cut problem is equivalent to the Quadratic Unconstrained Binary Optimization (QUBO) problem, which is related to the Ising model. This class of problems has been well studied in operations research, with numerous classical, quantum, and hybrid solvers available [6]. Classical solvers, such as semidefinite programming relaxations and heuristics like MADAM [7], have been used to solve Max-Cut efficiently, though scalability remains a key challenge for problems with larger datasets.

Quantum computing offers an innovative approach to solving the Max-Cut problem efficiently. The Quantum Approximate Optimization Algorithm (QAOA) leverages quantum superposition and entanglement to explore multiple solutions simultaneously, providing potential computational advantages for solving large-scale optimization problems. Recent studies have demonstrated QAOA’s ability to deliver approximate solutions to the Max-Cut problem with reduced computational effort compared to classical methods [8,9]. However, quantum annealers, such as those developed by D-Wave, also provide a native solution to the Max-Cut problem and offer complementary approaches to quantum optimization [10]. While QAOA is recognized as a promising quantum algorithm, quantum annealing represents another credible alternative for specific optimization tasks, and future scientific research could systematically compare the trade-offs between these approaches. It is also important to note that quantum annealers, while effective for certain problem classes, lack the versatility of gate-based quantum computers. Consequently, their commercialization remains confined to niche applications, and this dependency on one to two vendors may further complicate efforts to persuade compliance departments in the financial industry to adopt them.

Despite these advancements, solving large-scale financial asset recommendation problems using quantum methods remains a challenge due to the computational cost and the need for more efficient solutions. In highly dynamic financial markets, real-time computations require faster and more scalable algorithms [11]. In the context of financial asset recommendation systems, as compared to similar algorithms in e-commerce, the complexity is further compounded by several factors:

• Large User Profiles: Financial recommender systems typically deal with much larger and more complex user profiles (easily 50 to 100 fields, as required by regulations) compared to conventional recommendation systems in other domains (e.g., less than 5 fields in e-commerce that are actively used).
• Regulatory Considerations: A key challenge in financial asset recommendation is the need to address suitability concerns, which necessitate that recommendation systems produce piecewise linear—rather than smooth or continuous—outputs to align asset recommendations with each investor’s specific needs, risk appetite, and investment objectives.
• Expert System Integration: A financial recommender system must integrate expert input—typically provided by experienced financial analysts or investment managers, as often required by regulation. In our implementation, the expert system closely mirrors an investment analytics engine used by one of the world’s largest asset managers, thereby enhancing the likelihood that our recommendations comply with established industry practices. Looking ahead, we plan to incorporate advanced expert token routing (ETR) techniques, which differ from traditional mixture of experts methods by routing expert inputs more efficiently and offering significant improvements in computational scalability. This enhancement is vital for addressing high-dimensional problems that incorporate causality, rendering them considerably more complex than the recommendation systems developed for leading e-commerce platforms; for example, the financial product types we target are characterized by hundreds of factors—such as asset type, region, sector, corporate financials, news/social media sentiment, and regulatory filings—compared to the handful of attributes typically considered in conventional commercial merchandise.

Our work aims to enhance financial asset recommendation systems by applying QAOA to the Max-Cut algorithm for investor clustering. This work addresses the scalability and regulatory complexities inherent in financial portfolio management. The use of quantum simulators, such as cuQuantum [12] and Cirq-GPU [13], is tested and compared against brute-force enumeration to demonstrate the potential advantages of quantum optimization for large-scale financial problems.

Several works have contributed to the development of quantum computing applications in finance and graph theory. Lee and Constantinides (2023) investigated quantum applications in finance, focusing on computational experiments for quantum computing in financial optimization [14]. Their earlier work on quantumized graph cuts for portfolio construction and asset selection set the stage for further advancements in integrating quantum algorithms into financial systems [15]. However, the application of quantum computing in financial asset recommendation, a specific subfield, is still in development. Our work builds upon these contributions by applying QAOA to improve financial asset recommendation systems, specifically in large-scale, real-time financial contexts.

In this paper, we combine QAOA with investment analytics techniques to solve the Max-Cut algorithm for investor clustering in financial portfolio management. We demonstrate the application of QAOA on quantum simulators and compare its performance to brute-force enumeration. Our results show that quantum optimization through QAOA can significantly enhance the efficiency and accuracy of asset recommendations in large-scale financial decision-making, bridging the gap between quantum theory and practical financial applications.

2. Problem Statement and Modeling

The objective of this paper is to develop an efficient, scalable, and practical recommendation system for financial assets. Conventional asset recommendation methods often rely on predefined heuristics and simplistic—or even naïve—clustering techniques that fail to capture the high-dimensional and complex nature of financial data. Furthermore, these traditional approaches do not scale well when matching millions of investor profiles against thousands of approved financial products, as is common in typical commercial banking environments. To address these challenges, we propose a novel approach that clusters similar customers and recommends assets based on these clusters. This technique aims to provide more accurate and personalized recommendations by grouping customers with similar portfolio characteristics and preferences.

2.1. Data Structure Modeling: Graph Representation

In this study, we represent customers and their relationships using a graph. This allows us to model the problem of asset recommendation as a graph partitioning task. Each customer is represented as a node, and the relationship between customers is represented by an edge. The edges indicate the degree of similarity between customer profiles, with the weight of the edge reflecting how similar the customers’ profiles and portfolio information are. In the standard adjacency matrix, the higher the weight of an edge, the more similar the two customer profiles are. For the initial phase of deployment, this graph-based representation provides an intuitive way to group customers by clustering them based on their portfolio similarities. In subsequent phases, the investor graph analytics will likely integrate additional information, such as investor–investor social graphs as well as investor–product interaction graphs.

Let $G=(V,E)$ represent an undirected graph, where

• $V=\{v_1,v_2,\dots ,v_n\}$ is the set of vertices (or nodes), where each node represents an individual customer.
• $E=\left\{e_{ij}\right\}$ is the set of edges, where each edge $e_{ij}\in E$ connects customers $v_i$ and $v_j$, and the weight $w_{ij}$ represents the similarity between their portfolios.

The similarity $w_{ij}$ between customers $v_i$ and $v_j$ is computed using a similarity measure such as the correlation coefficient. The correlation coefficient is a measure of how closely the portfolio characteristics and other profile information of two customers may align. The formula for the correlation coefficient between two customer profiles’ data vectors ${\mathbf{p}}_i$ and ${\mathbf{p}}_j$ is given by

$$w_{ij}={\displaystyle \frac{{\sum }_{k=1}^m(p_{ik}-\overline{p_i})(p_{jk}-\overline{p_j})}{\sqrt{{\sum }_{k=1}^m{(p_{ik}-\overline{p_i})}^2}\sqrt{{\sum }_{k=1}^m{(p_{jk}-\overline{p_j})}^2}}}$$

where

• $p_{ik}$ and $p_{jk}$ represent the k-th profile feature for customers $v_i$ and $v_j$, respectively.
• $\overline{p_i}$ and $\overline{p_j}$ are the means of the profile features for customers $v_i$ and $v_j$.
• m is the number of profile features in the customer profile and portfolio data.

The result of this correlation coefficient is a value between $-1$ and 1, where a value closer to 1 indicates a high similarity between the two customers’ profiles, and a value closer to $-1$ indicates a large dissimilarity. In the context of our graph, this value directly translates to the edge weight $w_{ij}$. Higher edge weights indicate customers that are more similar, while lower values indicate greater dissimilarity. This correlation-based graph model forms the foundation for the subsequent clustering of customers. For more convenient computation, we use $1-w_{ij}$ as the weight of edges, ensuring all values are positive. Using this modified convention, a smaller value represents higher similarity.

2.2. Max-Cut Problem for Clustering

Once the graph is constructed as stated in the last subsection, the problem of customer clustering is identical to that of graph partitioning, specifically, solving the Max-Cut problem. The Max-Cut problem is an NP-complete combinatorial optimization problem that involves partitioning a graph into two sets such that the number of edges between the sets is maximized. This problem is naturally suited for clustering customers, as it seeks to split the graph in a way that maximizes the differences between clusters (i.e., thus ensuring that similar customers remain within the same cluster while dissimilar customers are placed in different clusters).

Formally, the Max-Cut problem can be defined as follows: given an undirected graph $G=(V,E)$ with weight function $w:E\to \mathbb{R}$, the task is to find a partition of the vertices into two sets S and T such that the sum of the weights of the edges between S and T is maximized:

$$\mathrm{Max}\text{-}\mathrm{Cut}=\underset{S,T}{max}\sum _{\begin{array}{c}i\in S,j\in T\\ (i,j)\in E\end{array}}{w}_{ij},$$

where $S\cup T=V$ and $S\cap T=\varnothing$.

The Max-Cut problem is NP-complete, meaning that it is often computationally intractable to solve precisely for large graphs. Therefore, we turn to approximate methods, specifically quantum computing techniques, to find near-optimal solutions more efficiently than using classical methods.

2.3. Quantum Approximate Optimization Algorithm (QAOA)

To solve the Max-Cut problem, we utilize the Quantum Approximate Optimization Algorithm (QAOA), which approximates solutions to combinatorial optimization problems. Introduced by Farhi et al. (2014) [16], QAOA leverages quantum superposition and entanglement to explore multiple solutions simultaneously, offering potential advantages over classical algorithms.

In this study, we selected the Quantum Approximate Optimization Algorithm (QAOA) as the primary quantum approach for solving our portfolio selection problem due to its ability to effectively address graph cut challenges, which are critical for identifying optimal solutions in both asset selection and asset allocation. Graph cut techniques play a foundational role in portfolio construction, as demonstrated in prior research [17]. Specifically, the portfolio max-cut problem is essential for ensuring robust asset selection and asset allocation strategies. Without an effective graph cut implementation, the use of a “dumb” optimizer may deliver results of limited value to investors.

While QAOA is well suited for solving combinatorial optimization problems like graph cuts, alternative quantum approaches were considered. For instance, quantum annealing has shown promise in solving optimization problems by leveraging adiabatic quantum computation [18]. However, its reliance on specific hardware architectures and sensitivity to noise can limit its applicability to solve more general problems. Hybrid quantum–classical methods, such as variational quantum eigensolvers (VQE), offer flexibility and adaptability but may require extensive parameter tuning and classical resources [19].

Ultimately, QAOA was chosen for its computational efficiency and alignment with the requirements of portfolio construction. By addressing graph cut challenges effectively, QAOA enables scalable quantum solutions that are practical for financial applications. QAOA operates on a quantum system of n qubits, where each qubit corresponds to a vertex in the graph. The QAOA algorithm uses a parameterized quantum circuit consisting of alternating layers of problem-specific unitary operations and mixing operations. The goal is to find the optimal set of parameters that minimize the expected value of the problem’s cost function.

The QAOA circuit can be described as follows.

2.3.1. Initialize the Qubits in an Equal Superposition State

We begin the construction of the QAOA circuit by preparing a uniform superposition across the qubits that correspond to the nodes of the graph. This is achieved by applying a Hadamard gate H to each qubit.

The Hadamard gate transforms the initial state ${|0\rangle }^{\otimes n}$ (where n is the number of nodes in the graph) into an equal superposition of all possible binary configurations of the qubits:

$$|{\psi }_0\rangle =H^{\otimes n}{|0\rangle }^{\otimes n}={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{x_1,x_2,\dots ,x_n\in \{0,1\}}|x_1,x_2,\dots ,x_n\rangle$$

This state prepares the system for the quantum search over all possible partitions of the graph. After the Hadamard gates, the qubits are in a superposition of all possible outcomes, representing different ways the graph can be split into two sets.

2.3.2. Problem Hamiltonian Evolution: ZZ Interactions

Next, we apply the problem Hamiltonian, which encodes the Max-Cut objective into the quantum system. The problem Hamiltonian $H_C$ for the Max-Cut problem can be written as follows:

$$H_C=\sum _{(u,v)\in E}{w}_{uv}(I-Z_u{Z}_v)$$

where

• E is the set of edges in the graph;
• $w_{uv}$ is the weight of the edge between nodes u and v;
• $Z_u$ and $Z_v$ are the Pauli-Z operators acting on the qubits corresponding to nodes u and v;
• I is the identity matrix.

The operator $Z_u{Z}_v$ acts as an energy penalty when both qubits u and v are in the same state (either both 0 or both 1), aligning with the goal of maximizing the cut by favoring opposite states for each pair of connected nodes.

In the circuit, we apply controlled-$ZZ$ gates between pairs of neighboring qubits. Specifically, for each edge $(u,v)$, we apply a $ZZ$ gate with a rotation angle proportional to the edge weight $w_{uv}$. The parameter $\alpha$ determines the strength of the evolution, which is controlled via the following transformation:

$$U_{\mathrm{problem}}\left(\alpha \right)=\prod _{(u,v)\in E}exp\left(-i\alpha w_{uv}{Z}_u{Z}_v\right)$$

This step ensures that the quantum state evolves according to the problem’s constraints, encoding the weight of each edge into the system’s entanglement.

2.3.3. Mixer Hamiltonian: X Rotation

After the problem Hamiltonian evolution, we apply the mixer Hamiltonian, which promotes superposition and the exploration of different possible solutions. The mixer Hamiltonian $H_M$ is typically chosen as the sum of Pauli-X operators for all qubits:

$$H_M=\sum _{i=1}^n{X}_i$$

where $X_i$ is the Pauli-X operator acting on qubit i. The corresponding unitary evolution under the mixer Hamiltonian is given by

$$U_{\mathrm{mixer}}\left(\beta \right)=\prod _{i=1}^{n}exp\left(-i\beta X_i\right)$$

where $\beta$ is a free parameter that controls the strength of the mixing. The application of X-rotation gates $X^{\beta }$ for each qubit induces transitions between computational basis states, promoting exploration of the solution space and helping to prevent the algorithm from getting trapped in local minima. The parameter $\beta$ is optimized during the quantum optimization process to achieve an optimal balance between exploration and exploitation, and guide the system toward a solution that maximizes the cut.

2.3.4. Cost Function and Optimization

The Quantum Approximate Optimization Algorithm (QAOA) seeks to minimize the expected value of the cost function C, which is defined based on the partitioning of the graph in the Max-Cut problem. In QAOA, the objective is to find the optimal cut that maximizes the number of edges cut by the partition of the graph, and this is achieved by appropriately selecting the quantum parameters $\alpha$ and $\beta$.

In QAOA, the quantum state $\left|\psi \right(\alpha ,\beta )\rangle$ is evolved through a series of unitary operations defined by the problem Hamiltonian $H_C$ and the mixer Hamiltonian $H_M$. The total evolution is governed by the unitary operators $U_{\mathrm{problem}}\left(\alpha \right)$ and $U_{\mathrm{mixer}}\left(\beta \right)$, which are applied sequentially. The quantum state after applying these unitaries is given by

$$|\psi (\alpha ,\beta )\rangle =U_{\mathrm{mixer}}\left(\beta \right)U_{\mathrm{problem}}\left(\alpha \right)|{\psi }_0\rangle$$

where $|{\psi }_0\rangle$ is the initial state, prepared as a uniform superposition of all possible configurations.

The cost function C is typically defined as the weight of the edges that are cut by the partition of the graph. In the QAOA framework, this cost is encoded in the problem Hamiltonian $H_C$. The expected cost $\langle C\rangle$ is the expectation value of $H_C$ with respect to the final quantum state $\left|\psi \right(\alpha ,\beta )\rangle$. This is expressed as follows:

$$\langle C\rangle =\langle \psi (\alpha ,\beta )\left|H_C\right|\psi (\alpha ,\beta )\rangle$$

The expectation value $\langle C\rangle$ represents the average cut or expected weight of the cut after measuring the quantum state in the computational basis. The partitioning of the graph is mapped to a classical bitstring upon measurement, and each bitstring corresponds to a different cut. The cost for each bitstring is computed and averaged to give $\langle C\rangle$. The goal of QAOA is to find the optimal parameters $\alpha$ and $\beta$ that minimize the expected cost function $\langle C\rangle$. The optimization procedure typically involves classical optimization techniques such as gradient descent, differential evolution, or other heuristic methods.

To find the optimal values of $\alpha$ and $\beta$, the following optimization problem is solved:

$$({\alpha }^{*},{\beta }^{*})=arg\underset{\alpha ,\beta }{min}\langle C\rangle =arg\underset{\alpha ,\beta }{min}\langle \psi (\alpha ,\beta )\left|H_C\right|\psi (\alpha ,\beta )\rangle$$

The optimization is performed iteratively by adjusting $\alpha$ and $\beta$ to minimize $\langle C\rangle$, most often through gradient-based methods that evaluate the cost function at different points in parameter space. The specific procedure can be summarized as follows:

• Initialization: Set initial values for $\alpha$ and $\beta$ (random or based on heuristics).
• Unitary Application: Apply the unitaries $U_{\mathrm{problem}}\left(\alpha \right)$ and $U_{\mathrm{mixer}}\left(\beta \right)$ to the initial quantum state $|{\psi }_0\rangle$.
• Measurement: Measure the quantum state in the computational basis and compute the corresponding cost $\langle C\rangle$ for the resulting partition.
• Optimization: Update the parameters $\alpha$ and $\beta$ based on the feedback from the measured cost, using a classical optimization algorithm.
• Convergence: Repeat the process until convergence is achieved, i.e., when the parameters no longer result in significant improvement in the cost.

The classical optimization routine used to adjust $\alpha$ and $\beta$ is typically based on minimizing the expected value of the cost function. As quantum circuits are inherently probabilistic, the cost $\langle C\rangle$ is obtained by repeatedly sampling from the quantum state, which corresponds to measuring the quantum state multiple times to gather statistics about the expected cut. The optimization process can be formalized as follows:

$$\langle C\rangle ={\displaystyle \frac{1}{N}}\sum _{x}P\left(x\right)·C\left(x\right)$$

where

• $P\left(x\right)$ is the probability of measuring bitstring x;
• $C\left(x\right)$ is the corresponding cut value for bitstring x;
• N is the number of measurements.

The parameters $\alpha$ and $\beta$ are adjusted to minimize this average cost, where the measurement probabilities $P\left(x\right)$ are obtained through the quantum operations described earlier.

3. Initial Results Based on Quantum Simulators

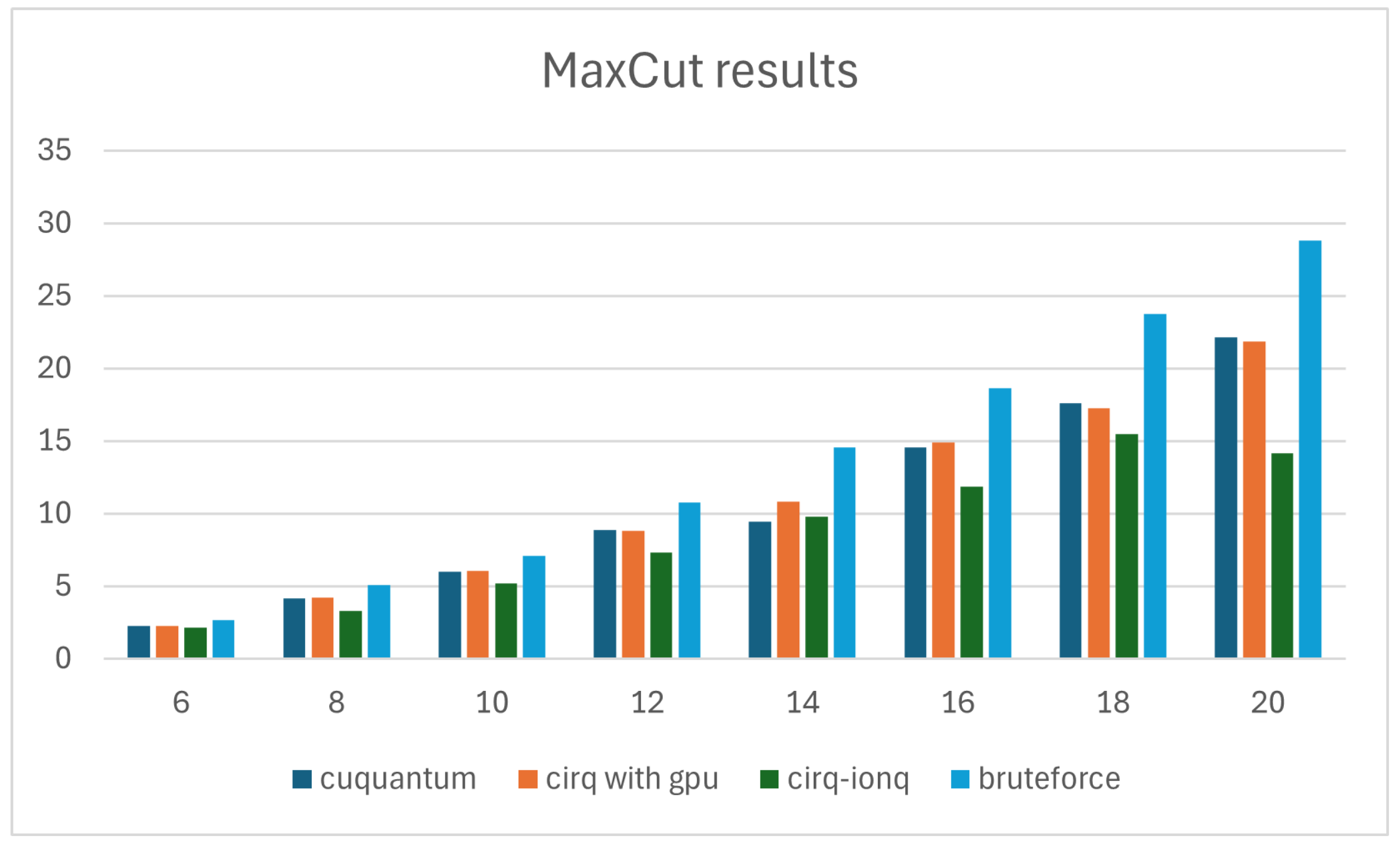
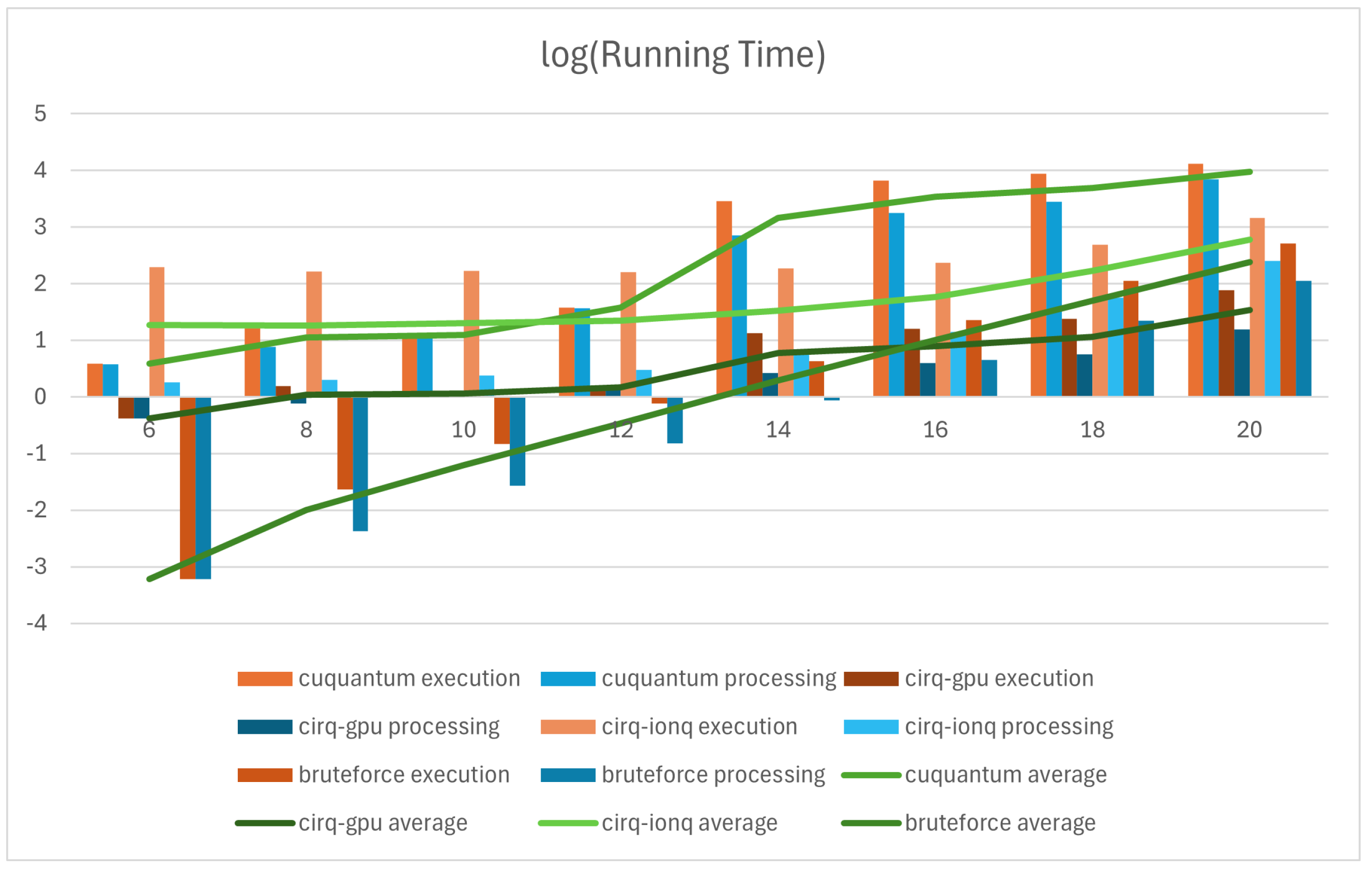
In the ongoing exploration of using the Quantum Approximate Optimization Algorithm (QAOA) to solving the Max-Cut problem, we conducted initial tests using multiple quantum simulators, including cuQuantum, Cirq with GPU, and the Cirq with IonQ simulator. These simulators are crucial for understanding the performance of quantum algorithms before accessing real quantum processing units (QPUs), which often cost more than USD 10,000 per test. The results are compared against the traditional brute-force method to evaluate the efficiency in terms of execution and processing time, as well as the accuracy in approximating the optimal Max-Cut solution.

In this study, brute-force enumeration was used as a reference point rather than a definitive baseline to evaluate the efficiency of quantum heuristics. As an exact algorithm, brute force is slower than heuristic approaches and does not fully capture comparative performance. To define a more practical baseline, intelligent sampling techniques were considered, which reduce the dataset to say 0.1% while retaining essential problem characteristics. Despite this reduction, the exponential complexity of the problem remains, making it computationally intractable for large-scale problems. This underscores the limitations of classical methods, including intelligent sampling, in tackling highly complex optimization tasks.

Although the Max-Cut problem remains inherently challenging, classical heuristics such as Fortet linearization offer viable solutions; in our study, we employ brute-force enumeration to obtain exact solutions that serve as a benchmark for assessing the trade-off between speed and precision. This approach demonstrates that, while quantum heuristics do not yield exact answers, they can considerably enhance efficiency while maintaining competitive accuracy in financial asset recommendations. Although real-world implementations would likely incorporate intelligent sampling techniques—raising practical compliance questions of whether a 1% or a 0.1% sample should be used, which is usually determined by empirical convergence speed—for the purposes of scientific investigation we contend that the baseline should be defined in a manner that remains indisputable from a compliance perspective.

The following chart (

Table 1. Comparison of various simulators and the brute-force method.

Sample Size	cuQuantum			Cirq with GPU			Cirq-IonQ			BruteForce
	Time (s)		Results	Time (s)		Results	Time (s)		Results	Time (s)		Results
	Execution	Processing	Maxcut (top20)	Execution	Processing	Maxcut (top20)	Execution	Processing	Maxcut (top20)	Execution	Processing	Maxcut
6	3.863313	3.819956	2.239370316	0.415386	0.414308	2.239370316	197.522825	1.799864	2.14402627	0.000604	0.000599	2.669099149
8	16.35116	7.739964	4.146999928	1.539764	0.763621	4.204704403	165.770192	1.99014	3.294080284	0.023033	0.004291	5.045877808
10	12.515796	12.431834	5.980810915	1.165031	1.158915	6.047812671	170.325591	2.382496	5.172855712	0.145999	0.026764	7.04879823
12	38.000989	37.03152	8.838397059	1.505424	1.429708	8.796282518	160.003448	3.012442	7.30643994	0.771684	0.151043	10.75412972
14	2894.44738	714.453489	9.45452126	13.230309	2.63625	10.83294122	184.860132	6.004671	9.805261103	4.337385	0.864996	14.52553876
16	6674.65008	1793.984631	14.54128637	16.028221	3.926569	14.90209752	234.33759	14.218993	11.82430494	22.834276	4.522856	18.60860883
18	8789.18914	2772.882752	17.5893638	24.192284	5.603362	17.23152697	495.057964	57.158453	15.48339957	113.048	22.475252	23.71913495
20	13299.4609	6930.772767	22.15522582	75.977552	15.665305	21.83568132	1437.816666	252.57063	14.14051707	517.04842	112.62169	28.79757136

) presents the execution time, processing time, and Max-Cut (top 20) results for varying sample sizes. The execution time represents the total time spent by the simulator to perform the QAOA algorithm, while the processing time refers to the time spent specifically on quantum operations, excluding any overhead. The Max-Cut (top 20) is the average value of the top 20 Max-Cut solutions obtained from the simulation runs.

3.1. Analysis of Results

Based on the data presented in Table 1, we can visualize the results in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6. From these visualizations, several observations can be made:

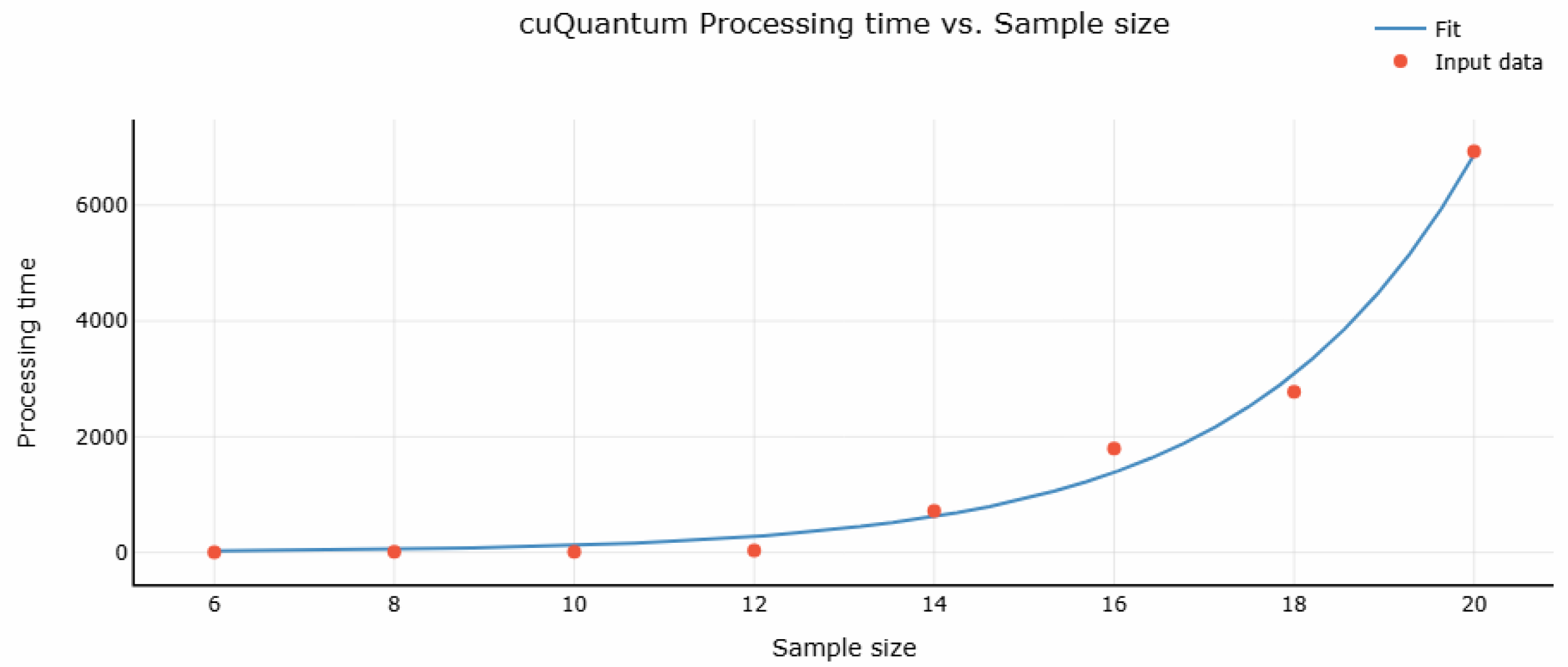
• cuQuantum: The analysis of the cuQuantum simulator demonstrates an exponential growth in execution time as the problem size increases. The empirical relationship between execution time (y) and input size (x) can be modeled by the equation

  $$y=2.27e^{0.401x}$$

  with a coefficient of determination

  $$R^2=0.99136,\mathit{Adj}.R^2=0.98791.$$
  These results demonstrate a strong correlation, indicating that cuQuantum exhibits predictable scalability as the graph size increases.
  Optimized for NVIDIA GPUs, cuQuantum efficiently handles smaller problem sizes (e.g., sample sizes of six and eight). However, its performance declines for larger instances due to increased computational demands and memory constraints. The processing time shows complex scaling, influenced by memory access patterns and tensor contractions. While cuQuantum is highly efficient for small to medium-sized instances, its execution time increases rapidly, posing scalability challenges for larger graphs. Despite this, it maintains high precision in Max-Cut solutions, making it valuable for benchmarking quantum algorithms before deployment on real quantum hardware.
• Cirq with GPU: Google’s Cirq with GPU acceleration provides a substantial performance boost for quantum circuit simulations. Unlike cuQuantum, which is optimized for tensor network-based simulations, Cirq with GPU leverages optimized state-vector evolution and batched quantum circuit execution, resulting in distinct scaling behavior.
  The execution time of Cirq with GPU can be modeled by the polynomial function

  $$y=0.0188x^3-0.60927x^2+6.4487x-20.82978$$

  with a coefficient of determination

  $$R^2=0.96481,\mathit{Adj}.R^2=0.91789.$$
  These values indicate a strong fit, suggesting that Cirq with GPU exhibits a more favorable scaling trend compared to purely exponential growth. The cubic term dominates for larger problem sizes, implying that execution time increases at a controlled rate relative to other approaches.
  Given its efficient handling of state-vector evolution and parallelized execution, Cirq with GPU emerges as the most effective simulator among those analyzed. It balances execution speed with scalability, making it a highly suitable candidate for benchmarking quantum algorithms before deployment on real quantum hardware.
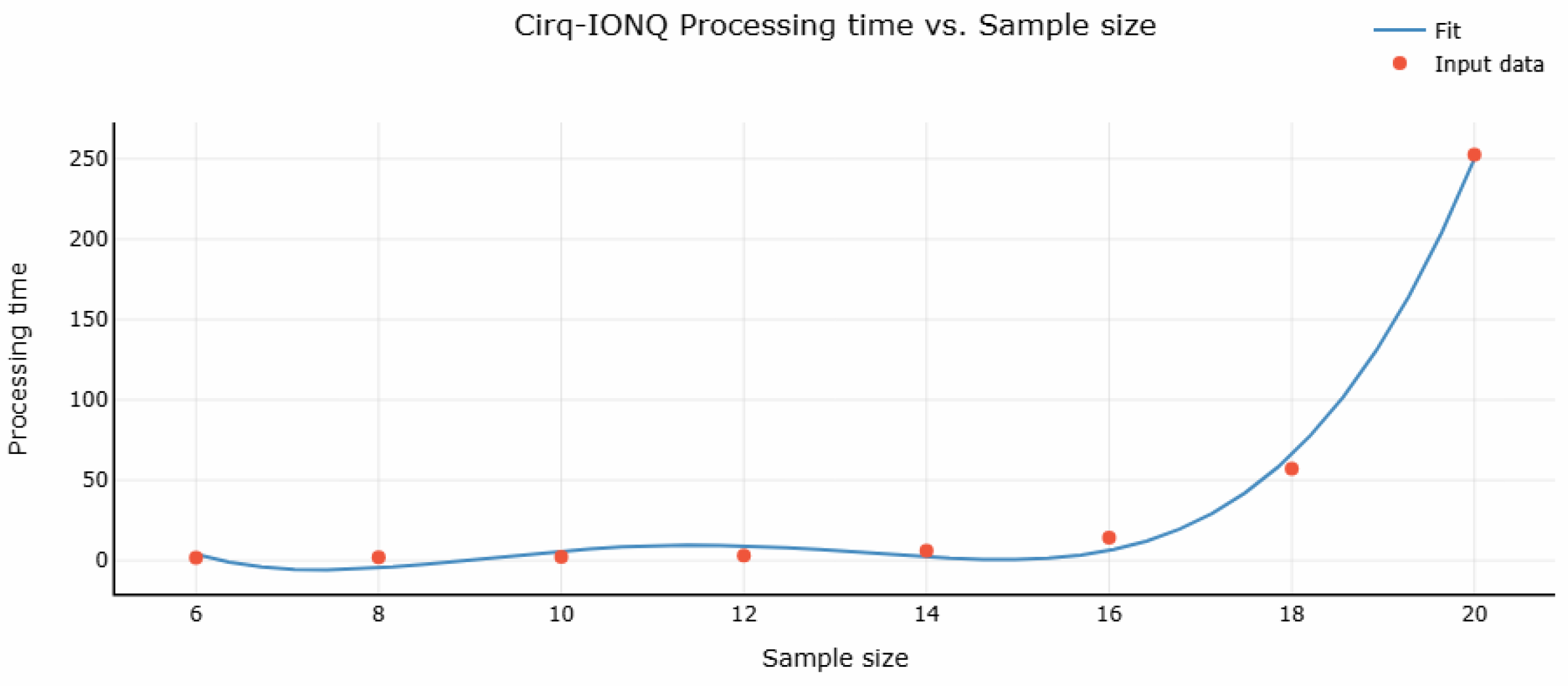
• Cirq-IonQ: The Cirq with IonQ simulator demonstrates the poorest performance in terms of accuracy among the simulators tested. While its execution times are much lower than cuQuantum but slightly higher than Cirq with GPU, it demonstrates less ability to approximate the Max-Cut solutions as compared to the other simulators. This may indicate additional simulation complexity or resource constraints inherent to the IonQ simulator.
  The execution time of the Cirq with IonQ simulator is modeled by the following polynomial function:

  $$\begin{array}{c}\hfill y=0.06173x^4-2.77198x^3+44.95119x^2-309.71821x+762.72271\end{array}$$

  with a coefficient of determination

  $$R^2=0.99507,\mathrm{Adj}.R^2=0.98276.$$
  These values indicate a strong fit, reflecting the behavior of execution time as the problem size increases. The quartic polynomial suggests that execution time grows sharply with increasing sample size, with the highest-degree term contributing to this rapid escalation.
  Although the IonQ simulator exhibits consistent execution times across varying sample sizes, it performs the worst in terms of accuracy, with results less precise than those of cuQuantum and Cirq with GPU. This may be due to limitations in simulation capabilities or resource constraints, which hinder its ability to achieve high-precision solutions.
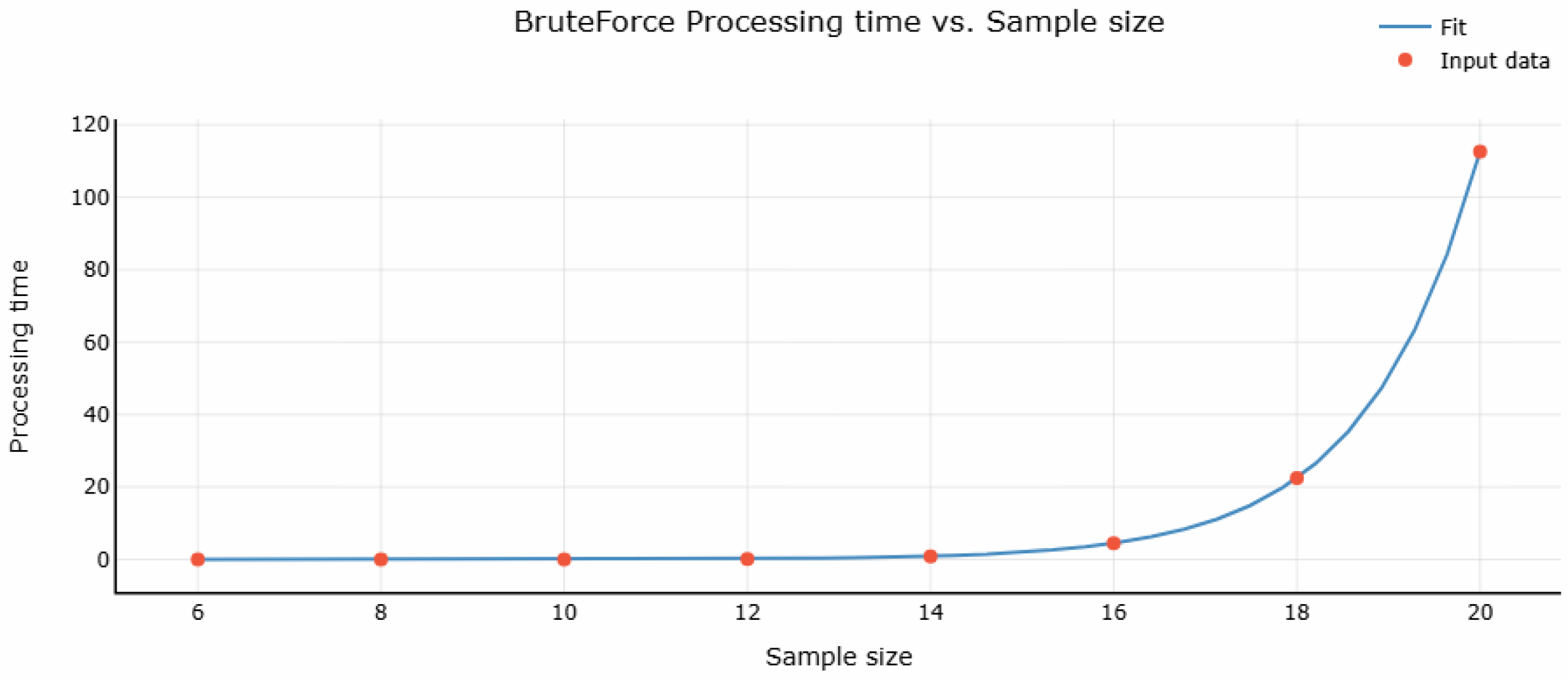
• Brute Force: The brute-force method exhibits an exponential increase in execution time as the problem size grows. The empirical relationship between execution time (y) and input size (x) is given by

  $$y=1.13\times {10}^{-5}{e}^{0.806x}$$

  with a coefficient of determination

  $$R^2=1.0,\mathrm{Adj}.R^2=1.0.$$
  These results confirm the exponential scaling behavior of the brute-force approach, highlighting its inherent computational complexity and inefficiency. Unlike heuristic or quantum methods, brute force exhaustively enumerates all possible Max-Cut partitions to obtain the exact solution. However, this exhaustive search quickly becomes computationally prohibitive for larger graphs, as evidenced by the exponential growth in execution time with increasing problem size.
  As expected, brute-force search is significantly more time-intensive than alternative methods, particularly for larger instances. Despite guaranteeing optimality, its scalability is fundamentally constrained by its exponential time complexity. This renders brute-force optimization impractical for real-world applications beyond small graph instances, reinforcing the necessity of heuristic and quantum approaches such as QAOA.

In our experiments, we analyzed the performance of cuQuantum, Cirq with GPU, the Cirq with IonQ simulator, and brute-force simulators for solving the Max-Cut problem using QAOA. CuQuantum demonstrated high accuracy but faced scalability issues with larger graphs. Cirq with GPU exhibited the best performance, particularly for larger sample sizes, with efficient scaling and high accuracy. The Cirq with IonQ simulator showed consistent performance but lagged in accuracy compared to both cuQuantum and Cirq with GPU. The brute-force method, while guaranteeing optimal solutions, was computationally infeasible for larger problems due to its exponential time complexity. Each method has distinct strengths and limitations, underscoring the importance of selecting the appropriate approach based on problem size and required accuracy.

Evaluating the results reveals a trade-off between accuracy and efficiency.

Table 2. Relative error and processing time of simulators and the brute-force method.

Sample Size	cuQuantum		Cirq with GPU		Cirq-IonQ		BruteForce
	Relative Error	Processing Time (s)	Relative Error	Processing Time (s)	Relative Error	Processing Time (s)	Relative Error	Processing Time (s)
20	23.07%	6930.772767	24.18%	15.665305	50.90%	252.57063	0%	112.62169

highlights the relative error and processing time for different simulators with a sample size of 20. As shown in the figure, the Cirq with GPU method offers significant computational efficiency, providing results much faster than the brute-force approach for large sample sizes. This highlights the trade-off between accuracy and running time, where a slight reduction in accuracy is compensated by a substantial gain in speed. Rapid computation time is particularly beneficial in real-time financial decision-making scenarios, where timely insights are crucial.

While quantum processing units (QPUs) are ideal due to their superior computational power, they remain quite expensive and not yet widely accessible. In the interim, GPUs present an affordable and convenient alternative, delivering commendable performance and making advanced quantum optimization techniques more accessible to a broader range of users. This accessibility ensures that significant improvements in computational efficiency and accuracy can still be achieved without dedicated quantum hardware, thereby democratizing the benefits of quantum computing.

Moving forward, the continued development of GPU-accelerated quantum simulations can bridge the gap between theoretical advancements and practical implementation. As QPUs become more accessible, these GPU-based approaches can serve as valuable intermediate solutions, enabling more researchers and industries to adopt quantum-inspired techniques. Optimizing computational frameworks and leveraging parallel processing capabilities will further enhance scalability, driving innovation in fields such as financial modeling, materials science, and complex optimization problems, where quantum computing is expected to play a transformative role.

3.2. Scalability Challenges and Future Testing on Quantum Hardware

Scalability challenges in financial datasets are driven by the complexity of large user profiles, which typically consist of 50 to 100 fields. These profiles are matched against extensive product lists while adhering to stringent regulatory suitability constraints, resulting in significantly higher computational demands compared to e-commerce systems. In contrast, well-known e-commerce platforms typically handle smaller user profiles with only three to five fields (although e-commerce platforms are capable of storing extensive user metadata, empirical evidence indicates that practical deployments typically restrict themselves to a handful of fields due to computational constraints associated with responding to tens of thousands of graph-based queries per minute), yielding simpler graph structures and lower computational complexity (despite much higher in volume). This disparity highlights the distinct challenges posed by financial datasets and the need for advanced computational methods to address them effectively.

Quantum algorithms, particularly the Quantum Approximate Optimization Algorithm (QAOA), present promising solutions to these scalability issues. QAOA is well suited for managing piecewise linear clustering and incorporating regulatory constraints, making it applicable to the complexities of large-scale financial datasets. By utilizing quantum hardware, QAOA offers the potential to drastically reduce computation time compared to classical brute-force methods, thus providing practical and scalable solutions for data-intensive financial applications.

Despite its potential, scaling QAOA to large investor datasets introduces significant challenges due to the exponential growth in problem size. Classical methods, such as heuristic approaches and mixed-integer programming, have proven effective in addressing scalability efficiently. However, quantum computing faces hardware limitations, including restricted qubit counts, short coherence times, and gate fidelity constraints. To overcome these barriers, future research should investigate hybrid quantum–classical algorithms that integrate quantum optimization with classical solvers and explore problem decomposition techniques that break large portfolio optimization tasks into smaller, manageable subproblems. Advances in quantum circuit design and error mitigation strategies will also be critical for enhancing computational stability.

At present, our results from IonQ are based on simulations, with access to the real IonQ quantum processing unit (QPU) anticipated in future research. The simulator data provide preliminary insights into the expected performance of actual quantum hardware. A key focus of ongoing work is graph sparsification, which is critical due to the unique qubit connectivity constraints in real quantum machines. The topology of a quantum processor significantly influences qubit entanglement and interaction, affecting the execution of quantum algorithms. Future testing on real quantum devices will provide valuable insights into the practical performance of QAOA and other quantum algorithms under realistic noise conditions. Comparative evaluations across different quantum hardware architectures will be crucial for assessing algorithmic efficiency and identifying optimization strategies tailored to specific quantum processors. The distinctive characteristics of these devices are expected to inform best practices for quantum algorithm design, particularly in the context of combinatorial optimization problems such as Max-Cut.

3.3. Practical Considerations

While Quantum Annealers have demonstrated potential for optimization tasks, they were not utilized in this study due to their limited computational advantages over classical methods and the uncertainty surrounding their commercial adoption. The more niche nature of their target audience has resulted in manufacturers such as D-Wave facing challenges in gaining widespread adoption. Given that the financial technology focus of this work is targeted at the banking and finance sector, it is essential to prioritize gate-based quantum devices with more promising commercial prospects that do not immediately draw negative attention among compliance departments of financial institutions due to dependency on one or two hardware vendors.

Instead, this study focuses on hardware platforms that are more likely to support practical applications in the longer term. Recent developments in quantum computing hardware, including new quantum chip designs by the technology giants and trapped ion systems that do not require supercooling, appear promising. These advancements not only mitigate operational complexity but also align with the typical industry requirements of scalable and reliable financial applications that simply do not accept any dependency on one or two hardware vendors. By targeting commercially feasible hardware devices, this work ensures relevance and applicability to real-world use cases in the banking and finance sector.

4. Analysis and Conclusions

This study explores the application of quantum computing in financial asset recommendation, specifically through the use of the Quantum Approximate Optimization Algorithm (QAOA) to solve the Max-Cut problem. Traditional portfolio optimization techniques often struggle with scalability and the complexity of large datasets. Quantum computing offers an alternative approach, leveraging its ability to tackle combinatorial optimization problems efficiently.

Our approach models the investor-to-asset recommendation problem as a graph, where nodes represent investors and edges denote similarities in asset choices. We have applied QAOA to partition this graph and tested its performance using quantum simulators such as cuQuantum, Cirq-GPU, and the Cirq-IonQ simulator. The results indicate that QAOA can effectively find optimal solutions. However, while quantum optimization shows potential advantages over brute-force classical methods, further comparisons with classical heuristics and hybrid algorithms are necessary to fully assess its computational benefits.

Future research will focus on advancing key aspects of quantum computing explored in this work. One priority will be the investigation of graph compression techniques, which, while improving computational efficiency, may introduce additional challenges and unique error patterns. Efforts will also be directed toward addressing device-level accuracy issues that arise from direct problem mapping, with proposed methods to mitigate these errors and enhance computational robustness. Furthermore, ongoing work with real quantum devices will expand the scope of analysis beyond simulations, enabling a thorough evaluation of QAOA’s performance across various hardware architectures. This transition to actual quantum processors will provide valuable insights into quantum circuit optimization, noise mitigation, and hardware-specific challenges. Additionally, alternative quantum approaches, such as quantum annealing and hybrid quantum–classical methods, will be explored to assess their comparative effectiveness in addressing financial optimization problems. These directions aim to refine and broaden the practical applicability of quantum solutions in the financial technology domain.

While this study contributes to the growing body of research on quantum computing in finance, it is important to acknowledge that QAOA’s scalability and real-world applicability remain non-conclusive. As quantum hardware continues to evolve, further advancements in error correction and algorithm design will be essential for achieving practical advantages over classical methods.