Abstract
Verifying sequential consistency (SC) in concurrent programs is computationally challenging due to the exponential growth of possible interleavings among read and write operations. Many of these interleavings produce identical outcomes, rendering exhaustive verification approaches inefficient and computationally expensive, especially as thread counts increase. To mitigate this challenge, this study introduces a novel approach that efficiently verifies SC by identifying a minimal subset of valid event orderings. The proposed method iteratively focuses on ordering write events and evaluates their compatibility with SC conditions, including program order, read-from (rf) relations, and SC semantics, thereby significantly reducing redundant computations. Corresponding read events are subsequently integrated according to program order once the validity of write events has been confirmed, enabling rapid identification of violations to SC criteria. Three algorithmic variants of this approach were developed and empirically evaluated. The final variant exhibited superior performance, achieving substantial improvements in execution time—ranging from 31.919% to 99.992%—compared to the optimal existing practical SC verification algorithms. Additionally, comparative experiments demonstrated that the proposed approach consistently outperforms other state-of-the-art methods in both efficiency and scalability.
1. Introduction
Concurrent programs are composed of multiple threads that operate simultaneously, sharing objects such as shared memory [1,2]. Each thread possesses its own set of instructions and a program counter, which tracks the execution of these instructions [3]. Executing concurrent programs can result in various types of interleaving between thread instructions. In essence, the execution of these programs often integrates the actions of multiple threads rather than treating each thread as a distinct, indivisible unit [4].
In addition to the operating system scheduler, the presence of cache hierarchies and store buffers in modern CPUs, designed to enhance performance, contribute to the diverse range of behaviors observed during the execution of concurrent programs. Therefore, the sequential arrangement of events within each thread may not be assured when these programs are executed on modern processors [5]. Frequently, the behavior of a concurrent program varies when executed in one processor model compared to another [6,7,8]. Moreover, compiler optimizations in contemporary programming languages, which alter the sequence of events within a thread to improve efficiency, can lead to diverse behaviors for the same concurrent program [9,10,11]. The behaviors resulting from the execution of concurrent programs may either conform to the programmer’s expectation—based on following the events in the exact order written in the source code—or deviate from it, as seen in modern processors and compilers where the execution order of instructions is rearranged from the source code sequence [7,12,13]. Due to this reordering, inconsistencies in shared memory among threads may arise [12]. As a result, developing such applications poses a challenging and significant task [13].
To fully leverage the capabilities of modern CPUs and ensure the proper functioning of concurrent applications, it is necessary for programmers to carefully analyze all conceivable combinations of events occurring simultaneously in separate threads [14], [15]. Verifying programs that exhibit unexpected behaviors due to specific sequences of thread events is a formidable challenge. Traditional testing methods may hinder the ability to reproduce the exact sequence of running events that lead to particular behaviors and achieve the intended results for maintenance purposes [15,16]. To illustrate the variety of behaviors that might occur in a concurrent program during multiple executions, Figure 1 demonstrates a small concurrent program known as the store buffer (SB). The SB program consists of two threads (T0 and T1) running concurrently with two shared variables (x and y). Variable a in T0 and variable b in T1 are private. Initially, all shared and private variables are set to 0. The code is organized as a set of events, with each thread containing two events. T0 writes the value 1 to the shared variable x and subsequently reads the value of y into the private variable a. Concurrently, T1 writes the value 1 to the shared variable y and then loads the value of x into the private variable b. The assertion of this program evaluates whether the two read events (e2 and e4) retrieve values from the initial state or the write events within T0 and T1 [17].
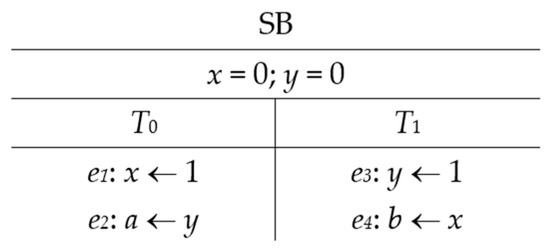
Figure 1.
The SB program.
The results listed in the Results column of Table 1 can be achieved by executing the SB program. Any result can be attained by following the prescribed sequence of events listed in the “Order of Events” column of Table 1.

Table 1.
Behaviors derived from executing the SB litmus test.
Table 1 illustrates that a small program like SB can yield a relatively large number of interleavings of threads and a significant number of behaviors. This illustrates the urgent need for what is referred to as the memory consistency model (MCM) [18]. MCMs define the order in which shared variables are accessed, thereby determining the allowed and disallowed behaviors of concurrent programs under a given MCM [19]. MCMs are categorized into strong models, such as sequential consistency (SC), and weak or relaxed models, such as TSO, ARM, and POWER [18]. In SC, the write operation is executed as an atomic operation, with events from different threads arbitrarily interleaved, while the order of operations within each thread is preserved [7,20]. For this reason, the SC model is often assumed by programmers and verification tools for the design and analysis of concurrent programs [21]. However, current multiprocessors and high-level programming languages provide permissive memory models that allow for the reordering of memory access activities [22,23,24]. As shown by behavior (d) in Table 1, the event order within each thread is reordered, which is prohibited in SC but permissible under weak memory models such as TSO and ARM. Although behavior (d) is allowed in TSO and ARM, it is not acceptable in concurrent program design or verification because event reordering compromises data consistency. This necessitates the consideration of all possible interleavings during the verification process. Concurrency errors, or heisenbugs, describe such behaviors as behavior (d). Testing such programs is challenging, as the program’s behavior may be altered by tracing objectionable behaviors, potentially causing these errors to disappear [25].
Although SC is considered a desirable memory model by users because it simplifies their tasks, implementing sequential consistency is exceedingly complex and prone to error. Consequently, it is crucial to develop automated methods and tools capable of verifying the sequential consistency of executions of a memory implementation for all potential clients or a specific client [20]. As a result, predicting the behaviors that a concurrent program will produce by simply running is impossible, as is determining the number of times a program must be executed to produce all behaviors to classify them as acceptable or unacceptable and investigate the causes of undesirable behaviors. For instance, it is unknown how many times the SB program must be executed to produce behavior (d). Table 2 displays the frequency with which the SB program in the TSO model produces each behavior. It is noteworthy that only 124 out of 1,000,000 execution cycles resulted in the acquisition of behavior (d). This demonstrates the difficulties associated with capturing all behaviors in concurrent programs and reproducing undesirable behaviors to investigate their causes [17]. In general, the absence of concurrency errors cannot be guaranteed by executing concurrent programs numerous times [25].

Table 2.
Frequency of behaviors acquired from executing the SB program.
On the other hand, program verification is a systematic procedure used to demonstrate a program’s accuracy in relation to its specifications. This process involves comparing the program’s specifications to each of its properties, such as whether it should or should not perform certain actions, whether it reaches a deadlock state, whether a data race occurs, or whether it exhibits a specific behavior, to determine if these properties hold [26,27].
Although numerous methods exist for ensuring the accuracy of sequential and concurrent programs, such as those described in [28,29,30], stateless model checking (SMC) is considered the most effective. SMC assumes responsibility for scheduling and systematically examines all potential interleavings (scheduling) of thread events. This approach enables the identification of the order of events that result in a concurrency error and the replication of these event orders to resolve the errors [25].
SMC must implement strategies to reduce the number of executions (event orderings) that are evaluated, as the number of possible thread schedulings increases exponentially with program length and the number of threads [14]. One of the most notable methods is partial order reduction [31,32,33], modified as dynamic partial order reduction (DPOR) for SMC [34]. Two executions can be considered equivalent if they result in the same ordering of conflicting statement executions (referred to as events). The fundamental principle of DPOR holds that it is sufficient to examine at least one execution in each equivalency class of event ordering. Such equivalency classes are referred to as Mazurkiewicz traces [35]. For example, it is evident in Figure 1 that there are four distinct sequences of events that result in behaviors C and D, and none of them contain conflicting events. It is sufficient to analyze one sequence for each behavior, as all four sequences produce the same result without conflict. This expedites the verification process.
The DPOR algorithm is employed to identify each execution, and subsequently, each execution is associated with a read-from (rf) relation that links each read event to the write event that initiated its value. Consequently, the set of events and its rf relation are the only parameters required to determine whether an execution aligns with the SC semantics [14]. The process of classifying executions involves evaluating all possible overlaps between write and read events from all threads concerning the rf relation while preserving the SC model’s semantics. As a result of the exponential increase in overlapping probabilities, this problem is classified as NP-hard [20].
Numerous studies have been conducted to determine whether executions are compatible with the SC model. One such study is presented in [36], where a trace is accepted as input and a search is conducted for a witness to an execution that adheres to SC if any exist. However, this study is constrained by the limited number of threads, memory locations, and values that each memory location can handle. Another approach is proposed in [37], where an execution is utilized as input to determine whether it conforms to the SC model. The authors suggested a method that enables the verification of SC in polynomial time for most practical scenarios while avoiding systematic failures in worst-case scenarios. This method employs a weaker MCM, such as causal consistency, as an intermediate phase to verify consistency in polynomial time before extending it to verify sequential consistency. However, despite these efforts, the method still experiences long processing times. The study [20] introduced a novel method that drastically narrowed the search space for SC checking by computing restrictions on write operations using a saturation-based strategy. By employing a straightforward saturation rule, they deterministically computed a partial storage order to approximate SC in their work, introducing the Weak Sequential Consistency (wSC) model. This model was shown to effectively identify SC violations and compute a significant portion of the SC kernel in polynomial time, covering 74% of the kernel completely and approximating the remaining cases with up to 99.9% accuracy. To further enhance SC checking, the authors combined wSC with external tools like SAT solvers and DBCOP, resulting in two algorithms: wSC + ENUM and wSC + DBCOP. These algorithms demonstrated superior performance and scalability compared to existing techniques, such as Convergent Causal Memory (CCM), achieving notable gains of up to 16 threads. However, the reproducibility of these results is hindered by the lack of specific benchmark information provided in the report.
Other studies [38,39] have focused on detecting SC violations by monitoring concurrent programs during execution. Although effective, this approach negatively impacts the performance of these programs. The study in [14] is notable for its comprehensive treatment of extracting equivalence rf classes, being recognized as the optimal DPOR algorithm for identifying all unique states that can be reached during the execution of any concurrent program. Each of these states is associated with an rf relation. Subsequently, three steps are applied to each state, using the rf relation as input.
In the initial step, a new relation known as “saturated happen-before” (shb) is generated, which must be cycle-free. If a cycle is detected, the execution is considered incompatible with the SC model. Although this step is necessary, it is not always sufficient, and step three is frequently required, as some traces at this stage may contain a cycle without violating SC conditions. If the shb relation is cycle-free, step two is employed to determine a sequence of events from all threads, if feasible, that results in the attainment of this state. This sequence serves as a witness to the program’s compatibility with SC. In cases where a witness cannot be identified, step three is designed to detect all possible overlaps between the threads’ events that lead to the previously specified state.
The primary principle of the third step involves generating a graph that consists of nodes, each representing the execution of an event by a thread. Following the application of numerous conditions, connections between these nodes are established. However, some nodes remain disconnected due to the failure to meet these conditions. A path is then searched from the initial node to a node where all threads have terminated upon fulfilling all conditions for all nodes. If such a path is identified, the case is considered consistent with the SC model, and this path is regarded as a witness to the case. Conversely, if no path is found, the conditions of the SC model are deemed violated. Regardless of the outcome, the execution time of this algorithm is exponential concerning the number of threads, as all potential sequences of event execution are examined.
From the foregoing, it is evident that there is a need for an algorithm that can verify the compatibility of concurrent programs with the SC model by searching for a witness, if any. Such an algorithm should exhibit faster execution than previous methods and should not be restricted by the number of threads, variables, or variable values.
The remainder of this paper is organized as follows. Section 2 provides the preliminary concepts necessary for understanding the proposed approach. In Section 3, an illustrative scenario is presented to clarify the preliminary concepts and demonstrate their application in a concurrent programming context. Section 4 details the proposed algorithms, which form the core of the approach to efficient sequential consistency verification. Implementation details are discussed in Section 5, where the practical aspects of applying the algorithms are elaborated. Section 6 presents a comprehensive performance evaluation of the proposed algorithms, comparing their execution times and accuracy. Finally, Section 7 concludes the paper with a summary of findings and outlines potential directions for future work.
2. Preliminary
2.1. Program
A program refers to a concurrent program consisting of a finite set T of threads that access a finite set X of shared variables. These shared variables can take values from a domain V. Prior to executing a concurrent program p, it is necessary to initialize the finite set X with the value 0.
2.2. Events
An event refers to a specific interaction with a shared variable x that is part of an extended trace Eτ. The structure of an event e varies depending on its category. Events are primarily classified into the following categories:
- Initializing Event: This event initializes the variable x with the value 0. It is essential that every variable x ∈ X undergoes an initialization event before any other events in Eτ are processed. The initialization event is exclusively present in Eτ. This type of event is represented by the tuple e = <id,−1,W,x,0>. Here, the first element represents the identifier of the event e, starting from 1 and incrementing by 1 for each variable initialization. The second element, denoted by −1, indicates that e does not belong to any thread. The type of memory access, specifically a write operation, is denoted by W. The variable x represents the name of the shared variable, and 0 denotes its initial value;
- Write Event: This event updates the value of a shared variable x. It is represented as e = <id,th,W,x,v>, where id is a unique identifier number within the same thread th. Each thread has its own set of identifiers, starting from 1 and incrementing in the order they appear in Eτ. In this context, th represents the thread to which e belongs, W denotes the write event type, x represents the shared variable to which the event e applies, and v ∈ V represents the value of the write;
- Read Event: This event is identified by id and belongs to thread th. It reads the value of a shared variable x that was written by event e’. The event e’ can be either a write event or an initialization event that precedes the read event in an execution if the execution conforms to SC. The tuple is represented as e = <id,th,R,x,e’>. To illustrate the source of reading, a combination of a thread id followed by a dot and then an event id will be used.
2.3. Incomplete Trace
An incomplete trace iτ is a collection of memory access operations (MAOs) that occurred during the execution of a program P. MAOs are obtained by injecting special codes into multi-threaded C and C++ compiled programs, which capture any memory access during runtime. Each operation in iτ is initiated by a thread th, where th ∈ T. The set of memory access operations MAOth in iτ belongs to the thread th, where th ∈ T. The MAOth ∈ MAOs are completely ordered. However, the set of MAOs from various threads is only partially ordered due to the interleaving of memory operations between threads. A recorded memory access operation (MAO) falls into one of the following categories:
- Write Operation: A write operation WO of a value v triggered by a thread th to a memory address addr. It can be represented as WO = <th,W,addr,v>;
- Read Operation: A read operation RO of a value v triggered by a thread th reads from a memory address addr. It can be represented as RO = <th,R,addr,v>. In this study, memory addresses will be referred to as shared variables.
2.4. Extended Trace
An extended trace Eτ is a set of all events of T in addition to the initialization events. It can be constructed through the following steps:
- Converting MAOs in a given iτ to events by attaching an event id to them;
- For each RO in iτ the source of the read event, which is e’, should be identified, and the value of the read in RO should be replaced by the found write event e’;
- All initialization events for all memory addresses or shared variables should be added at the beginning of Eτ.
Similar to iτ, events in Eτ from a thread th are totally ordered, whereas events from different threads remain unordered. Each thread’s events have identifiers starting from 1. Thus, it is possible to have multiple events with id = 1, but belonging to different threads.
For a given trace Eτ, the relation rf refers to the mapping between the read event eR and the source of the reading, which is either an initializing event or a write event eW. Extracting the rf relation is performed by relating eR to the last preceding eW in Eτ with the same value of reading and the same variable name. If no preceding eW is found, eR should be related to the nearest subsequent eW in Eτ, which writes the same value to the same variable as eR. The following structure will be used to represent any rf relation: (reading thread id. reading event id belongs to the reading thread, writing thread id. writing event id belongs to the writing thread).
2.5. Conflict Events
Two events are in conflict if they access the same variable or memory location, with at least one being a write event, and attempt to access memory without utilizing any synchronization techniques [40]. The initial two conditions of conflict events are sufficient to determine whether two events conflict, as this work is based on iτ and Eτ rather than source code. For instance, if two threads, T0 and T1, contain two events, e1 = <1,0,W,x,2> and e2 = <1,1,R,x,0>, respectively, the rf relation associates e2 with the initial write event of x, as e2 reads the value 0 from the initial write of x. Both e1 and e2 access the same shared variable x, and since e1 is a write event, they are considered conflict events. It is critical to focus on these events because their two ordering possibilities produce different outcomes. For example, if e2 executes before e1, it achieves the desired consistency by reading x as 0 from the initial write and primarily from the most recent write of x, as no other write event overrides the initial write before e2 executes. Conversely, if e1 executes before e2, e2 should read x as 2, but this is incorrect due to the rf relation associated with the extended trace.
2.6. Configuration
A configuration C is a set that contains the program counter for each thread, where C.length = T.length. It contains several pointers equal to the number of threads. For a given c ∈ C, c is a pointer that points to an event e that will be considered in the subsequent processing phase. The indicator “isProcessed” present in each configuration signifies whether it has undergone previous processing.
2.7. Transition
A transition t of a concurrent program P changes the configuration C from one state to another state C’ concerning SC semantics. It takes the form of , where e is either an initialization write, a write, or a read event.
2.8. Execution
A sequentially consistent execution E is a unique possible sequence of interleaving events for a given rf that corresponds to Eτ. It is possible for an Eτ to have one or more executions. However, if the rf relation is unable to commit to achieving an SC execution for a given Eτ, no executions should exist. An execution E, if it exists, is considered a witness for the compliance of Eτ with the SC semantics.
2.9. Model
A model refers to a state transition model representing an abstract mathematical formulation of a concurrent program. The states correspond to configurations, while the transitions refer to transitions between these configurations. This model is used to define the possible executions of the concurrent program.
2.10. Cut of Eτ
In general, when processing an extended trace Eτ to identify executions that are considered witnesses for compliance with SC, Eτ is not treated as a single unit. Instead, it is divided into multiple cuts of extended traces, each referred to as a cutTrace (cut Eτ), based on the events it contains and the dependencies between those events. A cutTrace Eτc is a subsequence of the extended trace Eτ. Consequently, for each Eτ, there is a set of cutTraces = Eτc1, Eτc2,..., Eτcn.
2.11. Conflict and Non-Conflict cutTraces
If two cuts of an extended trace Eτ, Eτc1, and Eτc2, contain the same conflicting events but differ in the order of these events, they are considered to be in conflict. Conversely, if the order of the conflict events is identical between Eτc1 and Eτc2, they are regarded as equivalent. In a given configuration C, if the pointer set of C contains more than one pointer to write events, it becomes feasible to transition to multiple subsequent configurations. Each candidate transformation should be examined in accordance with SC semantics, and the transformations will be classified into two categories: accepted and discarded. Each transformation consists of a collection of events that may be related to previously processed events. These transformations represent cuts of Eτ, and the set of transformations can be mapped into a set of cuts of Eτ as Eτc. The Eτc can then be divided into groups, each represented by an equivalent cut of Eτ. SC semantics for each group in Eτc can be verified by investigating a single Eτc.
3. An Illustrative Scenario Clarifying the Preliminary Concepts
Referring back to the SB concurrent program, it can be stated that SB is a program P. The set of threads T = {T0, T1} indicates that SB contains two threads, and the set of shared variables X = {x, y} shows that SB attempts to access two shared variables, x and y. The domain of both x and y is [0, 1], with x and y initialized to 0 and then updated to 1. To achieve the outcome of behavior d shown in Table 1, one possible iτ is as follows:
<0,W,x,1> , <1,W,y,1> , <0,R,y,0> , <1,R,x,0>
Converting the iτ to an Eτ yields the following:
<1,−1,W,x,0> ,<2, −1,W,y,0> , <1,0,W,x,1> , <1,1,W,y,1> , <2,0,R,y,(−1.2)> , <2,1,R,x,(−1.1)>
The corresponding read-from relation rf = {{(0,2),(−1,2)},{(1,2),(−1,1)}}
While execution set E = Ø
Following the verification of Eτ with the proposed algorithms, the set E remains empty due to the absence of a sequentially consistent sequence of events in Eτ that would result in the desired values of local variables a and b. In other words, SC prohibits the reading of the initialized values of shared variables x and y, as these values become inaccessible after the first two events of both T0 and T1. Consequently, this behavior is classified as non-SC. On the other hand, obtaining the outcome of behavior c in Table 1, one of the potential iτ is as follows:
<0,W,x,1> , <1,W,y,1> , <0,R,y,1> , <1,R,x,1>
Converting the iτ to an Eτ yields the following:
<1,−1,W,x,0> , <2,−1,W,y,0> , <1,0,W,x,1> , <1,1,W,y,1> , <2,0,R,y,(1.1)> , <2,1,R,x,(0.1)>
The corresponding read-from relation
rf = {{(0,2),(1,1)},{(1,2),(0,1)}}
After verifying this iτ with the proposed algorithms, the resulting execution set is as follows:
E = {e1 → e3 → e2 → e4 , e1 → e3 → e4 → e2 , e3 → e1 → e2 → e4 , e3 → e1 → e4 → e2}
It is evident that the non-empty execution set E causes this Eτ to be SC. Consequently, four possible orders of events exist that will result in this behavior, meaning this behavior has four witnesses.
4. The Proposed Algorithms
In this section, the approach for categorizing a collection of memory access operations (MAOs) to shared memory locations obtained from an executed concurrent program into two categories—Sequentially Consistent (SC) and non-SC—is introduced. As mentioned previously, these operations are referred to as incomplete traces, denoted as iτ. Applying a dynamic partial order reduction (DPOR) algorithm to a concurrent program yields a comprehensive list of all possible behaviors associated with the values that read operations may access. Typically, such verification involves identifying all possibilities of overlapping thread events and evaluating each possibility to determine if it aligns with SC conditions. However, exhaustively analyzing all possible combinations can be computationally impractical.
To address this limitation, the proposed approach establishes an order or arrangement of MAOs in the program under verification. By explicitly determining an order of events consistent with the values fixed by the DPOR algorithm, the method ensures adherence to sequential consistency criteria while significantly reducing computational overhead.
4.1. High-Level Methodological Framework
To enhance readability and clarify the interrelationships between algorithmic components, the overall methodological framework is briefly summarized here before presenting detailed algorithms. The verification approach introduced in this paper consists of two primary stages:
- Stage 1 (Trace Preparation):
An incomplete trace (iτ) obtained from the execution of a concurrent program is converted into an extended trace (Eτ). During this stage, initialization events for each shared variable are identified and explicitly included. Subsequently, all read and write operations within the incomplete trace are systematically converted into events, ensuring the creation of a well-defined extended trace. This step lays the groundwork for accurate SC verification in the next stage;
- Stage 2 (SC Verification via DAG Construction):
In this stage, a directed acyclic graph (DAG) is constructed from the extended trace to systematically represent dependencies among memory access events, particularly emphasizing write events. Utilizing the DAG, the proposed approach significantly reduces redundant explorations of execution paths. This stage involves specialized algorithms, including BuildGraph, AddReadEvent, GetWrite, and AddVertex, each except AddVertex ensuring adherence to SC semantics while systematically pruning unnecessary paths. The DAG-based approach efficiently classifies the program’s behavior as SC or non-SC by evaluating event interrelationships, culminating with the ClassifyProgram algorithm.
In brief, the proposed approach attempts to arrange the events of the concurrent program P in a way that ensures read values are consistent with the DPOR algorithm’s determinations while strictly adhering to sequential consistency semantics. Given that memory operations consist solely of read and write events—with reads inherently depending on writes—the main algorithm (BuildGraph) iteratively explores sequences of write events across threads. Each configuration c represents a set of pointers indicating the events to be processed in the current iteration. The BuildGraph algorithm systematically seeks a coherent ordering between write events based on SC semantics. After verifying write events, corresponding read events are integrated sequentially according to program order through the AddReadEvent algorithm.
If a write event eW’ precedes a read event eR, and if eR must be linked to another write event eW, the AddReadEvent algorithm adds eW’ as a node in the DAG after verifying its compliance with SC semantics. This algorithm recursively attaches all dependent read events that read from the added write event. If there is an earlier unprocessed read event eR’ that depends on an unprocessed write event, the GetWrite algorithm handles this dependency by recursively processing the relevant write events.
To manage nodes and edges effectively in the DAG, a specialized algorithm called AddVertex is employed. Once the DAG is fully constructed, the ClassifyProgram algorithm analyzes it comprehensively to determine whether the specified behavior is sequentially consistent (SC) or non-sequentially consistent (non-SC).
The following subsections provide detailed descriptions and formal algorithms involved in each stage of the proposed verification approach.
4.2. First Task: Converting iτ to Eτ
Algorithm 1: GenerateExtendedTrace
The initial task, as outlined in Algorithm 1, involves accepting the incomplete trace iτ as input. The task will then generate the extended trace Eτ of iτ by first identifying the shared variable set X and adding the initialization write operations for these variables into Eτ. Subsequently, all read and write operations within iτ are converted into events, which are appended to the end of Eτ. To optimize the processing performance of the subsequent task, it is more efficient to handle each thread independently. Therefore, the algorithm’s final phase determines Eτ for each thread individually. At the conclusion of the algorithm, a list that represents each Eτ for each thread is returned, which will be utilized by subsequent algorithms.
| Algorithm 1: GenerateExtendedTrace | |||||
| 1 | GenerateExtendedTrace (iτ) | ||||
| 2 | let Eτ is an empty list of events | ||||
| 3 | let X := Ø | ||||
| 4 | let ToT[noThreads][] := Ø | ||||
| 5 | let cT [noThread] := 1 for all items | ||||
| 6 | for each MAO ∈ MAOs where MAOs belongs to iτ do | ||||
| 7 | if ∄x ∈ X where x.name = MAO.variable then add MAO.variable to X | ||||
| 8 | for each x ∈ X | ||||
| 9 | create an initializing event ei for initializing x, attach ei to the tail of Eτ | ||||
| 10 | for each MAO ∈ MAOs where MAOs ∈ iτ do | ||||
| 11 | if MAO is WO then | ||||
| 12 | Create a write event eW for MAO where eW.id = cT[MAO.thread] | ||||
| 13 | increment cT[MAO.thread] by 1 | ||||
| 14 | add eW to the tail of Eτ | ||||
| 15 | else if MAO is RO then | ||||
| 16 | Create a read event eR for MAO where eR.id = cT[MAO.thread] | ||||
| 17 | let eR.e’ := null | ||||
| 18 | increment cT[MAO.thread] by 1 | ||||
| 19 | add eR to the tail of Eτ | ||||
| 20 | for each read event eR ∈ Eτ where eR.e’ = null do | ||||
| 21 | for each write event eW ∈ Eτ where index(ew) in Eτ < index(eR) in Eτ start from index(eR)-1 to beginning of Eτ | ||||
| 22 | if eW.variable = eR.variable and eW.value = (RO ↦ eR).value where RO ∈ iτ then eR.e’ := eW | ||||
| 23 | if eR.e’ = null then | ||||
| 24 | for each write event eW ∈ Eτ where index(eW) in Eτ > index(eR) in Eτ start from index(eR)+1 to end of Eτ | ||||
| 25 | if eW.variable = eR.variable and eW.value = (RO ↦ eR).value where RO ∈ iτ then eR.e’ := eW | ||||
| 26 | for each event e in Eτ do | ||||
| 27 | ToT[e.thread][e.id] = e | ||||
| 28 | return ToT | ||||
Initially, Eτ is defined as an empty set of events. To create an initialization write for each shared variable, a list of shared variables must be maintained. Therefore, the set X is initially defined as an empty set, which will hold the shared variables in subsequent steps. The set cT (counter of events in thread) is defined to track the last ID of the final event of each thread added to Eτ to assign an ID to each MAO that will be added as an event to Eτ. The number of threads in the concurrent program P is equivalent to the capacity of the cT set.
A two-dimensional array, ToT (Traces of Threads), is defined to hold all events for each thread separately. The number of rows in ToT is equal to the number of threads, while the number of columns is left undefined to minimize memory utilization, as the number of events per thread is generally unequal. The pseudo-code in lines 6 and 7 verifies whether the variable of each MAO in iτ has been included in the set X. If the variable has not yet been included, it is added to the set X. To ensure that Eτ includes initialization write events for all variables, which is initially empty, an initialization write event with a value of 0 is generated for each variable in the set X and appended to Eτ, as shown in lines 8 and 9.
In lines 10–19, each MAO in iτ is converted to an event and added to the end of Eτ, with an ID assigned to each MAO. Consequently, the order of operations in iτ matches the event order in Eτ. Lines 12 and 16 reference the current event’s ID, which is obtained from the cT set using the MAO’s thread as the index. Additionally, the event ID for the same thread is incremented by 1 in lines 13 and 18, ensuring that the new ID is available for the next event in the same thread.
Write operations are converted to events differently from read operations because a write assigns a value to a variable, whereas a read retrieves a value from a variable. In other words, a read event eR reads from a write event eW that was referred to by e’ previously. Consequently, the field eR.e’ is initially assigned a null value, as the source of the read has not yet been determined for the current read event. The sources for each read event eR in Eτ where eR.e’ = null are identified in lines 20–25 by examining whether preceding events include a write event eW, or an initialization event that operates on the same variable as eR and writes the same value recorded by the read operation MAO in iτ. If the search for such a write event is unsuccessful, the algorithm will search for a write event eW that writes to the same variable and has the same read value for eR in the subsequent events.
Once eW is found—whether preceding or following eR—the algorithm sets eR.e’ = eW, thus establishing the rf relation by linking all read events with their source write events. At this point, the extended trace Eτ is complete and is subsequently segregated and added into the two-dimensional array ToT (lines 26–27) for further processing by the subsequent algorithms.
4.3. Second Task: Processing ToT and Categorizing P into SC and Non-SC
The objective of this task is to classify the behavior of the concurrent program P represented by the two-dimensional array ToT as either sequentially consistent (SC) or non-sequentially consistent (non-SC). The core idea behind this task is to construct a graph G, consisting of a set of nodes and edges that connect these nodes. Each node in G represents a configuration of P, which can be reached by transitioning between thread events in a specific order that does not violate SC conditions. Therefore, in order to transition from one configuration c1 to another configuration c2, an event from c1 addressed by one of the pointers in c1 must be processed. This processing determines whether it is possible to add as c2 a node to G.
This processing provides the decision to either continue along the current path in G if it adheres to SC or terminate the path if it does not. In other words, the question is whether c2 can be reached from c1 by adding an event e to the path, where e is pointed to by a pointer in c1. In this approach, adding read events is always feasible, while violations of SC are detected only when write events are added. Therefore, at any level of G, it is guaranteed that any read event eR reads from the last write to the same variable.
The level of each node in G must be stored within each node, indicating the depth of the node in G and the number of events that have been processed in the current path from the root node in G to the current node across all threads. There may be more than one node at the same level if the program allows for more than one valid order of events. The concurrent program under verification must have at least one node at the final level of G, where the thread pointers point to the final event of each thread plus one, to qualify as SC-compliant. This indicates that the program has transitioned from its initial configuration to the final configuration in a specific order of thread events that complies with SC, and all events from all threads have been processed and arranged in an SC-compliant order.
In this task, the algorithm ClassifyProgram calls the BuildGraph algorithm, which generates the graph G. ClassifyProgram then analyzes G to determine whether the program is SC or non-SC. Event processing is divided into two types of operations:
- The GetWrite algorithm processes write events. This algorithm identifies the write event eW, which is the source of a read event eR, and then checks whether SC conditions permit the addition of a write node to G. If it is possible to add a write node to G, the AddReadEvent algorithm is invoked to add all read events that read from the newly added write event;
- The processing of read events searches for all read events that read from a specific write event currently added to G. The discovered read events are then added to G, and the AddReadEvent algorithm manages this process.
Note that the GetWrite algorithm invokes the AddReadEvent algorithm, and the AddReadEvent algorithm may also invoke the GetWrite algorithm. For instance, if a read event eR2 in a particular thread is to be added to G, which reads from the write event eW2, added by the GetWrite algorithm, and if eR2 is preceded by another read event eR1 that has not yet been processed because its source write event eW1 is not yet processed, the AddReadEvent algorithm will invoke the GetWrite algorithm to process eW1. GetWrite will subsequently call AddReadEvent to identify all read events that read from eW1 and add them to the graph. After processing eW1 and all associated read events, the AddReadEvent algorithm adds the event eR2.
The AddVertex algorithm has been introduced as a separate algorithm to handle the addition of nodes to the graph, as this is a repetitive step in the BuildGraph, AddWriteEvent, and GetWrite algorithms. The following sections provide a detailed explanation of each of the proposed algorithms in this approach.
4.3.1. Algorithm 2: ClassifyProgram
The approach is based on generating a directed acyclic graph (DAG) using the BuildGraph algorithm, which is then analyzed by the ClassifyProgram algorithm to determine whether the behavior of the concurrent program P is sequentially consistent (SC) or non-sequentially consistent (non-SC). If the behavior is classified as SC, the set of witnesses for this behavior will be identified by the algorithm.
| Algorithm 2: ClassifyProgram | ||||||
| 1 | ClassifyProgram (ToT, Eτ) | |||||
| 2 | G := BuildGraph(ToT, Eτ) | |||||
| 3 | let E := Ø | |||||
| 4 | V := {v: node in G|v.level = G.maxLevel} | |||||
| 5 | let isFinished = true | |||||
| 6 | C := configuraction of V [0] | |||||
| 7 | for each pointer p in C do | |||||
| 8 | if p < ToT[p.index].length+1 then isFinished = false | |||||
| 9 | if isFinished = false then return <NON-SC, E> | |||||
| 10 | else | |||||
| 11 | for each v in V do | |||||
| 12 | find paths from G [0] to v | |||||
| 13 | for each path in paths do | |||||
| 14 | add path to E | |||||
| 15 | return <SC, E> | |||||
It is assumed that the graph G consists of a set of nodes V and a set of edges connecting the nodes. In line 3, the relation E is defined as an empty set, which will later be populated with the possible order(s) of events representing the witness(es) of the behavior, provided it is classified as SC-compliant. In line 4, a set V is defined to contain all the nodes at the deepest level of G, where the level of these nodes corresponds to the largest level in the graph. Verifying the state of a single node in this set is sufficient for classification, as all nodes at the same level have processed the same number of events, though not necessarily the same events, in cases where the behavior is non-SC.
The process of verifying a single node from the set V involves determining whether all thread pointers in node v have passed the last event for each thread. Specifically, the algorithm checks whether all events for all threads have been processed and added as nodes to G. Lines 5–8 confirm whether each pointer in the first node v in set V equals the length of the thread it points to, plus one. In configuration c of v, the pointer p of thread T0 is compared to the length (number of events) of T0, which is based on the thread index 0 (the row index in the ToT array). As previously mentioned, the two-dimensional array ToT stores the events of each thread in its rows. Whether all events have been processed for all threads is indicated by the flag isFinished.
In line 9, if the isFinished flag is set to false, the behavior under verification is classified as non-SC. This indicates that an event violating SC semantics has been reached in the last level of the graph G. In this case, the algorithm terminates, returning the behavior as non-SC along with an empty set of executions or witnesses since there are no valid witnesses for this behavior. However, if the behavior is classified as SC, lines 10–14 analyze all possible paths, beginning from the root node in G and ending at a node in set V. The algorithm adds each path, representing an order of events, to the set E as a witness. Finally, the algorithm returns all the witnesses and the SC classification.
4.3.2. Algorithm 3: BuildGraph
This algorithm is invoked by the ClassifyProgram algorithm only once and is responsible for generating the graph G, which is then returned to the ClassifyProgram algorithm. Its functionality depends on the two-dimensional array ToT and Eτ. Below is the pseudo-code, followed by an explanation of the algorithm.
| Algorithm 3: BuildGraph | ||||||
| 1 | BuildGraph (ToT, Eτ) | |||||
| 2 | let configurationForProcessing := Ø | |||||
| 3 | let c := initial configuration | |||||
| 4 | create a vertex v for c | |||||
| 5 | add v to G | |||||
| 6 | parentVertex := v | |||||
| 7 | for each event e where e ∈ Eτ and e.thread = −1 do | |||||
| 8 | AddVertex (e) | |||||
| 9 | configurationForProcessing := G[G.size].configuration | |||||
| 10 | while configurationForProcessing != Ø | |||||
| 11 | start := G.size | |||||
| 12 | for each configuration c in configurationForProcessing do | |||||
| 13 | parentConfiguration := c | |||||
| 14 | let eventsForProcessing[] := Ø | |||||
| 15 | let existRead := false | |||||
| 16 | for each pointer p in c where p <= ToT[p.index].length do | |||||
| 17 | if ToT[p.index][p].type = R and (ToT[p.index][p].e’.thread = −1 or e.e’.id < c[e.e’.thread]) | |||||
| 18 | AddVertext (ToT[p.index][p]) | |||||
| 19 | existRead := true | |||||
| 20 | if existRead = true then set c.isProcessed = true and exit this iteration | |||||
| 21 | for each pointer p in c where p <= ToT[p.index].length do | |||||
| 22 | if ToT[p.index][p].type = W | |||||
| 23 | add p.index to eventsForProcessing | |||||
| 24 | for each thread number in eventsForProcessing do | |||||
| 25 | e = ToT[thread number][p[thread number]] | |||||
| 26 | if (∃ read event eR where eR.id >= c. pointers[eR.thread] and eR.variable = e.variable and eR.e’ != e and eR.e’.id < c. pointers[er.e’.thread]) or (∃ read event eR where eR.id >= c. pointers[eR.thread] and eR.variable = e.variable and ∃ write event eW where eW.thread = eR.thread eW.variable = e.variable and eW.id < eR.id and eW.id >= c. pointers[eW.thread]) then skip this currentRow | |||||
| 27 | AddVertext (e) | |||||
| 28 | addReadEvent(e, ToT) | |||||
| 29 | c.isProcessed = true | |||||
| 30 | configurationForProcessing := {c = v.configuration where index(v) in G > start & v ∈ G | v.configuration.isProcessed = false and ∀ p ∈ c | p <= ToT[p.index].length | |||||
| 31 | Return (G) | |||||
To process the previously unprocessed configurations that are candidates for the subsequent phase of this algorithm, the configurationForProcessing set is required to hold these configurations. This set is defined as an empty set in line 2. Once a specific configuration c is processed, it is immediately removed from the configurationForProcessing set. Periodically, new candidate configurations are added to the configurationForProcessing set until all configurations have been processed. In line 3, configuration c is defined as the initial configuration, where all thread pointers indicate the first event of each thread. Lines 4 and 5 describe the generation and incorporation of a node representing the initial configuration c into G. The graph consists of nodes representing events and edges connecting these nodes, with each edge linking a node at a specific level, known as the parent node, to a node at the next level, referred to as the child node. As a result, the parent node’s information must be saved for later use in defining the edges between parent and child nodes. Thus, in line 6, the parentVertex is defined as the parent node, which, at this point, is the initial or root node. In lines 7 and 8, all events corresponding to the initial values of the shared variables are appended to G by invoking the AddVetex algorithm, which is explained later. As described in the first task of this approach, these events exist in Eτ and are distinguished from other events by their association with thread −1. The order of these events is not important, but they must precede the processing of any event associated with a thread other than thread −1. Initially, these events are added to G as separate nodes, each with an edge connecting it to the previous event, while the first event is connected to the root node. Up to this point, the final node added to G, which represents the last initialization write event, will be used in the next phase of the algorithm and will be added to the configurationForProcessing set in line 9.
The algorithm then continues its cyclical execution until the configurationForProcessing set becomes empty. The algorithm initiates its cyclic operation by assigning the index of the last node added to G to the variable start in order to identify the nodes that will be processed next when determining the new configurationForProcessing set at the end of each cycle of the algorithm. This approach avoids searching through all nodes in the graph, which would be time-consuming. Each candidate configuration c in the configurationForProcessing set is selected individually for processing, as indicated in line 12. During the first iteration, the configurationForProcessing set contains only one configuration. Line 13 selects the current configuration c for processing as the parent node of the next nodes if one exists.
The algorithm examines the thread pointers for each configuration to determine if at least one points to a read event that either reads a previously published value from a write event or an initialization value. In such cases, the algorithm extends G by adding a node for each read event as a path originating from the node of c. Since these are not conflict occurrences, their sequence is immaterial. As adding write events is subject to rules that preserve SC semantics, as will be detailed later, adding read events is guaranteed to read from the most recent write to shared variables. Prioritizing the addition of read events in each cycle ensures that thread pointers eventually point to as many write events as possible, enabling the verification of their ordering. Lines 15–20 handle this task, and line 20 concludes the current cycle by marking the node representing the current configuration as processed when such read events are being processed.
When the pointers of threads do not point to read events that could be processed, the algorithm should process the write events. Write events that are candidates for processing are handled individually, with each event generating its own path branching from the parent node. Line 14 defines the array eventsForProcessing for handling write events. The algorithm evaluates the write events indicated by the parent node in lines 21–23 using its configuration pointers. The thread number to which the events belong is appended as a cell to the eventsForProcessing array if they are of the write type. Lines 24 iterate over the eventsForProcessing array, where each cell corresponds to a distinct path from the parent node. The event denoted by e in line 25 corresponds to the event mentioned in the configuration of the parent node, based on the thread number indicated in the eventsForProcessing array and the pointer of its thread. Next, the write events are processed, but before generating a node for a write event, it is necessary to verify that including the current write event eW in G does not violate the sequential consistency criteria.
The verification is conducted in line 26, where the algorithm identifies any unprocessed read event eR that retrieves a value written by a previously processed write event eW’, which has already been added to G. This occurs under the condition that the variable associated with eW matches the variable of both eR and eW’. In such a scenario, the occurrence of eW would modify the shared variable’s value previously written by eW’, while eR is expected to retrieve the earlier value as defined by the rf relation. Consequently, the sequential consistency criteria would be violated. Furthermore, the algorithm continues to search for an unprocessed read event eR within a thread, where eR reads from eW and an unprocessed write event eW’ belonging to the same thread as eR, and eW’ located before eR, ensuring that the variable written to by eW is identical to the variable of eW’. This condition necessitates that eW’ be processed before eW. If such an event eR is found, the current path is terminated, and a new path is initiated by processing the next candidate write event in the eventsForProcessing array. Once the current path has been processed, a new node for eW is appended to G. The addReadEvent(eW) method is then invoked to process all read events that access the value written by eW, adding them as nodes to G if that is possible.
After all candidate write events in the eventsForProcessing array have been processed, the isProcessed flag is set to true for the current configuration during the ongoing processing cycle. After evaluating all paths, configurations are examined within the newly created nodes from the current iteration. The search begins from the node indicated by the start variable (set in line 11) and continues until the last node added to G. This approach avoids the need to search through all graph nodes. The search examines the configurations of nodes with unprocessed events, as stated in line 30. The search may fail to find unprocessed configurations for two reasons: either all thread pointers have exceeded the number of thread events, indicating that all events have been processed and included in G, or a thread is stuck in a specific event due to a violation of the SC conditions. If no configurations remain in the configurationForProcessing set, the algorithm’s cycle terminates, and the generated graph is returned to the ClassifyProgram algorithm.
4.3.3. Algorithm 4: AddReadEvent
During the iterative execution of the BuildGraph algorithm, events involving writing are identified and incorporated into the graph G as individual nodes. For each processed writing event eW, it is necessary to process all reading events that read from eW. This task is assigned to the addReadEvent algorithm, with its pseudo-code presented below, followed by an explanation.
| Algorithm 4: AddReadEvent | |||||||
| 1 | AddReadEvent (eW, ToT) | ||||||
| 2 | let parentVertex := vertex of eW | ||||||
| 3 | let setOfReadsFromeW := {e ∈ ToT | e.e’ = eW} | ||||||
| 4 | let permutations := generate permutation for setOfReadsFromeW | ||||||
| 5 | for each permutation in permutations | ||||||
| 6 | for each read event eR in permutation | ||||||
| 7 | let indexOfRead := event id of eR.e’ | ||||||
| 8 | for each event e where e.thread = eR.thread and e.id >= eW.pointers[eR.thread] and e.id <= indexOfRead | ||||||
| 9 | if e.type = R | ||||||
| 10 | if e.e’.thread = −1 or e.e’ = eW or e.e’.id < eW.pointers[e.e’.thread] | ||||||
| 11 | AddVertex(e) | ||||||
| 12 | else if e.e’ != eW | ||||||
| 13 | getWrite (e, ToT) | ||||||
| 14 | else if e.type = W | ||||||
| 15 | if (∃ read event eR where eR.id >= eW.pointers[eR.thread] and eR.variable = e.variable and eR.e’ != e and eR.e’.id < eW.pointers[eR.e’.thread]) or (∃ read event eR where eR.id >= eW.pointers[eR.thread] and eR.variable = e.variable and ∃ write event eW’ where eW’.thread = eR.thread and eW’.variable = e.variable and eW’.id < eR.id and eW’.id >= eW.pointers[eW.thread]) then skip this permutation | ||||||
| 16 | AddVertex(e) | ||||||
| 17 | addReadEvent(e) | ||||||
Read events depend on write events, as they retrieve values written by a preceding write event. Upon processing each write event eW in the BuildGraph or GetWrite algorithms, it becomes essential to locate all read events associated with the recently added eW through the rf relation, which is embedded in the set ToT. This relation links each read event to its source, a write event. The search must account for the possible orders of read events from different threads, especially when multiple read events read from eW. The addReadEvent algorithm accepts the write event eW and the ToT array as inputs. The node associated with the event eW is treated as the parent node for the first read node in any conceivable order of read events. The set of read events linked to the write event eW is obtained by referencing the rf relation in line 3 and stored in the setOfReadsFromew set. In line 4, the collection of read events is permuted, as illustrated in the subsequent figures. In Figure 2, three threads contained in a concurrent program are displayed, while Figure 3 shows how the current algorithm’s processing could result in two different paths when processing events that read from event 1 of T0. After adding event 1 of T0, the addReadEvent algorithm is invoked to process the first two events of both T1 and T2. In this situation, there are two possible ways to process these events, with the difference depending on the order in which the read events are processed. Table 3 shows the permutation incorporated into this algorithm, where two event orders could be added to graph G.
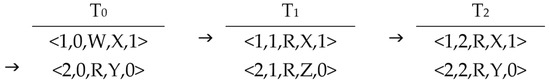
Figure 2.
A simple concurrent program depicted with events for each thread.

Figure 3.
The representation of all permutations illustrated in Table 3.

Table 3.
All possible orderings in iteration 1 when verifying the program illustrated in Figure 2.
Figure 3 displays the permutations of a two-dimensional array derived from generating the interference probability for configuration c stated above.
However, the number of overlaps is often calculated using the following equation:
noPermutation = numberOfEvents!
Afterward, all potential permutations of read events are considered. It is important to note that the read event eR may not be directly pointed to by the parent node’s configuration pointer. This indicates that antecedent events within the same thread may not yet have been processed. To ensure correct event processing order within the same thread with respect to program order, it is not valid to process the read event eR directly while leaving earlier events in the thread unprocessed. For this reason, the algorithm should create a set of events starting from the event pointed to by the parent configuration pointer within eR’s thread and ending with the read event eR. Each collected event is then processed individually. For example, in the following figure, it is evident that the only processed event is <1,0,W,X,1>, denoted as eW1, because the pointer of T0 is pointing to the second event of T0. This indicates that event 1 of T0 has been processed by the BuildGraph algorithm and already added as a node to G. Afterward, the BuildGraph algorithm invokes the AddReadEvent algorithm to add all read events that read from eW1. When the current algorithm searches for read events that read from eW1, it identifies the second event of T2 as eR. However, there is an earlier event in T2 that has not yet been processed. In this case, the algorithm processes the first event of T2, eW2, by adding a vertex for eW2 to G after confirming that eW2 does not violate SC semantics in line 15 of this algorithm. The AddReadEvent algorithm is then invoked with the parameter eW2 to include all its read events, after which the current algorithm resumes processing eR. small program that illustrates how the AddReadEvent algorithm invokes itself recursively is shown in Figure 4.
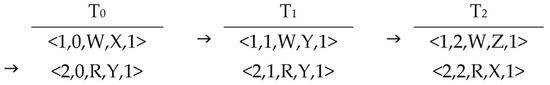
Figure 4.
A simple program illustrating how the AddReadEvent algorithm can invoke itself recursively.
During the processing of events that precede the read event eR, each event e is examined to determine whether it is a read event that reads from an already processed write event or from eW. If either condition is met, a node is generated for this event and added to G. If the event e reads from a different write event than eW, and the write event has not yet been processed, line 13 invokes the getWrite algorithm to process the write event that e reads from. If the event e is a write event, its addition to the graph is evaluated in line 15 to determine whether it violates the SC semantics, following the same procedure outlined in the BuildGraph algorithm. If adding the event e does not result in a violation of SC semantics, the sequence proceeds. The event e is then added to G, and the associated read events are identified through the recursive invocation of the algorithm.
A drawback that affects the algorithm’s speed is the number of potential sequences of read events. As the number of threads containing read events from the current write event increases, the number of potential permutations grows exponentially. This increase in the number of possible ordering alternatives results in a corresponding increase in execution time.
4.3.4. Algorithm 5: GetWrite
As stated in the previous algorithm, the inclusion of a read event eR reading from a write event eW that has not yet undergone processing necessitates the invocation of the GetWrite algorithm to include eW in G. As a result, the significance of this algorithm lies in its ability to efficiently complement the work with AddReadEvent algorithms to handle the tasks of writing and reading events.
This algorithm takes a read event eR and the ToT array as input. Line 2 will be elaborated later, as it necessitates proficiency in this algorithm. This algorithm will process the write event eW that eR reads from, as indicated by line 3. It is important to note that when verifying a certain Eτ, it may either correspond to the SC or not. An instance where Eτ does not align with the SC is when there is a failure to preserve the order of events within the same thread. Practically, it is feasible in certain scenarios that a read event within a specific thread reads a value from a later write event in the same thread in modern processors. However, the order of these events in the thread does not adhere to sequential consistency (SC) principles. To differentiate these events, line 4 verifies if the read event eR is reading from a write event eW that happens inside the same thread and the id of eR is smaller than the id of eW. In this scenario, the path’s processing will halt due to its violation of the specified SC requirements. As a consequence, the verification process will be stopped. Unless the current path is stopped, the algorithm will process the events beginning with the event indicated by the thread pointer associated with the eW’s thread. The algorithm will continue processing all events until it reaches the write event eW, as specified in line 6 of the algorithm. If the event being processed is a read event that read from a preprocessed write event, then a node for it will be created by calling the addVertex algorithm; otherwise, the algorithm is recursively invoked to include its corresponding write event eW’ along with all the read events that are dependent on eW’. This occurs in lines 10 and 11. On the other hand, if the event is a write event eW’, the algorithm will verify if appending eW’ to the graph will violate the SC conditions. This verification is identical to the checking consistency in both algorithms BuildGraph and AddRead. If this path is not interrupted after the verification, the algorithm will include the write event in the G and then identify all the read events that are dependent on event e, processing them all by using the addReadEvent algorithm.
| Algorithm 5: GetWrite | ||||||
| 1 | GetWrite (eR, ToT) | |||||
| 2 | check if there is a cycle in events of this path after adding eR.e’, if such cycle is exist then stop this path | |||||
| 3 | let eW := eR.e’ | |||||
| 4 | if eR.thread = eW.thread and eR.id < eW.id then // read from future write | |||||
| 5 | Break | |||||
| 6 | for each event e where e.thread = eW.thread and e.id >= eR.pointers[eW.thread] and e.id <= eW.id do | |||||
| 7 | if e.type = R | |||||
| 8 | if e.e’.thread = −1 or e.e’.id < er.pointers[e.e’.thread] | |||||
| 9 | AddVertex(e) | |||||
| 10 | else | |||||
| 11 | getWrite (e, ToT) | |||||
| 12 | else if e.type = W then | |||||
| 13 | if (∃ read event eR’ where eR’.id >= eR.pointers[eR.thread] and eR’.variable = e.variable and eR’.e’ != e and eR’.e’.id < eR.pointers[eR’.e’.thread]) or (∃ read event eR’ where eR’.id >= eR.pointers[eR.thread] and eR’.variable = e.variable and ∃ write event eW’ where eW’.thread = eR.thread and eW’.variable = e.variable and eW’.id < eR’.id and eW’.id >= eR.pointers[eR.thread]) then skip this path | |||||
| 14 | AddVertex(e) | |||||
| 15 | addReadEvent(v) | |||||
In the given example depicted in Figure 5, when the BuildGraph algorithm processes e4 and incorporates it into G, the AddReadEvent method is then invoked to handle all events that will read from e4. Therefore, event e7 is the event that has to be accessed and processed after events e5 and e6 have been handled. The AddWrite algorithm will be invoked to look for the event that adds the value 3 to the shared variable C in order to process event e5. Event e3 will serve as the source from which event e5 will read. The suggested approach requires the processing of event e2, which is reading from event e6, in order to process e3. Due to the fact that event e5 has not been handled and depends on e3, event e6 is completely inaccessible. In this case, the suggested approach would enter a closed loop where it continuously processes recurrent events without end. Therefore, the dependencies between events are depicted in Figure 6. Here, it is imperative to halt this sequence of events and seek an alternative sequence, as it fails to adhere to the SC requirements. When discussing the semantics of the SC based on the axiomatic model, such a series of occurrences also creates a prohibited cycle in the relation: po ∪ fr ∪ rf ∪ co. To verify whether the current iteration of the BuildGraph algorithm contains such a cycle, line 2 will examine all events in the current path. This path will be halted if a case of this nature is identified in the present path, as it does not comply with SC semantics.
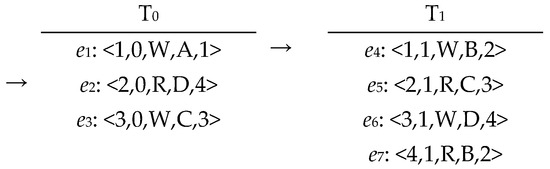
Figure 5.
An example containing a forbidden cycle of events during processing.

Figure 6.
A forbidden cycle of events identified by GetWrite algorithm.
4.3.5. Algorithm 6: addVertex
For the sake of abstraction, the following work is presented separately, as previous algorithms necessitate the addition of vertices to the graph G. The pseudo-code required for adding a vertex to G is provided below, followed by an explanation.
| Algorithm 6: AddVertex | ||
| 1 | AddVertex (e) | |
| 2 | let c:= e.pointers where c.pointers[e.thread] := c.pointers[e.thread] + 1 | |
| 3 | create a vertex v for e | |
| 4 | add v to G | |
| 5 | add an edge from parentVertex to v | |
| 6 | parentVertex.isProcessed = true | |
| 7 | parentVertex := v | |
| 8 | parentConfiguration := c | |
The algorithm is designed to generate a node for the input event e and incorporate it into the graph G, regardless of whether it is a read or write event. In line 2, a new configuration is created, where all pointers in this configuration are identical to those of the parent node’s configuration, except for the pointer corresponding to the thread to which event e belongs. This pointer is incremented by 1 to point to the subsequent event in the thread, ensuring it is processed in the next iteration. Subsequently, a node for event e is added to G, and an edge is established between the parent node and the newly created node. In line 6, the isProcessed field of the parent node is set to true, indicating that it has been processed and preventing it from being processed again in the subsequent iteration of the BuildGraph algorithm. The variable parentVertex in line 7 refers to the newly created node, while parentConfiguration in line 8 will also point to the new configuration.
Based on previous explanations of the algorithms, it is apparent that verifying consistency with SC involves two types of event processing. The first type concerns the handling of read events, which read from a write event eW. This requires the extraction of permutations for the sequence of events following the currently processed event eW. Simply put, the node for event eW may have multiple child nodes, leading to potential divergence after the node representing eW. Once the pathways that represent the permutations are complete, they may contain either similar or distinct nodes at their final level, as long as they do not violate SC criteria. This is because all permutations have the same number of events, differing only in their order. These nodes are added to the configurationForProcessing set for processing in the next iteration of the BuildGraph algorithm. The fewer nodes included in this set, the faster the execution time. Identifying similar nodes and merging them after the current iteration’s completion can help reduce execution time. In this study, a hash table approach was utilized to manage node redundancy.
The proposed approach ensures soundness by focusing on the correct sorting of write events, as demonstrated by section (Appendix A.1).
4.4. Illustrative Example
This section clarifies the proposed approach for verifying concurrent programs by using a simple program, as shown in Figure 7. The program consists of two threads, T0 and T1, and two shared variables, x and y. The first thread assigns the value 1 to the variable x, followed by assigning the value 1 to the shared variable y, and finally retrieves the value 1 from the variable x. Regarding thread T1, it first assigns the value 2 to the variable x and then retrieves the value 1 twice from the variable x.
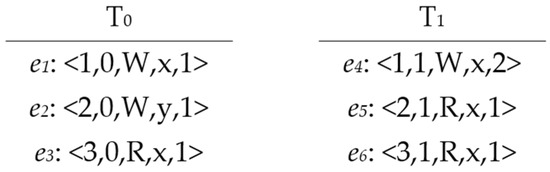
Figure 7.
A small concurrent program illustrating the operation of the proposed approach.
The work of the proposed approach is illustrated in Figure 8, which explains the graph obtained from verifying the previous program using the suggested algorithms. The process of obtaining iτ and subsequently converting it to Eτ and establishing the relation rf is omitted in this explanation, as it operates in the same manner described in the section “An illustrative scenario that clarifies the preliminary”. The figure contains a collection of nodes, each with its own code to unambiguously identify the node being referred to. This code is crucial for programming purposes when establishing a connection between nodes. Each node displays its code in the leftmost cell of the top row, while the right cell in the first row reflects the final event processed by the chosen path. The second row in each node contains the thread labels, with thread −1 appended to all nodes. The remaining rows correspond to the events associated with each thread. The processed events stand out due to their green cell background, and an indicator appears on the left side of the events in every unfinished thread, indicating the next event the thread will handle. Upon completing all events in the thread, the absence of a pointer becomes evident. The proposed approach is divided into three levels to provide clarity.
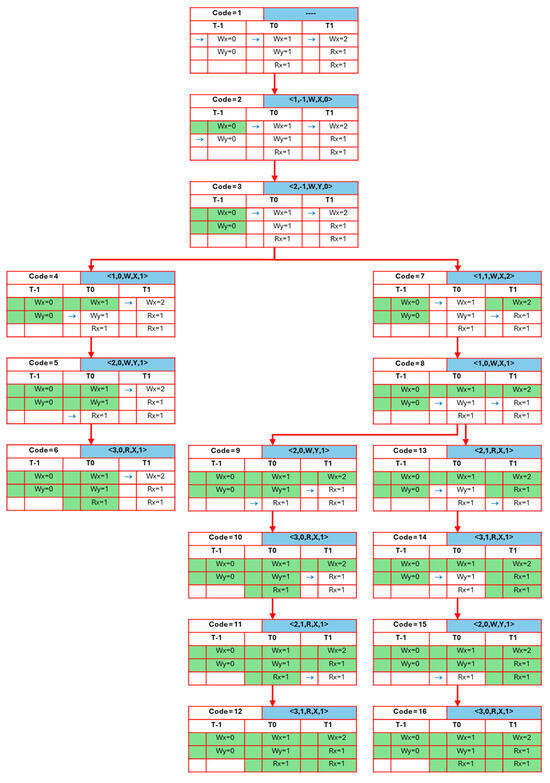
Figure 8.
The graph G generated from the processing of the program shown in Figure 7.
Level 1: During this level, the initial node, with code 1, is generated to encompass all events occurring in the threads before the start of the processing procedure. It can be seen that the first node does not contain any previously handled events. Nodes 2 and 3 are added to handle the assignment or writing of initial values to the shared variables. In node 2, the event pointer has shifted to the second event of thread −1. In node 3, thread −1 no longer has an event pointer, as all its events have been handled. At this point, the events of thread −1 do not coincide with other threads, as this is the initial phase. The pointers of T0 and T1 still refer to the first event in each thread. This level corresponds to lines 2–9 of the BuildGraph algorithm.
Level 2: At this stage, the cyclic process of the buildGraph algorithm begins by searching for events of the type “write” or “read”, which read initial values or depend on an already processed write event. This corresponds to line 10 and beyond in the buildGraph algorithm. From the previous level, node 3 is selected as the candidate node for processing because its pointers, for all threads except thread −1, point to the first event in each thread. Events e1 and e4 are chosen as candidates for processing, resulting in two nodes being attached to node 3. When processing e1, node 4 is added to the graph to represent e1. Upon completing the processing of e1, the AddReadEvent algorithm is used to locate read events that depend on it. The AddReadEvent algorithm generates permutations for read events occurring in T0 and T1, resulting in two possibilities. The first option is to process the read event from T0, beginning with e2 and continuing up to e3, which reads from e1, followed by processing the read events in T1. The second option is to start with the read events from T1, followed by T0. However, the read events in T1 that depend on e1 are preceded by e4, which writes to the variable x, violating the sequential consistency (SC) criteria, as e4 overwrites the value of x, on which the read events from e1 depend. Therefore, this option is disregarded, and only one path from node 4, related to events in T0, remains. The third event from T0, which reads from e1, is located after the write event e2, which writes to y in T0. As a result, the processing proceeds with e2, followed by e3. Upon including event e2, the AddReadEvent algorithm is invoked. Since no read events depend on e2, no further nodes related to y are added beyond node 5. Node 6, representing e3, is then added to G. Node 6 marks the end of this incomplete path due to the failure to add all read events dependent on e1. At this point, the first branch of node 3 is complete, and the second branch begins. This branch handles e4. During this process, the first event e4 from T1 is added as node 7 in the graph. Next, the AddReadEvent algorithm is invoked to search for events that depend on e4 (the value 2 of x). Since no such events exist, the AddReadEvent algorithm does not yield any events related to e4.
Level 3: This level involves searching for nodes added during the current iteration that have not yet been processed but have at least one thread pointer referring to unprocessed events. In other words, these nodes contain events that have not yet been handled. Nodes 6 and 7 are eligible for processing in the next iteration, which repeats levels two and three.
Returning to level two, node 6 cannot be processed because adding e4 would violate SC requirements. Therefore, the isProcessed value for this node is set to true. Upon further searching for unprocessed nodes, the algorithm concludes, as no additional nodes remain for processing. For node 7, the first event e1 from T0 is processed, which is referred to by node 8. A search for read events related to e1 follows. Since both threads T0 and T1 contain read events from e1, a permutation is generated for the AddReadEvent algorithm. This phase results in two permutations. Permutation 1 is represented by the nodes in path (9–12), which are processed using the same method as described earlier. Permutation 2 is represented by the nodes in path (13–16).
Upon analyzing this program using the classifyProgram algorithm, it is deemed SC-compatible, as nodes 12 and 16 are present in G, with the pointers of both nodes indicating the completion of all events in both T0 and T1. The classifyProgram algorithm then provides two witnesses of the specified behavior, as there are two paths from the initial node to nodes 12 and 16. These witnesses are as follows:
Witness 1: e4 → e1 → e2 → e3 → e5 → e6
Witness 2: e4 → e1 → e5 → e6 → e2 → e3
Discussion on Completeness and Validity
The proposed approach focuses on identifying a sequentially consistent ordering of events strictly adhering to the read-from relation. By concentrating explicitly on exploring sequentially consistent (SC) paths and disregarding non-SC paths, the method effectively reduces computational complexity without compromising accuracy. Specifically, Variant 2 eliminates the exploration of redundant paths, as formally justified in the provided proof (Appendix A.2), since each omitted set of paths is represented by an equivalent path already analyzed. Similarly, for Variant 3, while permutations involving ordering of read events with their ancestor unprocessed events are restricted—usually yielding SC paths—any non-SC path selected under these restrictions will have its nodes revisited and explored in subsequent iterations of the BuildGraph algorithm. This iterative exploration guarantees that all necessary event orderings are eventually considered, ensuring the completeness, accuracy, and validity of the classification results.
5. Implementation
The approach was implemented using the Java programming language. To assess its performance against the third algorithm from [14], referred to as ConsistencyDecision, the ConsistencyDecision algorithm was also implemented in Java. Both approaches rely on the same input type of iτ, which is provided as a text file. Additionally, the transformation process of iτ into Eτ remains identical in both approaches. While constructing the ConsistencyDecision algorithm, it was observed that the graph generated at multiple levels contained redundant nodes, causing a decline in performance during the processing of subsequent levels. Therefore, a procedure was introduced to eliminate duplicate nodes, retaining only one instance, which led to performance improvements. Both approaches utilized the mxgraph package to render the graph for analytical purposes. Furthermore, the depth-first search method was applied to identify a path from the initial node to a node where all events of all threads are processed in the ConsistencyDecision algorithm to classify a given behavior as SC or non-SC. Additionally, the depth-first search method was employed to determine the order of events to uncover witnesses substantiating behavior in both approaches.
Upon analyzing the execution time and its distribution across the various phases of the proposed approach, it became apparent that a significant portion of the execution time was spent processing the probabilities of the order of reading events in the AddReadEvent algorithm. To reduce execution time, three distinct variants of the proposed approach were developed while adhering to the previously defined algorithms. The three variants are described below:
- The first variant, referred to as V1 in the performance comparison tables, relies solely on the previously mentioned algorithms;
- The second variant, referred to by V2 in the comparison tables, builds upon the first variant but focuses on analyzing the permutations generated in the AddReadEvent algorithm by identifying equivalent groups of events. Only one path from each group is processed to minimize execution time. The concept behind the equivalent set of events is described below.
After adding a write event eW to the graph G through the buildGraph, AddReadEvent, or getWrite algorithms, the AddReadEvent algorithm begins adding the read events that read from eW. This addition process starts with the pointers of the configuration of eW and concludes with the intended read events for each thread containing read event(s) reading from eW. The number of paths generated depends on the number of threads containing read events that read from eW, with each path based on a different order of these events, but all paths maintain the same events. For example, the program shown in Figure 9, currently being verified, includes three threads, each with several events depicted in the figure.
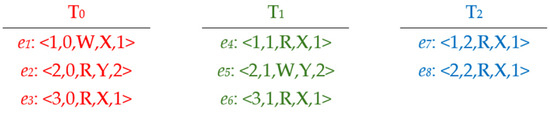
Figure 9.
A small program illustrating the concept of equivalent cutTraces. Colors are used to distinguish threads: red for T0, green for T1, and blue for T2.
When the buildGraph algorithm runs, event e1 from T0 is added to the graph G, as it is the only candidate event for processing, followed by invoking the AddReadEvent algorithm to add all read events that depend on e1. Table 4 shows six different event orders, called cutTrcaes, generated by the AddReadEvent algorithm. Each cutTrace represents a permutation from the set permutations generated in line 4 in the algorithm AddReadEvent. As explained in Table 4, each group of events belongs to the same thread represented by a distinct color. It is possible to process all determined events belonging to the same thread one after one as cutTraces 1 and 6 without interleaving between threads. On the other hand, it is also possible to process interleaving events from different threads like cutTraces 2, 3, 4, and 5.

Table 4.
All cutTraces obtained from processing event e1 in Figure 9 using the AddReadEvent algorithm. Colors are used to distinguish threads: red for T0, green for T1, and blue for T2.
After analyzing each cutTrace and its results, it was determined that these cutTraces could be grouped based on their final outcomes, with each group producing identical final outcomes. To achieve this, a signature should be extracted from each cutTrace, showing that cutTraces within the same group share the same signature. Consequently, instead of processing all cutTraces, only one cutTrace from each group is analyzed, reducing the time required for processing. In other words, this variant of the proposed approach focuses on collapsing multiple equivalent sequences of events as they are deemed equivalent. This concept aligns with the theory of Mazurkiewicz traces. The signature for each cutTrace is generated by first identifying the set of shared variables that the cutTrace interacts with. In fact, all cutTraces share the same set of variables, as they share the same events with different orders.
For the current example, the set of variables is {X and Y}. Then, events for each cutTrace are separated according to the variable name, ensuring that the order of events in the cutTrace remains the same for each shared variable after separation. In other words, this separation means sorting events of each cutTrace according to the variable names with respect to the order of events dealing with the same variable. The events of each cutTrace from the program in Figure 9 are presented in Table 5 after being separated based on the shared variable names. After that, the write events are encoded using these rules:
- –
- Write event: {thread number, W, variable name, value of write};
- –
- Read event: {R, variable name, value of read}.

Table 5.
The separation of events for all cutTraces in Table 4 based on variable names. Colors are used to distinguish threads: red for T0, green for T1, and blue for T2.
Table 5.
The separation of events for all cutTraces in Table 4 based on variable names. Colors are used to distinguish threads: red for T0, green for T1, and blue for T2.
| Variable | cutTrace1 | cutTrace2 | cutTrace3 | cutTrace4 | cutTrace5 | cutTrace6 |
|---|---|---|---|---|---|---|
| X | <1,0,W,X,1> | <1,0,W,X,1> | <1,0,W,X,1> | <1,0,W,X,1> | <1,0,W,X,1> | <1,0,W,X,1> |
| <3,0,R,X,1> | <1,1,R,X,1> | <1,2,R,X,1> | <1,2,R,X,1> | <1,1,R,X,1> | <3,0,R,X,1> | |
| <1,1,R,X,1> | <3,1,R,X,1> | <2,2,R,X,1> | <2,2,R,X,1> | <3,1,R,X,1> | <1,2,R,X,1> | |
| <3,1,R,X,1> | <3,0,R,X,1> | <3,0,R,X,1> | <1,1,R,X,1> | <1,2,R,X,1> | <2,2,R,X,1> | |
| <1,2,R,X,1> | <1,2,R,X,1> | <1,1,R,X,1> | <3,1,R,X,1> | <2,2,R,X,1> | <1,1,R,X,1> | |
| <2,2,R,X,1> | <2,2,R,X,1> | <3,1,R,X,1> | <3,0,R,X,1> | <3,0,R,X,1> | <3,1,R,X,1> | |
| Y | <2,0,R,Y,2> | <2,1,W,Y,2> | <2,0,R,Y,2> | <2,1,W,Y,2> | <2,1,W,Y,2> | <2,0,R,Y,2> |
| <2,1,W,Y,2> | <2,0,R,Y,2> | <2,1,W,Y,2> | <2,0,R,Y,2> | <2,0,R,Y,2> | <2,1,W,Y,2> |
Write event encoding includes the thread number to maintain the order of writes across threads. By combining event encodings within a cutTrace into a single string, a signature for each cutTrace is formed, as shown in Table 6. Each row in Table 6 represents a cutTrace signature, revealing that cutTraces {1, 3, 6} share the same signature as cutTraces {2, 4, 5}. Consequently, only one cutTrace per group is processed, which leads to reducing the number of cutTraces from six to two. Experiments show that this reduction becomes more significant as more threads read from eW. Referring to Figure 8, it is obvious that after the completion of processing event e1, which is displayed as node 8, two paths were processed by nodes {9, 10, 11, and 12} as cutTrace1 and {13, 14, 15, and 16} as cutTrace2. As a result of applying this variant concept, only one cutTrace is generated. The minimal set of cutTraces, where each cutTrace represents a group of equivalent cutTraces, is referred to as McutTraces. Algorithm 7 presents the revised pseudo-code for the AddReadEvent algorithm. In the updated version, lines 5–16 have been introduced to replace line 5 from the original algorithm in V1. Additionally, line 29 has been appended to the end of the old algorithm. Lines 5–16 are designed to extract the variable names that the first permutation, referred to as cutTrace1, handles. Since all permutations share the same set of variables, it is sufficient to rely solely on permutation [0] for this purpose. The subsequent lines ensure that the logic for encoding each permutation is maintained, combining these encodings into a single signature. Finally, the algorithm checks whether this signature has been processed before or not.

Table 6.
The encoded events for all cutTraces in Table 5.
| Algorithm 7: AddReadEvent | |||||||
| 1 | AddReadEvent (eW, ToT) | ||||||
| 2 | let parentVertex := vertex of eW | ||||||
| 3 | let setOfReadsFromeW := {e ∈ ToT | e.e’ = eW} | ||||||
| 4 | let permutations := generate permutation for setOfReadsFromeW | ||||||
| 5 | let setOfVariables := distinct variables names a permutations [0] deal with | ||||||
| 6 | let processedSignatures := Ø | ||||||
| 7 | for each permutation in permutations | ||||||
| 8 | Let signature := “” | ||||||
| 9 | let orderedEvents := events of permutation sorted based on setOfVariables | ||||||
| 10 | for each event e in orderedEvents | ||||||
| 11 | if e.type = W | ||||||
| 12 | signature := signature + e.thread + “W” + e.variable + e.value | ||||||
| 13 | else | ||||||
| 14 | signature := signature + “R” + e.variable + e.e`.value | ||||||
| 15 | if signature ⊆ processedSignatures | ||||||
| 16 | skip this permutation | ||||||
| 17 | for each read event eR in permutation | ||||||
| 18 | let indexOfRead := event id of eR.e’ | ||||||
| 19 | for each event e where e.thread = eR.thread and e.id >= eW.pointers[eR.thread] and e.id <= indexOfRead | ||||||
| 20 | if e.type = R | ||||||
| 21 | if e.e’.thread = −1 or e.e’ = eW or e.e’.id < eW.pointers[e.e’.thread] | ||||||
| 22 | AddVertex(e) | ||||||
| 23 | else if e.e’ != eW | ||||||
| 24 | getWrite (e, ToT) | ||||||
| 25 | else if e.type = W | ||||||
| 26 | if (∃ read event eR where eR.id >= eW.pointers[eR.thread] and eR.variable = e.variable and eR.e’ != e and eR.e’.id < eW.pointers[eR.e’.thread]) or (∃ read event eR where eR.id >= eW.pointers[eR.thread] and eR.variable = e.variable and ∃ write event eW’ where eW’.thread = eR.thread and eW’.variable = e.variable and eW’.id < eR.id and eW’.id >= eW.pointers[eW.thread]) then skip this permutation | ||||||
| 27 | AddVertex(e) | ||||||
| 28 | addReadEvent(e) | ||||||
| 29 | add signature to processedSignatures | ||||||
- 3.
- When examining the second variant, it was observed that the majority of cutTraces in the McutTraces set generate identical sequences of conflict events after being sorted using the addReadEvent and getWrite algorithms. This means that if these cutTraces are ordered by the algorithms before extracting their signatures, they will produce the same signatures. For instance, in Figure 9 and Table 4, cutTraces 1 and 2 are processed using addReadEvent and getWrite, resulting in the ordered cutTraces displayed in Table 7. The signatures extracted from these ordered cutTraces in Table 7 are identical, as demonstrated in Table 8, which shows the signatures obtained by encoding the events from Table 7’s cutTraces 1 and 2 in the same manner as in Variant 2, but the only difference is extracting signature here performed after applying addReadEvent and getWrite algorithms.
 Table 7. Two equivalent cutTraces after being processed in AddReadEvent and GetWrite algorithms.
Table 7. Two equivalent cutTraces after being processed in AddReadEvent and GetWrite algorithms. Table 8. The encoded events for the cutTraces presented in Table 7.
Table 8. The encoded events for the cutTraces presented in Table 7.
As a result, processing a single cutTrace can significantly reduce the processing time by eliminating the need to detect equivalent cutTraces, as required in Variant 2, or all cutTraces, as in Variant 1. Additionally, this approach decreases memory utilization. However, this method cannot be generalized due to rare exceptions where the signatures of cutTraces differ. Such cases can lead to the misclassification of behaviors. The primary issue lies in selecting one cutTrace from among several options, as this choice may deviate from exploring all possible interleavings of conflicting events. Consequently, this may result in a configuration that cannot be processed in subsequent iterations of the BuildGraph algorithm. In contrast, choosing an alternative cutTrace might have allowed the process to continue if the behavior conformed to SC. Moreover, this issue highlights that after processing the AddReadEvent and GetWrite algorithms, some cutTraces, each representing a set of equivalent cutTraces, could lead to different outcomes and behaviors.
It can therefore be concluded that the correctness of the verification process may be affected by the reduced exploration of interference cases. In such scenarios, the approach does not guarantee the exploration of all possible interleavings of events. To detail this, the proposed approach relies on the iterative execution of lines 10 to 30 in the BuildGraph algorithm, where each iteration invokes the AddReadEvent algorithm to process multiple write events sequentially. The processing of each write event considers a set of associated read and write events, as described previously. After examining all potential interleavings among the events in this set, the corresponding set of cutTraces is generated. In essence, the verification of a concurrent program is divided into independent chunks of events for processing. A fundamental principle is that if the behavior is SC, it is essential that each set of cutTraces processed during one iteration of the BuildGraph algorithm should include at least one cutTrace conforming to SC conditions. This cutTrace must encompass all read events that depend on the write event currently being processed. If the selected cutTrace fails to include all such read events due to consistency checks in both the AddReadEvent and GetWrite algorithms, then the choice of that cutTrace is deemed incorrect, and an alternative cutTrace should be selected for processing.
To address this issue, the addReadEvent algorithm was modified in a straightforward manner. The modification ensures that the chosen cutTrace contains all the required read events that must be added to the graph. If this condition is not met, the nodes of the corresponding path are not assigned a “true” value for the isProcessed variable within the AddVertex algorithm. This adjustment allows the subsequent iteration of the buildGraph algorithm to consider potential interference among events in this path, ensuring the identification of at least one valid path that maintains functionality when the concurrent program’s behavior aligns with SC. This enhancement was implemented in the third variant. The following algorithm, labeled as Algorithm 8, represents the third variant of this algorithm. Unlike previous versions that iterate over permutations, this variant iterates over setOfReadsFromeW, which contains all read events that read from eW. At the end of the algorithm, a check is performed to determine whether all events in setOfReadsFromeW have been appended to the graph G. If not all events in setOfReadsFromeW are added to G, the isProcessed flag for all vertices processed during this execution of the algorithm is set to false. This ensures that subsequent iterations of the BuildGraph algorithm can explore all possible orderings of the events.
| Algorithm 8: AddReadEvent | |||||||
| 1 | AddReadEvent (eW, ToT) | ||||||
| 2 | let parentVertex := vertex of eW | ||||||
| 3 | let setOfReadsFromeW := {e ∈ ToT | e.e’ = eW} | ||||||
| 4 | for each read event eR in setOfReadsFromeW | ||||||
| 5 | let indexOfRead := event id of eR.e’ | ||||||
| 6 | for each event e where e.thread = eR.thread and e.id >= eW.pointers[eR.thread] and e.id <= indexOfRead | ||||||
| 7 | if e.type = R | ||||||
| 8 | if e.e’.thread = −1 or e.e’ = eW or e.e’.id < eW.pointers[e.e’.thread] | ||||||
| 9 | AddVertex(e) | ||||||
| 10 | else if e.e’ != eW | ||||||
| 11 | getWrite (e, ToT) | ||||||
| 12 | else if e.type = W | ||||||
| 13 | if (∃ read event eR where eR.id >= eW.pointers[eR.thread] and eR.variable = e.variable and eR.e’ != e and eR.e’.id < eW.pointers[eR.e’.thread]) or (∃ read event eR where eR.id >= eW.pointers[eR.thread] and eR.variable = e.variable and ∃ write event eW’ where eW’.thread = eR.thread and eW’.variable = e.variable and eW’.id < eR.id and eW’.id >= eW.pointers[eW.thread]) then skip this iteration | ||||||
| 14 | AddVertex(e) | ||||||
| 15 | addReadEvent(e) | ||||||
| 16 | if ∃e ∈ setOfReadsFromeW , e ∉ V(G) | ||||||
| 17 | let Viter be the set of vertices created in the current call of AddReadEvent algorithm | ||||||
| 18 | ∀v ∈ Viter , isProcessed(v) = false | ||||||
- PKM Test
During the development phase, the approach was tested on various concurrent programs to validate the accuracy of Eτ classification. These programs, selected from [41], cover all forms of SC semantic violations. Additional concurrent programs were employed during the development and optimization of the approach and were used to evaluate its performance. The breaking of SC semantics can occur when appending a write event that produces invalid coherence order to the graph G. So, detecting SC violence is guaranteed to catch, but avoiding the omission of a path leading to SC behavior remains a challenging goal. To rigorously test the approach and generate SC behaviors, if any, a parameterized concurrent program called PKM was developed. The algorithm explaining PKM’s operation is shown below in Algorithm 9.
| Algorithm 9: ParameterizedCP | |||||
| 1 | let numberOfThreads := number | ||||
| 2 | let numberOfOperations := number | ||||
| 3 | let sizeOfSharedArray := numebr | ||||
| 4 | let count := 1 | ||||
| 5 | initialize SharedArray[sizeOfSharedArray] with 0 | ||||
| 6 | thread_routine() | ||||
| 7 | for i =0 and i < numberOfOperations | ||||
| 8 | let randomLocation := rand() | ||||
| 9 | if ((i mod 2) == 1) | ||||
| 10 | lock SharedArray[randomLocation] | ||||
| 11 | SharedArray[randomLocation] = count | ||||
| 12 | unlock SharedArray[randomLocation] | ||||
| 13 | count = count +1 | ||||
| 14 | else | ||||
| 15 | lock SharedArray[randomLocation] | ||||
| 16 | Let x := SharedArray[randomLocation] | ||||
| 17 | unlock SharedArray[randomLocation] | ||||
The parameterized concurrent program aims to generate balanced memory accesses, with the number of read events nearly equal to the number of write events, since the number of write operations strongly affects the performance of our approach, as will be explained in the next paragraph. This ensures the worst-case execution time for the approach. The program is provided with the number of threads, the number of operations per thread, and the size of the shared array for all threads. The program generates threads accordingly. The recursive nature of each thread’s task is determined by the number of specified operations. If the iteration count is odd, the variable count is added to a random location within the shared array during each cycle of work. The address is determined by generating a random number between 0 and the size of the array minus one. The variable count is then incremented by one. If the iteration count is even, a random location from the shared array is read. The read address is also determined randomly. To ensure that all iτ generated by this program are SC-compatible, each thread’s read and write operations are performed after the array location is locked. The lock is released after the completion of each operation. In the next section, the size of the array is set to 2 in order to increase the concurrent access of threads to the thread array.
6. Performance Evaluation
In this study, the performance of the three proposed variants was compared with the third algorithm from [14], referred to as “ConsistencyDecision”, by analyzing a collection of parametric concurrent programs containing a variable number of threads. These programs, sourced from SCTBench [42], sv-comp [43], and lastzero [34], were written in the C programming language. This program collection encompasses examples with both low and high numbers of Mazurkiewicz traces, depending on the trace count of each program. They fall into one of the following categories: concurrent programs where Reads-From coincides with Mazurkiewicz and concurrent programs where Reads-From is significantly coarser than Mazurkiewicz. The performance of the proposed approach is influenced by the number of write and read events, as well as the quantity of shared variables. These factors directly impact the frequency of shared variable accesses and the number of conflicting write events requiring proper ordering. Consequently, the number of shared variables varies significantly across programs, ranging from 25 in cases such as PKM to 465 in cases such as fsbench. The GNU Compiler Collection (GCC) was used to compile these programs into executable files, and the Intel PIN tool was employed to track read and write operations to and from memory, representing the iτ when the executable files were run. The experiments were conducted on an HP laptop equipped with 8 GB of RAM and 11th Gen Intel(R) Core(TM) i5-1135G7 @ 2.40GHz 2.42 GHz CPU, running Windows 10.
Three distinct sets of experiments were conducted as part of this evaluation. The first set, with results presented in Table 9, evaluates the performance of the proposed approach in comparison with the ConsistencyDecision algorithm, the third algorithm proposed in [14]. The second set, depicted in Figure 10, compares the performance of the proposed method with those described in [20,37]. Lastly, the third set examines the impact of varying the number of events while keeping the number of threads constant on the performance of the proposed approach.

Table 9.
A performance evaluation and comparison of the three variants of the proposed approach with the ConsistencyDecision algorithm.
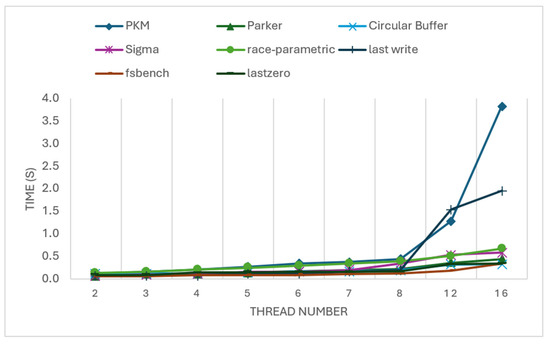
Figure 10.
The time required to verify SC for three distinct concurrent programs with varying thread counts.
Table 9 provides a practical comparison between the ConsistencyDecision algorithm and the three variants of the proposed approach. This comparison was conducted through a series of experiments involving the four verification methods. Three key factors were measured during this evaluation: the number of witnesses, the time required for verification (in milliseconds), and the memory usage (in megabytes). Memory usage was programmatically measured by calculating the difference between the total memory utilized during all iterations by the Java Virtual Machine (JVM) and the memory consumed by the JVM before the initiation of both the proposed approach and the ConsistencyDecision algorithm. In the “Test” column of Table 9, the name of each concurrent program is followed by the number of threads involved in each test. The tilde (˜) symbol in the time column indicates that the execution time exceeded two hours; in some cases, verification using the ConsistencyDecision algorithm extended beyond three days. If the number of witnesses is denoted by the tilde symbol, it signifies that the procedure for collecting witnesses exceeded one hour due to the large graph size, leading to impractical execution times for depth-first search (DFS) in recording witnesses. If the test is not completed due to time limitations, the memory usage remains unknown and is denoted by the tilde symbol. If the execution time of the ConsistencyDecision algorithm is uncertain and denoted by the tilde symbol, then the improvement achieved by our Variants is indicated using the triple minus sign (---).
Upon reviewing the results in Table 9, it is clear that all variants of the proposed approach outperformed the ConsistencyDecision algorithm in terms of execution time and usage of memory. However, the number of witnesses obtained by the ConsistencyDecision algorithm exceeds that of all the proposed variants. During witness analysis, it was observed that the ConsistencyDecision algorithm provides all witnesses without applying Mazurkiewicz trace theory. In terms of performance improvement, which is depicted in column Imp in Table 9, the third variant outperformed the others, with improvements ranging from 31.919% to 99.992% over the ConsistencyDecision algorithm. Furthermore, the percentage of improvement was significantly higher when the number of threads was greater compared to when the number of threads was low.
The execution time of a program is highly dependent on the number of memory write access operations, the number of threads, and the number of shared variables, as demonstrated in the analysis of the results in Table 9. However, predicting the execution time for two different programs remains a challenging and ambiguous task. For example, the execution time of the program “parker(6)”, which contains 143 memory access operations and 6 threads, is shorter than that of the program “dining(6)”, which contains 104 memory access operations and 6 threads. To investigate this discrepancy, the operations of each program were examined. Table 10 displays the number of operations performed by some programs for a variable number of threads, up to six. The operations in Table 10 are categorized into two types: write and read events denoted by (W and R), respectively. The program “Dining” has a greater number of write operations than the program “Parker”, as shown in Table 10. Additionally, the write-to-read event ratio in the “Dining“ program is higher than that in the “Parker” program. It is well established that execution time increases with the number of write operations when following the classification operations in the previous algorithms. This is because the BuildGraph algorithm treats each write event as an independent path for processing during each cycle, causing the number of paths to increase in proportion to the number of write events, while the read events follow a single sequential path according to the AddReadEvent algorithm in V3. The PKM program described earlier was designed with a balanced number of write and read events to simulate the worst-case scenario for the proposed approach.

Table 10.
The number of write and read events in the verified concurrent programs.
The execution times of V2 and V3 for classifying non-SC behavior are presented in Table 11. The iτ of the concurrent programs listed in Table 11 was modified by altering the last or penultimate event to cause a read value that violates SC conditions. These programs are identical to those in Table 9, with the only difference being the modified event for SC semantics violation, and they maintain the same number of threads and events. The table clearly demonstrates that execution time does not require full processing of program events, as the process terminates upon the initial detection of an SC condition violation. The execution time of a program violating SC conditions depends on the location of the write event causing the violation.

Table 11.
A performance evaluation of V2 and V3 of the proposed approach using a varying number of MAOs when behaviors are non-SC.
As shown in Table 11, it is clear that the third variant of the proposed approach produces better results compared to the first two variants. Therefore, the remaining experiments for the proposed approach will focus exclusively on the third variant.
A series of experiments was conducted to evaluate the performance of the proposed approach compared to the methods described in [20,37]. The concurrent programs utilized in these experiments are listed in Figure 10. The number of threads varied, starting at 4 and incrementally increasing to 16 in steps of 4 threads for each program. Each thread executed 50 operations. The test was repeated for 10 Eτs values, with the average execution time calculated for each program and thread count. The testing methodology employed in both studies was consistent; however, the hardware configurations used in [20,37] were not explicitly mentioned. This introduces an inherent limitation in direct performance comparisons, as execution time can be influenced by factors such as CPU clock speed, number of cores, memory bandwidth, and cache efficiency. Despite this uncertainty, the results indicate a significant reduction in verification time—from 60 s in [20] to 4 s in the worst case and from 15 s in [37] to 0.5 s—suggesting that the efficiency gains stem primarily from algorithmic improvements rather than hardware advantages alone. Future work could involve running all methods on a unified hardware platform to ensure direct comparability of execution times.
In order to analyze the effect of the number of events per thread on the verification time while considering the write-to-read operation ratio, two sets of Eτs were generated from the execution of the PKM program designed to represent the worst-case scenario for the proposed approach. This was conducted to illustrate the approach’s performance when verifying varying numbers of operations. In Figure 11, numerous experiments were conducted, resulting in the formation of five classes of Eτs for each ratio. The first ratio is 1:1, while the second is 1:3. Each class contains four threads, but the number of memory access operations differs between them. The first class begins with 100 operations, while each Eτ in the fifth class contains 500 operations, with an increment of 100 operations per class. Ten instances were constructed for each class, and the average execution time for each class was then calculated. Figure 11 illustrates the average execution time for each class. The shared array size in the PKM program is fixed as 2.
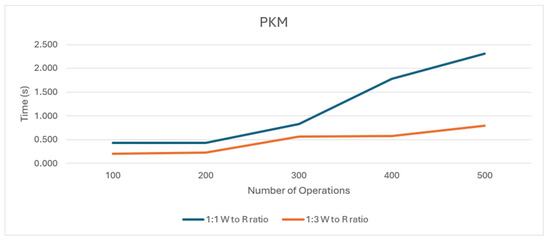
Figure 11.
The examination of SC while altering the number of operations for four threads in the PKM test.
According to Figure 11, the execution time of the verification process exhibits distinct growth patterns depending on the write-to-read ratio. When the ratio is 1:1, the execution time increases from 0.427 s at 100 operations to 2.305 s at 500 operations, showing a significant rise, particularly beyond 200 operations. This suggests a superlinear trend, likely quadratic (O(n²)), due to the increasing number of write operations that introduce dependency checks and ordering constraints. In contrast, when the write-to-read ratio is 1:3, the execution time remains consistently lower, starting at 0.203 s and reaching 0.798 s at 500 operations. The relatively moderate increase in execution time suggests a near-linear growth pattern, indicating that read operations have a reduced impact on verification complexity compared to writes. The widening gap between the two execution time series as the number of operations increases highlights the verification overhead imposed by frequent write operations. Since writes establish dependencies that must be checked for consistency, higher write ratios significantly affect scalability. Conversely, increasing the proportion of reads improves performance, as reads do not introduce additional constraints on execution order.
Threats to Validity
While the proposed approach demonstrates significant improvements in verification efficiency and scalability, some limitations and threats to validity must be discussed. One potential limitation involves managing complex cyclic dependencies (illustrated in Figure 5). The current method effectively handles cycles using a Java HashSet to detect and terminate cycles early. Another potential limitation concerns the heuristic approach employed in Variant 3, specifically regarding the selection of one cutTrace instead of all permutations like V1. A sensitivity analysis was conducted to investigate the heuristic’s impact on verification accuracy compared to performance gains. The results indicate that despite the heuristic’s aggressive pruning of redundant paths, the iterative nature of the BuildGraph algorithm ensures the eventual exploration of all essential event nodes, thus preserving accuracy while providing significant performance gains. Therefore, accuracy remains uncompromised, validating our heuristic choice.
Future work may involve deeper exploration of edge cases, especially those programs with unusually high write-to-read ratios, to further assess scalability and accuracy trade-offs.
7. Conclusions and Future Work
In this study, an approach was implemented to optimize the efficiency of verification concurrent programs to determine their compliance with SC. The proposed method either provides witnesses of SC compatibility or identifies the events that violate SC semantics in non-SC programs. The approach focuses on analyzing writing events, which led to significant performance improvements, as was the case with the first variant of the approach. Additionally, the second and third variants utilized the concept of analyzing event sequences and grouping them into equivalent groups that lead the program to the same state. By examining only one sequence from each equivalent group, execution time was reduced. Each variant employed a distinct methodology, and a directed acyclic graph was used to represent these sequences.
During the evaluation phase, the third variant demonstrated superior performance, with an improvement over the consistencyDecision algorithm ranging from 31.919% to 99.992%. All three variants shared six core algorithms, with slight variations in the addReadEvent algorithm. Both the variants and the consistencyDecision algorithm were developed and subsequently compared. The results revealed that all three variants outperformed the consistencyDecision algorithm, with the third variant yielding the most significant improvements. While the consistencyDecision algorithm iterates through the events in the concurrent program, the proposed approach reduces the number of iterations based on the number of write events in the program. The comparison demonstrates the superior efficiency of the proposed approach in verifying concurrent programs. Furthermore, the proposed method proved to be more effective than the two alternative approaches.
The following key findings were identified after analyzing the third variant:
- Execution time increases as the number of paths in the generated graph increases;
- Execution time is dependent on the ratio of write-to-read events;
- When a write event eW is sequenced at the start of a thread, and the read events dependent on eW are sequenced far from the last processed events in their threads, the execution time of a single cycle in the BuildGraph algorithm increases. But, the iterations required to verify the complete concurrent program will be decreased;
- A greater balance in the number of events across threads leads to increased overlap between thread events that access the same shared variables, resulting in longer execution times compared to threads with significant event count disparities.
The primary bottleneck in the proposed approach lies in the number of possible orderings of write events in each processing cycle of the BuildGraph algorithm. It is suggested that a new method, such as utilizing the happens-before relation, could be integrated into the BuildGraph algorithm to predict the order of conflicting events. By predicting the order of events, the proposed method processes the sequence as a single path, thereby avoiding the need to examine all possible orderings. This approach enhances scalability and efficiency. Additionally, the consistency-checking mechanism within the algorithm could be modified to accommodate weaker memory models, further extending its applicability.
Author Contributions
Conceptualization, M.H.A., P.A.A. and K.J.; methodology, M.H.A., P.A.A. and K.J.; software, M.H.A.; validation, M.H.A., P.A.A. and K.J.; formal analysis, M.H.A., P.A.A. and K.J.; investigation, M.H.A., P.A.A. and K.J.; resources, M.H.A., P.A.A. and K.J.; data curation, M.H.A., P.A.A. and K.J.; writing—original draft preparation, M.H.A. and K.J.; writing—review and editing, M.H.A., P.A.A. and K.J.; visualization, M.H.A., P.A.A. and K.J.; supervision, P.A.A. and K.J.; project administration, M.H.A., P.A.A. and K.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data supporting the findings of this study are available upon request from the corresponding author. No publicly archived datasets were used or generated during this study.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Formal Proof of the Soundness of the Proposed Approach
Appendix A.1.1. Definitions and Preliminaries
- Sequential Consistency (SC): A system is sequentially consistent if the result of any execution is equivalent to a sequential execution of operations from all threads, preserving each thread’s program order.
- Axiomatic Model of SC: An execution is sequentially consistent if the union of the following relations is acyclic:Program Order (po): Events from the same thread follow their program order:
- ○
- Read-From (rf): A read event ej reads the value written by a write event ei;
- ○
- From-Read (fr): A read event ej reads from write event ei, and a subsequent write event ek modifies the same variable after ei. So, ej and ek should be related in such a fr relation;
- ○
- Coherence Order (co): Write events to the same variable are ordered consistently with the po and rf relations.
- Operational Model of SC: Write events are considered atomic, with their values immediately visible to all threads. No intermediate writes intervene between a write event and its corresponding read events.
Appendix A.1.2. Formal Proof
The proposed approach is sound if all executions it identifies are sequentially consistent. The proof involves demonstrating that the approach adheres strictly to both the axiomatic and operational SC models.
Axiomatic Model
The proposed approach maintains the acyclicity of the union of po, rf, fr, and co relations as follows:
- rf Relation: The rf relation is either inherited from the initial trace (generated via DPOR) or derived explicitly using Algorithm 1. All read events are processed strictly after identifying their corresponding write events;
- po Relation: The po is preserved by explicitly managing thread pointers within the configurations. Algorithms (BuildGraph, AddReadEvent, GetWrite) process events strictly according to each thread’s program order, ensuring correct po relations;
- fr Relation: The fr relation is maintained explicitly by the conditions in the proposed algorithms:
- ○
- Line 26 (BuildGraph): Ensures subsequent write events cannot be considered until all dependent read events are processed;
- ○
- Line 15 (AddReadEvent): Ensures read events are correctly linked to preceding write events;
- ○
- Line 13 (GetWrite): Enforces coherence order consistency between write events.
- co Relation: Coherence order (co) is preserved through the same conditions employed to ensure the fr relation. Specifically, algorithms (BuildGraph, AddReadEvent, GetWrite) order writes to the same variable consistently, aligning with the SC semantics;
- Acyclicity: The union of po, rf, fr, and co relations is explicitly checked for cycles (line 2 in GetWrite). Detection of any cycle immediately terminates processing, thereby preserving SC.
Operational Model
The proposed approach aligns fully with the operational model by ensuring atomicity and immediate visibility of write events:
- Atomicity of Write Events: Write events are treated atomically. Algorithms (BuildGraph, AddReadEvent, GetWrite) ensure that read events directly follow their corresponding write events, with no intermediate conflicting write events intervening;
- Immediate Visibility of Writes: After a write event is processed, the associated read events from all threads are immediately linked, making the write value instantly visible across threads, complying with operational SC.
Therefore, the proposed approach satisfies both axiomatic and operational sequential consistency models and is sound.
Appendix A.2. Soundness of the Variant 2
Appendix A.2.1. Formal Proof of Validity of Variant 2 (V2)
- Definitions and Preliminaries: Consider the set of events E = {e1,e2,e3,e4}:
- ○
- e1 = ⟨1,0,W,x,1⟩ (Thread 0 writes 1 to x);
- ○
- e2 = ⟨2,0,R,x,1⟩ (Thread 0 reads x= 1);
- ○
- e3 = ⟨1,1,W,x,2⟩ (Thread 1 writes 2 to x);
- ○
- e4 = ⟨2,1,R,x,1⟩ (Thread 1 reads x = 1).
Define dependency relation D based on relations po, rf, co, and fr. Two events are independent if not related by D. Formally, independence relation I={(ei,ej)∣(ei,ej) ∉ D}.
Dependency Analysis:
- po: (e1,e2), (e3,e4);
- rf: (e1,e2), (e1,e4);
- co: (e3,e1) as e3 writes x= 2 before e1 writes x=1;
- fr: (Empty).
Thus, D = {(e1,e2),(e3,e4), (e1,e4),(e3,e1)}.
Independence Relation I: Events not related by D form independence relation I. Thus:
- I = {(e2,e4)}, as these events neither conflict nor depend on each other.
Trace Equivalence (Mazurkiewicz traces)
Consider traces:
- T1 = e3→ e1→e2→e4;
- T2 = e3→ e1→e4→e2.
Steps of equivalence:
- Both traces start identically (e3→ e1), consistent with D;
- e2 and e4 can be swapped (independent in I); the final state is unaffected since both read the same value x=1 from e1.
Signature Equivalence
Both traces T1 and T2 yield identical signatures due to the independence and identical read values:
- Signature(T1) = Signature(T2) = ⟨1,W,x,2⟩ → ⟨0,W,x,1⟩ → ⟨R,x,1⟩ → ⟨R,x,1⟩.
Appendix A.2.2. Formal Proof
Since read events that access the same value from the same variable produce identical encodings, the ordering of independent read events (e2, e4) does not alter the trace signature. Thus, the signature concept mirrors Mazurkiewicz’s trace theory, confirming trace equivalence despite reordered independent events. Both approaches guarantee identical execution outcomes, validating the robustness of our method.
References
- Schneider, F.B.; Andrews, G.R. Concepts for Concurrent Programming. In Current Trends in Concurrency. Overviews and Tutorials; Springer: Berlin/Heidelberg, Germany, 1986; pp. 669–716. ISBN 0-387-16488-X. [Google Scholar]
- Di Pierro, M.; Skinner, D. Concurrency in Modern Programming Languages [Guest Editors’ Introduction]. Comput. Sci. Eng. 2012, 14, 8–10. [Google Scholar] [CrossRef]
- Arpaci-Dusseau, R.H.; Arpaci-Dusseau, A.C. Operating Systems: Three Easy Pieces; Erscheinungsort Nicht Ermittelbar; Arpaci-Dusseau Books, LLC: Madison, WI, USA, 2018; ISBN 978-1-985086-59-3. [Google Scholar]
- Arlt, E. A Formally Verified Automatic Verifier for Concurrent Programs. Master’s Thesis, ETH Zürich, Zürich, Switzerland, 2023. [Google Scholar]
- Abdulwahhab, M.H. A Comparative Analysis of Memory Models: SC, TSO, and ARM in Concurrent Programming. Commun. Appl. Nonlinear Anal. 2024, 32, 100–117. [Google Scholar] [CrossRef]
- Atig, M.F. What Is Decidable under the TSO Memory Model? ACM SIGLOG News 2020, 7, 4–19. [Google Scholar] [CrossRef]
- Lamport. How to Make a Multiprocessor Computer That Correctly Executes Multiprocess Programs. IEEE Trans. Comput. 1979, C-28, 690–691. [CrossRef]
- Alglave, J.; Deacon, W.; Grisenthwaite, R.; Hacquard, A.; Maranget, L. Armed Cats: Formal Concurrency Modelling at Arm. ACM Trans. Program. Lang. Syst. 2021, 43, 1–54. [Google Scholar] [CrossRef]
- Moiseenko, E.; Podkopaev, A.; Koznov, D. A Survey of Programming Language Memory Models. Program. Comput. Softw. 2021, 47, 439–456. [Google Scholar] [CrossRef]
- Lahav, O.; Giannarakis, N.; Vafeiadis, V. Taming Release-Acquire Consistency. In Proceedings of the 43rd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, St. Petersburg, FL, USA, 20–22 January 2016; pp. 649–662. [Google Scholar] [CrossRef]
- Abdulla, P.A.; Atig, M.F.; Jonsson, B.; Ngo, T.P. Optimal Stateless Model Checking under the Release-Acquire Semantics. Proc. ACM Program. Lang. 2018, 2, 1–29. [Google Scholar] [CrossRef]
- Zhang, N.; Kusano, M.; Wang, C. Dynamic Partial Order Reduction for Relaxed Memory Models. In Proceedings of the 36th ACM SIGPLAN Conference on Programming Language Design and Implementation, Portland, OR, USA, 13–17 June 2015; pp. 250–259. [Google Scholar] [CrossRef]
- Ta, T.; Troendle, D.; Jang, B. Thread Communication and Synchronization on Massively Parallel GPUs. In Advances in GPU Research and Practice; Morgan Kaufmann: San Francisco, CA, USA, 2017; pp. 57–81. [Google Scholar] [CrossRef]
- Abdulla, P.A.; Atig, M.F.; Jonsson, B.; Lång, M.; Ngo, T.P.; Sagonas, K. Optimal Stateless Model Checking for Reads-from Equivalence under Sequential Consistency. Proc. ACM Program. Lang. 2019, 3, 1–29. [Google Scholar] [CrossRef]
- Lorch, J.R.; Chen, Y.; Kapritsos, M.; Parno, B.; Qadeer, S.; Sharma, U.; Wilcox, J.R.; Zhao, X. Armada: Low-Effort Verification of High-Performance Concurrent Programs. In Proceedings of the 41st ACM SIGPLAN Conference on Programming Language Design and Implementation, London UK, 15–20 June 2020; pp. 197–210. [Google Scholar] [CrossRef]
- Agarwal, P.; Chatterjee, K.; Pathak, S.; Pavlogiannis, A.; Toman, V. Stateless Model Checking Under a Reads-Value-from Equivalence. In Computer Aided Verification; Silva, A., Leino, K.R.M., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2021; Volume 12759, pp. 341–366. [Google Scholar] [CrossRef]
- Alglave, J.; Maranget, L.; Sarkar, S.; Sewell, P. Litmus: Running Tests against Hardware. In Tools and Algorithms for the Construction and Analysis of Systems; Abdulla, P.A., Leino, K.R.M., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6605, pp. 41–44. [Google Scholar] [CrossRef]
- Sorin, D.J.; Hill, M.D.; Wood, D.A. A Primer on Memory Consistency and Cache Coherence; Synthesis Lectures on Computer Architecture; Morgan & Claypool Publishers: San Rafael, CA, USA, 2011; ISBN 978-1-60845-564-5. [Google Scholar]
- Naeem, A.; Jantsch, A.; Lu, Z. Architecture Support and Comparison of Three Memory Consistency Models in NoC Based Systems. In Proceedings of the 2012 15th Euromicro Conference on Digital System Design, Cesme, Turkey, 5–8 September 2012; pp. 304–311. [Google Scholar] [CrossRef]
- Zennou, R.; Atig, M.F.; Biswas, R.; Bouajjani, A.; Enea, C.; Erradi, M. Boosting Sequential Consistency Checking Using Saturation. In Automated Technology for Verification and Analysis; Hung, D.V., Sokolsky, O., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2020; Volume 12302, pp. 360–376. [Google Scholar] [CrossRef]
- Abdulla, P.A.; Arora, J.; Atig, M.F.; Krishna, S. Verification of Programs under the Release-Acquire Semantics. In Proceedings of the 40th ACM SIGPLAN Conference on Programming Language Design and Implementation, Phoenix, AZ, USA, 22–26 June 2019; pp. 1117–1132. [Google Scholar] [CrossRef]
- Naeem, A.; Chen, X.; Lu, Z.; Jantsch, A. Realization and Performance Comparison of Sequential and Weak Memory Consistency Models in Network-on-Chip Based Multi-Core Systems. In Proceedings of the 16th Asia and South Pacific Design Automation Conference (ASP-DAC 2011), Yokohama, Japan, 25–28 January 2011; pp. 154–159. [Google Scholar] [CrossRef]
- Atig, M.F.; Bouajjani, A.; Burckhardt, S.; Musuvathi, M. What’s Decidable about Weak Memory Models? In Programming Languages and Systems; Seidl, H., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7211, pp. 26–46. [Google Scholar] [CrossRef]
- Nardelli, F.Z.; Sewell, P.; Sevcik, J.; Sarkar, S.; Owens, S.; Maranget, L.; Batty, M.; Alglave, J. Relaxed Memory Models Must Be Rigorous. In Exploiting Concurrency Efficiently and Correctly, CAV 2009 Workshop; University of Kent: Canterbury, UK, 2009; Available online: https://kar.kent.ac.uk/31904/ (accessed on 5 February 2024).
- Aronis, S. Effective Techniques for Stateless Model Checking; Acta Universitatis Upsaliensis: Uppsala, Sweden, 2018; ISBN 978-91-513-0160-0. [Google Scholar]
- Apt, K.R.; Boer, F.S.d.; Olderog, E.-R. Verification of Sequential and Concurrent Programs. In Texts in Computer Science, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-1-84882-745-5. [Google Scholar]
- Baier, C.; Katoen, J.-P. Principles of Model Checking; MIT Press: Cambridge, MA, USA, 2008; ISBN 978-0-262-02649-9. [Google Scholar]
- Floyd, R.W. Assigning Meanings to Programs. In Program Verification; Colburn, T.R., Fetzer, J.H., Rankin, T.L., Eds.; Studies in Cognitive Systems; Springer: Dordrecht, The Netherlands, 1993; Volume 14, pp. 65–81. [Google Scholar] [CrossRef]
- Hoare, C.A.R. An Axiomatic Basis for Computer Programming. In Programming Methodology; Gries, D., Ed.; Springer: New York, NY, USA, 1978; pp. 89–100. [Google Scholar] [CrossRef]
- Ashcroft, E.A. Proving Assertions about Parallel Programs. J. Comput. Syst. Sci. 1975, 10, 110–135. [Google Scholar] [CrossRef]
- Clarke, E.M.; Grumberg, O.; Minea, M.; Peled, D. State Space Reduction Using Partial Order Techniques. Int. J. Softw. Tools Technol. Transf. 1999, 2, 279–287. [Google Scholar] [CrossRef]
- Godefroid, P. (Ed.) Partial-Order Methods for the Verification of Concurrent Systems; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1996; Volume 1032. [Google Scholar] [CrossRef]
- Peled, D. All from One, One for All: On Model Checking Using Representatives. In Computer Aided Verification; Courcoubetis, C., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1993; Volume 697, pp. 409–423. [Google Scholar] [CrossRef]
- Abdulla, P.; Aronis, S.; Jonsson, B.; Sagonas, K. Optimal Dynamic Partial Order Reduction. In Proceedings of the 41st ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, San Diego, CA, USA, 22–24 January 2014; pp. 373–384. [Google Scholar] [CrossRef]
- Mazurkiewicz, A. Trace Theory. In Petri Nets: Applications and Relationships to Other Models of Concurrency; Brauer, W., Reisig, W., Rozenberg, G., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1987; Volume 255, pp. 278–324. [Google Scholar] [CrossRef]
- Qadeer, S. Verifying Sequential Consistency on Shared-Memory Multiprocessors by Model Checking. IEEE Trans. Parallel Distrib. Syst. 2003, 14, 730–741. [Google Scholar] [CrossRef]
- Zennou, R.; Bouajjani, A.; Enea, C.; Erradi, M. Gradual Consistency Checking. In Computer Aided Verification; Dillig, I., Tasiran, S., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2019; Volume 11562, pp. 267–285. [Google Scholar] [CrossRef]
- Qian, X.; Torrellas, J.; Sahelices, B.; Qian, D. Volition: Scalable and Precise Sequential Consistency Violation Detection. In Proceedings of the Eighteenth International Conference on Architectural Support for Programming Languages and Operating Systems, Houston, TX, USA, 16–20 March 2013; pp. 535–548. [Google Scholar] [CrossRef]
- Muzahid, A.; Qi, S.; Torrellas, J. Vulcan: Hardware Support for Detecting Sequential Consistency Violations Dynamically. In Proceedings of the 2012 45th Annual IEEE/ACM International Symposium on Microarchitecture, Vancouver, BC, Canada, 1–5 December 2012; pp. 363–375. [Google Scholar] [CrossRef]
- Marino, D.; Singh, A.; Millstein, T.; Musuvathi, M.; Narayanasamy, S. DRFX: A Simple and Efficient Memory Model for Concurrent Programming Languages. ACM SIGPLAN Not. 2010, 45, 351–362. [Google Scholar] [CrossRef]
- POWER and ARM Litmus Tests. Available online: https://www.cl.cam.ac.uk/~pes20/ppc-supplemental/ppc451.html#toc25 (accessed on 15 November 2024).
- Thomson, P.; Donaldson, A.F.; Betts, A. Concurrency Testing Using Controlled Schedulers: An Empirical Study. ACM Trans. Parallel Comput. 2016, 2, 1–37. [Google Scholar] [CrossRef]
- SV-COMP. Competition on Software Verification. 2024. Available online: https://sv-comp.sosy-lab.org/ (accessed on 20 June 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).