Abstract
Federated learning in heterogeneous data scenarios faces two key challenges. First, the conflict between global models and local personalization complicates knowledge transfer and leads to feature misalignment, hindering effective personalization for clients. Second, the lack of dynamic adaptation in standard federated learning makes it difficult to handle highly heterogeneous and changing client data, reducing the global model’s generalization ability. To address these issues, this paper proposes pFedKA, a personalized federated learning framework integrating knowledge distillation and a dual-attention mechanism. On the client-side, a cross-attention module dynamically aligns global and local feature spaces using adaptive temperature coefficients to mitigate feature misalignment. On the server-side, a Gated Recurrent Unit-based attention network adaptively adjusts aggregation weights using cross-round historical states, providing more robust aggregation than static averaging in heterogeneous settings. Experimental results on CIFAR-10, CIFAR-100, and Shakespeare datasets demonstrate that pFedKA converges faster and with greater stability in heterogeneous scenarios. Furthermore, it significantly improves personalization accuracy compared to state-of-the-art personalized federated learning methods. Additionally, we demonstrate privacy guarantees by integrating pFedKA with DP-SGD, showing comparable privacy protection to FedAvg while maintaining high personalization accuracy.
1. Introduction
Federated Learning (FL), a distributed machine learning paradigm, has demonstrated significant potential in privacy-sensitive domains such as medical diagnosis and intelligent IoT systems by adhering to the “Data Immobility and Model Mobility” principle. However, the prevalence of non-IID data in real-world applications presents critical challenges: global models often fail to adapt to diverse local data distributions, while purely local personalized models face data sparsity and isolated learning. Consequently, Personalized Federated Learning (PFL) has garnered increasing attention, aiming to provide client-specific models that maintain privacy.
Knowledge Distillation (KD) and Attention Mechanism (AM) have emerged as cornerstone techniques for addressing data heterogeneity and enhancing personalization effectiveness. Recent advancements span dynamic optimization and aggregation strategies leveraging Bayesian ensemble methods [1,2,3,4], attention-driven client selection [5], Transformer architectures [6,7], and instance-level optimization [8], all contributing to improved model adaptability. In the realm of KD, adversarial feature alignment [9] and spectral collaborative distillation [10] have enhanced generalization on heterogeneous datasets. Cross-domain frameworks—including hybrid healthcare models [11,12,13], edge caching [14], and mobile edge aggregation [15]—have facilitated real-world PFL deployment, while efficient training schemes [16] and standardized benchmarks [17] support rigorous evaluation. Despite these strides, persistent limitations remain in adapting to dynamic distributions, preserving privacy, and achieving multi-level collaborative optimization.
KD serves as a cornerstone for mitigating data heterogeneity by enabling knowledge transfer from global to local models [18,19]. However, existing KD-based methods face substantial challenges: First, many approaches risk privacy leakage by relying on public datasets (e.g., FedMD [20]) or uploading label information (e.g., FedGKT [21]), thus exposing sensitive data and undermining FL’s privacy-preserving principles. Second, most methods rely on static distillation strategies, assuming homogeneous and stable data sharing (e.g., FedDF [22]). In practice, however, local data distributions fluctuate significantly. This discrepancy results in feature misalignment, especially in non-IID environments, causing excessive distillation noise and a significant degradation in model performance. FedMD, for instance, assumes that global and local models can be aligned using public datasets, which introduces significant privacy concerns. When data distributions shift, the static distillation policy in FedMD causes misalignment between the global and local models, increasing distillation noise and reducing performance. Similarly, FedGKT relies on bidirectional distillation, but still depends on label sharing, leading to privacy concerns and misalignment in dynamic data environments.
In contrast, FedDF [22] employs soft labels to improve knowledge transfer. However, FedDF also assumes that the data distributions are homogeneous, which is unrealistic in most federated settings. The failure to accommodate heterogeneous data results in feature misalignment and ineffective distillation, further contributing to performance degradation in non-IID settings. Thus, the static distillation strategies in these methods are not adaptable to changing data distributions and lead to suboptimal performance.
AM enhances model adaptability through dynamic weighting, but it often addresses either client-side personalization or server-side aggregation in isolation. For example, FedAtt [23] employs a self-attention module on clients to bolster feature representation but lacks sufficient server-side aggregation optimization. FedAMP [24] clusters similar clients through attention message passing to promote personalization yet still relies on relatively static attention patterns that may struggle under severe non-IID heterogeneity. pFedHN [25] introduces Hypernetworks for parameter sharing, improving adaptability but encountering scalability issues. Additionally, frameworks like APFL [26], which rely on fixed model mixing, prove inadequate in highly heterogeneous environments and lack flexibility in accommodating varying client demands.
These methods, though significant, exhibit critical limitations, especially in managing both client-side personalization and server-side aggregation effectively. They may struggle with highly heterogeneous data distributions and diverse client behaviors, which can affect model robustness and adaptability in practical federated environments. FedAtt and FedAMP mainly focus on feature representation or client clustering but do not explicitly optimize server-side aggregation, while FedGKT and FedMD are constrained by their reliance on label sharing, raising privacy concerns.
Based on these shortcomings, pFedKA introduces a dual attention mechanism to overcome the limitations of both KD and AM. By utilizing cross-attention (CA) modules for feature alignment before distillation, pFedKA ensures better knowledge transfer even in the presence of data misalignment. This dynamic alignment allows for reduced distillation noise, particularly in non-IID environments, and ensures that knowledge transfer remains effective under heterogeneous client distributions. Furthermore, pFedKA incorporates a GRU-based aggregation strategy, which adjusts aggregation weights based on client data performance and historical states. The dual attention mechanism in pFedKA allows it to handle both client-side personalization and server-side aggregation simultaneously, overcoming the limitations of static attention and enabling adaptive aggregation across heterogeneous data. In addition, pFedKA is designed to be compatible with standard privacy-preserving mechanisms such as differentially private SGD [27] and secure aggregation [28]; in this work, we integrate DP-SGD as an instantiation to empirically assess the privacy–utility trade-off.
Based on these improvements, pFedKA provides the following contributions:
- (1)
- A dynamic KD framework employing CA modules and adaptive temperature coefficients to achieve feature alignment and noise suppression under non-IID data.
- (2)
- An adaptive aggregation strategy leveraging Gated Recurrent Unit (GRU) networks to exploit cross-round historical client metadata for dynamic weight assignment and improved robustness over static averaging.
- (3)
- A cross-level collaborative optimization scheme bridging client-side feature distillation with server-side dynamic aggregation, harmonizing global consistency with local personalization.
2. Related Work
The PFL approach based on KD and dual AM builds on foundational research across three key domains:
2.1. PFL
FL enables collaborative model training while preserving data privacy, yet global models often underperform for non-IID clients requiring personalization. FedAvg [29], which reduces communication by averaging parameters, struggles in highly heterogeneous environments due to its static aggregation rule. This limitation becomes even more pronounced when data distributions change over time, highlighting the need for more dynamic adaptation. FedProx [30] introduces regularization to align local and global models, yet its fixed regularization strength fails to handle shifts in local data distributions. Per-FedAvg [31], leveraging meta-learning, allows for faster personalization but still relies heavily on the global model, making it ineffective in highly diverse or sparse data scenarios.
In contrast, FedRep [32] separates shared and personalized layers to improve model adaptation but neglects feature misalignment, which can lead to misalignment between the global model and local features. FedMA [33] attempts to address this issue through neuron matching, but this approach introduces scalability problems as the number of clients increases. Ditto [34], which allows clients to maintain both global and personalized models, provides flexibility but incurs significant computational overhead, making it difficult to scale in real-world settings. FedCDA [35] introduces a cross-round aggregation approach to improve personalization by selecting models with minimal divergence, but relies on storing multiple historical models and assumes model homogeneity, limiting its flexibility. These methods, though significant, still struggle with feature misalignment, adaptability, and scalability in diverse environments.
2.2. PFL Based on KD
KD has long been a cornerstone for enabling knowledge transfer from global models to local models, especially in non-IID settings where feature spaces do not align. FedDF [22] aggregates client predictions as soft labels for global training, but its assumption of homogeneous data distributions leads to noisy aggregation and loss of personalization in heterogeneous environments. Similarly, FedMD [20] aligns client models using public datasets, which raises significant privacy concerns, as the reliance on label sharing exposes sensitive client data. FedGKT [21] enhances knowledge transfer through bidirectional distillation, yet still relies on label sharing, which compromises privacy and fails to address the dynamic nature of data distributions. These early methods often operate under static distillation policies, if client data distributions remain stable, which is rarely the case in real-world federated environments. This static nature leads to feature misalignment, excessive distillation noise, and performance degradation in non-IID settings.
Recent advancements have attempted to overcome these limitations. FedKT [36] introduces dynamic temperature adjustment based on each client’s data distribution, but is typically evaluated under relatively mild distribution shifts, limiting the evidence for its effectiveness in more challenging heterogeneous scenarios. FedDyn [37] addresses dynamic knowledge transfer by adjusting the strength of knowledge transfer, but this introduces scalability issues. CD2-pFed [38] applies cyclic distillation to improve feature alignment, yet it overlooks long-term knowledge evolution, causing suboptimal performance as data distributions drift. MH-pFLID [39] proposes a more efficient framework for heterogeneous PFL, but it still struggles with domain generalization, particularly in highly heterogeneous, non-IID settings.
Privacy remains a key challenge in federated distillation. FedRod [40] bridges generic and personalized federated learning via a two-loss, two-predictor framework, achieving strong global and personalized performance but without explicitly integrating formal privacy mechanisms. FedKADP [41] combines knowledge distillation with differential privacy and an adaptive feedback controller to mitigate membership inference attacks while maintaining high utility. KD3A [42] further explores privacy-preserving decentralized knowledge distillation for multi-source domain adaptation, distilling consensus knowledge from multiple source models while dynamically down-weighting malicious or irrelevant domains and significantly reducing communication cost. However, most DP-based distillation frameworks are evaluated in centralized or multi-source adaptation settings and typically do not simultaneously address client-level personalization, non-IID heterogeneity, and adaptive server-side aggregation in federated learning.
New approaches such as FedFomo [43] and FLUID [44] are making strides in improving privacy and distillation effectiveness. FedFomo allows clients to optimize aggregation weights without requiring prior knowledge of data distributions, enabling out-of-distribution personalization, a challenge for methods like pFedMe [45] and LG-FedAvg [46]. However, its reliance on local validation sets limits its applicability, and its first-order approximation for weight updates may not suffice in highly non-linear parameter spaces. FLUID, on the other hand, combines dynamic pruning with KD, allowing for model personalization in resource-constrained environments like maritime predictive maintenance. Yet, it does not integrate privacy-preserving mechanisms for logits transmission and lacks scalability analysis, limiting its broader applicability. Fed-DFA [47] provides a solution for heterogeneous model fusion by using adversarial distillation, optimizing models based on boundary perception. While it shows promise in non-IID environments, its high computational overhead, particularly from PGD-based boundary estimation, and the lack of theoretical convergence analysis, raise concerns regarding its robustness in large-scale, dynamic federated settings.
While these methods have made progress, they still face challenges related to privacy, scalability, and adapting to long-term data drift. These limitations suggest that while KD-based methods have advanced PFL, there is still a need for more flexible and privacy-preserving approaches.
2.3. PFL Based on AM
AM has been widely adopted in PFL for enhancing feature selection, aggregation, and alignment between global and local models. Despite its successes, existing AM-based methods face several limitations, particularly in addressing evolving data distributions and ensuring a balanced approach to both client-side personalization and server-side aggregation. For example, FedAtt [23] utilizes self-attention on the client side to improve feature representation, leading to better personalization. However, its static per-round weighting does not explicitly incorporate client metadata or historical behavior, which may limit its adaptability under strong non-IID heterogeneity and complex client dynamics. FedAMP [24] addresses this by using an attention-based message passing mechanism to cluster similar clients, but it still struggles with local feature alignment in highly heterogeneous environments. Both approaches lack explicit mechanisms to exploit cross-round historical information in aggregation, which can hinder robust adaptation under challenging client heterogeneity. Similarly, while FedRoD [40] improves personalization by introducing dynamic sub-model selection, it is still limited by its memoryless aggregation strategy, which fails to adapt to long-term changes in client data. pFedHN [25] employs hypernetworks for parameter sharing, which enhances adaptability but at the cost of increased computational complexity and architectural overhead.
These existing AM-based methods struggle with feature misalignment, data distribution shifts, and long-term data dependencies. They remain largely ineffective in dynamic, heterogeneous environments where client data continuously evolves. This emphasizes the need for more robust solutions that can simultaneously address these issues of feature misalignment, aggregation, and long-term adaptation in a scalable manner.
3. pFedKA
To ensure consistency, a global notation table is defined in Table 1, which is presented above the main text. Figure 1. illustrates the overall framework of pFedKA, whose core process is divided into the following three phases:

Table 1.
Notation Table.
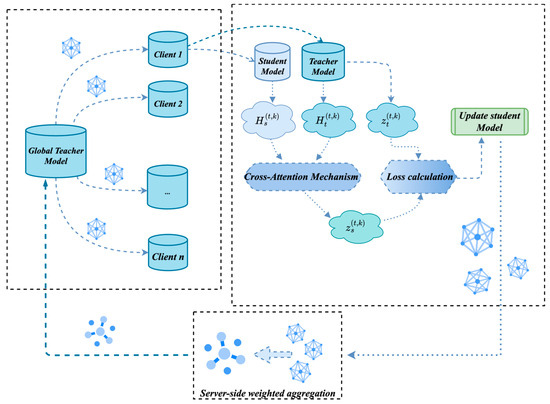
Figure 1.
pFedKA overview: (left) the global teacher model is broadcast to allocated clients, (right) clients perform local training with cross-attention and loss calculation, and (bottom) the server aggregates updated client models to form the new global model.
- (1)
- Global model distribution: the server sends the current global teacher model down to the client collection.
- (2)
- Client local training phase: each client initializes the student model on local data and optimizes it via CA-based feature alignment between teacher and student, combined with a dynamic distillation loss.
- (3)
- Server-side global aggregation phase: the server dynamically assigns weights to clients based on the gated attention network, and weightily aggregates local model parameters to update the global teacher model.
3.1. Problem Formulation
The core challenge in FL lies in reconciling the global model’s consistency with the local model’s personalization requirements while preserving data privacy. Given clients, each client holds a local dataset , drawn from a potentially non-IID distribution , which may deviate significantly from the global distribution . Traditional FL optimizes the global model parameters by minimizing the weighted empirical risk:
While effective under near-IID conditions, a single global model often underperforms on heterogeneous clients, yielding weak personalization.
To address this, PFL equips each client with a local model and augments the objective with a proximity term:
Here, measures the discrepancy between the local and global models—typically instantiated as an proximity (e.g., ) to encourage personalization while keeping the local solution close to the global one; however, a fixed cannot adapt across rounds or across clients, and the feature-space mismatch between and under non-IID data further hinders effective knowledge transfer.
To tackle these challenges, pFedKA proposes a dual-attention-driven framework that integrates KD and AM, replacing the fixed with dynamic, client-specific coefficients each round: a KD weight and a temperature . The round- objective is:
where the CA-guided distillation loss is:
Temperature softening rescales logit gaps and shrinks gradients by roughly in standard KD; multiplying by compensates for this shrinkage so the KD term remains on a comparable scale to . This follows common KD practice and avoids the KD term vanishing at higher temperatures.
For stability, the adaptive temperature is kept small in practice and numerically clipped to the open interval :
We use a narrow, upper-bounded window to provide moderate smoothing that empirically stabilizes KD on clients without over-flattening soft targets. This design is orthogonal to simulated annealing and is chosen for KD stability on heterogeneous data.
The dynamic KD weight balances local fitting and global guidance. To avoid circularity, it depends on the previous-round CE:
We bound the adaptive KD weight using the client’s sample proportion , preserving the original design and avoiding extra hyperparameters: larger clients are allowed a higher admissible KD influence, while smaller clients remain more regularized; this choice keeps scale-free and aligns the weighting with client representativeness.
And we map the KD/CE trade-off to with a boundary-consistent rule:
Thus , and as the KD term dominates, . where is a small constant (e.g., ) to ensure numerical stability. The in Equation (7) compresses extreme CE values, yielding smoother, numerically stable bounds so that neither CE nor KD can dominate.
3.2. Algorithm
The pFedKA algorithm coordinates client-side personalization and server-side aggregation, as illustrated in Figure 2a (dynamic, on-device distillation with cross-attention) and Figure 2b (GRU-based, adaptive aggregation on the server). Each round alternates between local updates on a sampled client subset and a server update of the global teacher , refining both and client students . By integrating CA with dynamic coefficients and (Section 3.1), and GRU-gated aggregation on the server, pFedKA addresses the static regularization and feature-mismatch limitations identified earlier.
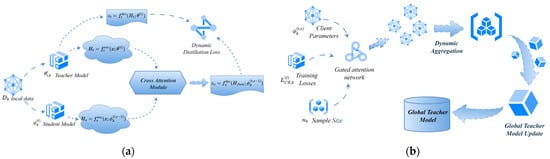
Figure 2.
Application of KD and Dual AM in pFedKA. (a) Client-Side Dynamic Distillation Process. (b) Server-Side Dynamic Aggregation Process.
The pFedKA procedure alternates client-side dynamic distillation (Figure 2a) and server-side GRU-gated aggregation Figure 2b. At round , the server broadcasts the global teacher to a sampled client subset . Each selected client initializes its student , then runs local training with CA–guided knowledge adaptation as follows. For an input mini-batch , the teacher and student encoders produce hidden maps via the original notation and :
To mitigate feature-space mismatch, CA aligns with . Using the original projections , , and key dimension :
Student features reflect local semantics; using them as queries lets the student “pull” only the relevant global components from the teacher’s bank (as keys/values). This asymmetry is intentional: it prevents forcing the teacher to attend to local idiosyncrasies, and instead projects global knowledge onto local needs, directly addressing the feature misalignment concern.
The fused representation is decoded by the student:
The teacher’s logits are generated by the global model on the same input and serve as soft targets for KD, while the student logits are the client’s local predictions based on the CA–aligned representation .
And the client minimizes the round- objective (consistent with Section 3.1):
The local update for epoch is:
where is the client-side learning rate and denotes the gradient with respect to. the student parameters . After local training, client uploads only , its sample size , and a scalar loss summary . No intermediate features or logits are transmitted, addressing the privacy-leakage concern raised for KD methods.
On the server, a compact per-client summary vector is constructed internally (e.g., ) and fed, with the previous hidden state , into a shared GRU with parameters :
which are normalized to attention weights:
The global teacher is then updated by weighted model averaging:
Finally, is broadcast for the next round, combining client-side alignment and on-device distillation with server-side history-aware weighting.
3.3. Generalization Analysis
We adopt established learning-theoretic results and specialize them to pFedKA without altering the training or communication protocol. For client with samples, augmenting its empirical risk with the KD penalty (Equation (4)) yields the following standard, temperature-scaled decomposition (cf. KD analyses and classical generalization bounds, e.g., [19], FedAvg/FedProx aggregation arguments [29,30]):
Averaging (Equation (18)) across clients with weights —as in standard federated averaging analyses [29,30]—gives the global form:
Equations (18) and (19) state that pFedKA’s improvement arises from reducing the KD term via CA feature alignment and stabilizing the student/teacher distributional gap with the adaptive temperature , while preserving the same capacity/concentration scaling as FedAvg/FedProx. Random client sampling with m participants per round retains the same order with the empirical terms concentrating as m grows [3,29].
The pFedKA algorithm is summarized in Algorithm 1, which outlines the iterative process of client-side training and server-side aggregation.
| Algorithm 1 pFedKA |
| . |
| do |
| ; |
| in parallel do |
| do |
| end for |
3.4. Convergence Analysis
We adopt standard FedAvg-family convergence results under nonconvex smooth objectives with partial participation and bounded heterogeneity (e.g., [3,29,30]). Let
Assume is -smooth:
and client-gradient divergence is bounded:
With clients sampled per round and local steps of step-size , canonical analyses yield.
where bounds stochastic gradient variance. pFedKA inherits (Equation (23)), because its local objective (Equation (13)) remains smooth and the protocol matches FedAvg. Moreover, CA (Equation (11)) and temperature-controlled KD (Equation (5)) reduce residual misalignment and prediction discrepancy—i.e., the effective constant multiplying improves—while the GRU produces nonnegative summing to one (Equation (16)), yielding convex combinations of client updates that do not worsen the variance term and, in practice, concentrate on more representative updates. Consequently, the round-averaged expected gradient norm decays at the standard FedAvg-family rate:
with improved constants when alignment and distillation reduce drift—matching the empirical behavior in Section 4 and consistent with proven rates for adaptive federated optimization under heterogeneity, while retaining the communication and privacy posture of FedAvg [29].
4. Experiment
4.1. Experiment Setup and Datasets
To comprehensively evaluate the generalization and personalization capability of pFedKA under heterogeneous federated scenarios, we conduct experiments on three widely used public datasets: Shakespeare for character-level language modelling, and CIFAR-10/100 [48] for visual classification. Shakespeare [49] contains roughly 1.2 million characters extracted from plays and poems; we follow the standard preprocessing in TensorFlow Federated to convert the text into 80-character subsequences and build a 90-character vocabulary. The corpus is naturally divided into 100 clients by treating each speaking role as a user, yielding consecutive yet non-overlapping text segments that preserve the temporal correlation and vocabulary bias across clients.
For CIFAR-10 and CIFAR-100, we simulate statistical heterogeneity by partitioning the training set into 100 clients using a symmetric Dirichlet distribution with concentration parameter . Specifically, for each class we draw a 100-dimensional Dirichlet vector and assign the corresponding fraction of class samples to each client. We adopt to produce highly skewed label distributions and for moderate heterogeneity; the same strategy is applied to both CIFAR-10 and CIFAR-100, giving a total of four image-based non-IID scenarios. All clients use a fixed batch size of 20, perform 5 local epochs per communication round, and the entire federation runs for 1000 rounds with a constant learning rate . For image tasks we instantiate a ResNet-18 [50] backbone, while for Shakespeare we employ a 2-layer LSTM [51] with 256 hidden units and an 80-dimensional character embedding. No public data, label leakage or server-side proxy datasets are involved, ensuring a strict FL protocol.
4.2. Baseline Methods
In this study, seven representative personalized federated-learning approaches are employed as baselines: FedAvg [29], FedProx [30], Ditto [34], FedRep [32], FedAvgFT [52], Flow [8] and FedCDA [35]. FedAvg and FedProx serve as canonical global and proximal-regularized FL methods, highlighting the gap between standard aggregation and personalized optimization under non-IID data. Ditto and FedRep represent parameter-decoupling and multi-task style personalization, where each client learns a customized local head or objective on top of a shared representation. FedAvgFT reflects a simple yet competitive two-stage strategy that first learns a global model and then performs local fine-tuning. Flow introduces dynamic per-instance routing to better adapt to client heterogeneity, while FedCDA performs cross-round divergence-aware aggregation and thus represents a recent class of adaptive aggregation schemes. Together, these methods span parameter regularization, multi-task personalization, dynamic routing, and adaptive aggregation, providing a comprehensive spectrum for evaluating pFedKA. All experiments adhere to the unified protocol and hyperparameter settings detailed in Section 4.1.
4.3. Experimental Results
The experimental results demonstrate that pFedKA achieves superior personalization accuracy compared to baseline methods across CIFAR-10, CIFAR-100, and Shakespeare (see Figure 3). Detailed comparisons in Table 2 highlight its advantages across diverse tasks and heterogeneity settings.
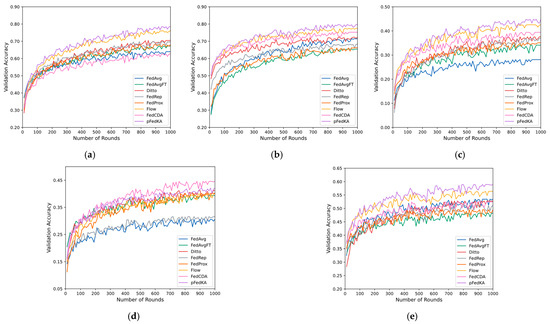
Figure 3.
Learning Curves of pFedKA and Baselines. (a) CIFAR-10 ; (b) CIFAR-10 ; (c) CIFAR-100 ; (d) CIFAR-100 ; (e) Shakespeare.

Table 2.
Personalized Accuracy Comparison with 7 Baseline Methods across Different Datasets.
On CIFAR-10, pFedKA demonstrates significantly faster convergence than all baseline methods under both high and moderate heterogeneity, highlighting its robust adaptability to varying data distributions. On CIFAR-100 with high heterogeneity, pFedKA achieves an accuracy of 44.78%, outperforming all competing methods by a notable margin. However, when the heterogeneity is moderate, FedCDA attains 44.57% while pFedKA achieves 42.11%. In this mild-heterogeneity regime, FedCDA’s cross-round divergence-aware aggregation simply selects historical models whose parameters are closest to the current global state, effectively acting as a lightweight denoiser that proves sufficient when client distributions are already well-aligned and consistent. In contrast, pFedKA’s client-side component alignment and dynamic temperature introduce additional optimization variables, which can potentially be overfit to local fluctuations and thus marginally dilute the global signal. This outlier case exposes a practical limitation: the dual-attention mechanism in pFedKA may become over-parameterized and less effective when heterogeneity is weak, suggesting that future work should explore heterogeneity-aware gating mechanisms to adaptively control model complexity.
For the Shakespeare dataset, pFedKA attains an accuracy of 58.92%, clearly outperforming Flow (56.36%) and exceeding FedAvg by more than 5%. This result demonstrates that the dual-attention design of pFedKA is particularly effective at capturing long-range sequential dependencies, outperforming both static aggregation strategies and pure local fine-tuning approaches.
For training loss, as presented in Figure 4, pFedKA demonstrates consistent reduction across all datasets. On CIFAR-10 with high heterogeneity, pFedKA’s loss decreases steadily from 0.3122 to 0.2238 over 1000 rounds, compared to higher final losses for FedAvg, FedAvgFT, Ditto, FedRep, FedProx, and Flow; notably, FedCDA descends even faster (0.9142 → 0.1580) but exhibits occasional jumps due to historical-model reuse. The smoother loss curve of pFedKA may result from its KD, which enhances feature alignment between the teacher and student models, and reduces variance in comparison to FedAvg’s basic averaging or FedAvgFT’s fine-tuning. On CIFAR-10 with moderate heterogeneity, pFedKA’s loss drops from 0.5023 to 0.2062, lower than the baselines, possibly due to its gated attention, which stabilizes convergence compared to the proximal term in FedProx or the dynamic adjustments in Flow. On CIFAR-100 with high heterogeneity, pFedKA achieves a loss of 0.3922, compared to higher losses observed in other baseline methods; FedCDA initially descends faster but rises around round 500 and ends at 0.2851, slightly above pFedKA’s 0.3922, indicating that its divergence-aware reuse can occasionally inject stale information under severe skew. On CIFAR-100 with moderate heterogeneity, FedCDA again converges fastest and reaches the lowest terminal loss (0.2427), outperforming pFedKA (0.3416), as its historical-model selection acts as an efficient denoiser when client distributions are already well-aligned. For Shakespeare, pFedKA’s loss declines from 0.3697 to 0.2791, compared to higher losses for FedAvg, FedAvgFT, Ditto, FedRep, FedProx, and Flow, while FedCDA records the steepest descent but occasional spikes. The consistent loss reduction across datasets suggests that pFedKA’s combination of cross-entropy optimization, KD, and AM mitigates data heterogeneity challenges, while baseline methods exhibit higher variance.
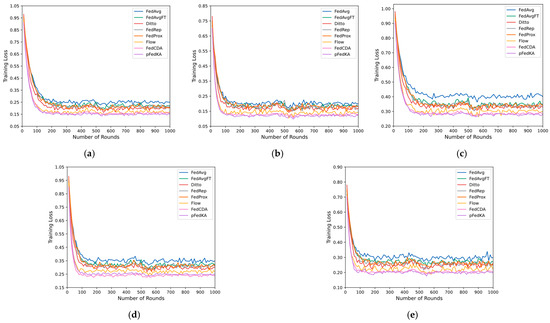
Figure 4.
Loss Curves of pFedKA and Baselines. (a) CIFAR-10 ; (b) CIFAR-10 ; (c) CIFAR-100 ; (d) CIFAR-100 ; (e) Shakespeare.
4.4. Ablation Experiments
We evaluate the contribution of each core component in pFedKA—knowledge distillation (KD), cross-attention (CA), and gated attention (GA)—by ablating them one at a time under identical data partitions, communication rounds, and hyperparameters. Concretely, the w/o KD, w/o CA, and w/o GA variants respectively remove the KD loss, the CA alignment module, and the GRU-based gated aggregation (the latter replaced by static FedAvg aggregation), while keeping all other settings unchanged. This design isolates the effect of each component and allows us to examine not only their individual benefits but also how they interact to stabilize training and improve personalization.
Results on CIFAR-10/100 under high and moderate heterogeneity and on Shakespeare are summarized in Table 3 (Accuracy) and visualized in Figure 5 for clearer comparison across variants.

Table 3.
Ablation Experiment Results.
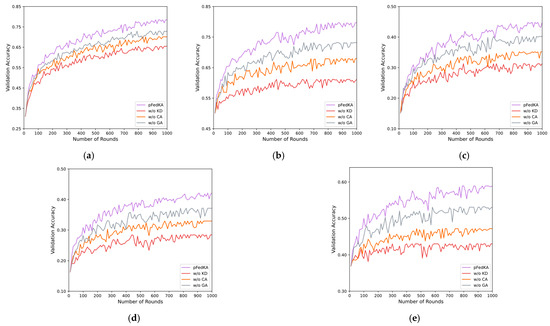
Figure 5.
Ablation Experiment Comparison. (a) CIFAR-10 ; (b) CIFAR-10 ; (c) CIFAR-100 ; (d) CIFAR-100 ; (e) Shakespeare.
Across all datasets, pFedKA consistently outperforms its ablations: removing KD produces the largest degradation, especially in high heterogeneity and on Shakespeare, confirming that KL-guided transfer of global knowledge is central for personalization under distribution shift. Removing CA also hurts markedly—most notably on CIFAR-100—indicating that feature-space alignment before decoding is important for fine-grained recognition with non-IID feature drift. Removing GA yields a steady drop (smaller than KD/CA removal), showing that history-aware, data-aware weighting based on client metadata improves robustness over static averaging. These components are complementary: KD provides a transferable soft-target prior, CA aligns global and local representations to reduce mismatch, and GA adaptively emphasizes stable, representative clients across rounds; their synergy explains the performance gap between pFedKA and any single ablation.
To complement accuracy and reflect per-class behavior under non-IID partitions, we report macro-averaged F1 (Macro-F1) to reflect per-class performance. For a -class, single-label task, we compute a per-class one-vs-rest F1 score and then average across classes:
The formulas for precision and recall are as follows:
Table 4 exhibits the same ordering and comparable gaps, reinforcing that each component yields non-redundant gains. KD contributes the largest share of improvement (e.g., CIFAR-100-High Macro-F1: 41.98 → 25.32 when removed), highlighting the necessity of shrinking the teacher–student KL under severe heterogeneity; CA provides the next most substantial gain (e.g., CIFAR-100-High: 41.98 → 27.57), consistent with mitigating feature misalignment prior to decoding; GA offers steady improvements (e.g., CIFAR-10-Moderate: 78.67 → 71.08), reflecting the benefit of history-aware, data-aware weighting that suppresses noisy or outlier updates. Interactions among components are also evident: with KD present, CA aligns richer soft-target structure into the local feature space; with CA present, GA more reliably emphasizes clients whose updates are stable and representative; when KD or CA is absent, the effectiveness of GA diminishes toward static averaging.

Table 4.
Macro-F1.
The ablation results show that pFedKA’s performance gains stem from three complementary components: (i) KD enables knowledge transfer and improves generalization across heterogeneous clients; (ii) CA aligns feature spaces to reduce non-IID drift; and (iii) GA provides history-aware, data-aware aggregation for more stable cross-round learning. KD accounts for the largest improvement, CA adds significant gains—especially on fine-grained tasks—and GA further refines aggregation. Their combined effect surpasses any single component, confirming both their individual and synergistic contributions.
4.5. Communication Overhead & Privacy Verification
4.5.1. Analysis of Communication Overhead
To quantify the bandwidth cost incurred by the CA module and the GRU-based aggregator, we record the exact payload exchanged between the server and ten randomly sampled clients during the first 100 communication rounds of CIFAR-10 training under Dirichlet heterogeneity . Each round begins with the server broadcasting the current global teacher to every selected client; the client then performs five epochs of CA-guided distillation and uploads its updated student together with two scalars (sample count and last-epoch cross-entropy ). No feature maps, gradients or logits are transmitted at any stage, so the uplink volume is identical to that of FedAvg, while the downlink carries one additional full model copy required by the distillation paradigm. Traffic is captured transparently via tcpdump, aggregated over three independent runs and reported with 95% bootstrap confidence intervals.
Table 5 summarizes communication volumes. All baselines transmit at least one model per round; methods with auxiliary variables or historical models increase traffic. FedAvg and FedProx exchange one model per direction (30.82 MB). Flow adds a small routing vector (0.07 MB), totaling 30.91 MB. FedCDA uploads an extra 128-bit digest per client (30.87 MB). pFedKA transmits 33.47 MB per round—an 8.61% increase—leading to 3.35 GB after 100 rounds and 33.47 GB after 1000 rounds. This ratio remains unchanged for CIFAR-100 and Shakespeare, as payload size is independent of label or vocabulary size.

Table 5.
Average communication volume (CIFAR-10, ).
Thus, the dual-attention design improves absolute accuracy on CIFAR-10 from 63.98% (FedAvg) to 78.45%a lift of 14.7%—while increasing the total traffic after 1000 rounds by only 8.61%. On CIFAR-10 (, 100 clients, 5 local epochs, batch 20), per-round iteration time on one RTX 3080 is 4.37 s for pFedKA vs. 3.98 s for FedAvg (+9.8%), negligible against the +8.6% traffic and +14.7% accuracy gain. The extra volume is constant per round and scales linearly with model size rather than client count, so the same ratio applies to cross-device federations with thousands of participants. It should be noted that the present analysis accounts only for payload bytes; wall-clock time per round, local FLOP overhead of the CA module, and server-side GRU latency were not measured. A full run-time profile will be included in future work. We therefore conclude that pFedKA achieves substantial personalization gains at a communication cost that remains negligible in practice.
4.5.2. Privacy Verification Mechanisms
We evaluate pFedKA under client-level -DP [53] with by integrating DP-SGD [27]. Gradients are clipped to unit norm and Gaussian noise is injected before the CA distillation step; no features or logits are transmitted. Each privacy setting is executed once with a fixed random seed, and the final personalized accuracy after 1000 rounds is reported in Table 6.

Table 6.
Privacy–utility trade-off under -DP after 1000 rounds.
Without noise pFedKA achieves 78.45% on CIFAR-10 and 44.78% on CIFAR-100, while FedAvg obtains 63.98% and 28.11%. At the privacy budget is for FedAvg and for pFedKA; the accuracy drop is markedly smaller for our method (0.31% vs. 2.12% on CIFAR-10). ( for FedAvg, for pFedKA) pFedKA still outperforms FedAvg by 48.9% on CIFAR-10 and 16.4% on CIFAR-100, confirming that the CA-guided alignment reduces effective gradient variance and thus requires less noise for the same privacy budget. We conclude that pFedKA maintains its accuracy advantage even under stringent differential privacy.
5. Conclusions and Future Work
In summary, pFedKA effectively balances global consistency and local personalization through knowledge distillation and dual-attention design. The client-side CA module aligns global and local features to address non-IID data challenges, while the server-side GRU-based gated aggregator dynamically adjusts client updates using metadata such as losses and sample counts. By leveraging historical information across rounds, this approach adapts the aggregation strategy to client-specific behavior and performance, providing more stability in federated learning. Experimental results show that pFedKA achieves superior convergence speed, training stability, and personalization accuracy compared to existing methods, making it a promising solution for federated learning under data heterogeneity. Furthermore, pFedKA provides strong privacy guarantees via DP-SGD integration, maintaining or even improving personalization accuracy compared to FedAvg.
Despite these advantages, pFedKA faces some limitations. The introduction of additional modules increases computational and memory overhead for both clients and servers, and maintaining the GRU’s historical state over many communication rounds requires extra resources. Additionally, the communication cost per round may rise slightly, though the overhead remains modest. Our experiments did not cover highly skewed data distributions or dynamic client participation, leaving these areas unverified and suggesting a key direction for future work.
Future work will focus on addressing these limitations, including exploring additional privacy mechanisms like secure aggregation to further safeguard client data. We also plan to evaluate pFedKA on larger, more diverse datasets, as well as under dynamic federated settings (e.g., time-varying client data or changing client membership), to validate its robustness and scalability in real-world applications.
Author Contributions
Conceptualization, Y.J. and K.Z.; methodology, Y.J. and K.Z.; software, Y.J.; validation, Y.J. and L.Z.; formal analysis, K.Z.; investigation, L.Z.; resources, C.M.; data curation, Y.J.; writing—original draft preparation, Y.J. and X.C.; writing—review and editing, K.Z., C.M. and H.Z.; visualization, X.C.; supervision, K.Z.; project administration, C.M.; funding acquisition, C.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 62172123) and the Key Research and Development Program of Heilongjiang (Grant No. 2022ZX01A36).
Data Availability Statement
This article encompasses the original contributions proposed in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, H.Y.; Chao, W.L. Fedbe: Making bayesian model ensemble applicable to federated learning. arXiv 2020, arXiv:2009.01974. [Google Scholar]
- Karimireddy, S.P.; Kale, S.; Mohri, M.; Reddi, S.; Stich, S.; Suresh, A.T. Scaffold: Stochastic controlled averaging for federated learning. In Proceedings of the 37th International Conference on Machine Learning (ICML 2020), Vienna, Austria, 12–18 July 2020; pp. 5132–5143. [Google Scholar]
- Reddi, S.; Charles, Z.; Zaheer, M.; Garrett, Z.; Rush, K.; Konečný, J.; Kumar, S.; McMahan, B. Adaptive federated optimization. arXiv 2020, arXiv:2003.00295. [Google Scholar]
- Jiang, Z.; Xu, J.; Zhang, S.; Shen, T.; Li, J.; Kuang, K.; Cai, H.; Wu, F. FedCFA: Alleviating Simpson’s Paradox in Model Aggregation with Counterfactual Federated Learning. arXiv 2024, arXiv:2412.18904. [Google Scholar] [CrossRef]
- Chen, Z.; Li, J.; Shen, C. Personalized Federated Learning with Attention-Based Client Selection. In Proceedings of the 2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 6930–6934. [Google Scholar]
- Li, H.; Cai, Z.; Wang, J.; Tang, J.; Ding, W.; Lin, C.-T.; Shi, Y. FedTP: Federated Learning by Transformer Personalization. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 13426–13440. [Google Scholar] [CrossRef]
- Marfoq, O.; Neglia, G.; Vidal, R.; Kameni, L. Personalized federated learning through local memorization. In Proceedings of the 39th International Conference on Machine Learning, PMLR 2022, Baltimore, MD, USA, 17–23 July 2022; pp. 15070–15092. [Google Scholar]
- Panchal, K.; Choudhary, S.; Parikh, N.; Zhang, L.; Guan, H. Flow: Per-instance personalized federated learning. In Proceedings of the Advances in Neural Information Processing Systems 36 (NeurIPS 2023), New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Yang, Z.; Zhang, Y.; Zheng, Y.; Tian, X.; Peng, H.; Liu, T.; Han, B. FedFed: Feature distillation against dataheterogeneity in federated learning. In Proceedings of the Advances in Neural Information Processing Systems 36 (NeurIPS 2023), New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Chen, Z.; Yang, H.H.; Quek, T.; Chong, K.F.E. Spectral co-distillation for personalized federated learning. In Proceedings of the Advances in Neural Information Processing Systems 36 (NeurIPS 2023), New Orleans, LA, USA, 10–16 December 2023; pp. 8757–8773. [Google Scholar]
- Zhao, Y.; Liu, Q.; Liu, P.; Liu, X.; He, K. Medical Federated Model With Mixture of Personalized and Shared Components. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 47, 433–449. [Google Scholar] [CrossRef]
- Guo, T.; Guo, S.; Wang, J. Pfedprompt: Learning personalized prompt for vision-language models in federated learning. In Proceedings of the ACM Web Conference 2023, Austin, TX, USA, 30 April–4 May 2023; pp. 1364–1374. [Google Scholar]
- Wang, J.; Yang, X.; Cui, S.; Che, L.; Lyu, L.; Xu, D.; Ma, F. Towards personalized federated learning via heterogeneous model reassembly. In Proceedings of the Advances in Neural Information Processing Systems 36 (NeurIPS 2023), New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Wu, Z.; Sun, S.; Wang, Y.; Liu, M.; Xu, K.; Wang, W.; Jiang, X.; Gao, B.; Lu, J. FedCache: A Knowledge Cache-Driven Federated Learning Architecture for Personalized Edge Intelligence. IEEE Trans. Mob. Comput. 2024, 23, 9368–9382. [Google Scholar] [CrossRef]
- Deng, D.; Wu, X.; Zhang, T.; Tang, X.; Du, H.; Kang, J.; Liu, J.; Niyato, D. FedASA: A Personalized Federated Learning With Adaptive Model Aggregation for Heterogeneous Mobile Edge Computing. IEEE Trans. Mob. Comput. 2024, 23, 14787–14802. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, W.; Shi, Y.; Zhao, J. A robustly optimized BERT pre-training approach with post-training. In Proceedings of the 20th China National Conference on Chinese Computational Linguistics, Hohhot, China, 13–15 August 2021; Springer International Publishing: Cham, Switzerland, 2021; pp. 471–484. [Google Scholar]
- Touvron, H.; Cord, M.; Douze, M.; Massa, F.; Sablayrolles, A.; Jegou, H. Training data-efficient image transformers & distillation through attention. In Proceedings of the 38th International Conference on Machine Learning PMLR, Vienna, Austria, 18–24 July 2021; pp. 10347–10357. [Google Scholar]
- Hinton, G. Distilling the Knowledge in a Neural Network. arXiv 2015, arXiv:1503.02531. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, J. A Data-Free Personalized Federated Learning Algorithm Based on KD. Netinf. Secur. 2024, 24, 1562–1569. [Google Scholar]
- Li, D.; Wang, J. Fedmd: Heterogenous federated learning via model distillation. arXiv 2019, arXiv:1910.03581v1. [Google Scholar] [CrossRef]
- He, C.; Annavaram, M.; Avestimehr, S. Group knowledge transfer: Federated learning of large cnns at the edge. Adv. Neural Inf. Process. Syst. 2020, 33, 14068–14080. [Google Scholar]
- Lin, T.; Kong, L.; Stich, S.U.; Jaggi, M. Ensemble distillation for robust model fusion in federated learning. Adv. Neural Inf. Process. Syst. 2020, 33, 2351–2363. [Google Scholar]
- Ji, S.; Pan, S.; Long, G.; Li, X.; Jiang, J.; Huang, Z. Learning private neural language modeling with attentive aggregation. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar]
- Huang, Y.; Chu, L.; Zhou, Z.; Wang, L.; Liu, J.; Pei, J.; Zhan, Y. Personalized cross-silo federated learning on non-iid data. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 2–9 February 2021; AAAI Press: Palo Alto, CA, USA; Volume 35, pp. 7865–7873. [Google Scholar]
- Shamsian, A.; Navon, A.; Fetaya, E.; Chechik, G. Personalized federated learning using hypernetworks. In Proceedings of the 38th International Conference on Machine Learning PMLR, Vienna, Austria, 18–24 July 2021; pp. 9489–9502. [Google Scholar]
- Deng, Y.; Kamani, M.M.; Mahdavi, M. Adaptive personalized federated learning. arXiv 2020, arXiv:2003.13461v3. [Google Scholar] [CrossRef]
- Abadi, M.; Chu, A.; Goodfellow, I.; McMahan, H.B.; Mironov, I.; Talwar, K.; Zhang, L. Deep learning with differential privacy. In Proceedings of the ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 308–318. [Google Scholar]
- Bonawitz, K.; Ivanov, V.; Kreuter, B.; Marcedone, A.; McMahan, H.B.; Patel, S.; Ramage, D.; Segal, A.; Seth, K. Practical secure aggregation for privacy-preserving machine learning. In Proceedings of the ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 1175–1191. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learningof deep networks from decentralized data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. In Proceedings of the Machine Learning and Systems 2 (MLSys 2020), Austin, TX, USA, 2–4 March 2020; Volume 2, pp. 429–450. [Google Scholar]
- Fallah, A.; Mokhtari, A.; Ozdaglar, A. Personalized federated learning: A meta-learning approach. arXiv 2020, arXiv:2002.07948. [Google Scholar] [CrossRef]
- Collins, L.; Hassani, H.; Mokhtari, A.; Shakkottai, S. Exploiting shared representations for personalized federated learning. In Proceedings of the 38th International Conference on Machine Learning PMLR, Vienna, Austria, 18–24 July 2021; pp. 2089–2099. [Google Scholar]
- Wang, H.; Yurochkin, M.; Sun, Y.; Papailiopoulos, D.; Khazaeni, Y. Federated learning with matched averaging. arXiv 2020, arXiv:2002.06440. [Google Scholar] [CrossRef]
- Li, T.; Hu, S.; Beirami, A.; Smith, V. Ditto: Fair and robust federated learning through personalization. In Proceedings of the 38th International Conference on Machine Learning PMLR, Vienna, Austria, 18–24 July 2021; pp. 6357–6368. [Google Scholar]
- Wang, H.; Xu, H.; Li, Y.; Xu, Y.; Li, R.; Zhang, T. Fedcda: Federated learning with cross-rounds divergence-aware aggregation. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Li, Q.; He, B.; Song, D. Practical One-Shot Federated Learning for Cross-Silo Setting. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 19–26 August 2021; pp. 1484–1490. [Google Scholar]
- Acar, D.A.E.; Zhao, Y.; Navarro, R.M.; Mattina, M.; Whatmough, P.N.; Saligrama, V. Federated learning based on dynamic regularization. In Proceedings of the 9th International Conference on Learning Representations, Vienna, Austria, 4–8 May 2021. [Google Scholar]
- Shen, Y.; Zhou, Y.; Yu, L. Cd2-pfed: Cyclic distillation-guided channel decoupling for model personalization in federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 21–24 June 2022; pp. 10041–10050. [Google Scholar]
- Xie, L.; Lin, M.; Luan, T.; Li, C.; Fang, Y.; Shen, Q.; Wu, Z. MH-pFLID: Model Heterogeneous personalized Federated Learning via Injection and Distillation for Medical Data Analysis. arXiv 2024, arXiv:2405.06822v1. [Google Scholar]
- Chen, H.Y.; Chao, W.L. On bridging generic and personalized federated learning for image classification. arXiv 2021, arXiv:2107.00778v2. [Google Scholar]
- Jiang, Y.; Zhao, X.; Li, H.; Xue, Y. A Personalized Federated Learning Method Based on Knowledge Distillation and Differential Privacy. Electronics 2024, 13, 3538. [Google Scholar] [CrossRef]
- Feng, H.-Z.; You, Z.; Chen, M.; Zhang, T.; Zhu, M.; Wu, F.; Wu, C.; Chen, W. KD3A: Unsupervised Multi-Source Decentralized Domain Adaptation via KD. ICML 2021, 4, 5. [Google Scholar]
- Zhang, M.; Sapra, K.; Fidler, S.; Yeung, S.; Alvarez, J.M. Personalized federated learning with first order model optimization. arXiv 2020, arXiv:2012.08565. [Google Scholar]
- Kalafatelis, A.S.; Pitsiakou, A.; Nomikos, N.; Tsoulakos, N.; Syriopoulos, T.; Trakadas, P. FLUID: Dynamic Model-Agnostic Federated Learning with Pruning and Knowledge Distillation for Maritime Predictive Maintenance. J. Mar. Sci. Eng. 2025, 13, 1569. [Google Scholar] [CrossRef]
- Dinh, C.T.; Tran, N.; Nguyen, J. Personalized federated learning with moreau envelopes. Adv. Neural Inf. Process. Syst. 2020, 33, 21394–21405. [Google Scholar]
- Liang, P.P.; Liu, T.; Ziyin, L.; Allen, N.B.; Auerbach, R.P.; Brent, D.; Salakhutdinov, R.; Morency, L.-P. Think locally, act globally: Federated learning with local and global representations. arXiv 2020, arXiv:2001.01523. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, F.; Wang, T.; Wang, C.; Shu, Y.; Cheng, P.; Chen, J. Fed-DFA: Federated distillation for heterogeneous model fusion through the adversarial lens. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; Volume 39, pp. 21429–21437. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Shakespeare. TensorFlow Federated Datasets. Available online: https://www.tensorflow.org/federated/api_docs/python/tff/simulation/datasets/shakespeare (accessed on 12 November 2024).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Graves, A. Supervised Sequence Labelling with Recurrent Neural Networks; Springer Nature: Durham, NC, USA, 2012; pp. 37–45. [Google Scholar]
- Collins, L.; Hassani, H.; Mokhtari, A.; Shakkottai, S. Fedavg with fine tuning: Local updates lead to representation learning. Adv. Neural Inf. Process. Syst. 2022, 35, 10572–10586. [Google Scholar]
- Dwork, C.; Roth, A. The Algorithmic Foundations of Differential Privacy. Found. Trends® Theor. Comput. Sci. 2013, 9, 211–407. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).