Machine Learning Models for Subsurface Pressure Prediction: A Data Mining Approach
Abstract
1. Introduction
2. Objectives
- The study performed a systematic integration and evaluation of a diverse set of ML methods including shallow as well as DL methods to capture complex, nonlinear relationships in geological datasets.
- The proposed study presents a scalable domain-aware data mining framework that fuses geoscientific knowledge with AI-based methods, advancing the field of subsurface prediction and contributing towards safe pore pressure prediction with improved accuracy and reduced risk of blowout.
- The proposed framework offers a transferable template for other geoscience challenges including porosity prediction, facies analysis, source rock maturity modeling, estimation of geothermal resource potential, carbon storage capacity evaluation and other such geoscience areas.
3. Materials and Methods
3.1. Machine Learning Algorithms
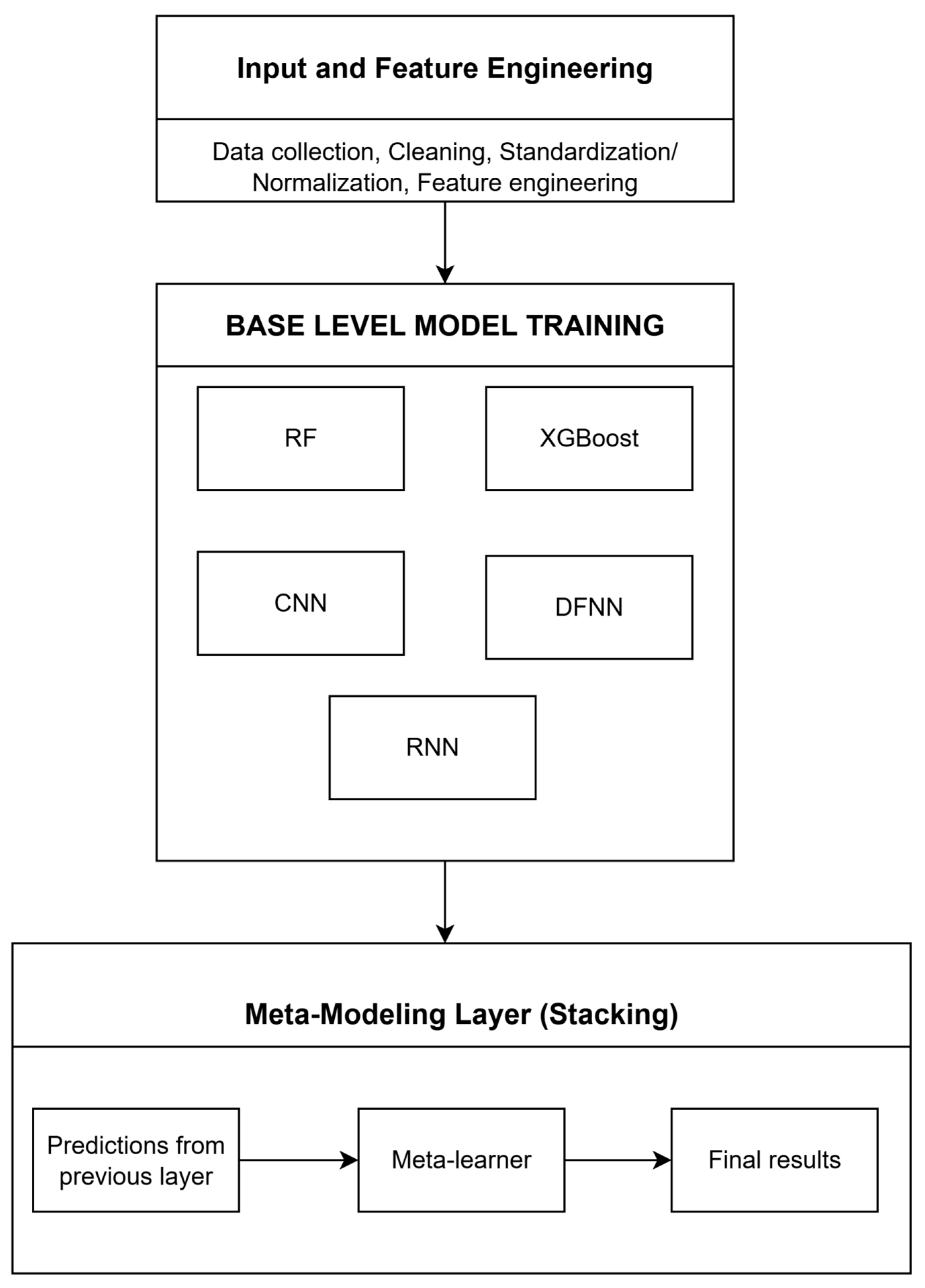
3.2. Proposed Hybrid Meta-Ensemble (HME) Framework
3.2.1. Data Preprocessing and Feature Engineering
3.2.2. Base-Level Model Training
3.2.3. Model Output Stacking
3.2.4. Meta Learner from Ensemble Integration
3.2.5. Evaluation and Generalizability
3.2.6. Domain Adaptation Through Controlled Fine-Tuning
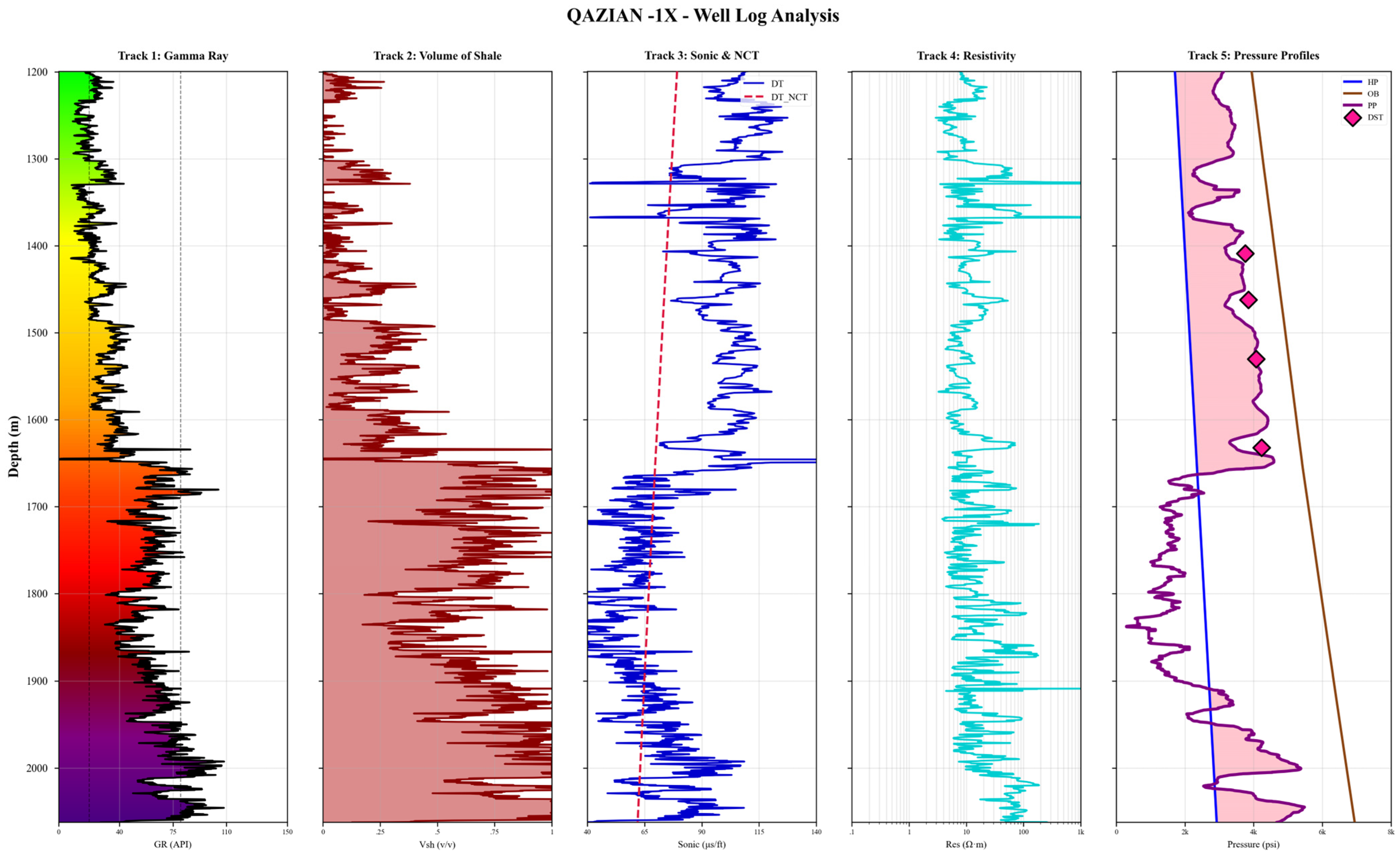
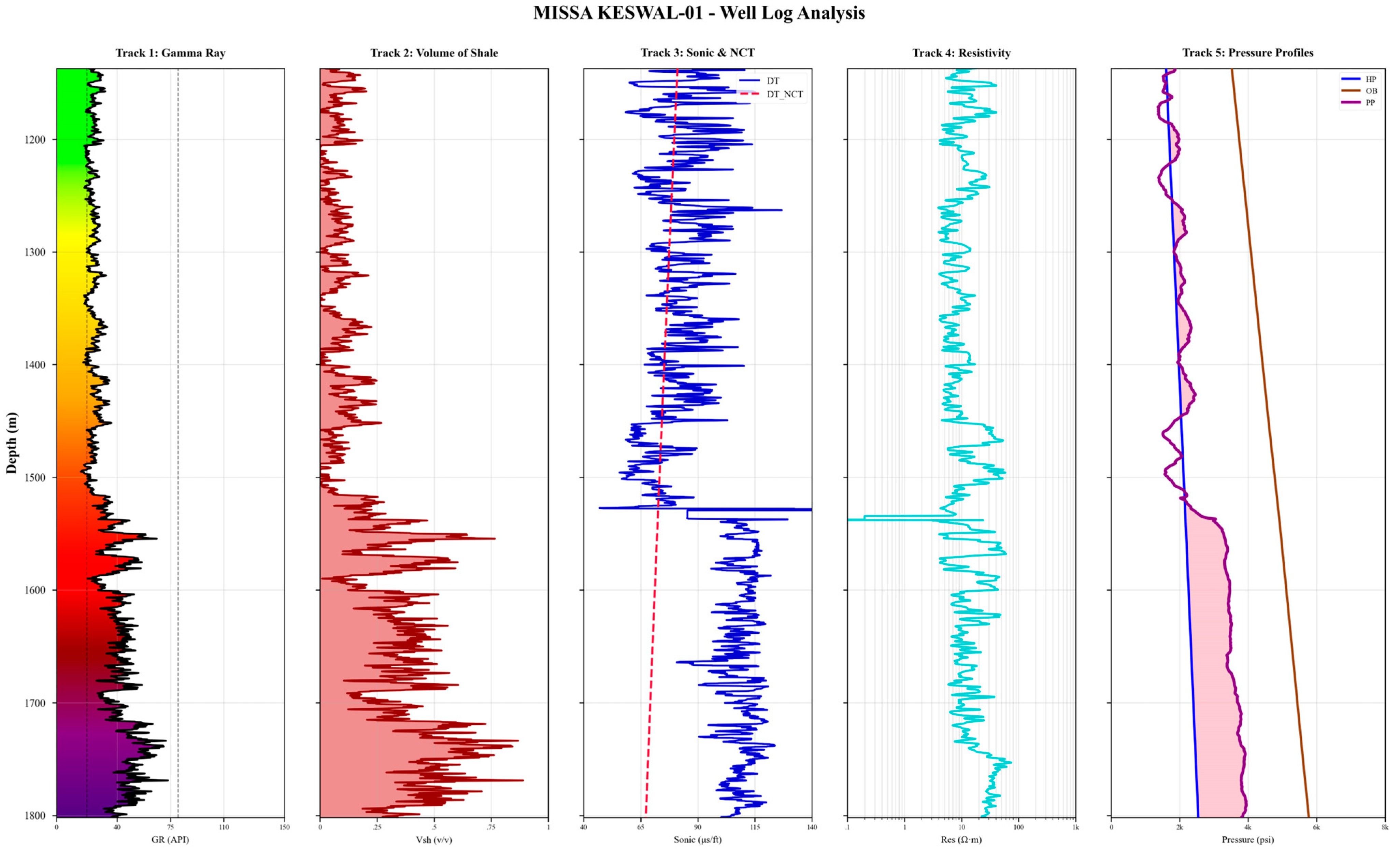
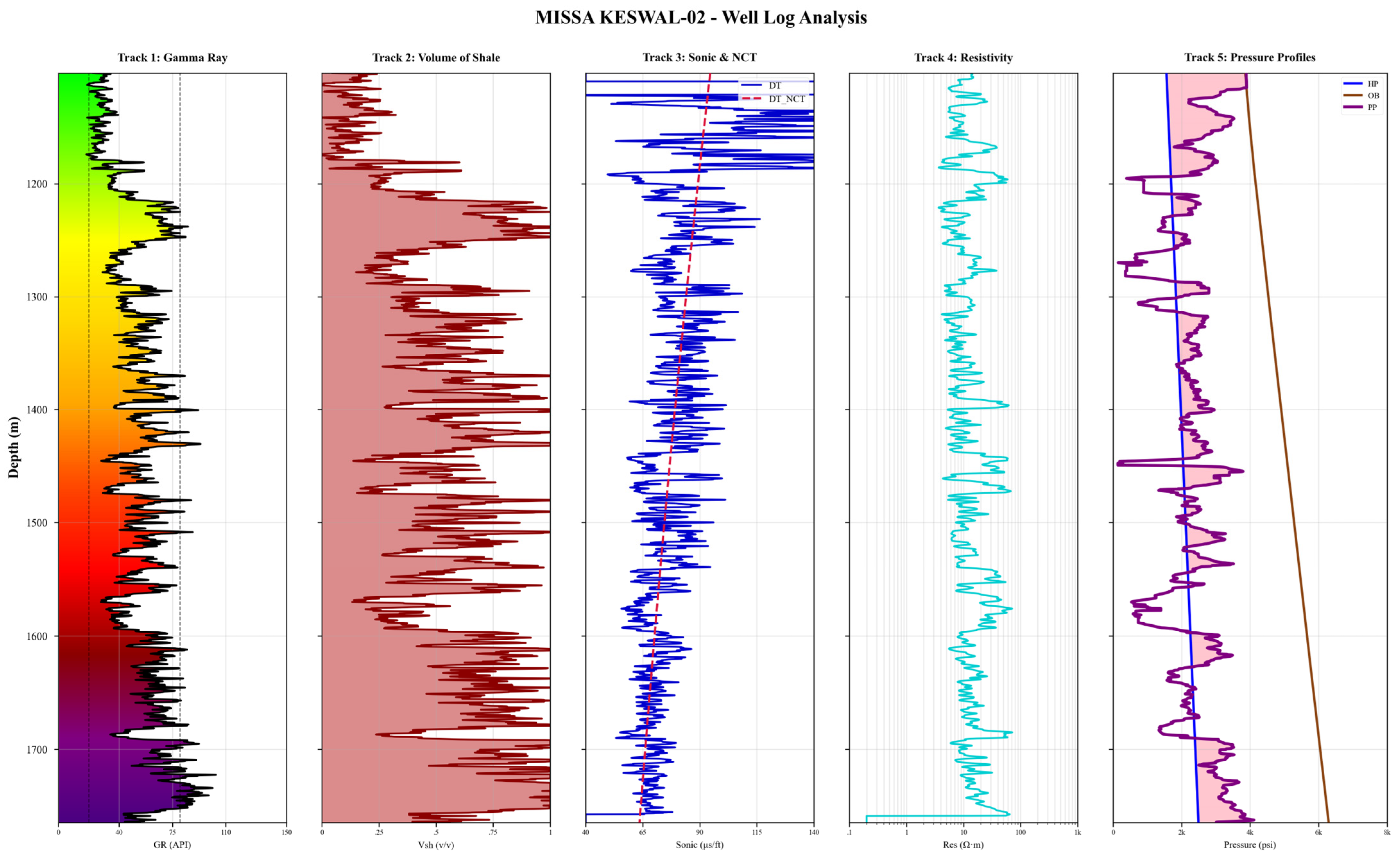
3.3. Well Logs Description
3.4. Performance Evaluation
3.4.1. Coefficient of Determination (R2)
3.4.2. Mean Absolute Error (MAE)
3.4.3. Root Mean Square Error (RMSE)
3.4.4. Relative Root Mean Square Error (RelRMSE)
4. Results
4.1. Base Models
4.1.1. Convolutional Neural Networks
4.1.2. Recurrent Neural Networks
4.1.3. Deep Feedforward Neural Networks
4.1.4. Random Forest
4.1.5. Extreme Gradient Boost
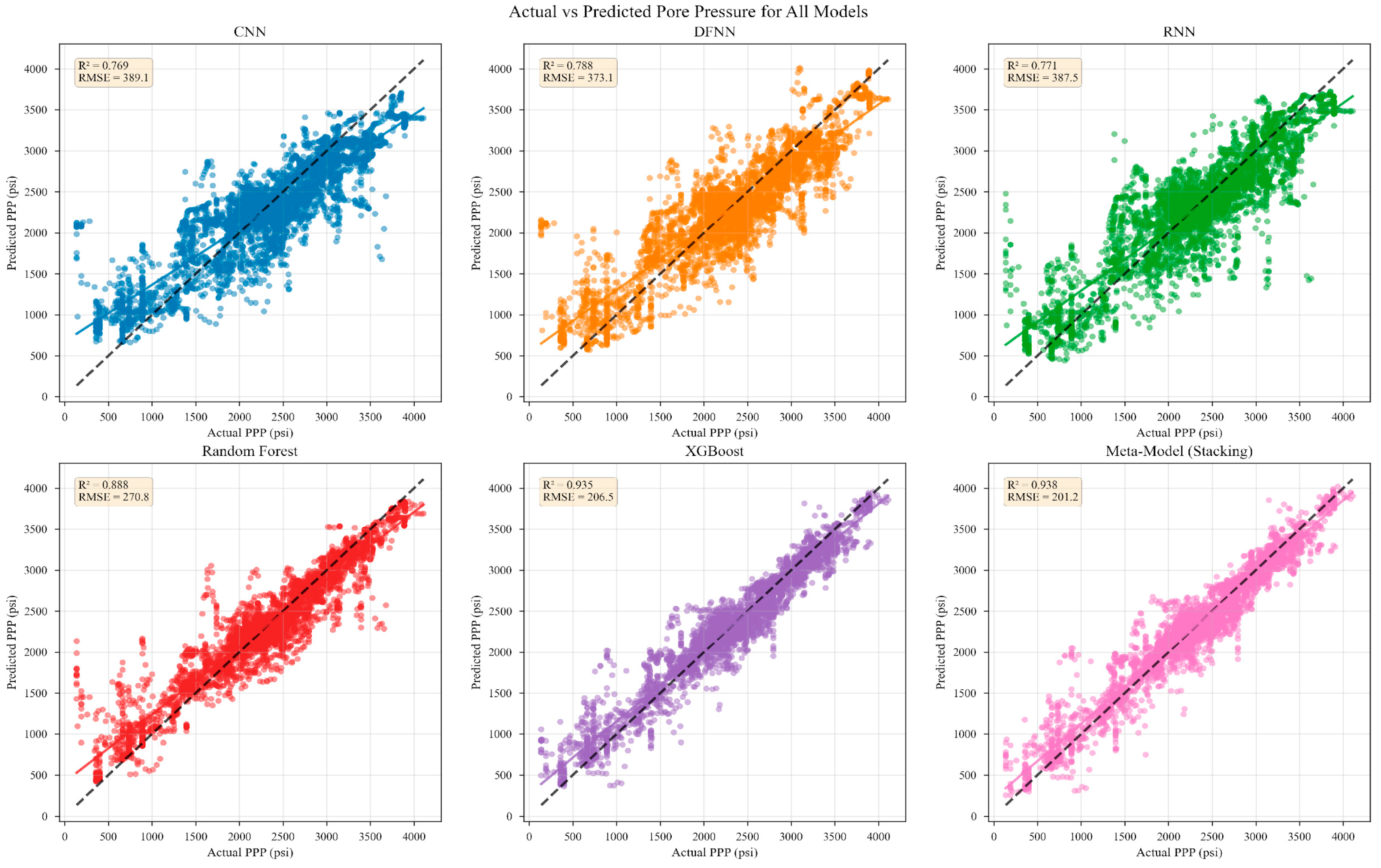
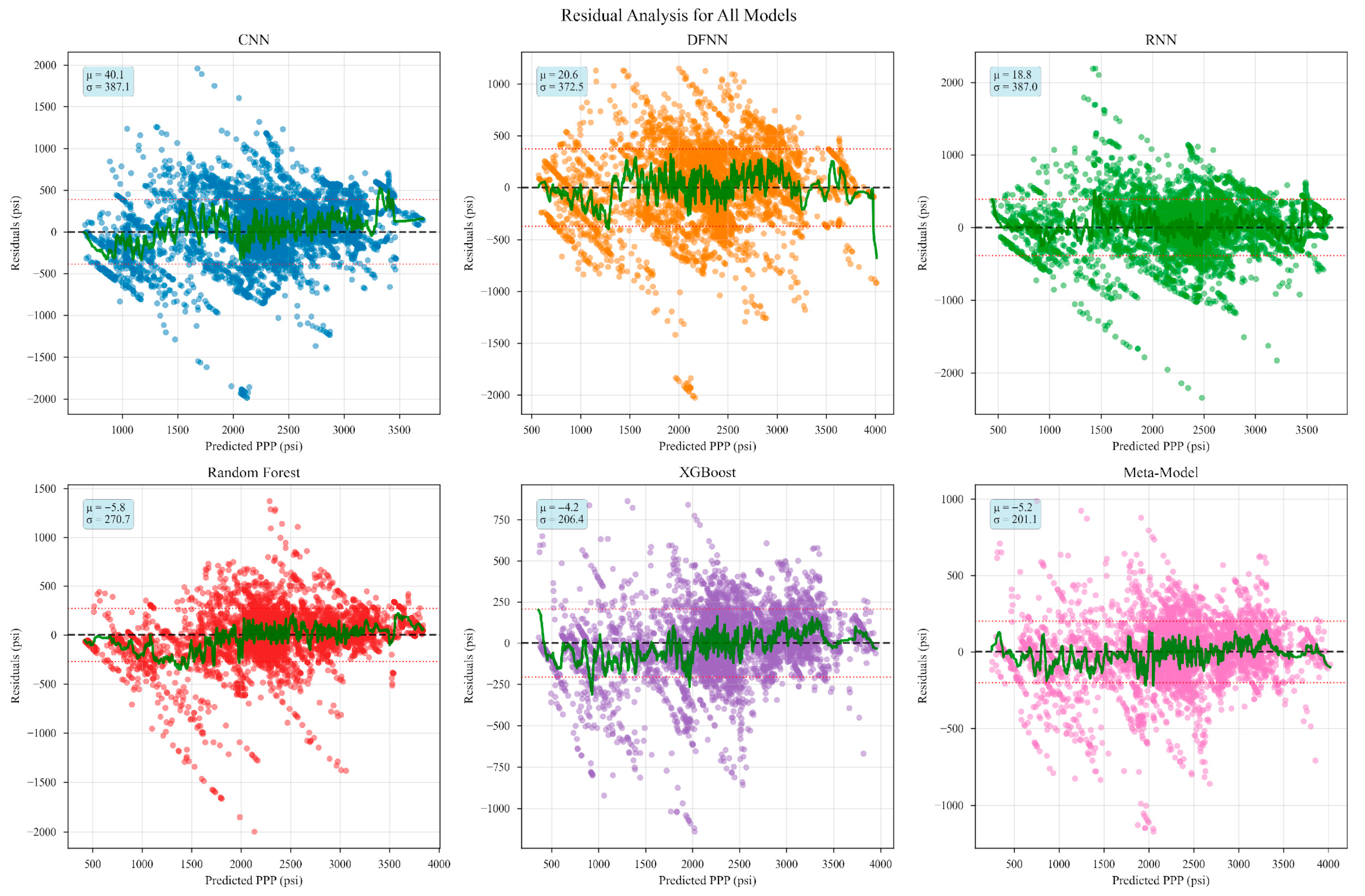
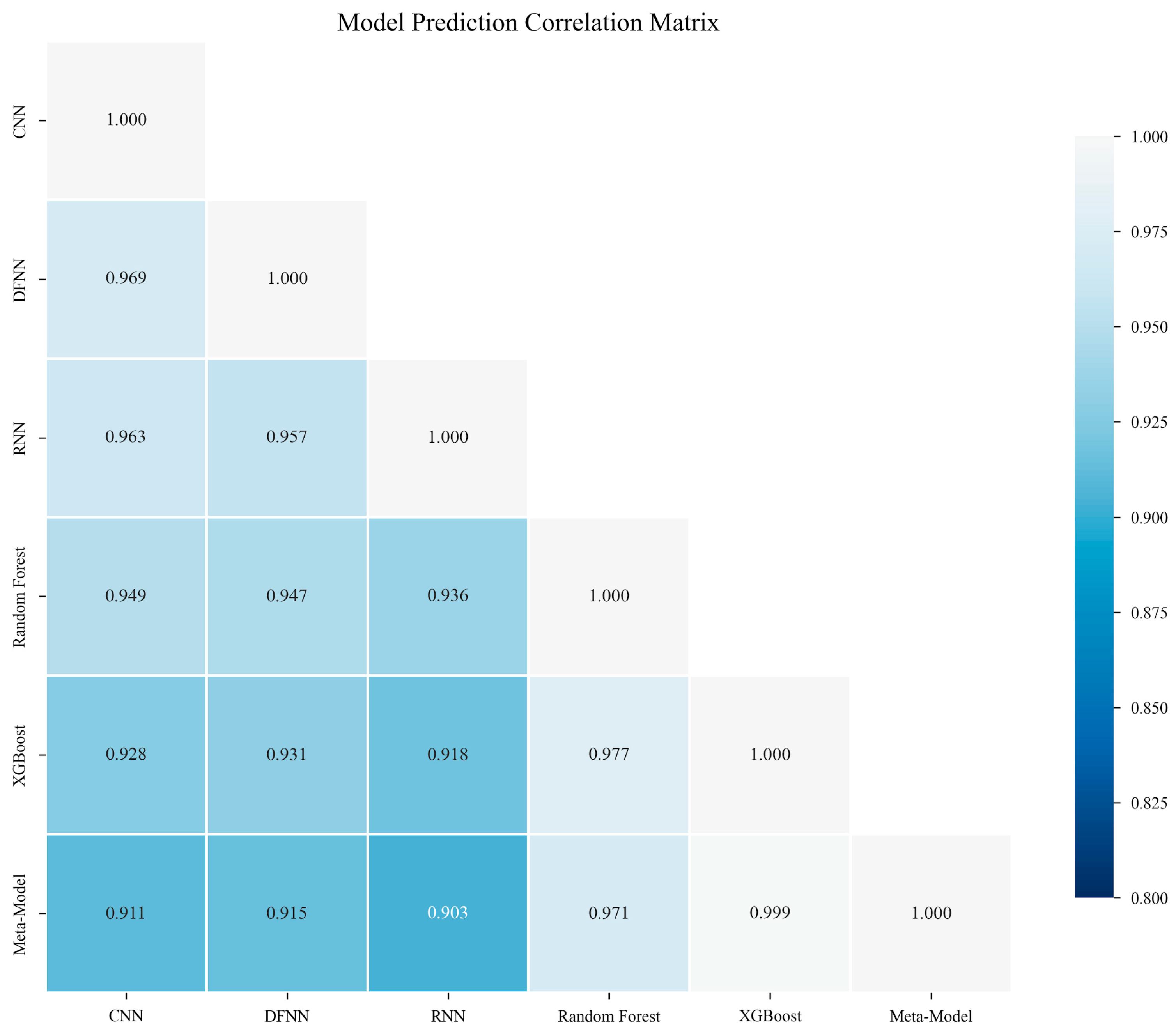
4.2. Hybrid Meta-Ensemble
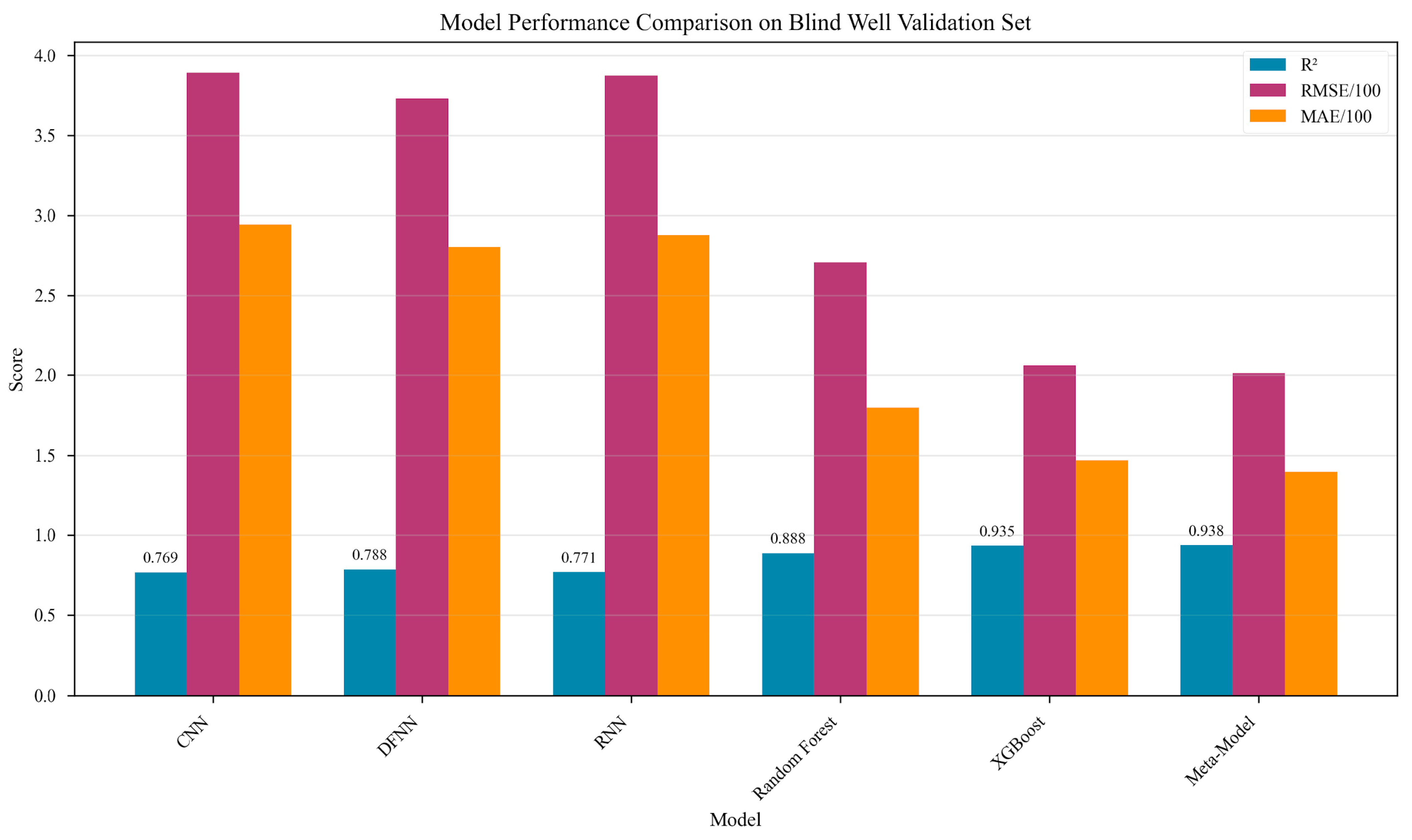
4.3. Comparative Analysis and Model Selection
- (a)
- Critical Importance of Fine-tuning: All models exhibited negative R2 values before fine-tuning, indicating unreliable predictions. Fine-tuning transformed these models into effective predictors, with R2 improvements ranging from 1.72 to 2.19 units.
- (b)
- Model Hierarchy: Among base models, performance ranking after fine-tuning was XGBoost > RF > RNN > DFNN > CNN. Tree-based ensemble methods (XGBoost and RF) demonstrated superior performance, likely due to their ability to capture complex nonlinear relationships without requiring extensive feature engineering.
- (c)
- Ensemble Superiority: The stacking meta-ensemble achieved the best overall performance (R2 = 0.9382), demonstrating that sophisticated model combination strategies can exceed individual model capabilities. The 39.9% improvement over simple averaging highlights the value of learned combination weights.
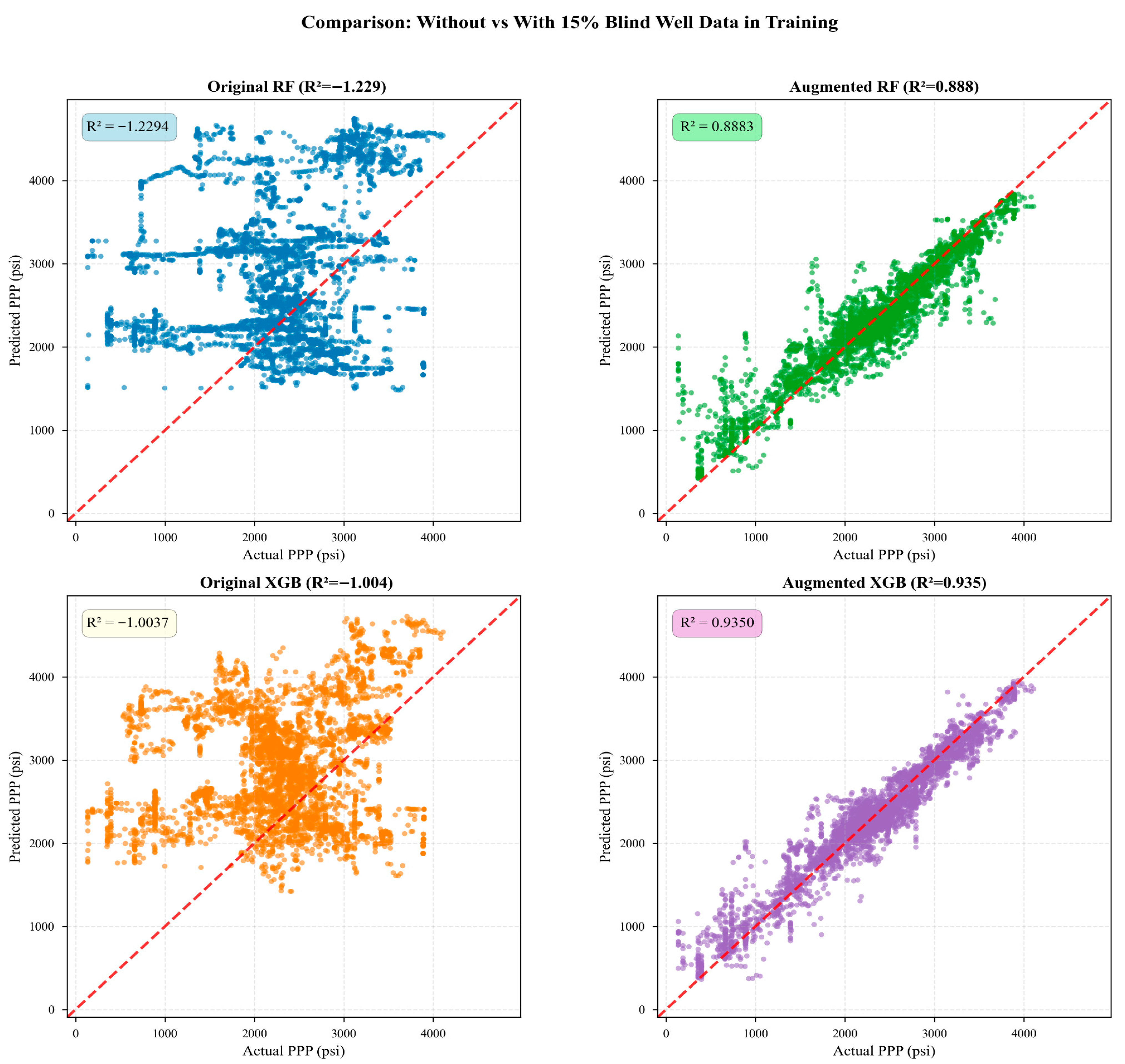
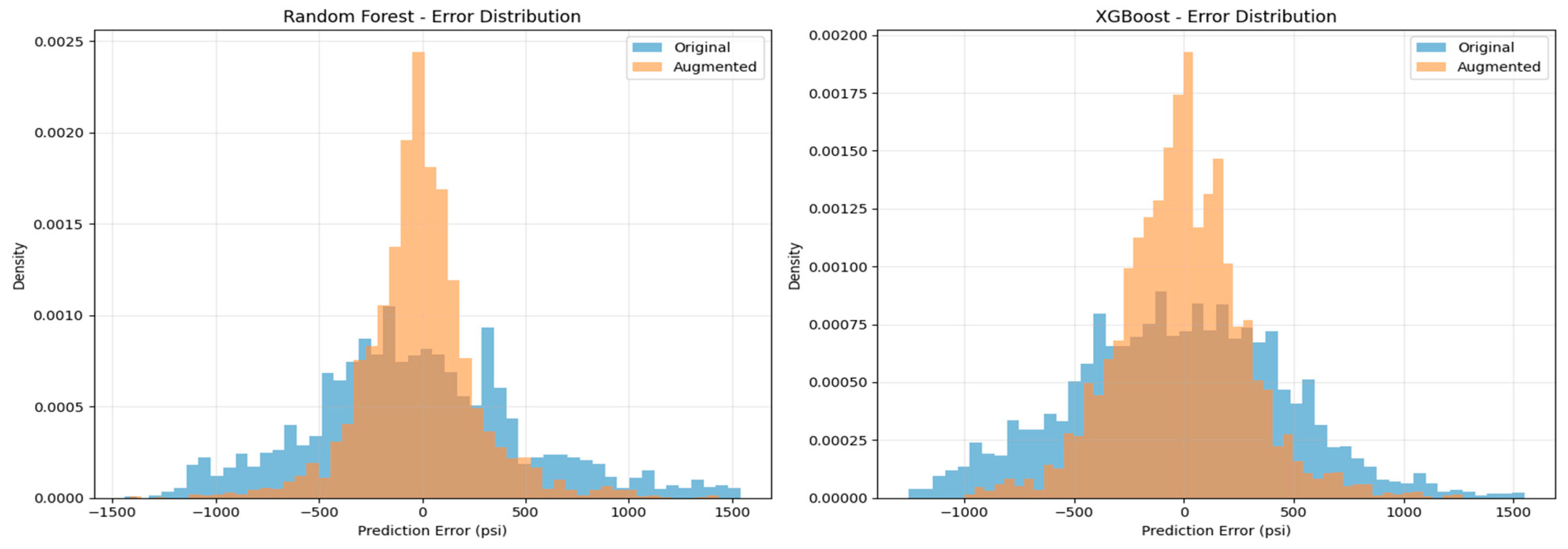
4.4. Pressure Prediction in Blind Well
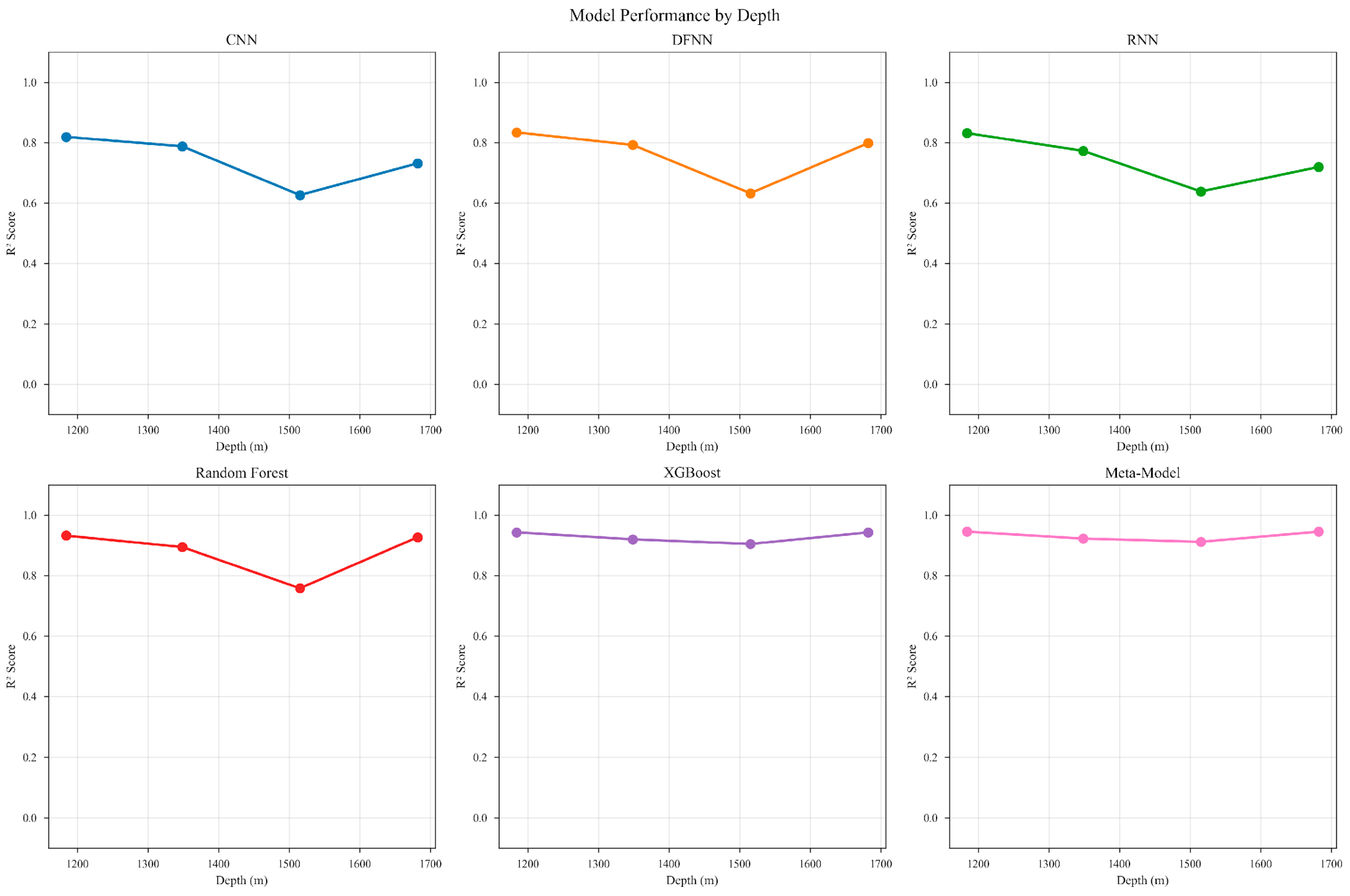
4.5. Leave-One-Well-Out Cross-Validation (LOOCV)
5. Discussion
6. Model Limitations
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ML | Machine Learning |
| PPP | Pore Pressure Prediction |
| HME | Hybrid Meta-Ensemble |
| CNN | Convolutional Neural Network |
| RNN | Recurrent Neural Network |
| DFNN | Deep Feedforward Neural Network |
| RF | Random Forest |
| XGBoost | Extreme Gradient Boost |
References
- Eaton, B.A. The equation for geopressure prediction from well logs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 28 September–1 October 1975; p. SPE-5544-MS. [Google Scholar]
- Bowers, G.L. Pore pressure estimation from velocity data: Accounting for overpressure mechanisms besides undercompaction. SPE Drill. Complet. 1995, 10, 89–95. [Google Scholar] [CrossRef]
- Amjad, M.R.; Zafar, M.; Malik, M.B.; Naseer, Z. Precise geopressure predictions in active foreland basins: An application of deep feedforward neural networks. J. Asian Earth Sci. 2003, 245, 105560. [Google Scholar] [CrossRef]
- Li, H.; Tan, Q.; Deng, J.; Dong, B.; Li, B.; Guo, J.; Zhang, S.; Bai, W. A Comprehensive Prediction Method for Pore Pressure in Abnormally High-Pressure Blocks Based on Machine Learning. Processes 2023, 11, 2603. [Google Scholar] [CrossRef]
- Lawal, A.; Yang, Y.; He, H.; Baisa, N.L. Machine learning in oil and gas exploration: A review. IEEE Access 2024, 12, 19035–19058. [Google Scholar] [CrossRef]
- Yu, H.; Chen, G.; Gu, H. A machine learning methodology for multivariate pore-pressure prediction. Comput. Geosci. 2020, 143, 104548. [Google Scholar] [CrossRef]
- Amjad, M.R.; Shakir, U.; Hussain, M.; Rasul, A.; Mehmood, S.; Ehsan, M. Sembar formation as an unconventional prospect: New insights in evaluating shale gas potential combined with deep learning. Nat. Resour. Res. 2023, 32, 2655–2683. [Google Scholar] [CrossRef]
- Naseer, Z.; Ehsan, M.; Ali, M.; Amjad, M.R.; Latif, M.A.U.; Abdelrahman, K. Lithofacies and sandstone reservoir characterization for geothermal assessment through artificial intelligence. Results Eng. 2025, 26, 105173. [Google Scholar] [CrossRef]
- Elmgerbi, A.; Thonhauser, G. Assessing the Potential of Advanced Sensor Technologies and IoT in Predicting Downhole Drilling Issues. In Proceedings of the SPE Gas & Oil Technology Showcase and Conference, GOTECH, Dubai City, UAE, 21–23 April 2025. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Mining, D. Concepts and techniques. Morgan Kaufmann 2006, 340, 94104–103205. [Google Scholar]
- Zhang, J. Pore pressure prediction from well logs: Methods, modifications, and new approaches. Earth-Sci. Rev. 2011, 108, 50–63. [Google Scholar] [CrossRef]
- Krishna, S.; Irfan, S.A.; Keshavarz, S.; Thonhauser, G.; Ilyas, S.U. Smart predictions of petrophysical formation pore pressure via robust data-driven intelligent models, Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 5611–5630. [Google Scholar] [CrossRef]
- Ahmed, A. New Model for Pore Pressure Prediction While Drilling Using Artificial Neural Networks. Arab. J. Sci. Eng. 2018, 44, 6079–6088. Available online: https://link.springer.com/article/10.1007/s13369-018-3574-7 (accessed on 11 September 2025).
- Abdelaal, A.; Elkatatny, S.; Abdulraheem, A. Data-Driven Modeling Approach for Pore Pressure Gradient Prediction while Drilling from Drilling Parameters. ACS Omega 2021, 6, 13807–13816. [Google Scholar] [CrossRef]
- Matinkia, M.; Amraeiniya, A.; Behboud, M.M.; Mehrad, M.; Bajolvand, M.; Gandomgoun, M.H.; Gandomgoun, M. A novel approach to pore pressure modeling based on conventional well logs using convolutional neural network. J. Pet. Sci. Eng. 2022, 211, 110156. [Google Scholar] [CrossRef]
- Huang, H.; Li, J.; Yang, H.; Wang, B.; Gao, R.; Luo, M.; Li, W.; Zhang, G.; Liu, L. Research on prediction methods of formation pore pressure based on machine learning. Energy Sci. Eng. 2022, 10, 1886–1901. [Google Scholar] [CrossRef]
- Radwan, A.E.; Wood, D.A.; Radwan, A.A. Machine learning and data-driven prediction of pore pressure from geophysical logs: A case study for the Mangahewa gas field, New Zealand. J. Rock Mech. Geotech. Eng. 2022, 14, 1799–1809. [Google Scholar] [CrossRef]
- Farsi, M.; Mohamadian, N.; Ghorbani, H.; Wood, D.A.; Davoodi, S.; Moghadasi, J.; Alvar, M.A. Predicting formation pore-pressure from well-log data with hybrid machine-learning optimization algorithms. Nat. Resour. Res. 2021, 30, 3455–3481. [Google Scholar] [CrossRef]
- Abdelaal, A.; Elkatatny, S.; Abdulraheem, A. Real-time prediction of formation pressure gradient while drilling. Nature 2022, 12, 11318. [Google Scholar] [CrossRef]
- Shi, L.; Tang, Z.; Zhang, N.; Zhang, X.; Yang, Z. A Survey on Employing Large Language Models for Text-to-SQL Tasks. ACM Comput. Surv. 2025, 58, 3737873. [Google Scholar] [CrossRef]
- Medsker, L.R.; Jain, L. Recurrent neural networks. Des. Appl. 2001, 5, 2. [Google Scholar]
- Osman, A.I.A.; Ahmed, A.N.; Chow, M.F.; Huang, Y.F.; El-Shafie, A. Extreme gradient boosting (Xgboost) model to predict the groundwater levels in Selangor Malaysia. Ain Shams Eng. J. 2021, 12, 1545–1556. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6999–7019. [Google Scholar] [CrossRef]
- Warwick, P.D. Overview of the geography, geology and structure of the Potwar regional framework assessment project study area, north-ern Pakistan. In Regional Studies of the Potwar Plateau Area, northern Pakistan. U.S. Geological Survey. Bulletin 2078–A; 2007; p. 2078. Available online: https://www.academia.edu/download/34058136/B2078_chapter_A.pdf (accessed on 19 October 2025).
- Paglia, J.; Eidsvik, J.; Grøver, A.; Lothe, A.E. Statistical modeling for real-time pore pressure prediction from predrill analysis and well logs. Geosci. World 2019, 84, ID1–ID12. Available online: https://pubs.geoscienceworld.org/seg/geophysics/article-abstract/84/2/ID1/569426/Statistical-modeling-for-real-time-pore-pressure (accessed on 12 May 2025). [CrossRef]
- Shakir, U.; Ali, A.; Amjad, M.R.; Hussain, M. Improved gas sand facies classification and enhanced reservoir description based on calibrated rock physics modelling: A case study. Open Geosci. 2021, 13, 1476–1493. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, M.; Liu, P.; Yan, G.; Sun, D.; Wu, J.; Liang, L.; Huang, Y.; Huang, Y.; Sun, M. Pore Pressure Prediction Using Machine Learning Method. In Proceedings of the Offshore Technology Conference Asia, Kuala Lumpur, Malaysia, 27 February–1 March 2024. [Google Scholar] [CrossRef]
- Hu, N.; Han, B.; Long, T.; Tan, Q.; Deng, J.; Liu, W.; Feng, Y.; Li, X.; Yang, H.; Shang, G.; et al. Pore Pressure Prediction Model Based on XGBOOST: A Case Study of Complex Geological Strata in Block K. In Proceedings of the ARMA/DGS/SEG International Geomechanics Symposium, ARMA, Kuala Lumpur, Malaysia, 18–20 November 2024; p. ARMA-IGS. Available online: https://onepetro.org/armaigs/proceedings-abstract/IGS24/IGS24/632582 (accessed on 18 June 2025).
- Shi, X.; Gou, J.; Gong, W.; Cao, J.; Cao, S.; Wang, G.; Ramezanzadeh, A. Machine Learning-Based Pore Pressure Prediction in Deep Reservoirs: Model Comparison and Optimized Application of XGBoost. In Proceedings of the ARMA US Rock Mechanics/Geomechanics Symposium, ARMA, Santa Fe, New Mexico, 8–11 June 2025; p. D032S041R013. Available online: https://onepetro.org/ARMAUSRMS/proceedings-abstract/ARMA25/ARMA25/786137 (accessed on 19 October 2025).
- Deng, S.; Pan, H.-Y.; Wang, H.-G.; Xu, S.-K.; Yan, X.-P.; Li, C.-W.; Peng, M.-G.; Peng, H.-P.; Shi, L.; Cui, M.; et al. A hybrid machine learning optimization algorithm for multivariable pore pressure prediction. Pet. Sci. 2024, 21, 535–550. [Google Scholar] [CrossRef]
- Ehsan, M.; Manzoor, U.; Chen, R.; Hussain, M.; Abdelrahman, K.; Radwan, A.E.; Ullah, J.; Iftikhar, M.K.; Arshad, F. Pore pressure prediction based on conventional well logs and seismic data using an advanced machine learning approach. J. Rock Mech. Geotech. Eng. 2024, 17, 2727–2740. [Google Scholar] [CrossRef]
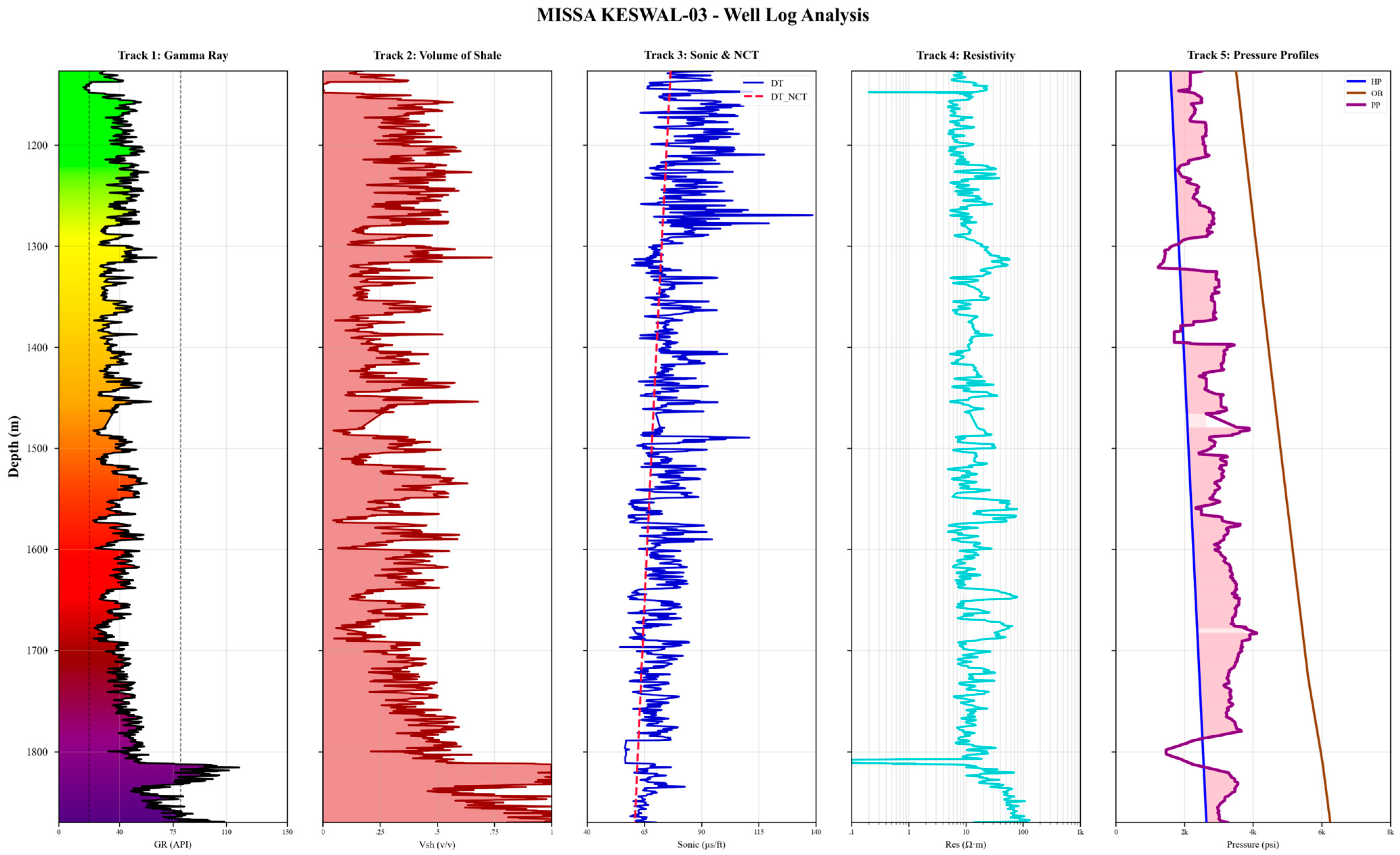
| Property | Formula | Parameters Description |
|---|---|---|
| Gamma Ray Index | Equation (1) | IGR = gamma ray index GRlog = GR log value GRmin = GR minimum value GRmax = GR maximum value |
| Shale Volume (Steiber Correction) | Equation (2) | Vsh = volume of shale |
| Density Porosity | Equation (3) | PHID = density porosity ρma = matrix density ρf = drilling fluid density ρb = bulk density |
| Porosity | Equation (4) | PHIS = sonic porosity DTma = matrix transit time DTf = drilling fluid transit time DT = transit time from sonic log |
| Hydrostatic Pressure | Equation (5) | HP = hydrostatic pressure g = gravity acceleration z = depth |
| Overburden Pressure | Equation (6) | OB = overburden pressure |
| Pore Pressure | Equation (7) | PP = Pore Pressure |
| Model | Configuration | R2 | RMSE (psi) | MAE (psi) | RelRMSE (%) |
|---|---|---|---|---|---|
| CNN | Original | −1.0355 | 1155.62 | 915.84 | 29.09 |
| Fine-tuned | 0.7692 | 389.13 | 294.32 | 10.03 | |
| RNN | Original | −0.8163 | 1091.64 | 874.46 | 27.47 |
| Fine-tuned | 0.7712 | 387.45 | 287.75 | 9.50 | |
| DFNN | Original | −1.3260 | 1235.35 | 928.66 | 31.09 |
| Fine-tuned | 0.7878 | 373.11 | 280.37 | 9.34 | |
| RF | Original | −1.2294 | 1209.40 | 976.97 | 30.44 |
| Fine-tuned | 0.8883 | 270.77 | 179.66 | 6.81 | |
| XGBoost | Original | −1.0037 | 1146.55 | 928.36 | 28.86 |
| Fine-tuned | 0.9350 | 206.46 | 147.12 | 5.20 |
| Ensemble Method | R2 | MAE | RMSE | RelRMSE (%) |
|---|---|---|---|---|
| Simple Average | 0.8645 | 219.83 | 298.21 | 7.51 |
| Weighted Average | 0.8711 | 213.82 | 290.85 | 7.32 |
| Stacking | 0.9382 | 140.05 | 201.2 | 5.07 |
| Model | Mean R2 | Std Dev | RMSE (psi) | MAE (psi) |
|---|---|---|---|---|
| Meta-Model | 0.959 | ±0.031 | 142.4 | 82 |
| XGBoost | 0.947 | ±0.034 | 145 | 84.4 |
| Random Forest | 0.944 | ±0.058 | 159.3 | 89.8 |
| CNN | 0.833 | ±0.118 | 299.3 | 215.1 |
| DFNN | 0.833 | ±0.115 | 298.3 | 214.7 |
| RNN | 0.825 | ±0.114 | 310.8 | 218.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amjad, M.R.; Varghese, R.B.; Amjad, T. Machine Learning Models for Subsurface Pressure Prediction: A Data Mining Approach. Computers 2025, 14, 499. https://doi.org/10.3390/computers14110499
Amjad MR, Varghese RB, Amjad T. Machine Learning Models for Subsurface Pressure Prediction: A Data Mining Approach. Computers. 2025; 14(11):499. https://doi.org/10.3390/computers14110499
Chicago/Turabian StyleAmjad, Muhammad Raiees, Rohan Benjamin Varghese, and Tehmina Amjad. 2025. "Machine Learning Models for Subsurface Pressure Prediction: A Data Mining Approach" Computers 14, no. 11: 499. https://doi.org/10.3390/computers14110499
APA StyleAmjad, M. R., Varghese, R. B., & Amjad, T. (2025). Machine Learning Models for Subsurface Pressure Prediction: A Data Mining Approach. Computers, 14(11), 499. https://doi.org/10.3390/computers14110499







