SACW: Semi-Asynchronous Federated Learning with Client Selection and Adaptive Weighting

Abstract

Federated learning (FL), as a privacy-preserving distributed machine learning paradigm, demonstrates unique advantages in addressing data silo problems. However, the prevalent statistical heterogeneity (data distribution disparities) and system heterogeneity (device capability variations) in practical applications significantly hinder FL performance. Traditional synchronous FL suffers from severe waiting delays due to its mandatory synchronization mechanism, while asynchronous approaches incur model bias issues caused by training pace discrepancies. To tackle these challenges, this paper proposes the SACW framework, which effectively balances training efficiency and model quality through a semi-asynchronous training mechanism. The framework adopts a hybrid strategy of “asynchronous client training–synchronous server aggregation,” combined with an adaptive weighting algorithm based on model staleness and data volume. This approach significantly improves system resource utilization and mitigates system heterogeneity. Simultaneously, the server employs data distribution-aware client clustering and hierarchical selection strategies to construct a training environment characterized by “inter-cluster heterogeneity and intra-cluster homogeneity.” Representative clients from each cluster are selected to participate in model aggregation, thereby addressing data heterogeneity. We conduct comprehensive comparisons with mainstream synchronous and asynchronous FL methods and perform extensive experiments across various model architectures and datasets. The results demonstrate that SACW achieves better performance in both training efficiency and model accuracy under scenarios with system and data heterogeneity.

1. Introduction

With the rapid advancement of Artificial Intelligence (AI) and Internet of Things (IoT) technologies [1], various terminal devices (e.g., smart vehicles, drones, mobile terminals) generate massive amounts of data. Under traditional machine learning and deep learning paradigms, these raw data must be uploaded to a central server for centralized training [2]. This approach not only consumes substantial communication resources but also poses significant risks of user privacy leakage. As data volume and computational requirements grow exponentially, centralized model training methods face severe challenges in terms of time costs and resource consumption. In this context, federated learning (FL) [3] emerges as an innovative distributed machine learning framework [4]. By employing local model training on client devices and transmitting only model parameters, FL effectively addresses the privacy security and resource bottleneck issues associated with raw data transmission. Currently, FL demonstrates significant application value across various domains, including smart finance, IoT applications, and healthcare [5].

Despite its notable successes, federated learning faces critical challenges in practical applications: its fundamental assumption—that all clients share similar local data distributions and homogeneous computational capabilities [6]—often fails to hold in real-world scenarios. Specifically, both statistical heterogeneity and system heterogeneity among clients [7,8] significantly degrade FL performance. Below we analyze these two types of heterogeneity in detail: (1) System heterogeneity stems from variations in client hardware configurations, including computing unit performance, communication bandwidth, storage capacity, and power supply. Such disparities lead to substantial differences in local model training and parameter upload times, thereby prolonging the overall FL training cycle. Taking the classic synchronous FedAvg algorithm [9] as an example, the server must wait for all clients (including the slowest devices) to upload their models before performing global aggregation. This waiting mechanism causes severe computational resource idling, known as the straggler effect [10]. More critically, in FL frameworks employing fixed global deadlines [11], clients with weaker hardware often fail to complete computations on time and are excluded from training, resulting in severe participation imbalance. (2) Statistical heterogeneity primarily manifests as divergent local data distributions across clients. For instance, in healthcare, specialty hospitals (e.g., orthopedic vs. oncology centers) collect patient data with significant variations in disease types and diagnostic metrics. Such distribution disparities are defined as the Non-IID (Non-Independent and Identically Distributed) problem [12]. Under Non-IID conditions, local model updates may exhibit substantial directional conflicts, and clients with larger datasets tend to disproportionately influence the global model [13]. This training inconsistency not only slows model convergence but may also compromise the final model’s generalization capability. Consequently, research on optimizing system and statistical heterogeneity has become pivotal for improving FL training efficiency and model accuracy. Addressing these challenges is essential to advancing FL’s practical deployment in complex real-world environments.

Synchronous federated learning approaches (e.g., FedAvg [9]) exhibit significant efficiency bottlenecks when addressing system heterogeneity challenges. In this framework, clients must synchronously wait for the server to distribute the global model before initiating local training. Simultaneously, the server must wait for all selected clients to complete training and upload their models before performing global aggregation. This bidirectional waiting mechanism generates substantial idle time, severely limiting the overall training efficiency of federated learning. To overcome this limitation, researchers have proposed the asynchronous federated learning (AFL) framework [14,15]. AFL employs a “first-come-first-train” asynchronous mechanism that effectively eliminates resource waste caused by synchronous waiting and significantly improves client participation efficiency. However, AFL still faces two critical issues in practice: First, due to uneven computational resource allocation, high-performance clients may complete multiple training iterations while resource-constrained clients can only finish a single round, leading to participation imbalance. Second, when stale models uploaded by lagging clients are directly aggregated with the continuously evolving global model, gradient deviation occurs, adversely affecting model convergence speed and stability. To address these challenges, semi-asynchronous federated learning [16] has emerged as an innovative compromise solution. This mechanism introduces dynamic aggregation triggers (e.g., reaching preset model quantity thresholds or fixed time windows), maintaining the efficiency advantages of asynchronous training while ensuring fair participation among all clients.

To address statistical heterogeneity challenges, optimizing client selection mechanisms has become a critical breakthrough for improving federated learning performance [17]. In practical application scenarios, a single server needs to coordinate and manage hundreds to thousands of clients for multiple rounds of iterative training. Adopting a full-client participation communication model would not only impose tremendous communication and computational pressure on the server but also lead to the excessive consumption of network bandwidth resources, severely reducing training efficiency. While the random client selection strategy employed by the traditional FedAvg algorithm is simple to implement, it fails to account for differences in client data distributions. This approach often cannot guarantee the representativeness of selected clients and may overlook those with critical data characteristics, ultimately affecting model performance. Therefore, an appropriate client selection method serves as a viable solution to statistical heterogeneity.

Based on the above research methodology, this paper proposes SACW: Semi-Asynchronous Federated Learning with Client Selection and Adaptive Weighting. SACW synergizes the strengths of synchronous and asynchronous federated learning, markedly mitigating biases induced by statistical and system heterogeneity to bring the training process closer to an ideal federated environment. First, we introduce a DBSCAN (Density-Based Spatial Clustering of Applications with Noise)-based clustering algorithm that selects representative clients according to the local data distributions of all participants, ensuring a balanced global data distribution in each round and effectively curbing statistical heterogeneity. Second, to balance communication efficiency and model convergence, we devise a semi-asynchronous communication paradigm: “clients train asynchronously, while the server performs synchronous adaptive-weighted aggregation.” On the one hand, clients are allowed to update their models locally on their own schedules, eliminating idle time and dropouts caused by synchronous waiting; on the other hand, during synchronous aggregation, the server adaptively weights each contribution based on both the client’s local data volume and its model staleness, suppressing the client bias inherent to fully asynchronous updates and thereby significantly alleviating system heterogeneity.

Our main contributions are summarized as follows:

• We propose the SACW framework, which adopts a semi-asynchronous strategy of “asynchronous client training–synchronous server aggregation.” This design balances training efficiency with model quality. In addition, an adaptive weighting algorithm based on model staleness and data volume improves system resource utilization and effectively mitigates system heterogeneity.
• We present a DBSCAN-based client selection strategy that automatically identifies clients with similar data distributions through density clustering, without requiring predefined cluster numbers. This approach forms a grouping structure with “inter-cluster heterogeneity and intra-cluster homogeneity.” Representative clients are then selected from each cluster for aggregation, which alleviates data heterogeneity. To further reduce the network load introduced by semi-asynchronous communication, we introduce a lattice-based quantization scheme for model compression. This method significantly decreases the transmission overhead between clients and the server.
• To evaluate the practicality of our method, we construct a realistic heterogeneous training environment. We simulate fast and slow clients by assigning different computing resources and generate Non-IID data distributions through non-uniform dataset partitioning. Experiments on three benchmark datasets show that SACW achieves high model accuracy while delivering faster convergence and better communication efficiency.

This paper is organized as follows: Section 2 surveys existing synchronous, asynchronous, and semi-asynchronous federated learning paradigms, highlighting their strengths and limitations in coping with both system and statistical heterogeneity. Section 3 briefly reviews the FedAvg framework and details the DBSCAN clustering algorithm. Section 4 presents our proposed algorithm through flowcharts, pseudocode, and an in-depth description of its key modules. Section 5 provides a comprehensive experimental evaluation: we describe the setup and conduct comparative, ablation, and parameter sensitivity analyses to validate the feasibility of SACW under system and statistical heterogeneity. Section 6 discusses the limitations observed during experimentation and outlines promising directions for future work. Finally, Section 7 concludes this paper.

2. Related Work

FedAvg [9], as the earliest proposed federated learning approach, represents the most classic synchronous federated learning framework, with most subsequent research building upon this foundation. In FedAvg, clients can synchronously perform local training and interact with the server for global model training. However, current studies demonstrate that FedAvg tends to diverge when faced with statistical and system heterogeneity [18]. Currently, most synchronous federated learning methods focus on addressing statistical heterogeneity while assuming the absence of system heterogeneity. For example, MOON [19] corrects local model update directions by constraining the differences between representations generated by local models. FedRS [20] mitigates model drift in Label Shift scenarios by introducing weight parameters to limit uncertain updates. FedLC [21] calibrates logits before softmax based on class occurrence probabilities and optimizes local cross-entropy loss through pairwise label margins for fine-grained class calibration. However, constrained by their synchronous nature, these methods still suffer from compromised convergence speed when system heterogeneity is present.

Federated learning based on asynchronous mechanisms serves as an effective solution to system heterogeneity. AFL enables clients to conduct local model training at their individual speeds while maintaining timely interaction with the server. After acquiring the updated global model, clients proceed with subsequent local training. This approach enhances client utilization efficiency while significantly reducing server waiting time. For instance, FedAsync [14] permits clients to upload updates at any time, where the server queues them in order of arrival and employs a staleness function combined with mixing hyperparameters to downweight obsolete models during global model updates. Concurrently, it optimizes the local training process through a proximal term. FedBuff [22] establishes a buffer on the server side, allowing clients to asynchronously upload updates to this fixed buffer, with batch aggregation performed to update the global model once the buffer reaches capacity. MAPA-S and MAPA-C [23] also equip the server with a buffer to enable asynchronous training across clients. Their distinction lies in adding noise to the buffer, thereby shielding the model parameters from potential leakage. However, these fully asynchronous methods may cause the global model to converge toward high-efficiency clients, consequently weakening the model’s generalization capability. Moreover, when local models exhibit higher staleness than the global model, the post-aggregation results may decelerate the overall convergence speed.

Federated learning frameworks based on semi-asynchronous mechanisms can combine the advantages of both synchronous and asynchronous approaches by performing aggregation when reaching specific model quantity thresholds or fixed time intervals. This approach reduces waiting time while ensuring each client can participate fairly in global training. For example, FedSA [24] dynamically adjusts the number of clients M participating in each round of aggregation to balance convergence speed and communication efficiency. SAFA [25] synchronously updates both current and outdated clients to maintain basic model consistency while allowing tolerable lagging clients to continue asynchronous local training. QuAFL [26] permits global model aggregation even when some clients have not completed local training but fails to consider the impact of model staleness and data heterogeneity on training performance.

In federated learning scenarios, focusing solely on data distribution differences would cause weak terminals to fall behind and slow down overall training progress. Conversely, considering only computational capability disparities would lead to slow convergence and accuracy degradation due to Non-IID data effects. Therefore, both system resource heterogeneity and statistical data differences must be incorporated into scheduling decisions to simultaneously achieve optimal model performance and training efficiency.

3. Preliminary

3.1. Federated Learning

To address challenges including data silos, privacy protection regulations, and distributed computing limitations, Google first proposed the concept of Federated Optimization in 2017 [27]. This groundbreaking work established the theoretical foundation for federated learning technology. As the first complete framework in this field, the Federated Averaging (FedAvg) algorithm [9] adopted the typical architecture shown in Figure 1: a two-tier topology consisting of a central server and distributed clients. Its core innovation lies in realizing the privacy-preserving paradigm of “data stays local; models move”—the server only aggregates model parameters trained locally by each client, while raw data always remains on local devices.

Table 1. Descriptions of notations in this paper.

Symbol	Descriptions
N	total number of clients
R	number of global model aggregation rounds
r	current round number
T	total training time of the global model
L	maximum number of local training steps
K	number of clusters for clustering all clients
$k_i$	$i^{th}$ client
$c_i$	adaptive weight of $i^{th}$ client
$C_i$	$i^{th}$ cluster
S	set of selected clients
$s_i$	selected representative client of $C_i$
$D_i$	dataset of $clien{t}_i$
$\left|·\right|$	size of dataset
$l_i(·)$	loss function of $k_i$
$p_i$	weight factor of $k_i$
$\beta$	parameters of the Dirichlet probability distribution
${\tau }_i$	model version number of $k_i$
${\omega }_i^{{\tau }_i}$	local model of $k_i$ after local training
${\omega }^r$	global model in the $r^{th}$ round
b	quantization bit-width
v	server visiting time
h	server handling time
$m_i$	actual local training steps of $k_i$
$P_i\left(y\right)$	local label distribution of $k_i$
$G_i(·)$	local gradient computation function of $k_i$

provides explanations of the key notations used throughout this paper. The standard workflow of this framework can be described in detail as follows:

• Initialization: The central server broadcasts initialization parameters to all clients. $k_i(i\in [1,N])$ performs local initialization after receiving the broadcast information from the server.
• Client Selection: The server randomly selects a subset of clients from all available clients, forming a candidate set $S=\{s_1,s_2,\dots ,s_i,\dots ,s_k\}$, and sends the global model ${\omega }^r(r\in [1,R])$ to the selected clients.
• Local Client Training: Each selected $s_i\in S$ trains the model using its local dataset based on ${\omega }^r$, obtaining updated parameters ${\omega }_{s_i}^{r+1}$, and then uploads the trained model parameters to the server. Upon completing training, the client stops local training and waits for subsequent selection by the server. The client state transitions as follows: $Idle\to Training\to Uploading\to Idle$.
• Server Aggregation: After collecting all updated parameters ${\omega }_{s_i}^{r+1}$, the server performs a weighted aggregation of local models based on each client’s data volume to obtain a new global model ${\omega }^{r+1}$.
• Model Evaluation: The system evaluates whether the global model’s accuracy meets the target threshold or whether the total training rounds reach R. If yes, the federated learning task terminates. Otherwise, the next training round begins immediately, repeating steps 2–5.

The global training objective of FedAvg is to obtain a global model that minimizes the loss function, expressed as follows:

$$min\left(l\left(\omega \right)\right):=\sum _{i=1}^N{\displaystyle \frac{|D_i|}{\left|D\right|={\sum }_{i=1}^N\left|D_i\right|}}{l}_i\left({\omega }_i\right)$$

(1)

where represents the trained global model, $D_i$ denotes the dataset of $k_i$, $\left|·\right|$ indicates the size of the dataset, and $l_i\left({\omega }_i\right)$ corresponds to the loss of $k_i$’s local model.

3.2. DBSCAN

Density-Based Spatial Clustering of Applications with Noise (DBSCAN) [28] is a powerful unsupervised clustering algorithm whose core concept lies in identifying “density regions” within datasets and recognizing these regions as clusters while simultaneously detecting and handling noise points located in sparse areas. The algorithm offers several advantages: First, in real-world data, the number of clusters is often unknown. DBSCAN automatically discovers the number of clusters through density expansion, avoiding clustering bias caused by inappropriate cluster number selection. Second, DBSCAN forms clusters through density expansion, enabling the discovery of non-convex and irregularly shaped clusters. Third, DBSCAN explicitly distinguishes between core points, border points, and noise points, marking points in sparse regions as noise to prevent them from interfering with the clustering results. The algorithm procedure is as follows:

• Parameter Initialization: Predefine the neighborhood radius $ϵ$(Eps) and minimum density threshold MinPts to characterize the density conditions for core points.
• Point Access and Core Point Determination: Randomly select a point f from the dataset and mark it as visited. If the $ϵ$-neighborhood of f contains at least MinPts objects, d is identified as a core point, and a new cluster C is created. Otherwise, f is temporarily marked as noise. If f is a core point, all objects within its neighborhood are added to the candidate set F.
• Cluster Expansion: While the candidate set F is non-empty, repeat the following operations: Extract any object d from F that has not been assigned to another cluster. If d has not been visited, mark it as visited and examine its $ϵ$-neighborhood. If d also satisfies the core point condition, append all objects in its neighborhood not yet assigned to the current cluster into F. Then, assign d to cluster C. This process continues until F is empty, at which point cluster C is fully constructed.
• Iteration: Randomly select another unvisited point and repeat steps 2 and 3 until all objects in the dataset have been visited.
• Output: Finally, all points successfully assigned to a cluster C form the clustering result, while points never incorporated into any cluster are treated as noise.

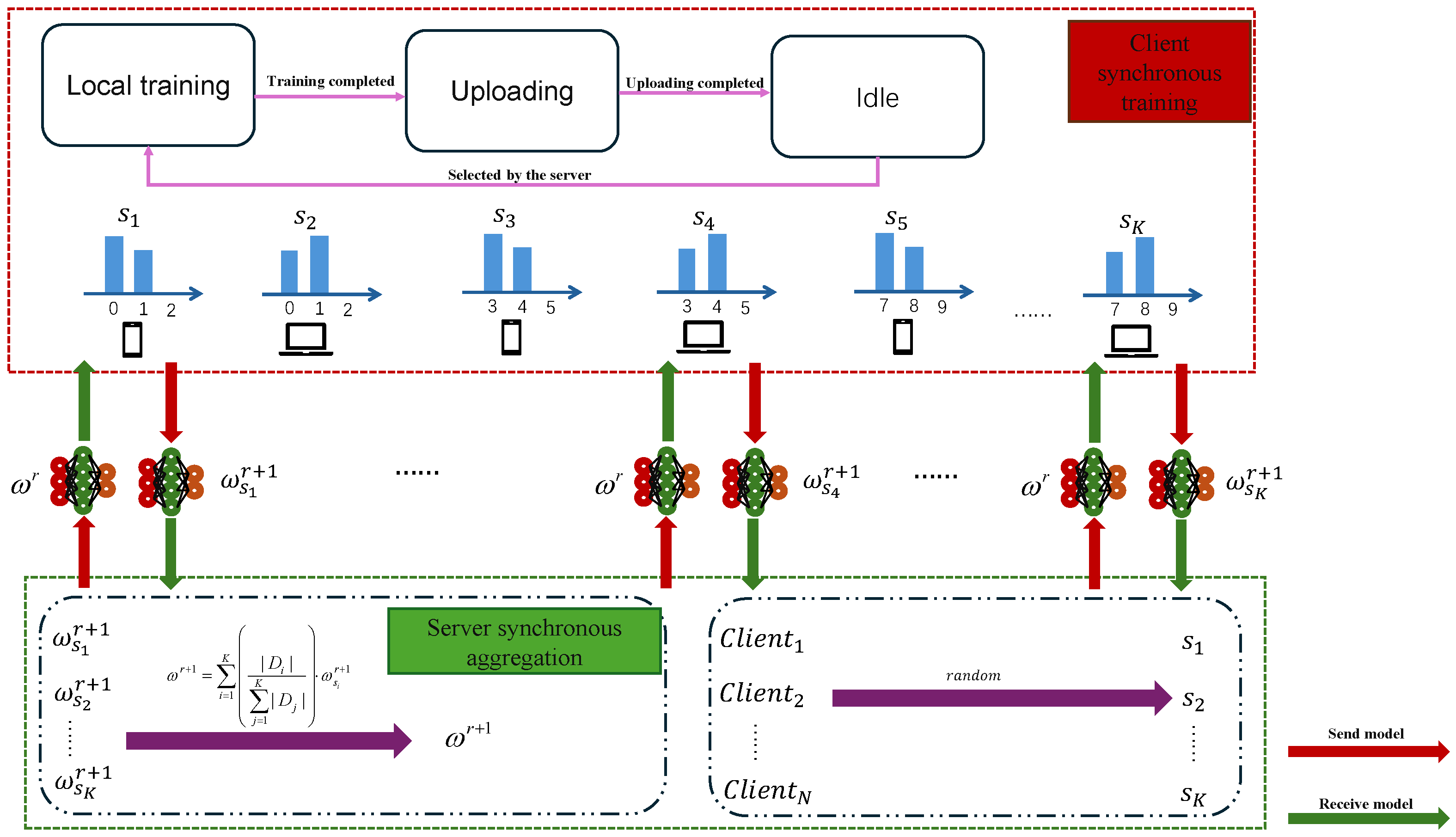
4. Proposed Method: SACW

4.1. Problem Description

In this paper, we consider a federated learning scenario with both system and statistical heterogeneity, where the system architecture consists of one central server and N local clients. To facilitate theoretical analysis, we make the following basic assumptions:

• The client set remains fixed during training, with no dynamic addition of new clients;
• Each client’s local dataset remains unchanged throughout the training process;
• The central server is honest and coordinates all clients for global training.

Under this framework, the optimization objective of federated learning can be formally expressed as follows: through the efficient scheduling of heterogeneous clients coordinated by the server, we aim to minimize the expected loss function of the global model. Specifically, we need to solve the following distributed optimization problem:

$$min\left(l\left(\omega \right)\right):=p_i·l_i\left({\omega }_i^{{\tau }_i^r}\right)$$

(2)

where $p_i$ represents the adaptive weight of $k_i$ based on both data volume and model staleness, and $l_i\left({\omega }_i^{{\tau }_i^r}\right)$ denotes the loss function of $k_i$’s local model with staleness ${\tau }_i^r$.

4.2. Algorithm Description

The semi-asynchronous federated learning framework proposed in this study innovatively integrates the advantages of asynchronous training mechanisms while preserving the core principles of FedAvg. In large-scale scenarios such as IoT, industrial IoT, and vehicular networks, our algorithm significantly outperforms synchronous federated learning. The reason is clear: when the number of clients is huge, some devices will inevitably lose power, go offline, or suffer from low training efficiency due to insufficient voltage or computing power. A simple synchronous scheme would introduce excessive waiting time and slow down global model training. SACW adopts a semi-asynchronous mechanism to eliminate this synchronization bottleneck, and quantization during communication further reduces the communication overhead. As illustrated in Figure 2, the framework introduces two key innovative features.

First, regarding client selection strategy, we advanced beyond the traditional random selection mechanism of FedAvg by proposing a DBSCAN density-based clustering intelligent selection algorithm. This algorithm analyzes the data distribution characteristics of clients and clusters those with similar data distributions into several groups, achieving optimized data distribution characterized by “inter-cluster heterogeneity and intra-cluster homogeneity.” This clustering selection mechanism ensures that the clients selected from each cluster are sufficiently representative, thereby effectively mitigating model bias caused by statistical heterogeneity.

Second, in terms of the training mechanism, we improved upon FedAvg’s synchronous waiting mode, specifically via the following: (1) Clients are permitted to continue local training even when not selected by the server. (2) Training is terminated only when clients are selected by the server or when the preset maximum training steps are reached. (3) We innovatively designed a client training scheduling mechanism incorporating three process states. This design enables clients to efficiently switch among three states: “training–waiting–uploading.” Compared with FedAvg, this approach allows for more effective local training iterations within the same time window. As shown in Figure 2, the framework’s operational workflow can be divided into five key steps:

• Initialization: All clients receive the initial model (${\omega }^0$) broadcast by the server, including the learning rate and local maximum training steps L. They subsequently transmit their local data distributions to the server.
• Client Clustering and Selection: The server performs clustering based on all clients’ local data distributions and periodically (with interval T) randomly selects clients from each cluster to receive the latest global model ${\omega }^r,r\in [1,R]$, where R represents the total number of global training rounds.
• Local Client Training: Each local client operates under one of three conditions:

  (a)

  When selected by the server, the client immediately uploads its compressed local model (full or partial) along with the model version number, then initiates local training based on the latest global model. State transition: $Localtraining/idle\to Uploading\to Localtraining$.

  (b)

  When not selected by the server but with local training steps below the maximum threshold, the client continues local model training. State transition: $Localtraining\to Idle$.

  (c)

  When not selected and having reached the maximum training steps, the client remains idle until scheduled by the server. State transition: Persists in $Idle$.

• Server Aggregation: Upon receiving all selected clients’ models and version numbers, the server decompresses the models, calculates their staleness, and computes adaptive weighting factors based on both model staleness and training data volume. It then performs weighted aggregation to update the global model ${\omega }^{r+1}$.
• Model Evaluation: The server evaluates whether the global model’s accuracy meets the target threshold or whether the training duration has expired. If yes, the federated learning task terminates; otherwise, it repeats steps 2–5 after waiting for period T.

Algorithm 1 presents the comprehensive procedure of the SACW algorithm.

4.3. Method Description

4.3.1. Client Selection

In ideal federated learning scenarios where all clients share identical label distributions (IID data), each round of global training involves balanced client data participation, enabling optimal model convergence speed [8]. However, this idealized assumption rarely holds in practice due to inherent disparities in client resources and data distributions. To mitigate the impact of data heterogeneity on global model training, our algorithm first clusters clients based on their local data label distributions, grouping those with similar patterns into the same cluster. This creates an “intra-cluster homogeneity, inter-cluster heterogeneity” structure among clients. The central server then employs a stratified random-sampling strategy to select representative clients from each cluster for participation in training. Moreover, randomly selecting clients with similar data within each cluster effectively prevents the system from persistently favoring high-performance and high-capacity clients. This mechanism ensures the global model learns comprehensive data characteristics while effectively reducing model bias caused by data heterogeneity. The detailed procedure operates as follows:

$k_i$ computes its data distribution $P_i\left(y\right)$ representation through the dataset $D_i$ as follows:

$$P_i\left(y\right)=\left({\displaystyle \frac{\left|D_{i,1}\right|}{\left|D_i\right|}},{\displaystyle \frac{\left|D_{i,2}\right|}{\left|D_i\right|}},\dots ,{\displaystyle \frac{\left|D_{i,\mathrm{m}}\right|}{\left|D_i\right|}}\right)$$

(3)

where $\left|D_i\right|$ represents $k_i$’s total data volume, and $\left|D_{i,\mathrm{m}}\right|$ denotes the data volume of the $m^{th}$ category’s training samples in $k_i$.

Algorithm 1: Pseudocode of SACW

The central server performs clustering based on the local label distributions of all clients, grouping those with similar label distributions into the same cluster. The similarity measurement process for the DBSCAN clustering algorithm follows the methodology described in Section 3.2.

$$C_1,C_2,\dots ,C_K\leftarrow Clustering\left(P_i{\left(y\right)}_{i=1}^N\right)$$

(4)

where $C_i,i\in [1,K]$ represents all partitioned clusters of clients. The central server randomly selects one representative client from each cluster to participate in global training.

$$S\leftarrow (s_1,s_2,\dots ,s_K)\stackrel{\mathrm{random}}{\leftarrow }(C_1,C_2,\dots ,C_K)$$

(5)

where S represents the set of clients participating in the next round of global training.

4.3.2. The Semi-Asynchronous Framework with Adaptive Weighting

Many optimization algorithms based on the FedAvg federated learning framework have been proposed, yet none can completely overcome the negative impacts inherent in synchronous federated learning mechanisms. In FedAvg, clients must wait to be selected by the server before initiating local model training, while the server must wait to collect models from all selected clients before performing model aggregation and starting the next round of global training.

Our algorithm overcomes this waiting constraint: local clients can continue training without needing to be selected by the server. In fact, clients that remain unselected for extended periods can perform more comprehensive model training, resulting in more complete local models. The central server only needs to periodically collect local training progress and distribute the latest global model, replacing the original operation that required waiting for all clients to complete training before aggregation. This “asynchronous client training with periodic server synchronization” approach significantly reduces bidirectional waiting time between clients and the server while greatly improving client utilization efficiency.

In heterogeneous environments, while this high-efficiency communication paradigm improves client utilization, it also increases the number of communication rounds between clients and the server by an order of magnitude compared to FedAvg. This consequently raises two critical problems:

• Problem 1: In each training round, the central server selects only a subset of clients to participate in global training (for instance, 200 out of 1000 clients). As communication rounds accumulate, certain clients may remain unselected for an extended period, resulting in local models that are excessively stale relative to the latest global model. Directly averaging these highly stale local models with the global model can severely impede convergence. Therefore, in SACW, a local model is assigned higher utility—and consequently a larger weight in server aggregation—when its host client possesses a larger dataset and exhibits lower staleness. This relationship is strictly linear: weight increases proportionally with data volume and decreases proportionally with staleness. Conversely, clients with smaller datasets and higher staleness receive proportionally smaller weights. This adaptive weighting strategy demonstrably accelerates convergence, as corroborated by the experimental results in Section 4.3.3.
• Problem 2: The server must communicate cyclically with all selected clients, transmitting the global model and receiving their local updates in every round. As both the number of communication rounds and participating clients grows, this imposes substantial communication overhead on the server. To mitigate this pressure, SACW incorporates model compression techniques, detailed in Section 4.3.4.

4.3.3. Adaptive Weighting

In our framework, whenever a client is accessed by the server, it immediately uploads its local model ${\omega }_i^{{\tau }_i^r}$ (either partial or complete) and the version number ${\tau }_i^r$ of the global model upon which this local model was last trained. The selected client then instantaneously performs local parameter updates and initiates a new round of local model training. The local update and training process proceeds as follows:

$${\tau }_i^r=\left\{\begin{array}{cc}r& i\in S\\ {\tau }_i^{r-1}& i\notin S\end{array}\right.$$

(6)

$${\omega }_i^{{\tau }_i^r}=\left\{{\omega }^r|i\in S\right\}$$

(7)

$${\omega }_i^{{\tau }_i^r}={\omega }_i^{{\tau }_i^r}-{\eta }_i\nabla g_i\left({\omega }_i^{{\tau }_i^r};D_i\right)$$

(8)

where ${\tau }_i^r$ and ${\omega }_i^{{\tau }_i^r}$ denote the version number of the global model received by client and the local model of the selected client, respectively, while ${\eta }_i$ and $\nabla g_i(·)$ represent the learning rate and optimizer employed by $k_i$.

Upon receiving ${\omega }_i^{{\tau }_i^{r-1}}$ and ${\tau }_i^{r-1}$ from $s_i$, the central server computes a staleness factor $stalenes{s}_i$. Subsequently, an adaptive weighting factor $q_i$ is assigned to each client based jointly on its staleness and dataset size. The formulation is as follows:

$$stalenes{s}_i=r-{\tau }_i^{r-1}$$

(9)

$$c_i={\displaystyle \frac{|D_i|}{{\sum }_{j\in S}\left|D_j\right|}}·e^{-\lambda ·stalenes{s}_i}$$

(10)

where $\lambda$ is a tunable hyperparameter that modulates the magnitude of staleness’s influence on the weight assignment; its tuning is elaborated in the dedicated ablation study.

The central server performs weighted aggregation on the local models of the selected clients to obtain the new global model, as follows:

$${\omega }^{r+1}=\alpha ·{\omega }^r+(1-\alpha )·\sum _{i\in S}\left({\displaystyle \frac{c_i}{{\sum }_{j\in S}{c}_j}}\right)·{\omega }_i^{{\tau }_i^{r-1}}$$

(11)

where $\alpha$ is an adjustable parameter, $\alpha \in [0,{\displaystyle \frac{1}{K+1}}]$. We treat the $r^{th}$ global model as an additional client; $\alpha$ thus determines the extent to which the $r^{th}$ global model is retained.

4.3.4. Lattice-Based Model Quantization

Lattice-based quantization [29] addresses distributed mean estimation (DME) and variance reduction while minimizing communication cost, making it well-suited to parallel SGD. This aligns closely with federated learning; hence, we adopt this quantization scheme for bidirectional communication between clients and the server to alleviate the central server’s communication burden. The procedure is as follows: Each client transmits its compressed local model, which the central server decompresses and then receives. Specifically, in the $r^{th}$ round, to encode ${\omega }_i^{{\tau }_i^{r-1}}$ ($encode\left({\omega }_i^{{\tau }_i^{r-1}}\right)$), the client randomly maps ${\omega }_i^{{\tau }_i^{r-1}}$ to a point z selected from a set of nearby lattice points forming a convex hull around ${\omega }_i^{{\tau }_i^{r-1}}$. It then sends z mod q under the lattice basis (where q is the quantization precision parameter). To decode ${\omega }_i^{{\tau }_i^{r-1}}$ ($decode(B,encode\left({\omega }_i^{{\tau }_i^{r-1}}\right))$), the server maintains the previous global model ${\omega }^r$ as the decoding key. After receiving all clients’ $encode\left({\omega }_i^{{\tau }_i^{r-1}}\right)$, it recovers the original model parameter ${\omega }_i^{{\tau }_i^{r-1}}$ for each dimension by leveraging the proximity between ${\omega }^r$ and the received $encode\left({\omega }_i^{{\tau }_i^{r-1}}\right)$.

5. Experimental Description

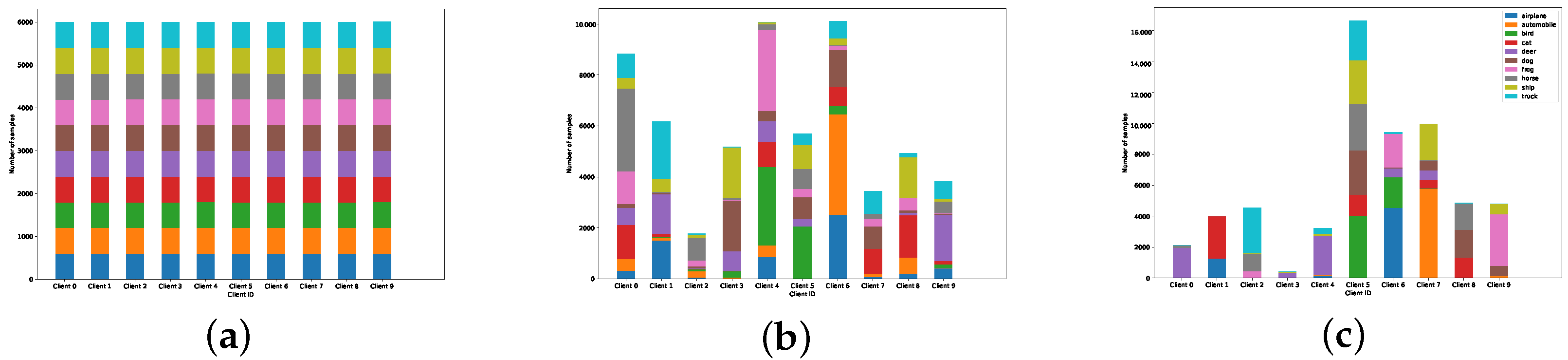
5.1. Dataset and Model

To systematically evaluate the algorithm under varying task complexities, we conduct comprehensive experiments on three benchmark datasets: [30], Fashion-MNIST [31], and CIFAR-10 [32]. For MNIST, we employ a fully connected MNISTNet network with a single hidden layer and ReLU activation; the optimizer is SGD with a learning rate of 0.1 and a batch size of 128. For Fashion-MNIST, we adopt the classical CNN architecture and use the Adam optimizer with a learning rate of 0.002 and a batch size of 128. For the more challenging CIFAR-10, we use ResNet-20 and retain SGD with a learning rate of 0.1.

5.2. Experimental Setup

In real federated learning scenarios, clients exhibit both data distribution and system performance heterogeneity. To reproduce these conditions, we introduce statistical and system heterogeneity in the federated setup. The details are described below.

Statistical heterogeneity: We employ Dirichlet-based data partitioning [33] ($p_k\sim Dir\left(\beta \right)$), which assigns non-identical class distributions and sample sizes to clients. The strength of statistical heterogeneity is controlled by $\beta$; as $\beta$ increases, the heterogeneity among clients becomes more pronounced, as illustrated in Figure 3.

System heterogeneity: To capture the uncertainty of local computation time, we model the duration of a single local update as a memoryless random variable X that follows an exponential distribution with parameter $\theta$. A larger $\theta$ indicates faster computation. Accordingly, we classify devices into two types: “fast” nodes with $\theta ={\displaystyle \frac{1}{2}}$ (expected time E[X] = 2 units) and “slow” nodes with $\theta ={\displaystyle \frac{1}{8}}$ (expected time E[X] = 8 units). By default, $25\%$ of the clients are slow nodes.

In our experiments, setting $\alpha$ = ${\displaystyle \frac{1}{K+1}}$ accelerates convergence. We attribute this to the fact that the previous global model is the closest approximation to the current one; retaining a fraction of it further alleviates the staleness effect.

Additionally, SACW advances the global model by periodically collecting a subset of client models. The period is determined by the handling time (h) and the server visiting time (v). The processing time h is governed by the quantization bit-width (b): fewer bits yield shorter processing. The access time v is set by the server according to local task complexity; simple tasks such as MNIST and Fashion-MNIST set v = 1, whereas the more complex CIFAR-10 task sets v = 6. For MNIST and Fashion-MNIST, we set the total number of clients to N = 50; for CIFAR-10, we set N = 40. The experimental setup for this study is outlined in

Table 2. Experiment environment configuration.

Experiment Environment	Configuration
CPU	Intel(R) Core(TM) i9-12900K (Intel Corporation, Santa Clara, CA, USA)
GPU	NVIDIA RTX A5000 (NVIDIA Corporation, Santa Clara, CA, USA)
RAM (random access memory)	64 GB
Programming language	Python 3.8
Pytorch version	1.8.2
CUDA toolkit	11.6

.

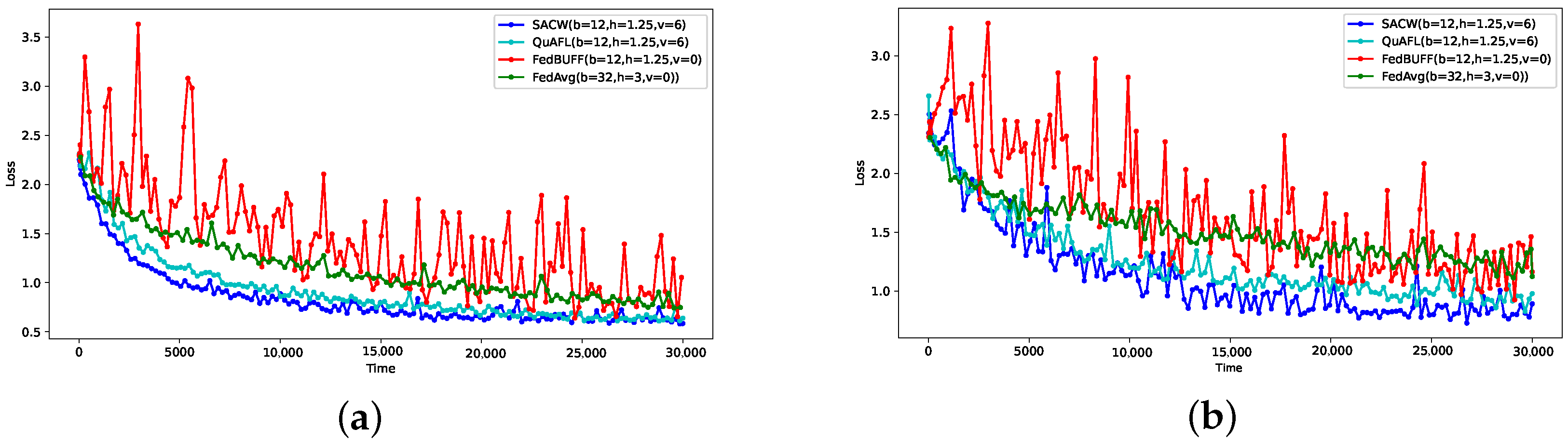
5.3. Comparative Experimental Results and Analysis

Figure 4, Figure 5 and Figure 6 adopt two degrees of data heterogeneity, namely $p_k\sim Dir\left(0.5\right)$ and $p_k\sim Dir\left(0.1\right)$. The label distributions of the clients are illustrated in Figure 3. In $p_k\sim Dir\left(0.5\right)$, heterogeneity among clients is mild and better reflects real-world data distributions. In $p_k\sim Dir\left(0.1\right)$, heterogeneity is severe.

In Figure 4, on the MNIST dataset, the federated learning task is relatively simple, and all four algorithms perform well. Under $\beta$ = 0.5, SACW exhibits rapid convergence and a smooth training trajectory, almost completely mitigating the effects of heterogeneity. The other three algorithms are visibly affected, with FedAvg and FedBUFF being the most sensitive. Under the harsher setting of $\beta$ = 0.1, SACW experiences the smallest degradation; accuracy drops by only $2.01\%$. The remaining algorithms fluctuate sharply, and FedAvg’s accuracy declines by $5.15\%$.

In Figure 5, on the Fashion-MNIST dataset, SACW outperforms the other three algorithms in both convergence speed and final accuracy under $\beta$ = 0.5 and $\beta$ = 0.1. When $\beta$ = 0.5, the training curve of SACW remains smooth despite the increased data and model complexity.

Figure 6 compares the global training loss curves using ResNet-20 on CIFAR-10, a more complex model and dataset. Figure 6a,b both exhibit fluctuations, yet SACW converges faster and achieves higher accuracy than the other methods. Under both $\beta$ = 0.5 and $\beta$ = 0.1, FedBUFF suffers from poor convergence and large oscillations. When $\beta$ = 0.1, QuAFL and FedAvg also display pronounced instability.

In summary, under system and statistical heterogeneity, SACW maintains stable training and rapid convergence across three datasets and neural networks of varying complexity. With $\beta$ = 0.5 and $25\%$ slow clients, SACW almost completely overcomes heterogeneity. Under the more challenging case of $\beta$ = 0.1, SACW experiences only minor fluctuations and outperforms the other three algorithms. To evaluate the model performance more comprehensively, we introduce precision, recall, and F1-score as core metrics, with the specific results of supplementary comparative experiments available in Appendix A.

5.4. Hyperparameter Analysis

5.4.1. Analysis of Core Hyperparameters (b, v, $\lambda$)

To examine the influence of three key hyperparameters—quantization bits b, weighting factor $\lambda$, and server access interval v—we conduct ablation studies on MNIST under $p_k\sim Dir\left(0.5\right)$ with $25\%$ slow clients, a setting that closely approximates real-world heterogeneity.

The parameter (b) represents the quantization bit-width, which controls the trade-off between communication cost and model accuracy. In our experiments, the server schedules clients for federative learning tasks based on server handling time (h) and waiting time (v). A larger quantization bit-width (b) means more precise model information, which increases processing time (h) but improves accuracy. As shown in Figure 7a, we conduct a hyperparameter analysis with b = $\{8,12,32\}$, where (b = 32) corresponds to the unquantized baseline. According to [29], the adopted lattice-based quantization guarantees bounded distortion, ensuring that quantization does not significantly degrade the global model. When (b = 12), the global accuracy curve closely matches that of the unquantized case, effectively reducing communication cost while maintaining training efficiency. Moreover, in unstable networks (high packet loss or jitter), the bit-width can be increased to compensate.

The parameter (v) denotes the server visiting time, which specifies the minimum local training duration allowed for clients. A larger (v) leads to more complete local training but may cause fast clients to wait for slow ones, making the system behave more synchronously. Conversely, a smaller (v) speeds up global updates but may reduce local model quality. As shown in Figure 7b, we tested (v = $\{1,2,5\}$) on the MNIST dataset and found that the global accuracy curve for (v = 1) is close to that for (v = 3). Thus, for simpler datasets such as MNIST and Fashion-MNIST, (v = 1) is sufficient. However, for the more complex CIFAR-10 dataset, a higher value (v = 5) is needed to balance local model completeness and overall training efficiency.

The parameter ($\lambda$) is a weighting coefficient that balances client data size and model staleness in global aggregation. A higher $\lambda$ imposes stricter penalties on client staleness, discarding more outdated information. As shown in Figure 7c, we ran extensive tests with $\lambda$ = $\{0.1,0.2,\dots ,1.0\}$. Performance stays stable when $\lambda$ is between 0.2 and 0.6. Setting $\lambda$ = 0.3 gives a good trade-off between letting data size dominate and penalizing delay, so this is the value we use in this paper.

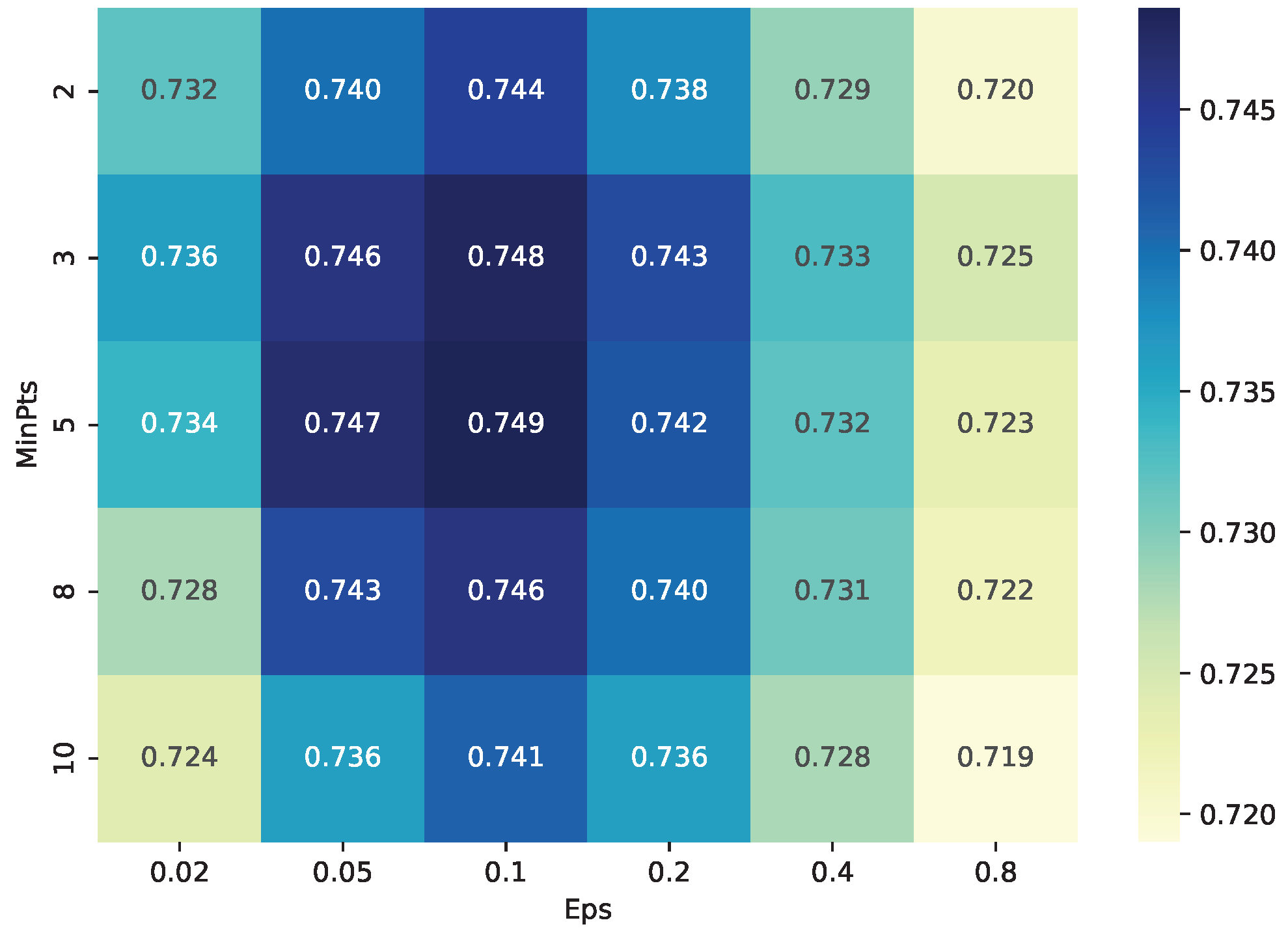
5.4.2. Sensitivity analysis to DBSCAN Clustering Parameters ($ϵ$, MinPts)

To examine the robustness of the proposed SACW framework with respect to the clustering hyperparameters used in the DBSCAN-based client selection, we conduct a systematic parameter sensitivity analysis. Specifically, we investigate the influence of the two key parameters—the neighborhood radius Eps and the minimum number of core points MinPts—on the clustering structure and global model performance.

Our analysis is conducted under the most heterogeneous and challenging setting: CIFAR-10 with Dirichlet $\beta$ = 0.1. The results on MNIST and Fashion-MNIST show similar trends. Both parameters are tuned within ranges that are empirically common.

• $ϵ$ is set to = $\{0.02,0.05,0.1,0.2,0.4,0.8\}$, covering a wide spectrum from very tight to loose clustering thresholds.
• MinPts is set to $\{2,3,5,8,10\}$, representing progressively stricter density constraints.

For each ($ϵ$, MinPts) pair, DBSCAN is applied to generate client clusters, and SACW is trained to converge with identical initialization and learning rate. The final global model accuracy is recorded and visualized as a heatmap (Figure 8).

Figure 8 illustrates the influence of DBSCAN parameters on model performance. The color intensity represents the final global accuracy. As observed, SACW achieves stable and consistent performance across a broad parameter range. The best accuracy of 0.7486 is obtained when $ϵ\in [0.1,0.2]$ and MinPts $\in [3,5]$. Within this range, accuracy fluctuations remain below $\pm 0.3\%$, indicating strong parameter robustness. When $ϵ$ is too small (≤0.05), the clustering becomes overly fine-grained, leading to insufficient data diversity representation. Conversely, when $ϵ\ge 0.4$ or MinPts $\ge 8$, the clustering becomes too coarse, merging heterogeneous clients and slightly degrading global performance.

5.5. Ablation Analysis

The SACW framework comprises two primary modules: (1) the DBSCAN-based client selection method (DBCS) and (2) the adaptive local model weighting method (ALMW). We decompose SACW into four variants:

• Default: Neither DBCS nor ALMW; employs random client selection and data-volume-based weighting.
• Default + DBCS: Replaces the client selection strategy with DBCS.
• Default + ALMW: Replaces the server-side weighting strategy with ALMW.
• SACW: The complete framework that combines both modules.

We evaluate these four variants on three datasets under two heterogeneity levels. The results are summarized in

Table 3. Ablation experiment results. (In the table, ✓ indicates the module is used, and × indicates it is not used).

Method		MNIST		Fashion MNIST		CIFAR 10
DBCS	ALMW	$\mathbf{\beta }$ = 0.1	$\mathbf{\beta }$ = 0.5	$\mathbf{\beta }$ = 0.1	$\mathbf{\beta }$ = 0.5	$\mathbf{\beta }$ = 0.1	$\mathbf{\beta }$ = 0.5
×	×	0.8928	0.9255	0.8548	0.8843	0.6541	0.786
✓	×	0.9105	0.9391	0.8689	0.8923	0.6705	0.7968
×	✓	0.9072	0.9324	0.875	0.8913	0.6758	0.8009
✓	✓	0.9276	0.9477	0.8902	0.9016	0.7486	0.8164

. DBCS yields the largest improvement when data heterogeneity is high. On MNIST with $\beta$ = 0.5, accuracy rises from $92.55\%$ to $93.91\%$. The gain is more pronounced on simpler datasets than on complex ones. ALMW plays a more critical role in complex datasets. On CIFAR-10 with $\beta$ = 0.1, ALMW alone improves accuracy by $2.17\%$. When both modules are active, SACW achieves the highest score in all 18 experimental settings and often surpasses the sum of individual gains. For example, on CIFAR-10 with $\beta$ = 0.1, SACW attains $74.86\%$, exceeding the second best result by $7.28\%$, indicating a synergistic amplification effect.

In summary, DBCS filters high-quality clients via clustering, and ALMW suppresses low-quality updates through adaptive weighting. They demonstrate complementary strengths across datasets of varying complexity and heterogeneity. Activating either module alone outperforms Default, while their joint activation yields non-linear synergy, ensuring SACW consistently achieves the best performance and validating the necessity of both DBCS and ALMW.

6. Discussion

Although our framework demonstrates robust performance in the presence of system and statistical heterogeneity, it leaves the local training phase of each client unoptimized; theoretically, both efficiency and convergence speed can therefore be further improved. Personalized federated learning [34]—tailoring local optimization to individual clients—will be a primary direction for future work. Moreover, when the number of client distribution vectors is small, the server can easily handle the load. However, once the system scales to millions of clients and thousands of labels, storing every vector becomes prohibitive and cripples training efficiency. Fortunately, an incremental clustering algorithm [35] copes with both streaming data and limited memory: new samples are merged into existing clusters on the fly, so the server only keeps the current cluster summaries instead of the full set of vectors.

A second concern arises during client-to-server uploads: vanilla gradient transmission is vulnerable to gradient inversion attacks [36], which can reconstruct private training data and thus violate the privacy-preserving tenet of federated learning. Differential privacy (DP) [37,38] offers a remedy: the Laplace or Gaussian mechanism can inject calibrated noise into the gradients before sharing, thereby thwarting such attacks. However, most DP-flavored defenses have been designed for synchronous federated protocols. Extending these guarantees to our semi-asynchronous setting—balancing privacy, utility, and convergence—constitutes another key avenue for future research. Additionally, malicious servers do exist in practice, and sending exact client distributions to them would clearly breach privacy. Recent works [39,40] show that deep models tend to predict the majority classes seen during training. Leveraging this, we can feed each client model a large set of random inputs and indirectly estimate its data distribution from the predicted labels. Such estimates are inherently coarse and noisy, mitigating the privacy threat posed by an untrusted server.

7. Conclusions

We propose SACW, a semi-asynchronous federated learning method that combines client selection with adaptive weighting to address training inefficiency under system and statistical heterogeneity. By periodically collecting local model progress while allowing clients to train asynchronously, SACW eliminates the mutual waiting inherent in synchronous schemes, thereby maximizing client utilization and mitigating system heterogeneity. An adaptive weighting mechanism that considers both data volume and model staleness suppresses the impact of low-quality local updates and accelerates convergence. To counteract statistical heterogeneity, a clustering-based client selection strategy enforces intra-cluster homogeneity and inter-cluster diversity, guiding the global model toward consistent optimization. Communication overhead is further reduced through model quantization for both uplink and downlink transmissions. Extensive experiments under heterogeneous conditions demonstrate that SACW outperforms state-of-the-art synchronous, asynchronous, and semi-asynchronous baselines in both convergence speed and final accuracy.