2. Background
In programming languages, date–time data types are rarely considered
primitive types, which can complicate their use and interoperability. However, certain languages provide built-in support for date and time handling, effectively treating them as primitive or near-primitive types. For example, the XML Schema provides a set of 19 primitive data types, among which are several dedicated to date and time: dateTime, date, time, gYearMonth, gYear, gMonthDay, gDay, and gMonth [
3]; C Standard Library (time.h) offers functions in the time.h header for date and time manipulation [
4]. The Unix-based systems timestamp uses a basic integer representation, facilitating compatibility across systems [
5]. However, the absence of a universally accepted primitive date–time type hinders interoperability.
The
range of a date–time system defines the earliest and latest date it can represent. For instance, the Unix times, which count the number of seconds elapsed since the Unix epoch (00:00:00 UTC on 1 January 1970), is commonly implemented using a signed 32-bit integer [
5]. This representation limits the range of representable dates from 13 December 1901, at 20:45:52 UTC, to 19 January 2038, at 03:14:07 UTC. Attempting to represent times beyond this range leads to an integer overflow, causing systems to interpret the time incorrectly. This limitation is referred to as the Y2K38 problem [
6]. In Visual Basic, the date data type holds IEEE 64-bit (8-byte) values that represent dates ranging from January 1 of the year 0001 through December 31 of the year 9999, and times from 12:00:00 AM (midnight) through 11:59:59.9999999 PM [
7].
Resolution refers to the smallest unit of time a system can accurately represent, such as seconds, milliseconds, or nanoseconds. Most systems have a fixed resolution; for example, Unix time traditionally offers a resolution of one second [
5]. However, modern implementations may extend this to higher precision, such as microseconds or nanoseconds, to accommodate applications requiring finer time measurements.
Time zones (
tz) are geographic regions where the same standard time is observed, defined by their offset from Coordinated Universal Time (UTC), expressed as UTC ± [offset] (e.g., UTC + 2, UTC-5) [
8]. Additionally, many regions implement
daylight saving time (DST), a system in which clocks are adjusted forward by one hour during the summer months and set back in the autumn to return to standard time. To manage these complexities, the
tz database [
9] serves as a widely used solution. It systematically compiles global time zone data and daylight-saving time rules, ensuring accurate timekeeping across different systems. Primarily designed for integration into programs and operating systems, the
tz database facilitates the correct handling of time zone differences and seasonal time changes [
9].
The
leap seconds problem [
10,
11,
12,
13] arises because leap seconds are added to, or subtracted from, UTC to adjust for irregularities in Earth’s rotation. While this adjustment has been implemented since 1972, many systems, particularly those requiring high precision like GPS, do not incorporate leap seconds [
14,
15]. For example, Java’s
LocalDateTime class [
16] allows input for leap seconds but fails to properly handle them in calculations. Similarly, Java’s
Date [
17] and
Calendar [
18] classes theoretically support leap seconds but do not account for them in practice. In Visual Basic 6, date–time is treated as a primitive type, yet leap seconds are unsupported, resulting in runtime errors if a leap second is entered. PostgreSQL’s [
19] timestamp type accepts leap seconds but merely adjusts the time by one second, storing the result as the next day at midnight.
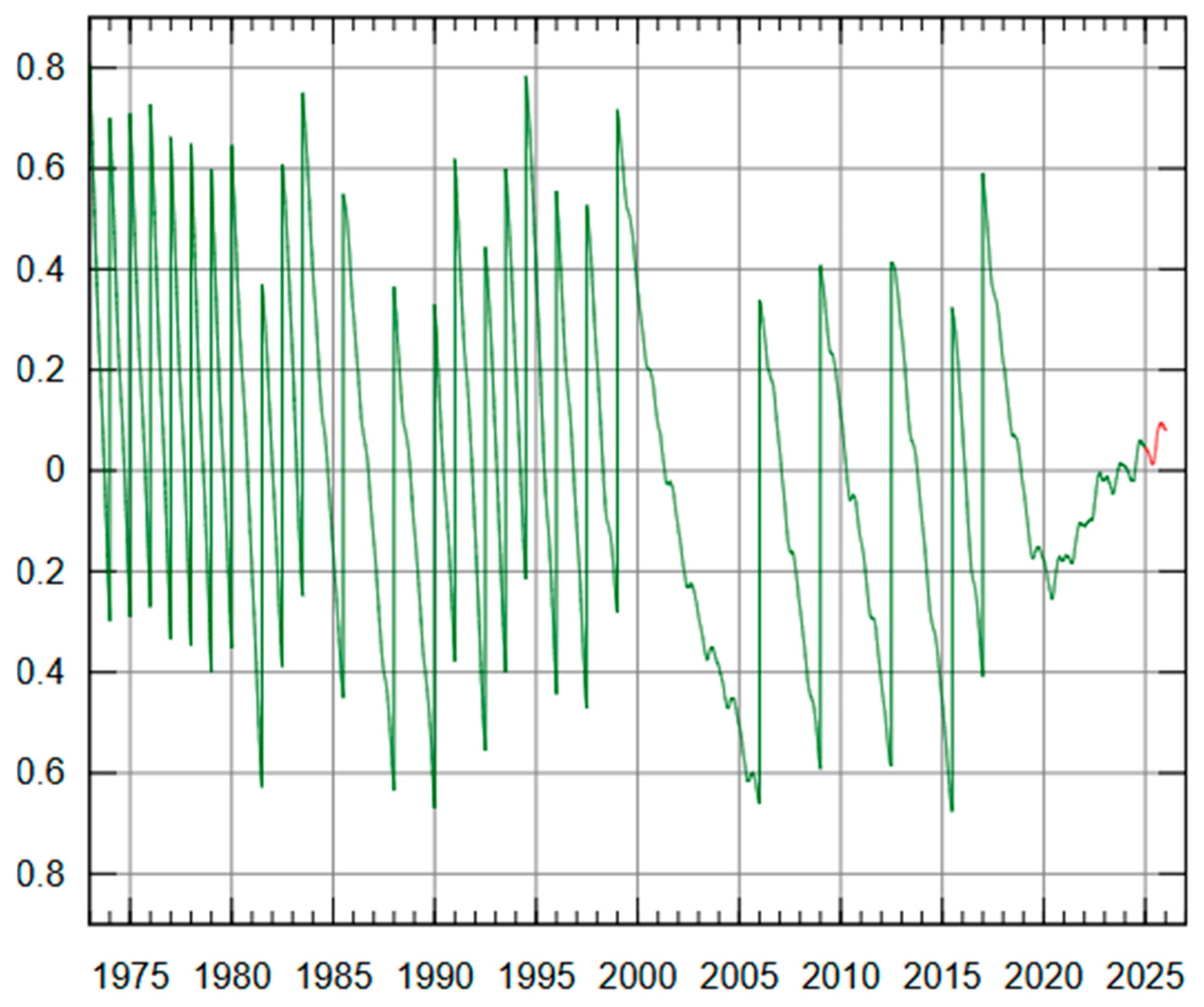
Figure 1 illustrates the difference between UTC and UT1 (Observed Solar Time), with vertical segments indicating the insertion of leap seconds [
20]. According to the current IERS policy, the time deviation between UTC and UT1 is maintained within a maximum limit of 0.9 s.
Several calendar systems around the world have been used historically or are still in use alongside the Gregorian calendar, including the Julian, Hijri (Islamic), Hebrew, Persian, Bahá’í, Ethiopian, Chinese, and Japanese calendars, among others. However, the Gregorian calendar is the most widely adopted, if not the only one universally accepted. Notably, all modern date–time data types rely on the Gregorian calendar, at least in their notation.
One significant challenge arising from this reliance is the
Year 1582 problem [
22,
23,
24,
25]. This issue originates from the introduction of the Gregorian calendar, which reformed the Julian calendar by skipping ten days to realign with the solstices (see
Figure 2). Some systems struggle to handle this transition properly, leading to inconsistencies when processing historical dates. This discrepancy particularly affects programming languages and database systems, which do not always account for the shift between the Julian and Gregorian calendars.
For instance, in Java [
27], dates from 1582 are processed as valid, overlooking the calendar shift, while Visual Basic 6 [
7] avoids this issue by not supporting dates before 1900, thus sidestepping the Gregorian reform entirely.
When providing a date such as 7 October 1582, Java fails to recognize the transition between the two calendars. The following code examples demonstrate this issue, where the results should be considered incorrect.
| Code example 1: |
| LocalDate oldDate = LocalDate.of(1582, Month.OCTOBER, 7); |
| System.out.println(oldDate); |
| Output: |
| > 1582-10-07 returns a valid date, even though this date should be invalid due to the calendar shift. |
| |
| Code example 2: |
| LocalDateTime start = LocalDateTime.of(1582, Month.OCTOBER, 4, 0, 0, 0); |
| LocalDateTime end = LocalDateTime.of(1582, Month.OCTOBER, 15, 0, 0, 0); |
| System.out.println(Duration.between(start, end).getSeconds() / 86400); |
| Output: |
| > 11 returns 11 days instead of 1, failing to account for the missing 10 days due to the calendar reform. |
Since Visual Basic 6 only supports dates starting from the year 1900, it does not encounter the Year 1582 problem at all, as it simply does not allow dates from that period.
Upon further research regarding the above problem, it is not necessarily an error when considering the
Proleptic Gregorian Calendar (PGC) [
25]. The PGC extends the Gregorian calendar backward in time, applying its rules even to dates before its official introduction in 1582. This means that
14 October 1582, in the Gregorian calendar, actually corresponds to
Thursday, 4 October 1582, in the Julian calendar [
25].
A notable real-world example is Christopher Columbus’s journal from his first voyage, which records
Friday,
12 October 1492, as the date of his arrival in the Americas (see
Figure 3) [
28]. However, this date follows the Julian calendar.
When handling historical dates in Java, this discrepancy becomes evident. A Java Date object incorrectly reports the weekday for
12 October 1492, as Wednesday, instead of the correct Friday. The issue arises because Java’s Date objects are not based on the Julian calendar. To obtain the correct weekday, the date must first be converted to its Proleptic Gregorian Calendar equivalent, which shifts it to
21 October 1492, where the correct weekday is Friday, as shown in Code examples 3 and 4:
| Code example 3: |
| LocalDate a = LocalDate.of(1492, Month.OCTOBER, 12, 0, 0, 0); |
| System.out.println(a.getDayOfWeek()); |
| Output: |
| > WEDNESDAY Incorrect due to Java’s default Gregorian implementation. |
| |
| Code example 4: |
| LocalDate a = LocalDate.of(1492, Month.OCTOBER, 21, 0, 0, 0); |
| System.out.println(a.getDayOfWeek()); |
| Output: |
| > FRIDAY Correct after converting to the Proleptic Gregorian Calendar. |
By applying the Proleptic Gregorian Calendar, historical dates can be aligned with modern computational frameworks, ensuring greater precision in date–time calculations. However, this also underscores the need for programming languages and database systems to provide built-in support for handling both Julian and Gregorian dates correctly, particularly for applications involving historical or archival data.
Another important issue is the representation of
Year Zero. In ISO 8601, [
4], Year zero exists and corresponds to 1 BC (Before Christ) in the Gregorian and Julian calendars. This discrepancy causes differences when interpreting ancient dates. The Java Date class uses ISO 8601, which introduces further complications when mapping historical events.
Regarding the date–time representation, it is important to note that Year zero in ISO corresponds to 1 BC in PGC. In both the Gregorian and Julian Calendars, year 1 BC is followed by year 1AD (Anno Domini), whereas in ISO 8601, year 0 is followed by year 1. This means, for example, that year 100 BC in PGC is represented as year −99 in ISO 8601 [
28]. This distinction is crucial when dealing with historical events in computing systems, as incorrect conversions could lead to misinterpretations of ancient dates.
Table 1 illustrates this difference:
These inconsistencies in historical date representations highlight the need for developers working with date–time libraries to be aware of the different conventions used across various systems. Ensuring accurate handling of ancient dates requires explicitly specifying the correct calendar system and being mindful of the differences between ISO 8601 and traditional calendar notations.
Beyond calendar-related discrepancies,
gravitational time dilation presents another challenge in precise timekeeping. As explained in Albert Einstein’s theory of general relativity, time passes more slowly near massive objects and faster farther away. This phenomenon, discussed in
Part II, Section 3 of The Foundation of the General Theory of Relativity [
29], implies that time at the top of a mountain runs slightly faster than at sea level due to weaker gravity at higher altitudes.
A date–time type incorporating additional parameters, such as the observer’s location, gravitational field strength, and relative motion to the gravitational source, would be valuable for high-precision time measurements, particularly in correcting for time dilation effects in satellite communication. Though this study does not address gravitational time dilation due to its complexity, it is acknowledged as a potential area for future research. Understanding and accounting for relativistic time effects will become increasingly important as technology advances and as more systems, such as GPS and deep-space communication, rely on extreme precision in time synchronization.
This contribution explores the challenges in date–time representations and proposes a new date–time data type design to address these issues. The proposed design enhances flexibility by supporting leap seconds, high time resolution, and time zone offsets. The goal is to highlight the necessity of a new date–time standard and to assess the feasibility of this approach.
However, several limitations remain. While the new design accounts for leap seconds and calendar discrepancies, it does not yet integrate relativistic effects such as gravitational time dilation or velocity-based time distortions, which could be significant in high-precision applications like space exploration and satellite-based systems. Additionally, the practical adoption of a new standard requires consensus among software developers, database designers, and timekeeping institutions, which poses an implementation challenge.
3. Related Work
Research on the date–time data type is a complex field that involves various challenges in areas such as programming, databases, operating systems, networking, and data storage. While a significant amount of information is available in forums and popular scientific publications on the internet, there is a noticeable lack of peer-reviewed articles specifically focusing on programming languages or databases concerning date time data types. In particular, research on handling leap seconds in database systems remains notably scarce, despite their critical role in ensuring accurate timekeeping and data consistency. To our knowledge, most available information on this topic comes from online discussions, such as [
30,
31], rather than formal academic studies.
Nelson et al. [
13] provide a comprehensive analysis of the theory, historical development of leap second in Coordinated Universal Time (UTC) and explore various possible future approaches for UTC, including maintaining the status quo, increasing the tolerance between UT1 (Universal Time) and UTC, periodically inserting leap seconds, implementing variable frequency adjustments, redefining the second, replacing UTC with TAI (International Atomic Time), or discontinuing leap seconds altogether. Additionally, the authors examine the transition from solar time to atomic time and the ongoing adjustments required to keep UTC aligned with Earth’s rotation. However, the article does not describe how leap second is implemented in computer systems and programming languages, including specific handling mechanisms in operating systems, timekeeping libraries, or the impact on software applications that rely on precise time synchronization.
Kuhn [
32] proposes Smoothed Coordinated Universal Time (UTS) as a refinement of UTC, specifically designed for information systems that struggle with leap second adjustments. The conversion from UTC to UTS is intended to take place only within an end system rather than in reference clock hardware or a time service broadcasting station, ensuring compatibility while minimizing disruptions caused by leap second insertions. An updated version of Smoothed Leap Seconds, known as the UTC-SLS standard, was developed to address the challenges of handling UTC leap seconds in computer protocols, operating system APIs, and standard libraries [
10]. Leap second considerations in distributed computer systems are further explored by Kuhn in [
33], where he defines a standardized UTC variant for computer applications. This approach adjusts the clock phase gradually by 1 s near a leap second, similar to
adjtime(), but with a more precise and well-defined specification. Additionally, Kuhn introduces a modernized <time.h> implementation for ISO C [
34], and addresses timekeeping challenges by providing an improved API for handling time calculations. This API accounts for inconsistencies introduced by leap seconds and historical calendar changes, enhancing time representation in software systems.
These efforts align with the work of Mills [
5], who explores leap second handling in Unix-based systems, and its impact on time synchronization and system stability, as well as modifications to Unix kernels aimed at enhancing precision time synchronization and effectively accommodating leap seconds. Unlike other methods, Unix clocks typically implement a non-synchronous approach. A commonly used Mills-style Unix clock initially allows the time value to decrease where a leap second occurs before abruptly adjusting to the correct time one second later. This approach simplifies implementation and is described in detail in [
23]. Additionally, Mills discusses leap second management in network time protocols and its implications for distributed systems in [
35]. This work provides further insight into how leap seconds are handled across interconnected systems, addressing challenges related to synchronization precision and system reliability.
Dimitrov in [
36] revisits Codd’s [
37] recommendations on date and time handling in relational databases, focusing on modern challenges and best practices. The study highlights inconsistencies in time representation across systems, issues with epoch definitions, and the need for standardized date–time handling in databases. It discusses key recommendations, such as storing dates in UTC, ensuring proper time zone conversions, and supporting flexible date–time arithmetic while maintaining logical consistency. While some database systems implement these best practices, further improvements are needed for full compliance with relational model principles.
One critical component in time zone management for databases and operating systems is the tz database, a collaborative compilation of global time zone information and daylight-saving time rules. Maintained by Eggert since 2005 with organizational backing from ICANN [
9,
38,
39], the tz database—also known as
tzdata, the zoneinfo database, or the IANA time zone database—serves as a crucial reference for ensuring accurate and up-to-date time zone handling in software systems. Originally founded by Olson [
40], this database plays a vital role in addressing the challenges of time representation across different geographical regions, reinforcing the importance of standardized time-handling practices as advocated by Dimitrov [
36].
5. Results
This contribution proposes a design in which date–time concepts are used to help avoid the issue demonstrated earlier. The terminology used, as outlined above, includes the following:
Moment—to describe a specific point on the timeline,
Period—to describe a duration spanning days and times, and
Date–time—as an umbrella term encompassing both concepts.
This terminology is intended to prevent confusion between the terms date and date–time.
5.1. Primitive Type
The proposed date–time data type is envisioned as a primitive system analogous to bit-based encoding systems like ASCII or UTF-8. This makes it universally exchangeable across different platforms. Unlike Unix timestamps (32/64-bit integers), which are limited and imprecise in certain contexts, the proposed format aims to be a more robust primitive alternative without those constraints.
5.2. Resolution and Range
The system introduces flexible resolution and range settings to optimize both storage and performance. For example, if only minute-level resolution is required (e.g., store opening hours), it should not store superfluous data at second or millisecond resolution. This adaptability ensures efficient use of storage and computational resources.
5.3. Time Zones
While most time zones use hour-based offsets (e.g., +01:00, 05:00), some use minute or even second offsets (e.g., India at +05:30, Nepal at +05:45). The proposed system accommodates such irregularities and remains future proof in case more granular time zones emerge.
5.4. Leap Seconds
Leap seconds, unlike leap years, are observational and not computationally derived, which makes them challenging to integrate. Current systems often ignore leap seconds or allow invalid values (e.g., “60” for seconds) without meaningful results. The proposed system incorporates leap second proximity, allowing results like “5 or 5 + 1 s” to represent both standard and leap-second inclusive outcomes.
Figure 4 illustrates how the proposal handles some examples of critical dates.
5.5. Accuracy
Moments like “2019-05-05” are often interpreted as “2019-05-05 00:00:00.000Z,” but this may not reflect the user’s intended precision. To resolve this, the system supports embedded accuracy metadata within Moments:
Start (s): Beginning of the specified unit.
- ○
2019-05-05 (A:s) → “2019-05-05 00:00”
Whole (w): Represents the entire unit without implying any finer resolution.
- ○
2019-05-05 (A:w) → Implies the entire day, not just midnight.
End (e): End of the unit but not extending into the next.
- ○
2019-05-05 11:00 (A:e) → “2019-05-05 11:00:59.999…”
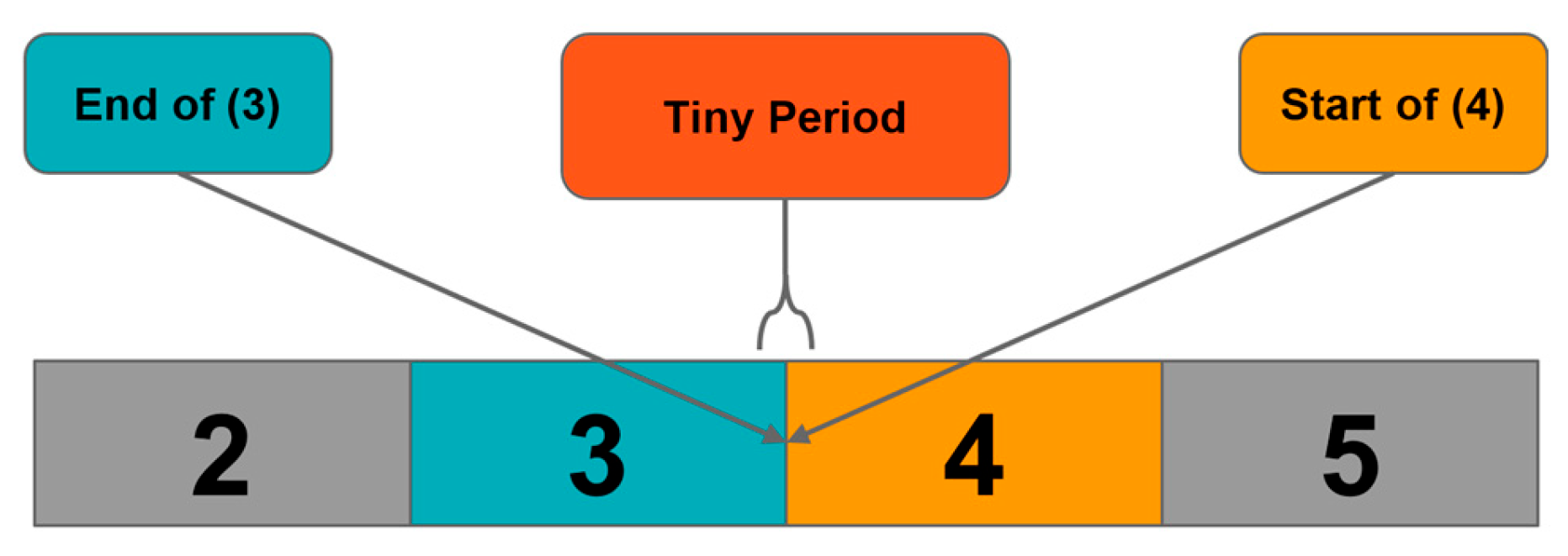
To formalize minute boundary transitions, the concept of a tiny period (tp) is introduced. It represents an infinitesimally small duration greater than zero. For instance, B = A + tp captures the Moment just after A but before the next full unit.
The system currently only supports Start precision for implementation but reserves flags for the other types.
Figure 5 and
Figure 6 illustrate how these accuracy types align across different resolutions, and where the tiny period exists between them.
5.6. Period and Moment
A Moment is a timestamp, while a Period spans across time. Periods have two counters: one for days, another for time within a 24 h window. These share the same resolution settings as Moments, account for one or more leap seconds, and can represent both positive and negative durations. Periods do not store time zone or accuracy metadata.
5.7. Arithmetics
Table 2 outlines notations and their associated meaning, where
M stands for a Moment,
P for a Period, and
n for a number. Note also that
Line and
Tilde over M and P are regenerated from Unicode. Then, calculations between two Moments will result in a Period as shown in
Table 3. That table also illustrates operations on the date–time type.
Again, performing calculations between two Moments results in a Period, as illustrated in
Table 3.
Table 3, furthermore, demonstrates the results of operations on Moments and Periods.
As observed, both Moment and Period can store leap second proximity values within them. For example, a Period of 3 days ± 1 s. In the forthcoming notations, an approximate Period or Moment and an absolute Period or Moment will be specified.
5.8. Moment Minus Moment
The subtraction of two Moments will give the results in proximity or absolute Period, depending on the value of the Moment, even if both Moments are absolute, but if one or both Moments are approximate, then the result is always an approximate Period. While
Table 4 outlines the result of subtraction between absolute and approximate Moments, it should be mentioned that
Moment Plus Moment is not supported by this design. The reason behind this decision is motivated by the absence of meaning of the
Plus operation. This can be exemplified by two dates of birth, where the difference between them shows a period of time, but where the sum of them lacks any corresponding meaning.
5.9. Moment Plus/Minus Period
Only an absolute Period with an absolute Moment will result in an absolute Moment; otherwise, the result will be an approximate Moment as outlined in
Table 5.
5.10. Period Plus/Minus Period
If both sides of an operation involve absolute Periods, the result will also be an absolute Period; otherwise, the result will be an approximate Period. see
Table 6.
5.11. Period Times/Divided Number
Multiplying Periods by numbers will result in the same kind of Period, as illustrated by
Table 7.
However, multiplication and division have other kinds of challenging details. For instance, multiplying a Period by a number will result in multiplying the day counter, time counter, and leap second counter. Then, it takes the exceeded time into days or a fraction of days into times without affecting the resolution level (R) of the Period. In cases with division, the calculation should be conducted correspondingly.
Example:
Assume R = hours, then
A = 3 days
A ÷ 2 = 1 day 12 h
Assume R = days, then
B = 3 days
B ÷ 2 = 1 day
While there is an awareness of such kinds of challenges, the study will leave those for future investigations and development.
5.12. Logical Comparison
When comparing two Moments or Periods, the outcome will determine if the relationship between the two values is equal, greater than, or less than one another.
5.13. Logical Comparison for Absolute Moment and Period
When performing logical comparisons between Moments or Periods, it is needed to perform a subtraction operation between the two Moments or Periods and check the result Period.
1 − 2
1 − 2
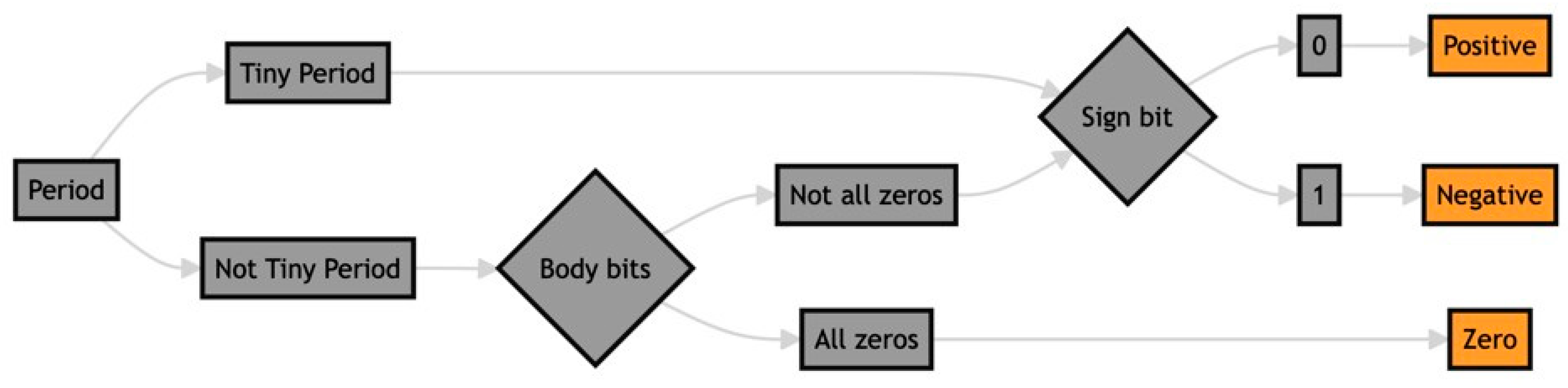
If now:
1 = 2 or 1 = 2 then is Zero
1 > 2 or 1 > 2 then is Positive
1 < 2 or 1 < 2 then is Negative
5.14. Reading Period
Table 8 and
Figure 7 illustrate how to determine if a Period is positive, negative, or zero.
Below are examples of the notation provided to represent Moments and Periods. The proposed date–time data type is primitive and basically consists of a bit pattern. Here, the symbol ‘@’ sets the start and the end of a bit pattern that represents a date or Period. The symbol ‘@G’ describes a Moment (‘G’ stands for the Proleptic Gregorian Calendar), while ‘@P’ stands for a Period. Generally, a bit pattern starts with one or more header bytes, and these header bytes describe the rest of the bit pattern. The system is totally independent of Gregorian, Julian, or any other calendar system. Moreover, the Julian Day Number (On Julian Day Number, JDN:
https://simple.wikipedia.org/wiki/Julian_day, accessed on 18 October 2025) (JDN) is used as a reference point alongside the date range level.
Example 1: Date 2019/05/05, resolution is day, no time zone, no leap seconds, accuracy is “start”. The notational representation of this date can be written as follows:
@G2019-05-05 {d:1, t:0, z:0, a:s, l:0-0}@ or as @2019-05-05@
Here
- -
d stands for the date range level, where
- ○
0: a bit that describes the Period,
- ○
1: start date is 0 × 258000 JDN (Julian Day Number, 0 × 258000 JDN = 2457600 JDN = 30 July 2016), with the pattern length of 15 bits, giving the range 0 × 258000…0 × 25FFFF,
- ○
2: start date 0 JDN, with the pattern length of 22 bits, giving the range: 0 × 0…0 × 3FFFFF,
- ○
3: start date is −0 × 80000000, with the pattern length of 32 bits, giving the range: −0 × 80000000…0 × FFFFFFFF,
- ○
4: start date is −0 × 800000000000, with the pattern length of 48 bits, giving the range: −0 × 800000000000…0 × FFFFFFFFFFFF.
- -
t for the time resolution level (from 0 to 20 value, where level 0 represents no time, 1: hourly resolution, … 5: second resolution, … 20: planck (the amount of time light takes to travel one Planck length = 5.39 × 10−44 s)),
- -
z for the time zone (from 0 to 10 value, where 0 value = no time zone, 1 for a time zone with 15 min resolution, etc.),
- -
a: for the accuracy (where the parameter s stand for start, w for whole, and e for end), and
- -
l: for the leap second (where, e.g., value 0-0 stands for plus 0 and minus 0).
The short form, @2019-05-05@, is motivated by the other values being default values. Here, the range level is 1, the resolution level is 0; z:0 meaning that there is no time zone; a:s meaning the start of the accuracy, and l:0-0 means that the leap second is plus 0 and minus 0. A header encodes the above-mentioned values and points out the contents of the following bytes that represent the date itself. A header is represented by one byte and has the following form: [IKDTTTZA], and is explained in more detail as follows:
- -
I: Indicator bit (0: more, 1: last) indicates whether this is the last header byte or another one will follow. In the above example, this bit has value 1.
- -
K: To determine whether this represents Period (0) or Moment (1). In the example above, this bit is 1.
- -
D: Date range (0: level-1, 1: level-2) determines the date range level. For levels above 2, there is a need for a two-byte header. In this example, this bit is 0.
- -
TTT: Time resolution (000: level-0 (no time), … 101: level-5 (sec), 111:level-6 (milli sec)). In the above example, these bits are 000.
- -
Z: Time zone (0: level-0, 1: level-1 (15 min resolution)). In the example, this means that this bit is 0.
- -
A: Accuracy (0: start, 1: whole). That is, this bit is 0.
In case of an approximate Moment with leap seconds, a header of two bytes with different patterns is needed. This implies the following pattern of the above-mentioned Moment: [11000000].
The JDN value for the date 2019/5/5 is 2458609, which is 0 × 2583F1. We subtract this value from the level start value, i.e., 0 × 2583F1 − 0 × 258000 = 0 × 03F1. This value is represented as a bit pattern: 0000 0011 1111 0001.
Because the last byte in the pattern contains a padding bit, the 15-bit data representation must be left-shifted by one bit. This produces the body 0000 0111 1110 0010 (0 × 07E2). With the header 0 × C0, the complete encoding is 0 × C0 0 × 07 0 × E2, and outlined as a Bin pattern in
Figure 8.
Example 2: Period of 1 Day, can be described as @P1D {d:1, t:0, l:0-0}@ or as short as @P1D@, since all values are default values. The bit representation for this has 3 bytes, for the header byte will have a pattern of [IKSDDTTT]:
- -
I: Indicator bit. So, in the example, this bit is 1.
- -
K: Kind bit (0: Period, 1: Moment). So, this bit is 0.
- -
S: Sign bit (0: Positive, 1: Negative). So, here, this bit is 0.
- -
DD: Date range (00: level-0, 01: level-2, … 11: level-3). Notice here, unlike a Moment range level that can be zero, for range level 4, a 2-byte header is needed with a different pattern. So, these bits are 01.
- -
TTT: Time resolution. So, these bits are 000.
In case of an approximate Period that contains leap seconds, a 2-byte header with different patterns will be needed. This means that the above Period properties will be represented as [10001000].
The body of the bit pattern will here be the same as in example 1. The complete bit pattern is outlined below, and in
Figure 9.
Hex: 0 × 88 00 02.
Bin: 0 b 1000 1000 0000 0000 0000 0010.
Figure 9.
A bit representation of @P1D {d:1, t:0, l:0-0}@, that is corresponding to example 2.
Figure 9.
A bit representation of @P1D {d:1, t:0, l:0-0}@, that is corresponding to example 2.
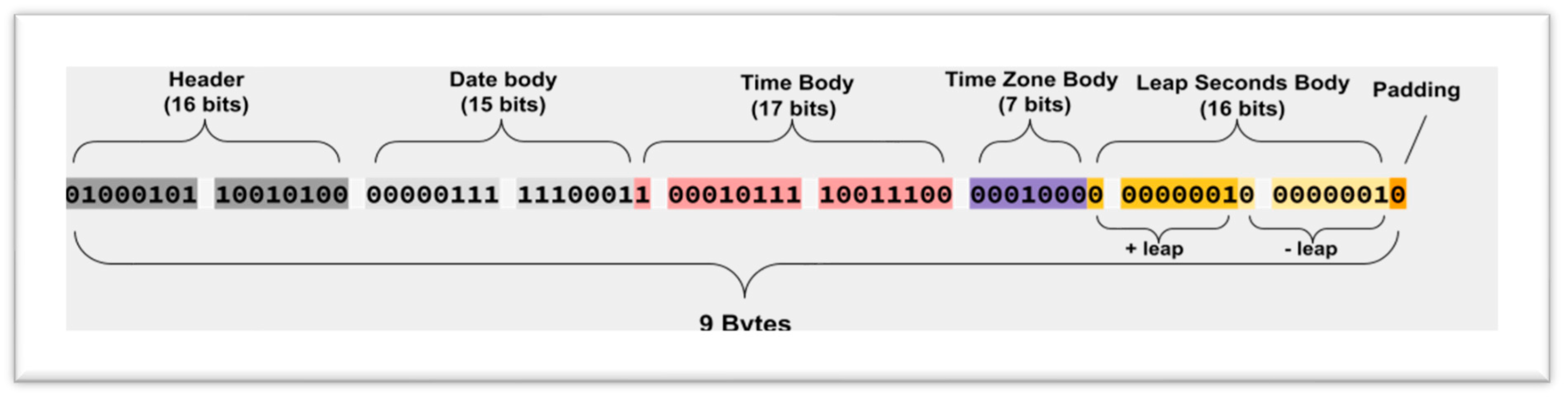
Example 3: 2019/5/5 19:53:00 + 02:00 is an example of a Moment with time and time zone. It also includes +1 or -1 leap seconds, noted as
@G2019-05-05T19:53:00+02:00 {d:1, t:5, z:1, a:s, l:1-1}@.
Here, t:5 means the resolution is level 5, which is the 2nd level. z:1 indicates that the time zone is level 1, which encodes to a resolution of 15 min (currently, this can cover all countries’ time zones, including the Nepal case), and l:1 − 1 means this Moment includes an approximate leap second of +1 −1 s. The bit pattern representation for this contains 9 bytes with two header bytes of the form [IKDDTTTT IZZZLLAA] and with the contents further described below:
- -
I: 0 more, this byte will have a following header byte.
- -
K: 1 Moment.
- -
DD: 00, Date range level: 1, like example 1 takes 15 bits.
- -
TTTT: 0101, time resolution level-5 (second); this level needs 17 bits to cover a day.
- -
I: 1 last; this is the last header byte.
- -
ZZZ: 001, time zone level-1; this level needs 7 bits.
- -
LL: 01, 2 bytes, one for positive and one for negative leap seconds. AA: 00, accuracy “start”.
Which means that the above-mentioned Moment is represented as [01000101 10010100].
The complete bit pattern is described below and outlined in
Figure 10:
- -
Hex: 0x45 94 07 E3 17 9C 10 02 02.
- -
Bin: 0b0100 0101 1001 0100 0000 0111 1110 0011 0001 0111 1001 1100 0001 0000 0000 0010 0000 0010.
Figure 10.
A bit representation of example 3.
Figure 10.
A bit representation of example 3.
5.15. Software Expressions in Pseudocode
The pseudocode presented below is Java-like. The proposed date–time data type here is, as has been outlined previously, a primitive data type, and can be described as a sequence of bytes or characters, as also proposed above. Sequences, as previously proposed, begin and end with the character @. The sequence @G…@ here corresponds to a Moment, M, while @P…@ corresponds to a Period, P.
| Examples: |
| Moment m1 = @G2019-01-01@; |
| Moment m2 = @G2019-01-02@; |
| boolean b1 = m2 > m1; // true; |
| boolean b2 = m1.isAbs(); // true (since there is no leap second); |
| Period p1 = m2 – m1; // The calculation produces an absolute Period; |
| boolean b3 = p1.isAbs(); // true; |
| Period p2 = m2 + m1; // compile error; |
| sout(p1.toString()); // print > @P+1D { d:1 t:0 l:0-0 }@. |
| |
| Period p3 = @P+1D@; |
| Period p4 = p3 + p3; |
| sout(p4.toString()): // print > @P+2D { d:1 t:0 l:0-0 }@; |
| Period p5 = p3 ∗ 2; |
| soutp5.toString()): // print > @P+2D { d:1 t:0 l:0-0 }@; |
| boolean b4 = p4 == p5 // true. |
| |
| Moment m3 = m1 + p1; |
| sout(m3.toString()); // print > @G2019-01-02 { d:1 t:0 z:0 a:s l:0-0 }@; |
| boolean b5 = m2 == m3 // true. |
Furthermore, while the example above shows expressions for date–time, it is proposed that Moment and Period be represented in a class hierarchy as shown below. This also enables clearer type affiliation and operations on these. See further Java-like examples below. Also, note the similarity with Java’s String data type, where strings may be seen as primitive as well as class instances.
| abstract class DateTime {...} |
| class Period extends DateTime {...} |
| class Moment extends DateTime {...} |
| |
| public Period diff(Moment Moment1, Moment Moment2) { ... |
| public Moment add(Moment m, Period p) { ... |
| public Moment sub(Moment m, Period p) { ... |
| public Period add(Period p, Period p) { ... |
| public Period sub(Period p, Period p) { ... |
| public Period multi(Period p, int n) { ... |
| |
| p instanceof Period // true |
| p instanceof Moment // false |
| p instanceof DateTime // true |
The results of this study show a conceptual investigation of the aforementioned problems in representing time and how these problems are met at the conceptual and design levels. For the presented concepts and designs to have concrete usability, those have also been investigated at the level of software development. Through these steps, consistency is reported, including concepts, design, and software development, which shows potential to form a robust base for further investigation and development.