Efficient Image Restoration for Autonomous Vehicles and Traffic Systems: A Knowledge Distillation Approach to Enhancing Environmental Perception ^†

Abstract

Image restoration tasks such as deraining, deblurring, and dehazing are crucial for enhancing the environmental perception of autonomous vehicles and traffic systems, particularly for tasks like vehicle detection, pedestrian detection and lane line identification. While transformer-based models excel in these tasks, their prohibitive computational complexity hinders real-world deployment on resource-constrained platforms. To bridge this gap, this paper introduces a novel Soft Knowledge Distillation (SKD) framework, designed specifically for creating highly efficient yet powerful image restoration models. Our core innovation is twofold: first, we propose a Multi-dimensional Cross-Net Attention(MCA) mechanism that allows a compact student model to learn comprehensive attention relationships from a large teacher model across both spatial and channel dimensions, capturing fine-grained details essential for high-quality restoration. Second, we pioneer the use of a contrastive learning loss at the reconstruction level, treating the teacher’s outputs as positives and the degraded inputs as negatives, which significantly elevates the student’s reconstruction quality. Extensive experiments demonstrate that our method achieves a superior trade-off between performance and efficiency, notably enhancing downstream tasks like object detection. The primary contributions of this work lie in delivering a practical and compelling solution for real-time perceptual enhancement in autonomous systems, pushing the boundaries of efficient model design.

1. Introduction

Image restoration—encompassing tasks such as deraining, deblurring, and dehazing—stands as a critical frontline defense for the safety and reliability of autonomous vehicles and traffic systems. These tasks are particularly important in challenging environmental conditions where image quality is often degraded by factors such as inclement weather, poor lighting, and low visibility, leading to perceptual results such as poor object detection, as shown in Figure 1a. Effective restoration of these images is essential for autonomous vehicles to perform critical tasks, including vehicle detection, pedestrian detection, and lane line identification, which are foundational to the safety and reliability of autonomous driving systems [1].

While transformer-based encoder–decoder models [2,3,4] have demonstrated exceptional performance in image restoration tasks, their computational demands—particularly in terms of FLOPs (floating-point operations), memory, and energy usage—make them less suitable for resource-constrained environments such as autonomous vehicles and traffic systems. These platforms typically operate under stringent resource limitations, where processing power, memory, and energy are at a premium. This constraint makes it infeasible to deploy computationally expensive models, as illustrated in Figure 1b. This creates a critical deployment gap: the very models that excel at restoring clarity are often unsuitable for the resource-constrained hardware of autonomous vehicles where power, memory, and processing capabilities are severely limited.

In response to this challenge, model compression techniques have gained attention as a way to reduce computational complexity while retaining the high performance of state-of-the-art image restoration models. Knowledge distillation, first introduced by Hinton et al. [5], has emerged as an effective method for model compression. In this approach, a lightweight student model is trained to emulate the behavior of a larger, more powerful teacher model, with various distillation strategies targeting different learning objectives such as logits, feature maps, and reconstruction outputs. Over time, distillation techniques have evolved to incorporate advanced methods like intermediate features [6,7], attention matrices [8,9], and instance relationships [10,11].

While these techniques have been successful in domains like classification and detection, their application to image restoration has remained less explored. Existing distillation strategies for image restoration typically involve direct mimicking of teacher features [12,13,14] or reconstruction outputs [15,16]. However, these methods often overlook the importance of implicit attention relationships between teacher and student networks. Such attention relationships are critical for preserving fine-grained details, such as edges and textures, which are vital for high-quality image restoration. Furthermore, traditional distillation approaches can suffer from instability due to the direct imitation of teacher features, limiting their scalability to resource-constrained platforms like autonomous vehicles.

To address these limitations, we propose a novel Soft Knowledge Distillation (SKD) strategy, synergistically integrated with a Multi-Dimensional Cross-Net Attention (MCA) mechanism. This work is specifically designed to bridge the critical performance–efficiency gap for image restoration in autonomous systems. The principal novelty and contributions of our work are fourfold:

• A Holistic distillation framework: We introduce a comprehensive SKD framework that moves beyond conventional feature mimicking. Unlike prior arts that often focus on a single aspect, our method orchestrates knowledge transfer at multiple levels, deliberately designed to equip a compact student model with the robust capabilities of a large teacher model, while being inherently suitable for resource-constrained platforms.
• Multi-dimensional attention transfer: A cornerstone of our innovation is the MCA mechanism. It enables the student to learn implicit, fine-grained attention relationships from the teacher across both spatial and channel dimensions. This is a significant departure from methods that directly mimic features, allowing the student to intrinsically understand what and where to attend for recovering critical details like edges and textures, which are paramount for high-quality restoration and subsequent detection tasks.
• Stable and efficient feature guidance: To circumvent the instability of direct feature imitation, we introduce a Gaussian kernel function to guide the student’s learning in a transformed kernel space. This novel approach ensures a more stable and efficient optimization process, enhancing the reliability of the distillation under strict computational budgets.
• Contrastive reconstruction learning: We pioneer a paradigm shift at the reconstruction level by replacing traditional pixel-wise loss functions with a contrastive learning loss. Here, the teacher’s high-quality reconstructions serve as positive anchors, explicitly pulling the student’s output towards them while pushing away from the degraded inputs. This strategy fundamentally boosts the perceptual quality of the student’s restorations, a critical factor for improving downstream task accuracy.

Our proposed SKD framework is not merely an incremental improvement but a cohesive solution that rethinks how knowledge is distilled for image restoration. Through extensive experiments on deraining, deblurring, and dehazing, as well as downstream detection tasks, we show that our approach significantly reduces computational complexity without sacrificing restoration quality, as shown in Figure 2. More importantly, we provide concrete evidence that our method leads to significant gains in critical downstream perception tasks, such as vehicle and pedestrian detection, thereby directly enhancing the safety and reliability of autonomous systems. These results underscore the potential of our SKD framework for real-time deployment, offering a practical and effective path forward for intelligent transportation systems.

2. Related Work

In this section, we review relevant works related to the core components of our research, specifically image restoration, knowledge distillation, and contrastive learning.

2.1. Image Restoration Methods

2.1.1. Prior-Based Methods

Prior-based image restoration techniques rely on physical scattering models and statistical priors to estimate parameters such as transmission maps, atmospheric light intensity, and other image characteristics based on clear image statistics [17,18,19,20,21,22,23]. For example, He et al. [17] proposed a dehazing method based on the dark channel prior (DCP), which estimates transmission maps and global atmospheric light. Subsequent works [21,24,25,26] extended the DCP approach to other image restoration tasks. Additionally, Li et al. [23] developed a layer prior method to effectively remove rain streaks from images. Chen et al. [27] introduced a unified prior loss committee that combines several well-established physical priors to improve restoration performance.

While prior-based methods are effective in certain scenarios, they often face limitations when dealing with more complex or diverse degradation types.

2.1.2. CNN-Based Methods

Convolutional neural networks (CNNs) have revolutionized image restoration by learning complex features and restoration functions directly from data. These methods have achieved state-of-the-art performance across various restoration tasks [28,29,30,31,32,33,34]. For instance, Dong et al. [28] introduced a Multi-Scale Boosted Dehazing Network built on the U-Net architecture, which improves dehazing performance through dense feature fusion. Shao et al. [30] proposed an end-to-end image translation and dehazing network, which achieved improved results for both tasks. Similarly, Zamir et al. [34] developed a multi-stage architecture that progressively learns restoration functions tailored to degraded inputs, enhancing overall restoration performance.

CNN-based methods have greatly advanced image restoration, enabling the learning of complex features and producing high-quality restored images across a wide range of degradation types.

2.1.3. Transformer-Based Methods

The integration of Vision Transformers (ViTs) into image restoration tasks has gained considerable attention due to their ability to capture long-range dependencies, which are essential for understanding the global context and relationships within an image. Recent works have demonstrated the effectiveness of ViTs in various restoration tasks [2,3,4,35,36,37]. For example, Wang et al. [3] proposed Uformer, a hierarchical encoder–decoder network utilizing Vision Transformer blocks, which effectively captures both local and global dependencies. Zamir et al. [2] introduced Restormer, a Transformer-based model that incorporates key design innovations in multi-head attention and feed-forward networks, allowing it to capture long-range pixel interactions while remaining computationally efficient. Similarly, Chen et al. [4] proposed DRSformer, which incorporates a learnable top-k selection operator within the transformer block, enhancing the model’s focus on the most critical features during restoration.

Transformer-based methods, such as Restormer, Uformer, and DRSformer, have demonstrated strong performance in image restoration by leveraging self-attention mechanisms to capture long-range dependencies and focus on important features, making them particularly effective for handling a wide range of image degradations.

2.2. Knowledge Distillation

Knowledge distillation [5] is a technique that transfers knowledge from a large teacher model to a smaller student network. The process involves training the student on a transfer set, using the soft target distribution provided by the teacher model. Both the teacher’s outputs and intermediate representations can significantly enhance the training process, improving the final performance of the student network.

This technique has been widely applied across high-level computer vision tasks such as object detection [38], face recognition [39], and semantic segmentation [40]. More recently, knowledge distillation has been employed in image restoration tasks [41,42], where it helps guide smaller models in restoring images degraded by noise, blur, or other distortions. These studies demonstrate how distillation can enhance the performance of lightweight models in challenging restoration tasks.

Knowledge distillation is a powerful technique that transfers both outputs and intermediate representations from a teacher model to a smaller student model, boosting performance across various computer vision and image restoration tasks.

2.3. Contrastive Learning

Contrastive learning is a self-supervised technique that constructs positive and negative pairs around an anchor point, encouraging the model to pull positive samples closer and push negative ones farther apart in the representation space [43]. Traditionally used in high-level tasks such as image classification and natural language processing, contrastive learning has recently been extended to low-level vision tasks, including image-to-image translation [44,45], deraining [46,47], and dehazing [43,48,49].

For instance, Zheng et al. [49] proposed curricular contrastive regularization for image dehazing, which focuses on achieving consensus within the contrastive space, providing advantages over non-consensual strategies. Ye et al. [46] introduced a non-local contrastive learning mechanism specifically designed for image deraining. This approach exploits the intrinsic self-similarity of images, enhancing deraining performance by effectively applying contrastive learning principles.

Contrastive learning, by encouraging the differentiation of positive and negative samples in the representation space, has proven effective in low-level vision tasks, such as deraining and dehazing, where it enhances performance through self-supervised learning mechanisms.

3. Methods

3.1. Overall Pipeline

The core objective of our Soft Knowledge Distillation (SKD) framework is to enable a compact student network to acquire the powerful image restoration capabilities of a large teacher model, not through direct feature imitation, but by learning the teacher’s underlying “reasoning” process and perceptual standards. This is achieved via a dual-pathway strategy encompassing both feature-level and image-level guidance. It is important to note that the proposed SKD framework is architecture-agnostic. In this work, to fairly demonstrate the effectiveness of our distillation method, we construct the student models as compact counterparts of their teachers by reducing the number of layers and feature channels while retaining the same fundamental building blocks. This ensures that any performance gain can be primarily attributed to the distillation process itself rather than to architectural modifications. The overall process is illustrated in Figure 3, where a degraded image $I\in {\mathcal{R}}^{H\times W\times 3}$ is input into both networks. The teacher network, which is pre-trained and equipped with a sophisticated architecture, excels at restoring clean images from degraded inputs by effectively mitigating various degradation factors such as noise, blur, and weather-related distortions. In contrast, the student model is designed to be smaller and more efficient by reducing the number of transformer layers and feature channels in its residual blocks, making it suitable for resource-constrained environments like autonomous vehicles or other traffic systems. The distillation process is carried out at two levels: feature-level distillation and image-level distillation.

Feature-level learning is accomplished through our proposed Multi-Dimensional Cross-Network Attention (MCA) mechanism. The intermediate features of the student network interact with features of corresponding blocks in the teacher network, allowing the student to implicitly absorb the attention knowledge embedded within the teacher. The resulting student and teacher features are then mapped to Gaussian kernel space, and the loss is computed based on their distance, enabling stable and efficient knowledge transfer.

At the image level, in addition to the reconstruction loss computed with ground truth, contrastive learning helps the student further refine its output. The student’s reconstructed image uses the teacher’s output as a positive example, aligning closely with it, while multiple original degraded images serve as negative examples, encouraging divergence from these degraded instances. What is more, we also utilize a feature extractor for both the student and teacher’s reconstruction images and conduct contrastive learning on corresponding features.

These components of the SKD strategy work together to indirectly but significantly enhance the efficiency and stability of the student network during the distillation process, distinguishing our approach from direct imitation methods.

3.2. Multi-Dimension Cross-Net Attention

A central component of the SKD strategy is the Multi-Dimensional Cross-Network Attention (MCA) mechanism, which facilitates the transfer of attention knowledge from the teacher to the student by interacting across both channel-wise and spatial-wise dimensions. In traditional distillation methods, features from the teacher and student networks are directly compared. However, the MCA mechanism enhances this process by enabling a more sophisticated interaction between these features, allowing the student to benefit from richer attention knowledge, as shown in Figure 4.

Given the features from corresponding blocks in the teacher and student networks, we first use projectors to map these features into a unified dimensional space, represented as $T_f^i$ and $S_f^i$. The interaction process, which yields the updated student features $S_{fc}^i$ (channel) and $S_{fs}^i$ (spatial), can be expressed as:

$$\begin{array}{c}\hfill S_{fc}^i=softmax(T_f^i·{(S_f^i)}^{\mathsf{T}}/\lambda )·S_f^i,\end{array}$$

(1)

$$\begin{array}{c}\hfill S_{fs}^i=S_f^i·softmax({(T_f^i)}^{\mathsf{T}}·S_f^i/\lambda ),\end{array}$$

(2)

where $\lambda$ is an optional temperature factor defined by $\lambda =\sqrt{d}$.

To quantify the similarity between the teacher and student features, we map both feature sets to a Gaussian kernel space, where the distance between the features is computed. This approach is motivated by its superior stability and effectiveness compared to direct distance measures like Euclidean or Cosine similarity. The Euclidean distance $D_{eucl}={\parallel x-y\parallel }_2$ is sensitive to the absolute magnitude of features and can lead to unstable optimization. In contrast, the Gaussian kernel measures relative proximity in a normalized, bounded space, providing a smoother gradient and greater robustness to outliers. While $\sigma$ denotes the width of Gaussian kernel function, the Gaussian kernel distance and loss are defined as

$$\begin{array}{c}\hfill GK(x,y)=1-exp(-{\displaystyle \frac{\left|\right|x-{y\left|\right|}_2^2}{2{\sigma }^2}}),\end{array}$$

(3)

$$\begin{array}{c}\hfill L_{GK}=\sum _{i=1}^n(GK(S_f^i,T_f^i))+\alpha 1(GK(S_{fc}^i,T_f^i)+GK(S_{fs}^i,T_f^i)).\end{array}$$

(4)

3.3. Contrastive Learning for Knowledge Distillation

To further enhance the student’s image restoration capabilities, we integrate contrastive learning into the SKD framework. Contrastive learning has been extensively used in representation learning [50] and image restoration [43,46] tasks, where it encourages the model to bring similar instances closer together while pushing dissimilar instances further apart. In our approach, this technique is applied to both the reconstructed images and the corresponding features during the distillation process (Figure 5).

In the contrastive learning setup, the student’s reconstructed images and their corresponding extracted features serve as anchors, while the teacher’s output acts as the positive example. A batch of degraded images and their corresponding features serve as negative examples. By minimizing the distance between the anchor and positive examples, while maximizing the distance from the negative examples, the student network is guided to improve its ability to reconstruct clean images. The contrastive learning loss $L_{CL}$ is composed of two components: the image contrastive learning loss $L_{ICL}$ and feature contrastive learning loss $L_{FCL}$:

$$\begin{array}{c}\hfill L_{ICL}(S_r,T_r,I)=-log{\displaystyle \frac{sim\left(S_r,T_r\right)}{sim\left(S_r,T_r\right)+{\sum }_{q=1}^{b}sim\left(S_r,I_q\right)}}\end{array}$$

(5)

$$\begin{array}{c}\hfill L_{FCL}(S_r,T_r,I)=-log{\displaystyle \frac{sim\left(\varphi \left(S_r\right),\varphi \left(T_r\right)\right)}{sim\left(\varphi \left(S_r\right),\varphi \left(T_r\right)\right)+{\sum }_{q=1}^{b}sim\left(\varphi \left(S_r\right),\varphi \left(I_q\right)\right)}},\end{array}$$

(6)

$$\begin{array}{c}\hfill L_{CL}(S_r,T_r,I)=L_{ICL}(S_r,T_r,I)+L_{FCL}(S_r,T_r,I),\end{array}$$

(7)

where $S_r$, $T_r$, I represent the student’s output, the teacher’s output (positive sample), and the degraded images (negative samples), respectively. The batch size is denoted by b, and $sim(u,v)=exp\left({\displaystyle \frac{u^{T}v}{\parallel u\parallel \parallel v\parallel \tau }}\right)$ measures the similarity between two feature vectors, with $\tau$ as the temperature parameter and $\varphi \left(\right)$ representing a feature extraction operation using VGG-19 [51].

3.4. Overall Loss

The final loss function combines the three components discussed above: reconstruction loss, Gaussian kernel loss, and contrastive learning loss. The reconstruction loss measures the difference between the student’s output $S_r$ and ground truth G is formulated as

$$\begin{array}{c}\hfill L_{REC}={\left|\right|G-S_r\left|\right|}_1.\end{array}$$

(8)

The overall loss function is then defined as

$$\begin{array}{c}\hfill L=L_{REC}+\alpha 2L_{GK}+\alpha 3L_{CL},\end{array}$$

(9)

where $\alpha 2$ and $\alpha 3$ are trade-off weights that balance the contributions of the Gaussian kernel loss and contrastive learning loss. These weights are tuned to ensure that each component of the loss function contributes optimally to the distillation process.

4. Results

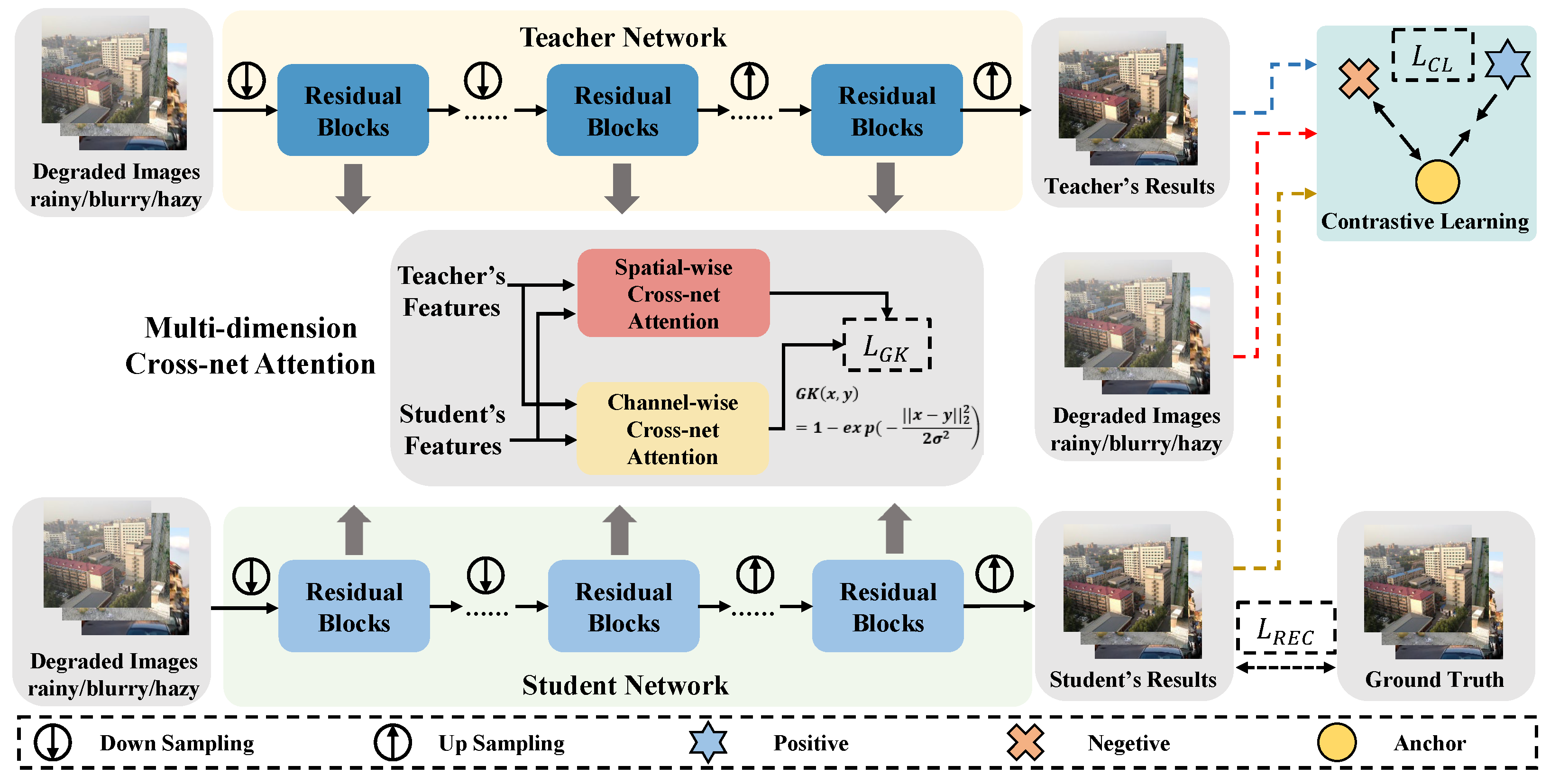
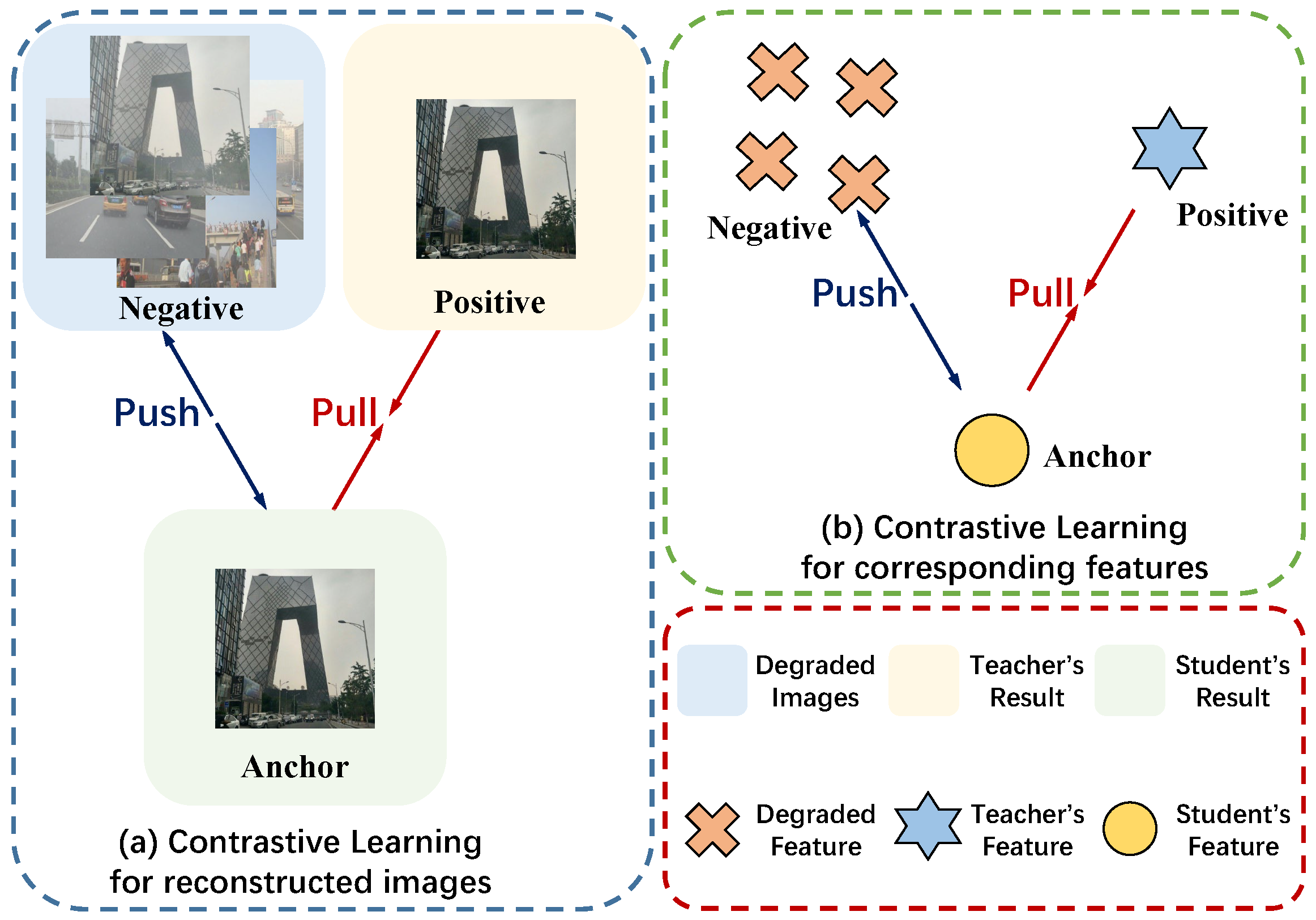
4.1. Implementation Details

We evaluate the proposed Soft Knowledge Distillation (SKD) strategy using a comprehensive set of eight datasets across three distinct image restoration tasks: deraining, deblurring, and dehazing. These tasks are critical for real-time traffic applications, where image quality must be restored under challenging environmental conditions.

For deraining, we use three datasets: the synthetic Rain1400 [52], Test1200 [53], and the real-world SPA [29]. For deblurring, we utilize the synthetic Gopro [54], HIDE [55], and the real-world BLUR-J [56]. Finally, for dehazing, we adopt the synthetic subset OTS and real-world subset RTTS from the RESIDE dataset [57].

To quantitatively assess the image restoration quality, we use a combination of full-reference and no-reference evaluation metrics. Specifically, for the synthetic datasets, we employ the Peak Signal-to-Noise Ratio (PSNR) [58] (in dB) and Structural Similarity Index (SSIM) [59], which measure pixel-level fidelity and structural similarity, respectively. For real-world datasets, where ground-truth references are unavailable, we use two no-reference metrics, the Blind/Referenceless Image Spatial Quality Evaluator (BRISQUE) [60] and Perception-based Image Quality Evaluator (PIQE) [61], which assess image quality based on perceptual and spatial features.

In addition to image quality, we evaluate the model complexity by measuring the Floating Point Operations (FLOPs) and inference time on each $512\times 512$ image. These metrics are critical for evaluating the feasibility of our SKD strategy in resource-constrained environments such as autonomous vehicles, where computational efficiency is paramount. We highlight the best results in bold and underline the sub-optimal results.

The entire SKD framework is implemented using PyTorch 1.10. We adopt Adam as the optimizer, with a temperature parameter set to $\tau$ = 1 × 10⁻⁶. The trade-off weights used in the SKD loss function are ${\alpha }_1=0.5$, ${\alpha }_2=0.2$, and ${\alpha }_3=0.2$. The student models are trained for 100 epochs with a batch size of 8. The learning rate starts at 2 × 10⁻⁴ and is reduced gradually to 1 × 10⁻⁶ using cosine annealing [62] to ensure stable convergence. During training, all input images are randomly cropped into $128\times 128$ patches, and pixel values are normalized to the range [−1, 1]. This augmentation strategy helps improve generalization and reduces the risk of overfitting, which is especially important when training on diverse and complex datasets like those used in this study.

For the teacher networks, we select three state-of-the-art transformer-based models known for their performance in image restoration tasks: Restormer [2], Uformer [3], and DRSformer [4]. These models were chosen due to their ability to capture long-range dependencies and complex features in the image restoration process. The architectures of these teacher models vary in terms of depth and dimensions:

• Restormer: 4, 6, 6, 8 layers per encoder–decoder level, with a feature dimension of 48.
• Uformer: 1, 2, 8, 8 layers, with a feature dimension of 32.
• DRSformer: 4, 4, 6, 6, 8 layers, with a feature dimension of 48.

The corresponding student models—Res-SKD, Ufor-SKD, and DRS-SKD—compress the hyper-parameters to more resource-efficient configurations:

• Res-SKD: 1, 2, 2, 4 layers, with a feature dimension of 32.
• Ufor-SKD: 1, 2, 4, 4 layers, with a feature dimension of 16.
• DRS-SKD: 2, 2, 2, 2, 4 layers, with a feature dimension of 32.

To ensure reproducibility, we clarify that the student models maintain the same fundamental architectural blueprint as their respective teachers (e.g., the same type and sequence of transformer blocks), with compression achieved solely by reducing the number of layers in each block and the dimensionality of the feature channels. It is worth noting that while our experiments utilize transformer-based models to construct a strong benchmark, the proposed SKD framework is not bound to any specific network family. The distillation mechanism operates on feature maps and output images, making it readily applicable to other architectures, such as CNNs. The exploration of its efficacy with CNN-based teachers is a valuable direction for future work. This compression results in significant reductions in both FLOPs and parameters, achieving an average reduction of 85.4% and 85.8%, respectively. Despite the reduced complexity, the student models retain much of the performance of their teacher counterparts, as demonstrated in the following experimental results.

4.2. Comparisons with State-of-the-Arts

Comparison with knowledge distillation methods. We begin by comparing our Soft Knowledge Distillation (SKD) strategy with two state-of-the-art (SOTA) image-to-image transfer knowledge distillation methods: Wave [16] and DCKD [13]. These methods are popular in the field of image restoration, particularly in distilling complex teacher models into simpler, more efficient student models. We present both qualitative and quantitative comparisons in Figure 6 and

Table 1. Quantitative results of knowledge distillation methods across three tasks. The best results are highlighted in bold.

Tasks	Deraining		Deblurring		Dehazing
Metrics	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
Restormer [2]	33.69	0.935	32.07	0.952	36.51	0.991
Res-Wave [16]	32.27	0.918	30.36	0.933	34.77	0.981
Res-DCKD [13]	32.42	0.921	30.46	0.937	34.81	0.983
Res-SKD	32.92	0.927	31.07	0.946	35.06	0.985
Uformer [3]	33.34	0.931	31.98	0.960	36.28	0.989
Ufor-Wave [16]	32.10	0.917	30.50	0.938	34.62	0.971
Ufor-DCKD [13]	32.13	0.918	30.50	0.937	34.85	0.979
Ufor-SKD	32.47	0.921	31.14	0.940	34.97	0.983
DRSformer [4]	33.82	0.937	31.97	0.949	36.10	0.988
DRS-Wave [16]	32.51	0.922	30.30	0.931	34.67	0.975
DRS-DCKD [13]	32.58	0.922	30.43	0.936	34.81	0.980
DRS-SKD	33.11	0.927	31.09	0.945	34.94	0.983

.

For the deraining task, results are averaged over the Rain1400 [52] and Test1200 [53] datasets, while for deblurring, results are averaged across the Gopro [54] and HIDE [55] datasets. In the dehazing task, we evaluate using the SOTS subset of the RESIDE dataset [57]. Our SKD-based model demonstrates a clear advantage over the other two SOTA methods in both visual quality and full-reference evaluation metrics (PSNR and SSIM). In particular, the restoration quality produced by SKD exhibits fewer artifacts, sharper edges, and more realistic details in both synthetic and real-world degradation scenarios.

Comparison with image restoration methods. In addition to comparing with knowledge distillation methods, we also benchmark our SKD strategy against seven image restoration models, including two for deraining (PReNet [63] and RCDNet [64]), two for deblurring (DMPHN [65] and MT-RNN [66]), two for dehazing (MSBDN [28] and PSD [27]), and one for generalized restoration (MPRNet [34]).

As shown in Figure 7 and

Table 2. Quantitative comparison (PSNR ↑/SSIM ↑) and efficiency metrics (FLOPs ↓/inference time ↓) with lightweight methods across deraining, deblurring, and dehazing tasks. Note that some compared methods are specialized for a single task, hence the missing entries, whereas general-purpose models (including ours) are evaluated on all tasks. PSD [27] employs an identical network architecture to MSBDN [28] during inference. The best and second-best results are highlighted in bold and underline, respectively.

Tasks	Deraining	Deblurring	Dehazing	FLOPs	Infer Time
PReNet [63]	31.56/0.914	-/-	-/-	192.1 G	0.0764 s
Std.	(0.10/0.003)
RCDNet [64]	32.24/0.918	-/-	-/-	842.5 G	0.1919 s
Std.	(0.12/0.003)
DMPHN [65]	-/-	30.14/0.932	-/-	780.4 G	1.694 s
Std.		(0.15/0.003)
MT-RNN [66]	-/-	30.15/0.931	-/-	579.0 G	0.0387 s
Std.		(0.14/0.004)
MSBDN [28]	-/-	-/-	33.79/0.984	617.4 G	0.1446 s
Std.			(0.09/0.002)
PSD [27]	-/-	-/-	33.21/0.972	617.4 G	0.1446 s
Std.			(0.11/0.003)
MPRNet [34]	33.28/0.927	31.81/0.949	31.31/0.971	565.0 G	0.0593 s
Std.	(0.10/0.003)	(0.13/0.004)	(0.12/0.003)
Res-SKD	32.92/0.927	31.08/0.946	35.06/0.985	85.0 G	0.0356 s
Std.	(0.11/0.003)	(0.14/0.003)	(0.08/0.002)
Ufor-SKD	32.47/0.921	31.14/0.940	34.97/0.983	57.1 G	0.0540 s
Std.	(0.08/0.002)	(0.12/0.004)	(0.09/0.002)
DRS-SKD	33.11/0.927	31.09/0.945	34.94/0.983	132.0 G	0.0599 s
Std.	(0.10/0.003)	(0.15/0.004)	(0.10/0.002)

, our SKD-based student models significantly outperform the baselines in terms of computational complexity while maintaining competitive image quality and performance metrics. Despite being more lightweight, the SKD models are able to restore images with a similar level of detail and clarity as the much more complex models such as MPRNet, which is known for its robust performance across various restoration tasks. This demonstrates the efficiency and potential of SKD in achieving high-quality image restoration with reduced resource consumption, making it particularly suitable for deployment in resource-constrained environments.

Comparison on real degraded images. In real-world applications, it is crucial to ensure that the model performs effectively on images that are not only synthetically degraded but also subjected to real-world conditions. To this end, we extend our evaluation to real degraded images, as shown in Figure 8 and

Table 3. Quantitative comparison (BRISQUE ↓/PIQE ↓) and efficiency metrics (FLOPs ↓/inference time ↓) with lightweight methods across three real-world datasets. Note that some compared methods are specialized for a single task, hence the missing entries, whereas general-purpose models (including ours) are evaluated on all tasks. PSD [27] employs an identical network architecture to MSBDN [28] during inference. The best and second-best results are highlighted in bold and underline, respectively.

Dataset	SPA [29]	BLUR-J [56]	RTTS [57]	FLOPs	Infer Time
PReNet [63]	59.64/53.18	-/-	-/-	192.1 G	0.0764 s
Std.	(1.25/1.85)
RCDNet [64]	59.62/51.23	-/-	-/-	842.5 G	0.1919 s
Std.	(1.30/1.72)
DMPHN [65]	-/-	70.42/50.33	-/-	780.4 G	1.694 s
Std.		(1.62/1.84)
MT-RNN [66]	-/-	63.92/53.32	-/-	579.0 G	0.0387 s
Std.		(1.45/1.88)
MSBDN [28]	-/-	-/-	28.74/50.66	617.4 G	0.1446 s
Std.			(0.97/1.61)
PSD [27]	-/-	-/-	25.24/30.63	617.4 G	0.1446 s
Std.			(0.86/1.33)
MPRNet [34]	76.63/46.76	64.643/36.165	36.15/38.70	565.0 G	0.0593 s
Std.	(1.21/1.45)	(1.42/1.21)	(1.12/1.57)
Res-SKD	46.53/44.15	44.37/42.78	24.76/27.93	85.0 G	0.0356 s
Std.	(1.07/1.36)	(0.93/1.18)	(0.88/1.23)
Ufor-SKD	45.83/46.27	47.37/45.83	26.37/29.52	57.1 G	0.0540 s
Std.	(1.03/1.42)	(1.11/1.19)	(0.92/1.17)
DRS-SKD	43.12/42.62	47.61/43.92	26.15/32.72	132.0 G	0.0599 s
Std.	(0.98/1.27)	(1.14/1.33)	(0.84/1.33)

.

Although the models are primarily trained on synthetic datasets, our SKD-based Res-SKD student model exhibits strong performance in handling multiple degradations in real-world images. The results in Figure 8 clearly demonstrate that Res-SKD can effectively mitigate rain, blur, and haze artifacts, yielding visually appealing and restored images that retain important fine-grained details. Furthermore, the no-reference evaluation metrics presented in Table 3 (BRISQUE and PIQE) confirm that the SKD-based student models achieve satisfactory image quality, reinforcing their applicability in practical scenarios where ground-truth references are unavailable.

Our findings highlight the versatility and robustness of the proposed SKD strategy, which excels not only on synthetic data but also when applied to real-world challenges. This is a key strength for the deployment of image restoration models in real-time autonomous vehicle applications and other resource-limited environments.

4.3. Object Detection Results

Object detection is a critical high-level computer vision task for traffic systems. However, the accuracy of object detection is heavily influenced by the quality of captured images. In complex outdoor environments, various degradation factors, including weather conditions, significantly degrade image quality, leading to reduced object detection performance.

To evaluate the impact of image restoration on object detection, we use the lightweight object detection model Yolov4 [67] as a downstream task and assess performance using the mean Average Precision (mAP) metric. We test on the synthetic RMTD-test dataset [68] and the real-world RMTD-real dataset [68], both of which include images with multiple coexisting degradation factors.

The visualization results in Figure 9 clearly demonstrate the benefit of using restored images. Object detection performance on images restored by our SKD-based Res-SKD model exhibits significantly higher recall and precision compared to low-quality images. Additionally, the detection results on Res-SKD-restored images outperform those of images restored by MPRNet [34], and approach the accuracy levels achieved on high-quality images.

Quantitative evaluations in

Table 4. Object detection results in mAP ↑ on RMTD [68]. The best results are highlighted in bold.

Datasets	RMTD-Test [68]	RMTD-Real [68]
Degraded	0.1053	0.4772
RCDNet [64]	0.2648	0.4864
DMPHN [65]	0.2701	0.4892
MPRNet [34]	0.2836	0.5071
Res-SKD	0.2977	0.5146
Ground Truth	0.3461	-

corroborate these observations, showing a significant improvement in mAP scores for images restored using Res-SKD. These results highlight the practical utility of our SKD strategy in enhancing the effectiveness of downstream tasks like object detection, particularly in autonomous vehicle applications where degraded image quality is a common challenge.

4.4. Ablation Studies

Ablation studies were conducted on the Gopro [54] dataset for the deblurring task to validate the effectiveness of our proposed distillation strategy and to analyze the contribution of its individual components. A critical baseline is established by training the student architecture solely with the reconstruction loss ($L_{REC}$) and without employing any knowledge distillation, which serves to isolate the impact of our SKD framework. The results, summarized in

Table 5. Quantitative ablation study results on Gopro [54]. The best results are highlighted in bold.

Sets	Teacher	Channel-Wise	Spatial-Wise	${\mathit{L}}_{\mathit{CL}}$	PSNR/SSIM
(a)					30.25/0.907
(b)	✓				32.20/0.924
(c)	✓	✓			32.61/0.929
(d)	✓		✓		32.71/0.930
(e)	✓	✓	✓		32.99/0.933
Res-SKD	✓	✓	✓	✓	33.24/0.937

and Figure 10, reveal the following:

• Student with $L_{REC}$ only: This setup reveals the native capacity of the compact student architecture. Its significantly lower performance, compared to all subsequent configurations that utilize the teacher network, clearly demonstrates that the performance gains are not merely a consequence of using a smaller model, but are primarily attributable to the proposed distillation method.
• Channel-wise attention: Adding this mechanism improves the student model’s learning capacity, yielding a 0.41 dB gain in PSNR.
• Spatial-wise attention: This mechanism contributes an additional 0.51 dB gain in PSNR.
• Full Multi-Dimensional Cross-Net Attention (MCA): When both channel-wise and spatial-wise attention mechanisms are combined, the model achieves a 0.79 dB increase in PSNR and a 0.009 improvement in SSIM over the baseline model.
• Contrastive learning loss ($L_{CL}$): This loss further enhances the model’s performance, adding a 0.25 dB gain in PSNR and a 0.004 improvement in SSIM.

The qualitative results in Figure 10 further validate these findings, illustrating that the inclusion of the MCA mechanism and contrastive learning significantly enhances the visual quality of restored images. These results demonstrate the effectiveness of our proposed components in improving the distilled model’s performance.

To validate the choice of the Gaussian kernel for feature-level distillation, we conducted a controlled experiment comparing different similarity measures while keeping all other components of our SKD framework identical. As shown in

Table 6. Ablation study on feature similarity measures for knowledge distillation. The experiment is conducted on the GoPro dataset for image deblurring, using the same student architecture and full SKD framework except for the feature-level distance metric. The best results are highlighted in bold.

Similarity Measure	Formula	PSNR ↑	SSIM ↑	Stability
Euclidean Distance	$L_{\mathrm{eucl}}={\parallel x-y\parallel }_2$	32.92	0.935	Medium
Cosine Similarity	$L_{\cos }=1-{\displaystyle \frac{x·y}{{\parallel x\parallel }_2{\parallel y\parallel }_2}}$	32.98	0.935	Medium
Gaussian Kernel (Ours)	$GK(x,y)=1-exp(-{\displaystyle \frac{\left|\right|x-{y\left|\right|}_2^2}{2{\sigma }^2}})$	33.24	0.937	High

, the Gaussian kernel achieves the best performance, outperforming both Euclidean distance and cosine similarity by 0.32 dB and 0.26 dB in PSNR, respectively.

The superior performance can be attributed to the Gaussian kernel’s unique properties: (1) Unlike Euclidean distance, which is sensitive to absolute feature magnitudes and can cause gradient instability, the Gaussian kernel operates in a normalized similarity space that is more robust to feature-scale variations. (2) Compared to cosine similarity, which only considers angular alignment and ignores feature magnitude information, the Gaussian kernel incorporates both directional and magnitude relationships through the Euclidean distance in its exponent. (3) The exponential decay characteristic of the Gaussian kernel provides a soft-thresholding effect, focusing the distillation on semantically meaningful feature relationships while being tolerant to minor variations.

Empirically, we also observed that training with the Gaussian kernel exhibited smoother convergence and lower loss variance, confirming its stabilization effect on the distillation process.

4.5. Model Complexity and Hyper-Parameter Analysis

We evaluate the computational complexity of our model by comparing the FLOPs (floating-point operations) and inference time of our distilled student model with those of the teacher model and other SOTA image restoration models. The results are shown in

Table 7. Comparison of model complexity.

Method	FLOPs	Infer Time
MPRNet [34]	565.0 G	0.0593 s
Restormer [2]	619.5 G	0.1103 s
Uformer [3]	347.6 G	0.1737 s
DRSformer [4]	972.0 G	0.3074 s
WGWS [69]	996.2 G	0.1919 s
Res-SKD	85.0 G	0.0356 s
Ufor-SKD	57.1 G	0.0540 s
DRS-SKD	132.0 G	0.0599 s

.

Our experiments demonstrate that the student model after distillation using the SKD strategy exhibits a substantial reduction in computational cost compared to the teacher models, with 85.4% reduction in FLOPs and 85.8% reduction in parameters. Moreover, our SKD-based model outperforms other SOTA models, including the relatively lightweight MPRNet [34], in terms of both computational efficiency and restoration quality. This confirms the efficacy of our SKD strategy in achieving high-performance image restoration with significantly reduced complexity, making it suitable for deployment on resource-constrained platforms such as autonomous vehicles.

Additionally, we conduct an analysis of key hyper-parameters to further optimize the SKD framework. The selection process for all hyper-parameters is directly illustrated by comparing the different experimental settings (a) to (e) within the table. Specifically, the results of these experiments are shown in

Table 8. Comparison of hyper-parameters on SOTS [57]. The best results are highlighted in bold.

Sets	${\mathit{\alpha }}_1$	${\mathit{\alpha }}_2$	${\mathit{\alpha }}_3$	PSNR/SSIM
(a)	0.2	0.2	0.2	34.95/0.981
(b)	0.5	0.1	0.1	34.74/0.974
(c)	0.5	0.1	0.2	34.89/0.978
(d)	0.5	0.2	0.1	34.91/0.979
(e)	0.5	0.2	0.2	35.06/0.985

, where we evaluate the impact of the trade-off weights (${\alpha }_1$, ${\alpha }_2$, and ${\alpha }_3$) used in the loss functions. We compare different settings for these hyper-parameters:

• The value of ${\alpha }_1$ is determined by comparing setting (a) (${\alpha }_1=0.2$) with setting (e) (${\alpha }_1=0.5$), while keeping ${\alpha }_2$ and ${\alpha }_3$ constant at 0.2. The superior performance of (e) demonstrates that a higher weight of ${\alpha }_1=0.5$ for the $L_{GK}$ loss strikes the best balance, providing more effective guidance from the teacher model.
• The values of ${\alpha }_2$ and ${\alpha }_3$ are analyzed by comparing settings (b), (c), (d), and (e). The optimal values are found to be ${\alpha }_2=0.2$ and ${\alpha }_3=0.2$, ensuring that the model prioritizes both the MCA mechanism and contrastive learning loss effectively.

These experiments highlight the importance of hyper-parameter tuning in optimizing the performance of the SKD strategy, ensuring that it achieves the best trade-off between image restoration quality, model complexity, and computational efficiency.

5. Conclusions

We introduced a Soft Knowledge Distillation (SKD) strategy with Multi-Dimensional Cross-Net Attention (MCA) for compressing transformer-based image restoration models, tailored for autonomous vehicles and traffic systems. Our method reduces computational complexity while maintaining high restoration quality, making it ideal for real-time deployment in resource-constrained environments. The MCA mechanism improves feature learning by capturing critical details across both spatial and channel dimensions, and contrastive learning loss further enhances image quality.

Experiments show that our SKD-based models significantly improve deraining, deblurring, and dehazing performance, confirming their suitability for autonomous vehicle applications. Moreover, the models enhance object detection performance, boosting recall and precision on degraded images. This demonstrates the effectiveness of our approach in improving environmental perception in autonomous driving and traffic systems. Future work will focus on optimizing the method for even more resource-limited devices.

While this work demonstrates the effectiveness of our SKD framework with state-of-the-art transformer architectures, a natural extension is to validate its generalizability across other network families, such as modern CNN-based models. We anticipate that the architecture-agnostic design of our method would yield similarly compelling results, and we identify this as an important direction for future research.