Improved Multi-Faceted Sine Cosine Algorithm for Optimization and Electricity Load Forecasting
Abstract
1. Introduction
2. Sine Cosine Algorithm (SCA)
| Algorithm 1: Sine Cosine Algorithm (SCA) |
| 1. Initialize the population {X1, X2, …, Xn} randomly in the search space 2. Assign initial values to the SCA parameters. 3. Determine the objective function value for every agent in the population. 4. Select the best solution found up to now as Pj 5. Initialize t = 0, where t is iteration counter 6. while Termination criteria are met do 7. Calculate r1 using Equation (3) and generate the parameters r2, r3, r4 randomly 8. for each search agent do 9. Update the position of search agents using Equations (1) and (2) 10. end for 11. Update the current best solution (or destination point) Pj 12. t = t + 1 13. end while 14. Return the best solution |
3. Proposed Modified SCA
3.1. Strategic Multi-Phase Enhancements of the MFSCA
3.1.1. Integration of Dynamic Opposition (DO) for Initialization
3.1.2. Incorporation of Adaptive Jumping Rate () Lévy Flight
3.1.3. Elite-Learning Strategy
3.1.4. Integration of Logistic Map as a Chaotic Mapping Mechanism
3.1.5. Incorporation of Adaptive Inertia Weight ()
3.1.6. Adaptive Local Search
4. Operational Flow of the Enhanced MFSCA
| Algorithm 2: Modified Sine Cosine Algorithm (MFSCA) |
|
5. Experiments and Results
5.1. Optimization Problems
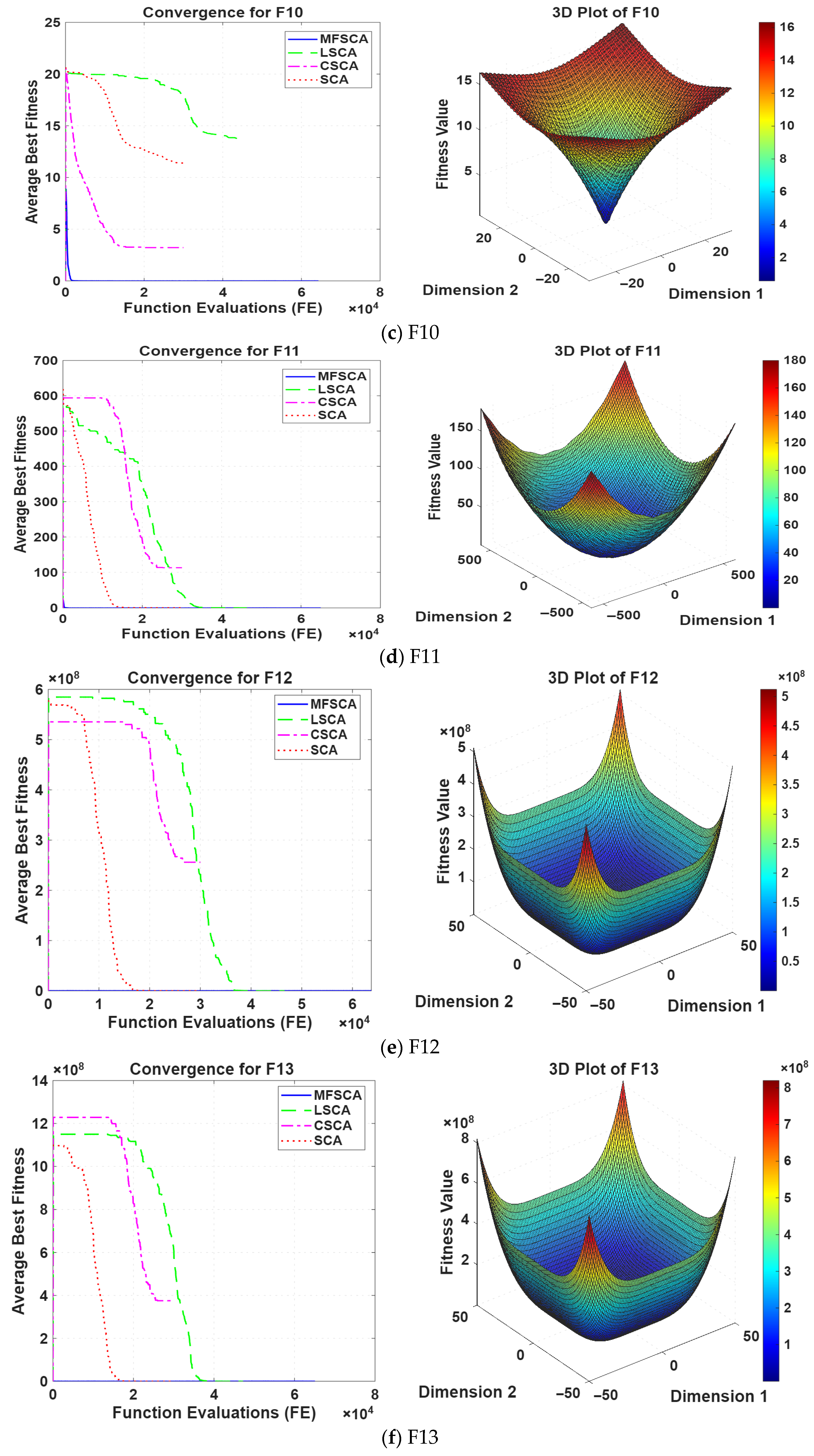
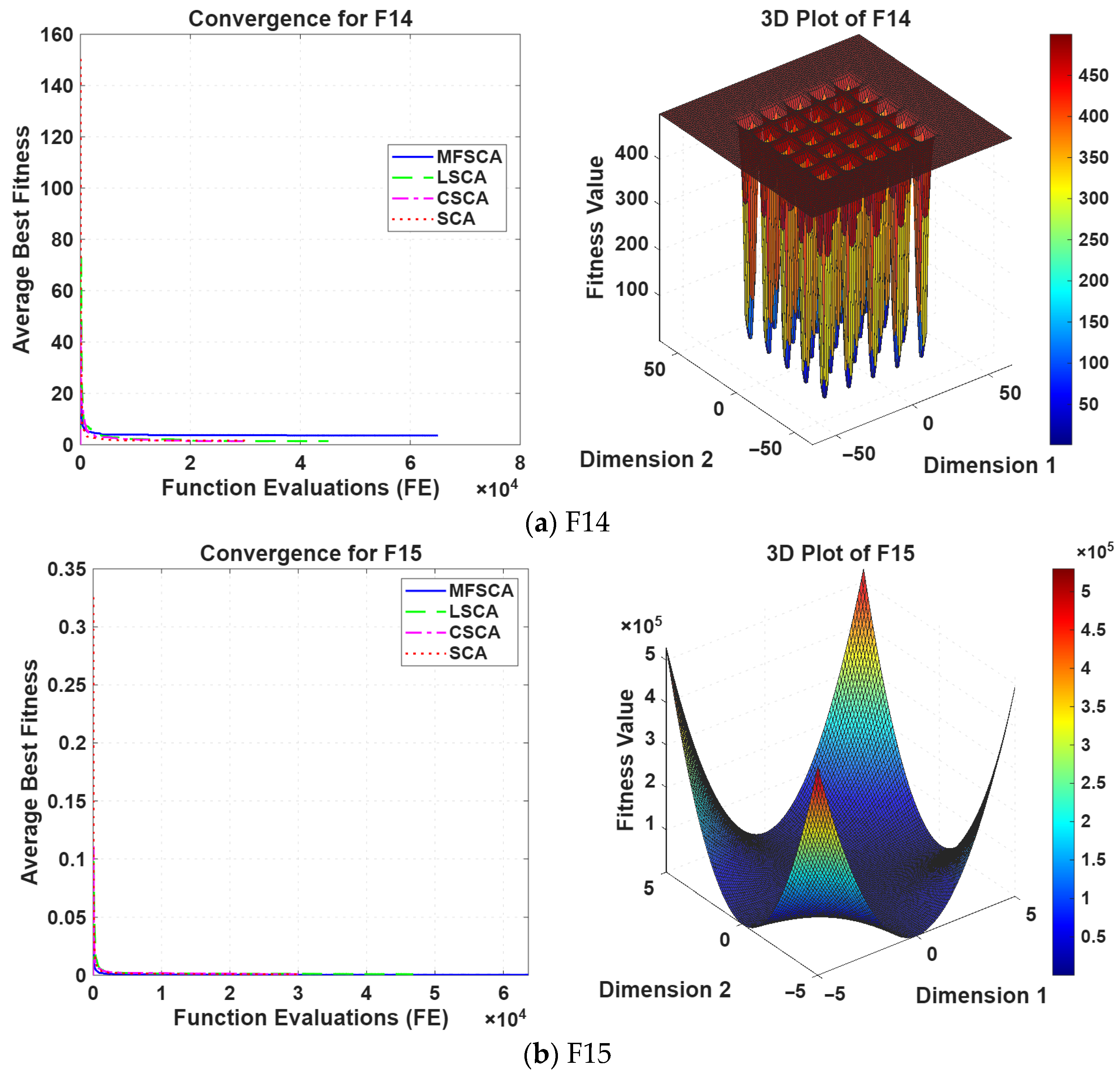
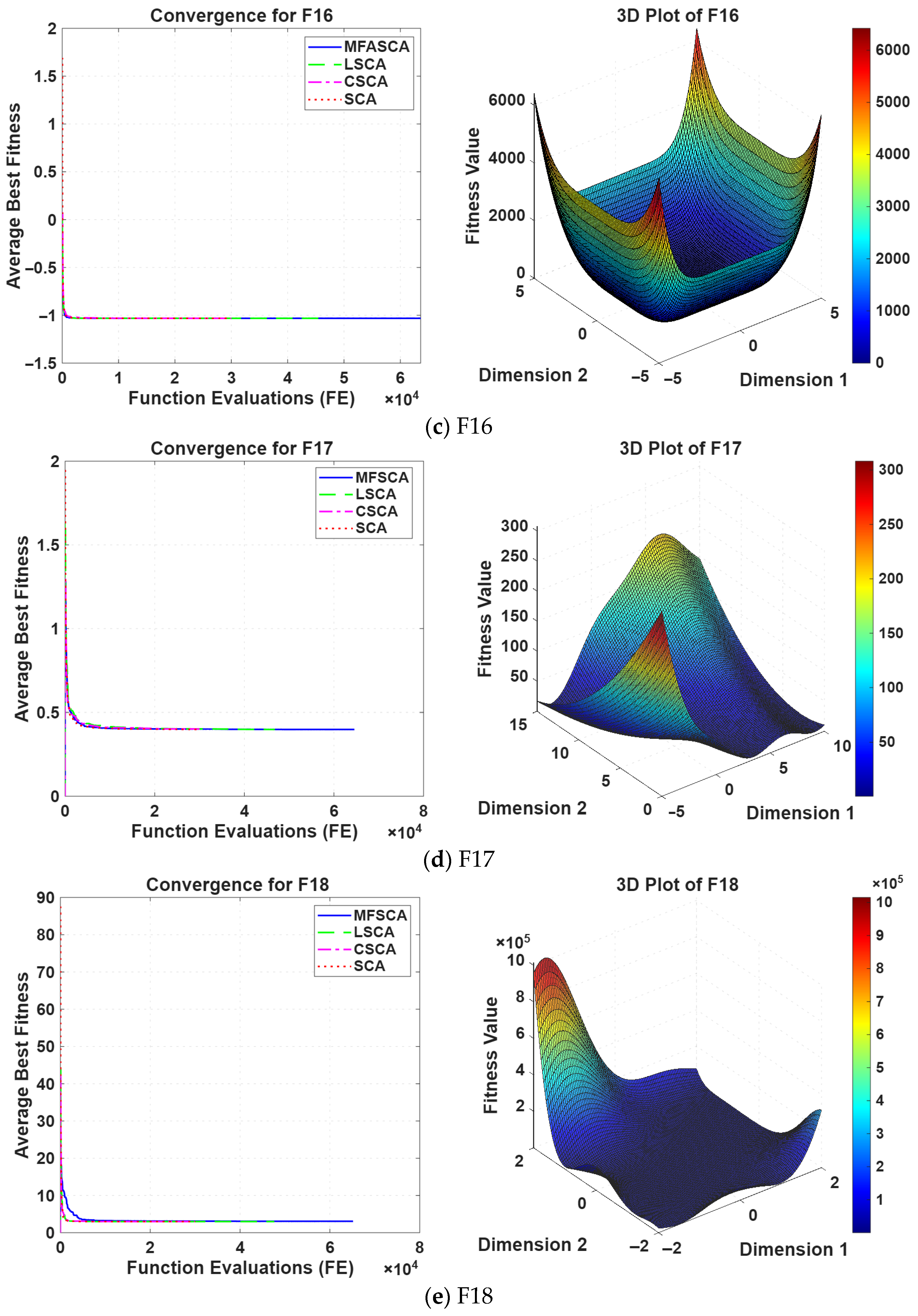
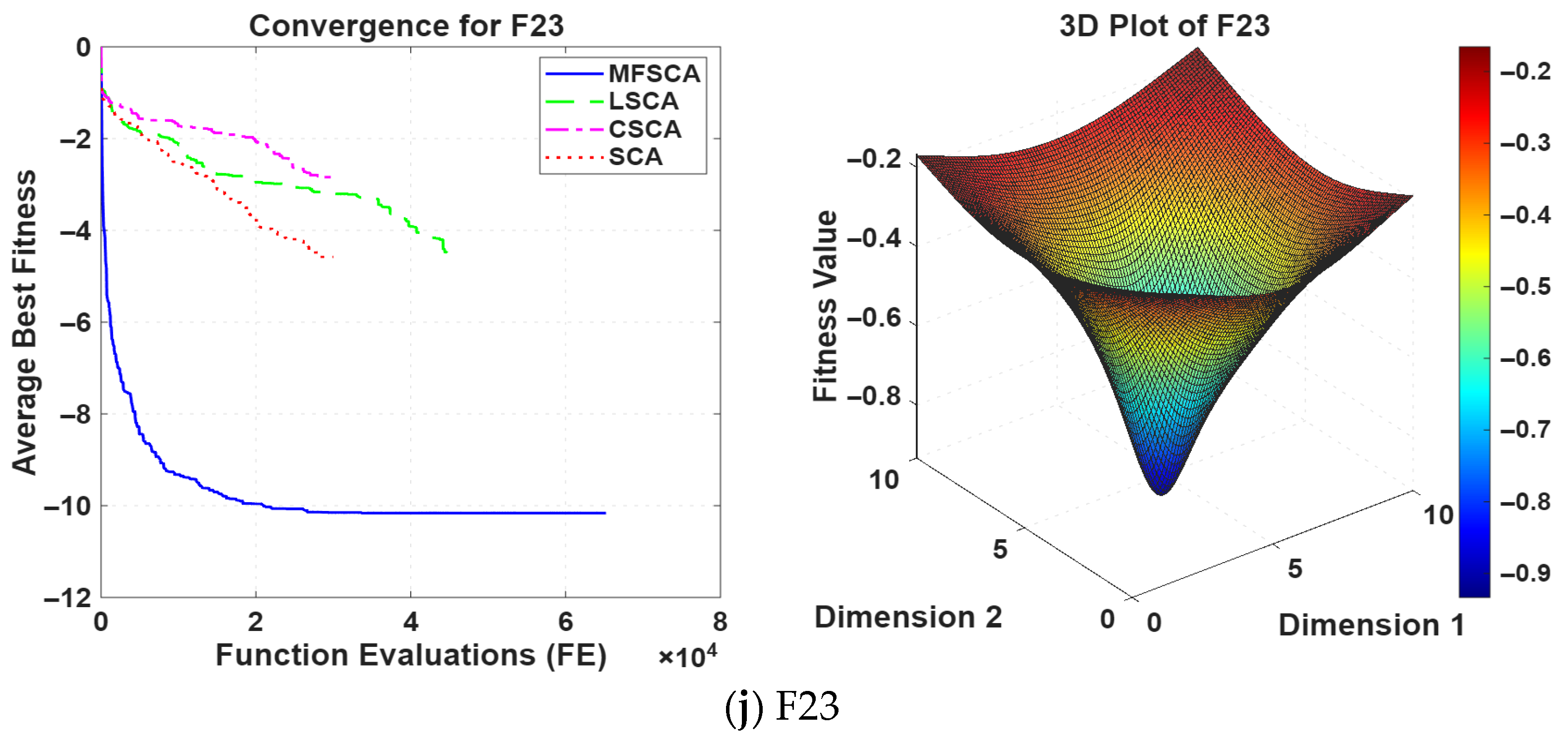
5.1.1. Evaluation of the Exploitation Capability
5.1.2. Evaluation of Exploration Capability
5.1.3. Fixed-Dimensional Multimodal Functions
5.2. Statistical Analyses
5.3. Algorithm Complexity
6. Performance Evaluation of the Proposed MFSCA on Adaptive Neuro-Fuzzy Inference System
6.1. Study Area Description and Data Collection
6.2. Adaptive Neuro-Fuzzy Inference System (ANFIS)
Clustering Technique
6.3. Modified Sine Cosine Algorithm (MFSCA)-ANFIS
Evaluating the Model Performance
6.4. Results and Discussion of the MFSCA-ANFIS with Other Hybrid Models
6.5. Limitations of the Study
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SCA | Sine Cosine Algorithm |
| DO | Dynamic Opposition |
| MFSCA | Multi-faceted |
| LSCA | Lévy Sine Cosine Algorithm |
| CSCA | Chaotic Sine Cosine Algorithm |
| NI | Nature Intelligence |
| MA | Metaheuristic Algorithm |
| JOS | Joint Opposition Selection |
| NFL | No Free Lunch Theorem |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| SAWS | South African Weather Service |
| MF | Membership Function |
| FIS | Fuzzy Inference System |
| FCM | fuzzy c-means |
References
- Bakır, H. Enhanced Artificial Hummingbird Algorithm for Global Optimization and Engineering Design Problems. Adv. Eng. Softw. 2024, 194, 103671. [Google Scholar] [CrossRef]
- Koop, L.; Maria, N.; Ramos, V.; Bonilla-Petriciolet, A.; Corazza, M.L.; Pedersen Voll, F.A. A Review of Stochastic Optimization Algorithms Applied in Food Engineering. Int. J. Chem. Eng. 2024, 2024, 3636305. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris Hawks Optimization: Algorithm and Applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, J.; Liu, C.; Su, K.; Ishibuchi, H.; Jin, Y. Synergistic Integration of Metaheuristics and Machine Learning: Latest Advances and Emerging Trends. Artif. Intell. Rev. 2025, 58, 268. [Google Scholar] [CrossRef]
- El-Shorbagy, M.A.; Bouaouda, A.; Abualigah, L.; Hashim, F.A. Stochastic Fractal Search: A Decade Comprehensive Review on Its Theory, Variants, and Applications. CMES Comput. Model. Eng. Sci. 2025, 142, 2339–2404. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Rashid, T.A.; Hassan, B.A.; Majidpour, J.; Noori, K.A.; Rahman, C.M.; Abdalla, M.H.; Qader, S.M.; Tayfor, N.; Mohammed, N.B. Balancing Exploration and Exploitation Phases in Whale Optimization Algorithm: An Insightful and Empirical Analysis. In Handbook of Whale Optimization Algorithm: Variants, Hybrids, Improvements, and Applications; Academic Press: Cambridge, MA, USA, 2024; pp. 149–156. [Google Scholar] [CrossRef]
- Selvam, R.; Hiremath, P.; Cs, S.K.; Ramakrishna Bhat, R.; Tomar, V.; Bansal, M.; Singh, P. Metaheuristic Algorithms for Optimization: A Brief Review. Eng. Proc. 2023, 59, 238. [Google Scholar] [CrossRef]
- Oladipo, S.; Sun, Y. Assessment of a Consolidated Algorithm for Constrained Engineering Design Optimization and Unconstrained Function Optimization. In Proceedings of the 2nd International Conference on Robotics, Automation and Artificial Intelligence (RAAI), Singapore, 9–11 December 2022; pp. 188–192. [Google Scholar] [CrossRef]
- Cotta, C. Harnessing Memetic Algorithms: A Practical Guide. TOP 2025, 33, 327–356. [Google Scholar] [CrossRef]
- Tsai, C.W.; Chiang, M.C. Handbook of Metaheuristic Algorithms: From Fundamental Theories to Advanced Applications. In Handbook of Metaheuristic Algorithms: From Fundamental Theories to Advanced Applications; Elsevier: Amsterdam, The Netherlands, 2023; pp. 1–584. [Google Scholar] [CrossRef]
- Bhattacharyya, T.; Chatterjee, B.; Singh, P.K.; Yoon, J.H.; Geem, Z.W.; Sarkar, R. Mayfly in Harmony: A New Hybrid Meta-Heuristic Feature Selection Algorithm. IEEE Access 2020, 8, 195929–195945. [Google Scholar] [CrossRef]
- Michalewicz, Z.; Hinterding, R.; Michalewicz, M. Evolutionary Algorithms BT. In Fuzzy Evolutionary Computation; Pedrycz, W., Ed.; Springer: Boston, MA, USA, 1997; pp. 3–31. ISBN 978-1-4615-6135-4. [Google Scholar]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Fogel, D.B.; Fogel, L.J. An Introduction to Evolutionary Programming. In Artificial Evolution; Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 1996; Volume 1063, pp. 21–33. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution-A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1997; Volume 11. [Google Scholar]
- Alavi, M.; Henderson, J.C. An Evolutionary Strategy for Implementing a Decision Support System. Manag. Sci. 1981, 27, 1309–1323. [Google Scholar] [CrossRef]
- Dutta, T.; Bhattacharyya, S.; Dey, S.; Platos, J. Border Collie Optimization. IEEE Access 2020, 8, 109177–109197. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 39–43. [Google Scholar]
- Dorigo, M.; Gambardella, L.M. Ant Colony System: A Cooperative Learning Approach to the Traveling Salesman Problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef]
- Shah-Hosseini, H. The Intelligent Water Drops Algorithm: A Nature-Inspired Swarm-Based Optimization Algorithm. Int. J. Bio-Inspired Comput. 2009, 1, 71–79. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- He, S.; Wu, Q.H.; Saunders, J.R. Group Search Optimizer: An Optimization Algorithm Inspired by Animal Searching Behavior. IEEE Trans. Evol. Comput. 2009, 13, 973–990. [Google Scholar] [CrossRef]
- Passino, K.M. Biomimicry of Bacterial Foraging for Distributed Optimization and Control. IEEE Control Syst. 2002, 22, 52–67. [Google Scholar] [CrossRef]
- Duman, E.; Uysal, M.; Alkaya, A.F. Migrating Birds Optimization: A New Metaheuristic Approach and Its Performance on Quadratic Assignment Problem. Inf. Sci. 2012, 217, 65–77. [Google Scholar] [CrossRef]
- Rahmani, R.; Yusof, R. A New Simple, Fast and Efficient Algorithm for Global Optimization over Continuous Search-Space Problems: Radial Movement Optimization. Appl. Math. Comput. 2014, 248, 287–300. [Google Scholar] [CrossRef]
- Cuevas, E.; González, A.; Zaldívar, D.; Pérez-Cisneros, M. An Optimisation Algorithm Based on the Behaviour of Locust Swarms. Int. J. Bio-Inspired Comput. 2015, 7, 402–407. [Google Scholar] [CrossRef]
- Odili, J.B.; Kahar, M.N.M.; Anwar, S. African Buffalo Optimization: A Swarm-Intelligence Technique. Procedia Comput. Sci. 2015, 76, 443–448. [Google Scholar] [CrossRef]
- Harifi, S.; Khalilian, M.; Mohammadzadeh, J.; Ebrahimnejad, S. Emperor Penguins Colony: A New Metaheuristic Algorithm for Optimization. Evol. Intell. 2019, 12, 211–226. [Google Scholar] [CrossRef]
- Jain, M.; Singh, V.; Rani, A. A Novel Nature-Inspired Algorithm for Optimization: Squirrel Search Algorithm. Swarm Evol. Comput. 2019, 44, 148–175. [Google Scholar] [CrossRef]
- Chen, Z.; Francis, A.; Li, S.; Liao, B.; Xiao, D.; Ha, T.T.; Li, J.; Ding, L.; Cao, X. Egret Swarm Optimization Algorithm: An Evolutionary Computation Approach for Model Free Optimization. Biomimetics 2022, 7, 144. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Yin, M. Animal Migration Optimization: An Optimization Algorithm Inspired by Animal Migration Behavior. Neural Comput. Appl. 2014, 24, 1867–1877. [Google Scholar] [CrossRef]
- Dehghani, M.; Trojovská, E.; Trojovský, P. A New Human-Based Metaheuristic Algorithm for Solving Optimization Problems on the Base of Simulation of Driving Training Process. Sci. Rep. 2022, 12, 9924. [Google Scholar] [CrossRef]
- Matoušová, I.; Trojovský, P.; Dehghani, M.; Trojovská, E.; Kostra, J. Mother Optimization Algorithm: A New Human-Based Metaheuristic Approach for Solving Engineering Optimization. Sci. Rep. 2023, 13, 10312. [Google Scholar] [CrossRef]
- Trojovská, E.; Dehghani, M. A New Human-Based Metahurestic Optimization Method Based on Mimicking Cooking Training. Sci. Rep. 2022, 12, 14861. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-Learning-Based Optimization: A Novel Method for Constrained Mechanical Design Optimization Problems. CAD Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Hubalovska, M.; Major, S. A New Human-Based Metaheuristic Algorithm for Solving Optimization Problems Based on Technical and Vocational Education and Training. Biomimetics 2023, 8, 508. [Google Scholar] [CrossRef] [PubMed]
- Elsisi, M. Future Search Algorithm for Optimization. Evol. Intell. 2019, 12, 21–31. [Google Scholar] [CrossRef]
- Askari, Q.; Younas, I.; Saeed, M. Political Optimizer: A Novel Socio-Inspired Meta-Heuristic for Global Optimization. Knowl. Based Syst. 2020, 195, 105709. [Google Scholar] [CrossRef]
- Kumar, M.; Kulkarni, A.J.; Satapathy, S.C. Socio Evolution & Learning Optimization Algorithm: A Socio-Inspired Optimization Methodology. Future Gener. Comput. Syst. 2018, 81, 252–272. [Google Scholar] [CrossRef]
- Askari, Q.; Saeed, M.; Younas, I. Heap-Based Optimizer Inspired by Corporate Rank Hierarchy for Global Optimization. Expert. Syst. Appl. 2020, 161, 113702. [Google Scholar] [CrossRef]
- Lian, J.; Hui, G. Human Evolutionary Optimization Algorithm. Expert. Syst. Appl. 2024, 241, 122638. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, S.; Zhou, C.; Yan, S.; Xue, J. Human Memory Optimization Algorithm: A Memory-Inspired Optimizer for Global Optimization Problems. Expert. Syst. Appl. 2024, 237, 121597. [Google Scholar] [CrossRef]
- Givi, H.; Dehghani, M.; Hubalovsky, S. Red Panda Optimization Algorithm: An Effective Bio-Inspired Metaheuristic Algorithm for Solving Engineering Optimization Problems. IEEE Access 2023, 11, 57203–57227. [Google Scholar] [CrossRef]
- Ni, L.; Ping, Y.; Yao, N.; Jiao, J.; Wang, G. Literature Research Optimizer: A New Human-Based Metaheuristic Algorithm for Optimization Problems. Arab. J. Sci. Eng. 2024, 49, 12817–12865. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J. Parameters Identification of Hydraulic Turbine Governing System Using Improved Gravitational Search Algorithm. Energy Convers. Manag. 2011, 52, 374–381. [Google Scholar] [CrossRef]
- Lam, A.Y.S.; Li, V.O.K. Chemical-Reaction-Inspired Metaheuristic for Optimization. IEEE Trans. Evol. Comput. 2010, 14, 381–399. [Google Scholar] [CrossRef]
- Hatamlou, A. Black Hole: A New Heuristic Optimization Approach for Data Clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Doğan, B.; Ölmez, T. A New Metaheuristic for Numerical Function Optimization: Vortex Search Algorithm. Inf. Sci. 2015, 293, 125–145. [Google Scholar] [CrossRef]
- Zheng, Y.J. Water Wave Optimization: A New Nature-Inspired Metaheuristic. Comput. Oper. Res. 2015, 55, 1–11. [Google Scholar] [CrossRef]
- Shareef, H.; Ibrahim, A.A.; Mutlag, A.H. Lightning Search Algorithm. Appl. Soft Comput. 2015, 36, 315–333. [Google Scholar] [CrossRef]
- Abedinpourshotorban, H.; Mariyam Shamsuddin, S.; Beheshti, Z.; Jawawi, D.N.A. Electromagnetic Field Optimization: A Physics-Inspired Metaheuristic Optimization Algorithm. Swarm Evol. Comput. 2016, 26, 8–22. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for Solving Optimization Problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Azizi, M.; Aickelin, U.; Khorshidi, H.A.; Baghalzadeh Shishehgarkhaneh, M. Energy Valley Optimizer: A Novel Metaheuristic Algorithm for Global and Engineering Optimization. Sci. Rep. 2023, 13, 226. [Google Scholar] [CrossRef] [PubMed]
- Kaveh, A.; Dadras, A. A Novel Meta-Heuristic Optimization Algorithm: Thermal Exchange Optimization. Adv. Eng. Softw. 2017, 110, 69–84. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S.; Loo, K.H. Propagation Search Algorithm: A Physics-Based Optimizer for Engineering Applications. Mathematics 2023, 11, 4224. [Google Scholar] [CrossRef]
- Wei, Z.; Huang, C.; Wang, X.; Han, T.; Li, Y. Nuclear Reaction Optimization: A Novel and Powerful Physics-Based Algorithm for Global Optimization. IEEE Access 2019, 7, 66084–66109. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Azeem, S.A.A.; Jameel, M.; Abouhawwash, M. Kepler Optimization Algorithm: A New Metaheuristic Algorithm Inspired by Kepler’s Laws of Planetary Motion. Knowl. Based Syst. 2023, 268, 110454. [Google Scholar] [CrossRef]
- Kundu, R.; Chattopadhyay, S.; Nag, S.; Navarro, M.A.; Oliva, D. Prism Refraction Search: A Novel Physics-Based Metaheuristic Algorithm. J. Supercomput. 2024, 80, 10746–10795. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. A Novel Heuristic Optimization Method: Charged System Search. Acta Mech. 2010, 213, 267–289. [Google Scholar] [CrossRef]
- Wang, M.; Lu, G. A Modified Sine Cosine Algorithm for Solving Optimization Problems. IEEE Access 2021, 9, 27434–27450. [Google Scholar] [CrossRef]
- Shang, C.; Zhou, T.; Liu, S. Optimization of Complex Engineering Problems Using Modified Sine Cosine Algorithm. Sci. Rep. 2022, 12, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Pham, V.H.S.; Nguyen Dang, N.T.; Nguyen, V.N. Enhancing Engineering Optimization Using Hybrid Sine Cosine Algorithm with Roulette Wheel Selection and Opposition-Based Learning. Sci. Rep. 2024, 14, 694. [Google Scholar] [CrossRef]
- Liu, J.; Bi, C.; Chen, H.; Heidari, A.A.; Chen, H. Triangular-Based Sine Cosine Algorithm for Global Search and Feature Selection. Sci. Rep. 2025, 15, 12992. [Google Scholar] [CrossRef]
- Cheng, J.; Lin, Q.; Xiong, Y. Engineering Optimization Sine Cosine Algorithm with Peer Learning for Global Numerical Optimization Sine Cosine Algorithm with Peer Learning for Global Numerical Optimization. Eng. Optim. 2024, 57, 963–980. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Dudek, G.; Piotrowski, P.; Baczyński, D. Forecasting in Modern Power Systems: Challenges, Techniques, and Emerging Trends. Energies 2025, 18, 3589. [Google Scholar] [CrossRef]
- Li, P.; Hu, Z.; Shen, Y.; Cheng, X.; Alhazmi, M. Short-Term Electricity Load Forecasting Based on Large Language Models and Weighted External Factor Optimization. Sustain. Energy Technol. Assess. 2025, 82, 104449. [Google Scholar] [CrossRef]
- Pachauri, R.K.; Pandey, J.K.; Sharma, A.; Nautiyal, O.P.; Ram, M. Applied Soft Computing and Embedded System Applications in Solar Energy; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Oladipo, S.; Sun, Y.; Wang, Z. Pelican Optimization Algorithm-Based ANFIS for Bolstered Electricity Usage Prediction. In Proceedings of the 8th International Conference on Computer Science and Artificial Intelligence, Beijing, China, 8–9 December 2024; pp. 537–543. [Google Scholar] [CrossRef]
- Du, P.; Ye, Y.; Wu, H.; Wang, J. Study on Deterministic and Interval Forecasting of Electricity Load Based on Multi-Objective Whale Optimization Algorithm and Transformer Model. Expert Syst. Appl. 2025, 268, 126361. [Google Scholar] [CrossRef]
- Wei, H.L.; Abhishek, S. 7 Overview of Swarm Intelligence Techniques for Harvesting Solar Energy. In Recent Advances in Energy Harvesting Technologies; River Publishers: Gistrup, Denmark, 2023; pp. 161–176. [Google Scholar]
- Oladipo, S.; Sun, Y.; Adegoke, S.A. Hybrid Neuro-Fuzzy Modeling for Electricity Consumption Prediction in a Middle-Income Household in Gauteng, South Africa: Utilizing Fuzzy C-Means Method. In Neural Computing for Advanced Applications; Springer: Berlin/Heidelberg, Germany, 2025; pp. 59–73. [Google Scholar] [CrossRef]
- Al-Qaness, M.A.A.; Elaziz, M.A.; Ewees, A.A. Oil Consumption Forecasting Using Optimized Adaptive Neuro-Fuzzy Inference System Based on Sine Cosine Algorithm. IEEE Access 2018, 6, 68394–68402. [Google Scholar] [CrossRef]
- Yılmaz, S.; Yıldırım, A.A.; Feyzullahoğlu, E. Erosion Rate of AA6082-T6 Aluminum Alloy Subjected to Erosive Wear Determined by the Meta-Heuristic (SCA) Based ANFIS Method. Mater./Mater. Test. 2024, 66, 248–261. [Google Scholar] [CrossRef]
- Ehteram, M.; Yenn Teo, F.; Najah Ahmed, A.; Dashti Latif, S.; Feng Huang, Y.; Abozweita, O.; Al-Ansari, N.; El-Shafie, A. Performance Improvement for Infiltration Rate Prediction Using Hybridized Adaptive Neuro-Fuzzy Inferences System (ANFIS) with Optimization Algorithms. Ain Shams Eng. J. 2021, 12, 1665–1676. [Google Scholar] [CrossRef]
- Bansal, J.C.; Bajpai, P.; Rawat, A.; Nagar, A.K. Sine Cosine Algorithm. In Sine Cosine Algorithm for Optimization; SpringerBriefs in Applied Sciences and Technology; Springer: Berlin/Heidelberg, Germany, 2023; pp. 15–33. [Google Scholar] [CrossRef]
- Rahnamayan, S.; Tizhoosh, H.R.; Salama, M.M.A. Quasi-Oppositional Differential Evolution. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 2229–2236. [Google Scholar]
- Ergezer, M.; Simon, D.; Du, D. Oppositional Biogeography-Based Optimization. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 1009–1014. [Google Scholar]
- Xu, Y.; Yang, Z.; Li, X.; Kang, H.; Yang, X. Dynamic Opposite Learning Enhanced Teaching–Learning-Based Optimization. Knowl. Based Syst. 2020, 188, 104966. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. Modified Particle Swarm Optimizer. In Proceedings of the IEEE Conference on Evolutionary Computation, ICEC, Nayoya, Japan, 20–22 May 1996; IEEE: Anchorage, AK, USA, 1998; pp. 69–73. [Google Scholar]
- Feng, H.; Ni, H.; Zhao, R.; Zhu, X. An Enhanced Grasshopper Optimization Algorithm to the Bin Packing Problem. J. Control Sci. Eng. 2020, 2020, 3894987. [Google Scholar] [CrossRef]
- Dao, P.B. On Wilcoxon Rank Sum Test for Condition Monitoring and Fault Detection of Wind Turbines. Appl. Energy 2022, 318, 119209. [Google Scholar] [CrossRef]
- Adeleke, O.; Akinlabi, S.; Jen, T.C.; Dunmade, I. A Machine Learning Approach for Investigating the Impact of Seasonal Variation on Physical Composition of Municipal Solid Waste. J. Reliab. Intell. Environ. 2022, 9, 99–118. [Google Scholar] [CrossRef]
- Masebinu, S.O.; Holm-Nielsen, J.B.; Mbohwa, C.; Padmanaban, S.; Nwulu, N. Electricity Consumption Data of a Student Residence in Southern Africa. Data Brief 2020, 32, 106150. [Google Scholar] [CrossRef]
- Oladipo, S.; Sun, Y.; Adeleke, O. An Improved Particle Swarm Optimization and Adaptive Neuro-Fuzzy Inference System for Predicting the Energy Consumption of University Residence. Int. Trans. Electr. Energy Syst. 2023, 2023, 8508800. [Google Scholar] [CrossRef]
- Rahman, M.S.; Ali, M.H. Adaptive Neuro Fuzzy Inference System (ANFIS)-Based Control for Solving the Misalignment Problem in Vehicle-to-Vehicle Dynamic Wireless Charging Systems. Electronics 2025, 14, 507. [Google Scholar] [CrossRef]
- Petković, D.; Ćojbašić, Ž.; Nikolić, V.; Shamshirband, S.; Mat Kiah, M.L.; Anuar, N.B.; Abdul Wahab, A.W. Adaptive Neuro-Fuzzy Maximal Power Extraction of Wind Turbine with Continuously Variable Transmission. Energy 2014, 64, 868–874. [Google Scholar] [CrossRef]
- Jayaprabha, M.; Felcy, P. A Review of Clustering, Its Types and Techniques. Int. J. Innov. Sci. Res. Technol. 2018, 3, 127–130. [Google Scholar]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium Optimizer: A Novel Optimization Algorithm. Knowl. Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-Based Optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Mohammed, H.; Rashid, T. FOX: A FOX-Inspired Optimization Algorithm. Appl. Intell. 2023, 53, 1030–1050. [Google Scholar] [CrossRef]





| Formula | Dim | Range | fmin | |
|---|---|---|---|---|
| Sphere | 30 | [−100, 100] | 0 | |
| Schwefel 2.22 | 30 | [−10, 10] | 0 | |
| Schwefel 1.2 | 30 | [−100, 100] | 0 | |
| Schwefel 2.21 | 30 | [−100, 100] | 0 | |
| Rosenbrock | 30 | [−30, 30] | 0 | |
| Step | 30 | [−100, 100] | 0 | |
| Quartic | 30 | [−1.28, 1.28] | 0 |
| Formula | Dim | Range | fmin | |
|---|---|---|---|---|
| Schwefel 2.26 | 30 | [−100, 100] | −418.982 | |
| Rastrigin | 30 | [−5.12, 5.12] | 0 | |
| Ackley | 30 | [−32, 32] | 0 | |
| Griewank | + 1 | 30 | [−600, 600] | 0 |
| Penalised 1 | + | 30 | [−50, 50] | 0 |
| Penalised 2 | 30 | [−50, 50] | 0 |
| Formula | Dim | Range | fmin | |
|---|---|---|---|---|
| Shekel’s Foxholes | 2 | [−65, 65] | 1 | |
| Kowalik | 4 | [−5, 5] | 0.00030 | |
| Six-Hump Camel | 2 | [−5, 5] | −1.0316 | |
| Branin RCOS | 2 | [−5, 5] | 0.398 | |
| Goldstein–Price | 2 | [−2, 2] | 3 | |
| Hartman 3 | 3 | [1, 3] | −3.86 | |
| Hartman 6 | 6 | [0, 1] | −3.32 | |
| Shekel 5 | 4 | [−10, 10] | −10.1532 | |
| Shekel 7 | 4 | [−10, 10] | −10.4028 | |
| Shekel 10 | 4 | [−10, 10] | −10.5363 |
| Parameter Name | Description | Values |
|---|---|---|
| Population size | 30 | |
| Max_iteration | Maximum number of iterations (generations) | 1000 |
| No of Runs | Number of independent runs for statistical analysis | 30 |
| Initial jumping rate (probability of applying Lévy Flight) | 0.4 | |
| Final jumping rate (at end of iterations) | 0.05 | |
| Initial JOS correlation threshold | 0.8 | |
| Final JOS correlation threshold | 0.1 | |
| Lévy flight exponent | 1.5 | |
| Maximum inertia weight (exploration phase) | 0.9 | |
| Minimum inertia weight (exploitation phase) | 0.4 |
| Function | Index | LSCA | CSCA | SCA | MFSCA |
|---|---|---|---|---|---|
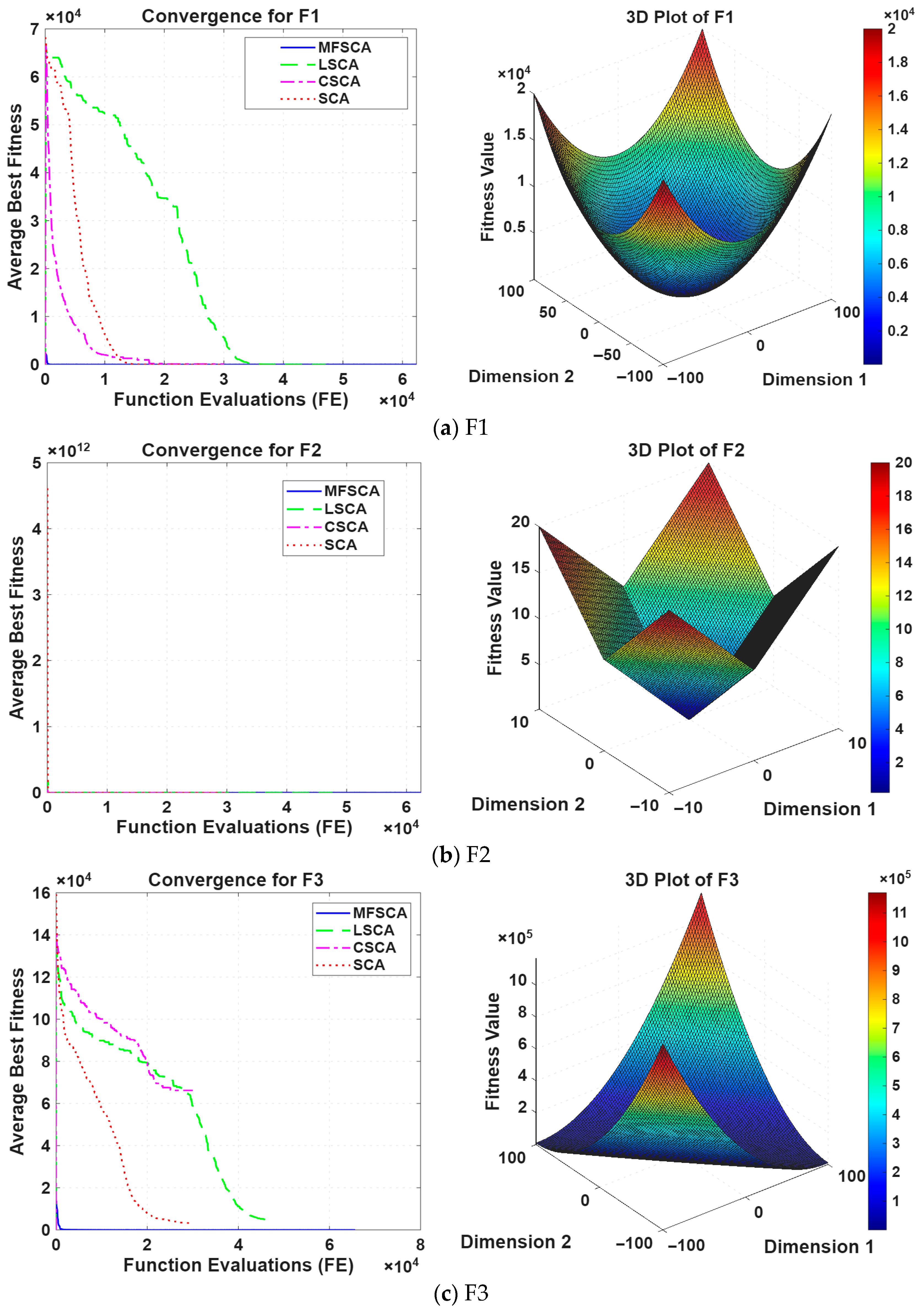
| F1 | mean | 1.3239 × 10−2 | 4.9167 × 103 | 6.4023 × 10−2 | 1.5128 × 10−292 |
| std dev | 2.5811 × 10−2 | 7.5235 × 103 | 2.5917 × 10−1 | 0.0000 × 100 | |
| best | 6.5244 × 10−5 | 5.6762 × 10−3 | 1.5496 × 10−6 | 2.7208 × 10−311 | |
| worse | 1.1480 × 10−1 | 3.2108 × 104 | 1.4291 × 100 | 3.5091 × 10−291 | |
| F2 | mean | 1.5982 × 10−3 | 1.3377 × 101 | 4.3640 × 10−5 | 1.2148 × 10−147 |
| std dev | 4.5484 × 10−3 | 7.7438 × 100 | 1.1194 × 10−4 | 6.1385 × 10−147 | |
| best | 1.3090 × 10−5 | 8.9444 × 10−1 | 9.4433 × 10−8 | 1.8933 × 10−156 | |
| worse | 2.0576 × 10−2 | 2.8724 × 101 | 5.9650 × 10−4 | 3.4207 × 10−146 | |
| F3 | mean | 3.8034 × 103 | 6.9461 × 104 | 4.1215 × 103 | 6.7108 × 10−285 |
| std dev | 3.5314 × 103 | 1.6756 × 104 | 2.6475 × 103 | 0.0000 × 100 | |
| best | 2.2755 × 101 | 3.0973 × 104 | 8.4659 × 101 | 5.0353 × 10−304 | |
| worse | 1.3020 × 104 | 9.7126 × 104 | 8.5914 × 103 | 1.9838 × 10−283 | |
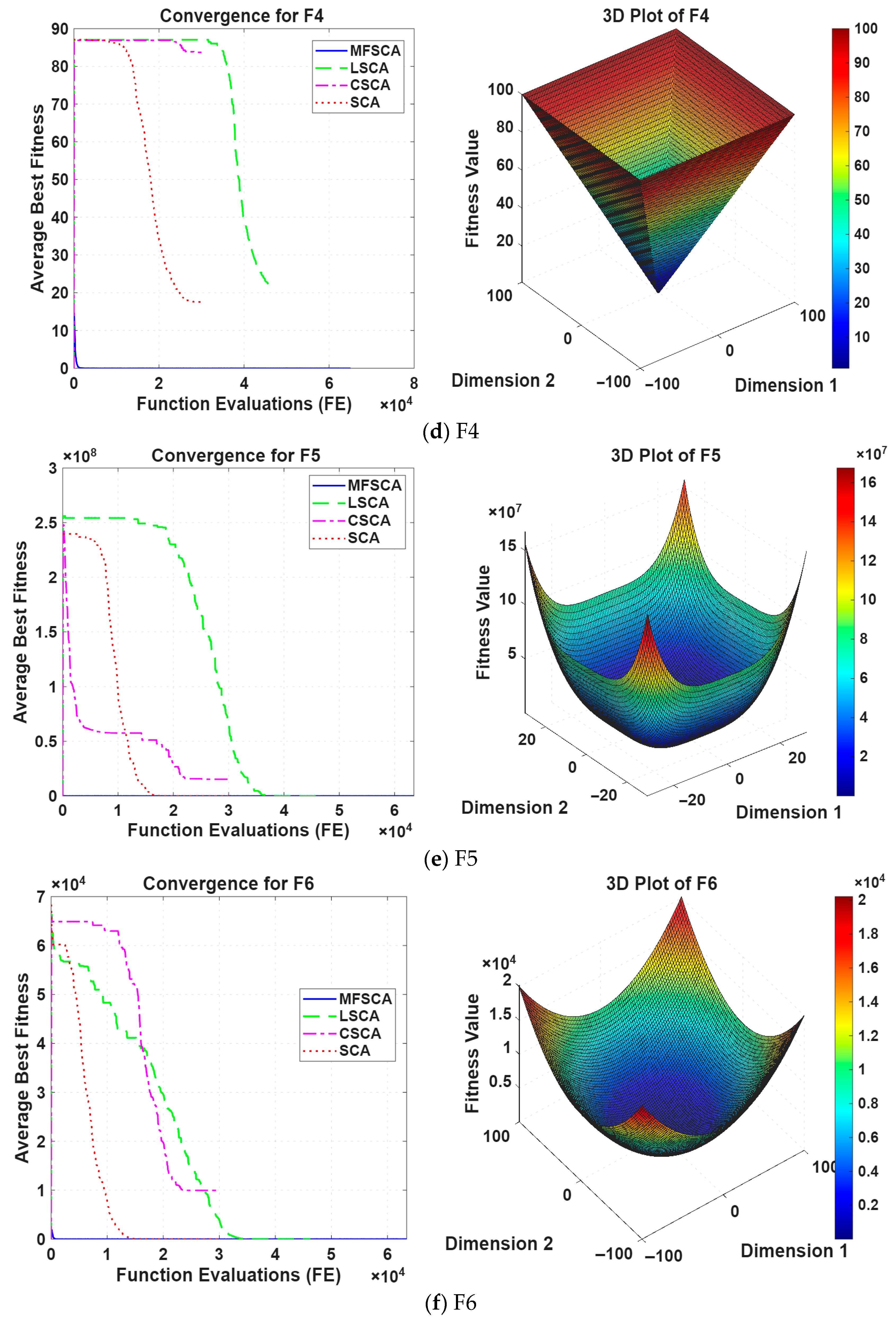
| F4 | mean | 1.8457 × 101 | 8.2936 × 101 | 2.2749 × 101 | 1.4519 × 10−148 |
| std dev | 1.0481 × 101 | 4.2911 × 100 | 1.1918 × 101 | 4.9468 × 10−148 | |
| best | 2.8740 × 100 | 7.3349 × 101 | 3.0020 × 100 | 7.7029 × 10−154 | |
| worse | 5.4362 × 101 | 9.1188 × 101 | 4.7403 × 101 | 2.0212 × 10−147 | |
| F5 | mean | 1.0865 × 103 | 2.3110 × 10+8 | 2.9458 × 103 | 2.7609 × 101 |
| std dev | 3.2565 × 103 | 7.7823 × 10+7 | 1.4919 × 104 | 4.5281 × 100 | |
| best | 2.8920 × 101 | 1.3186 × 10+7 | 2.8183 × 101 | 3.2302 × 100 | |
| worse | 1.6814 × 104 | 3.3317 × 10+8 | 8.3240 × 104 | 2.8649 × 101 | |
| F6 | mean | 3.8470 × 100 | 9.3676 × 103 | 4.5810 × 100 | 9.5481 × 10−1 |
| std dev | 4.7945 × 10−1 | 6.6317 × 103 | 3.9778 × 10−1 | 2.6351 × 10−1 | |
| best | 2.8578 × 100 | 1.1857 × 103 | 3.5479 × 100 | 1.9119 × 10−1 | |
| worse | 4.8576 × 100 | 2.8349 × 104 | 5.4797 × 100 | 1.3502 × 100 | |
| F7 | mean | 4.8382 × 10−2 | 3.2463 × 101 | 3.8258 × 10−2 | 6.7878 × 10−4 |
| std dev | 3.2868 × 10−2 | 2.2221 × 101 | 2.5948 × 10−2 | 3.8460 × 10−4 | |
| best | 5.9055 × 10−3 | 7.3722 × 10−1 | 9.2360 × 10−3 | 6.1001 × 10−5 | |
| worse | 1.4665 × 10−1 | 9.6816 × 101 | 1.0329 × 10−1 | 1.6042 × 10−3 |
| Function | Index | LSCA | CSCA | SCA | MFSCA |
|---|---|---|---|---|---|
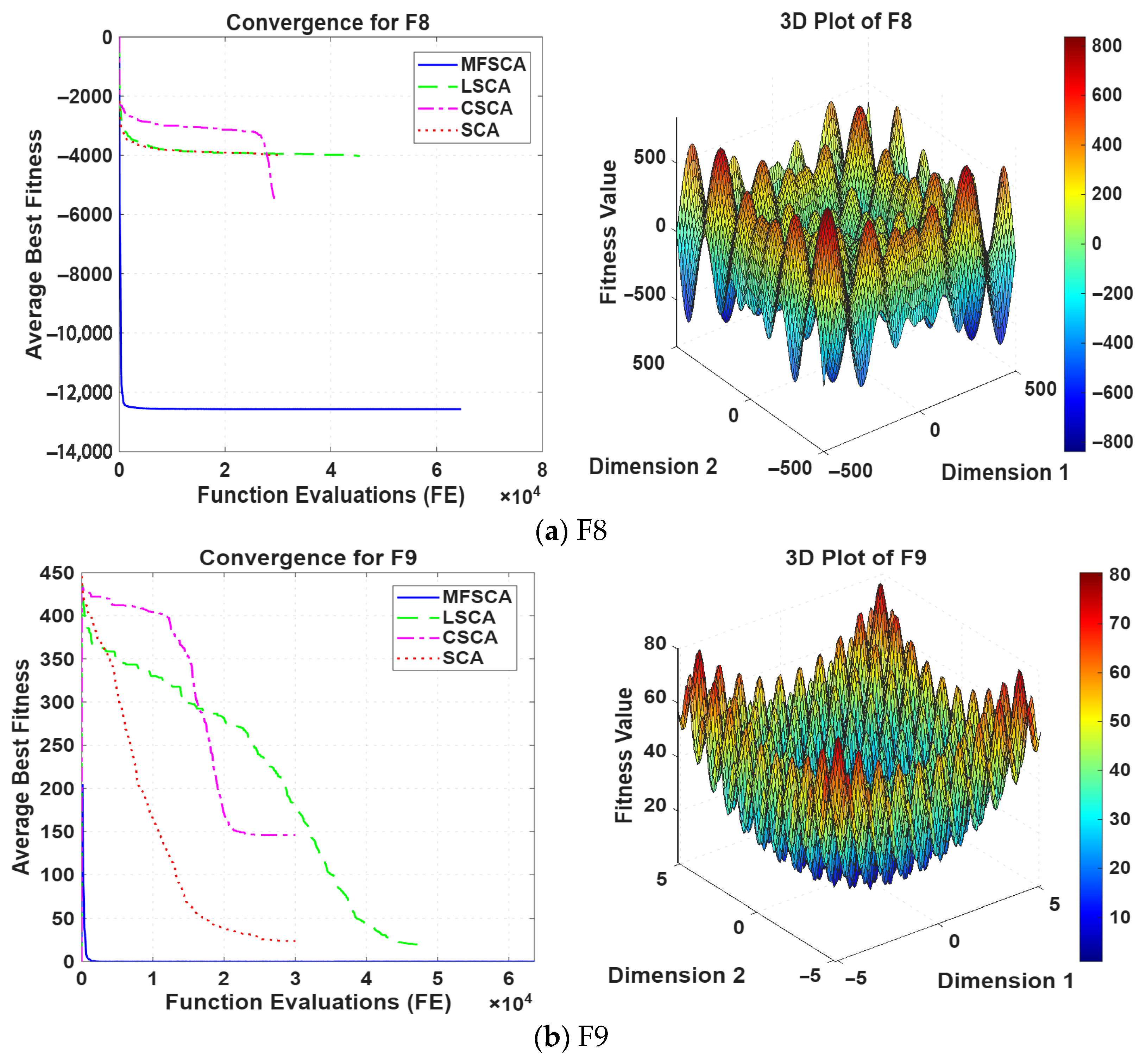
| F8 | mean | −4.1429 × 103 | −3.3918 × 103 | −3.9020 × 103 | −1.2569 × 104 |
| std dev | 2.5230 × 102 | 1.4781 × 103 | 3.1481 × 102 | 1.3996 × 100 | |
| best | −4.7642 × 103 | −6.5177 × 103 | −4.6415 × 103 | −1.2569 × 104 | |
| worse | −3.7047 × 103 | −1.7939 × 103 | −3.3789 × 103 | −1.2564 × 104 | |
| F9 | mean | 1.8196 × 101 | 1.5417 × 102 | 1.2460 × 101 | 0.0000 × 100 |
| std dev | 2.2446 × 101 | 6.1792 × 101 | 1.8611 × 101 | 0.0000 × 100 | |
| best | 4.6940 × 10−3 | 3.6497 × 101 | 3.6142 × 10−5 | 0.0000 × 100 | |
| worse | 8.7569 × 101 | 2.9273 × 102 | 7.2897 × 101 | 0.0000 × 100 | |
| F10 | mean | 1.8380 × 101 | 1.9622 × 101 | 1.3229 × 101 | 4.4409 × 10−16 |
| std dev | 5.1914 × 100 | 1.7115 × 100 | 9.4088 × 100 | 0.0000 × 100 | |
| best | 1.9170 × 10−2 | 1.2685 × 101 | 5.7757 × 10−5 | 4.4409 × 10−16 | |
| worse | 2.0275 × 101 | 2.0241 × 101 | 2.0295 × 101 | 4.4409 × 10−16 | |
| F11 | mean | 1.8314 × 10−1 | 1.1176 × 102 | 2.6762 × 10−1 | 0.0000 × 100 |
| std dev | 1.9729 × 10−1 | 7.4096 × 101 | 2.9975 × 10−1 | 0.0000 × 100 | |
| best | 4.6766 × 10−5 | 3.0870 × 100 | 3.6286 × 10−6 | 0.0000 × 100 | |
| worse | 5.6422 × 10−1 | 2.7323 × 102 | 9.6518 × 10−1 | 0.0000 × 100 | |
| F12 | mean | 1.9979 × 100 | 2.6200 × 108 | 4.8974 × 100 | 3.5533 × 10−2 |
| std dev | 3.9103 × 100 | 1.3261 × 108 | 8.2148 × 100 | 8.3218 × 10−3 | |
| best | 2.3684 × 10−1 | 4.8965 × 107 | 3.9145 × 10−1 | 1.3955 × 10−2 | |
| worse | 2.0807 × 101 | 5.4519 × 108 | 3.1427 × 101 | 4.7450 × 10−2 | |
| F13 | mean | 9.7529 × 100 | 8.0702 × 108 | 2.0497 × 102 | 3.0042 × 10−1 |
| std dev | 2.5412 × 101 | 4.6422 × 108 | 8.8400 × 102 | 7.8152 × 10−2 | |
| best | 1.7283 × 100 | 1.2377 × 108 | 2.2512 × 100 | 9.9412 × 10−2 | |
| worse | 1.3188 × 102 | 1.6065 × 109 | 4.8964 × 103 | 4.5018 × 10−1 |
| Function | Index | LSCA | CSCA | SCA | MFSCA |
|---|---|---|---|---|---|
| F14 | mean | 1.2626 × 100 | 1.5109 × 100 | 1.3288 × 100 | 3.3848 × 100 |
| std dev | 6.7443 × 10−1 | 8.2413 × 10−1 | 7.3936 × 10−1 | 2.5377 × 100 | |
| best | 9.9800 × 10−1 | 9.9800 × 10−1 | 9.9800 × 10−1 | 9.9800 × 10−1 | |
| worse | 2.9821 × 100 | 2.9821 × 100 | 2.9821 × 100 | 1.0233 × 101 | |
| F15 | mean | 9.1213 × 10−4 | 1.2035 × 10−3 | 9.5708 × 10−4 | 3.6054 × 10−4 |
| std dev | 3.1543 × 10−4 | 3.6961 × 10−4 | 3.1599 × 10−4 | 3.2864 × 10−5 | |
| best | 4.4250 × 10−4 | 7.6235 × 10−4 | 3.6017 × 10−4 | 3.1243 × 10−4 | |
| worse | 1.5416 × 10−3 | 1.9971 × 10−3 | 1.4646 × 10−3 | 4.6114 × 10−4 | |
| F16 | mean | −1.0316 × 100 | −1.0314 × 100 | −1.0316 × 100 | −1.0316 × 100 |
| std dev | 9.6483 × 10−6 | 1.5574 × 10−4 | 2.6599 × 10−5 | 7.6678 × 10−5 | |
| best | −1.0316 × 100 | −1.0316 × 100 | −1.0316 × 100 | −1.0316 × 100 | |
| worse | −1.0316 × 100 | −1.0311 × 100 | −1.0315 × 100 | −1.0313 × 100 | |
| F17 | mean | 3.9869 × 10−1 | 4.0189 × 10−1 | 3.9904 × 10−1 | 3.9838 × 10−1 |
| std dev | 1.3201 × 10−3 | 5.1719 × 10−3 | 1.3252 × 10−3 | 3.9497 × 10−4 | |
| best | 3.9789 × 10−1 | 3.9799 × 10−1 | 3.9793 × 10−1 | 3.9790 × 10−1 | |
| worse | 4.0505 × 10−1 | 4.1883 × 10−1 | 4.0277 × 10−1 | 3.9922 × 10−1 | |
| F18 | mean | 3.0000 × 100 | 3.0004 × 100 | 3.0000 × 100 | 3.0260 × 100 |
| std dev | 5.4367 × 10−5 | 5.7192 × 10−4 | 5.3464 × 10−5 | 2.3369 × 10−2 | |
| best | 3.0000 × 100 | 3.0000 × 100 | 3.0000 × 100 | 3.0003 × 100 | |
| worse | 3.0002 × 100 | 3.0023 × 100 | 3.0003 × 100 | 3.0838 × 100 | |
| F19 | mean | −3.8555 × 100 | −3.8541 × 100 | −3.8549 × 100 | −3.8534 × 100 |
| std dev | 2.6570 × 10−3 | 3.5946 × 10−3 | 1.9906 × 10−3 | 7.7607 × 10−3 | |
| best | −3.8626 × 100 | −3.8617 × 100 | −3.8614 × 100 | −3.8619 × 100 | |
| worse | −3.8531 × 100 | −3.8474 × 100 | −3.8524 × 100 | −3.8290 × 100 | |
| F20 | mean | −3.0456 × 100 | −2.9485 × 100 | −2.9234 × 100 | −3.2459 × 100 |
| std dev | 9.3065 × 10−2 | 2.3600 × 10−1 | 3.5629 × 10−1 | 3.4049 × 10−2 | |
| best | −3.2131 × 100 | −3.1985 × 100 | −3.1599 × 100 | −3.3009 × 100 | |
| worse | −2.7777 × 100 | −1.9686 × 100 | −1.4556 × 100 | −3.1689 × 100 | |
| F21 | mean | −3.2530 × 100 | −1.9648 × 100 | −2.1995 × 100 | −9.7752 × 100 |
| std dev | 2.1675 × 100 | 1.3852 × 100 | 1.8367 × 100 | 2.7572 × 10−1 | |
| best | −7.9025 × 100 | −4.7872 × 100 | −4.9654 × 100 | −1.0098 × 101 | |
| worse | −4.9728 × 10−1 | −4.9648 × 10−1 | −4.9727 × 10−1 | −9.1400 × 100 | |
| F22 | mean | −3.8301 × 100 | −2.3090 × 100 | −3.8547 × 100 | −1.0159 × 101 |
| std dev | 1.9243 × 100 | 1.3657 × 100 | 1.8090 × 100 | 2.1813 × 10−1 | |
| best | −7.8549 × 100 | −5.2511 × 100 | −9.0406 × 100 | −1.0401 × 101 | |
| worse | −5.2242 × 10−1 | −5.2103 × 10−1 | −5.2403 × 10−1 | −9.3796 × 100 | |
| F23 | mean | −4.6740 × 100 | −2.5928 × 100 | −5.0394 × 100 | −1.0211 × 101 |
| std dev | 1.9238 × 100 | 8.8996 × 10−1 | 1.8895 × 100 | 2.8059 × 10−1 | |
| best | −9.0163 × 100 | −4.1503 × 100 | −9.8090 × 100 | −1.0524 × 101 | |
| worse | −9.4336 × 10−1 | −5.5446 × 10−1 | −9.4206 × 10−1 | −9.3350 × 100 |
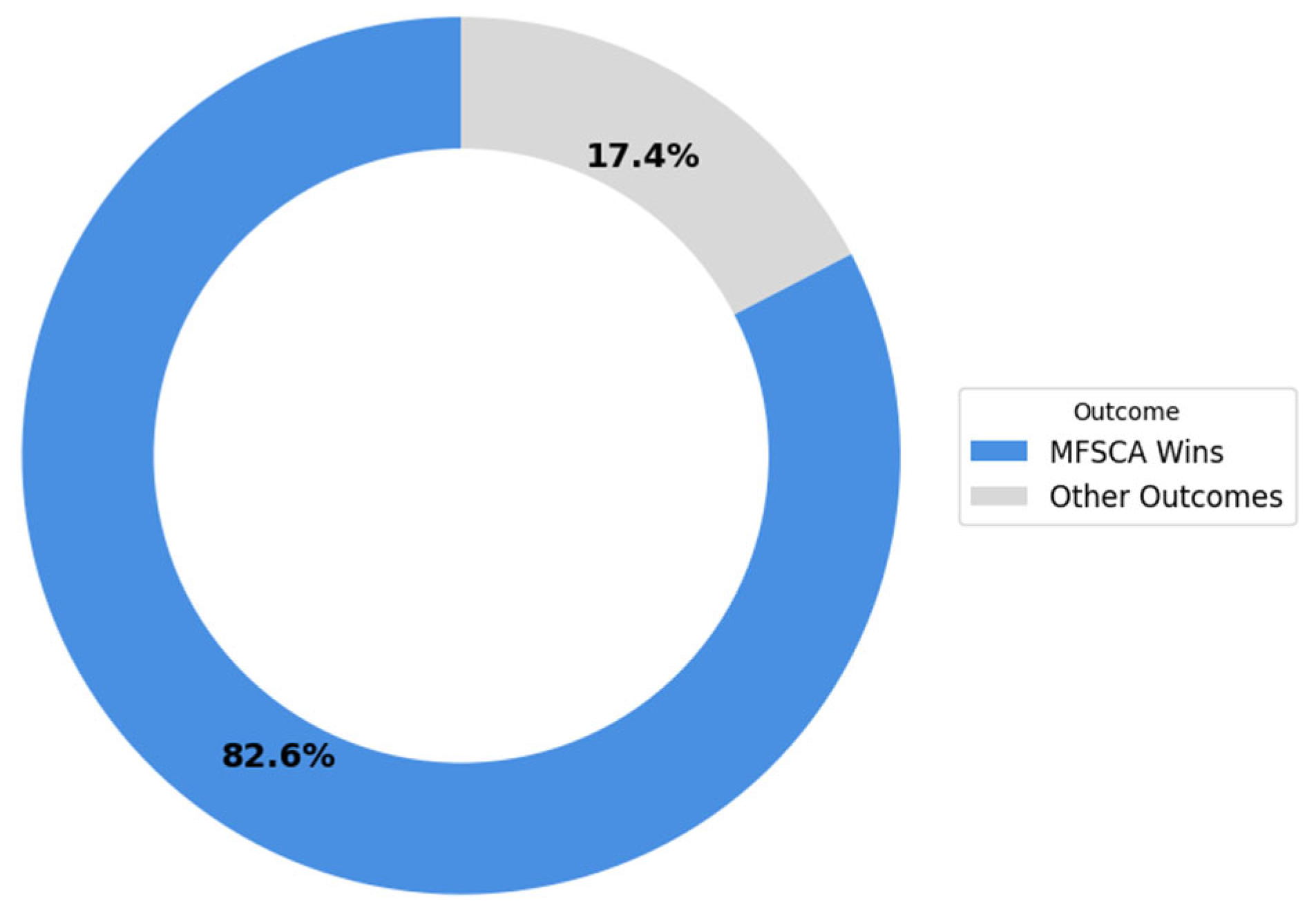
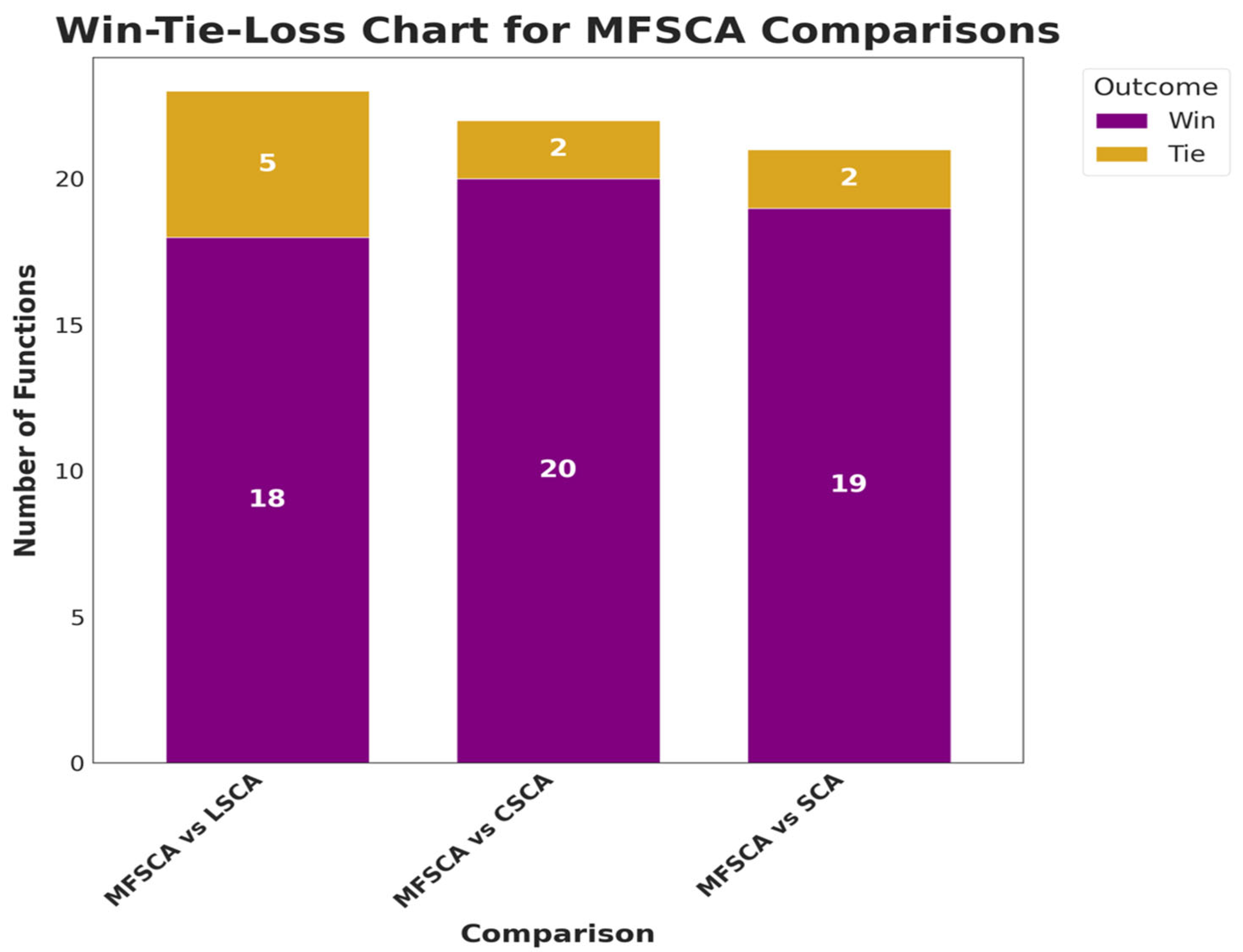
| Functions (F) | MFSCA vs. LSCA | MFSCA vs. CSCA | MFSCA vs. SCA |
|---|---|---|---|
| 1 | “” | “” | “” |
| 2 | “” | “” | “” |
| 3 | “” | “” | “” |
| 4 | “” | “” | “” |
| 5 | “” | “” | “” |
| 6 | “” | “” | “” |
| 7 | “” | “” | “” |
| 8 | “” | “” | “” |
| 9 | “” | “” | “” |
| 10 | “” | “” | “” |
| 11 | “” | “” | “” |
| 12 | “” | “” | “” |
| 13 | “” | “” | “” |
| 14 | “” | “” | “” |
| 15 | “” | “” | “” |
| 16 | “” | “” | “” |
| 17 | “” | “” | “” |
| 18 | “” | “” | “” |
| 19 | “” | “” | “” |
| 20 | “” | “” | “” |
| 21 | “” | “” | “” |
| 22 | “” | “” | “” |
| 23 | “” | “” | “” |
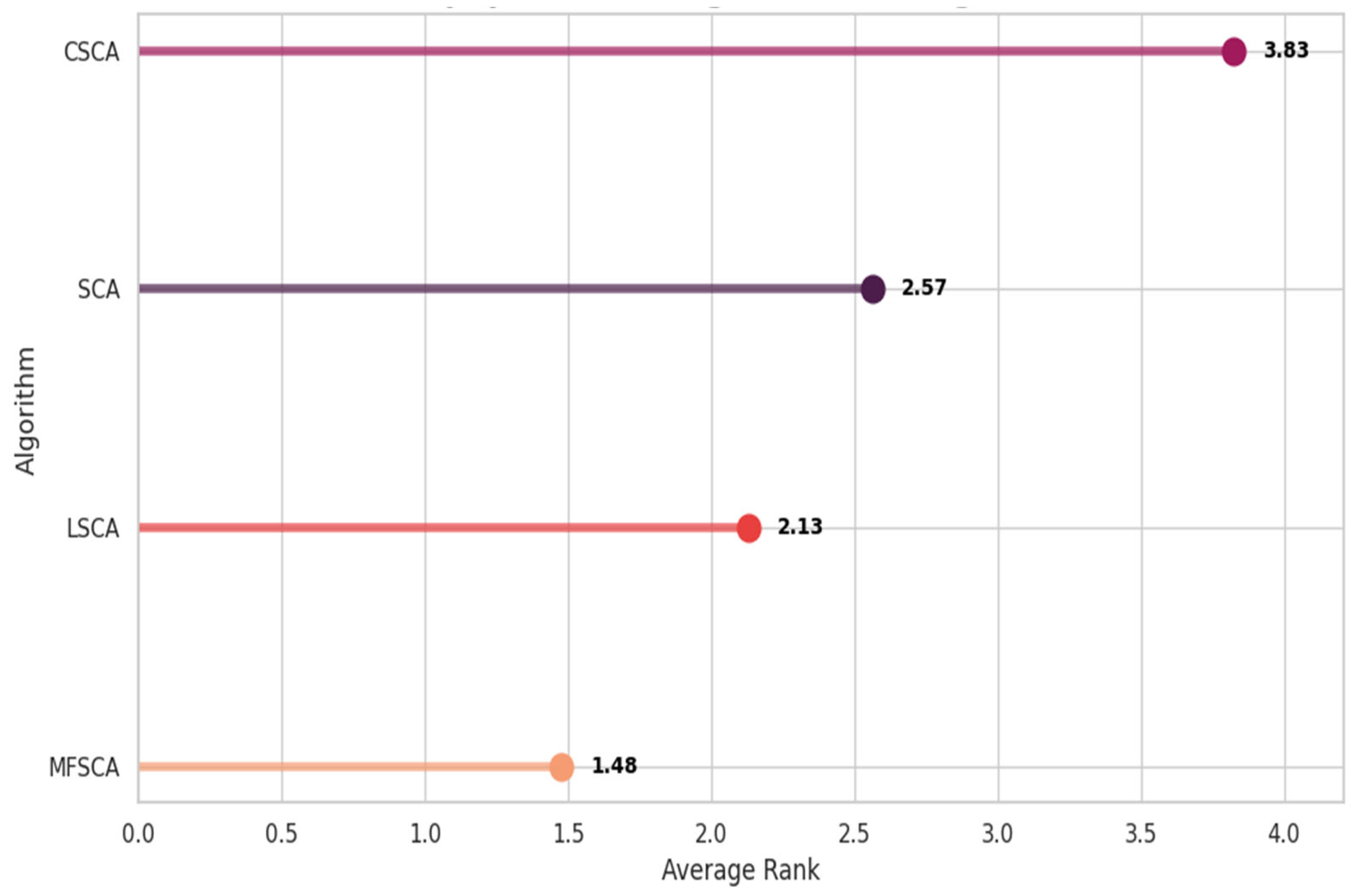
| Algorithm | Average Rank |
|---|---|
| LSCA | 2.1304 |
| CSCA | 3.8261 |
| SCA | 2.5652 |
| MFSCA | 1.4783 |
| Metrics | Mathematical Expression |
|---|---|
| Theil’s U | |
| SD |
| Hybrid Models | Parameter Setting |
|---|---|
| General parameters | dim = 25, pop = 30, Max_it = 100 |
| GA | = 0.15, roulette wheel |
| EO | = 1, GP = 0.5 |
| HHO | = 1.5 |
| FO | = 0.82 |
| BBO | Keep rate = 0.2, mutation probability = 0.1 |
| PSO | = 1 |
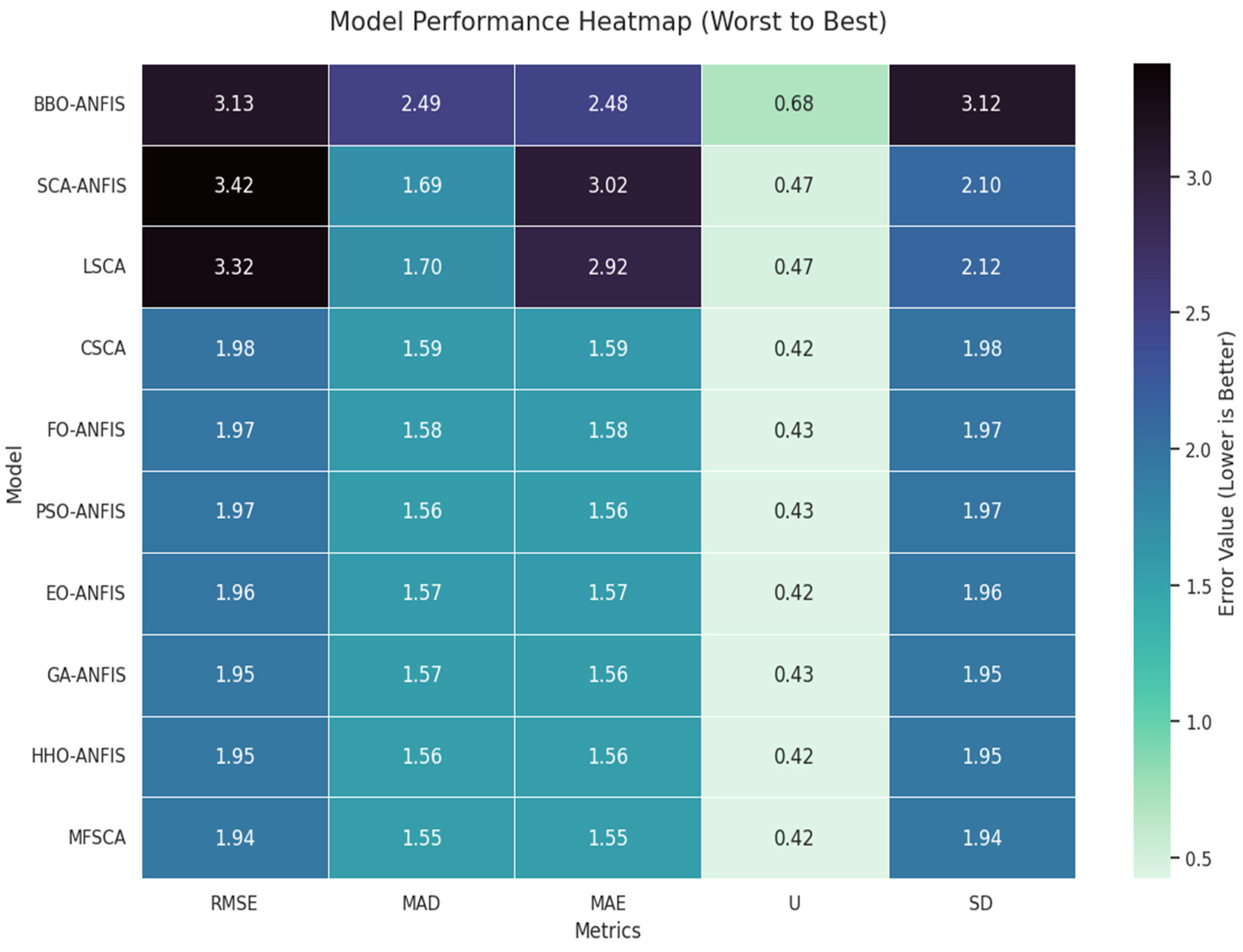
| Model | Phase | RMSE | MAD | MAE | CVRMSE | U | SD |
|---|---|---|---|---|---|---|---|
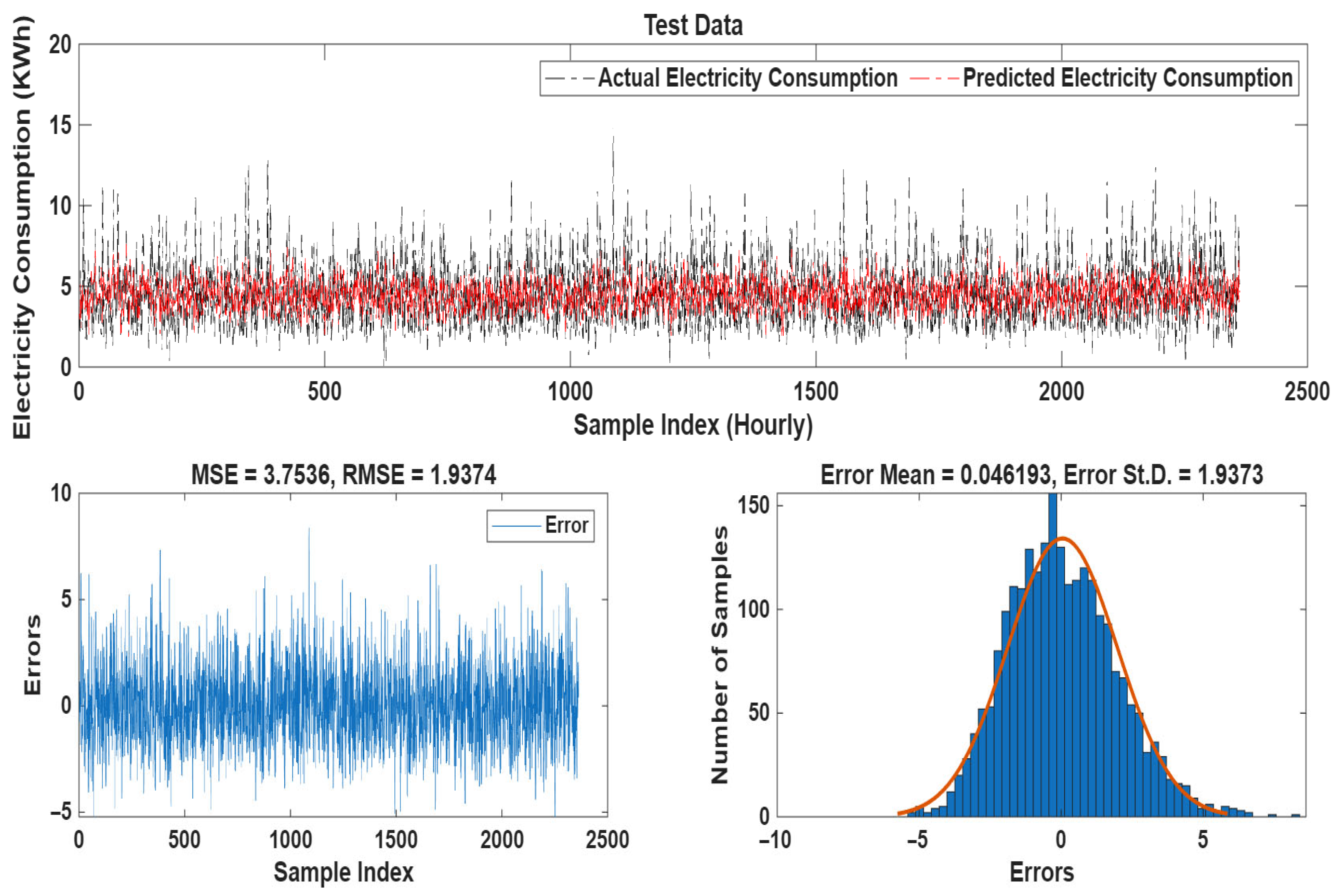
| MFSCA-ANFIS | Training | 1.9696 | 1.5635 | 1.5607 | 43.5676 | 0.4319 | 1.9685 |
| Testing | 1.9374 | 1.5483 | 1.5457 | 42.8463 | 0.4224 | 1.9373 | |
| PSO-ANFIS | Training | 1.9318 | 1.5502 | 1.5500 | 42.7007 | 0.4213 | 1.9320 |
| Testing | 1.9698 | 1.5637 | 1.5631 | 43.6367 | 0.4308 | 1.9702 | |
| GA-ANFIS | Training | 1.9403 | 1.5547 | 1.5550 | 42.9580 | 0.4232 | 1.9405 |
| Testing | 1.9532 | 1.5660 | 1.5637 | 43.1072 | 0.4273 | 1.9535 | |
| EO-ANFIS | Training | 1.9388 | 1.5496 | 1.5497 | 42.8734 | 0.4224 | 1.9389 |
| Testing | 1.9581 | 1.5723 | 1.5745 | 43.3341 | 0.4245 | 1.9583 | |
| CSCA-ANFIS | Training | 1.9515 | 1.5501 | 1.5618 | 43.2607 | 0.4145 | 1.9477 |
| Testing | 1.9847 | 1.5860 | 1.5950 | 43.6713 | 0.4209 | 1.9827 | |
| FO-ANFIS | Training | 1.9346 | 1.5447 | 1.5450 | 42.8861 | 0.4221 | 1.9348 |
| Testing | 1.9656 | 1.5767 | 1.5751 | 43.2528 | 0.4280 | 1.9660 | |
| SCA-ANFIS | Training | 3.3997 | 1.6798 | 2.9927 | 75.1010 | 0.4719 | 2.0944 |
| Testing | 3.4177 | 1.6861 | 3.0216 | 75.8226 | 0.4743 | 2.0990 | |
| LSCA-ANFIS | Training | 3.3125 | 1.6743 | 2.9077 | 73.3531 | 0.4672 | 2.0848 |
| Testing | 3.3218 | 1.6994 | 2.9179 | 73.2723 | 0.4685 | 2.1213 | |
| BBO-ANFIS | Training | 3.1366 | 2.4773 | 2.4683 | 69.4851 | 0.6893 | 3.1239 |
| Testing | 3.1284 | 2.4934 | 2.4811 | 68.9480 | 0.6838 | 3.1163 | |
| HHO-ANFIS | Training | 1.9584 | 1.5638 | 1.5619 | 43.3066 | 0.4272 | 1.9583 |
| Testing | 1.9454 | 1.5556 | 1.5558 | 43.0532 | 0.4209 | 1.9458 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oladipo, S.O.; Akuru, U.B.; Amole, A.O. Improved Multi-Faceted Sine Cosine Algorithm for Optimization and Electricity Load Forecasting. Computers 2025, 14, 444. https://doi.org/10.3390/computers14100444
Oladipo SO, Akuru UB, Amole AO. Improved Multi-Faceted Sine Cosine Algorithm for Optimization and Electricity Load Forecasting. Computers. 2025; 14(10):444. https://doi.org/10.3390/computers14100444
Chicago/Turabian StyleOladipo, Stephen O., Udochukwu B. Akuru, and Abraham O. Amole. 2025. "Improved Multi-Faceted Sine Cosine Algorithm for Optimization and Electricity Load Forecasting" Computers 14, no. 10: 444. https://doi.org/10.3390/computers14100444
APA StyleOladipo, S. O., Akuru, U. B., & Amole, A. O. (2025). Improved Multi-Faceted Sine Cosine Algorithm for Optimization and Electricity Load Forecasting. Computers, 14(10), 444. https://doi.org/10.3390/computers14100444









