Abstract
This research introduces a new approach for detecting mobile phone use by drivers, exploiting the capabilities of Kolmogorov-Arnold Networks (KAN) to improve road safety and comply with regulations prohibiting phone use while driving. To address the lack of available data for this specific task, a unique dataset was constructed consisting of images of bus drivers in two scenarios: driving without phone interaction and driving while on a phone call. This dataset provides the basis for the current research. Different KAN-based networks were developed for custom action recognition tailored to the nuanced task of identifying drivers holding phones. The system’s performance was evaluated against convolutional neural network-based solutions, and differences in accuracy and robustness were observed. The aim was to propose an appropriate solution for professional Driver Monitoring Systems (DMS) in research and development and to investigate the efficiency of KAN solutions for this specific sub-task. The implications of this work extend beyond enforcement, providing a foundational technology for automating monitoring and improving safety protocols in the commercial and public transport sectors. In conclusion, this study demonstrates the efficacy of KAN network layers in neural network designs for driver monitoring applications.
1. Introduction
Increasing traffic density necessitates safer individual and public transport, where drivers continue to play a pivotal role despite advancements in Advanced Driver-Assistance Systems (ADAS), such as emergency braking [1]. The passenger-kilometers for passenger cars show a general increasing trend from 2000 to 2019, peaking at 4298.3 billion in 2019 [2]. There was a notable decline in 2020 (3516.9 billion), likely due to the COVID-19 pandemic and subsequent lockdowns, with a partial recovery in 2021 (3742.2 billion). The impact of the pandemic is evident, showing a significant dip in 2020, but the numbers started to rebound in 2021. Despite a decrease in overall usage, buses still represent a significant part of European public road transport. In 2022, over 108 thousand million passengers and 97 thousand million passenger-kilometers were recorded across selected European countries (Table 1).

Table 1.
Passenger-kilomteres and fatalities with Passenger Cars, Buses, and Coaches in selected EU-17 countries [2].
The literature has investigated the relationship between mobile phone usage and accidents. One of the research projects uses data from a questionnaire sent to 15,000 Finnish working-age individuals, with 6121 responses analyzed [3]. A more significant number of accidents and near-miss incidents associated with the usage of mobile phones were reported by males and younger individuals. Individuals in employment reported a higher rate of incidents related to the use of mobile phones. A slight increase was observed in the number of incidents reported by those experiencing sleep disturbances or minor aches and pains. Another paper examined the correlation between smartphone adoption and traffic accident rates in areas with 3G coverage in California from 2009 to 2013 [4]. The study revealed an approximate 2.9% increase in accident rates in areas with 3G coverage. This magnitude of increase is comparable to that observed in other studies, which have linked elevated accident rates to higher minimum wages and alcohol consumption. Therefore, the authors recommend introducing more rigorous regulations and effective enforcement measures to mitigate the risks associated with smartphone use while driving. Another paper focused on drivers’ various issues due to mobile device usage, including visual and cognitive distraction [5]. Using mobile phones while driving reduces concentration and situational awareness, leading to slower reaction times and improper driving behaviors. The findings emphasize the need to understand mobile phone usage laws better and enforce them to enhance road safety.
One paper presents a nonintrusive computer vision system designed to monitor driver vigilance in real time [6]. The system uses multiple visual parameters, such as percent eye closure, blink frequency, and nodding frequency, combined through a fuzzy classifier to determine driver inattentiveness, offering a promising tool for enhancing road safety. Another review highlights the potential of physiological-based DMS to enhance driver safety by monitoring states such as alertness, fatigue, and drowsiness [7]. These systems use physiological signals (e.g., EEG, ECG, EMG) to provide more accurate monitoring compared to behavior-based or vehicle-based systems. The authors’ previous work introduces Capsule Networks (CapsNets) for image processing and face detection tasks within DMS [8]. The study aimed to create a fast and more accurate system than state-of-the-art Neural Network (NN) algorithms. The results demonstrate that the capsule-based solution performs superiorly in degradation tests compared to other networks. This highlights the robustness and efficiency of the solution in real-world applications such as public transport.
An early study investigated the association between cellular phone use in vehicles and traffic accident risk using an epidemiological case-control design and logistic regression techniques [9]. The research included 100 drivers involved in accidents and 100 control drivers. It was found that talking more than 50 min per month on a cellular phone while driving increased the risk of a traffic accident by 5.59 times. The research examined the impact of handheld and hands-free mobile phone use on driving performance in a simulated environment [10]. Participants exhibited impaired peripheral detection task (PDT) performance and increased mental workload during both dialing and conversations, regardless of phone type. Dialing caused increased lateral position deviation and reduced speed, while conversations led to decreased speed. Despite compensatory behavior to mitigate these effects, the overall mental workload remained elevated. Another paper assessed drivers’ awareness of their performance decrements while using cell phones [11]. Results indicated that many drivers are unaware of their decreased performance, such as increased brake response time and impaired ability to maintain lane position, during cell phone use. It highlighted a disconnect between drivers’ confidence in their multitasking ability and performance. One paper explored the prevalence and risks associated with mobile phone use while driving in Qatar [12]. A high rate of mobile phone use was found among drivers involved in road traffic crashes, with 82.6% using handheld phones. Significant factors associated with mobile phone use included vehicle type, speeding, educational level, and running red lights. The study concluded that mobile phone use while driving is a significant public health issue. Ortega et al. assessed the impact of mobile phone use on driving performance, focusing on workload and traffic violations [13]. The study used a driving simulator to find significant differences in vehicle control between distracted and non-distracted young drivers. The results indicated that mobile phone use increases overall workload and leads to more traffic violations. Recent studies use an ordered probit model to investigate the factors influencing intra-city bus drivers’ use of cell phones while driving [14]. The study identified significant variables associated with using mobile phones while driving, such as age, driving experience, and perceived risk. It emphasized the need for targeted interventions and policies to mitigate the risks posed by distracted driving among professional drivers. A research group conducted a comprehensive study on the impact of mobile phone use on driving behavior and the associated risks of traffic accidents [15]. By surveying a representative sample of drivers in Jordan, the study revealed significant correlations between mobile phone use and increased incidences of traffic violations and accidents. Another aspect is explored when the usability, advantages, and disadvantages of the Bring-Your-Own-Device (BYOD) concept within In-Vehicle Information Systems (IVIS) are tested [16]. One study used a complex simulation environment with eye-tracking technology to assess participants’ gaze patterns and attention allocation. The results suggest that integrating mobile phones as part of the BYOD concept enhances usability and reduces distraction, promoting the development of user-centric and sustainable automotive interfaces.
Focusing on algorithms and methods, the recent study by Braun examines Sprecher’s algorithm, focusing on the monotonicity and continuity of the inner function ψ [17]. While Sprecher’s original definition of ψ lacked these properties, a revised definition by Köppen ensures monotonicity and continuity on the interval [0, 1] [18]. The paper demonstrates that Sprecher’s algorithm, with Köppen’s ψ, converges effectively, providing a robust theoretical foundation for continuous and monotone increasing functions within the specified interval. More recent work delves into deep ReLU network constructions derived from the Kolmogorov–Arnold (KA) representation [19]. They present novel KA representations that transfer smoothness from multivariate functions to outer functions, optimizing neural network parameters for better approximation. The paper contrasts the efficiency of these networks with prior models, highlighting their advantages in parameter optimization and smooth function approximation. Some researchers explore the Kolmogorov Superposition Theorem (KST) to overcome the curse of dimensionality in approximating multivariate continuous functions [20]. They detail how KST can be applied in deep learning to approximate high-dimensional functions efficiently. The theorem’s application is shown to break dimensionality barriers, enabling more accurate and efficient neural network computations. Liu et al. introduce KANs as alternatives to Multi-Layer Perceptrons (MLPs) [21]. Unlike MLPs, with fixed activation functions on neurons, KANs feature learnable activation functions on edges, replacing linear weights with univariate functions parametrized as splines. KANs demonstrate superior accuracy and interpretability, performing better in function-fitting tasks with smaller network sizes compared to larger MLPs. These networks also exhibit faster neural scaling laws and are more intuitive, facilitating user interactions. Through applications in mathematics and physics, KANs are shown to assist in rediscovering mathematical and physical laws, suggesting their potential for further advancements in deep learning models heavily reliant on MLPs.
DropKAN, a novel regularization method, was proposed and explicitly designed for KANs [22]. Unlike traditional dropout methods, which can lead to unpredictable behaviors in KANs, DropKAN applies dropout directly to the activations within the KAN layers. This approach improves generalization and is validated through experiments on multiple real-world datasets, demonstrating superior performance compared to standard dropout techniques. Others introduce Convolutional KANs, which integrate KAN’s non-linear, spline-based activations into convolutional layers, forming an alternative to standard CNNs [23]. This architecture aims to reduce the number of parameters while maintaining comparable accuracy levels, as evidenced by experiments on the MNIST and Fashion-MNIST datasets. The results suggest that Convolutional KANs can match the performance of traditional CNNs with fewer resources.
Chebyshev Kolmogorov–Arnold Network (Chebyshev KAN), a novel neural network architecture that utilizes Chebyshev polynomials for function approximation, was presented recently [24]. The architecture builds on the Kolmogorov–Arnold representation theorem by employing learnable functions parametrized by Chebyshev polynomials along the network’s edges. This design significantly improves the parameter efficiency and interpretability of the network, resulting in tasks such as digit classification and synthetic function approximation. Some researchers recently comprehensively compared KANs and MLPs across various tasks, including machine learning, computer vision, Natural Language Processing (NLP), audio processing, and symbolic formula representation [25]. By controlling the number of parameters and floating-point operations (FLOPs), they found that MLPs generally outperform KANs in most tasks except symbolic formula representation, where KANs excel due to their B-spline activation functions. The study highlights that KANs suffer more severe forgetting issues in continual learning settings than MLPs, which retain better performance across tasks.
Focusing on driver attention and cognitive load is vital for optimizing working conditions and enhancing accident prevention. In this context, Kolmogorov–Arnold Networks have been integrated into a professional camera-based DMS for public transport, aiming to improve safety by detecting phone usage while driving. The following is a description of the structure of the paper: In Section 2, the authors present the theoretical background, the models employed in the research, and the datasets used. Subsequently, Section 3 details the conditions for training the proposed networks and illustrates the results achieved in several ways. Finally, the section discusses the achieved results. Section 4 presents a discussion of the present work, while Section 5 offers a conclusion.
2. Materials and Methods
This section presents the theoretical background applied in the current research, and the networks and datasets implemented are described. This research investigated the applicability of KAN networks for a specific sub-task. For this purpose, the theory and operation of KAN networks are presented. In total, neural networks have been designed where KAN theory has been applied. After a detailed presentation of these, the created dataset is described.
2.1. Kolmogorov–Arnold Network Theory
The application of the Kolmogorov–Arnold representation theorem [26,27] in the world of artificial neural networks promises to be a new and exciting field. The proposed approach is expected to enhance the efficiency of networks, potentially leading to improved solutions for specific problems. The theory of KAN [21] was developed primarily as a better alternative to multilayer perceptron. It is, therefore, beneficial to undertake a comparative analysis of its efficiency.
For the multilayer perceptron, fixed, non-learnable activation functions and learning weights between the neurons were applied to the neurons. The KAN network breaks with this idea. The MLP’s non-learnable and non-linear activation function is learnable, but linear weights are replaced by non-linear and learnable functions in the KAN network. It does this by using spline functions that can be parameterized. These parameters appear as learnable values in the neural network.
In the case of a multilayer perceptron, let
where is the input of the layer, is the learnable, linear weight matrix, is the bias, and is the non-linear activation function, which may take one of several forms, like ReLU [28], sigmoid or tanh.
It is asserted in KAN theory that there is a multivariate function (see Equation (1)),
where is the number of input parameters. Let
where is the number of inputs, is the -th input, is a univariate function that is mapping the inputs, such that
and the univariate function performs the following mapping:
For KAN networks, each layer can be represented as a matrix of these functions:
where is the number of inputs in the given layer, and is the output features generated by that layer. Each , where and , can be mapped to a B-spline function:
where is the Sigmoid Linear Unit [29,30] activation function
and s is the linear combination of B-splines
where is trainable.
ϕx = wbbx + wssx
bx = SiLUx
SiLUx = x 1 + e − x
2.2. Network Architectures
In the present research, different neural network designs were implemented; in cases, KAN layers were used, and in cases, they were not used. In the design, an effort has been made to create a multitude of networks with varying architectures, encompassing both more straightforward and intricate solutions. The KAN network layer is primarily comparable to the linear layers. Consequently, such networks have been devised.
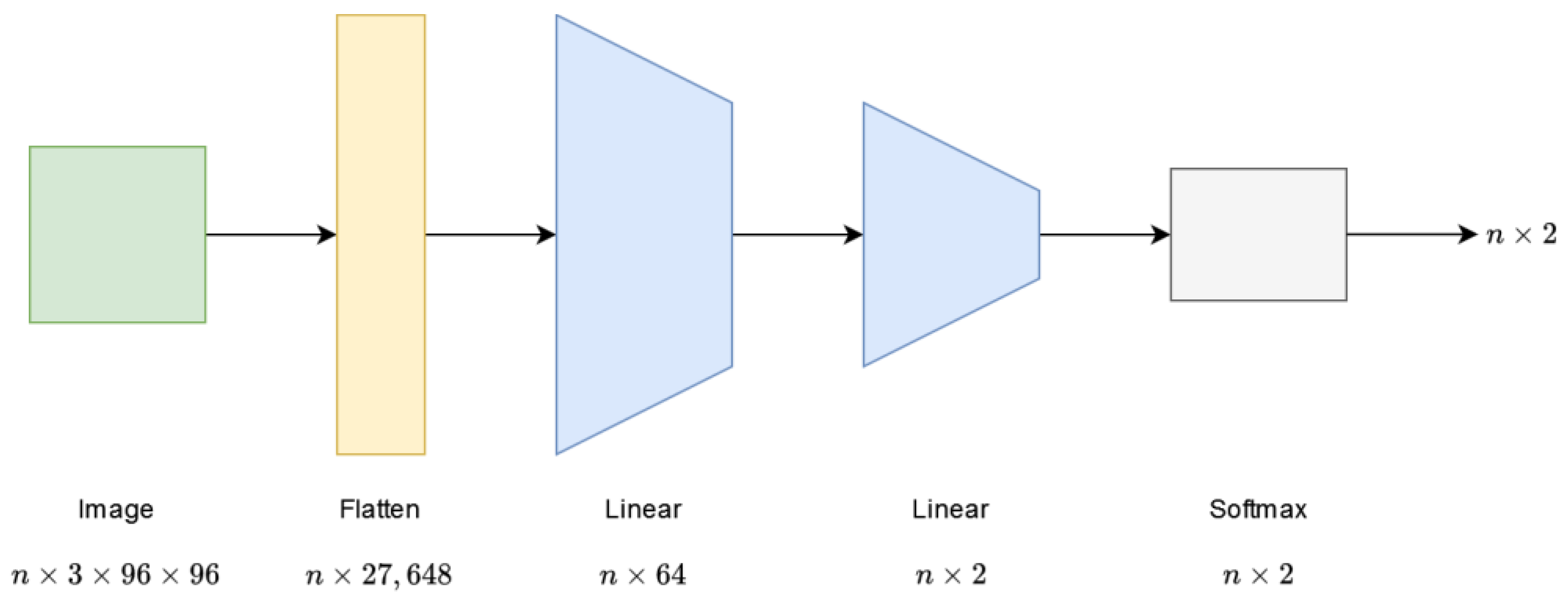
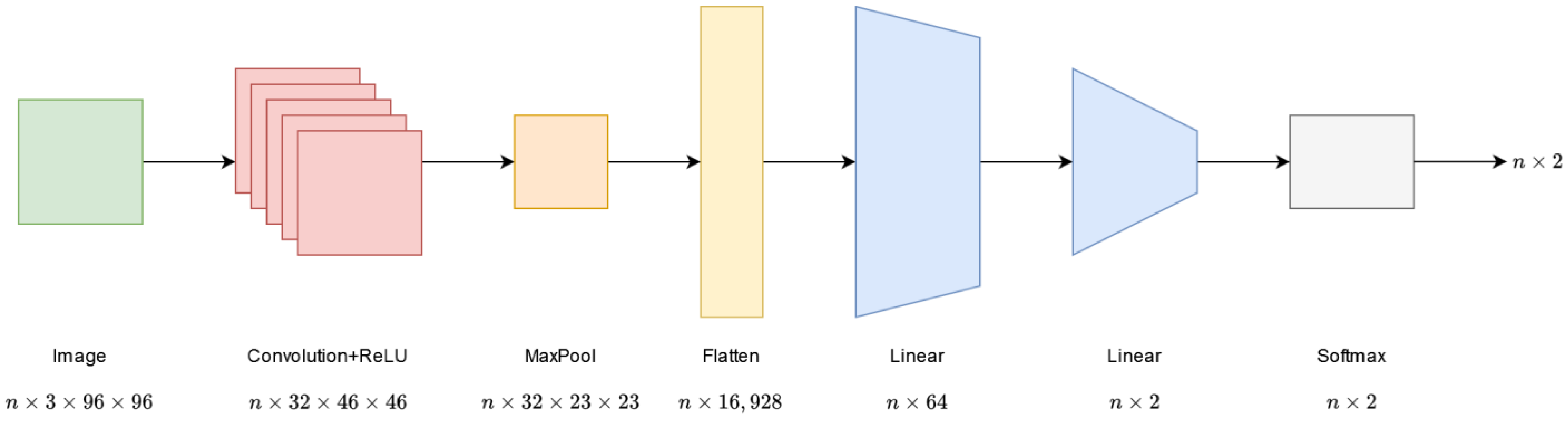
The first architecture is the LinNet, which does not include a KAN network layer. The network is built from fully connected layers. The first layer has an input of size and an output of size , where is the batch size. The second linear layer has an output of , since binary classification is performed. After the last layer, a softmax function is used to obtain the network output. The first linear layer contains parameters. The high number of parameters here is due to the size of the input image. The second layer is simpler, with only parameters. Figure 1 visualizes the LinNet architecture.
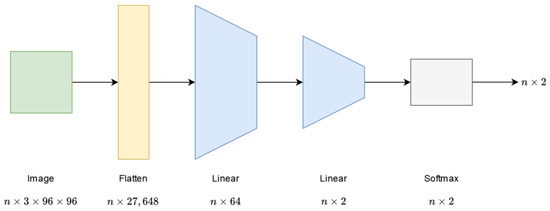
Figure 1.
Architecture of the LinNet network.
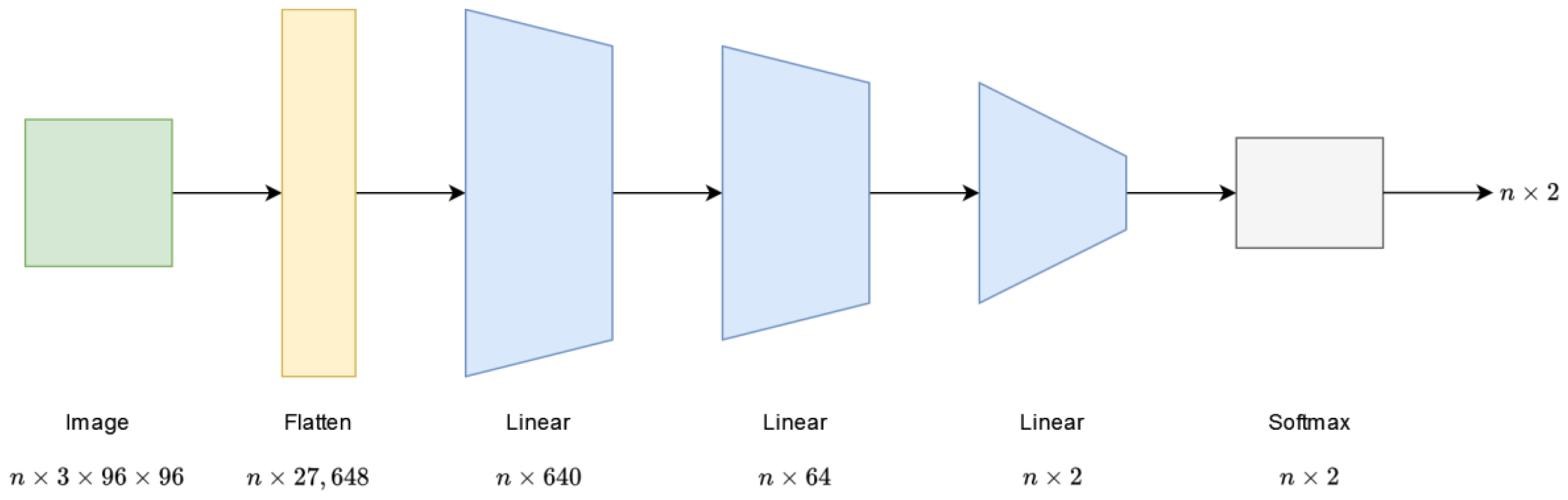
The second network design is based on the LinNet architecture. The main difference is that here, a third fully connected layer appears. This design has been named LinNet L, where “L” stands for “large”. In this case, the output of the first linear layer is . The size of the following two layers is equal to the size of the LinNet layers. The first layer still has a high number of parameters, in total; the second layer has , and the last linear layer has parameters. In this case, the network is also closed with a softmax function. Figure 2 shows the LinNet L model.
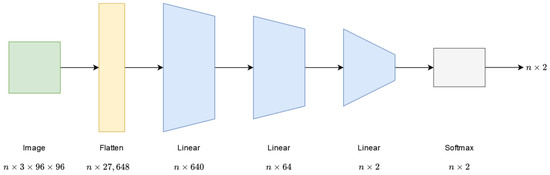
Figure 2.
Architecture of the LinNet L network.
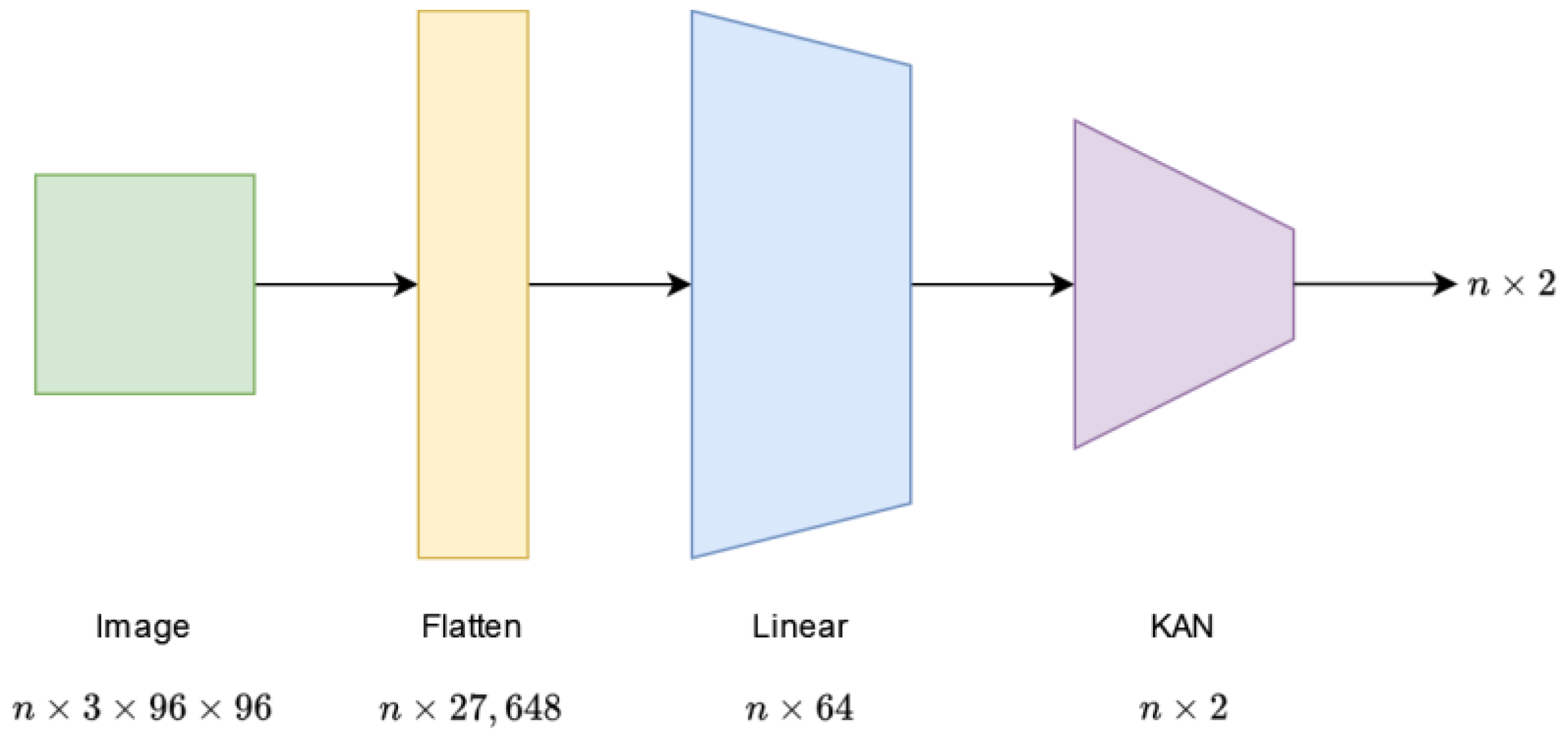
Our next solution is the LinKAN network, which already includes a KAN-based layer. Its structure is most similar to the LinNet network, with one crucial difference. The authors replaced the last fully connected layer with a KAN layer of the same size. In this case, the first linear layer has a parameter number of . The subsequent KAN layer has parameters. The structure of the LinKAN network is shown in Figure 3.
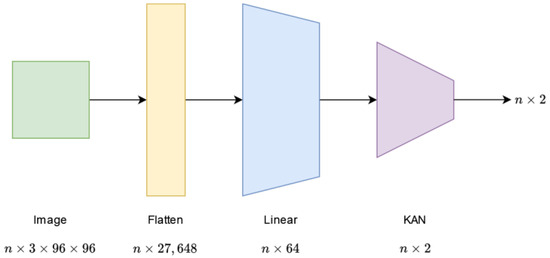
Figure 3.
Architecture of the LinKAN network.
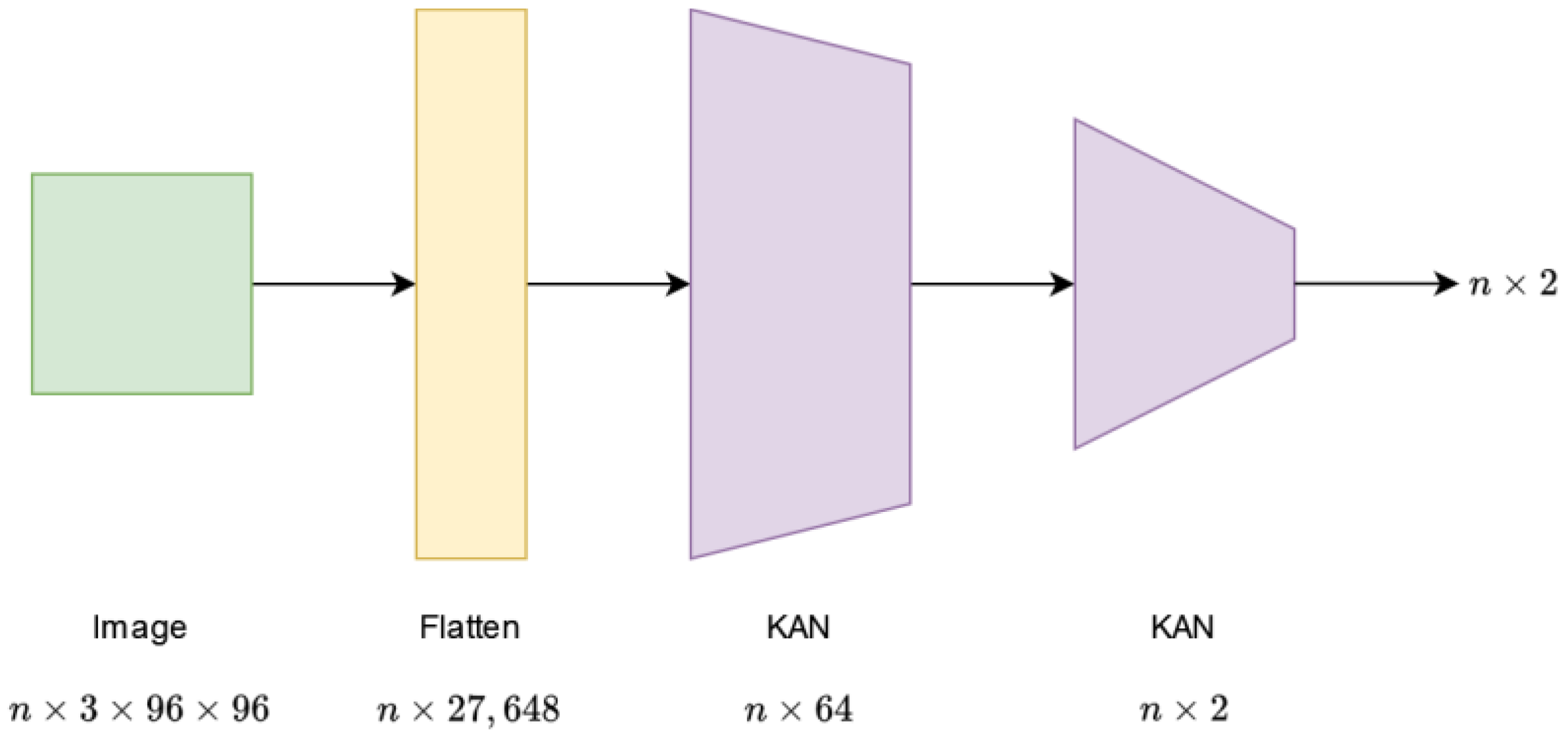
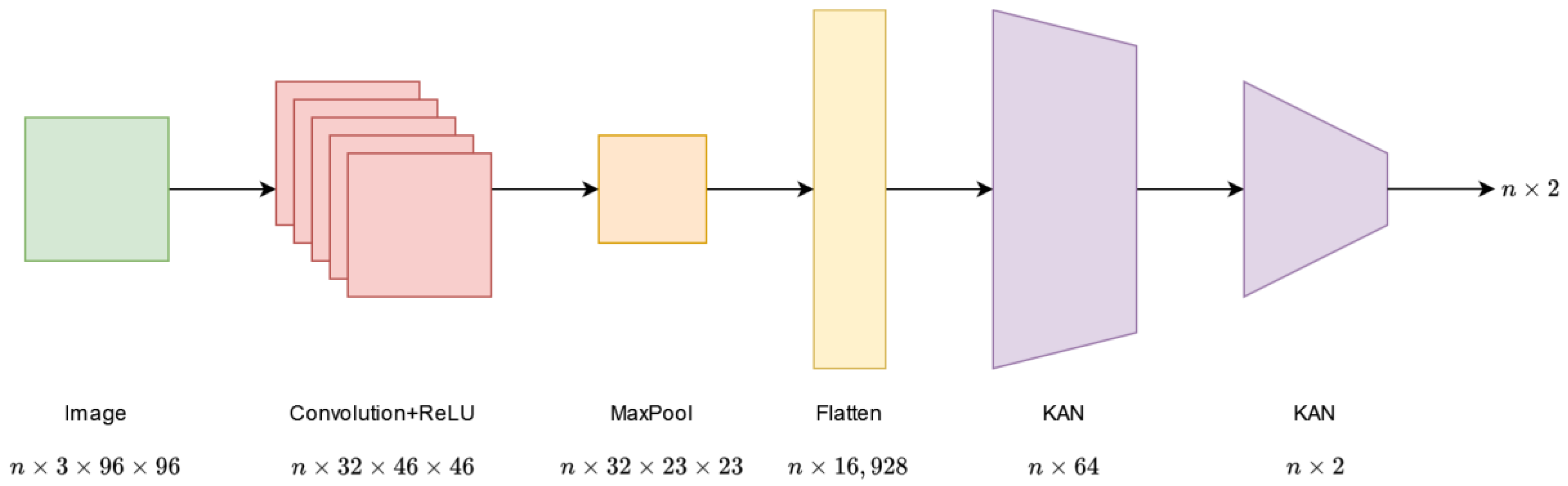
The fourth solution is called KAN because it is a purely KAN-based solution. It contains two KAN layers in total. The first one expects an input of size , from which it produces an output of size . The output of the second KAN layer is , which is also the output of the network. The value also refers to the batch size. The first KAN layer contains parameters. For the second, this value is . The structure of this design is shown in Figure 4.
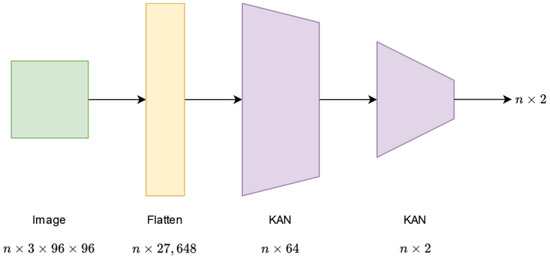
Figure 4.
Architecture of the KAN network.
The following solution now includes a convolutional layer aiming to test the efficiency of more complex convolutional networks. This network is called ConvNet, where the first layer is a convolutional filter. The convolution has channels on the input side and channels on the output side. The kernel size is , while the stride value is . The convolution was performed with padding, and the value of dilation is . The number of the parameters in the convolutional layer is . The convolution is followed by a ReLU activation [28] function and then a maxpool layer with a kernel size of . After a flatten layer, the network is completed with two linear layers. The first fully connected layer has an input of and an output of . The output of the second layer is , where a softmax function is used to generate the output of the network. In all cases, the value of refers to the batch size. The number of the parameters in the linear layers is and . The structure of this network is shown in Figure 5.
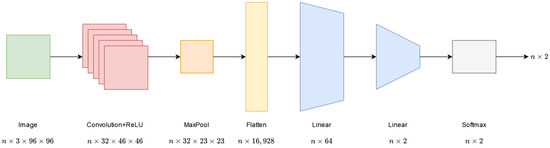
Figure 5.
Architecture of the ConvNet network.
Our last implementation is also a convolution-based network called ConvKANNet. The architecture of this network is very similar to the ConvNet network. The only difference is that KAN layers have replaced the two linear layers in the last layers of the network. The first KAN layer has parameters, while the last layer has parameters. Figure 6 shows the structure of this network.
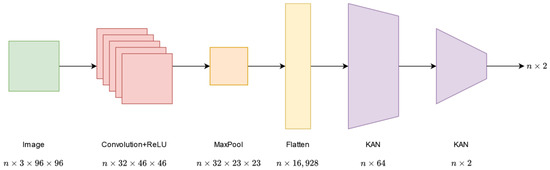
Figure 6.
Architecture of the ConvKANNet network.
2.3. Dataset
In the current study, the usability of KAN networks was investigated using a custom dataset for drivers’ mobile phone use, which was created for the authors’ research. Numerous datasets examine drivers’ actions in different situations. Abouelnaga et al. observed drivers via a camera mounted in a passenger car [31]. They identified different activities in their work, such as drinking or talking to a passenger. Ferreira et al. created a dataset using the built-in sensors in a mobile phone, where they monitored changes in sensor data during various events, like braking, turning, or changing lanes [32]. Ortega et al. used a variety of cameras, including an infrared camera, to monitor drivers of passenger vehicles [33]. Various actions were observed, including phone use, drinking, and radio. Montoya et al. also monitored drivers of cars using a camera mounted on board the vehicle [34]. Various events were observed and recorded. These activities included driving a passenger car, talking to passengers, or talking on the phone. Many researchers are working in this area, but the authors specifically aimed to observe bus drivers under natural working conditions in the current study. However, there is currently no existing dataset for such conditions. As a result, it was necessary to create our own dataset. This has been a lengthy process, and the first milestone was achieved with a dataset of minimal size that can be used. The long-term goal is to investigate the potential of AI-based monitoring of drivers. This will contribute to safer transport. As part of this project, the following dataset was created.
The dataset contains images taken while driving a vehicle. This is done in two cases: some images show bus drivers without using a phone, just driving. In contrast, other samples show drivers while using a phone. The images were taken in cooperation with a partner in the passenger transport industry. Thus, the dataset only contains images of real bus drivers driving while making a phone call.
The resulting dataset contains a total of samples. The dataset was created for a classification exercise. Therefore, for each image, it contains the information whether the driver is on the phone or not. Half of the pictures show bus drivers talking on the phone, and the other half show them without using a phone. The images are divided into training and test datasets. The training set contains samples, while the test set includes images. Figure 7 shows images from the dataset where drivers are not using mobile phones, and Figure 8 shows images taken while using a mobile phone.

Figure 7.
Sample images from the dataset without phone use.

Figure 8.
Sample images from the dataset when using the phone.
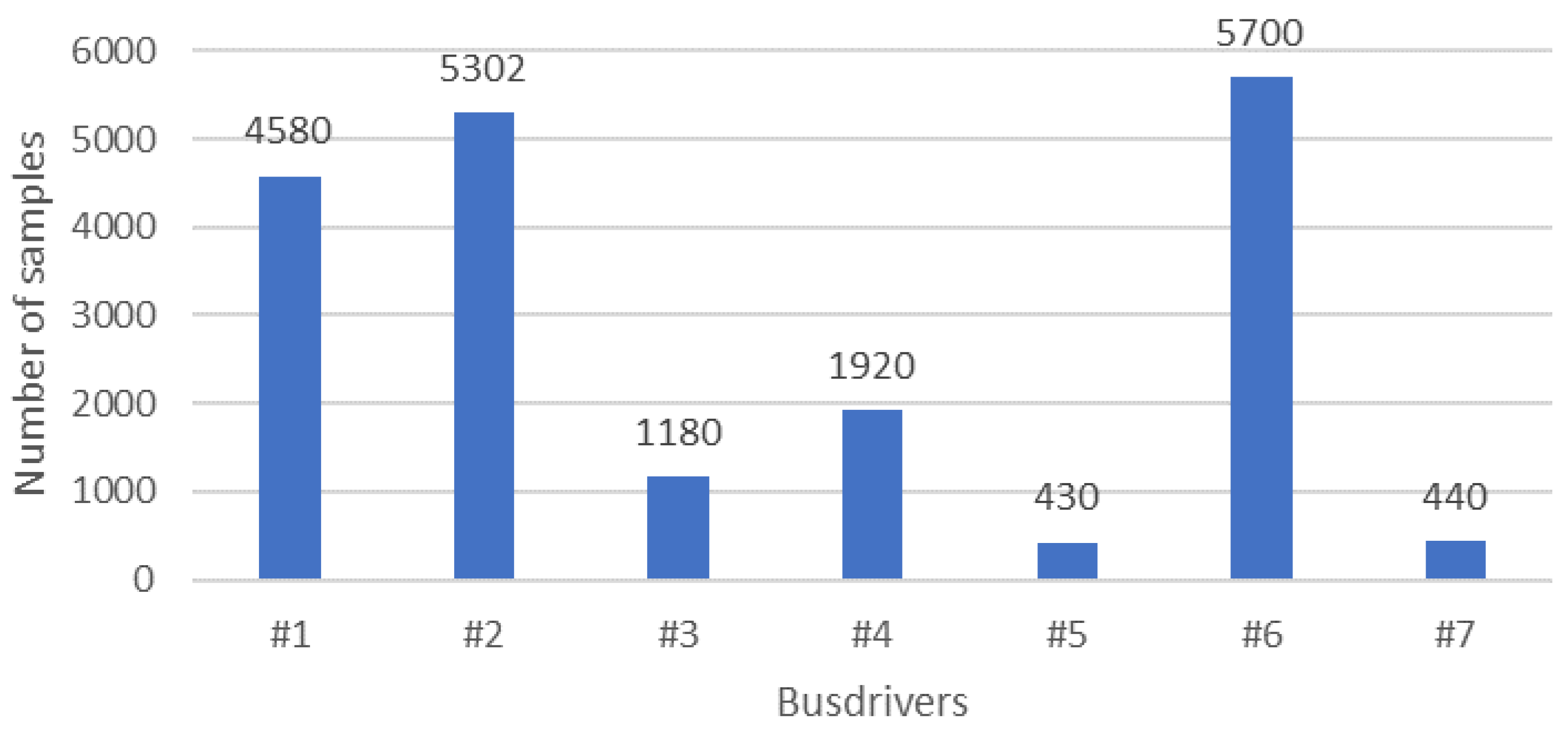
Each image is pixels high and pixels wide. These are color images with color channels in the RGB color space. The images were taken of a total of different bus drivers in various quantities. Figure 9 shows the number of recordings for each bus driver. In preparing the dataset, care was taken to ensure that the physical appearance and behavior of the drivers involved were varied. The images contain only the driver’s face and immediate surroundings so that it is still clearly visible to a human participant whether or not the driver is engaged in a telephone conversation. For the same driver, the images were always taken from the same viewpoint; however, slight variations were observed between drivers.
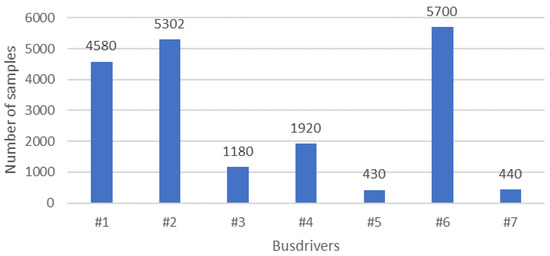
Figure 9.
Distribution of images in the dataset by bus driver.
3. Results
This section presents the research findings, emphasizing their significance and the insights gained from the process. The six networks outlined in Section 2 were examined for the created dataset in the present study. This study aims to demonstrate the efficacy of the KAN network theory in addressing this significant sub-task. The training process was conducted in four distinct approaches, employing diverse data augmentation techniques. In the initial approach, no modifications were made to the original dataset. In the second approach, random flips were applied to the images. In the third approach, the images were randomly inverted. In the fourth approach, both random image flipping and random image inverts were utilized. In order to avoid overfitting, the augmentations were performed so that their appearance was random, and not all input data were modified, but only a specific slice of the dataset.
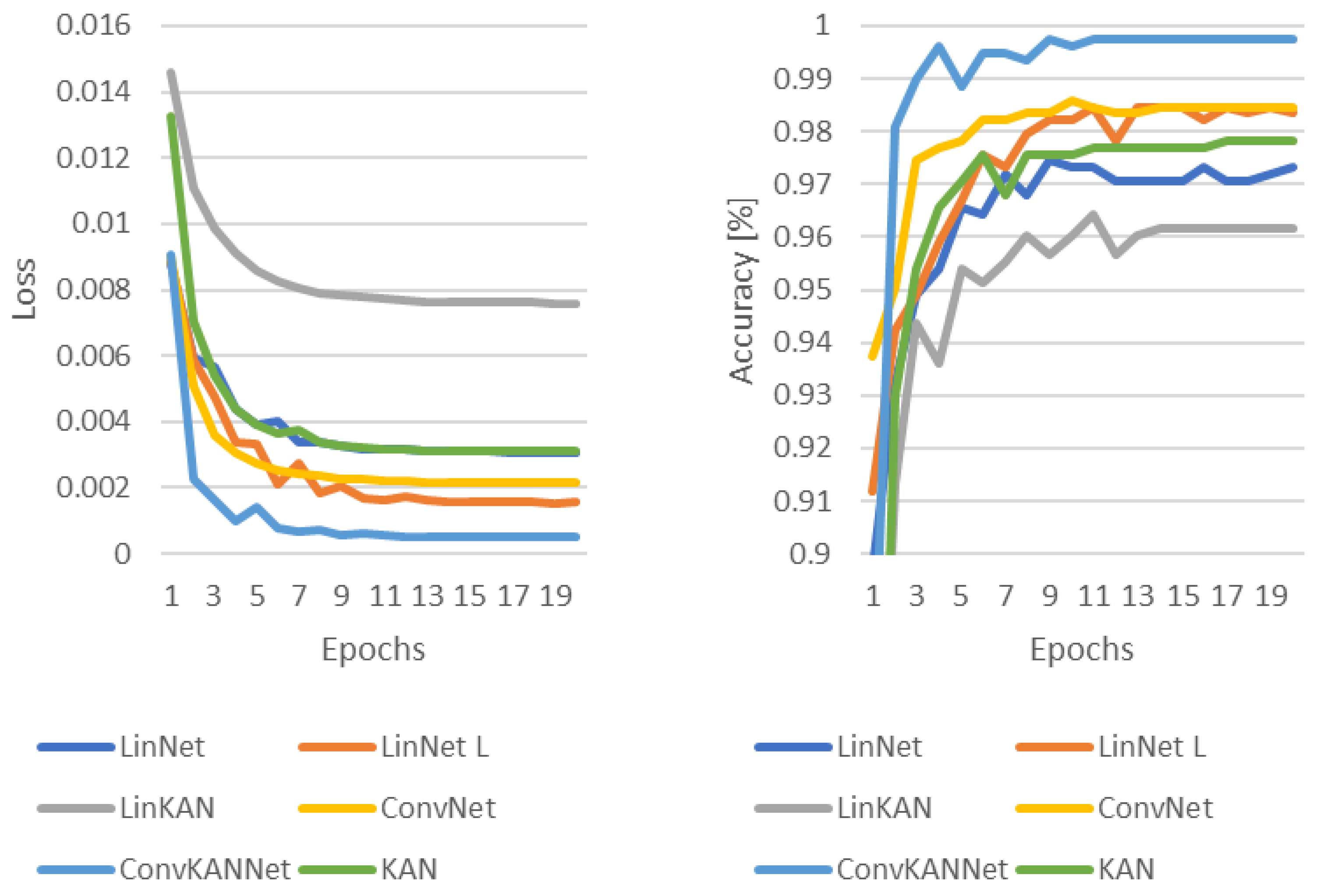
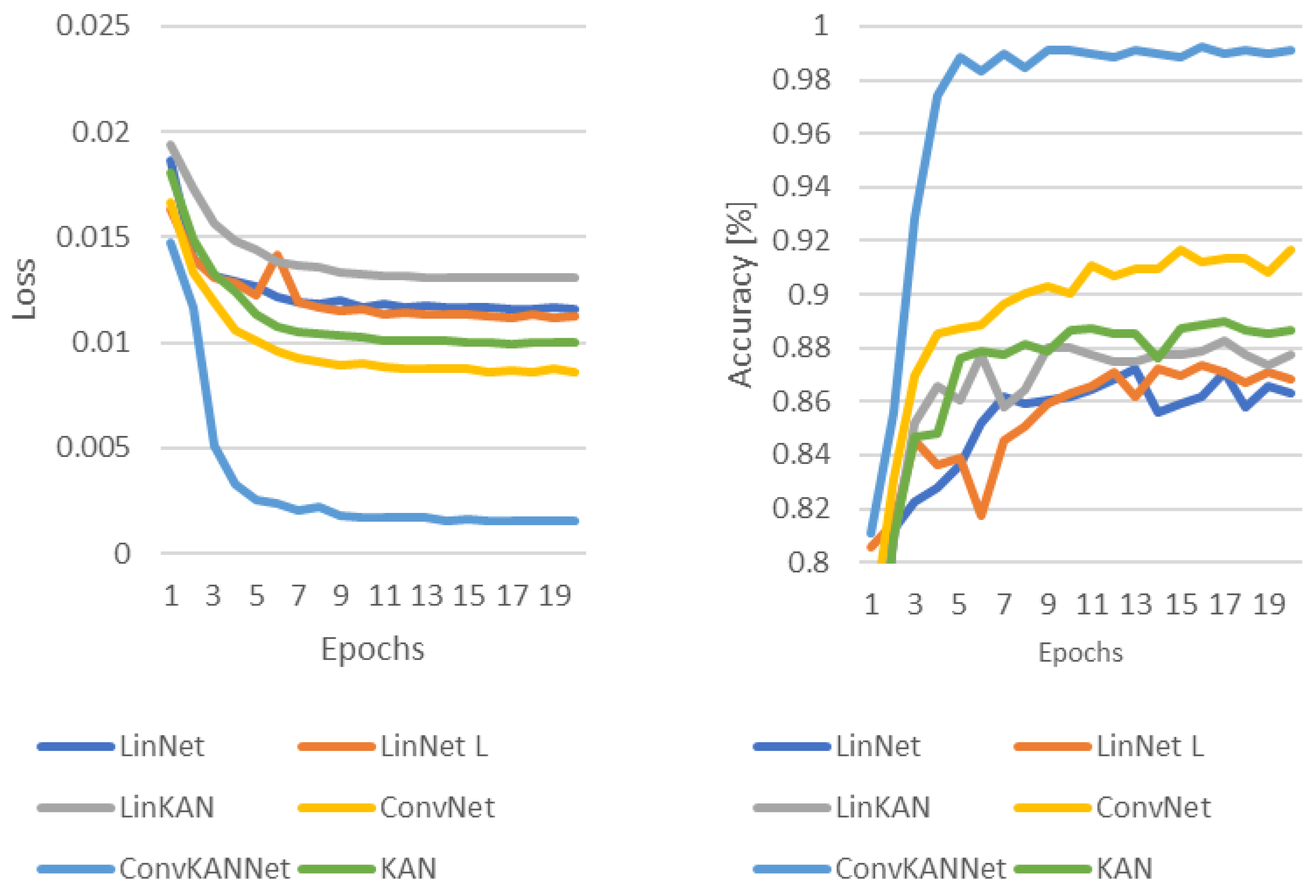
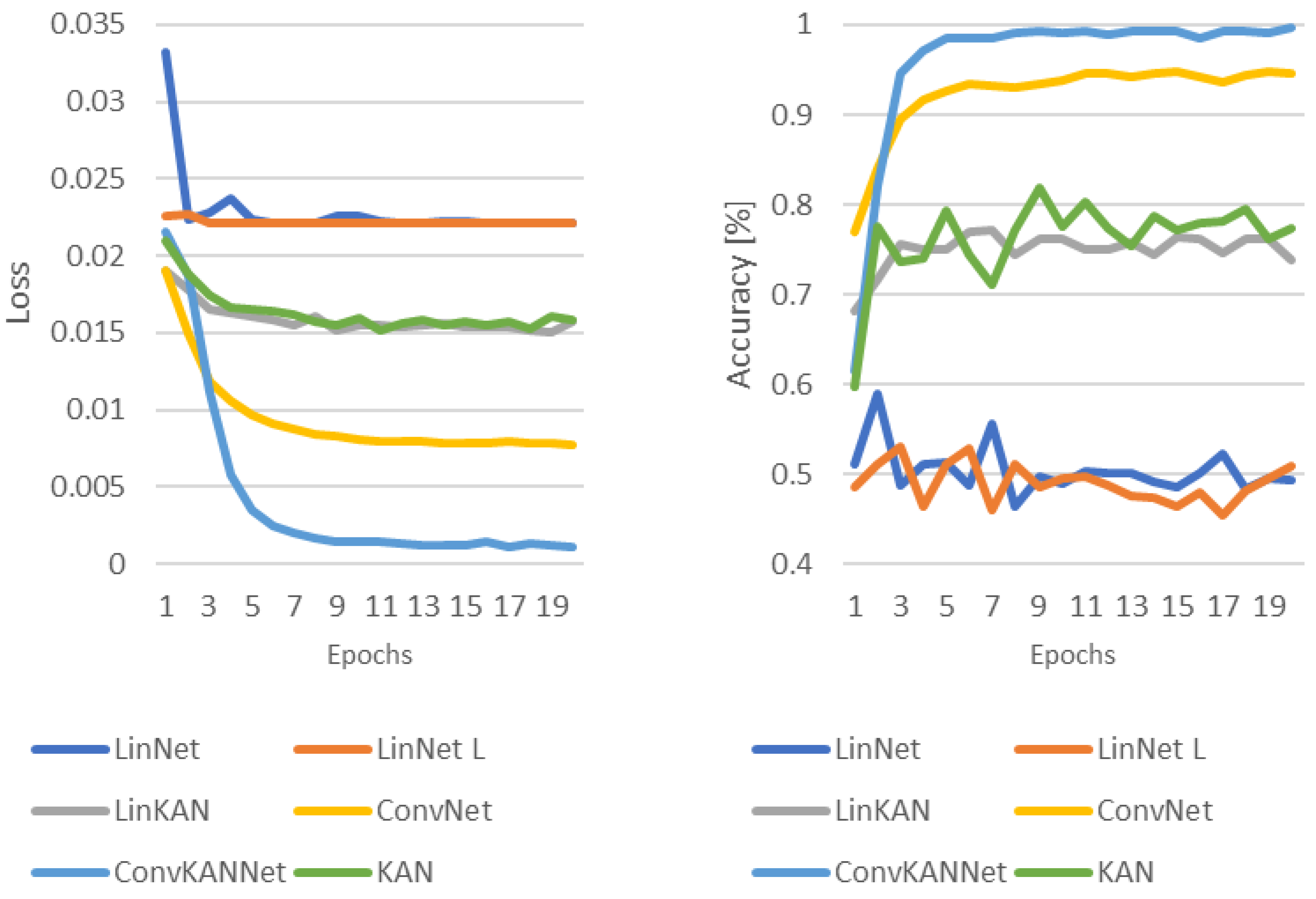
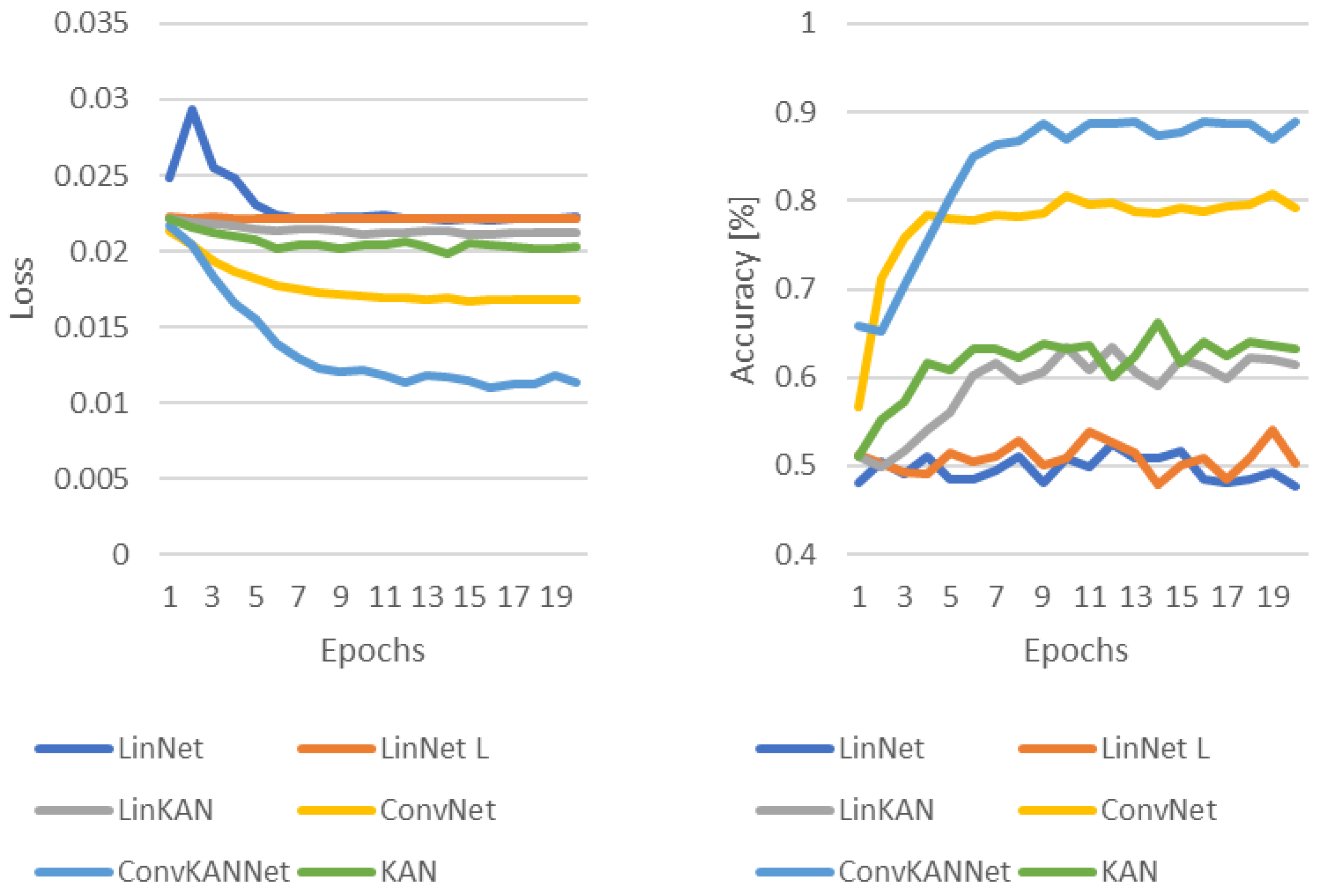
In each case, the authors used the Adam optimization algorithm [35], where the value of the learning rate is and the value of the weight decay is also . The Cross-Entropy loss function was used to determine the loss during the training process. The results of the training processes are summarized in Figure 10, Figure 11, Figure 12 and Figure 13, where the loss and accuracy values measured during the training process are shown.
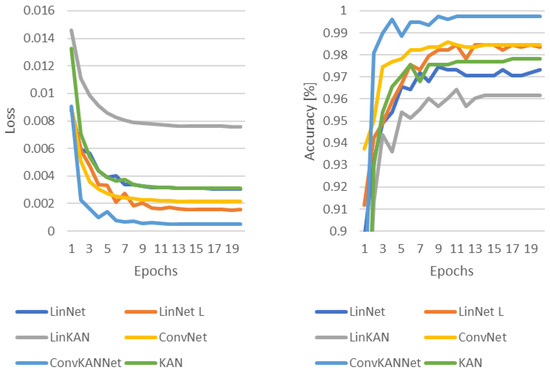
Figure 10.
Loss and accuracy in the training process without the use of any transformations.
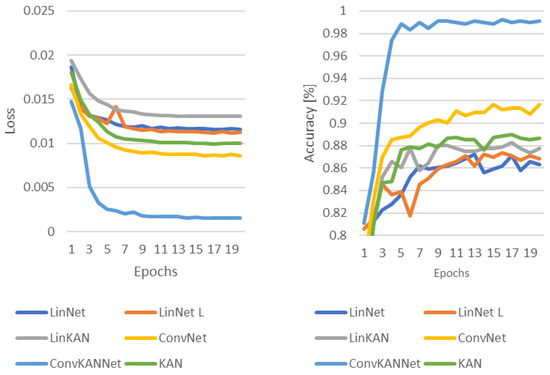
Figure 11.
Loss and accuracy in the training process with random image flips.
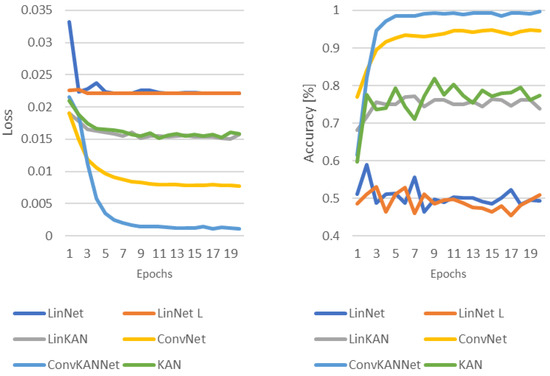
Figure 12.
Loss and accuracy in the training process with random image inverting.
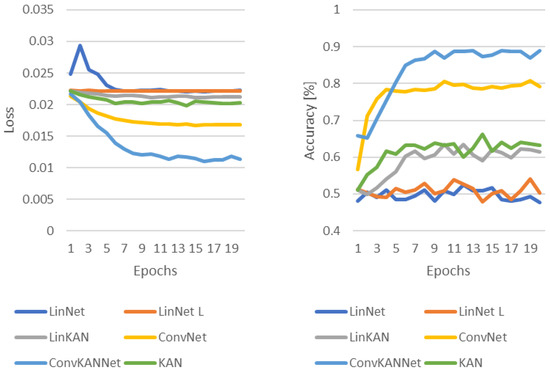
Figure 13.
Loss and accuracy in the training process with random image flips and inverting.
In the initial scenario, wherein no transformation is applied, all networks demonstrate satisfactory performance. This is shown in Figure 10. However, someone can also see that the ConvKANNet network performs best, followed by the other convolution-based solution, the ConvNet. The LinNet L architecture performs very similarly to the ConvNet. This is followed by the KAN network and then LinNet. The LinKAN model has the worst performance.
The introduction of random image flips results in a notable alteration. This is demonstrated in Figure 11. The efficiency of ConvKANNet remains high, whereas the efficiency of all other solutions has decreased. ConvNet remains the second-most effective performer. Subsequently, a ranking shift is observed compared to the results obtained without data augmentation. The KAN-based solutions occupied the third and fourth positions. At the conclusion of the evaluation, LinNet L was identified as the most effective solution, followed by LinNet networks.
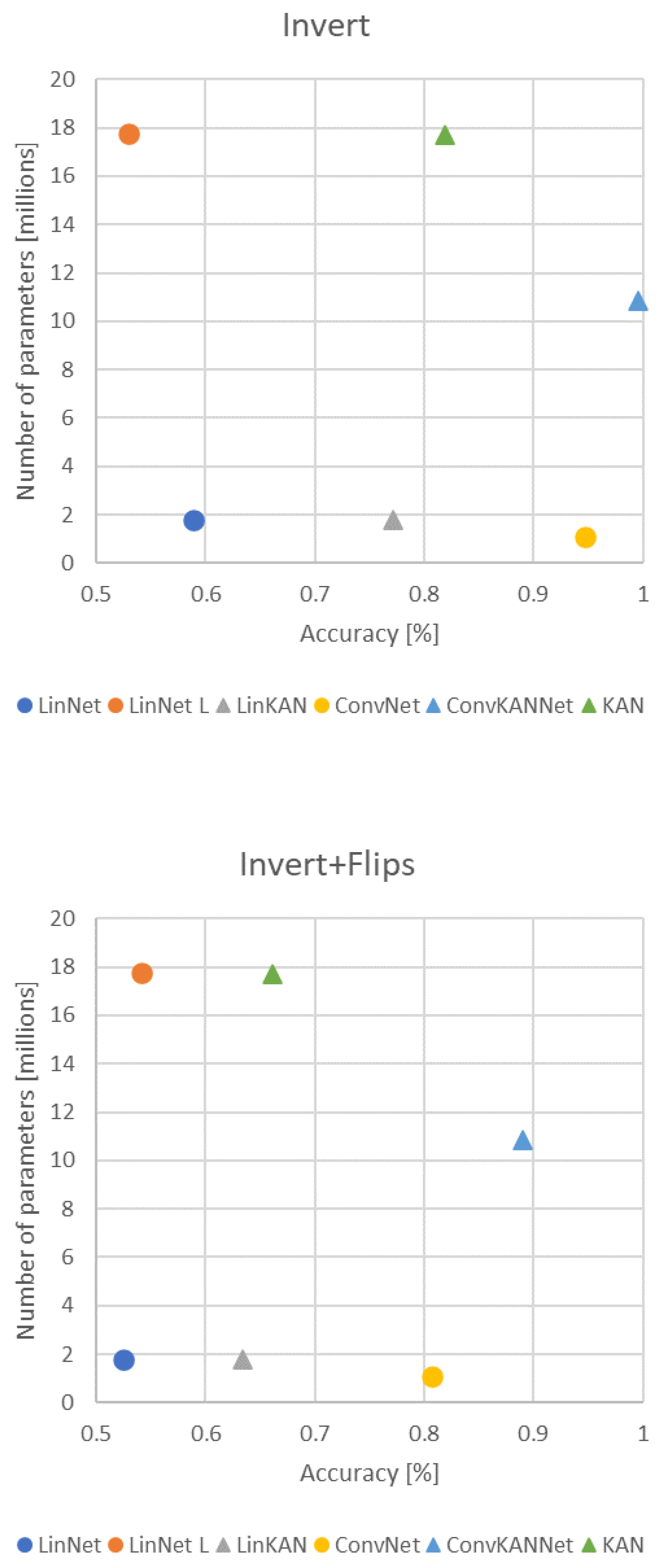
Random image inverts separate the solutions much better. This phenomenon can be observed in Figure 12. The results demonstrate that convolution solutions continue to perform optimally. Among these, the KAN-based solution was observed to achieve the best results. This is followed by the authors’ two other KAN-based implementations. The worst-performing solutions were observed to be the LinNet L and LinNet networks.
Both transformations were employed in the final test. The outcome is illustrated in Figure 13. The outcome is analogous to that observed in the preceding instance, wherein random image inversions were employed. The order of the networks remains unchanged. In other words, the convolutional KAN network is once again the most effective. Subsequently, the convolutional solutions are followed by the other KAN-based models. Ultimately, the two fully connected networks demonstrated the poorest performance.
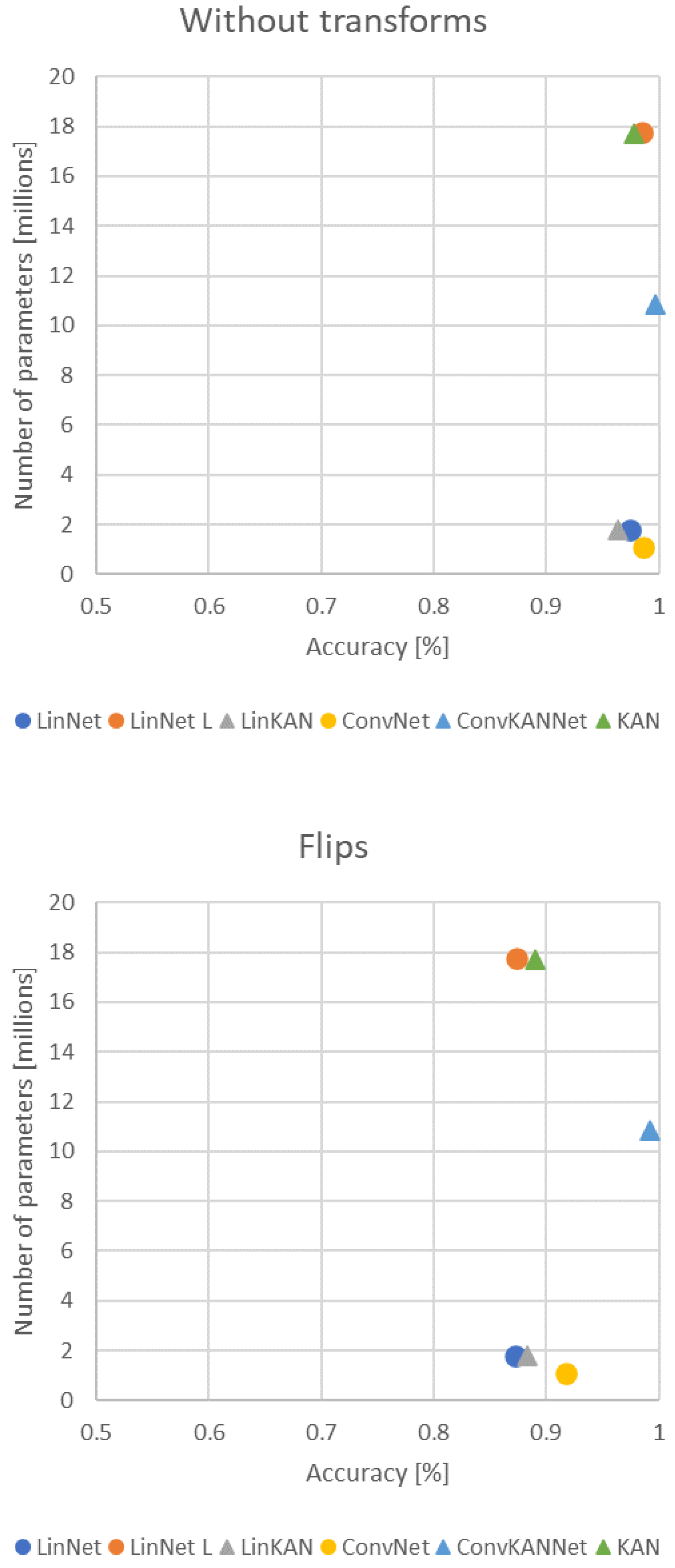
Figure 14 shows the best results and the number of parameters for each network. It is evident that the networks exhibit comparable complexity in terms of the number of parameters. In this case, the KAN and LinNet L networks are comparable regarding their underlying characteristics. In the absence of transformation, their performance was observed to be relatively similar and satisfactory in both cases. However, in the other three scenarios, the divergence of the two solutions becomes more pronounced. The LinNet L network exhibited a notable decline in performance, particularly due to the introduction of augmentations. In contrast, the KAN solution demonstrated resilience and stability.
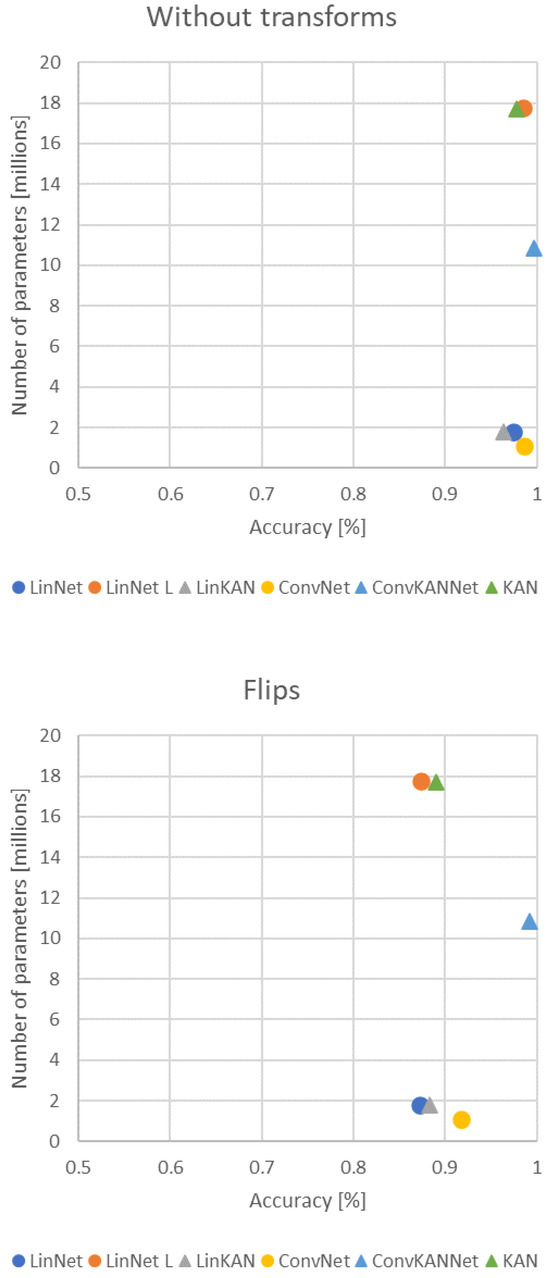
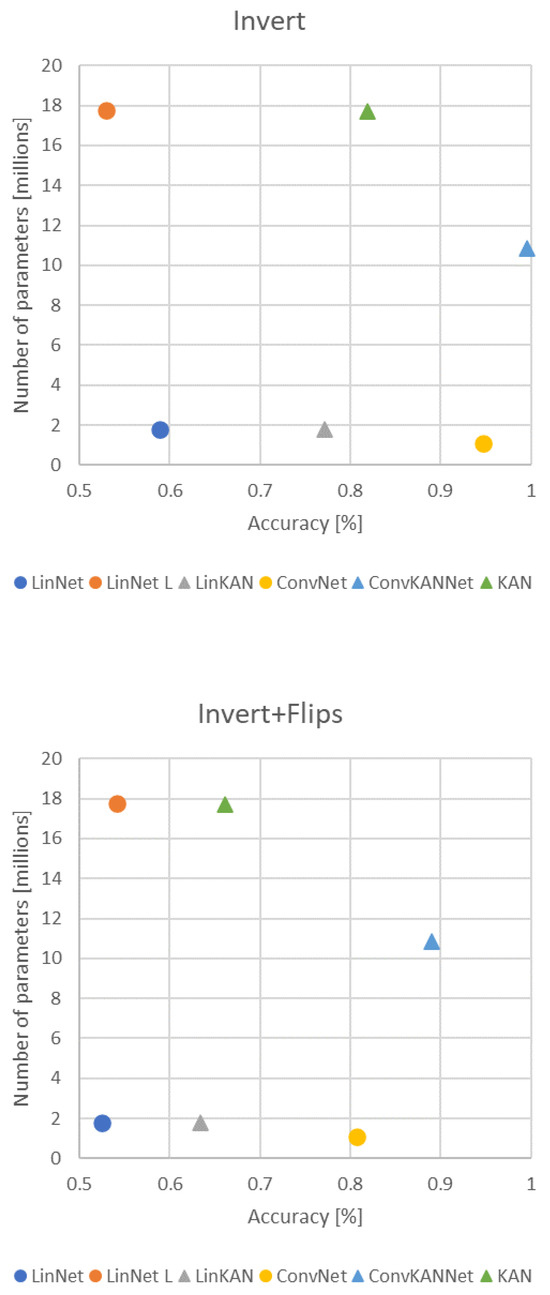
Figure 14.
Comparison of best accuracies.
A further comparison may be made between the LinNet and LinKAN networks, which exhibit a similar number of parameters. In the initial case, the efficiency of the two solutions was found to be comparable, with the linear solution exhibiting a slight advantage. In the subsequent cases, the KAN-based solution consistently demonstrated superior performance. However, it is noteworthy that the ConvNet network exhibited a slightly lower number of parameters than LinKAN. Nevertheless, in all cases, the ConvNet network yielded more favorable results.
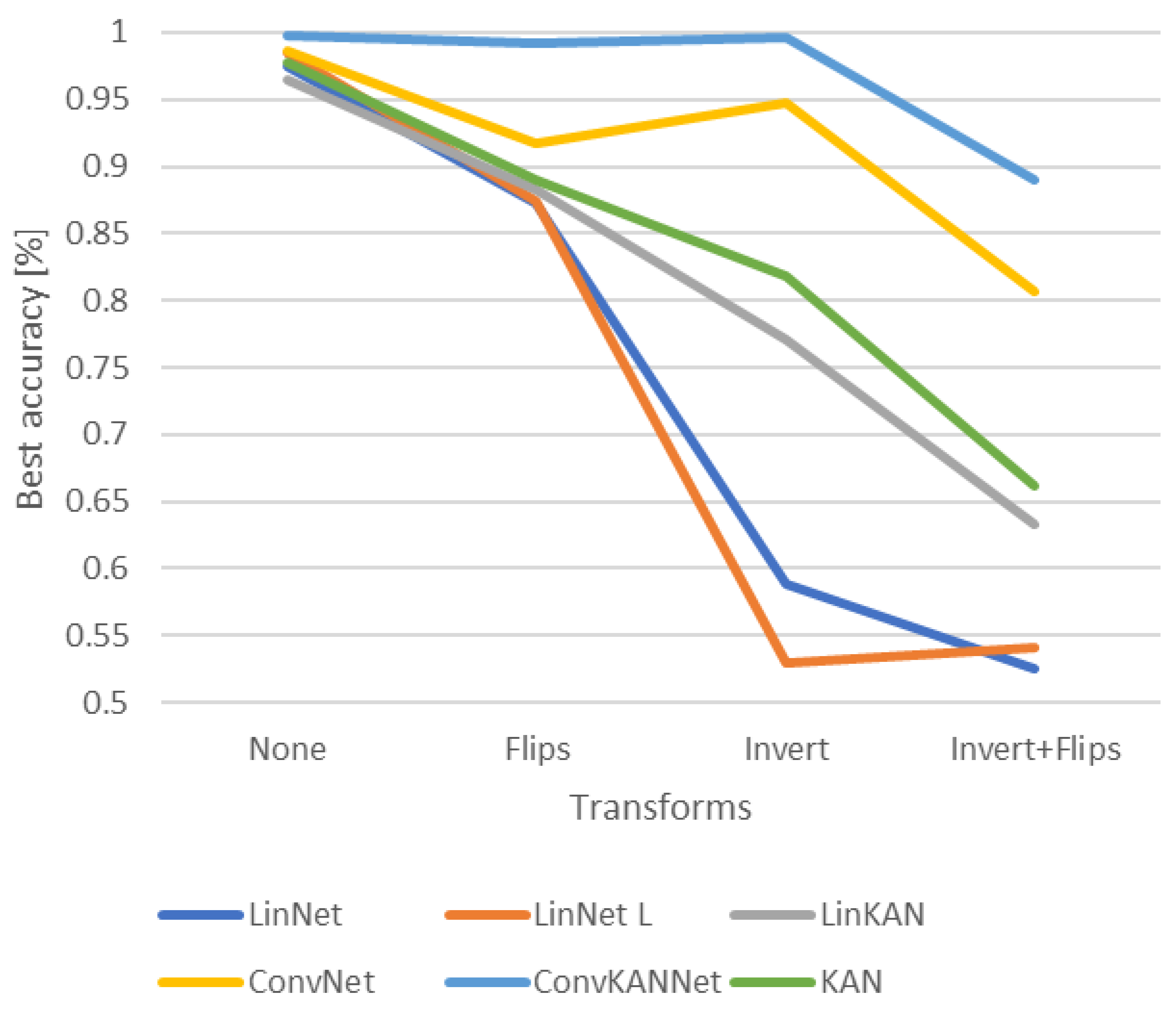
Figure 15 illustrates the optimal outcomes for each transformation. The order of each network remains consistent across the various transformations. In the case of the ConvKANNet network, the two transformations separately could not significantly impair the network’s efficiency. This was only achieved in the most complex case, when the two transformations were applied together. The situation is slightly worse for the ConvNet model, where no KAN layer was used. Additionally, the random flipping of images was observed to cause further degradation. Degradation was also observed in KAN and LinKAN networks but much less than in traditional linear networks (LinNet L, LinNet).
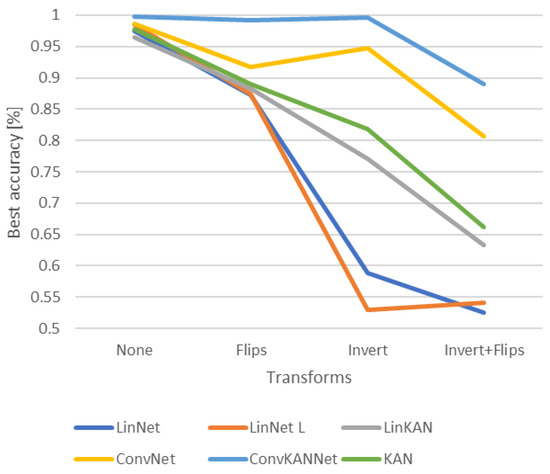
Figure 15.
Changes in the efficiency of networks under different transformations.
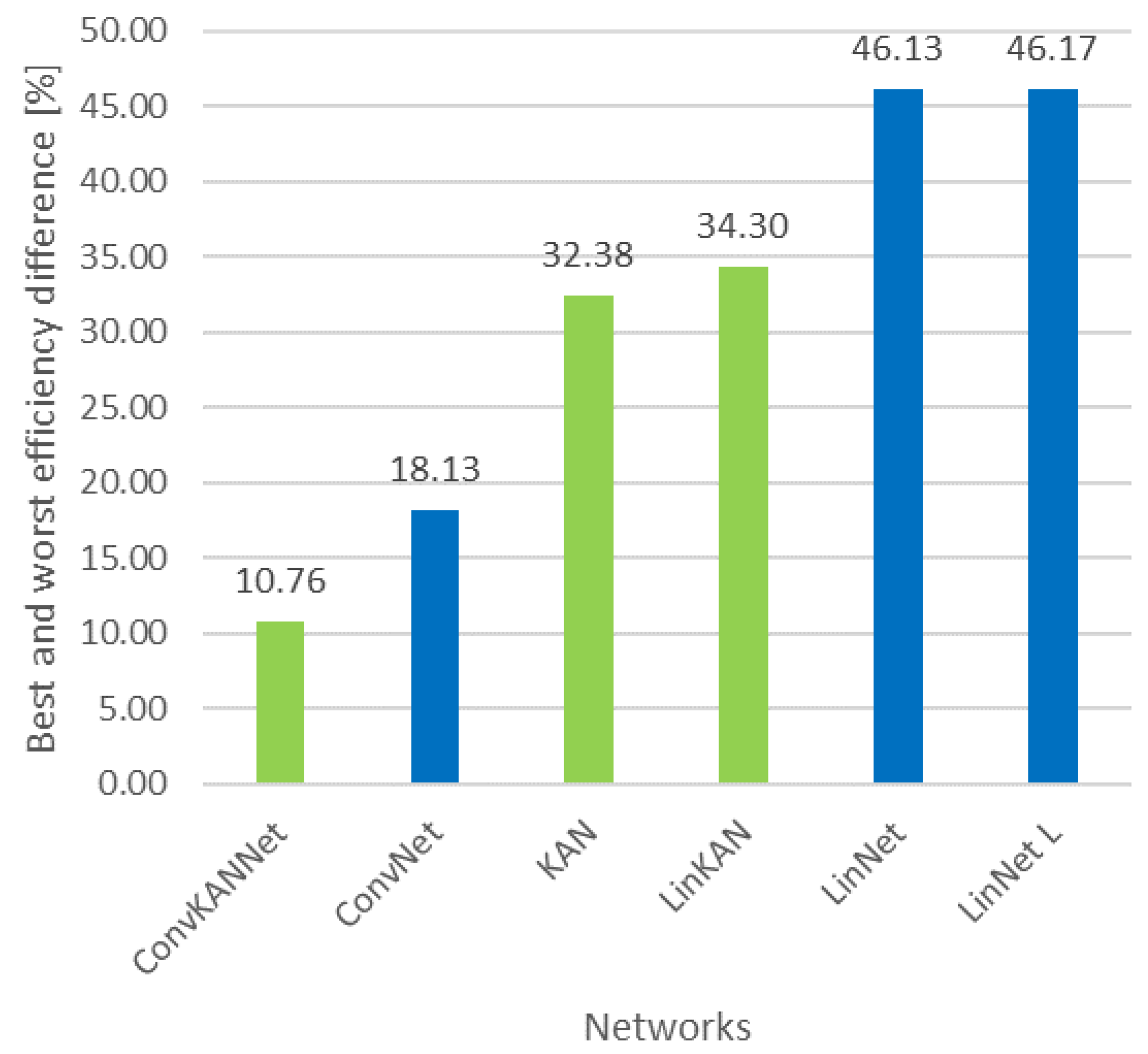
Furthermore, the discrepancy between each network’s optimal and suboptimal outcomes was examined. This demonstrates the influence of disparate transformations on the efficacy of each solution. This is illustrated in Figure 16, which depicts the percentage of the most significant degradation. Overall, the KAN-based solutions exhibited a comparatively lower degree of degradation.
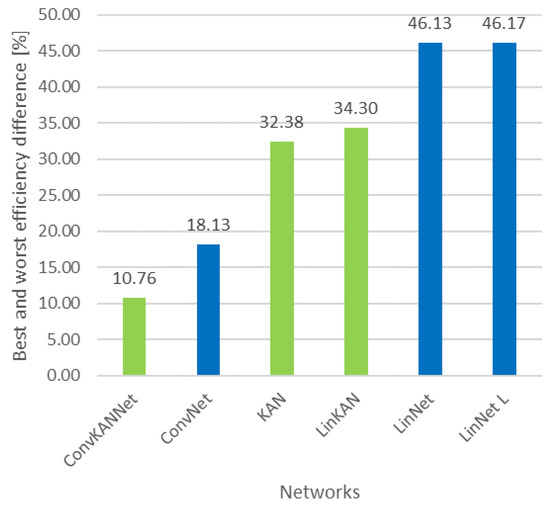
Figure 16.
The highest rate of efficiency degradation during the transformations. (green: KAN-based solutions, blue: MLP-based solutions).
4. Discussion
The primary focus of this study was to evaluate the performance of KAN network layers compared to traditional linear layers within various neural network architectures. This research highlights several key points:
- Custom Dataset: Creating a bespoke dataset tailored to the specific requirements of this study represents a significant strength. The dataset predominantly comprises male drivers aged 40 to 55 of European descent, mirroring the demographic composition of the partner company, which employs relatively few female or ethnically diverse drivers. This limited diversity may introduce biases, potentially compromising the accuracy and fairness of the model, particularly if it is implemented in contexts with a higher representation of female or ethnically diverse drivers. To mitigate these limitations, future research will focus on expanding the dataset to encompass a more diverse range of drivers, including variations in gender, age, and ethnicity. Such efforts will aim to enhance the representativeness of the data and thereby improve the robustness and fairness of the KAN algorithm.
- Data Augmentation Techniques: Employing various data augmentation techniques is paramount for enhancing model robustness. This study’s four-pronged approach, comprising no modifications, random flips, random inversions, and combined flips and inversions, provided comprehensive insights into the models’ performances under different conditions.
- Performance of ConvKANNet: The consistently superior performance of the ConvKANNet network across all scenarios indicates that KAN layers offer a meaningful advantage over traditional linear layers. This is particularly evident in scenarios involving random image inversions, where the ConvKANNet outperformed all other models.
- Comparison of Network Complexity: The networks exhibit comparable complexity regarding the number of parameters. The KAN and LinNet L networks showed similar performance without transformation, but the LinNet L network declined significantly with augmentations, while the KAN network remained resilient and stable. Despite having similar parameters, the LinNet and LinKAN networks saw the KAN-based solution outperform the linear one in most scenarios. Despite having fewer parameters than LinKAN, the ConvNet network generally produced more favorable results.
- Impact of Transformations: This study examined the impact of various transformations on network performance. The ConvKANNet network maintained high efficiency with single transformations and only showed significant performance degradation with combined transformations. In contrast, the ConvNet model without KAN layers performed worse, particularly with random flips. The KAN and LinKAN networks experienced less degradation from transformations than traditional linear networks (LinNet L, LinNet).
- Resilience of KAN-based Solutions: The KAN-based solutions demonstrated reduced performance degradation across diverse transformational operations. This resilience is demonstrated in Figure 16, which illustrates the percentage of the most significant degradation for each network. The robustness of KAN networks highlights their potential for real-world applications where data variability is a significant consideration.
The findings highlight the potential of KAN networks to enhance the accuracy and reliability of AI-based systems in ensuring safer transportation. Further research and development could facilitate their integration into practical monitoring solutions, thereby contributing to improved road safety and driver behavior analysis.
5. Conclusions
This research implemented six different neural network designs to assess the usability of KAN network layers compared to traditional linear layers. This study aimed to create diverse network architectures, ranging from simple to complex. Three designs incorporated KAN layers, while the other three did not. The overarching goal is to explore AI-based monitoring of drivers, contributing to safer transportation systems.
A custom dataset was created for this research, consisting of 19,552 images captured while bus drivers were either using a phone or driving without it. The dataset is evenly split between these two scenarios and is divided into training (15,640 images) and test sets (3912 images). The current dataset’s demographic limitations, predominantly male drivers of European descent, may introduce biases that affect the model’s accuracy and fairness. Future research will address this by broadening the dataset to include a more diverse range of drivers, thereby enhancing the representativeness, robustness, and fairness of the KAN algorithm.
This study tested the efficacy of KAN networks through four different data augmentation approaches: no modification, random flips, random inversions, and a combination of flips and inversions. The results indicated that the ConvKANNet, a convolution-based solution with KAN layers, consistently performed best across all scenarios, demonstrating the potential superiority of KAN networks for this application.
This research aims to develop AI-based systems for monitoring drivers, ultimately enhancing road safety. The promising results of KAN networks in this study indicate their potential utility in real-world applications, such as detecting driver distraction due to phone usage.
Author Contributions
Conceptualization, J.H. and V.N.; methodology, J.H. and V.N.; software, J.H.; validation, J.H. and V.N.; formal analysis, J.H. and V.N.; investigation, J.H. and V.N.; resources, J.H. and V.N.; data curation, J.H. and V.N.; writing—original draft preparation, J.H., Á.B., G.K., S.F. and V.N.; writing—review and editing, J.H., Á.B., G.K., S.F. and V.N.; visualization, J.H.; supervision, J.H., Á.B., G.K., S.F. and V.N.; project administration, J.H., S.F. and V.N.; funding acquisition, J.H., S.F. and V.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no specific grant from any funding agencies.
Data Availability Statement
All data in this research were presented in the article.
Acknowledgments
The authors wish to acknowledge the support received from the Vehicle Industry Research Centre and Széchenyi István University, Győr. This research was carried out as a part of the Cooperative Doctoral Program supported by the National Research, Development, and Innovation Office and the Ministry of Culture and Innovation.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| ADAS | Advanced Driver-Assistance Systems |
| BYOD | Bring-Your-Own-Device |
| CapsNets | Capsule Networks |
| DMS | Driver Monitoring Systems |
| ECG | Electrocardiogram |
| EEG | Electroencephalogram |
| EMG | Electromyogram |
| FLOPs | Floating-Point Operations |
| GELU | Gaussian Error Linear Unit |
| IVIS | In-Vehicle Information Systems |
| KAN | Kolmogorov-Arnold Networks |
| KST | Kolmogorov Superposition Theorem |
| MLP | Multi-Layer Perceptrons |
| NN | Neural Network |
| PDT | Peripheral Detection Task |
| ReLU | Rectified Linear Unit |
| RGB | Red, Green, Blue (color space) |
| SiLU | Sigmoid Linear Unit |
References
- Blades, L.; Douglas, R.; Early, J.; Lo, C.Y.; Best, R. Advanced Driver-Assistance Systems for City Bus Applications. In Proceedings of the SAE Technical Papers; SAE International: Warrendale, PA, USA, 2020; Volume 2020-April. [Google Scholar]
- European Commission and Directorate-General for Mobility and Transport: EU Transport in Figures—Statistical Pocketbook 2023; Publications Office of the European Union: Luxembourg, 2023. [CrossRef]
- Korpinen, L.; Pääkkönen, R. Accidents and Close Call Situations Connected to the Use of Mobile Phones. Accid. Anal. Prev. 2012, 45, 75–82. [Google Scholar] [CrossRef]
- Hersh, J.; Lang, B.J.; Lang, M. Car Accidents, Smartphone Adoption and 3G Coverage. J. Econ. Behav. Organ. 2022, 196, 278–293. [Google Scholar] [CrossRef]
- Horsman, G.; Conniss, L.R. Investigating Evidence of Mobile Phone Usage by Drivers in Road Traffic Accidents. In Proceedings of the Digital Forensic Research Conference, DFRWS 2015 EU; Digital Forensic Research Workshop, Dublin, Ireland, 23–26 March 2015; pp. S30–S37. [Google Scholar]
- Bergasa, L.M.; Nuevo, J. Real-Time System for Monitoring Driver Vigilance. In Proceedings of the IEEE International Symposium on Industrial Electronics, Dubrovnik, Croatia, 20–23 June 2005; Volume III, pp. 1303–1308. [Google Scholar]
- Razak, S.F.A.; Yogarayan, S.; Aziz, A.A.; Abdullah, M.F.A.; Kamis, N.H. Physiological-Based Driver Monitoring Systems: A Scoping Review. Civ. Eng. J. 2022, 8, 3952–3967. [Google Scholar] [CrossRef]
- Hollósi, J.; Ballagi, Á.; Kovács, G.; Fischer, S.; Nagy, V. Face Detection Using a Capsule Network for Driver Monitoring Application. Computers 2023, 12, 161. [Google Scholar] [CrossRef]
- Violanti, J.M.; Marshall, J.R. Cellular Phones and Traffic Accidents: An Epidemiological Approach. Accid. Anal. Prev. 1996, 28, 265–270. [Google Scholar] [CrossRef] [PubMed]
- Törnros, J.E.B.; Bolling, A.K. Mobile Phone Use—Effects of Handheld and Handsfree Phones on Driving Performance. Accid. Anal. Prev. 2005, 37, 902–909. [Google Scholar] [CrossRef] [PubMed]
- Lesch, M.F.; Hancock, P.A. Driving Performance during Concurrent Cell-Phone Use: Are Drivers Aware of Their Performance Decrements? Accid. Anal. Prev. 2004, 36, 471–480. [Google Scholar] [CrossRef] [PubMed]
- Bener, A.; Lajunen, T.; Özkan, T.; Haigney, D. The Effect of Mobile Phone Use on Driving Style and Driving Skills. Int. J. Crashworthiness 2006, 11, 459–465. [Google Scholar] [CrossRef]
- Catalina Ortega, C.A.; Mariscal, M.A.; Boulagouas, W.; Herrera, S.; Espinosa, J.M.; García-Herrero, S. Effects of Mobile Phone Use on Driving Performance: An Experimental Study of Workload and Traffic Violations. Int. J. Environ. Res. Public Health 2021, 18, 7101. [Google Scholar] [CrossRef]
- Ahmed, S.; Uddin, M.S.; Feroz, S.I.; Bin Alam, M.R.; Farabi, F.A.; Uddin, M.M.; Rifaat, S.M. Tendency of Intra-City Bus Drivers to Use Cell Phone While Driving Using Ordered Probit Model. In Proceedings of the AIP Conference Proceedings; American Institute of Physics Inc.: College Park, MD, USA, 2023; Volume 2643. [Google Scholar]
- Al-Ajlouny, S.A.; Alzboon, K.K. Effects of Mobile Phone Using on Driving Behavior and Risk of Traffic Accidents. J. Radiat. Res. Appl. Sci. 2023, 16, 100662. [Google Scholar] [CrossRef]
- Nagy, V.; Kovács, G.; Földesi, P.; Sándor, Á.P. Car Simulator Study for the Development of a Bring-Your-Own-Device (BYOD) Dashboard Concept. Chem. Eng. Trans. 2023, 107, 415–420. [Google Scholar] [CrossRef]
- Braun, J.; Griebel, M. On a Constructive Proof of Kolmogorov’s Superposition Theorem. Constr. Approx. 2009, 30, 653–675. [Google Scholar] [CrossRef]
- Köppen, M. On the Training of a Kolmogorov Network. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin, Germany, 2002; Volume 2415 LNCS, pp. 474–479. [Google Scholar]
- Montanelli, H.; Yang, H. Error Bounds for Deep ReLU Networks Using the Kolmogorov—Arnold Superposition Theorem. Neural Netw. 2020, 129, 1–6. [Google Scholar] [CrossRef]
- Lai, M.-J.; Shen, Z. The Kolmogorov Superposition Theorem Can Break the Curse of Dimensionality When Approximating High Dimensional Functions. arXiv 2021, arXiv:2112.09963. [Google Scholar]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. KAN: Kolmogorov-Arnold Networks. arXiv 2024, arXiv:2404.19756. [Google Scholar]
- Altarabichi, M.G. DropKAN: Regularizing KANs by Masking Post-Activations. arXiv 2024, arXiv:2407.13044. [Google Scholar]
- Bodner, A.D.; Tepsich, A.S.; Spolski, J.N.; Pourteau, S. Convolutional Kolmogorov-Arnold Networks. arXiv 2024, arXiv:2406.13155. [Google Scholar]
- Sidharth, S.S.; Keerthana, A.R.; Gokul, R.; Anas, K.P. Chebyshev Polynomial-Based Kolmogorov-Arnold Networks: An Efficient Architecture for Nonlinear Function Approximation. arXiv 2024, arXiv:2405.07200. [Google Scholar]
- Yu, R.; Yu, W.; Wang, X. KAN or MLP: A Fairer Comparison. arXiv 2024, arXiv:2407.16674. [Google Scholar]
- Schmidt-Hieber, J. The Kolmogorov-Arnold Representation Theorem Revisited. arXiv 2020, arXiv:2007.15884. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. On the Representation of Continuous Functions of Several Variables as Superpositions of Continuous Functions of One Variable and Addition. Dokl. Akad. Nauk. Russ. Acad. Sci. 1957, 114, 953–956. [Google Scholar]
- Agarap, A.F. Deep Learning Using Rectified Linear Units (ReLU). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian Error Linear Units (GELUs). arXiv 2016, arXiv:1606.08415. [Google Scholar] [CrossRef]
- Elfwing, S.; Uchibe, E.; Doya, K. Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning. arXiv 2017, arXiv:1702.03118. [Google Scholar] [CrossRef]
- Abouelnaga, Y.; Eraqi, H.M.; Moustafa, M.N. Real-Time Distracted Driver Posture Classification. arXiv 2017, arXiv:1706.09498. [Google Scholar]
- Ferreira Júnior, J.; Carvalho, E.; Ferreira, B.V.; De Souza, C.; Suhara, Y.; Pentland, A.; Pessin, G. Driver Behavior Profiling: An Investigation with Different Smartphone Sensors and Machine Learning. PLoS ONE 2017, 12, e0174959. [Google Scholar] [CrossRef] [PubMed]
- Ortega, J.D.; Kose, N.; Cañas, P.; Chao, M.-A.; Unnervik, A.; Nieto, M.; Otaegui, O.; Salgado, L. DMD: A Large-Scale Multi-Modal Driver Monitoring Dataset for Attention and Alertness Analysis. In Proceedings of the Computer Vision—ECCV 2020 Workshops, Glasgow, UK, 23–28 August 2020. [Google Scholar] [CrossRef]
- Anna Montoya Dan Holman, S.T.S.W.K. State Farm Distracted Driver Detection 2016. Available online: https://kaggle.com/competitions/state-farm-distracted-driver-detection (accessed on 10 July 2024).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).