Dynamic Opinion Formation in Networks: A Multi-Issue and Evidence-Based Approach

Abstract

In this study, we present a computational model for simulating opinion dynamics within social networks, incorporating cognitive and social psychological principles such as homophily, confirmation bias, and selective exposure. We enhance our model using Dempster–Shafer theory to address uncertainties in belief updating. Mathematical formalism and simulations were performed to derive empirical results from showcasing how this method might be useful for modeling real-world opinion consensus and fragmentation. By constructing a scale-free network, we assign initial opinions and iteratively update them based on neighbor influences and belief masses. Lastly, we examine how the presence of “truth” nodes with high connectivity, used to simulate the influence of objective truth on the network, alters opinions. Our simulations reveal insights into the formation of opinion clusters, the role of cognitive biases, and the impact of uncertainty on belief evolution, providing a robust framework for understanding complex opinion dynamics in social systems.

1. Introduction

Computational social science is an interdisciplinary field that utilizes computational methods and data analysis to study social phenomena and human behavior. Agent-based modeling in computational social science can uncover patterns, predict trends, and simulate social processes. When integrated with statistical models, it enhances our understanding of complex social dynamics, a goal of social physics [1,2,3]. Social physics covers a wide range of topics, such as the spread of information or misinformation through social networks, much like the diffusion of particles in a medium [4]. It also examines patterns of human mobility and crowd dynamics to improve urban planning and public safety [5]. Another application is understanding collective behavior, where reputation models in decision-making can help explain social phenomena [6]. By leveraging big data and advanced analytics, social physics offers a quantitative approach to solving complex social problems. In this article, we focus on a specific domain in the study of social physics—opinion dynamics. The dynamics of opinion formation within social networks have garnered significant attention due to their applicable impact on public discourse and societal cohesion [7]. Social networks serve as critical platforms for information dissemination and exchange, facilitating connectivity and synchronicity among individuals and influencing public opinion in complex and multifaceted ways [8].

The simulation of opinion dynamics within these networks is crucial for understanding how opinions evolve and spread, providing insights into polarization and consensus formation [9,10]. By modeling these processes, researchers can predict potential outcomes of information dissemination, identify factors that contribute to the stability or volatility of public opinion, and develop strategies to mitigate the negative impacts of misinformation and polarization. Online communities allow for the rapid spread of information and ideas, connecting people across diverse geographical locations and cultural backgrounds. This interconnectedness can lead to the swift formation of public sentiment on various issues, shaping societal norms and influencing political, economic, and social landscapes. However, online social settings can lead to formations of echo chambers where algorithms feed viewers based on the preference of material they engage with through selective exposure [11,12].

Key social phenomena, such as homophily, bias, influence, and selective exposure, are also integral to studying opinion dynamics. Homophily, the tendency of individuals to associate and bond with similar others, often leads to the formation of echo chambers—closed loops where information that aligns with existing beliefs is amplified while dissenting views are minimized [13,14]. This phenomenon is exacerbated by selective exposure, where individuals preferentially seek information that confirms their preexisting beliefs and avoid information that challenges them. Biases in information processing and social influence, where individuals’ opinions are swayed by those they interact with, further reinforce these echo chambers [15,16]. For example, social media algorithms are designed to cause one to be “hooked” into remaining on the platform by learning one’s browsing and trace history, thereby recommending content of the same form and topic, potentially reinforcing the echo chamber. This selective exposure can significantly influence the convergence or divergence of opinions within social networks, reinforcing existing biases and potentially leading to increased polarization [17,18]. Such polarization can have profound implications for social cohesion, as it can create deep divides between different groups within society, making it challenging to reach a consensus on critical issues. Selective exposure, the tendency of individuals to seek out information that reinforces their existing beliefs while avoiding contradictory viewpoints, plays a crucial role in the formation and persistence of echo chambers [19]. Understanding the mechanisms behind these dynamics is essential for addressing the challenges of echo chambers, especially in the context of misinformation and truth propagation.

One commonly adopted opinion dynamics model is the bounded confidence model first proposed by Hegselmann and Krause [20]. The bounded confidence model is a framework to study how individual opinions evolve within a population. Each individual updates their opinion by considering only those opinions within a confidence interval of their own opinions.

Mathematically, let $x^i\left(t\right)$ denote the opinion of individual i at time t, where $x^i\left(t\right)\in \left[-1,1\right]$, $\forall t$. Each i has a confidence interval ${ϵ}^i$, where i only considers the opinion of agent j if

$$\left|x^j\left(t\right)-x^i\left(t\right)\right|\le {ϵ}^i.$$

(1)

Consequently, the opinion of i at $t+1$ is updated based on the average opinions of all individuals whose opinions lie within i’s neighborhood of acceptance, $I(i,x)$, where

$$I(i,x):=\left\{j:\left|x^j-x^i\right|\le {ϵ}^i\right\},$$

(2)

and the updated opinion can be expressed as

$$x^i(t+1)={\left|I(i,x)\right|}^{-1}\sum _{j\in I(i,x)}{x}^j\left(t\right).$$

(3)

Tan and Cheong extended this work to include multi-issue consensus [21], by including an issue index k, where the opinions are now defined as $x_k^i\left(t\right)$. Tan and Cheong further specified three interaction instances, where the opinions are updated based on the dynamics of the modified update rule defined by a new neighborhood of acceptances. Exclusivist interaction represents one extreme where an agent considers the opinion of another only if it is sufficiently close in all dimensions. In this model, an agent will only take into account opinions that fall within a specific range for every issue simultaneously. This exclusivity leads to a narrow scope of accepted viewpoints, thereby reducing the chances for multi-issue consensus. Inclusivist interaction is the opposite extreme, where an agent considers the opinion of another if it is sufficiently close in any one dimension. Here, even if two agents disagree on most issues, they can still influence each other’s opinions if they share a similar view on at least one issue. This inclusivity allows for a broader acceptance of diverse viewpoints and promotes a greater potential for consensus. However, neither the exclusivist nor inclusivist models are entirely realistic. It is more reasonable to assume that agreement on one issue will only partially encourage agreement on another issue. To that end, Tan and Cheong defined a model that interpolates between the two extremes called general interaction:

$$I_k^{\prime }(i,x):=\left\{j:\left|x_k^j-x_k^i\right|\le {ϵ}_k\mathrm{and}\left|x_l^j-x_l^i\right|\le {\alpha }_k{ϵ}_l,\forall l\ne k\right\},$$

(4)

and

$$x^i(t+1)={\left|I^{\prime }(i,x)\right|}^{-1}\sum _{j\in I^{\prime }(i,x)}{x}^j\left(t\right),$$

(5)

where $I^{\prime }(i,x)={\cup }_{k=1}^m{I}_k^{\prime }(i,x)$. ${\alpha }_k$ is a factor that is termed the degree of inclusivity. What these equations say is that an agent i will consider the opinion of another agent j if, for any issue k, $x^j$ is within the latitude of acceptance ${ϵ}_k^i$ of $x^i$ and for every other issue $l\ne k$, also within an expanded latitude of acceptance of ${\alpha }_k{ϵ}_l^i$. The idea is that as long as agent i agrees sufficiently with agent j on one issue k, they are more willing to hear each other out on all other issues $l\ne k$. ${\alpha }_k$ is the parameter that describes how much more willing the agents are to consider each other’s opinions. If we set ${\alpha }_k=1,\forall k$, we obtain the exclusivist model, and if ${\alpha }_k\to \infty ,\forall k$, we obtain the inclusivist model of opinion intersection. Figure 1 illustrates the results from this model for the two extremes and the general interaction.

While these works have deepened our theoretical understanding of social interaction and opinion dynamics, there remain research gaps for potential further investigation. Two of such gaps are the homogeneity in agent behavior and the simplified interactions based entirely on a static network. Firstly, the network does not evolve due to interaction behaviors, which do not reflect reality. Real-life social interaction changes are influenced by homophily, belief, and influence, which are not fully captured in their models. Secondly, all agents behave the same way with a uniform $\alpha$ for all agents across all issues. In reality, agents have varied tolerance thresholds, differing levels of influence, and personal biases. Critically, uncertainty plays a significant role in social interactions, influencing behaviors, communication patterns, decision-making processes, and the formation of social networks. Understanding how uncertainty impacts social dynamics can help analyze and predict social phenomena. The Dempster–Shafer theory (DST), also known as the Theory of Evidence, is a mathematical framework for modeling epistemic uncertainty [22,23]. Unlike traditional probability theory, DST represents uncertainty without requiring precise probability assignments. Mathematically, DST is described with a frame of discernment $\mathsf{\Theta }$ as a finite set of mutually exclusive and exhaustive hypotheses representing all possible states. The Basic Probability Assignment (BPA), denoted by m, assigns a probability mass to each subset A of $\mathsf{\Theta }$ such that $m:2^{\mathsf{\Theta }}\to \left[0,1\right]$ satisfying

$$\sum _{A\subseteq \mathsf{\Theta }}m\left(A\right)=1,\mathrm{where}m(\varnothing )=0.$$

(6)

The belief function $Bel$ for a subset $A\subseteq \mathsf{\Theta }$ is defined as the sum of the masses of all subsets B that are contained within A, given by

$$Bel\left(A\right)=\sum _{B\subseteq A}m\left(B\right).$$

(7)

Consequently, Dempster’s rule of combination combines two independent sets of evidence represented by the BPAs $m_1$ and $m_2$ [24]. The combined BPA m is computed as

$$m\left(A\right)={\displaystyle \frac{1}{1-K}}\sum _{B\cup C=A}{m}_1\left(B\right)m_2\left(C\right),$$

(8)

where K is a normalization factor given by

$$K=\sum _{B\cup C=\varnothing }{m}_1\left(B\right)m_2\left(C\right).$$

(9)

While the use of other models to describe belief has been adopted in the context of opinion dynamics [25], and DST has been used to model decision-making [26], DST has yet to be used to handle uncertainty and combine multiple sources of evidence for opinion formation using the bounded confidence model.

Lastly, “truth” often refers to an objective reality or a widely accepted fact that individuals in a society aim to converge upon. The concept of truth in social networks is pivotal, as it influences how information spreads, how consensus is formed, and how public opinion evolves. Researchers have employed various models to study how opinions converge towards the truth or diverge from it due to the influence of different factors, including social pressure, misinformation, and the small presence of influential agents [27,28,29]. Furthermore, it is known that truth is perceived and formed within social groups and networks, leading to democratic faultlines and subgroup polarization [30]. However, balancing subgroup consensus and global diversity can lead to a dynamic and evolving perception of truth [31]. Collectively, these studies underscore the fact that a small number of resolute individuals (analogous to truths) profoundly influence the collective opinions of larger groups. Consequently, further research is needed to explore the role of truths in complex opinion dynamics systems, especially in the case of shifting evidence and beliefs.

This article attempts to introduce a robust model of opinion dynamics that addresses these research gaps. The rest of the article describes the formalism of our opinion dynamics model in Section 2. We then study the general behavior of such opinion dynamics using three interaction types and conduct computational experiments to show how different types of truths affect the convergence and divergence of opinions in Section 3. Finally, we conclude in Section 4.

2. Formalism and Methods

2.1. Network Formalism

We consider a population $N=\{1,2,\dots ,n\}$ of interacting agents belonging to a social group $G=(N,E)$, where E are all the edges in the network. Each $i\in N$ is a node in the network and is connected to a subset of $M^i\subseteq N\backslash \left\{i\right\}$ by undirected weighted edges $E^{ij}=\left((i,j),w^{ij}\right)$. Associated with each agent i is a vector of opinions $x^i$ of dimension p. The k-th component of the vector is denoted by $x_k^i$. For each issue index k, we also define the population opinion vector, $x_k:=\left(x_k^1,x_k^2,\dots ,x_k^n\right)$. Similarly, belief masses are assigned to agents where $m_k^i$ denotes the belief mass of agent i regarding issue k. The belief mass represents the degree of confidence agent i assigns to its opinion on issue k.

2.2. Opinion Dynamics Formalism

To expand the model under the general interaction, we first define an agent-wise partition on the set of issues, K. For each agent, i, the set of issues can be partitioned $K=P^i\cup \overline{P^i}$, where $P^i$ is the set of issues which i considers under the strict latitude of acceptance. The modified neighborhood of acceptance is

$$I_k^{\prime }(i,x):=\left\{j:\left|x_k^j-x_k^i\right|\le {ϵ}_k^i\wedge \left|x_l^j-x_l^i\right|\le {\alpha }_l^i{ϵ}_l^i,\forall l\ne k,k\in P^i,j\in M^i\right\},$$

(10)

where ${\alpha }_l^i>1$ is the modified degree of inclusivity, which gives us the expanded latitude of acceptances on the set of issues $l\in P^i$. This expanded model not only allows for each individual to have a different set of issues considered under the strict latitude of acceptance, but each issue can also have a different degree of inclusivity. This is a significant generalization of the general interaction previously introduced in Equation (4).

Next, to update agent i’s opinion based on the influence of other connected agents, we consider intrinsic and extrinsic factors. First, for the intrinsic factor, consider the case where each agent has a bias parameter $\beta \in \left[0,1\right]$. Agent i’s bias parameter ${\beta }_i$ indicates the weight of how strong an agent’s bias is towards its own opinion. An agent with a high $\beta$ tends to gravitate one’s opinions towards neighbors’ opinions, while a low $\beta$ places greater weight on one’s own opinion. This allows us to calculate the intrinsic influence of agent i on issue k:

$$J_k^i=(1-{\beta }_i)x_k^i\left(t\right)+{\beta }_i{x}_k^j\left(t\right),\mathrm{if}j\in I_k^{\prime }(i,x).$$

(11)

For the extrinsic factor, this is influenced by the weight of the connection between i and neighboring agents j, $w^{ij}\left(t\right)$ and the belief mass of neighbors j regarding issue k, $m_k^j$. The total combined influence is therefore

$$A_k^i={\displaystyle \frac{1}{W}}\sum _{j\in j\in I_k^{\prime }(i,x)}{w}^{ij}\times m_k^j\times J_k^i,$$

(12)

where W is the normalizing factor for extrinsic factors given by

$$W=\sum _{j\in j\in I_k^{\prime }(i,x)}{w}^{ij}\times m_k^j.$$

(13)

Consequently, the new opinion of agent i on issue k accounts for one to respond to the influence of others, which is also a factor in opinion evolution. The parameter $h\in \left[0,1\right]$, termed homophily in social settings, indicates the tendency of agents to be influenced by others similar to them. Thus, an agent i with a low $h_i$ makes minimal adjustments based on the neighbors’ opinions. The updated opinion evolution is thus

$$x_k^i(t+1)=x_k^i\left(t\right)+h_i\left(A_k^i-x_k^i\left(t\right)\right).$$

(14)

The scaling by $h_i$ of the difference in the overall influence and the agent’s current opinion ensures that agents with higher homophily are more likely to conform to the opinions of their social circle.

Finally, to update agent i’s belief mass, the beliefs from neighboring agents j are combined using Dempster’s rule of combination, given by Equation (8). To reinforce the echo chamber effect, we incorporate a mechanism of selective exposure to adjust the strength of connections between nodes based on opinion similarity. Specifically, for each agent i, if a neighbor’s opinion j is sufficiently close to that of the node, within the threshold ${ϵ}_k^i$, we strengthen the connection by increasing the edge weight by 1. Conversely, if the opinions are dissimilar, we weaken the connection by decreasing the edge weight by 1, ensuring that the edge weight does not drop below 1 so that no edges are removed from the original social network given by

$$w^{ij}(t+1)=\left\{\begin{array}{cc}{w}^{ij}\left(t\right)+1\hfill & \mathrm{if}\left|x_k^j\left(t\right)-x_j^j\left(t\right)\right|\le {ϵ}_k^i\hfill \\ max\left(w^{ij}\left(t\right)-1,1\right)\hfill & \mathrm{otherwise}\hfill \end{array}\right..$$

(15)

2.3. Modeling Truth

The “truth” can be incorporated into this model by introducing node(s) T. We will model two types of truths in this work:

• Exoteric Truth: This type of truth is general and accessible to everyone. It is meant for the public and is openly shared and disseminated. Exoteric truths are designed to be easily understood and widely accepted by the general populace. This type of truth is characterized by its high degree of connection and influence over a wide population. To model this, the node T is connected to every existing node in the network with a very high initial edge weight to ensure that T acts as an initial dominant source of influence. The other nodes’ opinions are continually pulled towards the truth T, given by $x_k^T$, simulating the concept of convergence towards a truth. $x_k^T$ is a constant in this case.
• Privileged Truth: This type of truth is initially accessible only to a select group of people who have privileged information. Although it is not meant to be a secret, it is not immediately available to the general public. Over time, this information might spread and become more widely known. To model this, the node T is connected to the neighbors of the node with the highest degree in the network with a very high initial edge weight to ensure that T acts as an initial dominant source of influence. The other nodes’ opinions are pulled indirectly towards the truth T, given by $x_k^T$, a constant in time.

2.4. Simulations

To investigate the dynamics of opinion formation and the influence of echo chambers in social networks, we will employ Python for our simulations, utilizing the NetworkX package to construct and analyze the networks. The pseudo-codes are found in the Supplementary Information. Our simulations will encompass three distinct experiments as follows:

• The behavior of opinion dynamics in a network for opinion evolution with DST;
• The comparison between presence and various types of truth and how they alter the dynamics of opinion evolution;
• The strength and pervasiveness of truth affecting opinion consensus and fragmentation.

3. Results and Discussion

In our simulations, we use the parameters and randomized domain found in

Table 1. Initial parameters used in simulations.

Symbol	Initial Value	Description
$\left|N\right|$	50	Number of agents in population
$\tau$	$\mathrm{10,000}$	Steps in simulation
$x_k^i\left(0\right)$	$\mathcal{U}(-1,1)$ *	Range of initial opinions
$m_k^i\left(0\right)$	$\mathcal{U}(0.5,1)$ *	Range of initial belief masses
$w^{ij}\left(0\right),i\ne T$	1	Weights of network edges between agents
$h_i$	$\mathcal{U}(0,1)$ *	Homophily parameter
${ϵ}_k^i$	$\mathcal{U}(0.1,0.25)$ *	Latitude of acceptance of agent i, for issue k
${\beta }_i$	$\mathcal{U}(0.1,0.3)$ *	Bias parameter
${\alpha }_k$	$\mathcal{U}(1.5,3.0)$ *	Expanded latitude of acceptance factor

* $\mathcal{U}(a,b)$ denotes the uniform distribution from the interval [a,b].

. The network used is generated by the function

$$\mathtt{barabasi}\mathtt{\_}\mathtt{albert}\mathtt{\_}\mathtt{graph}\mathtt{(}\mathtt{n}\mathtt{=}\mathtt{50}\mathtt{,}\mathtt{m}\mathtt{=}\mathtt{3}\mathtt{,}\mathtt{initial}\mathtt{\_}\mathtt{graph}\mathtt{=}\mathtt{H}\mathtt{)},$$

(16)

where H = erdos_renyi_graph(n=50,p=0.1) [32,33]. While the scale-free network is chosen for simulation in this work, the method introduced here can be applied to different network topologies. Many real-world networks naturally exhibit scale-free properties. Examples include the Internet, social networks, and biological networks. Leveraging a scale-free structure aligns well with the inherent topology of these systems and the potential generalizability of the results presented in this work to the social dynamics settings.

3.1. Interaction Outcomes

Firstly, we want to investigate how the number of issues $\left|K\right|$ affects opinion consensus. Figure 2 shows the outcome of simulating interactions on the scale-free Barabási–Albert (BA) network, a common network topology in social settings. In all simulations, the number of agents in the network is 50, averaged over 1000 experiments for $\left|K\right|=\{2,5,10\}$ number of issues, with each agent having a varying number of issues considered for the extended latitude of acceptance.

The multi-issue simulation demonstrates that as the number of issues under consideration increases, the potential for a dominant consensus to form also rises. This phenomenon occurs because including multiple issues allows for a broader range of perspectives and preferences to be integrated into the decision-making process. Consequently, individuals and groups are more likely to find common ground across various issues, leading to the emergence of a dominant consensus. This consensus reflects a more comprehensive agreement that accommodates the diverse interests and priorities of the individuals. Furthermore, the simulation indicates that the dynamics of negotiation and compromise become more intricate with multiple issues at play, ultimately fostering a more inclusive and representative outcome.

However, we further note that when the number of issues under consideration becomes too plentiful, it can decrease the potential or delay the formation of a dominant consensus, as seen in the case when comparing $\left|K\right|=5$ and $\left|K\right|=10$. This phenomenon occurs due to several factors. Firstly, the complexity of discussions can increase significantly with more issues, making it difficult for individuals to focus on and thoroughly understand each other. This complexity overload can lead to fragmented conversations where no single issue receives the attention needed for a strong consensus to emerge. Additionally, with more issues, there is a higher likelihood of divergent interests and opinions. Individuals may prioritize different issues based on their personal interests, leading to conflicts and disagreements rather than a unified agreement.

This is one of the key factors for employing Focus Group Discussions (FGDs) in research and decision-making processes. FGDs gather diverse individuals to discuss multiple issues, enabling the collection of varied opinions and insights. The interactive nature of FGDs encourages individuals to share their views and consider different perspectives, promoting a deeper understanding of the issues at hand [34]. Through this process, FGDs help to identify commonalities and divergences among individuals, facilitating the formation of a dominant consensus that reflects a broad spectrum of interests and opinions. Integrating multiple issues into the discussion allows FGDs to achieve a more holistic and representative outcome, similar to the dynamics observed in multi-issue simulations. However, as the name suggests, FGDs must be focused on a fixed number of issues. When the number of issues discussed becomes too diverse, the increased complexity can overwhelm individuals, making it difficult for them to focus on and deeply engage with each issue. This often leads to fragmented discussions where no single topic is thoroughly explored, diminishing the likelihood of a strong consensus [35].

Next, we examine the dynamic difference resulting from including evidence-based DST. We consider a system where the opinions are affected by the frame of discernment and the evolution of belief masses, reflecting the new confidence level in the updated opinions. We compare it to a topologically similar system, with opinions being affected only by influence. That is, Equations (12) and (13) can be collectively rewritten as

$$A_k^i={\displaystyle \frac{{\sum }_{j\in I_k^{\prime }(i,x)}{w}^{ij}\times J_k^i}{{\sum }_{j\in I_k^{\prime }(i,x)}{w}^{ij}}},$$

(17)

where the updated opinion evolution remains unchanged, as given by Equation (14).

When comparing the two models of opinion update from Figure 3, it is immediately apparent that the inclusion of evidence affects the evolution of opinions in two significant ways. Firstly, the presence of evidence accelerates the process of achieving a dominant consensus. This implies that when individuals incorporate evidence into decision-making, the overall time required to reach a unified opinion is reduced. Secondly, the inclusion of evidence also affects the final distribution of opinions among agents. It notably increases the number of agents whose opinions converge towards the dominant consensus. This indicates that evidence serves as a moderating force, leading the majority to align with the prevailing viewpoint quickly. Consequently, in a bounded confidence opinion dynamical system, the integration of evidence fosters a more nuanced and potentially stable opinion dynamic, enhancing the pathway to consensus.

3.2. Dynamics under the Influence of Truth

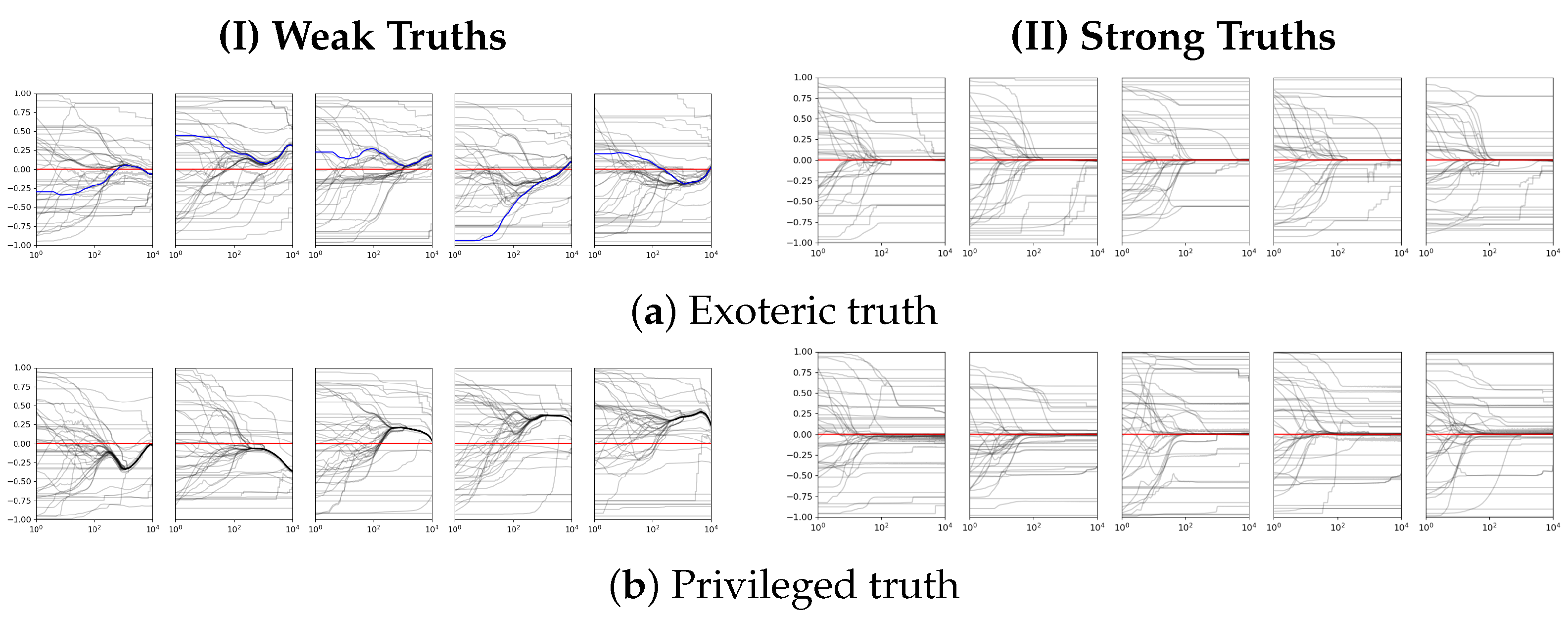
Next, we simulate opinion dynamics in the presence of truth, beginning with scenarios involving weak truth and progressing to those with strong truth for both exoteric and privileged truths. Here, we define weak truth as truths with influence that are similar to a smaller order of magnitude as agent–agent connections, i.e., $O\left(w^{Tj}\right)\le O\left(w^{ij}\right)$, for an eligible j. Conversely, strong truth is one where $O\left(w^{Tj}\right)\gg O\left(w^{ij}\right)$. This simulation is important because it provides insights into how varying degrees of truthful information influence the evolution of public opinion. We first define a central truth to compare the degree of truths, set as $x^T={\left[0.0\right]}_k,\forall k$, where ${\left[0.0\right]}_k$ denotes a vector of zeros of length k.

Figure 4 shows the extremes of the strength of exoteric and privileged truths. By simulating weak truth, we can observe how a limited or diluted form of truth, regardless of its type, impacts opinion formation, potentially leading to a slower consensus building or the persistence of misinformation, as seen in both cases of (I). Weak truths with little to no influence in the system of opinion dynamics often do not affect any changes to the evolution of opinions, leading key individuals to drive opinions instead. Simulating strong truth allows us to understand how robust, clear, and undeniable truths can accelerate consensus and reduce the prevalence of false beliefs. These simulations are crucial for policymakers, educators, and communicators as they highlight the effectiveness of truth in shaping public discourse. They can inform strategies for combating misinformation, designing educational campaigns, and understanding the resilience of truth in diverse social contexts.

Our results comparing strong truth in exoteric and privileged cases reveal intriguing dynamics in how consensus forms around societal truths, whether these truths are universally accessible (exoteric) or confined to an influential subset (privileged). Common in both scenarios, there is a convergence towards a dominant consensus at a similar rate. However, the characteristics of the final spread of opinions differ. While both exoteric and privileged truths ultimately lead to a dominant consensus, the nature of this consensus differs significantly. The exoteric model fosters a strong, cohesive agreement, whereas the privileged model shows multiple and diverse opinion formation, not amounting to fragmentation, around the core truth (haze around the truth, $t\to \tau$). This has applications in the real world. For instance, in scientific consensus (an exoteric truth), widespread access to information and data has led to a strong, unified agreement about its reality and causes. On the other hand, in contexts where truth is privileged, such as insider financial information available only to select investors, there tends to be a greater diversity of opinions and strategies surrounding the dominant consensus. This diversity stems from the varying interpretations and applications of the privileged information.

3.3. Dynamics under the Presence of Varied Truth

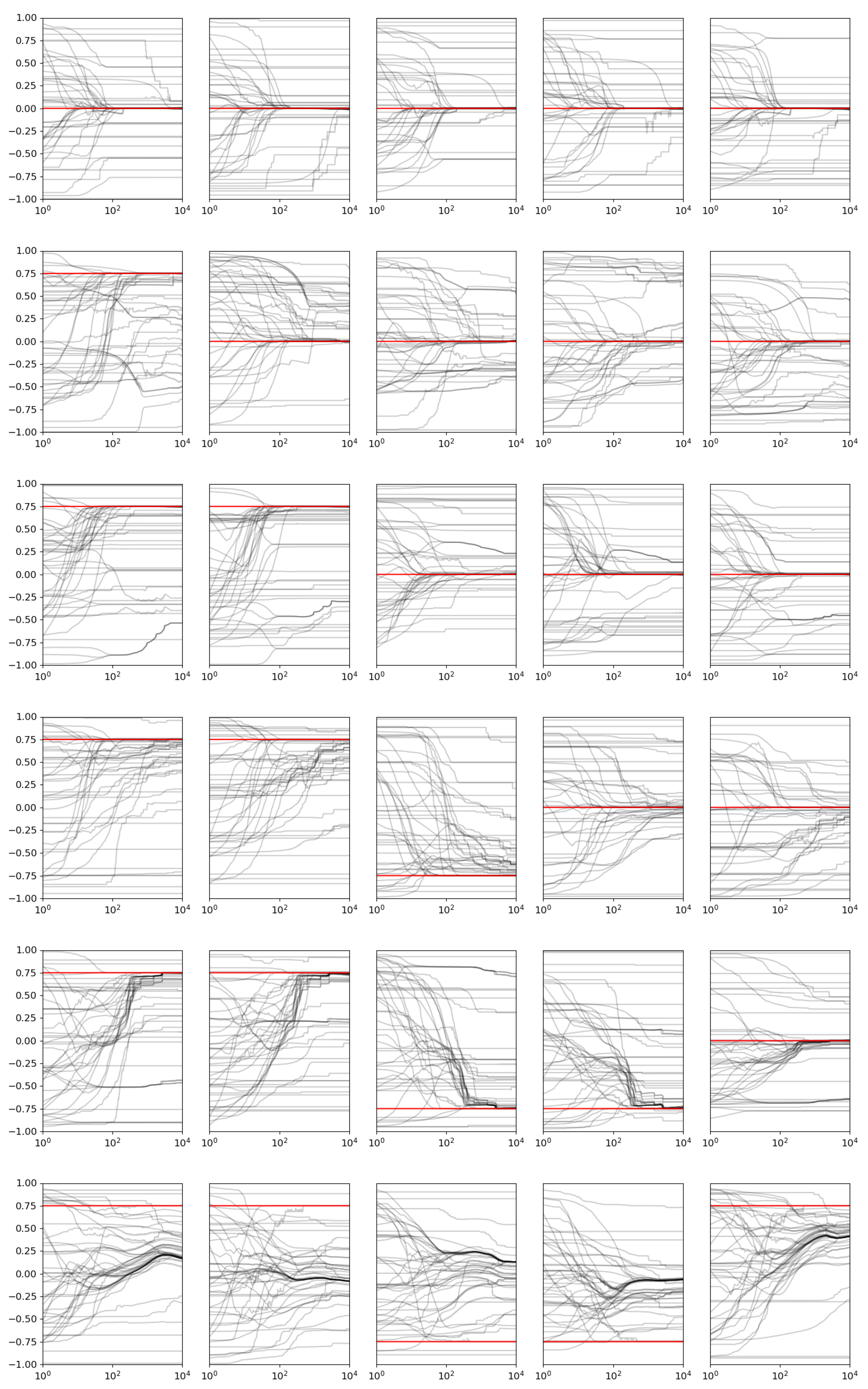
In exploring opinion dynamics, it is essential to acknowledge that not all truths occupy a centrist position; some may reside at the extremes. This understanding is critical as we delve into simulations incorporating strong truths within scenarios characterized by extreme and centrist exoteric truths. Examining these diverse truth positions, we aim to identify the tipping points for opinion formation. This approach allows us to investigate how extreme truths can influence overall opinion dynamics and under what conditions they might dominate or coexist with centrist truths. Understanding these tipping points is vital for predicting shifts in public opinion, managing societal polarization, and fostering environments where a plurality of truths can be discussed and understood. Through these simulations, we can gain deeper insights into the mechanisms driving opinion changes and the resilience of centrist positions in the face of extreme viewpoints. A centrist truth for issue k is defined as $x_k^T\left(t\right)=0.0,\forall t$, while an extreme truth is defined as $x_k^T\left(t\right)=\pm 0.75,\forall t$.

Figure 5 shows the results of $\left|K\right|=5$, where the number of extreme truths incrementally increases. The introduction of extreme truths continues to result in opinion convergence for most agents within the population. This outcome suggests that even when the truths are extreme, the inherent dynamics of the system encourage agents to gravitate towards the truth. However, a notable observation is a distinct delay in achieving consensus, even for the issues with centrist truths. This delay can be attributed to several factors inherent in the nature of extreme truths and the opinion dynamics model. Firstly, agents require time to adjust their opinions as they are exposed to extreme truths. This adjustment period is longer because agents may hold an initial opinion on the issue that diametrically opposes the truth. The process of repeatedly interacting with and adjusting to extreme truths introduces additional iterations before a stable consensus can be reached. Secondly, the delay in achieving a consensus may also be due to the complex interactions between agents influenced by extreme truths and their interaction with other agents. These interactions create a more complex landscape for opinion evolution, requiring more time to navigate and converge. This means that it takes more time and more interactions for the opinions to shift significantly towards consensus. As the number of extreme truths increases, the collective inertia of the system increases, thereby prolonging the convergence time.

While introducing extreme truths—in the presence of centrist truths—does not prevent the eventual convergence of opinions within the population, it does introduce complexities that delay the process. The initial polarization, longer adjustment periods, stronger influence of extremes, and complex inter-agent interactions all contribute to this delay. Moreover, an important detail is that if all the issues in the model are characterized by extreme truths, with no centrist truths present, the population will never converge to any of these extreme truths. This phenomenon occurs because the presence of only extreme truths exacerbates polarization without providing a moderating influence that centrist truths typically offer. In such a scenario, the agents’ opinions remain perpetually divided and oscillate without ever stabilizing. This lack of convergence highlights the critical role of centrist truths in facilitating consensus by acting as a balancing force that tempers the influence of extreme truths.

We note several other permutations, unexplored in this work, of how opinions evolve based on different forms and methods of simulating truths. For example, we have focused exclusively on strong truths across all issue dimensions in the last simulation. However, examining a combination of both strong and weak truths, spanning both centrist and extreme positions, might yield interesting and nuanced results that warrant future research. Such combinations could reveal more complex dynamics of opinion formation, highlighting how varying intensities and positions of truths interact to shape public consensus, polarization, and the stability of different opinion clusters. Future investigations into these permutations can provide a more comprehensive understanding of the multifaceted nature of opinion dynamics, offering valuable insights for fields ranging from social psychology to political science.

4. Conclusions

In conclusion, we develop a computational model to investigate the dynamics of opinion formation and the emergence of echo chambers in a network through evidence-based opinion updates. We model a network where each node represents an agent with opinions on multiple issues. Agents interact based on a modified general interaction where each agent has varying numbers and issues considered under the expanded latitude of acceptance. We also introduced selective exposure by varying the strength of connections (edge weights) based on opinion similarity. “Truth” nodes with high connectivity are used to simulate the influence of various types of truth on the network. Our model and findings collectively hold significant theoretical and practical implications, directly impacting the understanding of truth in networks. For example, by formalizing intuitive descriptions of how people interact with truth and engage in multi-issue discussions online, our work enables opinion dynamics to encompass a broader range of phenomena. The conclusions from our models can guide how online platforms manage discourse and interactions. This approach helps refocus debates on divisive online issues by moving beyond simplistic assumptions about multi-issue dialogue, promoting inclusivity in cross-issue interactions, which benefits users and platform administrators alike.