Abstract
Network visualization, in mathematics often referred to as graph visualization, has evolved significantly over time, offering various methods to effectively represent complex data structures. New methods and devices advance the possibilities of visualization both from the point of view of the quality of displayed information and of the possibilities of visualizing a larger amount of data. Immersive visualization includes the user directly in presented visual representation but requires a native 3D environment for direct interaction with visualized information. This article describes an approach to creating a force-directed immersive 3D network visualization algorithm available for application in immersive environments, such as a cave automatic virtual environment or virtual reality. The algorithm aims to address the challenge of creating visually appealing and easily interpretable visualizations by utilizing 3D space and the Unity engine. The results show successfully visualized data and developed interactive visualization methods, overcoming limitations of basic force-directed implementations. The main contribution of the presented research is the force-directed algorithm with springs and controlled placement as an immersive visualization technique that combines the use of springs and attractive forces to stabilize a network in a 3D environment.
1. Introduction
Increasing volumes of data require advanced methods for the presentation of insights, structures, and results included in explored datasets. Currently, it is possible to see a growing effort to visualize high-dimensional data with direct user involvement in the form of immersive visualization methods []. Detailed studies of immersive visualization methods include several aspects of the data visualization process, while in addition to the technical area of data preparation, they also include methods for analyzing the accuracy of interpretation and user interaction [].
Related areas of visualization research focus on removing the limitations of conventional methods for representing data (often static and with narrow scope) so that the available information contained in the analyzed data can be extracted [,]. The optimal way to achieve such advanced enhancements is to exploit the potential of interactivity to support complex data analysis. Such interactive systems enriched with integrated visual interfaces (synergy of simulation, analysis, and visualization modules) are designed to overcome the limited human analytical capacity to synthesize a multitude of heterogeneous data into informative insights [].
Linking visualization with interactive features is a key aspect in the design of visual analytics systems []. The focus of such interfacing has traditionally been on 2D displays containing abstract data. These techniques are quite appropriate when considering the visualization of continuous numerical attributes to reveal potential relationships, patterns, and correlations between these attributes. However, 2D representations are not suitable for some tasks, mostly including large amounts of data, and do not work at all in certain contexts. For example, when analyzing large datasets, such visualizations experience overlap (occlusion), leading to loss of information []. This is mainly due to the large number of data points that overlap each other, making it difficult for a human analyst to see individual data points and make inferences about potential relationships. Similar situations can potentially interfere with visual perception and inferences related to discovery (locating a geometric representation), access (retrieving a shape, color, or other property), and spatial relationships (the interrelationship of geometric representations) [].
Furthermore, relative positioning in 2D space is not equally suitable for performing the task of absolute positioning in 3D space, because the inherent physical limitations of 2D space make it impossible to account for the full range of other multidimensional attributes []. Alternative visualizations using 3D representations enriched with complex navigation features may therefore be more appropriate when exploring the internal structure of such data. Three-dimensional visualizations essentially capture the full spectrum of dimensions of the underlying data and supporting information, while interaction and navigation techniques mimic the sense of exploring the real-world environment in a familiar way.
The motivation for developing a novel method for 3D immersive visualization arose from the necessity to effectively display a substantial amount of network data (consisting of thousands of vertices) within an immersive virtual environment known as CAVE (cave automatic virtual environment). A cave automatic virtual environment (CAVE) is a fully immersive virtual reality setup in which projectors are aimed at three to six walls of a room-sized cube []. The software utilized in CAVE mostly relies on physical game engines. Consequently, we chose to develop an algorithm utilizing the physical environment that is already established in game engines.
The following immersive visualization principles are defined by (1) a three-dimensional environment supporting 3D vision, (2) user interaction support, (3) consistent physics (motion-oriented approach), and (4) intuitive navigation [].
In accordance with the defined taxonomy, we focus on the area of graph data transformation for immersive visualization, while we define transformation as the mechanism of the initial presentation of the graph in a 3D space without user interaction. Our defined goal for 3D visualization algorithm design and development is to provide a visual representation of the complex internal structure of networks to facilitate the understanding and analysis of network structures, and to reveal patterns and relationships within network data.
The main contributions of this paper are in (1) the analysis of graph visualization algorithms suitable for 3D implementation, and (2) the development of an algorithm for optimal graph placement with respect to immersive visualization principles.
The presented paper is structured as follows: the Introduction is followed by Section 2 with principles of force-directed visualization algorithms suitable for modification using a 3D environment, Section 3 defines our basic goals, principles, and algorithms together with our modifications of formally used techniques, Section 4 summarizes the experimental observations and results, Section 5 summarizes the main findings and solutions based on the experimental results, and Section 6 briefly concludes the article with defined steps for future research.
2. Related Work
Force-directed graph drawing algorithms are a type of algorithm that can be used to create visually appealing representations of graphs. Their purpose is to arrange the nodes of a graph in a way that minimizes the number of crossing edges and ensures that the edges have similar lengths. This is achieved by assigning forces to the nodes and edges based on their positions, and then using these forces to simulate the movement of the nodes and edges or to reduce their energy []. Force-directed algorithms are a class of algorithms that are among the most effective at calculating the distributions of simple undirected graphs. These algorithms, referred to as spring embedders, determine the arrangement of a graph only based on the network’s structure, without relying on any specific knowledge provided by the vertices, edges, or attributes. Graphs generated using these techniques possess natural aesthetic appeal, demonstrate symmetry, and tend to yield layouts without any intersecting edges for planar graphs. Research conducted in this area has been documented in publications by Di Battista et al. [] and Brandes [].
One of the first force-directed methods for drawing (visualizing) graphs is an algorithm based on barycentric representations []. More traditionally, the force representation decomposition method is based on Eades [], but the most common implementation of the algorithm is based on Fruchterman and Reingold []. Both implementations rely on spring forces defined analogously to Hooke’s law. In these methods, there are repulsive forces between all nodes and attractive forces between nodes that are mutually incident.
The advantages of force-directed algorithms in 2D space lie in their simplicity and comprehensibility. This form of visualization provides fast and intuitive data presentations, which is advantageous for various applications of social network visualizations or data structures. However, despite these advantages, 2D space also carries disadvantages. The limited space can lead to overlapping vertices and edges, which reduces the readability of the graph. Also, the lack of realism can limit the ability to capture details of relationships and distances between vertices.
Figure 1 shows 2D visualization using the Fruchterman–Reingold algorithm with different numbers of vertices and respective edges. As seen, the edges gradually overlap the vertices, which causes the loss of the original information about groups of vertices, as can be seen, for example, in the visualization of a graph with the number of vertices of 500.
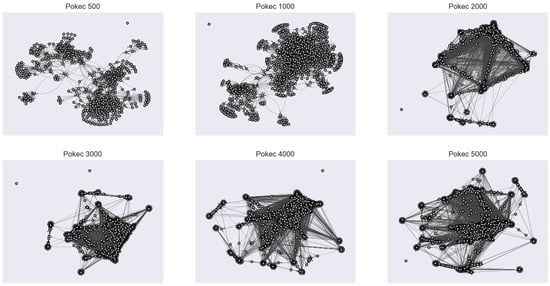
Figure 1.
Two-dimensional visualizations of Pokec dataset with different numbers of vertices and edges using Fruchterman–Reingold algorithm. With an increasing number of vertices (from 500 to 5000 with respective edges/links), the occlusion problem arises.
Using a different approach, forces between nodes can be calculated based on their theoretical distances in the graph, determined by the lengths of the shortest paths between them. For example, the algorithm of Kamada and Kawai [] uses spring forces proportional to the theoretical distances of the graph. In general, force-directed methods define an objective function that maps each graph layout to a number in that represents the energy of the layout. This function is defined such that low energies correspond to layouts in which neighboring nodes are close to each other based on some pre-specified distance and in which non-adjacent nodes are well spaced [].
The current research on 3D graph drawing algorithms primarily focuses on addressing specific problems and constructing specialized types of graphs. Notable algorithms in this field include those developed by Cohen, Eades, Lin, and Ruskey []. The algorithms for general graphs in three dimensions are well summarized by Gajer, Goodrich, and Kobourov [].
The main problem of research and development in 3D visualization algorithms is that there are only a limited number of works directly describing algorithms for three-dimensional space [,,]. Practical implementations for 3D visualizations or graph drawing are usually based on 2D algorithms adapted for 3D, typically Fruchterman–Reingold. Applications based on this approach include, e.g., Cytoscape [] or Pajek []. Other applications based on 3D visualizations are mostly experimental and provide limited guidelines and recommendations for algorithm development [].
Kobourov describes the problems with the force-directed approach for 3D as being two main limitations. First, basic force-directed approaches have a fundamental limitation in terms of the number of vertices to be processed. This approach shows poor results for graphs with more than a few hundred vertices. Second, problems with scalability are caused by the existence of multiple local minima in the physical model which is represented by a graph. Even with the help of sophisticated mechanisms, basic force-directed and barycentric methods are not able to consistently produce good distributions of vertices for large graphs and thus the minimum vertex separation is very small, leading to unreadable visualizations [].
Our approach follows basic principles introduced for 2D algorithms with respect to specifics of 3D space and implementation based on physical forces. We apply an incremental development approach to identify problems during the transformation to higher dimensional space and find solutions for effective and useful visualization in three-dimensional space.
3. Materials and Methods
The defined goal for 3D visualization algorithm design and development is to provide a visual representation of the complex internal structure of networks to facilitate the understanding and analysis of network structures, and to reveal patterns and relationships within network data. In addition, the requirement for immersive visualization presupposes the arrangement of the resulting graph structure in accordance with the principles of immersive 3D visualization in space so that the user is part of the visualized information.
We are following a general definition of a mathematical graph where graph is a mathematical structure consisting of a set of vertices V (also called nodes) and a set of edges E (also called links), where the elements of E are disordered pairs of distinct vertices, where .
The basic implementation of the force-directed algorithm uses the principle of attractive and repulsive forces based on the analogy of electro-magnetic force interaction. The simple spring algorithm is also known as the spring embedder algorithm. The heuristic algorithm was formulated in 1984 by Eades [] with three basic principles.
First, to represent the graph, we replace the vertices with steel rings and replace each edge with a spring to create a mechanical system. The vertices are placed in a certain initial arrangement and spaced so that the spring forces acting on the ring vertices move the system to a state of minimum energy.
The second principle defines logarithmic force springs: attractive forces. The force defined by the spring is then expressed in the following form:
where d is the length of the spring and and are constants. Experience shows that Hooke’s law springs (linear springs) are too strong when their ends (vertices) are far apart. The solution is to use the logarithmic definition of force. In the case when , the springs do not evolve any force.
Finally, the third principle defines repulsive forces. Non-adjacent vertices repel each other, and thus, the inverse power is applied, defined as follows:
where is constant and is the distance between the vertices. The original pseudocode of the defined algorithm is as follows (Algorithm 1):
| Algorithm 1: Spring algorithm by Eades [] |
| 1. algorithm SPRING(G: graph); 2. place vertices of G in random locations; 3. repeat M times; 4. calculate the force on each vertex; 5. move the vertex by applying force on vertex * c4; 6. draw graph on CRT or plotter. |
The values used in Algorithm 1 are suitable for most of the visualization. Not previously mentioned, the constant is used in multiplication with the resulting force when the vertex is moved to its new position. Almost all graphs reach the minimum energy state after running the simulation step M = 100 times.
The principles of the spring algorithm can be applied in 3D directly by using internal representation of the spring components in the Unity engine as described in the first implementation using spring joints.
3.1. Implementation Using Spring Joints: Naïve Implementation
As the simplest implementation in 3D, we decided to use an algorithm based on the internal spring system implementation used by the Unity engine []. The Unity engine is most widely known for its use in the development of video games, but it also possesses remarkable applicability in the field of scientific computing.
Since it excels in specific domains, it can be an extremely useful instrument when employed strategically. Unity specializes in the creation of dynamic real-time 3D visualizations with implemented physical environments and a variety of tools for work in 3D space. Built-in 3D physics includes the concept of joints, which, in principle, could be used for the definition of force-based connections between two physical objects or between a physical object and a fixed point in space. Joints can apply forces that move physical objects, and joint limits can restrict that movement []. The spring joint concept in the Unity engine allows the distance between two physical objects to change as though they were connected by a spring.
Following the principle introduced by Eades, the algorithm represents a graph as a physical system, where nodes are connected by springs. Each node is assigned two types of forces, attractive forces and repulsive forces, represented by joint parameters. The goal of the algorithm is to minimize the total energy of the spring system by moving nodes to new positions.
The naïve force-directed algorithm pushes the boundaries of using the physics of the individual components of the graph through the physical engine (Unity engine) further in order to obtain a better graph layout in 3D by incorporating other properties of the data. The proposed algorithm creates graphical representations using an emulated physical force system. Gravity assigns nodes mass proportional to their network centrality, allowing more central nodes to be visualized in central locations of physical space. In addition, the principle of granting the acceleration of the node using the resulting calculated force is used, as opposed to the original calculation of the resulting position of the node after the application of the resulting force calculation.
The main problem with implementation using spring joints is that the produced cluster distances and average distances between vertices are large and thus not suitable for immersive visualization. The more frequently used method accommodates the original Fruchterman–Reingold algorithm for three-dimensional environments.
3.2. Modified Fruchterman–Reingold Algorithm for 3D
By principle, the Fruchterman–Reingold algorithm [] is a graph layout technique that operates based on forces. Force-based refers to a method that considers each vertex and edge as a physical entity that is affected by surrounding forces, influencing its position. Transformation of the original algorithm into 3D is quite straightforward, since it is possible to replace coordinates defined in 2D by 3D coordinates.
The vertices are first placed randomly in either a 2D or 3D space. The algorithm then iteratively modifies the vertex placements by considering the repulsion between vertices and the attraction between connected vertices. The vertices that are linked by an edge experience attraction, causing them to move closer to one other, while the vertices that are not linked experience repulsion, causing them to move further away.
The Fruchterman–Reingold algorithm aims to minimize the total energy of the system by finding an equilibrium state where the forces between the nodes and edges are evenly distributed. The algorithm iteratively adjusts the positions of the nodes until it reaches a state of equilibrium. The result is a visually appealing layout of the graph that allows one to easily understand the connections and relationships between the nodes.
The problem with the implementation is the significant time for the preparation of the resulting visualization. Nevertheless, since this algorithm is one of the main implementations available for 3D, we used it for evaluation purposes.
Another observed effect of Fruchterman–Reingold application is the densification of clusters and creation of components in the graph not suitable for immersive visualization. Hence, the principle of uniform spreading was defined in the next evolution of the algorithm.
3.3. Motivation for New Force-Directed Immersive 3D Graph Visualization Algorithm
Both defined algorithms in 3D show some drawbacks and limitations. The naïve spring algorithm is extremely sensitive, and it does not converge to the state when it is possible to accept the final visualization. Not only is it jittering, but the unbalanced state of the whole 3D model is changing frequently in time. The modified Fruchterman–Reingold algorithm, on the other hand, shows excessive clustering and node repulsion problems.
Combining these two defined algorithms, we were able to eliminate both observed problems. We created a combined algorithm for standard Euclidean space and its modification with a spherical border used to ensure higher compactness and readability of the resulting visualization.
Using springs (spring joints) allows us to create a system in which the vertices are pulled together by attractive forces. This approach leads to a faster stabilization of the network, as the springs ensure a stable operation of the force system. In this approach, edges are represented by attractive forces that pull connected vertices together. This model is advantageous because of fast vertex joining and good internal implementation in physics engines.
In the case of a combination of string and force algorithms, we achieve a balanced approach where springs and attractive forces work together to stabilize the graph. However, it is important to set the force parameters and springs appropriately to achieve an optimal balance between quickly settling the network and minimizing model obscurity. The combination of procedures will also prevent the creation of one large cluster, which could impair the quality of the resulting visualization.
3.4. Force-Directed Algorithm with Springs and Controlled Placement
Drawbacks of both previously defined algorithms led us to define our own use of physical possibilities provided by the Unity engine. We defined additional forces on springs to eliminate the observed jittering and kept spring joints to avoid problems with vertex separation and undesired repulsion of the vertex outside the display space.
The attractive force () acts on neighboring nodes connected by a spring, while the repulsive force () acts on all nodes of the graph. Attractive and repulsive forces in 3D are defined with respect to the original 2D algorithm:
where the original is defined as ; thus does not appear in our formula, and is defined as . The coefficient .1 for the first 3D implementation is with respect to the original definition. The distance is defined as an abstract unit of distance in accordance with the Unity engine implementation.
Even though the basic identified difference is in the use of three vertex coordinates in the defined algorithm instead of the original two, we identified several fundamental limitations and specificities, which we discuss in more detail in the experimental results section.
The algorithm first calculates the direction vector by using a value for repulsive force and attractive force equal to the edge value or in the case the graph has no edge values. Edge values are assigned based on data features selected or based on other analytical needs. The resulting vector then indicates the direction in which the appropriate node should be moved. The resulting movement in the computed direction is defined by the impulse given to the node by the application of the force . This force is calculated as the sum of attractive forces for incident vertices minus the sum of repulsive forces for non-incident vertices. A node that has its mass defined based on its degree then gains velocity based on the initial acceleration applied by the force . The resulting movement is defined as uniformly slowed motion by using not only mass but also friction force defined for the node, as seen in Formula (4). Since in the case of the application of the force-directed approach it is a uniformly decelerated motion, the resulting velocity of the node is equal to its initial velocity minus the acceleration with respect to time . The friction force is defined by the drag parameter for objects in the Unity engine and is used for calculation of the final deceleration for the evaluated time interval.
It is important to mention that the time is specific to physical engine implementation. In our experiments, s, which corresponds to 60 FPS (Frames Per Second) defined for real-time visualization of a graph. Another observation comes with the friction force, which is in fact used as the primary parameter for the resulting velocity instead of mass, which is used mostly for collision with other physical objects. Based on the experimental evaluation, velocity is internally computed as
The algorithm can be applied to the graph with a defined number of steps; in our case, we used the definition of the stopping condition. It is obvious that the algorithm does not have a final state, when no force is applied to individual nodes, and therefore, after applying a certain number of steps, oscillations occur between the equilibrium states of the system defined by this graph. This situation is often referred to as jittering. To eliminate this situation, we defined a stop condition based on the experimental results when we stop the algorithm if the velocity of 90 percent of the nodes in the graph is less than 1.
Additionally, for immersion purposes we defined a special abstract point in the space for controlled vertex placement: an anchor. An anchor is defined as a point that prevents unwanted large distances between the visualized nodes of the graph. The reason for this is the problem with network stabilization in the field of view of the camera. This problem is partially solved for nodes that are pushed out of view, but it does not solve the problem of creating one large cluster. One cluster is formed if the attractive forces of the anchor are greater than the sum of the other acting forces in the network. To avoid this undesirable condition, we implemented a spherical constraint that keeps the nodes always at the same distance from the anchor, while at the same time preventing them from moving away in the opposite direction.
The implemented algorithms utilize the internal properties of graphs, which facilitates their straightforward application to various types of data. Since the naïve spring joint algorithm and 3D implementation of the Fruchterman–Reingold algorithm are built on a 2D base, it is critical to evaluate the problems and issues associated with moving algorithms to 3D. In 2D space, the absence of the third dimension acts as a constraint, eliminating several undesired viewing states such as vertex overlap in space, among others.
The proposed force-directed algorithm with springs and controlled placement for data visualization in 3D was created iteratively, with new procedures and constraints being gradually introduced, leading to new findings that contributed to the current state of development. In the first iteration, we focused on representing edges in the graph using spring connections. The results of experiments revealed limitations of 3D space and especially the physical gaming environments themselves, determining the maximum usable data volumes that can be visualized using these tools.
Another significant finding from the experiments conducted in the first iteration is that vertices in the graph tend to oscillate to levels where the graph can no longer be stabilized when using spring connections. Furthermore, we discovered that spring connections, as represented in game engines, are extremely sensitive to changes in their internal characteristics, which are not well specified for the type of data. Therefore, in our proposed algorithm, we decided to set spring connections as constants, with the only parameter being the normalized force.
The experimental findings demonstrated that while this strategy reduces the model’s inclination to oscillation, it also brings additional issues in keeping the model within the camera’s field of view. The forces applied to individual vertices are determined by the nature of the data, and in many cases, vertices subjected to large forces gained so much acceleration that they became disconnected from the rest of the model. This phenomenon can also be seen in 2D environments with algorithms such as Force Atlas 2 []. Another undesirable behavior was the formation of a single huge cluster containing most of the data, making the visualization unreadable and not suitable for immersive needs.
To overcome this issue, in the following iteration we introduced a gravitational force known as an anchor, which maintains the model centered on a single point. The anchor applies the same constant attractive force to each vertex in the model, regardless of the interactions between individual vertices. This method is simple to use, but with an incorrect set constant force, the entire model may end up in a single cluster, as in the second iteration. To address the issue of a single huge cluster, the entire picture was converted into a spherical projection. In this scenario, the sphere serves as a barrier for vertices, guaranteeing that all vertices are at the same distance from the stated anchor. This iteration of our algorithm ensures clear visualization for most datasets while eliminating most of the undesirable occurrences from the first three rounds.
In successive versions in the algorithm’s development, our focus was on eliminating obstacles that hinder the clear viewing of 3D objects, such as the overlapping of vertices or the inadequate representation of data on the sphere. In contrast to 2D space, where the lack of one dimension simplifies the issue of vertex overlap, in 3D, we had to use an alternative method including a constant vertex constraint and dynamic repulsive forces.
When using a constant vertex constraint, each vertex defines its own space, preventing other vertices from approaching within a certain distance to avoid being occluded. However, a problem arises with larger data volumes because vertices may indirectly affect the relationships around them by unnaturally pushing everything away from their center. On the other hand, according to experiments, this approach proved to be effective for smaller volumes, mainly due to computational complexity and implementation simplicity. The second method involves the integration of dynamic repulsive forces, which are active only when vertices approach a defined distance. Each vertex has a distance defined according to its degree, ensuring that vertices with a high degree do not hinder the movement of vertices with a low degree around the sphere. These approaches can be combined, but the condition that dynamic repulsive forces will be active before the vertex approaches the distance defined in the constant constraint must be maintained.
3.5. Datasets
During our experimental work with network visualization, we used publicly available datasets with minimal modifications, which were mostly caused only by customizing for import in the form of a graph. To verify the use of the proposed methods and algorithms, we used a basic, comparative benchmark dataset from previous research [] that is publicly available on the Snap portal of Stanford University []. A general overview of the datasets with their basic characteristics is presented in Table 1. All the datasets are publicly available.

Table 1.
Datasets derived from the original social network Pokec dataset used for algorithm evaluation.
3.6. Evaluation Metrics
Evaluation of 3D visualizations is more complex and requires a specific approach. In 3D visualization, empty space is common and fills most of the resulting space of visualized data. The resulting visualization with no additional constraints can lead into two main unsatisfactory outcomes for visualization:
- A single, unreadable cluster forms within the displayed graph.
- The distance between nodes always increases, without ever reaching a stable state.
When a single cluster emerges, it is due to the sum of attractive forces between nodes vastly outweighing the sum of repulsive forces in the graph. This cluster, comprising most or all graph nodes, becomes illegible due to the obscuration of edges and nodes by other graph elements. Conversely, when node distances continuously increase, or when the sum of repulsive forces exceeds that of attractive forces, the graph fails to reach a stable state in real time, rendering the visualization unusable.
To evaluate the defined algorithms, is necessary to define metrics for comparison. Since the use of the criterion of aesthetics of the resulting visualization is problematic without conducting research on users, we used quantitative criteria following two basic problems of visualization algorithms in 3D space. The first criterion is the average distance of the nodes of the graph in the resulting visualization; the second is the average density of the created clusters. The last monitored parameter is the average distance of the created clusters.
Average vertex distance defines the overall density of a graph. Since both too sparse and too dense a graph represents a problem for the resulting interpretation of the visualization, it is necessary to monitor the average distance of the vertices as a criterion for the quality of the resulting visualization.
Average cluster density tells how close nodes with similar properties are in the final visualization. In the case of a small distance between the nodes in the cluster, the resulting information is difficult to read without interaction with the user in the form of zooming. In the case of excessive zooming, information about the overall context of the visualized subset of data is subsequently lost. On the contrary, in the case of too low a density, the membership of the nodes within the cluster is not obvious.
Finally, average cluster distance works on a similar basis as the distance between vertices, except that it takes groups of vertices into account. Again, the resulting visualization should not lead to an extreme distance between clusters or to their excessive proximity.
4. Results
In the following section, we present the experimental verification of the force-directed immersive 3D graph visualization algorithm based on the principle of force-directed algorithms and needs for immersive visualization. Our approach enables visualization in 3D space, but also integrates immersive representation, normalization, clustering, spring connections, and gravitational interactions to create a robust tool for visualizing complex data networks.
The primary goal is to ensure that edge values in the visualized graph are appropriately normalized, thereby maximizing the interpretability and efficiency of the resulting 3D visualization. Data normalization (min–max normalization) is necessary for parameters used to represent forces and springs, because without normalization spatial complications can occur with vertices on which too much force is applied.
Additionally, we focused on the graph’s edges as an additional source of structural information, including their color, shape, and other features that can be used for edge visualization. Edge coloring can be related to a variety of data-derived features; in our presented version, it is tied to Euclidean distance to improve spatial awareness. Furthermore, this attribute is consistent with the concept of force-directed algorithms in that spatial distance is an internal property of the graph; therefore, no external intervention is required to identify it, and thus the generated algorithm can continue to function in the traditional fashion. In the presented results, the red color indicates a distance of mutual vertices greater than the radius of the resulting visualization (space defined by introduced anchor-controlled placement), the yellow color is used for edges with a mutual distance smaller than the radius and greater than 1/3 of the radius, and the green color is associated with the edges smaller than 1/3 of the radius.
Detailed visualization results can be observed in 3D in captured videos by using the link at the end of this paper.
4.1. Implementation Using Spring Joints: Naïve Implementation
Figure 2 shows the result of the simple spring algorithm in 3D on a randomly generated graph. In the initial experiments, spring connections between nodes that represent attractive forces were tested. At the same time, they also ensure the corresponding repulsive forces, because one of the properties of springs is the contraction of their length. Nodes and edges are generated with random properties such as color and position to remove possible bias caused by any specific dataset.
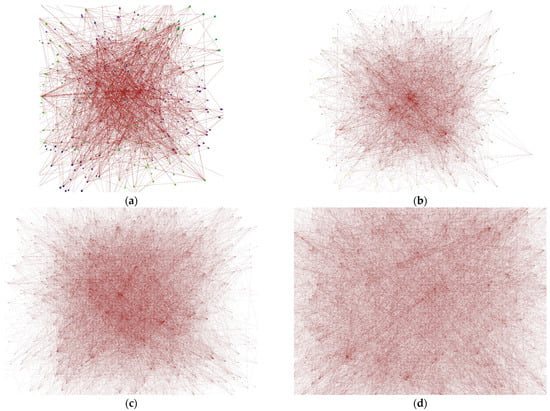
Figure 2.
Results of naïve implementation using spring joints rendered as the default view with no additional user interaction in 3D: (a) Pokec 500 containing 500 vertices and 3084 edges; (b) Pokec 1000 containing 1000 vertices and 6297 edges; (c) Pokec 2000 containing 2000 vertices and 18,313 edges; (d) Pokec 3000 containing 3000 vertices and 29,177 edges.
We used random positions to remove the initial distortion caused by the accumulated force that is applied when the nodes are placed at the beginning of the scene. Additionally, to direct the edges in the graph, nodes are assigned a color that represents their type. Based on the start and end node types, edges are created, and spring joint strength is set. Spring connections allow a quick and sufficiently clear visualization of the graph, while using the correct settings, they control the expansion of the nodes in space. Their disadvantage lies in the limited forces exerted in one direction and the increased load on the computing unit. Each spring joint must be represented by one specific object in the scene, which causes an increased load not only on the physics but also on the rendering engine.
Although this method produces clean, symmetric layouts for medium-sized graphs, it is considered a demanding algorithm. Its time complexity is often high, making the algorithm impractical in many cases. Additionally, it suffers from inadequate predictability, meaning that repeated runs of the algorithm can lead to different results. This can pose challenges in maintaining the user’s mental map during interaction with unstable layouts. Despite these drawbacks, force-directed algorithms are widely used in many visualization frameworks. In our work, the algorithm has been redesigned and optimized to eliminate its characteristic drawbacks, primarily for use in 3D space.
The resulting visualizations show the fundamental flaw of the algorithm, which is the creation of too-dense clusters of vertices, while at the same time the clusters are placed at a large distance from each other, as seen by the color associated with the edges and the results in Table 2. This is a basic identified shortcoming that led to efforts to improve the visualization method used. In the Unity engine, one unit equals one meter in the general physical environment based on the assumptions of most physical systems, including immersive systems and CAVE.

Table 2.
Experimental results for naïve algorithm using spring joints (in units/meters used by Unity engine).
It is important to mention that for a dataset with more than 3000 vertices, the overall execution time is long and resulting visualization is not useful for immersive visualization. As seen, the average distance grows as the number of vertices increases, while visualization in an immersive environment where one abstract unit is equal to one meter becomes problematic due to the average distance of vertices in the order of kilometers.
In practice, a naïve algorithm using spring joints can be used to display social networks, relationships in biological systems, or the structure of the web. The advantage is that this approach to graph visualization can reveal patterns and groups of vertices that might be difficult to see in other forms of visualization. This type of produced visualization also has its use in data analysis and complex system exploration, as its dynamic approach to vertex placement can help reveal structures and relationships that might otherwise remain hidden.
4.2. Modified Fruchterman–Reingold Algorithm for 3D
The proposed modified Fruchterman–Reingold algorithm for 3D creates graphical representations using an emulated physical force system. The main feature of the algorithm implemented on the Fruchterman–Reingold principle is the physical expansion of nodes (repulsion force) and then the application of attraction to reach the final rendered state as in Figure 3. Physical forces enable the creation of clear and understandable node and edge layouts in 3D space without requiring user intervention in the graph assembly process.
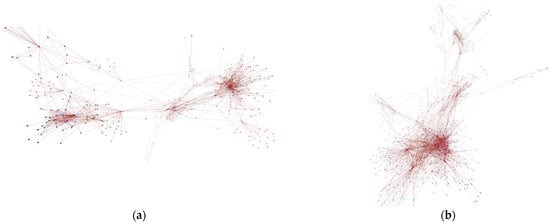
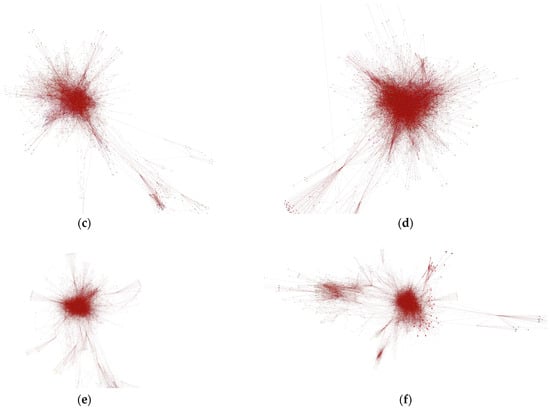
Figure 3.
Results of modified Fruchterman–Reingold algorithm for 3D implementation rendered as the default view with no additional user interaction in 3D: (a) Pokec 500 containing 500 vertices and 3084 edges; (b) Pokec 1000 containing 1000 vertices and 6297 edges; (c) Pokec 2000 containing 2000 vertices and 18,313 edges; (d) Pokec 3000 containing 3000 vertices and 29,177 edges; (e) Pokec 4000 containing 4000 vertices and 41,363 edges; (f) Pokec 5000 containing 5000 vertices and 52,182 edges.
The results of the Fruchterman–Reingold algorithm for 3D are listed in Table 3. In the comparison with the naïve spring algorithm, it is clear that the final visualization needs less space to display results, there is a lower average density of clusters, and there is an even smaller average cluster distance. Thus, it better fits the needs for acceptable immersive 3D visualization. However, there are still some drawbacks and limitations observed.

Table 3.
Modified Fruchterman–Reingold algorithm for 3D experimental results (in units/meters used by Unity engine).
The problem with Fruchterman–Reingold implementation is with vertex separation and the very tight clusters it produces. For more than thousands of vertices, visualization is defined by a small number of large clusters where each cluster is similar to the results for naïve spring implementation. Thus, for immersive visualization, even this approach in 3D is not perfect if observation is necessary within the cluster with high vertex density. Another problem is overall execution time, which is significant for more than one thousand vertices and increases with an increasing number of vertices and edges to be processed.
4.3. Force-Directed Algorithm with Springs and Controlled Placement
By the combination of two previously defined approaches, we were able to achieve a balanced approach where springs and attractive forces collaborate to stabilize the graph, as depicted in Figure 4. The visualization shows how important it is to appropriately adjust the force parameters and springs to achieve an optimal balance between rapid network stabilization and minimizing model clutter. Combining these approaches also prevents the formation of a single large cluster.
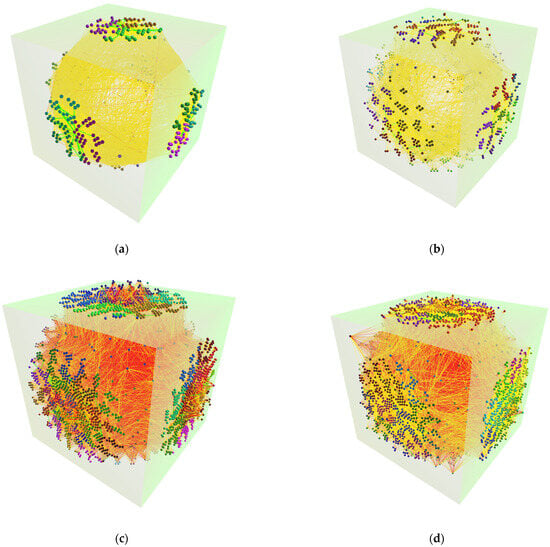
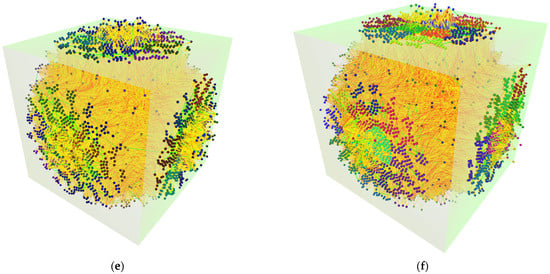
Figure 4.
Results of force-directed algorithm with springs and controlled placement rendered as the default view with no additional user interaction in 3D: (a) Pokec 500 containing 500 vertices and 3084 edges; (b) Pokec 1000 containing 1000 vertices and 6297 edges; (c) Pokec 2000 containing 2000 vertices and 18,313 edges; (d) Pokec 3000 containing 3000 vertices and 29,177 edges; (e) Pokec 4000 containing 4000 vertices and 41,363 edges; (f) Pokec 5000 containing 5000 vertices and 52,182 edges.
The results of the force-directed algorithm with springs and controlled placement rendered as the default view with no additional user interaction in 3D show an increasing density of edges (relations) but an even distribution of vertices on the sides of the projection space defined as the user’s view for an immersive environment for datasets with vertices numbering from 500 to 5000 and respective edges.
To establish the appropriate methodology for setting constraints in 3D space used for immersive layout, a series of measurements focused on detecting limitations and possibilities within the gaming environment were conducted. Recommended limits for the number of gaming objects in one scene were derived from our previous research [] to create a graph while maintaining temporal and computational complexity below the threshold where visualization becomes unusable. Free 3D space network visualization has several disadvantages that must be considered via the construction of limiting conditions. For instance, the emergence of clusters obstructs network clarity because nodes affected by lesser attractive forces or nodes influenced by excessive repulsive forces obstruct the camera view.
The experimental results in Table 4 show the best performance based on the metrics used. Moreover, by using the force-directed algorithm with springs and controlled placement we were able to eliminate drawbacks observed in previous implementations based on springs or a general force-directed approach. The defined algorithm helps users in 3D quickly identify distant and close parts of the graph, as well as areas requiring further attention or analysis.

Table 4.
Experimental results for the force-directed algorithm with springs and controlled placement (in units/meters used by Unity engine).
5. Discussion
Three-dimensional visualization allows users to explore and interact with a network in a three-dimensional space, providing a more comprehensive and intuitive way of working. The main discovery is that not all algorithms designed for two-dimensional space are appropriate for use in a three-dimensional setting and even algorithms available for three dimensions are not good for the visualization of more than one thousand vertices. The greatest obstacle to the advancement of immersive visualization tools for handling large amounts of data is the absence of appropriate algorithms designed for 3D space.
Our experimental results are summarized in Figure 5, where the overall comparison of evaluation metrics is presented.
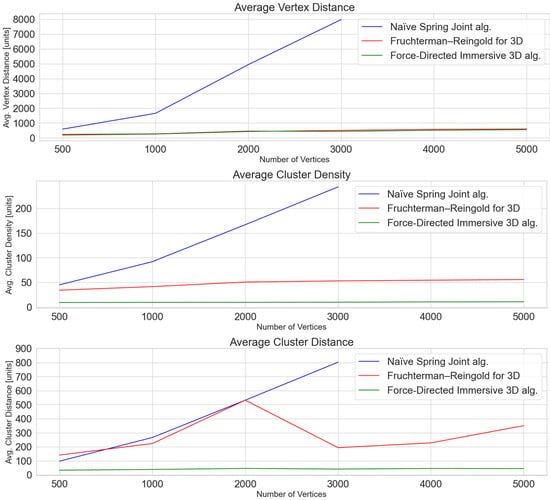
Figure 5.
Evaluation metric results for implemented algorithms.
For the naïve spring joint algorithm, only datasets with a maximum of 3000 vertices were used. For structures with more than 3000 vertices, the overall execution time increased significantly, and more than an hour of computing time was required for the final visualization to be rendered.
The average vertex distance metric shows the tendency of the naïve spring joint algorithm to move vertices far from each other to find a good, non-overlapping final visualization. As can be seen, for more than 1000 vertices, this trend is almost linear. The result is the final average distance in kilometers (1 unit = 1 m), which is not acceptable for the immersive visualization. The other two implementations are placing vertices at average distances of less than one kilometer which puts them in the field of view of the user and is fine for immersive environments.
A similar situation is represented by average cluster density. As shown in the second graph (Figure 5), the tendency of the naïve spring joint algorithm is to form one large and dense cluster. A significant drawback of the resulting visualization is the lack of structure available for intuitive navigation as one of the aspects of good immersive visualization. The other two implementations are similarly acceptable for immersive needs with no significant difference.
Finally, the third metric, average cluster distance, shows the main difference between Fruchterman–Reingold implementation in 3D and our force-directed immersive 3D algorithm. The clusters created for naïve implementation are sparse, and distances between vertices are large. For Fruchterman–Reingold implementation in 3D, it is possible to see the tendency to create one cluster, and with an increased number of vertices (about 2000), to split results into more clusters and dense newly created clusters again. The force-directed immersive 3D algorithm keeps the distance of vertices within the clusters constant and thus allows fulfilling all needs for good immersive visualization with the user involved inside the created space (between the clusters) with consistent physics and intuitive navigation (motion-oriented approach).
The specific visual results are presented in Figure 6. Figure 6a shows the comparison of our force-directed algorithm with the Fruchterman–Reingold 3D algorithm, and Figure 6b with the naïve spring joint algorithm. It is clear that our algorithm, shown as the cube placed on the initial coordinates of the rendering space for both visualization algorithms shown in red, renders data in a smaller 3D space, and thus the immersive projection is more natural than the potential projections of Fruchterman–Reingold or naïve spring joints. A specific situation is seen with our algorithm and naïve spring joint implementation, which produces an almost random graph visualization layout.
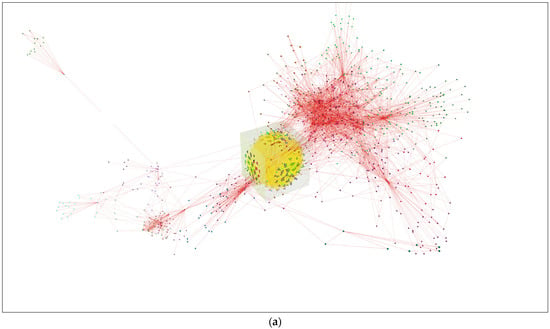
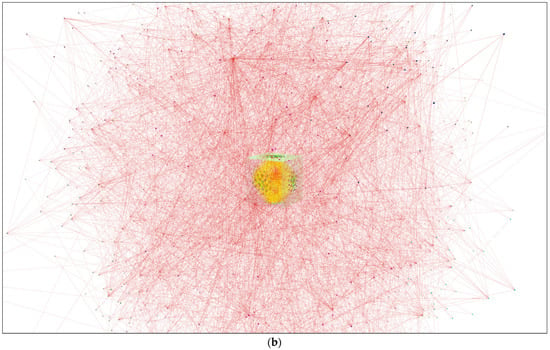
Figure 6.
Results of force-directed algorithm with springs and controlled placement for Pokec 1000 dataset containing 1000 vertices and 6297 edges in comparison with (a) Fruchterman–Reingold modification for 3D and (b) naïve spring joint algorithm.
For better understanding, since the final implementation of our force-directed algorithm with springs and controlled placement is in 3D and an immersive environment, the link in the Supplementary Materials section at the bottom of this article can be followed to find videos with the final 3D-rendered visualizations.
Within the experimental results, we observed a number of drawbacks and limitations of 3D visualization approaches based on well-developed 2D graph visualization methods. As presented, some of the main shortcomings can be eliminated by techniques inherent in physical game environments such as Unity, but others require the application of new methods based on heuristic procedures and methods.
An important factor is time complexity, which is high for the force-directed algorithms []. We defined the algorithm for high resolution, 4K with antialiasing (2x multisampling), due to the non-trivial display area consisting of several display areas of CAVE.
Table 5 summarizes the overall times necessary for rendering the initial view in minutes. As seen, algorithms originating in 2D, the naïve spring joint algorithm and Fruchterman–Reingold 3D adaptation, are very time-consuming for datasets with more than hundreds of vertices and associated edges.

Table 5.
Execution times of different implementations in 3D for initial visualization rendering (in minutes).
In general, time complexity exceeds where is the total number of vertices [,,]. This was identified as the main problem with the naïve spring joint implementation and even the Fruchterman–Reingold adaptation in 3D. Nevertheless, some new approaches based on parallel execution are available as concepts for application.
6. Conclusions
We introduced a new force-directed algorithm with springs and controlled placement for immersive data visualization in 3D. The graph, as a representation of connected data, is a very useful structure, since it can gain an advantage by graph theory and methods, but producing a nice and readable visualization is always a difficult task which requires advanced user interaction. Using 3D space, we were able to visualize data with the help of the Unity engine, namely its implementation of a physical environment, and create immersive interactive visualizations suitable for CAVE and VR environments with the drawbacks of basic force-directed implementations eliminated.
In the process of gradual implementation of principles for visualization of networks in 3D, we implemented a simple spring algorithm, a modification of the Fruchterman–Reingold algorithm and our own implementation of a force-directed algorithm with spring joints and controlled placement. The experimental evaluation shows acceptable results for all algorithms for networks of up to 1000 vertices, but significant drop-offs in both quality and performance for the first two algorithms were observed when dealing with thousands of vertices. Our implementation of a force-directed algorithm with controlled placement, on the other hand, keeps distances in the visualized network in an acceptable range for immersive visualization needs.
Future development will be focused on implementation for larger datasets and the development of extensive visual analytics features into the application for 3D visual data exploration. As can be seen, even simple implementations of the force-directed principle and spring embedders show potential for further development and modifications, which we are using in 3D visualization in preparation for domain-specific data.
Supplementary Materials
The following supporting information can be downloaded at https://github.com/AllexB1/ForViz3D_datasets/ (accessed on 2 July 2024) (videos showing 3D results of presented algorithms).
Author Contributions
Conceptualization, A.B. and M.Z.; methodology, A.B. and J.K.; software, A.B.; resources, A.B.; writing—original draft preparation, A.B.; writing—review and editing, J.K.; visualization, A.B.; supervision, M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the research grant VEGA 1/0654/22: Cost-effective design of combined charging infrastructure and efficient operation of electric vehicles in public transport in sustainable cities and regions.
Data Availability Statement
The datasets mentioned in this article are available at https://github.com/AllexB1/ForViz3D_datasets/ (accessed on 2 July 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Keim, D.A.; Mansmann, F.; Schneidewind, J.; Thomas, J.; Ziegler, H. Visual Analytics: Scope and Challenges. In Visual Data Mining; Simoff, S.J., Böhlen, M.H., Mazeika, A., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 4404, pp. 76–90. ISBN 978-3-540-71079-0. [Google Scholar]
- Zhang, Y.; Wang, Z.; Zhang, J.; Shan, G.; Tian, D. A Survey of Immersive Visualization: Focus on Perception and Interaction. Vis. Inform. 2023, 7, 22–35. [Google Scholar] [CrossRef]
- Anouncia, S.M.; Gohel, H.A.; Subbiah, V. Data Visualization: Trends and Challenges toward Multidisciplinary Perception, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2020; ISBN 978-981-15-2281-9. [Google Scholar]
- Schmidt, J. Visual Data Science. In Data Science, Data Visualization, and Digital Twins; Shirowzhan, S., Ed.; IntechOpen: Rijeka, Croatia, 2022; ISBN 978-1-83962-944-0. [Google Scholar]
- Vuckovic, M.; Schmidt, J.; Ortner, T.; Cornel, D. Combining 2D and 3D Visualization with Visual Analytics in the Environmental Domain. Information 2022, 13, 7. [Google Scholar] [CrossRef]
- Fisher, B.D. Visual Representations and Interactions Technologies. In Illuminating the Path: A Research and Development Agenda for Visual Analytics; Thomas, J., Cook, K., Eds.; IEEE Press: Piscataway Township, NJ, USA, 2005; pp. 69–104. [Google Scholar]
- Amini, F.; Rufiange, S.; Hossain, Z.; Ventura, Q.; Irani, P.; McGuffin, M.J. The Impact of Interactivity on Comprehending 2D and 3D Visualizations of Movement Data. IEEE Trans. Vis. Comput. Graph. 2015, 21, 122–135. [Google Scholar] [CrossRef] [PubMed]
- Elmqvist, N.; Tsigas, P. A Taxonomy of 3d Occlusion Management for Visualization. IEEE Trans. Vis. Comput. Graph. 2008, 14, 1095–1109. [Google Scholar] [CrossRef] [PubMed]
- Bleisch, S.; Nebiker, S. Connected 2D and 3D Visualizations for the Interactive Exploration of Spatial Information. In Proceedings of the The International Archives of Photogrammetry, Remote Sensing and Spatial Information Science, Beijing, China, 3–11 July 2008; Volume XXXVII. Part B2. [Google Scholar]
- Manjrekar, S.; Sandilya, S.; Bhosale, D.; Kanchi, S.; Pitkar, A.; Gondhalekar, M. CAVE: An Emerging Immersive Technology—A Review. In Proceedings of the 2014 UKSim-AMSS 16th International Conference on Computer Modelling and Simulation, Cambridge, UK, 26–28 March 2014; IEEE: Cambridge, UK, 2014; pp. 131–136. [Google Scholar]
- Kobourov, S.G. Force-Directed Drawing Algorithms. In Handbook of Graph Drawing and Visualization; Tamassia, R., Ed.; CRC Press: Boca Raton, FL, USA, 2013; pp. 383–408. [Google Scholar]
- Battista, G.; Eades, P.; Tamassia, R.; Tollis, I. Graph Drawing; Prentice Hall: Englewood Cliffs, NJ, USA, 1999. [Google Scholar]
- Brandes, U. Drawing on Physical Analogies. In Drawing Graphs: Methods and Models; Kaufmann, M., Wagner, D., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2001; Volume 2025, pp. 71–86. ISBN 978-3-540-42062-0. [Google Scholar]
- Tutte, W.T. How to Draw a Graph. Proc. Lond. Math. Soc. 1963, 13, 743–767. [Google Scholar] [CrossRef]
- Eades, P. A Heuristic for Graph Drawing; Congressus Numerantium: Winnipeg, MB, Canada, 1984; Volume 42. [Google Scholar]
- Fruchterman, T.M.; Reingold, E.M. Graph Drawing by Force-Directed Placement. J. Softw. Pract. Exp. 1991, 21, 1129–1164. [Google Scholar] [CrossRef]
- Kawai, S.; Kamada, T. An Algorithm for Drawing General Undirected Graphs. Inf. Process. Lett. 1989, 31, 7–15. [Google Scholar] [CrossRef]
- Cohen, R.F.; Eades, P.; Lin, T.; Ruskey, F. Three-Dimensional Graph Drawing. Algorithmica 1997, 17, 199–208. [Google Scholar] [CrossRef]
- Gajer, P.; Goodrich, M.T.; Kobourov, S.G. A Fast MultiDimensional Algorithm for Drawing Large Graphs? In Proceedings of the 8th International Symposium Graph Drawing, Colonial Williamsburg, VA, USA, 20–23 September 2000; pp. 211–221. [Google Scholar]
- Lu, J.; Si, Y.W. Clustering-Based Force-Directed Algorithms for 3D Graph Visualization. J. Supercomput. 2020, 76, 9654–9715. [Google Scholar] [CrossRef]
- Spritzer, A.; Freitas, C. Navigation and Interaction in Graph Visualizations. Rev. Informática Teórica Apl. 2008, 15, 111–136. [Google Scholar] [CrossRef]
- Cytoscape. Available online: https://cytoscape.org (accessed on 24 April 2024).
- Pajek. Available online: http://vlado.fmf.uni-lj.si/pub/networks/pajek/ (accessed on 24 April 2024).
- Unity Technologies Unity Engine. Available online: https://unity.com/products/unity-engine (accessed on 17 April 2024).
- Unity Technologies Unity Manual: Joints. Available online: https://docs.unity3d.com/2023.2/Documentation/Manual/joints-section.html (accessed on 17 April 2024).
- Jacomy, M.; Venturini, T.; Heymann, S.; Bastian, M. ForceAtlas2, a Continuous Graph Layout Algorithm for Handy Network Visualization Designed for the Gephi Software. PLoS ONE 2014, 9, e98679. [Google Scholar] [CrossRef] [PubMed]
- Takac, L.; Zabovsky, M. Data Analysis in Public Social Networks. In Proceedings of the International Scientific Conference & International Workshop Present Day Trends of Innovations, Lomza, Poland, 28–29 May 2012. [Google Scholar]
- Leskovec, J. Stanford Network Analysis Project. Available online: http://snap.stanford.edu (accessed on 17 April 2024).
- Brezani, A.; Zabovsky, M. 3D Graph Visualization Performance Using Physical Engine. Int. J. Inf. Technol. Eng. Manag. Sci. 2022, 6, 1–4. [Google Scholar]
- Tarawaneh, R.M.; Keller, P.; Ebert, A. A General Introduction To Graph Visualization Techniques. In Visualization of Large and Unstructured Data Sets: Applications in Geospatial Planning, Modeling and Engineering—Proceedings of IRTG 1131 Workshop 2011 (VLUDS 2011); Leibniz-Zentrum für Informatik: Wadern, Germany, 2013; Volume 27, pp. 151–164. [Google Scholar] [CrossRef]
- Tollis, I.G.; Di Battista, G.; Eades, P.; Tamassia, R. Graph Drawing: Algorithms for the Visualization of Graphs; Pearson: Englewood Cliffs, NJ, USA, 1998; ISBN 978-0-13-301615-4. [Google Scholar]
- Kaufmann, M.; Wagner, D. (Eds.) Drawing Graphs: Methods and Models; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2001; Volume 2025, ISBN 978-3-540-42062-0. [Google Scholar]
- Herman, I.; Melancon, G.; Marshall, M.S. Graph Visualization and Navigation in Information Visualization: A Survey. IEEE Trans. Vis. Comput. Graph. 2000, 6, 24–43. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).