Abstract
The distinguishing feature of hash-based algorithms is their high confidence in security. When designing electronic signature schemes, proofs of security reduction to certain properties of cryptographic hash functions are used. This means that if the scheme is compromised, then one of these properties will be violated. It is important to note that the properties of cryptographic hash functions have been studied for many years, but if a specific hash function used in a protocol turns out to be insecure, it can simply be replaced with another one while keeping the overall construction unchanged. This article describes a new post-quantum signature algorithm, Syrga-1, based on a hash function. This algorithm is designed to sign r messages with a single secret key. One of the key primitives of the signature algorithm is a cryptographic hash function. The proposed algorithm uses the HAS01 hashing algorithm developed by researchers from the Information Security Laboratory of the Institute of Information and Computational Technologies. The security and efficiency of the specified hash algorithm have been demonstrated in other articles by its authors. Hash-based signature schemes are attractive as post-quantum signature schemes because their security can be quantified, and their security has been proven.
1. Introduction
Confidential communications, financial transactions, and critical infrastructures—all of these are at risk if encryption can be broken. Active research on quantum computing is currently underway worldwide. Creating a computer that implements the quantum model of computation will have negative consequences for a range of cryptographic mechanisms. These computers promise significant advantages for information technology, especially in combination with artificial intelligence. However, quantum computers can also be turned into unprecedented surveillance machines, leading to a race between quantum computers and quantum-resistant cryptography.
As is well known, cryptographic schemes can be divided into symmetric and asymmetric types. In symmetric schemes, encryption and decryption keys are the same, while in asymmetric ciphers, encryption and decryption keys differ, but are linked by some mathematical function. The most common modern asymmetric cryptographic schemes are based on complex problems, such as factoring large natural numbers (e.g., the RSA algorithm), discrete logarithms in finite fields (DSA, DH, GOST R 34.10-94), and discrete logarithms in the group of points on elliptic curves (ECDSA, ECDH, GOST R 34.10-2012) [1,2].
When parameters for cryptographic schemes are correctly chosen, their compromise is considered infeasible for the foreseeable future. Quantum computers use fundamentally different techniques that can significantly speed up the solution to certain computational problems with specialized quantum algorithms. However, a breakthrough in the field of symmetric cryptography is not expected, as currently known quantum algorithms for analyzing hash functions and block ciphers (e.g., the Ambainis method for collision search and Grover’s algorithm for preimage search) still have exponential complexity, although it is smaller than that of classical algorithms.
Post-quantum algorithms currently work successfully on classical computers. Thus, it is possible to implement quantum-resistant algorithms now and thereby protect critical data for decades to come. It is understood that transitioning to quantum-resistant cryptography is reasonable in cases where the value of the protected information exceeds the cost of its protection [3,4].
In 2016, the National Institute of Standards and Technology (NIST) in the United States initiated a project to evaluate and standardize one or more post-quantum public key algorithms. The call for submissions continued until 2018. After the first round of evaluation, 69 candidates continued to participate in the competition, and after the second round, 26 candidates remained. It is planned that NIST will present the first post-quantum secure standard project by 2025.
It is important to understand that transitioning to post-quantum algorithms immediately after the adoption of standards will not be possible. Significant preparatory work will be required. New keys may be somewhat larger, and the infrastructure must be designed to transfer them without sacrificing the accustomed communication speed.
Several primary cryptographic systems are considered quantum-resistant: hash-based cryptography, code-based cryptography, matrix-based cryptography, cryptography based on multidimensional quadratic systems, and secret key cryptography. It is believed that all these schemes can withstand classical and quantum attacks when sufficiently long keys are used [5,6].
Among these systems, electronic signature schemes based on cryptographic hash functions are considered. In such schemes, the following approach is used: the foundation is a one-time signature scheme (where only one message can be signed), which is then combined with a Merkle tree to obtain a multi-time signature. Various patterns of this approach are possible to achieve greater efficiency. Algorithms in this direction are applied to generate and verify digital signatures and use only a cryptographically strong hash function [7,8].
2. Related Works
Cryptosystems based on hash functions offer a promising direction for post-quantum cryptography. These cryptosystems have the unique characteristic of a limited number of signatures that can be generated using a single key. The initial algorithms in this class allowed only one message to be signed, which led to their limited popularity. To overcome this limitation, hash trees based on one-time signatures were proposed, followed by hypertrees composed of hash trees.
The article [9] extensively discusses global efforts in the design, development, and standardization of various quantum-secure cryptographic algorithms as well as the performance analysis of some potential quantum-secure algorithms. Most quantum-secure algorithms require more processor cycles, increased memory usage, and larger key sizes. The feasibility of various quantum-secure cryptographic algorithms is also analyzed.
NIST has selected the first group of encryption tools designed to withstand attacks from future quantum computers. In the work [10], it is demonstrated that three of the chosen NIST algorithms, namely CRYSTALS-Khyber, CRYSTALS-Dilithium, and FALCON, utilize lattice-based cryptography, while SPHINCS+ employs hash functions. NIST advises security professionals to study the new algorithms and consider their application in their systems, but refrain from integrating them, as the standard is still in the development stage.
Considering the relevance of public key cryptography and the increasing threat it faces from quantum computers, it is essential to develop practical and secure post-quantum cryptography. The article [11] aims to study the impact of quantum computing on modern cryptography, provide a brief overview of key post-quantum algorithms, describe the differences between quantum and classical computing, and explore key quantum algorithms, such as Shor’s and Grover’s algorithms. The section on “Post-Quantum Cryptography” is dedicated to various methods of quantum key distribution and mathematical solutions.
In the work [12], information about the current state and significant challenges in post-quantum cryptography is presented, along with discussions on transitioning real systems to new technologies. Examples of one-time signatures include the Lamport and Winternitz signatures. It is worth noting that when using the Winternitz signature, the public key is significantly shorter. In the article [13], a new post-quantum digital signature scheme designed for cryptocurrencies is proposed. This scheme is based on a hash-based signature scheme that is a variant of the Winternitz one-time signature. The distinctive feature of this approach is that, unlike previously proposed variants, it avoids the need for computationally expensive operations.
The work [14] presents a highly secure post-quantum hash-based signature scheme without state retention, capable of signing hundreds of messages per second on a modern 4-core Intel processor with a frequency of 3.5 GHz. The signatures are 41 KB in size, public keys are 1 KB, and private keys are 1 KB. This signature scheme is designed to provide long-term security, even against adversaries equipped with quantum computers. Unlike most hash-based projects, this signature scheme does not maintain state, which allows it to replace current signature schemes.
In the article [15], it is demonstrated that the Winternitz one-time signature scheme is resistant to forgery under attacks with adaptive message selection when implemented using a family of pseudorandom functions. It also discusses security in a strict sense. Several security concepts based on keys for function families are formally defined in the work, and their relationship with pseudorandomness is investigated. In the article [16], it is proposed to replace the hash function in the standard Merkle scheme with a lattice-based hash function and use a lattice-based one-way function as a replacement for the one-way function.
In [17], several stateless optimizations for SPHINCS proposed by Bernstein et al. are presented. Based on a detailed analysis of the subset-resilience problem, the authors demonstrate that algorithm parameters can be adjusted to reduce the signature size while maintaining a similar level of security and computation time. SPHINCS is a stateless hash-based signature scheme that represents the HORST one-time signature scheme, which is an improvement over HORS. The article [18] proposes an algorithm called HORSIC+, which is an improvement over HORSIC. HORSIC+ uses a chain function similar to W-OTS+ [19]. This provides strict security without the need for the function family used to resist permutations or collisions. The authors claim that HORSIC+ cannot be forged under chosen message attacks, assuming a second preimage-resistant family of indistinguishable one-way functions and cryptographic hash functions in a random oracle model.
3. Materials and Methods
3.1. Cryptographic Hash Functions
To construct a secure one-time signature scheme, only a one-way function is required. As Rompel demonstrated, the existence of a one-way function is a necessary and sufficient condition for ensuring the security of digital signatures. Thus, one-time signature schemes can be considered the foundation of digital signature schemes.
One of the primary directions in the synthesis of quantum-resistant, or post-quantum, cryptographic schemes is the use of cryptographic hash functions. These functions are employed in all digital signature schemes. Therefore, the security of such schemes directly depends on the collision resistance of the hash function.
A hash function is a deterministic function that takes a binary string of arbitrary length as input and produces a fixed-length binary string of length n as output. Hash functions are used as building blocks in many applications.
Let us provide a formal definition of a hash function. Let be the set of all binary strings of length m, and be the set of all finite-length binary strings. Then, a hash function h is a transformation of the form
where m is the length of the hash output.
There are various approaches to constructing cryptographic hash functions today. Among them, the “sponge construction” stands out, meeting a broad spectrum of security requirements.
This construction was developed by a group of cryptographers led by John Daemen to replace the outdated Merkle–Damgård construction. It was first introduced in 2007 at the ECRYPT symposium and represents a mapping of variable-length input data to output data of variable length as well. The transformation f operates with a fixed number of bits b = r + c, where r is called the bitrate and c is the capacity. At the initial stage, similar to the Merkle–Damgård construction, the input data is extended according to a specified algorithm, after which it is divided into blocks of r bits. Next, b bits of state are initialized to zeros.
The construction includes two phases. In the first phase (“absorption”), r-bit blocks of the message are summed (XOR operation) with the first r bits of the internal state—the result of transformation f. When this operation is done for all message blocks, the phase concludes.
Next, in the “squeezing” phase, the first r bits of the internal state are returned as output blocks of f. This action is repeated until the desired length of the hash sum is obtained.
3.2. Primary Methods of Cryptanalysis of One-Way Hash Functions
Brute force attack. Having the hash value of a message , the cryptanalyst must, through trial and error, find a message for which (then the analyst can claim that the presented hash corresponds to the message , not ). If the hash function produces an n-bit output, the complexity of this method is .
The attack, based on a known statistical problem—the “birthday paradox”—is a universal method for finding collisions in hash functions.
We reduce the task of cryptanalysis of hash functions to the problem of finding collisions: how many messages need to be inspected to find messages with the same hashes? The probability of encountering identical hashes for messages from two different sets containing and texts is approximately . If = , then the success probability of the attack is , and the complexity of the attack is operations.
The avalanche effect is a property of block ciphers and cryptographic hash function algorithms, where even a slight change in input data should result in a significant change in most output data. This property is often a requirement in cryptography. For the avalanche criterion, the avalanche parameter value is determined by the formula
where i is the number of the changed bit in the input sequence and is the probability of changing half of the bits in the output when the ith bit is changed in the input.
3.3. The Main Properties of the Post-Quantum Signature Scheme
A distinctive characteristic of hash-function-based algorithms is the high confidence that developers place in their security. When constructing electronic signature schemes, proofs of security reduction to specific properties of cryptographic hash functions are employed. This implies that if the scheme were to be compromised, one of these properties would be violated. It is crucial to note that the properties of cryptographic hash functions have been studied for many years. However, if the hash function used in a specific protocol is found to be insecure, it would suffice to replace it with another, while the overall structure remains unchanged [20].
As of now, no information is available regarding quantum algorithms that could effectively be employed to generate collisions or find preimages for first and second preimage attacks.
The best results in the analysis of hash functions are as follows: Grover’s algorithm reduces the complexity of the preimage search procedure from to . Brassard’s algorithm decreases the complexity of the collision search procedure from to .
The signature size in post-quantum algorithms refers to the number of bits or bytes required to represent the digital signature generated by a specific algorithm. Various mathematical methods and data structures, such as hash functions, cryptographic lattices, and others, are used in the creation of signatures. The signature size in such schemes may be comparable to or exceed the sizes of signatures in classical cryptographic schemes. Factors influencing signature size in post-quantum schemes include the type and characteristics of the algorithm, the required level of security and performance, and the chosen parameters, among others.
Post-quantum signature schemes have unique security parameters associated with protection against quantum attacks. The security level “b” for specific post-quantum schemes depends on various factors, including the choice of scheme parameters, vulnerability analysis, theoretical attacks on the scheme, research in quantum algorithms, and more. The security level “b” is typically expressed in bits (b-bit), and one standard for its assessment in post-quantum cryptography is the approximate equivalence with classical algorithms in terms of the bit security level. For instance, if a post-quantum signature scheme has a 128-bit security level, breaking this scheme would require computational resources equivalent to breaking a classical cryptography algorithm providing a 128-bit security level.
4. Results
The scientific novelty of the developed algorithm lies in its ability to sequentially hash the original set of secret keys, leading to the generation of an intermediate set of secret keys. This intermediate set enables the one-time signing of multiple messages. Another distinctive feature of the algorithm is its relatively small signature size and low implementation time, which are attributed to the absence of an authentication path, a characteristic present in some algorithms utilizing Merkle trees.
In more formal terminology, an intermediate set of one-time keys is created through the sequential hashing of the original set of secret keys. This set is considered as the ith set of secret keys, where , and the final result of the sequential hashing, i.e., the rth result, is accepted as the public key. Consequently, the pair comprising the ith set of secret keys and the set of public keys is used to authenticate the ith message.
4.1. Development of a New Post-Quantum Multi-Signature Algorithm Syrga-1
In this section, we provide a detailed description of the new post-quantum signature algorithm, Syrga-1, which is based on hash functions. This algorithm is designed for signing r messages using a single secret key. To overcome the limitation of having one secret key for one signed message, r-fold hashing of the original secret key is used. In other words, each subsequent hashing of the secret key results in new one-time secret keys. One crucial property of a hash function is its one-wayness or irreversibility—the practical impossibility of finding the hash preimage. This property of the hash function plays a vital role in structuring the multi-use of the same secret key . Here, it is evident that the secret key SK consists of t component subkeys , where . The algorithm uses G—a pseudorandom number generator (PRG)—which is employed to generate a set of secret signing subkeys as needed. The parameter r determines the number of hash operations on the secret key SK using the hash function , i.e., r-fold hashing of SK. For clarity, q-fold hashing of the secret key SK using the function will be denoted as , where 0. The results of the qth intermediate hashing of the secret key SK are taken individually as one-time secret signing keys and will be further used for signing subsequent messages. It is important to note that the result of the final hashing of SK is taken as the public signing key and is denoted as where =, . Thus, in the key generation section, using the results of intermediate hashing and , a key pair KG: is formed for signing messages, where 0 .
An essential condition for using intermediate secret keys is their reverse order of usage. In other words, for signing and verifying the first message, the key pair is used, for the second message—, and so on. For the ()th message—. The signing process involves a counter q, where , , which determines the sequential number of the message being signed. This formulation is illustrated in Figure 1.
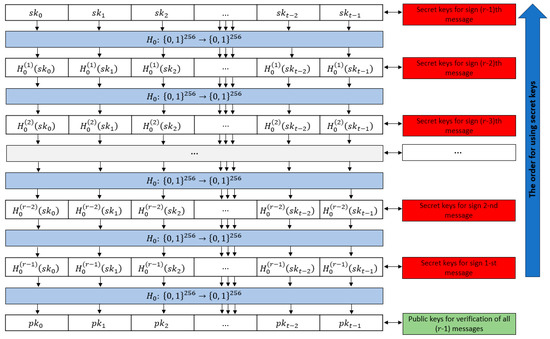
Figure 1.
Scheme for generating intermediate secret keys from the public key and the order of their use.
Additionally, the algorithm can make use of another property of the hash function—transforming messages of arbitrary length into a predefined fixed length, which is the length of the hash code. This property can be applied when generating the original secret key SK to optimize or minimize the size of the secret key. However, in the proposed algorithm, the length of the secret subkey is fixed and equal to 256 bits, where .
In the algorithm, the message to be signed, , is processed by the hash function . is considered to be the HAS01 hashing algorithm developed by the Information Security Laboratory of the Institute of Information and Computational Technologies. The scheme and key characteristics of the algorithm are briefly described in the following sections.
In Table 1, data on the key characteristics of the developed post-quantum signature algorithm based on hash functions are presented.

Table 1.
Parameters of the Syrga-1 signature algorithm.
In brief, the Syrga-1 algorithm can be summarized with respect to the technological stages of signing a message as follows:
- I.
- Key Generation (action by the sender):
- (1)
- Generate a set of secret subkeys using PRG—G:
- (2)
- Compute a set of public keys:
In this way, a pair of public and private keys KG is created. The public key PK is then distributed to the recipients.
- II.
- Message Signing Algorithm (action by the sender):
- Given the hashable message , where
- (1)
- Calculate the hash value .
- (2)
- Divide into 32 parts , each of length bits.
- (3)
- Interpret each as an integer ,
- (4)
- Calculate , , and determine .
- (5)
- Form the signature sign: . The sender sends to the recipient.
- III.
- Message Signature Verification Algorithm (action by the recipient):
- The recipient has a set of public keys PK and the hash algorithm .
- The verification algorithm is carried out as follows:
- (1)
- The recipient receives .
- (2)
- Calculate the hash value .
- (3)
- Divide into 32 parts , each of length bits.
- (4)
- Interpret each as an integer ,
- (5)
- Calculate ,
- (6)
- Check the following condition: If for all , where , is true, then it is asserted that the signature of the message is valid; otherwise, it is not.
4.2. Hashing Algorithm HAS01
The algorithm HAS01 is based on the “sponge” construction. A sponge function is a simple iterative construction with variable-length input and arbitrary-length output based on a transformation function denoted as f, which operates on a fixed number of bits, referred to as b, where b is called the width. The sponge construction operates on a state consisting of bits, where is the bitrate and c is the capacity of the sponge. The sponge function has two phases—absorbing and squeezing [21,22].
HAS01 transforms input plaintext of arbitrary length, consisting of 192-bit blocks, into a hash value of 256 or 512 bits. The hash value is represented as a byte sequence . For the Syrga-1 algorithm, we consider the variant where , making the hash value size 256 bits. A full mathematical description of the HAS01 hashing algorithm, as well as its security and efficiency analysis, can be found in references [23,24], where it is demonstrated to meet all the properties and requirements expected of hash functions, showing excellent performance in all aspects.
The structure of the input and output data for the HAS01 hashing algorithm is as follows:
- -
- Input data block has a size of 24 bytes and can be represented as a 24-byte sequence or as a matrix of size [3 × 8].
- -
- The external hash state has the same size as the input data block (24 bytes) and can be represented as a matrix of size [3 × 8].
- -
- The internal hash state has a size of 40 bytes and can be represented as a matrix of size [5 × 8].
- -
- Thus, the complete hash state is the combination of the external and internal states, i.e., , and can be represented as a matrix of size [8 × 8].
The main difference between HAS01 and the classical “sponge” structure is that during the absorbing phase, the function f, which is part of the F function, is called more than once (Figure 2). Additionally, when forming the hash value , each element of the sequence is obtained by copying a specific column from the current hash state matrix that has been formed up to that point.
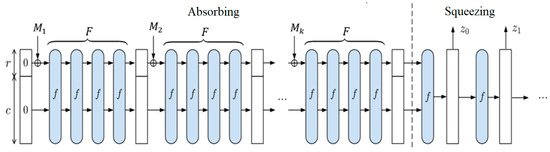
Figure 2.
Sponge construction used by the HAS01 hash algorithm —input, —hashed output.
The function : [8 × 8] → [8 × 8] transforms a 64-byte matrix A of size [8 × 8], containing the current hash state, into a 64-byte matrix of size [8 × 8], which contains the new hash state. The function f is a composition of functions , , and : , where the function performs a non-linear transformation of the matrix, the function transposes the matrix, and the function transforms the matrix by rows.
During the squeezing phase, the elements of the hash value are generated for . When , the size of the hash value is 256 bits. In each iteration of the squeezing phase, the elements are obtained by copying the sixth column of the current hash state matrix if the hash size is 256 bits, and by copying the fourth column if the hash size is 512 bits. Therefore, when the hash value length is 256 bits, the squeezing phase will consist of four iterations.
5. Discussion
5.1. Statistical Properties of HAS01 Hash Function
Digital signatures based on hash functions are a promising direction in post-quantum cryptography. The security of quantum-resistant cryptographic algorithms in this category is based on the properties of cryptographic hash functions. Among these properties, we can highlight resistance to preimage attacks, collisions, and second preimage attacks. Research has been conducted to study the resistance of the HAS01 hash functions.
The avalanche effect of the HAS01 hash algorithm for the F-function is shown in Figure 3. 512-bit blocks are chosen as inputs to the F-function, each of which differs from the first one in only one bit (with all bits being different). The probability of matching corresponding bits of the encrypted text when transforming (encrypting) these blocks using the F-function falls between 0.4277 and 0.5722. Therefore, the bit spread of the F-function indicates that this function satisfies the avalanche effect criterion.
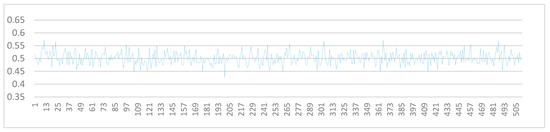
Figure 3.
Avalanche effect diagram of the F-Function.
Using the birthday paradox, the method of brute force estimates the occurrence of at least one collision in an attack as having a probability of 0.5, with a search space of for 256-bit hash values and for 512-bit hash values.
When searching for collisions, it is necessary to identify weak points in the algorithm and thus help avoid brute force. One such weak point in the algorithm under consideration is the function . The functions and perform permutations of bytes and bits, so attacking them with collision search methods does not pose a threat. The only weak point in the F-function is the nonlinear function because the input to the S-box is the sum of values modulo 2. If different values result in the same sum, the S-box will produce the same output. Therefore, one needs to check all inputs to the F-function that yield the same sum in the function. This means that it is necessary to check only those elements that are located at a distance from each other equal to the length of a matrix row. Let us check the hash values of two texts in hexadecimal format.
First text:
Second text:
The hash values for the two texts are as follows:
256-bit hash value for the first text: 4b d2 de fd 01 1f 52 a9 8e 46 16 83 4c 07 2b 4c 28 43 f5 27 df 34 bc a9 da 58 45 0b 63 88 eb ad
256-bit hash value for the second text: 46 df 0f 4d a0 3d cf c4 ea d2 59 d9 46 ae 7b bc 77 3e 8e 67 f6 5a d4 d5 f1 60 f9 4a f0 c1 00 65
512-bit hash value for the first text: 3f e0 ef 8a a9 6f 80 bf d0 49 3f 7a 7d f1 84 fb 98 b4 87 42 e4 65 7b a6 2e 7c 71 7 19 78 fc 6 25 bf 5c ae 8c 63 49 b2 82 7f 1c 38 b9 e6 80 38 6e 59 6d 7a f3 44 68 d6 e0 23 99 ce 42 e3 df 74
512-bit hash value for the second text: f6 a8 51 d9 80 be 62 66 3c 0a ae 10 b8 c3 7e 3e 42 35 ae 66 2f 26 16 81 90 10 4a fd 38 66 a9 3c 31 c6 7c d4 4b be 88 eb bf c0 61 cf 89 67 80 83 c0 49 e7 e7 e5 ef db e8 00 cd 05 13 1b 63 d7 55
It is necessary to check all such cases for the occurrence of collisions. If this check does not yield a result, then the probability of collisions occurring corresponds to the probability of an exhaustive search, the value of which was provided above.
First of all, we examined all 512 positions with a one-bit shift at the input of the function based on bitwise diffusion (avalanche effect). As a result, we found that they produce different values, so the input to function does not lead to collisions.
5.2. Security Level of Syrga-1
Table 2 presents comparative data on classical and quantum security levels regarding the length of hash values and types of attacks. The HAS01 algorithm is designed for computing hash values with lengths of 256 and 512 bits. From the table, it can be observed that the hash value computed by HAS01 currently provides the required level of data security.

Table 2.
Hash function security levels [13,25].
Table 3 provides comparative data on the types of keys and signatures for well-known post-quantum digital signature schemes and the proposed Syrga-1 scheme.

Table 3.
A comparative summary of the hash-based signature scheme.
From Table 3, it is evident that the developed Syrga-1 scheme requires the use of a long key but generates a minimal signature size compared to similar schemes. Since the designed scheme allows for the use of the public key r times, this can be considered one of the advantages of this scheme.
Table 4 presents a comparative analysis of the security level of the developed Syrga-1 signature algorithm with other post-quantum signature schemes, indicating the calculation formula and parameters.

Table 4.
The security level of some post-quantum signature schemes.
Table 4 displays the security levels of the Syrga-1 signature scheme compared to other commonly used signature schemes. From the table, it can be observed that the security level for Syrga-1 is practically indistinguishable from the security levels in other schemes. The formulas for calculating the security level for Syrga-1 and HORS are similar. However, in HORS, there is a parameter “r” that determines how many times the same key is used, gradually reducing the security level. For example, with , it decreases to 80 bits.
5.3. Software Implementation and Performance Evaluation of the Scheme
The primary goal of creating post-quantum signature schemes is to ensure the security of signatures in practical quantum computer deployment scenarios. However, the performance of post-quantum signature schemes is also a crucial factor in their development.
The development of the post-quantum Syrga-1 scheme aims to strike a balance between security, practical applicability, and performance.
Based on the key generation, signing, and verification algorithms presented below (Algorithms 1–3), software has been implemented to assess performance.
| Algorithm 1. Key generation of Syrga-1(KgSyrga(PRG(initial parameters))) |
| System parameters: Parameters , Output: and 1: for to do 2: Compute 3: for to do 4: Compute 5: return |
| Algorithm 2. Message Signing Algorithm of Syrga-1(SignSyrga()) |
| System parameters: Parameters , Input: Secret key , and message Output: Signature 1: Compute 2: Split : 3: for to do 4: interpret : 5: for to do 6: for to do 7: 8: 9: return Signature |
| Algorithm 3. Verification of Syrga-1(VfSyrga()) |
| System parameters: Parameters , Input: Public key and signature Output: “accept” or “reject” 1: Compute 2: Split : 3: for to do 4: interpret : 5: for to do 6: for to do 7: 8: . 9: for to do 10: if then 11: return “reject” 12: return “accept” |
Table 5 provides a comparative analysis of the performance of the Syrga-1 scheme and other algorithms. Computational performance experiments were conducted on a personal computer with the specifications of an Intel(R) Core(TM) i5-7500T CPU 2.70 GHz and 8.00 GB RAM, running a 64-bit Windows 10 Pro 21H2 operating system.

Table 5.
Average running time (ms).
When evaluating the execution time of all three Syrga-1 algorithms, we did not account for standard minor computational overheads and presented the average values. From Table 5, it can be observed that the numerical values obtained for Syrga-1 significantly exceed the corresponding values for the HORS scheme. This is explained by the generation of public keys (PKs) in the Syrga-1 scheme intended for multi-use, whereas in HORS, public keys are used only once. Specifically, in Table 5, the numerical values for Syrga-1 result from calculations performed for the formation of a public key (PK) used 1024 times.
Based on the above, it is recommended that research and development efforts be continued to enhance the performance of the Syrga-1 signature scheme and make it more competitive among other algorithms.
6. Conclusions
We have developed the HAS01 hashing algorithm based on the cryptographic sponge construction. The reliability of this algorithm has been studied through an analysis of the avalanche effect, and the F-function of the HAS01 algorithm has been investigated using methods such as exhaustive search and collision search through chain and differential cryptanalysis [22].
In algorithms such as WOTS and HORS, part of the secret key becomes known when the key is used more than once. This reduces the security of such algorithms. The main difference between the post-quantum algorithm presented in the article and other algorithms is that, depending on the choice of the parameter , it allows for signing a message times with just one secret key without compromising security. This is because it is impossible to recover an intermediate secret key from the hashed intermediate secret keys . This is related to one of the fundamental requirements of a hash function, which is providing irreversibility. Currently, further research on the algorithm’s reliability is underway.
Author Contributions
Conceptualization, K.A. and K.S.; methodology, K.S.; software, A.K.; validation, K.S. and K.A.; formal analysis, D.D.; investigation, K.S.; resources, K.A.; data curation, A.K.; writing—original draft preparation, K.S.; writing—review and editing, K.A.; visualization, D.D.; supervision, K.A.; project administration, K.S.; funding acquisition, K.A. All authors have read and agreed to the published version of the manuscript.
Funding
The research work was funded by the Ministry of Science and Higher Education of Kazakhstan and carried out within the framework of the project AP14870719 “Development and study of post-quantum cryptography algorithms based on hash functions” at the Institute of Information and Computational Technologies.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors are grateful to all lab members of the Information Security Laboratory (Institute of Information and Computational Technologies) for their useful suggestions and support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Song, F. A Note on Quantum Security for Post-Quantum Cryptography. In Post-Quantum Cryptography. PQCrypto 2014. Lecture Notes in Computer Science; Mosca, M., Ed.; Springer: Cham, Switzerland, 2014; Volume 8772. [Google Scholar] [CrossRef]
- Bernstein, D.J. Introduction to post-quantum cryptography. In Post-Quantum Cryptography; Bernstein, D.J., Buchmann, J., Dahmen, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Begimbayeva, Y.; Zhaxalykov, T.; Ussatova, O. Investigation of Strength of E91 Quantum Key Distribution Protocol. In Proceedings of the 19th International Asian School-Seminar on Optimization Problems of Complex Systems (OPCS), Novosibirsk, Moscow, Russia, 14–22 August 2023; pp. 10–13. [Google Scholar] [CrossRef]
- Yalamuri, G.; Honnavalli, P.; Eswaran, S. A Review of the Present Cryptographic Arsenal to Deal with Post-Quantum Threats. Procedia Comput. Sci. 2022, 215, 834–845. [Google Scholar] [CrossRef]
- Nejatollahi, H.; Dutt, N.; Ray, S.; Regazzoni, F.; Banerjee, I.; Cammarota, R. Post-quantum lattice-based cryptography implementations. ACM Comput. Surv. 2022, 51, 129. [Google Scholar] [CrossRef]
- Fouque, P.; Hoffstein, J.; Kirchner, P.; Lyubashevsky, V.; Pornin, T.; Prest, T.; Ricosset, T.; Seiler, G.; Whyte, W.; Zhang, Z. Falcon: Fast-Fourier Lattice-Based Compact Signatures over NTRU. 2019. Available online: https://api.semanticscholar.org/CorpusID:231637439 (accessed on 6 November 2023).
- Suhail, S.; Hussain, R.; Khan, A.; Hong, C.S. On the Role of Hash-Based Signatures in Quantum-Safe Internet of Things: Current Solutions and Future Directions. IEEE Internet Things J. 2021, 8, 1–17. [Google Scholar] [CrossRef]
- Sjöberg, M. Post-Quantum Algorithms for Digital Signing in Public Key Infrastructures. Master’s Dissertation, KTH Royal Institute of Technology, Stockholm, Sweden, 2017. Available online: https://urn.kb.se/resolve?urn=urn:nbn:se:kth:diva-210909 (accessed on 8 November 2023).
- Kumar, M. Post-quantum cryptography Algorithm’s standardization and performance analysis. Array 2022, 15, 100242. [Google Scholar] [CrossRef]
- Boutin, C. NIST Announces First Four Quantum-Resistant Cryptographic Algorithms, NIST. Available online: https://www.nist.gov/news-events/news/2022/07/nist-announces-first-four-quantum-resistant-cryptographic-algorithms (accessed on 8 August 2022).
- Hegde, S.B.; Jamuar, A.; Kulkarni, R. Post Quantum Implications on Private and Public Key Cryptography. In Proceedings of the 2023 International Conference on Smart Systems for Applications in Electrical Sciences (ICSSES), Tumakuru, India, 7–8 July 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Buchmann, J.; Lauter, K.; Mosca, M. Postquantum Cryptography—State of the Art. IEEE Secur. Priv. 2017, 15, 12–13. [Google Scholar] [CrossRef]
- Shahid, F.; Khan, A.; Malik, S.U.R.; Choo, K.-K.R. WOTS-S: A Quantum Secure Compact Signature Scheme for Distributed Ledger. Inf. Sci. 2020, 539, 229–249. [Google Scholar] [CrossRef]
- Bernstein, D.J.; Hopwood, D.; Hülsing, A.; Lange, T.; Niederhagen, R.; Papachristodoulou, L.; Schneider, M.; Schwabe, P.; Wilcox-O’Hearn, Z. SPHINCS: Practical Stateless Hash-Based Signatures. In EUROCRYPT 2015. Lecture Notes in Computer Science; Oswald, E., Fischlin, M., Eds.; Advances in Cryptology—EUROCRYPT 2015; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9056. [Google Scholar] [CrossRef]
- Buchmann, J.; Dahmen, E.; Ereth, S.; Hülsing, A.; Rückert, M. On the Security of the Winternitz One-Time Signature Scheme. In AFRICACRYPT 2011. Lecture Notes in Computer Science; Nitaj, A., Pointcheval, D., Eds.; Progress in Cryptology—AFRICACRYPT 2011; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6737. [Google Scholar] [CrossRef]
- Iavich, M.; Avtandil, G.; Iashvili, G. Hybrid Post Quantum Crypto System. Sci. Pract. Cyber Secur. J. (SPCSJ) 2019, 2, 92–98. [Google Scholar]
- Aumasson, J.P.; Endignoux, G. Improving Stateless Hash-Based Signatures. In Topics in Cryptology—CT-RSA 2018. CT-RSA 2018. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2018; Volume 10808. [Google Scholar] [CrossRef]
- Lee, J.; Park, Y. HORSIC+: An Efficient Post-Quantum Few-Time Signature Scheme. Appl. Sci. 2021, 11, 7350. [Google Scholar] [CrossRef]
- Hülsing, A. W-OTS+—Shorter Signatures for Hash-Based Signature Schemes. In Progress in Cryptology—AFRICACRYPT 2013. AFRICACRYPT 2013. Lecture Notes in Computer Science; Youssef, A., Nitaj, A., Hassanien, A.E., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7918. [Google Scholar] [CrossRef]
- Lenstra, A.K. Key Lengths Contribution to The Handbook of Information Security. 2010. Available online: https://api.semanticscholar.org/CorpusID:13203339 (accessed on 6 January 2024).
- Morris, J.D. Sha-3-standard: Permutation-based-hash-and extendable-output-functions. In Federal Information Processing Standards (FIPS-202); Information Technology Laboratory National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015. Available online: https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.202.pdf (accessed on 3 January 2024).
- Algazy, K.; Sakan, K.; Kapalova, N.; Nyssanbayeva, S.; Dyusenbayev, D. Differential Analysis of a Cryptographic Hashing Algorithm HBC-256. Appl. Sci. 2022, 12, 10173. [Google Scholar] [CrossRef]
- Kapalova, N.; Dyusenbayev, D.; Sakan, K. A new hashing algorithm—HAS01: Development, cryptographic properties and inclusion in graduate studies. Glob. J. Eng. Educ. 2022, 24, 155–164. [Google Scholar]
- Sakan, K.S.; Dyusenbaev, D.S.; Algazy, K.T.; Lizunov, O.A.; Khompysh, A. Development and analysis of the hashing algorithm “HAS01”. In Proceedings of the Collection of Articles of the IV International Scientific and Technical Conference “Minsk Scientific Readings-2021”, Minsk, Belarus, 29–30 March 2021; Volume 3, pp. 190–196. (In Russian). [Google Scholar]
- Jogenfors, J. Quantum Bitcoin: An Anonymous, Distributed, and Secure Currency Secured by the No-Cloning Theorem of Quantum Mechanics. In Proceedings of the 2019 IEEE International Conference on Blockchain and Cryptocurrency (ICBC), Seoul, Republic of Korea, 14–17 May 2019; pp. 245–252. [Google Scholar] [CrossRef]
- Reyzin, L.; Reyzin, N. Better than BiBa: Short One-Time Signatures with Fast Signing and Verifying. In Australian Conference on Information Security and Privacy; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).