Abstract
Online information cascades (tree-like structures formed by posts, comments, likes, replies, etc.) constitute the spine of the public online information environment, reflecting its various trends, evolving with it and, importantly, affecting its development. While users participate in online discussions, they display their views and thus contribute to the growth of cascades. At the same time, users’ opinions are influenced by cascades’ elements. The current paper aims to advance our knowledge regarding these social processes by developing an agent-based model in which agents participate in a discussion around a post on the Internet. Agents display their opinions by writing comments on the post and liking them (i.e., leaving positive assessments). The result of these processes is dual: on the one hand, agents develop an information cascade; on the other hand, they update their views. Our purpose is to understand how agents’ activity, openness to influence, and cognitive constraints (that condition the amount of information individuals are able to proceed with) affect opinion dynamics in a three-party society. More precisely, we are interested in what opinion will dominate in the long run and how this is moderated by the aforementioned factors, the social contagion effect (when people’ perception of a message may depend not only on the message’s opinion, but also on how other individuals perceive this object, with more positive evaluations increasing the probability of adoption), and ranking algorithms that steer the order in which agents learn new messages. Among other things, we demonstrated that replies to disagreeable opinions are extremely effective for promoting your own position. In contrast, various forms of like activity have a tiny effect on this issue.
1. Introduction
Individuals receive new information through communications with their peers and mass media outlets. While proceeding with new messages, people reorganize their belief systems in an attempt to approach logically coherent cognitive constructions in their minds [1,2]. However, external information is rarely unbiased. Facts and inferences based on them may be subject to inadvertent or intended distortions. As a result, corrupted chunks of belief systems are spreading across societies.
When social media began to appear, there was a point of view that low-cost access to online information, not limited by geographical and economical boundaries, should facilitate the formation of an unbiased and faithful perception of the world [2,3]. However, this never happened—social networks are divided into conflicting groups of individuals espousing similar views, so that people in these groups (aka echo-chambers) rarely have access to challenging messages, preferring to consume information that aligns with their opinions [4]. As a result of such segregation, disagreement, polarization, and fake news persist in societies [5,6].
Longstanding debates around possible reasons for such social phenomena are going on in the scientific community. Among other explanations, scholars hypothesize individuals’ intrinsic cognitive mechanisms—selective exposure (the tendency to avoid information that could bring any form of ideological discomfort) and biased assimilation (when new information is perceived in a form that aligns with existing belief systems) [6]. Next, the online domain is subject to moderation by ranking algorithms that may push people into closed information loops with no access to challenging content [7].
It is worth noting that interactions in the online environment differ from those in the offline world because online platforms provide a rich set of specific communication tools [8]. First, apart from private text messages, it could be messages with media content (images, videos, music). Further, most online platforms provide the opportunity to participate in public conversations whereby users can display their thoughts overtly, thus making them visible to a huge audience. Such public discussions are usually structured into specific tree-like hierarchies in which rooted messages (posts, tweets, etc.) are followed by replies/retweets/comments/reposts and different forms of evaluation displaying various types of emotions (likes, dislikes, etc.). These structures—information cascades—can grow very rapidly achieving, thereby, large audiences in a very short time [9].
Information cascades constitute the spine of the public online information environment, reflecting its various trends, evolving with it, and affecting its development. While users participate in online discussions, they display their views and thus contribute to the growth of the cascades. At the same time, users’ opinions are affected by the cascades’ contents. It is worth noting that due to the large sizes of cascades and users’ limited attention [10], each individual is able to attend only a limited number of a cascade’s elements. Further, the order of these elements when they appear in a user’s news feed is governed by the social network’s ranking systems [11].
To the best of our knowledge, there are no studies that capture all the points raised above. Some papers have already concerned the issue of users’ interactions in the online domain subject to moderation by personalization systems [7,8,12]. However, all these studies were drawn from minimal models of online interactions, ignoring the rich nature of online communication tools. The current paper aims to advance our knowledge regarding these social phenomena by developing an agent-based model in which agents participate in a discussion around a post on the Internet. While agents display their opinions by writing comments to the post and liking them (i.e., leaving positive evaluations), they also contribute to the development of the corresponding information cascade. At the same time, agents update their views as they communicate with the cascade’s contents. What is important is that all these processes are governed by a ranking algorithm that decides which comments will appear in the agents’ news feeds first. Using this model, we attempt to figure out what crucial factors determine the macro-scale outcomes of opinion dynamics that unfold in information cascade settings.
The rest of the paper is organized as follows. Section 2 lists the relevant literature. In Section 3, we elaborate on the model. Section 4 describes the design of numerical experiments, and Section 5 presents their results. Section 6 makes concluding remarks. The Appendix A includes supporting information.
2. Literature Review
To date, a huge number of opinion dynamics models have been elaborated; we refer the reader to excellent review papers [13,14,15,16,17,18,19,20]. Relatively recently, such models started to account for the fact that online interactions differ from those unfolding in the offline world and are hardly influenced by ranking algorithms—specific intelligent systems incorporated in social media platforms that affect the order in which new content appears in users’ news feeds. Ranking algorithms base their decisions on the information in a user’s profile, the history of the user’s actions on the Internet, and current trends in the online domain: if a message is rapidly emerging as popular, then it will be suggested to users foremost, as there is a high probability that it will get a positive evaluation from them. One of the main objectives of ranking algorithms is to ensure that users will appreciate the time they spend on the platform and thus do so repeatedly. We should say that the term “ranking algorithm” stands rather for content ordering. In turn, recommendation algorithms suggest something to a user (for example, new information sources that could be appreciated by the user or potential friends). However, content ordering can also be understood as a sort of recommendation as it implicitly assumes that contents that have higher priority are recommended by the platform. In this regard, in some situations where it is possible, we will use the terms “ranking algorithm” and “recommendation algorithm” interchangeably.
A near first attempt to investigate how ranking algorithms affect opinion formation dates back to Ref. [5], where the authors analyzed the polarizing effects of several prominent recommendation algorithms. The Ref. [12] focused on the interplay between a recommendation algorithm (operationalized as a parameter that measures to what extent like-minded individuals have more chances to communicate) and two alternative opinion formation models (the rejection model and the persuasion model) in order to figure out what opinion dynamics mechanisms lead to opinion polarization. They demonstrated that the emergence of polarization sufficiently depends on what social influence mechanisms are implemented. In the case of the persuasion model, if the effect of the ranking algorithm is strong, then opinion polarization will proliferate. In turn, the rejection model leads to a consensus in the same situation. Perra and Rocha [8] investigated how different ranking algorithms affect opinion dynamics by controlling for basic network features. They revealed that the effect of ranking algorithms is reinforced in networks with topological and spatial correlations. De Marzo et al. [21] upgraded the classical Voter model [22] with a recommendation algorithm that with some probability, on each iteration, replaces the standard Voter model protocol by exposing an interacting agent to an external opinion that is designed to be maximally coherent to the agent’s current opinion. For this advanced model, the authors obtained a mean-field approximation and derived conditions under which a consensus state can be achieved. In [7], the authors developed a model in which an agent communicates with an online news aggregator. They showed that ranking algorithms, while pursuing their commercial purposes, make users’ opinions more extreme. The Ref. [11] demonstrated that the macroscopic properties of opinion dynamics are seriously affected by how agent interactions are organized: in the case of pairwise interactions, ranking algorithms contribute to polarization, whereas group interactions do not display the same tendency. The empirical study by Huszár et al. [23] showed that ranking algorithms treat various information sources differently, with statistically significant variations along political lines. The Ref. [24] analyzed the effect of link recommendation algorithms (that moderate the dynamics of the social graph connecting users) on opinion polarization. They obtained that algorithms that rely on structural similarity (measured, for example, as the number of common online friends) enhance the creation of unintentional echo-chambers and thus strengthen opinion polarization.
All these papers ignored the fact that users’ interactions in online public debates are structured into complex tree-like structures—information cascades. Apparently, it is conditioned by the fact that information cascades (and other issues of information diffusion in the online domain) are historically studied by a parallel research branch whereby approaches from the percolation and social contagion theories are widely used [9,25,26,27,28,29].
In this paper, we try to combine perspectives from both opinion formation models and the social contagion theory by elaborating an agent-based model that, on the one side, describes the opinion dynamics of interacting agents and, on the other side, accounts for threshold effects and the rich nature of online information diffusion processes.
It is worth noting that due to the burgeoning development of social media, the large diversity of various online networking platforms, and the vast number of studies with social media as a research object therein, there is a need to craft frameworks that could systematically describe such complex systems. Indeed, social media are characterized by multilayer communication networks, with different layers standing for various information channels—it could be networks of personal (private) messages, networks of replies, comments, likes, dislikes, etc., [30]. Further, some social platforms come with specific communication architectures. For example, on Reddit, there are subreddits—special key words that stand for various discussion niches. Participation in such a discussion can be operationalized as being a part of one community [30]. As a result, we end up with a new communication dimension that should be properly acknowledged in analysis. As well as this, models representing online social platforms should account for various behavior types of users [31].
Despite recent models of online social platforms doing a nice job of describing various facets of online social interactions, our model focuses on an extremely simple scenario when an (unstructured) group of users publicly discusses a post on the Internet. We assume individuals interact with each other only by writing comments and making positive assessments (liking) of them. Further, we exclude any structural restrictions from our model by assuming that these users are random followers of an information source that has published the focal post. This is a quite strong assumption that could bring down our approach. For instance, individuals who have many friends (or who have a high rating on the platform—as, for example, in Stack Overflow) may have a larger effect on the discussion than other (less rated) individuals. Next, users may display more trust towards their friends than if they were random online strangers [32]. All these issues are ignored in our model, but should be carefully incorporated into future research.
As a final remark, we would like to say that despite previous studies successfully examining how ranking algorithms affect opinion formation by implementing them in poorly structured news feeds (in which elements are not connected to each other), the current paper presents the first (to the best of our knowledge) attempt to investigate how opinion forms in a highly structured information environment.
3. Methodology of Research
We consider a group of agents who participate in an online discussion on a social network. This discussion grows around a post published by an information source (say, by a social media account of a news outlet). The post bears a message which is characterized by an opinion that belongs to an opinion space , whereby variables represent an opinion alphabet. One could think of these opinions as arranged in such a way that the first and the last elements and stand for polar positions, whereas the middle opinion represents a neutral stance. More complex interpretations are also allowed.
Agents start the discussion by being assigned opinions that are also conceptualized as elements of the space . Following online interactions, agents may change their views, whereas the opinion of the post remains constant. Agents interact with each other by translating their views via special actions allowed by the online platform. Model dynamics proceed in a discrete time: . At time , the post appears and agents’ opinions are initialized. After that, at each time moment , a randomly chosen agent communicates with their news feed. Two actions are allowed for the agent: (1) write a reply (comment) to the post/comment and (2) like the post/comment. Therefore, each comment at time is characterized by the number of replies and likes it has received by this time. The post is characterized by the similar quantities and . Note that and counts only direct replies. As a result of agents’ actions, new comments and likes appear—the information cascade is growing.
Let us assume that at time , agent is selected. At this moment, they observe the news feed —an online display that contains textual elements (the post, comments) from the cascade arranged in some way as well as associated metrics demonstrating the corresponding numbers of likes/replies. The agent proceeds through the news feed in a sequential fashion, starting from the first element (which is always the post: ). The order of the news feed elements is subject to a ranking algorithm, which will be introduced below. It is important to clarify that the news feed essentially includes all the cascade textual elements (numbered as ). However, the agent may not be willing to attend all of them—it could be the case that they do not have enough time for this or, say, the topic of discussion is not important for this particular agent. As such, to define the agent’s behavior, one should pinpoint what of the cascade elements will be attended to by the agent. We denote the set of these elements by . It is worth noting that may be subject to dynamic updates as a result of the agent’s communications—for example, because of changes in the agent’s level of engagement in the discussion (as the agent’s opinion becomes more extreme, the agent may want to discuss the topic at stake fiercely).
While proceeding with an element from the news feed, agent may:
- -
- Change their opinion.
- -
- Put a like on the element.
- -
- Write a reply to the element.
These options are not mutually exclusive. The order of these events can vary, but it would be meaningful to assume that the agent updates their opinion first. The motivation behind this assumption is that, prior to displaying any reaction, the agent should first read the message. While reading the text, the agent updates their views according to the arguments presented in the message. After that, the agent may put a like on the element and write a reply. We assume that the order of these two reactions is subject to the model’s specification. As a basic configuration, we will suppose that the like appears first (as an estimation that does not require much time and cognitive resources to be displayed) and that only after that the agent may write the reply.
Here, we would like to emphasize that we do not use dislikes or other ways of evaluation (such as various sorts of emotions) in our model. On the one hand, a number of social media platforms are restricted to only one way of assessment: liking (the example of YouTube, which decided to reject public dislikes, is pertinent here). On the other hand, the inclusion of other sorts of reactions may substantially complicate the model. As a result, we do not consider them in our model, but leave this room for future studies.
3.1. Opinion Update Protocol
Following the approach from Ref. [33], we model opinion updates as a function of the focal agent’s opinion and the element’s properties. Being exposed to the textual element of the news feed, the agent can switch its current opinion to one of alternatives with some probabilities that add up to one. These probabilities may depend on the agent’s and the element’s opinions or, say, on the number of likes the element has. In Ref. [33], the author outlined that the probability of an opinion update , subject to the influencing opinion is , is determined by a quantity , where the lower indices are synchronized with the lower indices of the interacting opinions and the potential opinion . The variables constitute a 3D mathematical construction , which was called the transition matrix in Ref. [33]. In fact, this object is not a matrix per se: many matrix operations are not applicable here. In this regard, we will adopt a different notation strategy throughout this paper, and we will refer to as the transition table. The components of the transition table meet the restriction for any fixed and . The transition table can be straightforwardly represented as a list of square row-stochastic matrices:
where the matrix encodes how agents with the opinion react to social influence:
This approach can be modified to account for the fact that our perception of the post/comment may depend not only on its opinion, but also on how other individuals perceive this object. For example, if a person notices that a comment has acquired many likes, the person receives the signal that the society appreciates this message. In this regard, they will likely adopt the message’s opinion attempting to conform to society’s norms [34]. The social contagion theory posits that the probability of accepting the message is positively associated with the number of positive appraisals the message has received, and empirical studies witness that the dependency typically features a diminishing returns character [35,36,37]. These ideas can be incorporated into our framework by adding a special term to the transition table’s elements, which is responsible for the effect of social contagions:
where a monotonically increasing (upward convex) function represents the social contagion factor (it is assumed that ). In this case, the probability depicts the situation when the agent is exposed to the message that has not been liked by anyone yet.
As agents communicate, their opinions evolve. This process can be monitored both at the individual and the macroscopic levels. To investigate opinion dynamics at the macroscopic level, we use the quantities . Thus said, represents the number of agents having opinion at time .
3.2. Replies and Likes
Let us now outline how agents display reactions to textual messages. Still, we follow the probabilistic framework by encoding agents’ behavior using specific probability distributions. First, we assume that if the agent writes a reply, then the agent’s opinion is translated into the message. In principle, it is also possible to introduce a specific alphabet of textual opinions, accounting for the fact that our views cannot be transferred into textual form without any deformations (from this perspective, the opinion of the post should also be represented using this textual alphabet) [38]. However, we do not do so here, and we assume that both agents’ opinions and textual messages are elements of the same opinion alphabet. We now introduce the probability that a user with opinion will write a reply to the post/comment with opinion . Grouping these quantities into the matrix (hereafter, the Reply matrix)
we get a full description of agents’ textual-reaction behavior. Within this notation strategy, denotes how often agents with opinion respond to like-minded messages, whereas and encode the chances of replying to messages with opposite stances. In this paper, we do not account for the semantic facets of textual messages. However, one can think of responses to opposite opinions as those that translate negative emotions and represent animosity (hostile replies). In turn, replies to similar opinions are likely to bear positive sentiments (supporting replies).
Elaborating analogously, we introduce the Like matrix
whose entry is the probability that an agent with opinion will put a like on a message with opinion . Since the act of liking tends to display a positive evaluation, it would be rational to suppose that the like matrix’s elements should occupy predominantly the main diagonal, showing thus that agents tend to like content that aligns with their views. In contrast, in the Reply matrix, elements beyond the main diagonal can appear to be positive, indicating individuals’ intentions to debate with challenging arguments. For the sake of brevity, we will refer to the Reply and Like matrices as to the Activity matrices. Note that the Activity matrices are not restricted to being row-stochastic.
The Activity matrices can also be modified to account for the social contagion factor in a similar fashion as the transition table. For example, we can outline that the components of the Like matrix are additively incremented by a special term , which governs agents’ sensitivity towards how the audience evaluates the post/comment. As a result, the probability that an agent with opinion will put a like on the post/comment with opinion that has likes is given by
where the quantity describes the situation when the post/comment has no likes (we assume that ).
These specifications end the description of the model. The model’s sketch is depicted in Figure 1.
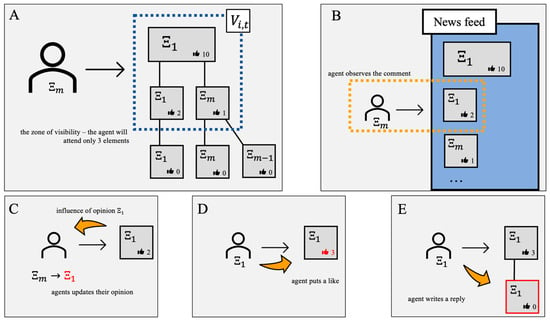
Figure 1.
(Panel A). We investigate how an agent with opinion (rightist) participates in the discussion initiated by a leftist post with opinion (large rectangle). After being selected at some time , the agent observes the news feed (see panel B), whose elements (the number of which equals 6—see panel A) are prioritized according to the number of likes. The zone of visibility of the agent () includes only three elements—the post and two comments that are direct replies to the post (see panels A,B). These two comments were chosen by the ranking algorithm because they have more likes than others. In this example, the agent does not change their opinion and does not display any reactions after reading the post. Instead, the second element of the news feed (the leftist comment with two likes) makes the agent change their opinion (panel C), induces a like reaction (panel D), and receives a reply from the focal agent (in which the agent translates their newly formed opinion )—see panel (E). All updates are highlighted in red. As a result, the information cascade is replenished with one more comment, one of its previous comments receives one additional like, and the opinion of the selected agent is flipped to the opposite side.
4. Design of Numerical Experiments
4.1. Baseline Settings
We use the model introduced above to investigate a stylized situation in which a generally neutral population of agents are exposed to a radical post. We consider an opinion alphabet with three elements (), whereby opinions and are opposite radical positions, whereas stands for the neutral stance. Without a loss of generality, we assume that the post has opinion . The initial opinion distribution is given by ; that is, the majority of agents in the system hold the neutral position, whereas the number of individuals with radical opinions (leftists) and (rightists) are balanced.
We assume that opinion updates are governed by the following transition table:
According to (1), agents with radical positions are not subject to opinion changes, whereas the neutral opinion can be reconsidered after communications with leftists or rightists. However, this occurs in only 10 cases out of 100. Such an assumption relies on empirical studies that witness the generally low tendency of individuals to change their views and the high resistance to social influence among individuals with strong opinions [38,39]. What is important is that we assume only assimilative opinion shifts—agents cannot adopt opinions opposite to those they were exposed to (in terms of the transition table, it means that ).
Next, we focus on the following Activity matrices:
which indicate that
- -
- Only leftists and rightists (that is, only individuals with clear positions) can take part in public debates and thus contribute to the information cascade, whereas neutral individuals are silent (until they change opinions).
- -
- Agents put likes only on those messages with opinions similar to their own.
- -
- Agents may reply to cross-ideological messages, but they do it two times less frequently than they reply to coherent messages.
- -
- The probability of a like is at least three times greater that the chance of writing a comment.
All these patterns are empirically motivated and can be observed in real life. For example, users far more often put likes than comments on social media. Perhaps only the one assumption—regarding the balance between cross-ideological and coherent replies—may raise some concerns, but we will proceed from the notice that people prefer to avoid conflict situations and communicate primarily with those espousing similar views, as reported by empirical studies of online communication networks [40].
4.2. Social Contagions
We incorporate social contagions into our model by adding adjustments to the Activity matrices, ignoring any modifications in the transition table. This assumption relies on the general notion that threshold effects are widely observed in how people perform physical actions (express their opinions publicly, subscribe to mass media accounts, lead a healthy lifestyle, and choose accommodations) [41,42], whereas opinion formation processes (that concern the transformation of internal individual characteristics) are moderated by a different family of mechanisms [13]. Amendments and in the Reply and Like matrices are defined as
and
where and , as well as their powers, represent the marginal revenue from each additional like or reply. In agreement with the empirics [43], and feature diminishing returns in the sense that the marginal increment decreases as the number of likes or replies goes up. If the number of likes or replies is huge, then we obtain:
4.3. Ranking Algorithms and Specification of the Visibility Zone
As was previously said, agents interact with each other through an interface (the news feed), in which they observe the post and comments sorted in a special fashion. The order of comments is defined by a ranking algorithm. We consider three ranking algorithm specifications:
- -
- “Time”—comments are sorted according to their time of appearance, from the newest to the oldest (this ranking algorithm is usually considered basic on social media sites).
- -
- “Likes Count”—comments that have more likes appear at the top of the news feed.
- -
- “Replies Count”—comments are prioritized according to the number of direct replies. The more replies a comment has, the higher its priority.
In fact, the real ranking algorithms that are employed on social media sites are much more complex and account for a wide range of metrics, including the history of users’ actions. However, our approach gives us an opportunity to isolate the effects of some, perhaps the most simple, metrics and study them separately—a similar methodology was implemented in Ref. [8].
Apart from defining the organization of the news feed, we should also clarify how many of its elements a given agent is willing to attend. The process of learning is a complex operation, in which many factors govern the volume of information with which the user is able to proceed, such as: cognitive constraints, the amount of free time, the level of the user’s engagement in the discussion topic, etc. In this paper, we will rely on the assumption that the majority of agents are able to learn only a few news feed elements, whereas the number of agents who can proceed with more comments decays exponentially. More specifically, we define the size of using the exponential distribution:
To avoid situations where this random variable is a non-integer, we round it down and then increment by one. By doing so, we ensure that at least one of the elements of the news feed (the post, which is always located at the top) will be looked at. In addition, we assume that while proceeding with the news feed, the agent does not skip its elements. As a result, they learn the first elements of the news feed.
4.4. Experiment Design
The dynamics of the social system presented above can be understood as a competition between the left () and right () opinions. Settings introduced in the previous subsection imply that the competing opinions have no advantage over each other—the transition table and the activity matrices are symmetric with respect to the radical positions. However, the left opinion has one sticking privilege—it is translated by the post and thus each agent when observing the news feed, is first exposed to . As a result, in the long run, the left opinion should prevail. Inspired by this observation, we focus on answering the following questions:
- (Q1) “What way should the rightists alter their activity rates to turn things around?”
- (Q2) “What way should the rightists modify the persuasiveness of their arguments which they use to influence neutral agents to facilitate proliferation of the right opinion?”
- (Q3) “What way should the rightists alter their presence in discussion to turn things around?”
- (Q4) “How the presence of social contagions, strength of cognitive constraints, and the type of the ranking algorithm affect the outcome of the opinion competition?”
From a mathematical point of view, our purpose is to find a hyperplane in the parameter space that marks the draw in the opinion competition. To address the questions formulated above, we conduct Monte-Carlo simulations in which the one-variable-at-a-time approach is applied. We manipulate the Activity matrices via the variables and (question Q1) just as follows:
Parameter alters the probability of writing a reply to the hostile opinion , regulates the probability of replying to the coherent opinion , changes the probability of liking opinion , and varies the probability of liking the congruent opinion .
Next, we isolate the effect of opinion ’s persuasiveness (question Q2) by introducing the parameter in the following fashion:
In other words, the greater is, the more often neutral agents adopt after being exposed to this opinion.
Question Q3 is addressed just by controlling the initial opinion distribution as the total number of agents is fixed.
While altering all these parameters, we also control for the social contagion factor and type of the ranking algorithm. The former covariate is operationalized via two stylized situations: (i) and (ii) . The second case covers the settings when there are no social contagions. In turn, in the first case, the Activity matrices are subject to amendments that depend on the post’s /comment’s metrics. It is straightforward to calculate that; in this case, the probability of writing a reply to the post/comment with a huge number of replies is described by the following Reply matrix:
Analogously, a comment/post that has already received many likes will get one more according to the following Like matrix:
The issue of cognitive constraints is operationalized via two regimes: (i) (strong cognitive constraints) and (ii) (weak cognitive constraints). We recognize that the term “cognitive constraints” is not fully correct here as other factors different to cognitive limitations do also affect the value of , but for the sake of simplicity we will adopt this terminology. In Appendix A (see Figure A1), we show the distributions of that appear in these two regimes.
Each experiment lasts until the agents’ opinions converge (it happens when the faction of neutral agents disappears). Each simulation run is associated with the convergence time and the quantity (the dependent variable) that signifies the relative advantage of opinion over after iterations. For each combination of parameters, we perform 100 independent experiments. In ongoing analysis, if we say “the draw can be achieved”, it means that the value of the dependent variable averaged over independent simulations equals 0.
5. Results
Figure 2 and Figure 3 show how the result of the discussion depends on how active the rightists are. More precisely, Figure 2 investigates the effect of reply activity, whereas Figure 3 outlines that of like activity. We see that the most straightforward way for rightists to mitigate the dominance of the left opinion is to write comments more often. What is more, replies to the disagreeable opinion are most effective—see panels A, C, E, and G. However, the draw is more real in the case of weak cognitive constraints (see panels C and G). A more detailed analysis (see Figure A2, Appendix A) revealed that the presence of social contagions favors the leftists. Under the most propitious for rightists conditions (see panel G), the draw can be achieved at (ranking algorithm: Likes Count) and (ranking algorithm: Time). Apparently, if rightists reply to opposite comments more often, then the ranking algorithm Replies Count favors leftists as their comments become more visible to neutrals on this occasion. In contrast, panels D and H indicate that this ranking algorithm contributes to the proliferation of right opinion in the case of the rightists interacting with congruent-opinion comments more often. The same can be said about the ranking algorithm Time. Again, the settings of weak cognitive constraints and the absence of social contagions are more advantageous for rightists if the value of goes up. However, in such settings, the draw can be achieved only at (see panel H). Panel D, however, indicates that the draw becomes real at (raking algorithm Replies Count), but the further increase in leads to lower values of the dependent variable, indicating thus that this extremum could be just an artefact of statistical fluctuations.
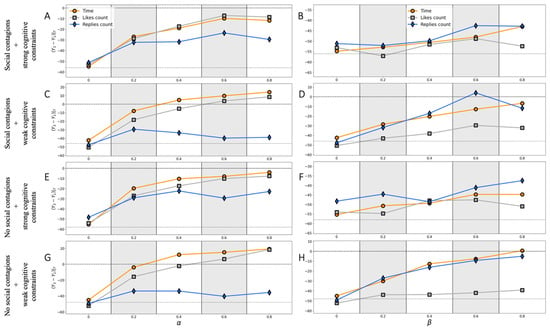
Figure 2.
We study the effect of reply activity on the advantage of opinion over opinion after iterations (averaged over 100 independent simulation runs). The left panels (A,C,E,G) show how replies to opposite comments (with opinion ) condition the dependent variable, whereas the right panels (B,D,F,H) showcase how the outcome of the opinion competition varies with how frequently agents reply to comments with congruent opinion . On each subplot, two dashed lines signify (i) the draw () and (ii) the median value of the dependent variable in the case of the Activity matrices holding the baseline configuration given by (2).
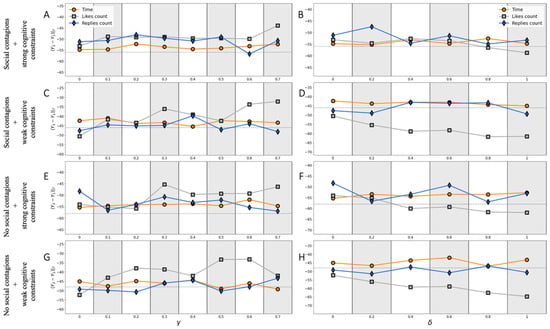
Figure 3.
We study the effect of like activity on the advantage of opinion over opinion after iterations (averaged over 100 independent simulation runs). The left panels (A,C,E,G) show how likes to opposite comments (with opinion ) condition the dependent variable, whereas the right panels (B,D,F,H) showcase how the outcome of the opinion competition varies with how frequently agents like comments with coherent opinion . On each subplot, the dashed line showcases the median value of the dependent variable in the case of the activity matrices holding the baseline configuration defined by (2). The line (the draw) did not fit into the figure.
Figure 3 clearly indicates that the potentiation of like activity cannot significantly strengthen the positions of rightists. Nonetheless, some positive relationships between the focal quantity and the value of can be found on panels C, E, and G in Figure 3 (see the gray curves). However, these curves are very far from the line that fixes the draw.
The left panels of Figure 4 demonstrate how the changes in the transition table related to the growth of the persuasiveness of rightists affect the final opinion distribution. As expected, the more influential the rightists are, the larger the value of the dependent variable is. We report that the ranking algorithm Time more favors rightists than other algorithms on this occasion. The critical value at which the draw appears strongly depends on how strong the cognitive constraints are. Weak cognitive constraints make the draw more feasible for rightists: such settings ensure the draw at regardless of the presence of social contagions (subject to the ranking algorithm, Time is in charge). Note that setting leads to the following transition table:
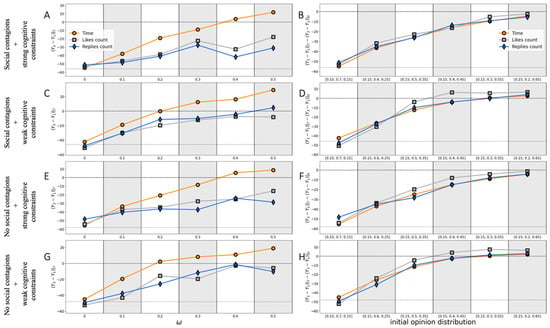
Figure 4.
The left panels (A,C,E,G) of this figure investigate the effect of the persuasiveness of rightists on the outcome of the discussion, measured as the advantage of opinion over opinion after iterations (averaged over 100 independent simulation runs). The right panels (B,D,F,H) study how the initial opinion distribution impacts the outcome of conversations. However, since the system is not opinion-balanced at the beginning on this occasion, we now use a different dependent variable: , which accounts for the fact that the initial number of rightists can be greater than that of leftists (in fact, this quantity just compares how many neutrals were convinced by rightists against those that were persuaded by leftists). On each subplot, two dashed lines signify (i) the draw (when the dependent variable is zero) and (ii) the median value of the dependent variable in the case of the activity matrices holding the baseline configuration defined by (2).
Finally, we investigate if the outcome of the opinion competition can be challenged by increasing the number of rightists in the discussion. From panels B, D, F, and H in Figure 4, we conclude that the rightists should have a significant numerical advantage to combat the effect of the left-opinion post. Panels D and H indicate that in the case of weak cognitive constraints and under the assumption that the ranking algorithm Likes Count moderates the news feeds, the draw can be achieved if the discussion starts from the opinion distribution . That is, the number of rightists should be comparable to the number of neutral agents. Other settings are less favorable for rightists.
6. Discussion
In general, our results demonstrate that, despite the initial advantage of leftists (ensured by the influence of the rooted message (the post) that bears the left opinion), the rightists would have more success in the discussion if the agents were able to proceed with more information. This result is intuitively clear: given that the first element in the news feed is a left-opinion message (the post itself), individuals that come with a higher information capacity have more chances to learn somewhat beyond the first news feed message.
Further, we obtained that the ranking algorithm Time, which is unbiased to how popular comments are in terms of likes or replies favors rightists in most situations. However, if rightists try to challenge the result of the discussion, then the ranking algorithm Likes Count will be more appropriate. We also report that social contagions typically inhibit the proliferation of the right-side position. We hypothesize that this result is conditioned by the post’s ability to reinforce its persuasiveness with social contagions, as the post has more chances to receive the very first replies and likes just because it has the ultimate advantage of the first exposition for each user.
In various scenarios, we found the critical values at which the advantage of the left opinion in the discussion disappears. Among other things, we found that replies to opposite comments have an extremely strong effect on the outcome of the opinion competition. We were surprised to learn that the like-type activity of rightists has a tiny effect on the outcome of the opinion competition and cannot challenge the prior dominance of leftists. This result is counterintuitive—we expected that if rightists were more active in supporting their comments with likes, then, in the case of the ranking algorithm Likes Count, right-opinion comments would become more visible and thus affect more neutral agents. Despite finding positive associations between and the dependent variable for some settings, however, we have to admit that these results are far from our expectations.
7. Conclusions
This paper introduces a model that simulates how users openly debate a post on a social media website in a three-party society (leftists–neutrals–rightists). In this model, individuals communicate by writing comments to the post and each other’s comments and by liking them. The key assumption of our model is that users’ actions are structured into tree-like structures—information cascades. Users learn textual information via their news feeds, with the elements of the news feed being processed sequentially. The post always appears first in the news feed, whereas the order of the comments is subject to the moderation of a ranking algorithm that may be sensitive to how popular a comment is in terms of likes or replies. Importantly, we account for the fact that, at some point, the cascade becomes too large in size so that users are unable to learn all elements therein due to individual cognitive constraints and limited attention. As a final ingredient, we assume that an individual’s perception of a message depends on how other people evaluate it. We suppose that the strong point of our approach is the systematic description of all relevant facets of online communication.
Assuming that the post itself is biased (has a left-side opinion), we studied how users’ activity patterns, their persuasiveness rates, and the initial populations of opinion camps affect the opinion dynamics at the macroscopic level. Specifically, we were interested in how rightists can challenge the prior dominance of leftists. Perhaps our main contribution is that for various settings, we precisely characterized the points of the parameter space at which the balance is shifted to the right opinion.
It is worth noting that we did not discuss how the corresponding modifications in the parameter space (e.g., an increase in activity rates or persuasiveness) can be achieved in reality. For example, from the technical point of view, changes in activity patterns or the numerical relation between opinion camps seem more feasible than an increase in persuasiveness. In the first two cases, rightists should just consolidate their efforts (call like-minded persons for help) and behavior (for example, writing replies to hostile comments more often), whereas any modifications in the transition table require more subtle behavioral transformations.
The current paper concerned only one stylized situation when a discussion unfolds around one post on the Internet. We did not touch more realistic scenarios where posts appear one after another, as it happens on social media sites. In addition, there could be several conflicting mass media accounts that may fight for followers. Further, we did not include in the model social bots that may act strategically and in a coordinated manner. Such artificial accounts are not bound by cognitive constraints and may display abnormal activity. Importantly, they could be configured to give immediate answers to posts and thus be extremely effective in moderating the discussion. All these ideas constitute promising avenues for further model development.
As we mentioned before, in the current paper, we did not account for how agents are connected in a social network, nor for how they diverge in statuses and activity rates. However, these factors may sufficiently affect the underlying processes. Further, we focused on only one reaction (like), whereas other sorts of reactions, such as dislikes or various types of emotions (smiles) are also of great interest. In particular, it would be interesting to investigate how the introduction of dislikes may affect the behavior of the social system (especially in view of the withdrawal of public dislikes undertaken by YouTube).
Finally, we did not study the structure of the information cascades generated by our model. From this perspective, it would be interesting to compare cascades that appear in the model with those that were observed on social media sites throughout empirical studies [27,28].
Supplementary Materials
The following are available online at https://doi.org/10.7910/DVN/FZOGGZ.
Funding
This research was funded by the Russian Science Foundation grant number 23-21-00408.
Acknowledgments
I thank the anonymous reviewers for their invaluable comments.
Conflicts of Interest
The author declare no conflict of interest.
Appendix A
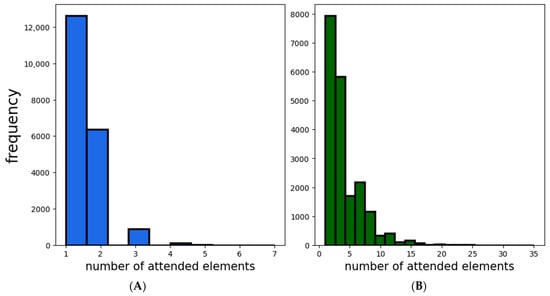
Figure A1.
Panel (A) shows the distribution of the number of attended elements in the case of the strong cognitive constraints regime. Panel (B) stands for the regime of weak cognitive constraints.
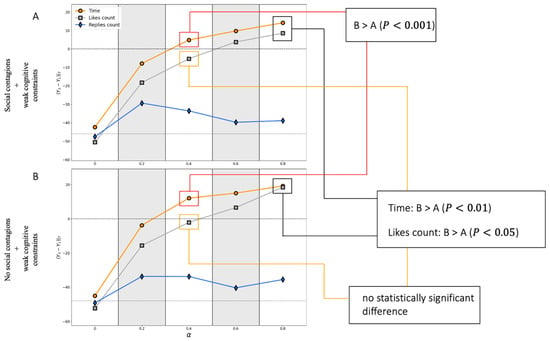
Figure A2.
This Figure replicates two panels from Figure 2C,G. Using the Mann–Whitney U test, we compare distributions of the dependent variable obtained with social contagions (denoted A) and without (denoted B), other things being equal.
References
- Banisch, S.; Olbrich, E. An Argument Communication Model of Polarization and Ideological Alignment. J. Artif. Soc. Soc. Simul. 2021, 24, 18564. [Google Scholar] [CrossRef]
- Zafeiris, A. Opinion Polarization in Human Communities Can Emerge as a Natural Consequence of Beliefs Being Interrelated. Entropy 2022, 24, 1320. [Google Scholar] [CrossRef]
- Baumann, F.; Lorenz-Spreen, P.; Sokolov, I.M.; Starnini, M. Modeling Echo Chambers and Polarization Dynamics in Social Networks. Phys. Rev. Lett. 2020, 124, 048301. [Google Scholar] [CrossRef]
- Bail, C.A.; Argyle, L.P.; Brown, T.W.; Bumpus, J.P.; Chen, H.; Hunzaker, M.B.F.; Lee, J.; Mann, M.; Merhout, F.; Volfovsky, A. Exposure to opposing views on social media can increase political polarization. Proc. Natl. Acad. Sci. USA 2018, 115, 9216–9221. [Google Scholar] [CrossRef]
- Dandekar, P.; Goel, A.; Lee, D.T. Biased assimilation, homophily, and the dynamics of polarization. Proc. Natl. Acad. Sci. USA 2013, 110, 5791–5796. [Google Scholar] [CrossRef]
- Haghtalab, N.; Jackson, M.O.; Procaccia, A.D. Belief polarization in a complex world: A learning theory perspective. Proc. Natl. Acad. Sci. USA 2021, 118, 44118. [Google Scholar] [CrossRef]
- Rossi, W.S.; Polderman, J.W.; Frasca, P. The Closed Loop Between Opinion Formation and Personalized Recommendations. IEEE Trans. Control. Netw. Syst. 2021, 9, 1092–1103. [Google Scholar] [CrossRef]
- Perra, N.; Rocha, L.E.C. Modelling opinion dynamics in the age of algorithmic personalisation. Sci. Rep. 2019, 9, 7261. [Google Scholar] [CrossRef]
- Goel, S.; Watts, D.J.; Goldstein, D.G. The structure of online diffusion networks. In Proceedings of the 13th ACM Conference on Electronic Commerce; ACM Digital Library: New York, NY, USA, 2012; pp. 623–638. [Google Scholar] [CrossRef]
- Weng, L.; Flammini, A.; Vespignani, A.; Menczer, F. Competition among memes in a world with limited attention. Sci. Rep. 2012, 2, 335. [Google Scholar] [CrossRef]
- Peralta, A.F.; Neri, M.; Kertész, J.; Iñiguez, G. Effect of algorithmic bias and network structure on coexistence, consensus, and polarization of opinions. Phys. Rev. E 2021, 104, 044312. [Google Scholar] [CrossRef]
- Maes, M.; Bischofberger, L. Will the Personalization of Online Social Networks Foster Opinion Polarization? SSRN 2015, 2553436. [Google Scholar] [CrossRef]
- Flache, A.; Mäs, M.; Feliciani, T.; Chattoe-Brown, E.; Deffuant, G.; Huet, S.; Lorenz, J. Models of Social Influence: Towards the Next Frontiers. J. Artif. Soc. Soc. Simul. 2017, 20, 18564. [Google Scholar] [CrossRef]
- Mäs, M. Challenges to simulation validation in the social sciences. A critical rationalist perspective. In Computer Simulation Validation: Fundamental Concepts, Methodological Frameworks, and Philosophical Perspectives; Beisbart, C., Saam, N.J., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 857–879. [Google Scholar] [CrossRef]
- Mastroeni, L.; Vellucci, P.; Naldi, M. Agent-Based Models for Opinion Formation: A Bibliographic Survey. IEEE Access 2019, 7, 58836–58848. [Google Scholar] [CrossRef]
- Noorazar, H. Recent advances in opinion propagation dynamics: A 2020 survey. Eur. Phys. J. Plus 2020, 135, 521. [Google Scholar] [CrossRef]
- Peralta, A.F.; Kertész, J.; Iñiguez, G. Opinion dynamics in social networks: From models to data. arXiv 2022, arXiv:2201.01322. [Google Scholar]
- Proskurnikov, A.V.; Tempo, R. A tutorial on modeling and analysis of dynamic social networks. Part I. Annu. Rev. Control 2017, 43, 65–79. [Google Scholar] [CrossRef]
- Proskurnikov, A.V.; Tempo, R. A tutorial on modeling and analysis of dynamic social networks. Part II. Annu. Rev. Control 2018, 45, 166–190. [Google Scholar] [CrossRef]
- Vazquez, F. Modeling and Analysis of Social Phenomena: Challenges and Possible Research Directions. Entropy 2022, 24, 491. [Google Scholar] [CrossRef]
- De Marzo, G.; Zaccaria, A.; Castellano, C. Emergence of polarization in a voter model with personalized information. Phys. Rev. Res. 2020, 2, 043117. [Google Scholar] [CrossRef]
- Clifford, P.; Sudbury, A. A model for spatial conflict. Biometrika 1973, 60, 581–588. [Google Scholar] [CrossRef]
- Huszár, F.; Ktena, S.I.; O’brien, C.; Belli, L.; Schlaikjer, A.; Hardt, M. Algorithmic amplification of politics on Twitter. Proc. Natl. Acad. Sci. USA 2021, 119, 34119. [Google Scholar] [CrossRef] [PubMed]
- Santos, F.P.; Lelkes, Y.; Levin, S.A. Link recommendation algorithms and dynamics of polarization in online social networks. Proc. Natl. Acad. Sci. USA 2021, 118, 41118. [Google Scholar] [CrossRef] [PubMed]
- Aral, S.; Walker, D. Creating Social Contagion Through Viral Product Design: A Randomized Trial of Peer Influence in Networks. Manag. Sci. 2011, 57, 1623–1639. [Google Scholar] [CrossRef]
- Centola, D.; Macy, M. Complex Contagions and the Weakness of Long Ties. SSRN Electron. J. 2007, 113, 702–734. [Google Scholar] [CrossRef]
- Iribarren, J.L.; Moro, E. Branching dynamics of viral information spreading. Phys. Rev. E 2011, 84, 046116. [Google Scholar] [CrossRef] [PubMed]
- Juul, J.L.; Ugander, J. Comparing information diffusion mechanisms by matching on cascade size. Proc. Natl. Acad. Sci. USA 2021, 118, 86118. [Google Scholar] [CrossRef]
- Liben-Nowell, D.; Kleinberg, J. Tracing information flow on a global scale using Internet chain-letter data. Proc. Natl. Acad. Sci. USA 2008, 105, 4633–4638. [Google Scholar] [CrossRef]
- Bonifazi, G.; Cauteruccio, F.; Corradini, E.; Marchetti, M.; Pierini, A.; Terracina, G.; Ursino, D.; Virgili, L. An approach to detect backbones of information diffusers among different communities of a social platform. Data Knowl. Eng. 2022, 140, 102048. [Google Scholar] [CrossRef]
- Corradini, E.; Nocera, A.; Ursino, D.; Virgili, L. Investigating negative reviews and detecting negative influencers in Yelp through a multi-dimensional social network based model. Int. J. Inf. Manag. 2021, 60, 102377. [Google Scholar] [CrossRef]
- Bond, R.M.; Fariss, C.J.; Jones, J.J.; Kramer, A.D.; Marlow, C.; Settle, J.E.; Fowler, J.H. A 61-million-person experiment in social influence and political mobilization. Nature 2012, 489, 295. [Google Scholar] [CrossRef]
- Kozitsin, I.V. A general framework to link theory and empirics in opinion formation models. Sci. Rep. 2022, 12, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Cialdini, R.B.; Goldstein, N.J. Social Influence: Compliance and Conformity. Annu. Rev. Psychol. 2004, 55, 591–621. [Google Scholar] [CrossRef] [PubMed]
- Centola, D. The Spread of Behavior in an Online Social Network Experiment. Science 2010, 329, 1194–1197. [Google Scholar] [CrossRef] [PubMed]
- Christakis, N.A.; Fowler, J.H. Social contagion theory: Examining dynamic social networks and human behavior. Stat. Med. 2013, 32, 556–577. [Google Scholar] [CrossRef]
- Guilbeault, D.; Centola, D. Topological measures for identifying and predicting the spread of complex contagions. Nat. Commun. 2021, 12, 4430. [Google Scholar] [CrossRef]
- Carpentras, D.; Maher, P.J.; O’Reilly, C.; Quayle, M. Deriving an Opinion Dynamics Model from Experimental Data. J. Artif. Soc. Soc. Simul. 2022, 25, 4. [Google Scholar] [CrossRef]
- Kozitsin, I.V. Opinion dynamics of online social network users: A micro-level analysis. J. Math. Sociol. 2023, 47, 1–41. [Google Scholar] [CrossRef]
- Cota, W.; Ferreira, S.C.; Pastor-Satorras, R.; Starnini, M. Quantifying echo chamber effects in information spreading over political communication networks. EPJ Data Sci. 2019, 8, 1–13. [Google Scholar] [CrossRef]
- Aral, S.; Nicolaides, C. Exercise contagion in a global social network. Nat. Commun. 2017, 8, 14753. [Google Scholar] [CrossRef]
- Schelling, T.C. Models of segregation. Am. Econ. Rev. 1969, 59, 488–493. [Google Scholar]
- Backstrom, L.; Huttenlocher, D.; Kleinberg, J.; Lan, X. Group formation in large social networks: Membership, growth, and evolution. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; ACM Digital Library: New York, NY, USA, 2006; pp. 44–54. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).