Unbalanced Web Phishing Classification through Deep Reinforcement Learning
Abstract
1. Introduction
- It extends the current state-of-the-art in DRL algorithms that addresses the web phishing detection task.
- It extends the algorithm proposed in [13] since:
- The ICMDP formulation is used to tackle class skew in web phishing detection;
- DQN is replaced with DDQN.
- It shows a benchmark between the proposed DDQN-based classifier and some state-of-the-art DL algorithms combined with data-level sampling techniques, in which metric scores suitable for unbalanced classification problems and algorithm timing performance are evaluated.
2. Background and Related Work
2.1. Reinforcement Learning
Q-Learning
2.2. Deep Reinforcement Learning
2.2.1. Deep Q-Network
2.2.2. Double Deep Q-Network
2.3. Deep Reinforcement Learning for Intrusion Detection
2.4. Handle Class Imbalance in Web Phishing Classification
3. Combining ICMDP with DDQN for Unbalanced Web Phishing Classification
3.1. ICMDP Environment Setting
- The observation space S is given by the training set, i.e., . As a consequence, each training sample represents an observation on a given t. In our model, positive samples are the phishing URLs and represent the minority class denoted with . On the other hand, the negative class comprises legitimate URLs representing the majority class . Hence, .
- The action space A consists of the set of predictable class labels. In particular, , where 0 and 1 are the negative and positive sample labels, respectively. Therefore, guides the agent classification actions according to .
- The reward function gives feedback on the quality of classification actions performed by the agent during its learning phase. In particular, the agent is positively rewarded if it correctly classifies a sample belonging to , i.e., if the action performed results in a true positive (TP). On the contrary, the agent is negatively rewarded if the classification action performed on a sample belonging to results in a false positive (FP). The classification actions related to samples belonging to the majority classes are rewarded based on the actual balancing ratio . In particular, corresponds to a misclassification of a sample belonging to , i.e., a false negative (FN); otherwise, is assigned to a correct classification of a sample belonging to , i.e., a true negative (TN). Since of the minority class is higher (in absolute value) than that of the majority class, the agent will be more sensitive in classifying samples belonging to . Finally, can be expressed as:where refers to the true value of the class to which the observed sample belongs. Furthermore, , and under such a hypothesis, the reward changes in a formulation as well as in the same expression used in [13].
- Following the definition of S, the states-transition probability function is deterministic, since the agent moves from to according to the order in which the samples appear in S.
- All the samples within S are classified.
- The agent classification action results in a FP.
3.2. Reward-Sensitive DDQN Training Phase
4. Experimental Setup
4.1. Web Phishing Dataset Description
4.2. Metrics Used to Evaluate Classification Performance
- Geometric mean: In binary classification problems, the geometric mean (G-Mean) is calculated as the square root of the product between the TPR and the true negative rate (TNR), where . It measures the balance between classification performances in both minority and majority classes in terms of TPR and TNR, respectively. A very high value of TPR (TNR) can be due to a biased classification that cannot handle data imbalance. This scenario will not result in an acceptable G-Mean value.
- Index of balanced accuracy: Introduced in [55], it measures the degree of balance between two scores. This is achieved using the so-called dominance , which is computed as the difference between TPR and TNR. Since . As a consequence, both rates are balanced if is close to 0. The correlation of the G-Mean (for simplicity, the authors suggest the use of ) and the results in a curve, namely balanced accuracy graph (BAG). The index of balanced accuracy (IBA) is defined as the area of the rectangle obtained considering the following series of points in the BAG: , where the point represents the trade-off between and . The highest value corresponds to . The weighting factor is introduced to make the influence of more stable. In our experiments , according to the default value of the Imbalanced-learn library [56].
4.3. DDQN-Based Classifier Implementation Details and Hyperparameter Settings
4.4. Deep Learning Classifiers and Data Sampling Techniques Selected for Benchmark
4.4.1. Deep Learning Classifiers
- Deep neural network (DNN): This is a conventional feed-forward neural network having two hidden layers with 256 nodes, with each node having a RELU activation function. The data are then forwarded to the classification layer, which has a unique node with a sigmoid activation function.
- Convolutional neural network (CNN): This model combines convolutional and pooling layers. The first aims at detecting local conjunctions between features, while the second tries to merge semantically similar features into a single one. Therefore, the convolutional layer extracts the relevant features, and the pooling layer reduces their dimensions. Finally, a fully connected layer is used to perform the classification. Datasets that present one-dimensional data, i.e., vector structure, can be processed using a one-dimensional CNN (CONV1D) [63] layer. In particular, the model employs a CONV1D layer with 128 filters, 3 as the kernel size, and a hyperbolic tangent activation function. The data are then forwarded through a flatten layer to a classification node that has a sigmoid activation function.
- Long short-term memory: This is a model belonging to the class of RNN. Unlike a classical feed-forward neural network, an RNN can create cycles. The architecture of long short-term memory (LSTM) introduced in [64] consists of three gates in its hidden layers, namely an input gate, an output gate, and a forget gate. These entities form the so-called cell, which controls the information flow necessary for prediction purposes. The LSTM used in our experiments has 128 units (size of hidden cells) connected to a final layer, which is a classification layer having a sigmoid activation function.
- Bidirectional long short-term memory (BiLSTM): This differs from the above mentioned for the adoption of a bidirectional layer, which can improve prediction accuracy by pulling future data in addition to the previous data captured as input [65].
4.4.2. Data Sampling Techniques
- Oversampling:
- –
- Random oversampling (ROS): This technique is the simplest since it randomly duplicates samples within to obtain .
- –
- Synthetic minority oversampling technique (SMOTE) [66]: This balancing technique initially finds the K-NNs for each sample x within by computing the Euclidean distance between it and all other samples in . Then, according to the actual value, a sampling rate is established, and for each sample in , elements are randomly selected from its K-NNs, to build a new set , such that . Finally, a new synthetic sample is created for each sample , with , using the following formula: , where the function randomly selects a number between 0 and 1.
- –
- Adaptive synthetic (ADASYN) [67]: This strategy initially computes and the number of synthetic data to be generated, which is given by , where indicates the value to achieve after applying the balancing algorithm. In our experiment, is considered. For each sample within , the algorithm finds the K-NNs based on the Euclidean distance calculated according to the feature space and computes the coefficient , where defines the dominance of the majority class in each specific neighborhood, since it is equal to the number of samples belonging to the majority class within the nearest K. Since , such a value is normalized using the sum of all coefficients (), resulting in the density distribution . Finally, the number of total synthetic samples generated for each neighborhood is calculated as .
- Undersampling:
- –
- Random undersampling (RUS): This technique randomly selects the samples to be removed from until is obtained.
- –
- Tomek-Links (T-Link) [68]: This technique is applied considering the following strategy. Let be two samples, respectively, in and . The Euclidean distance in the feature space is then computed. This value represents a T-Link if, for any sample z, one of the following inequality , , holds. In such a case, y will be removed.
- –
- One-sided selection (OSS) [69]: This technique first employs T-Link; thus, the condensed closest-neighbor rule is applied to remove the consistent subsets. A subset is consistent if using a K-NN , C correctly classifies D.
- Hybrid:
4.5. Hardware Settings Used in the Experimental Phase
5. Performance Evaluation
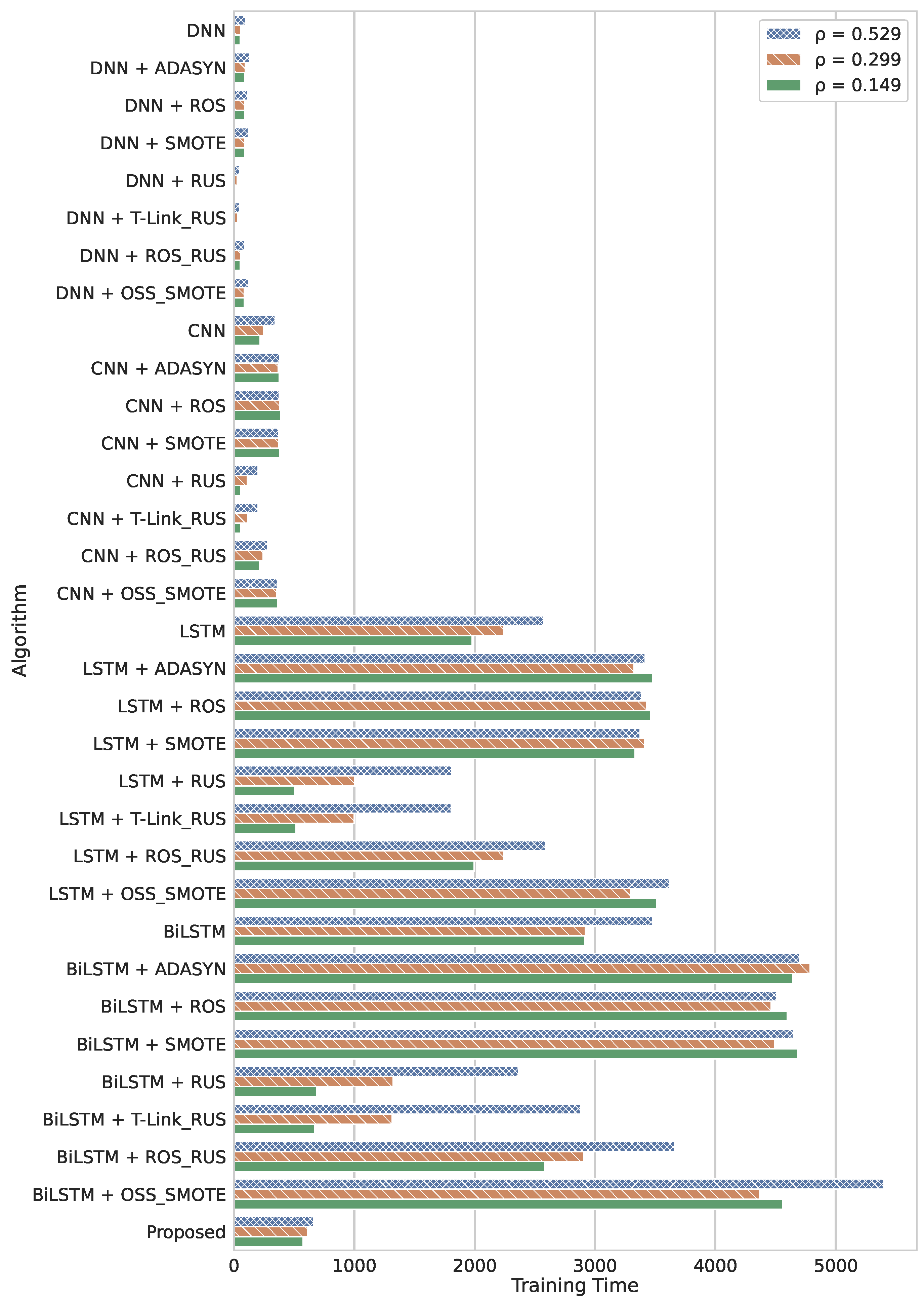
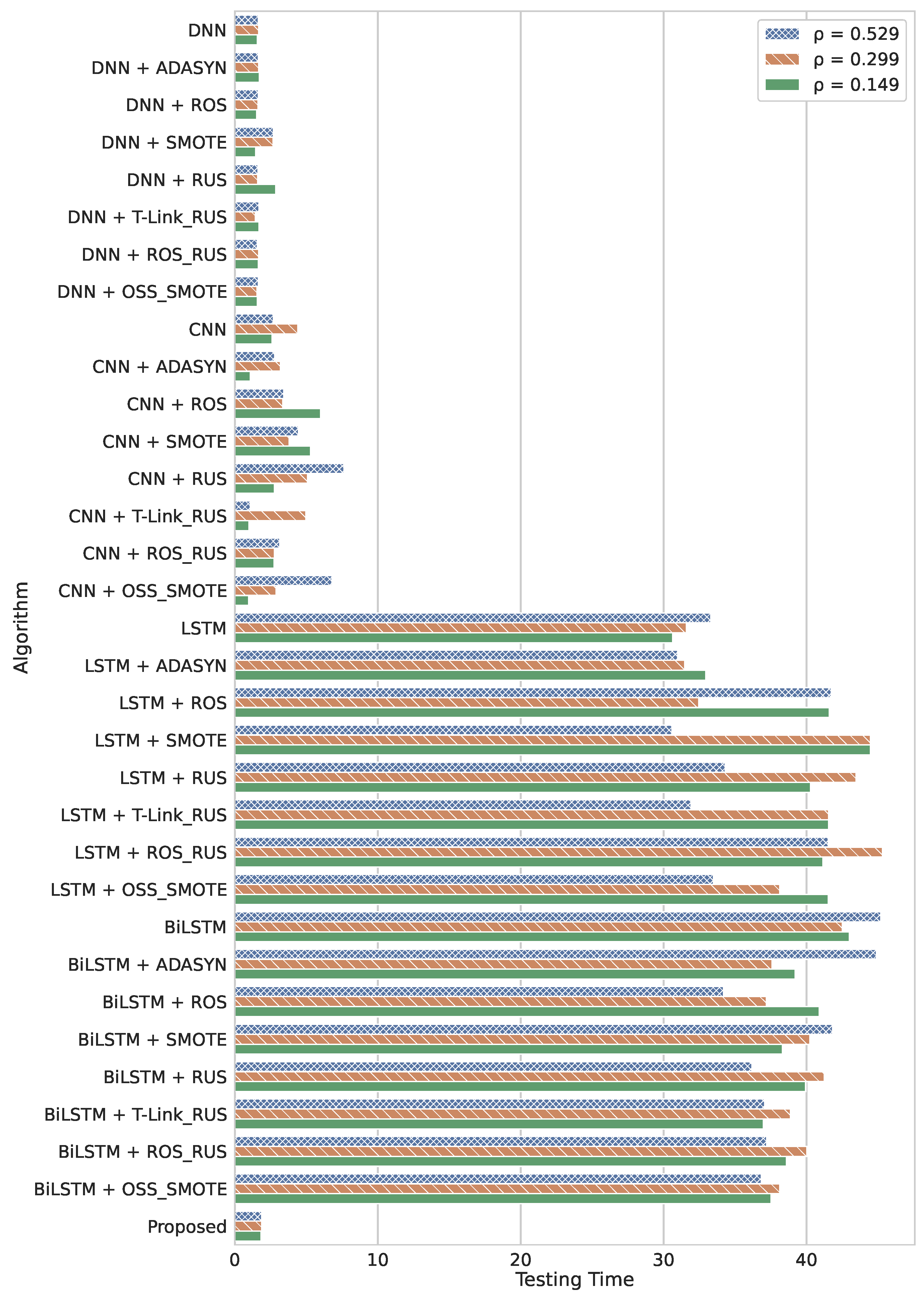
5.1. Timing Performance
5.1.1. Training Time
5.1.2. Testing Time
5.2. Classification Performance
- The CNN, LSTM, and BiLSTM algorithms share the same overall trend in the results obtained. In particular, we can observe that these algorithms are able to minimize the FN (i.e., high recall) score, but they result in many FPs (i.e., low precision) in each case. As a consequence of the low precision value, the maximum F1 score does not reach for any of them. In some cases, CNN and LSTM achieve the best recall score (∼98%) among all algorithms compared. This results in G-Mean and AUC close to and IBA∼0.8. The highest precision score (∼98.5%) is obtained by the LSTM combined with RUS. However, in this case, other metrics show that LSTM becomes a random guessing classifier. Therefore, data imbalance affects the performance achieved by the minority class. Furthermore, the combination with data-level balancing techniques does not improve classification performance. G-Mean and AUC are influenced by a high recall value, while the low IBA reflects that these algorithms are not suitable in any case for dealing with the unbalanced classification problem.
- The DNN algorithm shows good performance, especially when combined with SMOTE or OSS-SMOTE. In these two cases, the high-recall-low-precision trend is less evident since a higher precision value is shown than that achieved by LSTM, BiLSTM and CNN trio. The good trade-off between precision and recall results in an F1 score close to . Furthermore, the high recall score results in a high G-Mean (both in the range of ) and AUC. Finally, an IBA equal to ∼0.86 and ∼0.845 is reached, respectively. Moreover, DNN achieves the best recall score when combined with ROS. However, in this case, the precision score obtained (high value of FP) penalizes the overall unbalanced classification performances. DNN combined with ADASYN works similarly to DNN without prior data-level sampling techniques. Finally, RUS usage leads to worse overall performance unless used in hybrid approaches. For example, T-Link with RUS results in classification metrics very close to those achieved by OSS with SMOTE.
- The proposed DDQN-based classifier outperforms the compared algorithms in terms of G-Mean, IBA, F1 score, and AUC. The highest value of F1 score () denotes the best trade-off between precision and recall, equal to and , respectively. The TNR equal to results in a very high G-Mean value (∼94%) due to the TPR-TNR balance and the dominance very close to 0. As a consequence of high , a very high IBA value (∼0.885) is obtained. Finally, the AUC is very close to .
- The results obtained using CNN, LSTM and BiLSTM show the same low-precision-high-recall of Table 5. In this case, LSTM achieves the best precision score () when combined with ROS-RUS hybrid technique, while the highest recall value () is obtained by LSTM and BiLSTM combined with T-Link-RUS. However, these results are misleading, since other classification metric scores are very poor and denote random guessing classifications performed by all three algorithms. In this case, an F1 score that does not reach is obtained, and again G-Mean and AUC are positively influenced by the high recall. Finally, IBA the trend is worse than those achieved by the same algorithms as evaluated in the previous test ().
- DNN does not result in acceptable scores if not combined with data-level sampling techniques. Despite achieving a high precision, the recall score is very low, denoting several FNs. Therefore, in such an experiment, DNN requires using data-level sampling techniques. Performances improve significantly when DNN is combined with ROS, resulting in an F1 score close to , a G-Mean∼92%, and an AUC∼0.92. The IBA score is in the range of , which is similar to the one achieved by combining DNN with ADASYN. However, the latter is disadvantageous due to a high FP (i.e., low precision score). On the other hand, the usage of ROS and RUS techniques increased FN, while SMOTE and RUS led DNN to results comparable to the low-precision-high-recall trend of CNN, LSTM and BiLSTM. Finally, combining OSS-SMOTE with DNN does not improve performances better than the case in which no data-level balancing technique is adopted.
- In this case, the proposed DDQN-based classifier achieves better G-Mean, IBA, F1 score, and AUC scores than other benchmark algorithms. The F1 score is ∼90.5% due to the trade-off between precision () and recall (). Both TPR and TNR achieved high results (). Therefore, the high G-Mean score () denotes the balance between TPR and TNR. Furthermore, IBA is equal to due to superb dominance , which is equal to . Finally, the achieved AUC is . The overall performances are very similar to those obtained for the experiment reported in Table 5 i.e., .
- CNN, LSTM, and BiLSTM confirm the low-precision-high-recall trend already observed in both the above-discussed tests. In this case, BiLSTM achieves the best precision () when combined with RUS. However, other classification metric scores reveal that it is a random guess classifier. None of these algorithms achieve a G-Mean equal to and an IBA greater than . The maximum F1 score () is achieved by combining CNN with RUS and LSTM with ROS, respectively.
- DNN shows good performance in handling class imbalances when combined with SMOTE or RUS. In the first case, a low number of FPs is highlighted by a high precision score (), which combined with a recall equal to results in an F1 score equal to . DNN with RUS outperforms DNN with SMOTE in terms of G-Mean, IBA, and AUC due to a high recall (∼93%). Combining DNN with ROS results in the best recall score () achieved by all algorithms for this experiment. However, many FPs (precision ∼67%) affect the overall classifier performances. This trend is very similar to the one observed by using ADASYN instead of ROS as an oversampling technique. DNN combined with ROS-RUS or T-Link-RUS results in high FN. Finally, using OSS-SMOTE as a data-level sampling strategy achieves good performances, but a very low IBA value (∼0.7) is obtained.
- The proposed algorithm achieved better results in terms of G-Mean, IBA, F1 score, and AUC compared with other DL algorithms. Despite the limited availability of minority class samples, the proposed DDQN-based classifier is capable of balancing performance in both classes. It achieves since recall = 92.6% and TNR = 92.8%. As a consequence, G-Mean is the average mean between these two values, i.e., . The IBA of ∼0.86 follows. A very good precision value () positively influences the F1 score, which is close to . Finally, AUC denotes good performance thanks to an overall score of .
Effectiveness of the Proposed Unbalanced Classifier
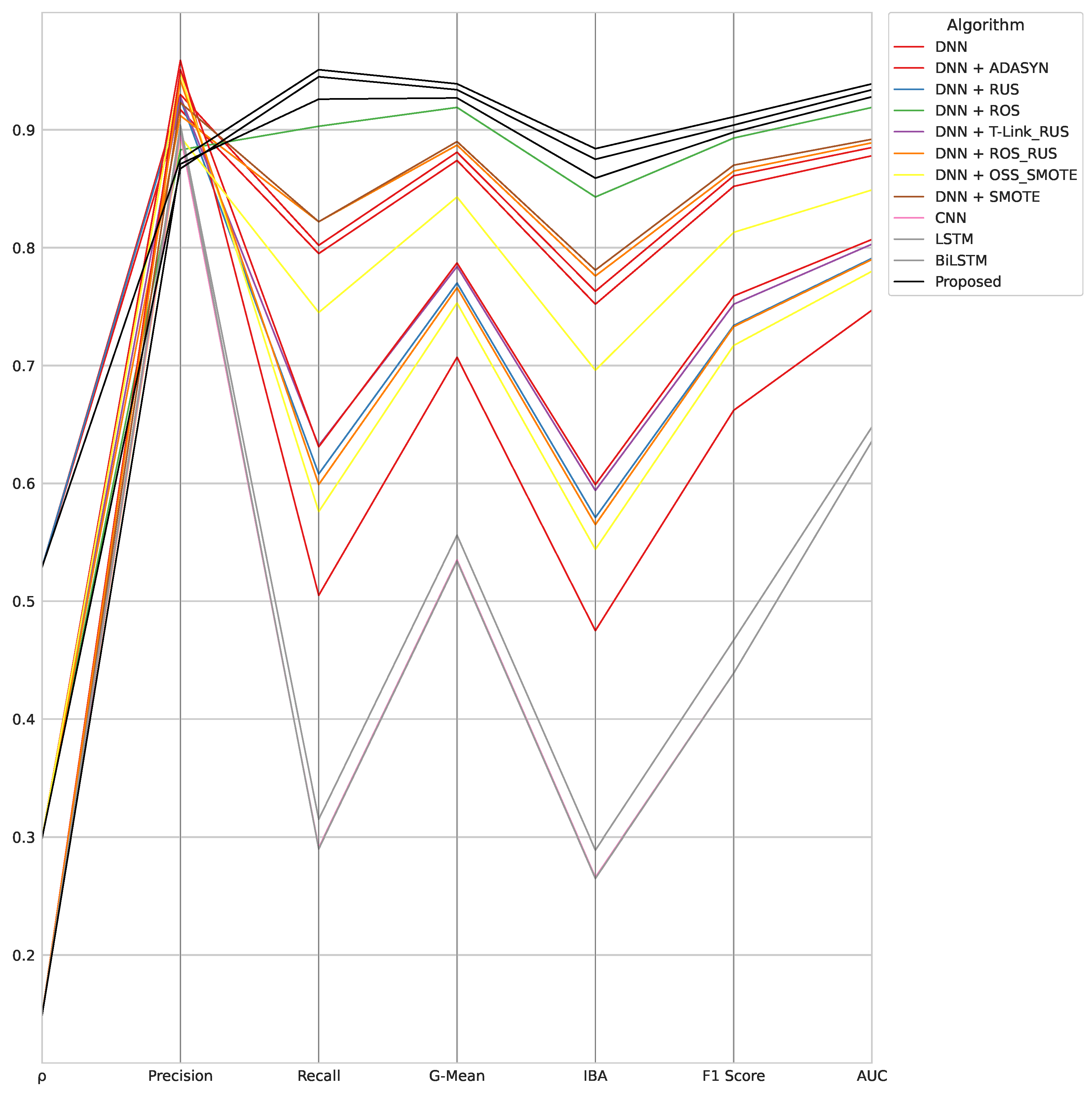
- The algorithmic robustness of the best performers for each algorithmic framework, i.e., for each different DL classifier involved (Figure 5). In such an analysis, in the cases where two classifiers belonging to the same framework (same classifier and a different data-level sampling strategy) achieve the same metric score, and the algorithm that appears most frequently in the top performers is selected.
- The DNN combined with ROS is the second-best performer in terms of problem-specific metrics achieved for . However, in the other experiments, it achieves only the best recall score for . DNN combined with RUS is the second-best performer in terms of G-Mean, IBA, and AUC only for . In the same experiment, the same DL classifier achieves the second-best F1 score when combined with SMOTE. However, DNN combined with SMOTE shows an irregular trend, as it alternates good results for different experiments in different metrics. In particular, it achieves the second-best G-Mean, IBA, and AUC for and the fourth-best recall value for . DNN combined with OSS-SMOTE achieves only the best F1 score score for . DNN without data-level sampling techniques only obtains the best precision scores for and , respectively. Similarly, DNN combined with ADASYN achieves only the best precision for . Finally, DNN combined with ROS-RUS is the fourth-best performer in the recall ranking for .
- The CNN without data-level sampling strategies is the fourth-best performer in terms of problem-specific metrics achieved for . Furthermore, in the same experiment, it appears in the precision top performers, as well as for . In the case of , it achieves the best recall score. For the latter experiment, CNN combined with T-Link-RUS is ranked as the fourth-best performer in terms of G-Mean, IBA, F1 score, and AUC. The CNN combined with RUS performs similarly for . Moreover, such an algorithm achieves the best recall for . CNN combined with SMOTE achieves only the second-best recall score for .
- The LSTM combined with OSS-SMOTE represents the top performer in each metric evaluated for the DL framework considered in the case of . Furthermore, it achieves the best problem-specific metric scores (again according to the DL framework) for . In the case of , LSTM achieves the second-best recall score without using data-level sampling techniques. The same algorithm results in the best unbalanced classification metrics for its category in such an experiment.
- The BiLSTM achieves the third-best recall score when combined with T-Link-RUS for . In the same experiment, the fourth-best precision and the fifth-best F1 score metrics are obtained by BiLSTM combined with RUS. A similar ranking level is recorded for BiLSTM combined with ROS-RUS for G-Mean, IBA, and AUC metrics. The latter algorithm appears in the same position also in the evaluation of problem-specific metrics for . In the same experiment, it reaches the fourth-best recall score, while the second-best precision is obtained for the BiLSTM without the support of data-level sampling techniques. For , BiLSTM combined with SMOTE is the best performer per category in all metrics evaluated.
- A compared classifier may be better than the proposed DDQN-based in either precision or recall, but not in both.
- A classifier that identifies a large portion of malicious samples, avoiding FP (FN), i.e., achieving a high precision (recall), is not necessarily satisfactory for addressing the present research problem, which requires a balanced precision-recall trend.
- The algorithms that outperform the proposed one in precision are divided per experiment as follows:
- –
- DNN, DNN with ADASYN, and DNN with RUS for ;
- –
- DNN, DNN with ROS, DNN with T-Link-RUS, DNN with ROS-RUS, and DNN with SMOTE for ;
- –
- DNN, DNN with SMOTE, DNN with ROS-RUS, DNN with OSS-SMOTE, CNN, LSTM, BiLSTM for .
On the other hand, our algorithm scores better on the remaining metrics, including recall, regardless of . - Focusing on classifiers that achieve a higher precision score than the proposed one, a common triangular pattern can be observed in the middle part of the parallel coordinate plot, due to similar recall and IBA scores, and a higher G-Mean value. Therefore, given the triangle built by the trio of points <Recall, G-Mean, IBA>, the higher its height, the greater the influence of precision on the G-Mean, i.e., low FP (high precision, high TNR) and high FN (low recall). As a consequence, the classifier correctly predicts positive samples but is not able to distinguish them from negative ones in more cases. This is a serious issue in real-life applications because legitimate URLs outnumber malicious ones.
- The algorithms that outperform the proposed one in recall are divided per experiment as follows:
- –
- CNN combined with one of the selected data-level sampling techniques, LSTM with ADASYN, LSTM with ROS, LSTM with SMOTE, LSTM with OSS-SMOTE, and BiLSTM with ADASYN, BiLSTM with ROS, BiLSTM with SMOTE, BiLSTM with ROS-RUS and BiLSTM with OSS-SMOTE in all the experiments;
- –
- CNN, LSTM, and BiLSTM with RUS for and ;
- –
- DNN with ROS, LSTM with ROS-RUS, and LSTM with T-Link-RUS for and ;
- –
- DNN with ADASYN and DNN with RUS for and ;
- –
- DNN with ROS-RUS, BiLSTM, BiLSTM with T-Link-RUS for ;
- –
- DNN with SMOTE for .
On the other hand, our algorithm scores better on the remaining metrics, including precision, regardless of . - Focusing on classifiers that achieve a higher precision score than the proposed one, a triangle formed by the trio of points <Precision, Recall, IBA> having a high height (recall spike very far from precision and IBA) denotes the high influence of the recall on the G-Mean, i.e., low FN (high recall) and high FP (low precision). In these cases, the classifier correctly predicts positive samples but classifies the negative samples as positive in more cases. Such a result is undesired, as in real-life scenarios, navigating to legitimate URLs must be guaranteed.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADASYN | ADAptive SYNthetic |
| AUC | Area Under ROC Curve |
| BAG | Balanced Accuracy Graph |
| BiLSTM | Bidirectional Long Short Term Memory |
| CNN | Convolutional Neural Network |
| DDPG | Deep Deterministic Policy Gradient |
| DDQN | Double Deep Q-Network |
| DL | Deep Learning |
| DNN | Deep Neural Network |
| DQN | Deep Q-Network |
| DRL | Deep Reinforcement Learning |
| FN | False Negative |
| FP | False Positive |
| IBA | Index of Balanced Accuracy |
| ICMDP | Imbalanced Classification Markov Decision Process |
| LSTM | Long Short-Term Memory |
| MDP | Markov Decision Process |
| ML | Machine Learning |
| MLP | Multi-Layer Perceptron |
| OSS | One Sided Selection |
| RL | Reinforcement Learning |
| RNN | Recurrent Neural Network |
| ROC | Receiver Operating Characteristic |
| ROS | Random Oversampling |
| RUS | Random Undersampling |
| SDN | Software Defined Network |
| SMOTE | Synthetic Minority Oversampling TEchnique |
| SVM | Support Vector Machine |
| T-Link | Tomek-Links |
| TN | True Negative |
| TNR | True Negative Rate |
| TP | True Positive |
| TPR | True Positive Rate |
| URL | Uniform Resource Locator |
| USA | United States of America |
References
- Lu, J.; Liu, A.; Dong, F.; Gu, F.; Gama, J.; Zhang, G. Learning under Concept Drift: A Review. IEEE Trans. Knowl. Data Eng. 2019, 31, 2346–2363. [Google Scholar] [CrossRef]
- Menon, A.G.; Gressel, G. Concept Drift Detection in Phishing Using Autoencoders. In Proceedings of the Machine Learning and Metaheuristics Algorithms, and Applications (SoMMA), Chennai, India, 14–17 October 2020; Thampi, S.M., Piramuthu, S., Li, K.C., Berretti, S., Wozniak, M., Singh, D., Eds.; Springer: Singapore, 2021; pp. 208–220. [Google Scholar] [CrossRef]
- Raza, M.; Jayasinghe, N.D.; Muslam, M.M.A. A Comprehensive Review on Email Spam Classification using Machine Learning Algorithms. In Proceedings of the 2021 International Conference on Information Networking (ICOIN), Jeju, Republic of Korea, 13–16 January 2021; pp. 327–332. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep Reinforcement Learning: A Brief Survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Liang, X.; Zhao, D.; Huang, J.; Xu, X.; Dai, B.; Miao, Q. Deep Reinforcement Learning: A Survey. IEEE Trans. Neural Netw. Learn. Syst. 2022, in press. [Google Scholar] [CrossRef] [PubMed]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar] [CrossRef]
- Stekolshchik, R. Some approaches used to overcome overestimation in Deep Reinforcement Learning algorithms. arXiv 2022, arXiv:2006.14167. [Google Scholar] [CrossRef]
- van Hasselt, H.; Guez, A.; Silver, D. Deep Reinforcement Learning with Double Q-learning. arXiv 2015, arXiv:1509.06461. [Google Scholar] [CrossRef]
- Lopez-Martin, M.; Carro, B.; Sanchez-Esguevillas, A. Application of deep reinforcement learning to intrusion detection for supervised problems. Expert Syst. Appl. 2020, 141, 112963. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Reddi, V.J. Deep Reinforcement Learning for Cyber Security. IEEE Trans. Neural Netw. Learn. Syst. 2021, in press. [Google Scholar] [CrossRef]
- Sarker, I.H. Deep Cybersecurity: A Comprehensive Overview from Neural Network and Deep Learning Perspective. SN Comput. Sci. 2021, 2, 154. [Google Scholar] [CrossRef]
- Do, N.Q.; Selamat, A.; Krejcar, O.; Herrera-Viedma, E.; Fujita, H. Deep Learning for Phishing Detection: Taxonomy, Current Challenges and Future Directions. IEEE Access 2022, 10, 36429–36463. [Google Scholar] [CrossRef]
- Chatterjee, M.; Namin, A.S. Detecting Phishing Websites through Deep Reinforcement Learning. In Proceedings of the 2019 IEEE 43rd Annual Computer Software and Applications Conference (COMPSAC), Milwaukee, WI, USA, 15–19 July 2019; Volume 2, pp. 227–232. [Google Scholar] [CrossRef]
- Do, N.Q.; Selamat, A.; Krejcar, O.; Yokoi, T.; Fujita, H. Phishing Webpage Classification via Deep Learning-Based Algorithms: An Empirical Study. Appl. Sci. 2021, 11, 9210. [Google Scholar] [CrossRef]
- Thabtah, F.; Hammoud, S.; Kamalov, F.; Gonsalves, A. Data imbalance in classification: Experimental evaluation. Inf. Sci. 2020, 513, 429–441. [Google Scholar] [CrossRef]
- Dablain, D.; Krawczyk, B.; Chawla, N.V. DeepSMOTE: Fusing Deep Learning and SMOTE for Imbalanced Data. IEEE Trans. Neural Netw. Learn. Syst. 2022, in press. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.; Khoshgoftaar, T. Survey on deep learning with class imbalance. J. Big Data 2019, 6, 27. [Google Scholar] [CrossRef]
- Hu, X.; Chu, L.; Pei, J.; Liu, W.; Bian, J. Model complexity of deep learning: A survey. Knowl. Inf. Syst. 2021, 63, 2585–2619. [Google Scholar] [CrossRef]
- Siddhesh Vijay, J.; Kulkarni, K.; Arya, A. Metaheuristic Optimization of Neural Networks for Phishing Detection. In Proceedings of the 2022 3rd International Conference for Emerging Technology (INCET), Belgaum, India, 27–29 May 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Ul Hassan, I.; Ali, R.H.; Ul Abideen, Z.; Khan, T.A.; Kouatly, R. Significance of machine learning for detection of malicious websites on an unbalanced dataset. Digital 2022, 2, 501–519. [Google Scholar] [CrossRef]
- Pristyanto, Y.; Dahlan, A. Hybrid Resampling for Imbalanced Class Handling on Web Phishing Classification Dataset. In Proceedings of the 2019 4th International Conference on Information Technology, Information Systems and Electrical Engineering (ICITISEE), Yogyakarta, Indonesia, 20–21 November 2019; pp. 401–406. [Google Scholar] [CrossRef]
- Lin, E.; Chen, Q.; Qi, X. Deep Reinforcement Learning for Imbalanced Classification. Appl. Intell. 2020, 50, 2488–2502. [Google Scholar] [CrossRef]
- Jang, B.; Kim, M.; Harerimana, G.; Kim, J.W. Q-Learning Algorithms: A Comprehensive Classification and Applications. IEEE Access 2019, 7, 133653–133667. [Google Scholar] [CrossRef]
- Hasselt, H. Double Q-learning. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 6–11 December 2010; Lafferty, J., Williams, C., Shawe-Taylor, J., Zemel, R., Culotta, A., Eds.; Curran Associates, Inc.: La Jolla, CA, USA; Volume 2, pp. 2613–2621. [Google Scholar]
- Mishra, P.; Varadharajan, V.; Tupakula, U.; Pilli, E.S. A Detailed Investigation and Analysis of Using Machine Learning Techniques for Intrusion Detection. IEEE Commun. Surv. Tutorials 2019, 21, 686–728. [Google Scholar] [CrossRef]
- Sewak, M.; Sahay, S.K.; Rathore, H. Deep Reinforcement Learning in the Advanced Cybersecurity Threat Detection and Protection. Inf. Syst. Front. 2022, 25, 589–611. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, M.; Ota, K.; Li, J.; Wu, J. Deep Reinforcement Learning based Smart Mitigation of DDoS Flooding in Software-Defined Networks. In Proceedings of the 2018 IEEE 23rd International Workshop on Computer Aided Modeling and Design of Communication Links and Networks (CAMAD), Barcelona, Spain, 17–19 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Shi, G.; He, G. Collaborative Multi-agent Reinforcement Learning for Intrusion Detection. In Proceedings of the 2021 7th IEEE International Conference on Network Intelligence and Digital Content (IC-NIDC), Beijing, China, 17–19 November 2021; pp. 245–249. [Google Scholar] [CrossRef]
- Dong, S.; Xia, Y.; Peng, T. Network Abnormal Traffic Detection Model Based on Semi-Supervised Deep Reinforcement Learning. IEEE Trans. Netw. Serv. Manag. 2021, 18, 4197–4212. [Google Scholar] [CrossRef]
- Gülmez, H.; Angin, P. A Study on the Efficacy of Deep Reinforcement Learning for Intrusion Detection. Sak. Univ. J. Comput. Inf. Sci. 2020, 4, 834048. [Google Scholar] [CrossRef]
- Hsu, Y.F.; Matsuoka, M. A Deep Reinforcement Learning Approach for Anomaly Network Intrusion Detection System. In Proceedings of the 2020 IEEE 9th International Conference on Cloud Networking (CloudNet), Virtual, 9–11 November 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Sujatha, V.; Prasanna, K.L.; Niharika, K.; Charishma, V.; Sai, K.B. Network Intrusion Detection using Deep Reinforcement Learning. In Proceedings of the 2023 7th International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 23–25 February 2023; pp. 1146–1150. [Google Scholar] [CrossRef]
- Caminero, G.; Lopez-Martin, M.; Carro, B. Adversarial environment reinforcement learning algorithm for intrusion detection. Comput. Netw. 2019, 159, 96–109. [Google Scholar] [CrossRef]
- Yang, B.; Arshad, M.H.; Zhao, Q. Packet-Level and Flow-Level Network Intrusion Detection Based on Reinforcement Learning and Adversarial Training. Algorithms 2022, 15, 453. [Google Scholar] [CrossRef]
- Alavizadeh, H.; Alavizadeh, H.; Jang-Jaccard, J. Deep Q-Learning Based Reinforcement Learning Approach for Network Intrusion Detection. Computers 2022, 11, 41. [Google Scholar] [CrossRef]
- Wheelus, C.; Bou-Harb, E.; Zhu, X. Tackling Class Imbalance in Cyber Security Datasets. In Proceedings of the 2018 IEEE International Conference on Information Reuse and Integration (IRI), Salt Lake City, UT, USA, 6–9 July 2018; pp. 229–232. [Google Scholar] [CrossRef]
- Abdelkhalek, A.; Mashaly, M. Addressing the class imbalance problem in network intrusion detection systems using data resampling and deep learning. J. Supercomput. 2023, 79, 10611–10644. [Google Scholar] [CrossRef]
- Fdez-Glez, J.; Ruano-Ordás, D.; Fdez-Riverola, F.; Méndez, J.R.; Pavón, R.; Laza, R. Analyzing the impact of unbalanced data on web spam classification. In Proceedings of the Distributed Computing and Artificial Intelligence, 12th International Conference, Skövde, Sweden, 21–23 September 2015; Springer: Berlin/Heidelberg, Germany, 2015; Volume 373, pp. 243–250. [Google Scholar] [CrossRef]
- Livara, A.; Hernandez, R. An Empirical Analysis of Machine Learning Techniques in Phishing E-mail detection. In Proceedings of the 2022 International Conference for Advancement in Technology (ICONAT), Goa, India, 21–22 January 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Gutierrez, C.N.; Kim, T.; Corte, R.D.; Avery, J.; Goldwasser, D.; Cinque, M.; Bagchi, S. Learning from the Ones that Got Away: Detecting New Forms of Phishing Attacks. IEEE Trans. Dependable Secur. Comput. 2018, 15, 988–1001. [Google Scholar] [CrossRef]
- Ahsan, M.; Gomes, R.; Denton, A. SMOTE Implementation on Phishing Data to Enhance Cybersecurity. In Proceedings of the 2018 IEEE International Conference on Electro/Information Technology (EIT), Rochester, MI, USA, 3–5 May 2018; pp. 531–536. [Google Scholar] [CrossRef]
- Priya, S.; Uthra, R.A. Deep learning framework for handling concept drift and class imbalanced complex decision-making on streaming data. Complex Intell. Syst. 2021, in press. [Google Scholar] [CrossRef]
- Abdul Samad, S.R.; Balasubaramanian, S.; Al-Kaabi, A.S.; Sharma, B.; Chowdhury, S.; Mehbodniya, A.; Webber, J.L.; Bostani, A. Analysis of the Performance Impact of Fine-Tuned Machine Learning Model for Phishing URL Detection. Electronics 2023, 12, 1642. [Google Scholar] [CrossRef]
- He, S.; Li, B.; Peng, H.; Xin, J.; Zhang, E. An Effective Cost-Sensitive XGBoost Method for Malicious URLs Detection in Imbalanced Dataset. IEEE Access 2021, 9, 93089–93096. [Google Scholar] [CrossRef]
- Tan, G.; Zhang, P.; Liu, Q.; Liu, X.; Zhu, C.; Dou, F. Adaptive Malicious URL Detection: Learning in the Presence of Concept Drifts. In Proceedings of the 2018 17th IEEE International Conference on Trust, Security and Privacy in Computing and Communications/12th IEEE International Conference on Big Data Science and Engineering (TrustCom/BigDataSE), New York, NY, USA, 1–3 August 2018; pp. 737–743. [Google Scholar] [CrossRef]
- Zhao, C.; Xin, Y.; Li, X.; Yang, Y.; Chen, Y. A Heterogeneous Ensemble Learning Framework for Spam Detection in Social Networks with Imbalanced Data. Appl. Sci. 2020, 10, 936. [Google Scholar] [CrossRef]
- Bu, S.J.; Cho, S.B. Deep Character-Level Anomaly Detection Based on a Convolutional Autoencoder for Zero-Day Phishing URL Detection. Electronics 2021, 10, 1492. [Google Scholar] [CrossRef]
- Xiao, X.; Xiao, W.; Zhang, D.; Zhang, B.; Hu, G.; Li, Q.; Xia, S. Phishing websites detection via CNN and multi-head self-attention on imbalanced datasets. Comput. Secur. 2021, 108, 102372. [Google Scholar] [CrossRef]
- Anand, A.; Gorde, K.; Antony Moniz, J.R.; Park, N.; Chakraborty, T.; Chu, B.T. Phishing URL Detection with Oversampling based on Text Generative Adversarial Networks. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 1168–1177. [Google Scholar] [CrossRef]
- Naim, O.; Cohen, D.; Ben-Gal, I. Malicious website identification using design attribute learning. Int. J. Inf. Secur. 2023, in press. [Google Scholar] [CrossRef]
- Vrbančič, G.; Fister, I., Jr.; Podgorelec, V. Datasets for phishing websites detection. Data Brief 2020, 33, 106438. [Google Scholar] [CrossRef]
- Vrbančič, G. Phishing Websites Dataset. 2020. Available online: https://data.mendeley.com/datasets/72ptz43s9v/1 (accessed on 30 November 2022).
- Safi, A.; Singh, S. A systematic literature review on phishing website detection techniques. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 590–611. [Google Scholar] [CrossRef]
- Wang, G.; Wong, K.W.; Lu, J. AUC-Based Extreme Learning Machines for Supervised and Semi-Supervised Imbalanced Classification. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 7919–7930. [Google Scholar] [CrossRef]
- García, V.; Mollineda, R.; Sánchez, J. Index of Balanced Accuracy: A Performance Measure for Skewed Class Distributions. In Proceedings of the Pattern Recognition and Image Analysis: 4th Iberian Conference, Póvoa de Varzim, Portugal, 10–12 June 2009; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5524, pp. 441–448. [Google Scholar] [CrossRef]
- Lemaître, G.; Nogueira, F.; Aridas, C.K. Imbalanced-learn: A Python Toolbox to Tackle the Curse of Imbalanced Datasets in Machine Learning. J. Mach. Learn. Res. 2017, 18, 1–5. [Google Scholar]
- van den Berg, T. imbDRL: Imbalanced Classification with Deep Reinforcement Learning. 2021. Available online: https://github.com/Denbergvanthijs/imbDRL (accessed on 16 November 2022).
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; van der Walt, S., Millman, J., Eds.; pp. 56–61. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI Gym. arXiv 2016, arXiv:1606.01540. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: https://www.tensorflow.org/ (accessed on 18 January 2023).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Yerima, S.Y.; Alzaylaee, M.K. High Accuracy Phishing Detection Based on Convolutional Neural Networks. In Proceedings of the 2020 3rd International Conference on Computer Applications & Information Security (ICCAIS), Riyadh, Saudi Arabia, 19–21 March 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar] [CrossRef]
- Elhassan, T.; Aljurf, M. Classification of imbalance data using tomek link (t-link) combined with random under-sampling (rus) as a data reduction method. Glob. J. Technol. Optim. 2016, 1, 111. [Google Scholar] [CrossRef]
- Kubat, M.; Matwin, S. Addressing the curse of imbalanced training sets: One-sided selection. In Proceedings of the Fourteenth International Conference on Machine Learning (ICML ’97) Citeseer, San Francisco, CA, USA, 8–12 July 1997; Volume 97, pp. 179–186. [Google Scholar]
- Johnson, J.M.; Khoshgoftaar, T.M. Deep Learning and Data Sampling with Imbalanced Big Data. In Proceedings of the 2019 IEEE 20th International Conference on Information Reuse and Integration for Data Science (IRI), Los Angeles, CA, USA, 30 July–1 August 2019; pp. 175–183. [Google Scholar] [CrossRef]
- Johnson, J.M.; Khoshgoftaar, T.M. The effects of data sampling with deep learning and highly imbalanced big data. Inf. Syst. Front. 2020, 22, 1113–1131. [Google Scholar] [CrossRef]




| No. Phishing URLs | No. Legitimate URLs | No. Features |
|---|---|---|
| 30,647 | 58,000 | 111 |
| 23,012 | 43,473 | |
| 13,012 | ↑ * | |
| 6506 | ↑ |
| No. Training Episodes | Optimizer | * | b ** |
|---|---|---|---|
| Adam | 128 |
| Algorithm | No. Training Epochs | Optimizer | * | Batch Size |
|---|---|---|---|---|
| DNN | 100 | Adam | 512 | |
| CNN | 40 | ↑ ** | ↑ | 256 |
| LSTM | 20 | ↑ | 128 | |
| BiLSTM | ↑ | ↑ | ↑ | ↑ |
| DL Classifier | Data-Level Sampling | Precision | Recall | G-Mean | IBA | F1 Score | AUC |
|---|---|---|---|---|---|---|---|
| DNN | None | 0.917 | 0.795 | 0.874 | 0.752 | 0.852 | 0.878 |
| ADASYN | 0.930 | 0.802 | 0.881 | 0.763 | 0.861 | 0.885 | |
| ROS | 0.784 | 0.960 | 0.907 | 0.832 | 0.863 | 0.909 | |
| SMOTE | 0.831 | 0.947 | 0.924 | 0.858 | 0.886 | 0.924 | |
| RUS | 0.926 | 0.608 | 0.770 | 0.571 | 0.734 | 0.791 | |
| T-Link with RUS | 0.868 | 0.887 | 0.908 | 0.821 | 0.877 | 0.908 | |
| ROS with RUS | 0.747 | 0.973 | 0.895 | 0.814 | 0.845 | 0.898 | |
| OSS with SMOTE | 0.864 | 0.914 | 0.919 | 0.844 | 0.888 | 0.919 | |
| CNN | None | 0.725 | 0.977 * | 0.886 | 0.799 | 0.832 | 0.890 |
| ADASYN | 0.724 | 0.977 | 0.888 | 0.803 | 0.832 | 0.892 | |
| ROS | 0.723 | 0.974 | 0.885 | 0.797 | 0.830 | 0.889 | |
| SMOTE | 0.727 | 0.976 | 0.886 | 0.799 | 0.834 | 0.890 | |
| RUS | 0.724 | 0.973 | 0.883 | 0.794 | 0.830 | 0.888 | |
| T-Link with RUS | 0.733 | 0.976 | 0.889 | 0.803 | 0.838 | 0.893 | |
| ROS with RUS | 0.728 | 0.977 | 0.888 | 0.803 | 0.834 | 0.892 | |
| OSS with SMOTE | 0.723 | 0.974 | 0.885 | 0.797 | 0.830 | 0.889 | |
| LSTM | None | 0.728 | 0.974 | 0.887 | 0.801 | 0.833 | 0.891 |
| ADASYN | 0.730 | 0.972 | 0.887 | 0.800 | 0.834 | 0.891 | |
| ROS | 0.723 | 0.976 | 0.886 | 0.799 | 0.831 | 0.890 | |
| SMOTE | 0.732 | 0.976 | 0.889 | 0.804 | 0.837 | 0.894 | |
| RUS | 0.984 | 0.016 | 0.129 | 0.015 | 0.032 | 0.508 | |
| T-Link with RUS | 0.730 | 0.974 | 0.888 | 0.801 | 0.835 | 0.891 | |
| ROS with RUS | 0.721 | 0.973 | 0.885 | 0.796 | 0.828 | 0.889 | |
| OSS with SMOTE | 0.733 | 0.977 | 0.891 | 0.807 | 0.838 | 0.894 | |
| BiLSTM | None | 0.732 | 0.975 | 0.886 | 0.799 | 0.836 | 0.890 |
| ADASYN | 0.730 | 0.975 | 0.888 | 0.802 | 0.835 | 0.892 | |
| ROS | 0.725 | 0.974 | 0.885 | 0.797 | 0.831 | 0.889 | |
| SMOTE | 0.727 | 0.972 | 0.887 | 0.800 | 0.832 | 0.891 | |
| RUS | 0.733 | 0.974 | 0.888 | 0.802 | 0.837 | 0.892 | |
| T-Link and RUS | 0.725 | 0.976 | 0.887 | 0.800 | 0.832 | 0.891 | |
| ROS with RUS | 0.731 | 0.974 | 0.889 | 0.804 | 0.835 | 0.893 | |
| OSS with SMOTE | 0.731 | 0.976 | 0.888 | 0.803 | 0.836 | 0.892 | |
| Proposed | None | 0.875 | 0.951 | 0.939 | 0.884 | 0.911 | 0.939 |
| DL Classifier | Data-Level Sampling | Precision | Recall | G-Mean | IBA | F1 Score | AUC |
|---|---|---|---|---|---|---|---|
| DNN | None | 0.959 | 0.505 | 0.707 | 0.475 | 0.662 | 0.747 |
| ADASYN | 0.786 | 0.965 | 0.911 | 0.840 | 0.867 | 0.913 | |
| ROS | 0.883 | 0.903 | 0.919 | 0.843 | 0.893 | 0.919 | |
| SMOTE | 0.744 | 0.972 | 0.893 | 0.810 | 0.843 | 0.896 | |
| RUS | 0.741 | 0.966 | 0.891 | 0.805 | 0.839 | 0.894 | |
| T-Link with RUS | 0.928 | 0.632 | 0.784 | 0.594 | 0.752 | 0.803 | |
| ROS with RUS | 0.912 | 0.822 | 0.887 | 0.776 | 0.865 | 0.889 | |
| OSS with SMOTE | 0.948 | 0.576 | 0.753 | 0.544 | 0.717 | 0.780 | |
| CNN | None | 0.733 | 0.978 | 0.889 | 0.804 | 0.838 | 0.893 |
| ADASYN | 0.730 | 0.975 | 0.888 | 0.802 | 0.835 | 0.892 | |
| ROS | 0.728 | 0.977 | 0.889 | 0.803 | 0.835 | 0.893 | |
| SMOTE | 0.723 | 0.979 | 0.886 | 0.799 | 0.832 | 0.890 | |
| RUS | 0.728 | 0.974 | 0.887 | 0.800 | 0.833 | 0.891 | |
| T-Link with RUS | 0.724 | 0.978 | 0.888 | 0.802 | 0.834 | 0.892 | |
| ROS with RUS | 0.728 | 0.973 | 0.887 | 0.800 | 0.833 | 0.891 | |
| OSS with SMOTE | 0.731 | 0.975 | 0.887 | 0.800 | 0.836 | 0.891 | |
| LSTM | None | 0.729 | 0.978 | 0.890 | 0.806 | 0.835 | 0.894 |
| ADASYN | 0.721 | 0.975 | 0.884 | 0.796 | 0.829 | 0.889 | |
| ROS | 0.730 | 0.976 | 0.887 | 0.801 | 0.835 | 0.891 | |
| SMOTE | 0.724 | 0.973 | 0.883 | 0.793 | 0.830 | 0.887 | |
| RUS | 0.340 | 0.988 | 0.011 | 0.001 | 0.505 | 0.494 | |
| T-Link with RUS | 0.348 | 0.999 * | 0.049 | 0.002 | 0.516 | 0.501 | |
| ROS with RUS | 0.990 | 0.016 | 0.128 | 0.014 | 0.032 | 0.508 | |
| OSS with SMOTE | 0.724 | 0.975 | 0.886 | 0.799 | 0.831 | 0.890 | |
| BiLSTM | None | 0.696 | 0.801 | 0.795 | 0.619 | 0.745 | 0.802 |
| ADASYN | 0.732 | 0.976 | 0.886 | 0.800 | 0.837 | 0.891 | |
| ROS | 0.724 | 0.975 | 0.884 | 0.796 | 0.831 | 0.888 | |
| SMOTE | 0.732 | 0.976 | 0.888 | 0.802 | 0.837 | 0.892 | |
| RUS | 0.717 | 0.975 | 0.883 | 0.794 | 0.827 | 0.888 | |
| T-Link with RUS | 0.347 | 0.999 | 0.001 | 0.001 | 0.515 | 0.500 | |
| ROS with RUS | 0.726 | 0.972 | 0.886 | 0.798 | 0.831 | 0.890 | |
| OSS with SMOTE | 0.726 | 0.975 | 0.886 | 0.800 | 0.832 | 0.890 | |
| Proposed | None | 0.867 | 0.945 | 0.934 | 0.875 | 0.904 | 0.934 |
| DL Classifier | Data-Level Sampling | Precision | Recall | G-Mean | IBA | F1 Score | AUC |
|---|---|---|---|---|---|---|---|
| DNN | None | 0.951 | 0.631 | 0.787 | 0.599 | 0.759 | 0.807 |
| ADASYN | 0.699 | 0.977 | 0.873 | 0.777 | 0.815 | 0.878 | |
| ROS | 0.666 | 0.983 * | 0.854 | 0.747 | 0.794 | 0.862 | |
| SMOTE | 0.923 | 0.822 | 0.890 | 0.781 | 0.870 | 0.892 | |
| RUS | 0.816 | 0.929 | 0.908 | 0.829 | 0.869 | 0.908 | |
| T-Link with RUS | 0.869 | 0.673 | 0.798 | 0.620 | 0.759 | 0.809 | |
| ROS with RUS | 0.942 | 0.599 | 0.766 | 0.565 | 0.733 | 0.790 | |
| OSS with SMOTE | 0.894 | 0.745 | 0.843 | 0.696 | 0.813 | 0.849 | |
| CNN | None | 0.896 | 0.291 | 0.535 | 0.266 | 0.439 | 0.636 |
| ADASYN | 0.727 | 0.975 | 0.884 | 0.796 | 0.833 | 0.889 | |
| ROS | 0.727 | 0.976 | 0.886 | 0.799 | 0.834 | 0.890 | |
| SMOTE | 0.727 | 0.974 | 0.886 | 0.799 | 0.833 | 0.890 | |
| RUS | 0.729 | 0.978 | 0.889 | 0.804 | 0.836 | 0.893 | |
| T-Link with RUS | 0.728 | 0.974 | 0.887 | 0.800 | 0.833 | 0.891 | |
| ROS with RUS | 0.722 | 0.975 | 0.885 | 0.798 | 0.829 | 0.890 | |
| OSS with SMOTE | 0.722 | 0.972 | 0.884 | 0.796 | 0.829 | 0.888 | |
| LSTM | None | 0.901 | 0.290 | 0.534 | 0.265 | 0.439 | 0.636 |
| ADASYN | 0.721 | 0.972 | 0.883 | 0.793 | 0.828 | 0.887 | |
| ROS | 0.731 | 0.977 | 0.889 | 0.803 | 0.836 | 0.892 | |
| SMOTE | 0.723 | 0.976 | 0.886 | 0.789 | 0.830 | 0.890 | |
| RUS | 0.961 | 0.016 | 0.126 | 0.014 | 0.031 | 0.507 | |
| T-Link with RUS | 0.727 | 0.977 | 0.888 | 0.802 | 0.833 | 0.892 | |
| ROS with RUS | 0.729 | 0.977 | 0.886 | 0.800 | 0.835 | 0.891 | |
| OSS with SMOTE | 0.738 | 0.976 | 0.890 | 0.805 | 0.841 | 0.894 | |
| BiLSTM | None | 0.904 | 0.315 | 0.556 | 0.289 | 0.467 | 0.648 |
| ADASYN | 0.730 | 0.974 | 0.887 | 0.801 | 0.834 | 0.891 | |
| ROS | 0.725 | 0.976 | 0.887 | 0.801 | 0.832 | 0.891 | |
| SMOTE | 0.729 | 0.974 | 0.885 | 0.797 | 0.834 | 0.889 | |
| RUS | 0.983 | 0.016 | 0.126 | 0.014 | 0.031 | 0.507 | |
| T-Link with RUS | 0.852 | 0.016 | 0.128 | 0.014 | 0.032 | 0.507 | |
| ROS with RUS | 0.727 | 0.976 | 0.890 | 0.805 | 0.834 | 0.893 | |
| OSS with SMOTE | 0.726 | 0.976 | 0.887 | 0.801 | 0.833 | 0.891 | |
| Proposed | None | 0.871 | 0.926 | 0.927 | 0.859 | 0.898 | 0.928 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maci, A.; Santorsola, A.; Coscia, A.; Iannacone, A. Unbalanced Web Phishing Classification through Deep Reinforcement Learning. Computers 2023, 12, 118. https://doi.org/10.3390/computers12060118
Maci A, Santorsola A, Coscia A, Iannacone A. Unbalanced Web Phishing Classification through Deep Reinforcement Learning. Computers. 2023; 12(6):118. https://doi.org/10.3390/computers12060118
Chicago/Turabian StyleMaci, Antonio, Alessandro Santorsola, Antonio Coscia, and Andrea Iannacone. 2023. "Unbalanced Web Phishing Classification through Deep Reinforcement Learning" Computers 12, no. 6: 118. https://doi.org/10.3390/computers12060118
APA StyleMaci, A., Santorsola, A., Coscia, A., & Iannacone, A. (2023). Unbalanced Web Phishing Classification through Deep Reinforcement Learning. Computers, 12(6), 118. https://doi.org/10.3390/computers12060118








