End-to-End Delay Bound Analysis for VR and Industrial IoE Traffic Flows under Different Scheduling Policies in a 6G Network
Abstract
1. Introduction
- Performance measurement of a 6G-based computer network system, where the edge computing node is shared between two concurrent traffic flows, related to two different services, and, hence, having different e2e delay deadlines;
- Formulation of the per flow e2e delay bound for heterogeneous services (VR and industrial IoE), evaluating performance assuming different scheduling policies in order to identify the best solution. The formulation provided is pursued involving SNC theory applied with martingale envelopes describing traffic behavior.
- System performance validation, devoted to measuring the reliability of the network in completing services before corresponding flow deadlines and goodness of the obtained analytical predictions in comparison with simulations results.
2. Related Works
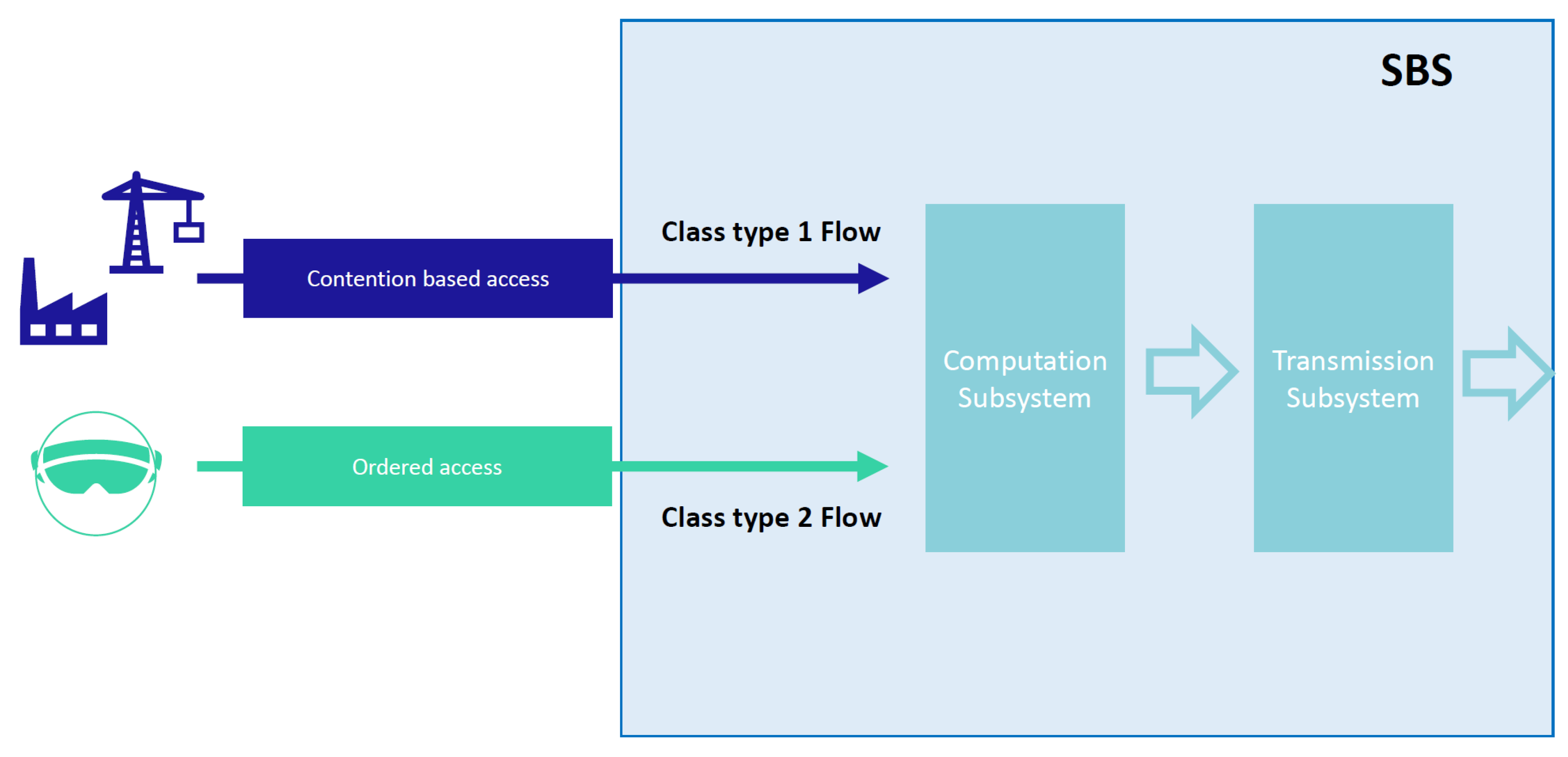
3. System Model
3.1. Channel Model
3.2. Channel Access Scheme
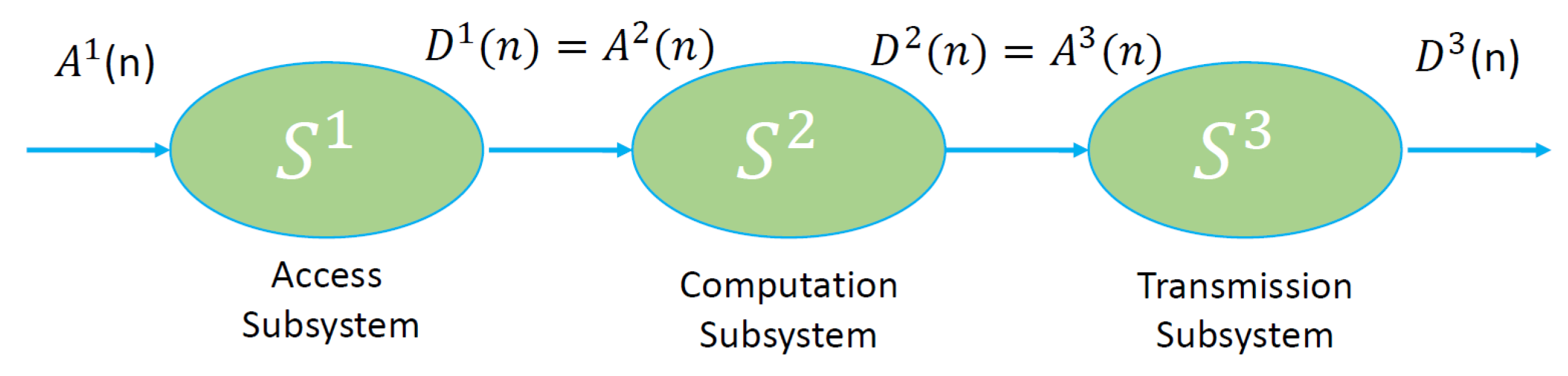
4. End-To-End Delay Analysis
4.1. Martingale Bound for FIFO Policy
4.2. Martingale Bound for EDF Policy
- , ;
- ;
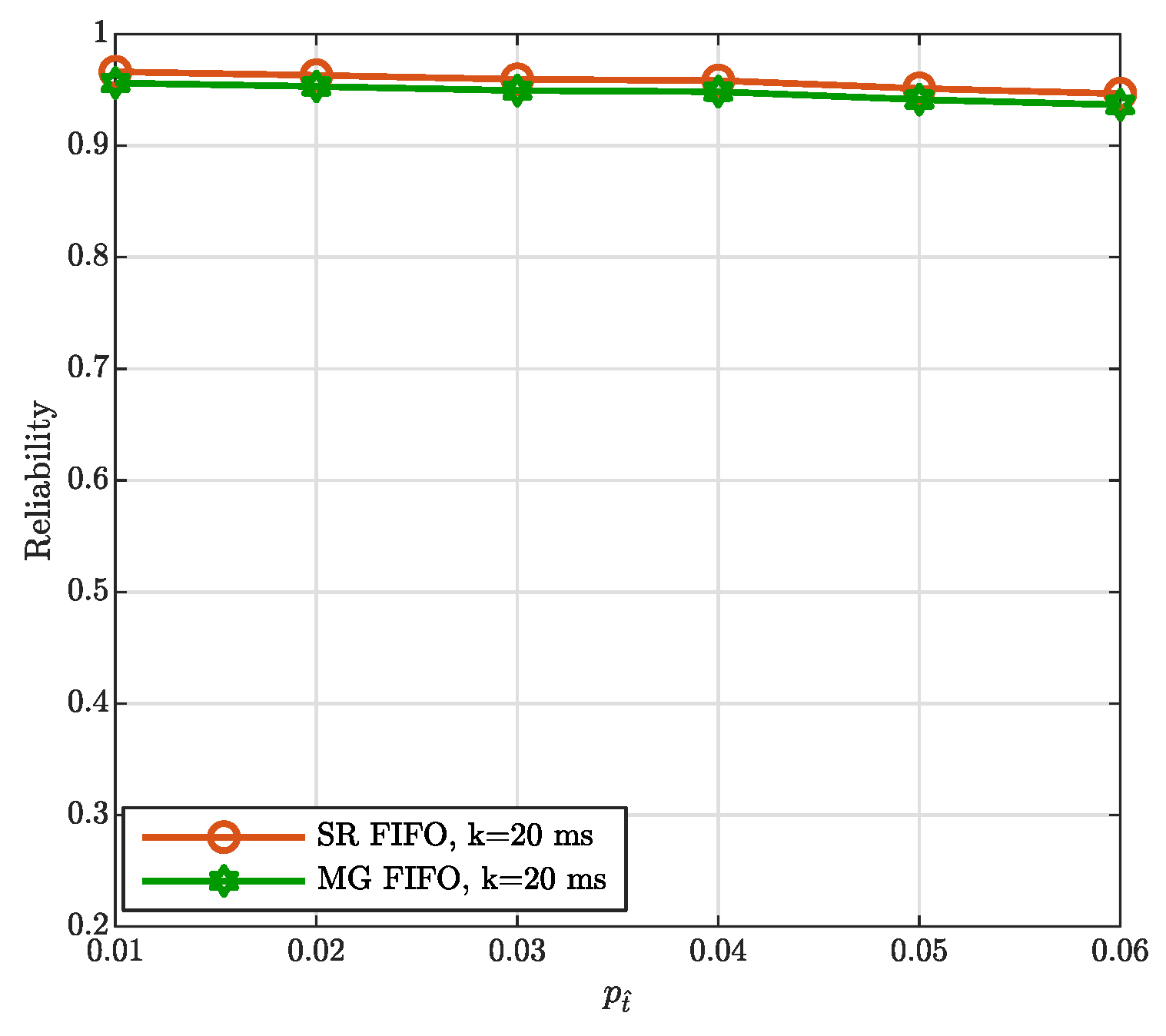
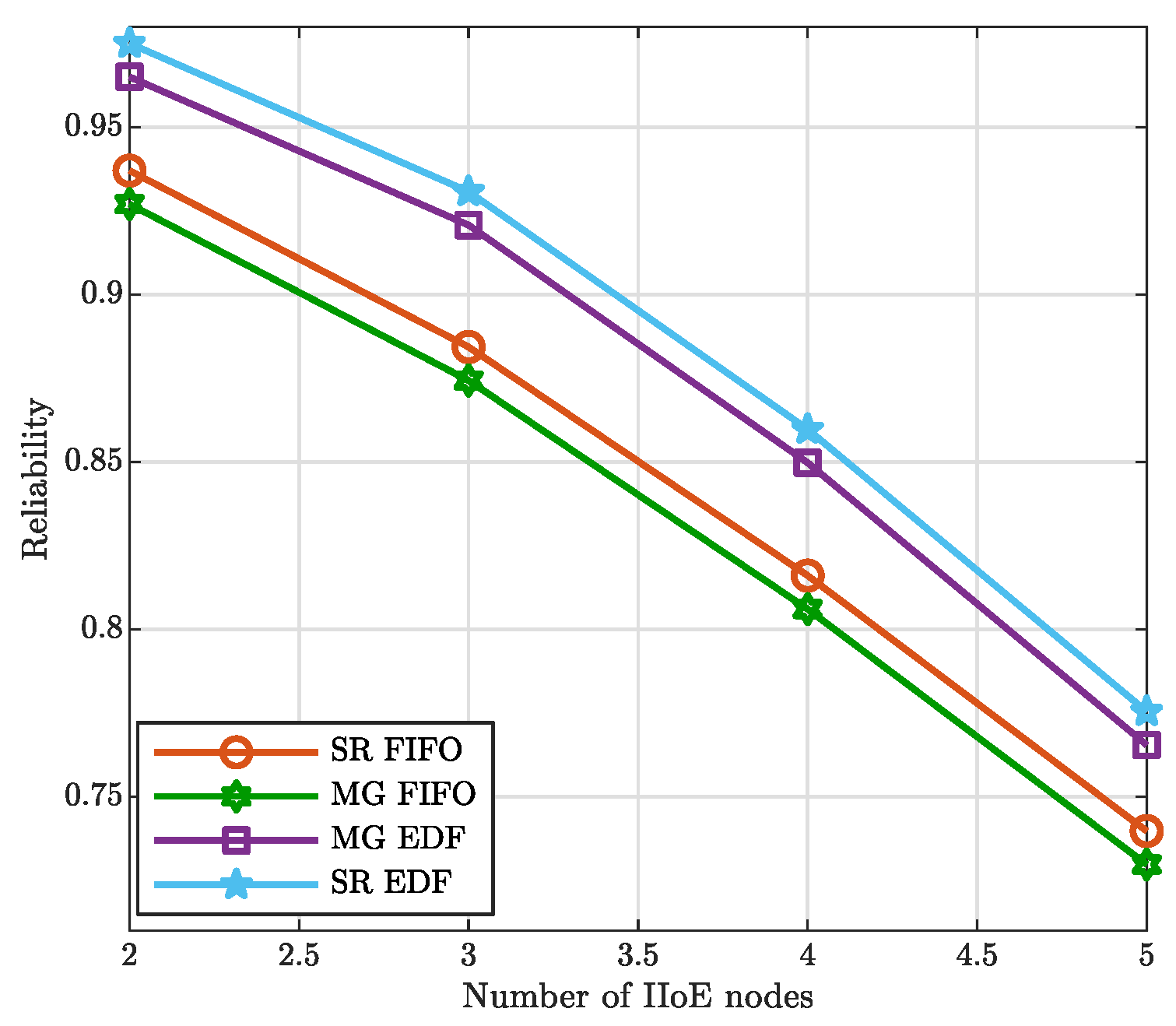
5. Performance Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Wang, M.; Lin, Y.; Tian, Q.; Si, G. Transfer learning promotes 6g wireless communications: Recent advances and future challenges. IEEE Trans. Reliab. 2021, 70, 790–807. [Google Scholar] [CrossRef]
- Fantacci, R.; Picano, B. End-to-end delay bound for wireless uvr services over 6g terahertz communications. IEEE Internet Things J. 2021, 8, 17090–17099. [Google Scholar] [CrossRef]
- Picano, B.; Fantacci, R.; Han, Z. Nonlinear dynamic chaos theory framework for passenger demand forecasting in smart city. IEEE Trans. Veh. Technol. 2019, 68, 8533–8545. [Google Scholar] [CrossRef]
- Gomes de Sa, A.; Zachmann, G. Virtual reality as a tool for verification of assembly and maintenance processes. Comput. Graph. 1999, 23, 389–403. [Google Scholar] [CrossRef]
- Lin, P.; Song, Q.; Wang, D.; Yu, R.; Guo, L.; Leung, V. Resource management for pervasive edge computing-assisted wireless vr streaming in industrial internet of things. IEEE Trans. Ind. Inform. 2021, 17, 7607–7617. [Google Scholar] [CrossRef]
- Qi, Y.-M.; Xie, B.; Deng, S.-P. Research on intelligent manufacturing flexible production line system based on digital twin. In Proceedings of the 2020 35th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Zhanjiang, China, 16–18 October 2020; pp. 854–862. [Google Scholar]
- Liu, Y.; Liu, J.; Argyriou, A.; Ci, S. Mec-assisted panoramic vr video streaming over millimeter wave mobile networks. IEEE Trans. Multimed. 2019, 21, 1302–1316. [Google Scholar] [CrossRef]
- Bastug, E.; Bennis, M.; Medard, M.; Debbah, M. Toward interconnected virtual reality: Opportunities, challenges, and enablers. IEEE Commun. Mag. 2017, 55, 110–117. [Google Scholar] [CrossRef]
- Singh, P.; Singh, L.K. Reliability and safety engineering for safety critical systems: An interview study with industry practitioners. IEEE Trans. Reliab. 2021, 70, 643–653. [Google Scholar] [CrossRef]
- Huang, C.-F.; Huang, D.-H.; Lin, Y.-K. Reliability evaluation of a cloud–fog computing network considering transmission mechanisms. IEEE Trans. Reliab. 2021, 71, 1355–1367. [Google Scholar] [CrossRef]
- Fidler, M.; Rizk, A. A guide to the stochastic network calculus. IEEE Commun. Surv. Tutor. 2015, 17, 92–105. [Google Scholar] [CrossRef]
- Jiang, Y. A basic stochastic network calculus. SIGCOMM Comput. Commun. Rev. 2006, 36, 123–134. [Google Scholar] [CrossRef]
- Poloczek, F.; Ciucu, F. Service-martingales: Theory and applications to the delay analysis of random access protocols. In Proceedings of the 2015 IEEE Conference on Computer Communications (INFOCOM), Hong Kong, China, 26 April–1 May 2015; pp. 945–953. [Google Scholar]
- Park, J.; Bennis, M. Urllc-embb slicing to support VR multimodal perceptions over wireless cellular systems. In Proceedings of the IEEE Global Communications Conference (GLOBECOM) 2018, Abu Dhabi, United Arab Emirates, 9–13 December 2018. [Google Scholar]
- Sun, Y.; Chen, Z.; Tao, M.; Liu, H. Communication, computing and caching for mobile vr delivery: Modeling and trade-off. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Popovski, P.; Stefanovic, C.; Nielsen, J.J.; de Carvalho, E.; Angjelichinoski, M.; Trillingsgaard, K.F.; Bana, A. Wireless access in ultra-reliable low-latency communication (urllc). IEEE Trans. Commun. 2019, 67, 5783–5801. [Google Scholar] [CrossRef]
- Angjelichinoski, M.; Trillingsgaard, K.F.; Popovski, P. A statistical learning approach to ultra-reliable low latency communication. IEEE Trans. Commun. 2019, 67, 5153–5166. [Google Scholar] [CrossRef]
- Faidley, G.; Hero, J.; Lee, K.; Lwakabamba, B.; Walstrom, R.; Chen, F.; Dickerson, J.; Rover, D.; Weber, R.; Cruz-Neira, C. Developing an integrated wireless system for fully immersive virtual reality environments. In Proceedings of the Eighth International Symposium on Wearable Computers, Arlington, VA, USA, 31 October–3 November 2004; Volume 1, pp. 178–179. [Google Scholar]
- Ahn, J.; Kim, Y.Y.; Kim, R.Y. Delay oriented vr mode wlan for efficient wireless multi-user virtual reality device. In Proceedings of the 2017 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 8–10 January 2017; pp. 122–123. [Google Scholar]
- Fantacci, R.; Picano, B. Edge-Based Virtual Reality over 6G Terahertz Channels. IEEE Netw. 2021, 35, 28–33. [Google Scholar] [CrossRef]
- Picano, B. End-to-End Delay Bound for VR Services in 6G Terahertz Networks with Heterogeneous Traffic and Different Scheduling Policies. Mathematics 2021, 9, 1638. [Google Scholar] [CrossRef]
- Hu, Y.; Li, H.; Chang, Z.; Han, Z. End-to-end backlog and delay bound analysis for multi-hop vehicular ad hoc networks. IEEE Trans. Wirel. Commun. 2017, 16, 6808–6821. [Google Scholar] [CrossRef]
- Hu, Y.; Li, H.; Han, Z. Delay bound analysis using martingale for multimedia dtn under heterogeneous network for high-speed trains. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar]
- Qi, R.; Chi, X.; Zhao, L.; Yang, W. Martingales-based aloha-type grant-free access algorithms for multi-channel networks with mmtc/urllc terminals co-existence. IEEE Access 2020, 8, 37608–37620. [Google Scholar] [CrossRef]
- Ferko, E.; Bucaioni, A.; Behnam, M. Architecting digital twins. IEEE Access 2022, 10, 50335–50350. [Google Scholar] [CrossRef]
- Ding, Z.; Lei, X.; Karagiannidis, G.K.; Schober, R.; Yuan, J.; Bhargava, V.K. A survey on non-orthogonal multiple access for 5g networks: Research challenges and future trends. IEEE J. Sel. Areas Commun. 2017, 35, 2181–2195. [Google Scholar] [CrossRef]
- Seo, J.; Jung, B.C.; Jin, H. Nonorthogonal random access for 5g mobile communication systems. IEEE Trans. Veh. Technol. 2018, 67, 7867–7871. [Google Scholar] [CrossRef]
- Yin, Y.; Peng, Y.; Liu, M.; Yang, J.; Gui, G. Dynamic user grouping-based noma over rayleigh fading channels. IEEE Access 2019, 7, 110964–110971. [Google Scholar] [CrossRef]
- Mutairi, A.; Roy, S.; Hwang, G. Delay analysis of ofdma-aloha. IEEE Trans. Wirel. Commun. 2013, 12, 89–99. [Google Scholar] [CrossRef]
- Jain, I.; Kumar, R.; Panwar, S. The impact of mobile blockers on millimeter wave cellular systems. IEEE J. Sel. Areas Commun. 2019, 37, 854–868. [Google Scholar] [CrossRef]
- Petrov, V.; Moltchanov, D.; Koucheryavy, Y. Interference and sinr in dense terahertz networks. In Proceedings of the 2015 IEEE 82nd Vehicular Technology Conference (VTC2015-Fall), Boston, MA, USA, 6–9 September 2015; pp. 1–5. [Google Scholar]
- Kleinrock, L.; Lam, S. Packet switching in a multiaccess broadcast channel: Performance evaluation. IEEE Trans. Commun. 1975, 23, 410–423. [Google Scholar] [CrossRef]
- Liu, T.; Li, J.; Shut, F.; Han, Z. Quality-of-service driven resource allocation based on martingale theory. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Fidler, M. An end-to-end probabilistic network calculus with moment generating functions. In Proceedings of the2006 14th IEEE International Workshop on Quality of Service, New Haven, CT, USA, 19–21 June 2006; pp. 261–270. [Google Scholar]
- Fidler, M. Survey of deterministic and stochastic service curve models in the network calculus. IEEE Commun. Surv. Tutor. 2010, 12, 59–86. [Google Scholar] [CrossRef]
- Liebeherr, J.; Ghiassi-Farrokhfal, Y.; Burchard, A. On the impact of link scheduling on end-to-end delays in large networks. IEEE J. Sel. Areas Commun. 2011, 29, 1009–1020. [Google Scholar] [CrossRef]
- Chaccour, C.; Soorki, M.; Saad, W.; Bennis, M.; Popovski, P. Can terahertz provide high-rate reliable low latency communications for wireless vr? IEEE Internet Things J. 2022, 9, 9712–9729. [Google Scholar] [CrossRef]



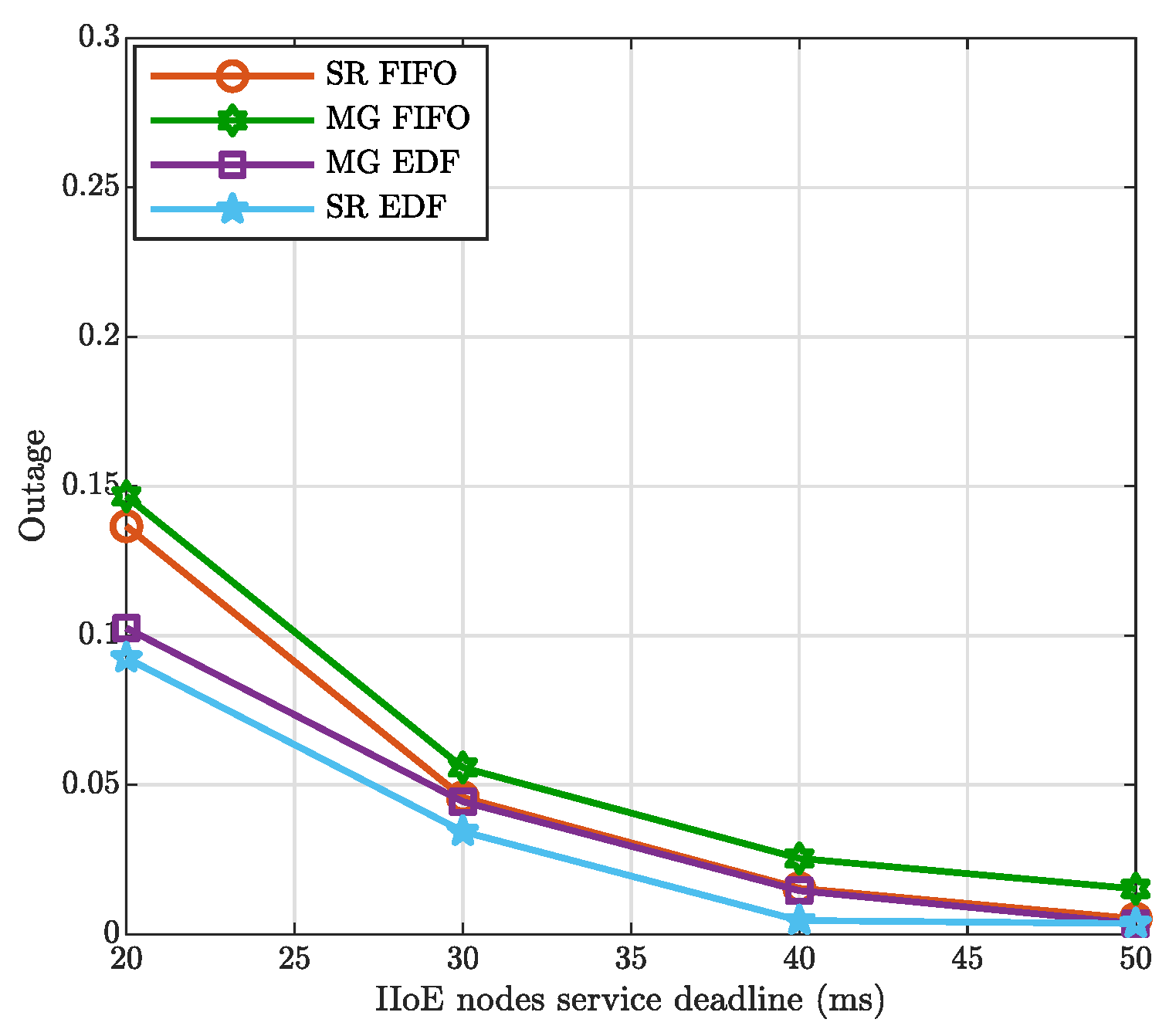


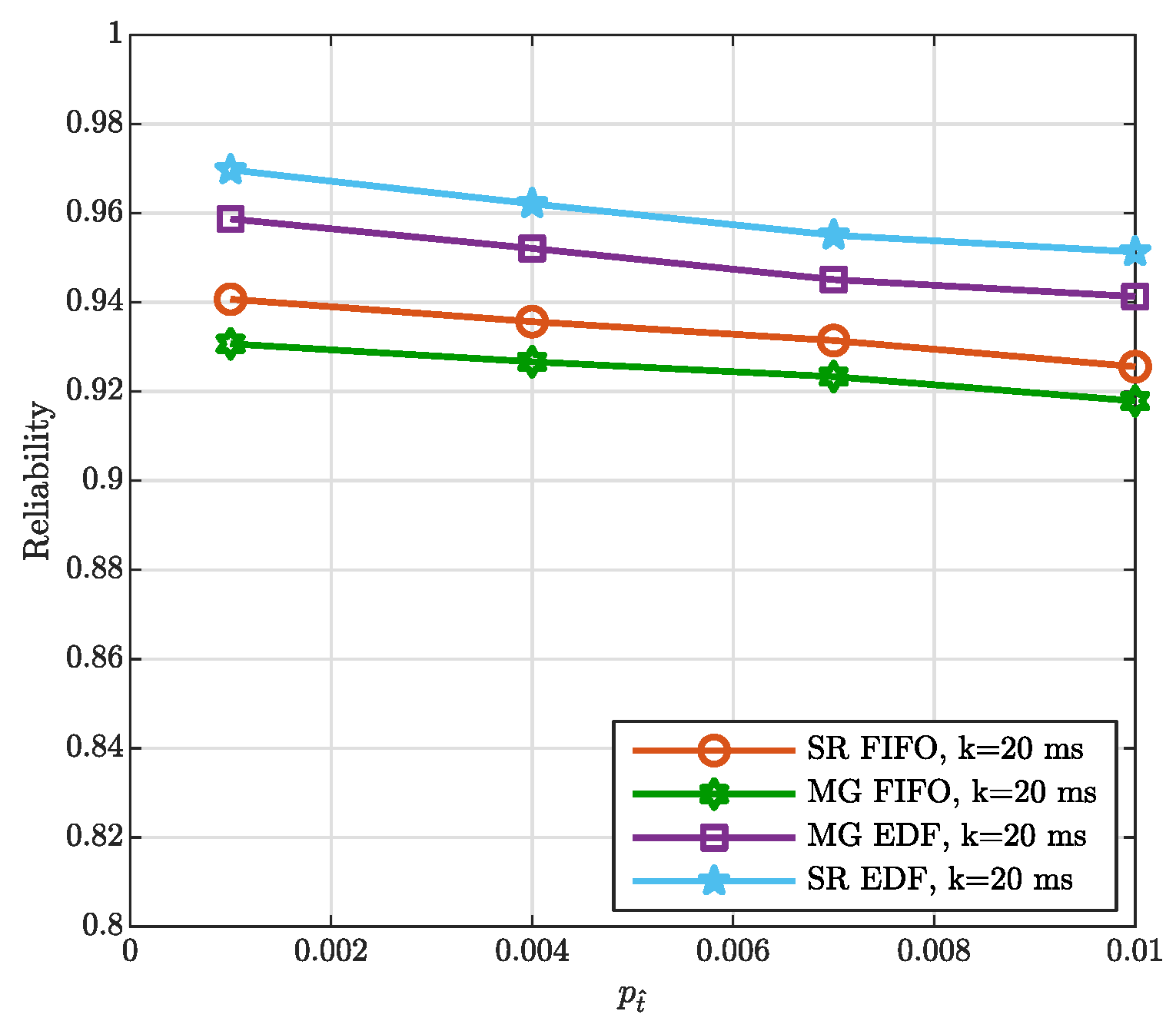
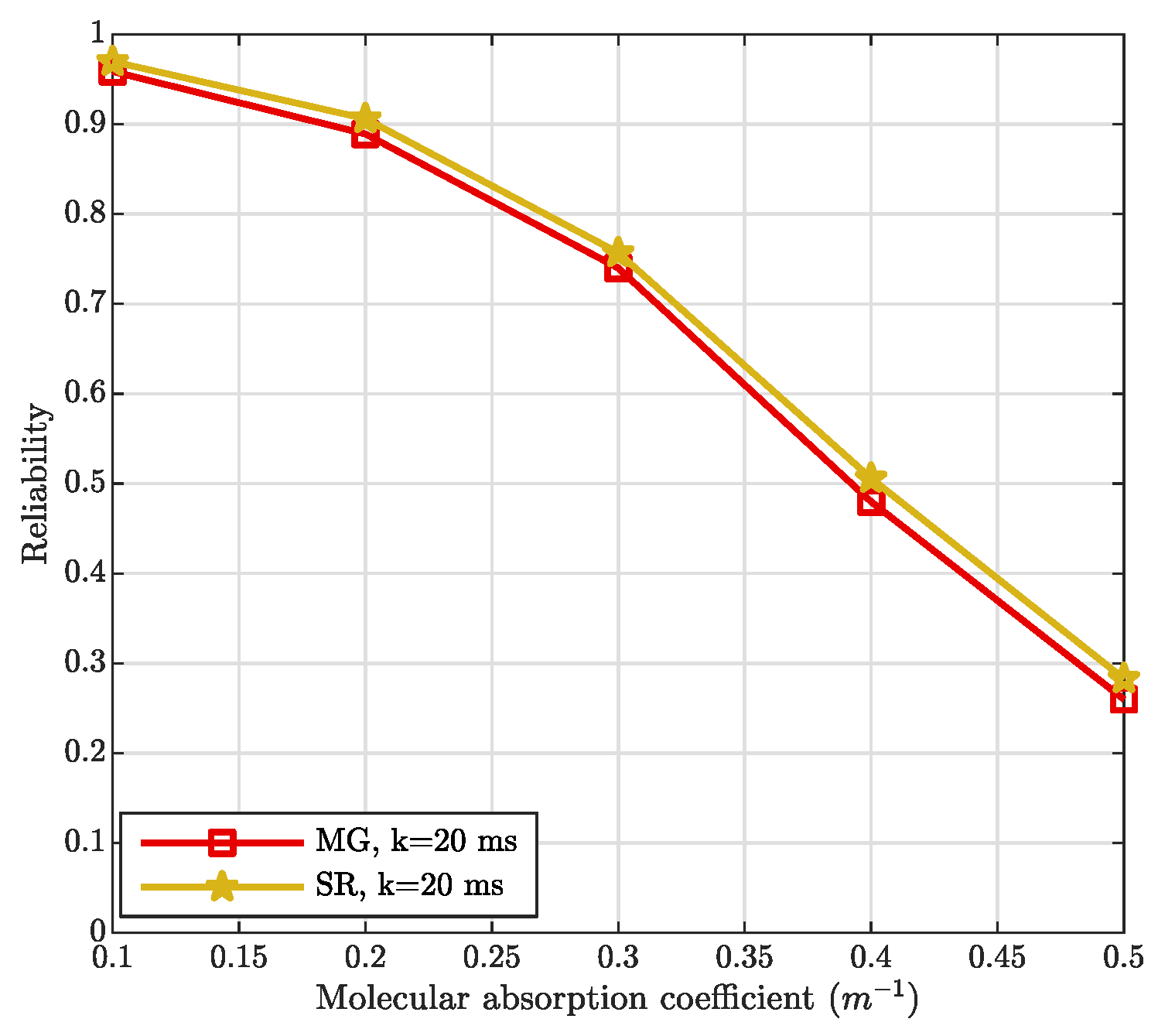
| Paper | Problem Addressed to Provide VR Services |
|---|---|
| [14] | Network slicing |
| [15] | Content caching and computational offloading |
| [16] | Design of a massive MIMO and a multi-connectivity access protocol |
| [17] | Packet error rate minimization |
| [18] | Implementation of a wireless sensors system |
| [19] | Network latency minimization |
| [22,23] | End-to-end delay minimization |
| [24] | Throughput maximization |
| [13] | Martingale-based random access protocols analysis |
| Bound | |
|---|---|
| EDF | , with |
| FIFO | with |
| Advantages | tightness between theoretical bound and simulation results |
| Parameter | Values |
|---|---|
| f | [0.2 THz, 1THz] |
| 0.0016 m | |
| packet size | 10 Mbits |
| 20 ms | |
| side of the network area | 20 m |
| deadlines | 20 and 25 ms |
| NLoS probability | |
| mean computation time | ms |
| 13 GHz | |
| Water vapor percentage |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Picano, B.; Fantacci, R. End-to-End Delay Bound Analysis for VR and Industrial IoE Traffic Flows under Different Scheduling Policies in a 6G Network. Computers 2023, 12, 62. https://doi.org/10.3390/computers12030062
Picano B, Fantacci R. End-to-End Delay Bound Analysis for VR and Industrial IoE Traffic Flows under Different Scheduling Policies in a 6G Network. Computers. 2023; 12(3):62. https://doi.org/10.3390/computers12030062
Chicago/Turabian StylePicano, Benedetta, and Romano Fantacci. 2023. "End-to-End Delay Bound Analysis for VR and Industrial IoE Traffic Flows under Different Scheduling Policies in a 6G Network" Computers 12, no. 3: 62. https://doi.org/10.3390/computers12030062
APA StylePicano, B., & Fantacci, R. (2023). End-to-End Delay Bound Analysis for VR and Industrial IoE Traffic Flows under Different Scheduling Policies in a 6G Network. Computers, 12(3), 62. https://doi.org/10.3390/computers12030062







