1. Introduction
The advent of quantum computing marks a revolutionary leap in computational technology, characterized by its ability to perform complex calculations at speeds unattainable by classical computers. This breakthrough is driven by the principles of quantum mechanics, enabling quantum computers to process vast amounts of data simultaneously and solve problems that are currently intractable for traditional computing systems [
1]. Despite its promising advancements, quantum computing poses significant security risks, particularly to traditional cryptographic systems used in classical computing, as illustrated by past research revealing susceptibilities in classical key establishment methods when faced with quantum computing [
2]. In response to these challenges, a new wave of algorithms, known as post-quantum cryptography (PQC), has been developed as a countermeasure to withstand cryptoanalytic attacks facilitated by quantum computing [
3,
4,
5]. These algorithms are designed to provide security in the age of quantum computing. Among the array of PQC algorithms tailored for key establishments [
6], the
Nth-degree truncated-polynomial ring units (NTRU) [
7] approach has emerged as an especially promising cryptosystem. Impressively, since its inception in 1996, NTRU has demonstrated resilience and remains uncompromised. Diverging from classical key establishment algorithms [
8,
9], NTRU employs a key encapsulation mechanism (KEM). This mechanism utilizes an asymmetric key to encrypt a symmetric key, such as a session key, establishing a secure communication channel. This strategy aligns with the overarching objective of ensuring security in the realm of quantum computing, positioning NTRU as a robust solution within the domain of post-quantum cryptography.
However, like other PQC algorithms, NTRU-KEM requires increased storage space and computation resources compared to classical cryptosystems, resulting in substantial memory and performance overheads [
10,
11,
12]. To address these overheads, researchers have focused on enhancing the efficiency of the NTRU-KEM algorithm, particularly in encapsulation and decapsulation functions [
13,
14,
15]. Previous studies exclude the third function,
key generation (KEYGEN), proposing that keys can be generated in advance and stored for repeated use. While this approach limits NTRU-KEM to a long-term key scenario, previous research relying on software for KEYGEN in a session-key context has led to a significant increase in latency.
Our approach differs, aiming to implement an efficient NTRU-KEM algorithm with full functionality, including KEYGEN. We adopt a hardware and software co-design methodology, a well-established platform for PQC algorithm accelerators [
16,
17], proven effective in addressing challenges associated with NTRU-KEM. This approach combines the strengths of both hardware and software components. Our implementation strategy aims to accelerate repetitive and parallelizable operations through hardware, focusing on increasing the utilization of limited hardware resources. Functions with high inherent parallelism and significant execution time are implemented in hardware, utilizing available resources for substantial performance gains. In contrast, functions with no repetitions or minor execution time are implemented in software to avoid unnecessary hardware resource allocation.
In our previous work [
18], we concentrated on operating the NTRU-KEM functions using as few hardware resources as possible. However, this approach led to relatively high latencies, limiting the performance efficiency in terms of area. We also observed that during approximately 55% of the NTRU-KEM function’s processing time, hardware components like the bus interface were idle. To improve this, we explored in a more in-depth way the data dependencies between the various sub-functions, identifying opportunities for greater parallelism. This led to the development of a new scheduling technique that maximizes the use of hardware resources, including bus interfaces and ALUs. Our approach allows for different ALU operations, such as addition and multiplication, to be executed concurrently. However, running these operations simultaneously necessitates an increase in the number of registers to prevent data overwriting. To address this without significantly increasing the hardware size, we designed an integrated register array that can be efficiently reused throughout NTRU-KEM processes. The specifics of this implementation are detailed in
Section 4.
Our implementation is designed to run on 45 nm process technology at a 1 GHz clock frequency for the hardware components, and a CPU (i5-8550) operating at 2.5 GHz for the software components. In our experimental comparisons, our implementation demonstrates higher efficiency in hardware resource usage compared to previous studies that implemented only the encapsulation and decapsulation functions, leaving out KEYGEN. We achieved this by optimizing the utilization of a smaller area, resulting in an improved performance ranging from 1.82 to 51.38 times greater per area.
A list of the contributions of this work is provided below:
Efficient full-functionality implementation: Unlike previous studies that focused only on encapsulation and decapsulation functions, this work aims to efficiently implement the entire NTRU-KEM algorithm, including the key generation (KEYGEN) function, using a hardware and software co-design methodology.
Optimized use of hardware resources: Our work addresses the challenge of high latencies and underutilized hardware resources (like bus interfaces) observed in previous work [
18]. Our approach achieves this by developing a new scheduling technique that maximizes hardware resource usage, particularly for cross-functional operations that can be executed in parallel.
Minimized area for registers: To run concurrent operations without data overwriting, we design an integrated register array. This design allows for efficient reuse of registers throughout NTRU-KEM processes, minimizing hardware size while maintaining performance.
Enhanced performance efficiency: Our implementation demonstrates a significant improvement in hardware resource efficiency, showing a performance increase of 1.82 to 51.38 times per area compared to previous work.
2. Background
This section provides a brief introduction to the fundamentals of the NTRU-KEM algorithm, as well as lattice-based cryptography as the theoretical basis of NTRU.
2.1. Lattice-Based Cryptography
Lattice-based cryptography refers to a cryptosystem constructed over mathematical grounds that involves lattices in the security proof. It is currently widely used for PQC and other cryptosystems, including NTRU. A lattice in an n-th dimension refers to the end-points of vectors that can be formed by linear combinations of a given basis . The security guarantees of cryptosystems over the lattice are bound to hardness based on problems such as the shortest vector problem or the closest vector problem.
In several cryptosystems, such n-th dimension vectors are interpreted as polynomials bound in integer rings. Lattice-based encryption schemes are constructed by adding a random lattice point to a plaintext vector and the resulting ciphertext is sent to the receiver, who decrypts it using their private key to find the lattice point closest to the ciphertext. Lattice-based cryptography is resistant to quantum attacks due to the hardness of the underlying problems, even for quantum computers, which makes it superior to other public-key cryptosystems. Furthermore, the efficiency properties of lattice-based cryptographic schemes make them suitable for resource-constrained environments like the Internet of Things (IoT).
2.2. NTRU Cryptosystem
NTRU is a latticed-based public-key cryptosystem that was first introduced in 1996 [
7]. The NTRU cryptosystem is based on operations between polynomials over integer quotient rings
and
, where
n and
p are prime integers and
q is coprime with both
p and
n while
,
and
. The coefficients of
and
are encoded in two’s complement modulo
q. The existing variants of NTRU [
7] use
, which leads rings and polynomials to have coefficients using 2 bits, −1, 0, or 1. Let
be the set of ternary polynomials in
with at most
degrees of order. The NTRU cryptosystem samples four polynomials,
and
m from
, which are used as will be described in
Section 2.3.
2.3. NTRU-KEM Algorithm
NTRU-KEM consists of three functions,
KEYGEN, encapsulation, and decapsulation.
KEYGEN generates a key pair
and
. The process starts by sampling the four polynomials and then computing
and
. The public key
h is a polynomial in
calculated from
. The last component of the private key,
, is a precomputed polynomial
. Using the polynomials above, encapsulation and decapsulation are computed as depicted in
Figure 1.
Table 1 depicts the four parameter sets considered as standards for NTRU. The HPS and HRSS parameters show small difference in the preprocessing of the algorithm (e.g., sorting the seed data before the start of the KEM function itself). All parameters have distinct polynomial degree
N and modulus prime
q. Accordingly, they have different security strengths and computational complexity, for which reason users should choose parameters with care, according to their need.
3. Design Overview
Our work focuses on designing a single ASIC accelerator for a generic purpose—to be able to compute all four parameters in
Table 1. We focused on an area of the ASIC design and maximizing the utilization. This approach aligns with the goal stated in our paper, which is to maximize the area efficiency. This design allows for efficient implementation without the need to aggregate separate hardware modules designated for each parameter set to support each function, such as
KEYGEN, encapsulation and decapsulation in
Figure 1. Our hardware design methodology focuses on area efficiency and hardware utilization, including the memory bus and ALU.
Figure 2 illustrates the design overview of our hardware implementation. At the center of our hardware setup, we have two ALUs responsible for executing arithmetic operations, and finite state machine (FSM) modules that manage and orchestrate the ALUs to perform the NTRU-KEM functions. Communication between these components is facilitated through a 64-bit bus interface, which transmits control and data signals. Specifically, each ALU is equipped with 64 instances of both multipliers and adders, handling 16-bit integers for input and output data types. The bus interface serves as a crucial path for all data that needs to be read or written. In addition to this, our design includes a general purpose register array with 56 entries, used for storing intermediate values during the execution of various sub-functions. These register entries are directly and in parallel connected to the ALUs to enable simultaneous computing. A key aspect of our design is the balanced allocation of resources across each module, ensuring an optimized trade-off between the area and performance. The specifics of this resource allocation are detailed in subsequent sections.
4. Implementation
This section presents the details of our accelerator and the design of the modules. Our architecture targets a hardware and software co-design, emphasizing area-efficient hardware design. First, we profiled the sub-functions to select the portions to be implemented as dedicated hardware modules. In other words, we selected heavy tasks to be implemented as dedicated hardware and let small tasks be implemented as the software part. As such, we designed four separate FSM modules, each dedicated to a specific sub-function: polynomial multiplication (
poly_*_mul), polynomial inversion (
poly_*_inv), integer sorting (
crypto_sort_int32), and binary conversion (
2B_conversion). These FSMs were designed based on their respective common arithmetic patterns.
poly_*_mul includes
poly__mul,
poly__mul,
poly__mul, and
poly__inv_to__inv sub-functions for polynomial multiplication with specific ring modulus. And
poly_*_inv includes
poly__inv and
poly__inv sub-functions for polynomial inverse operation. This approach is similar to our previous work [
18]. However, we observed that while our previous work was efficient in terms of area, its use of resources was not optimal. This was due to uneven allocation of resources, leading to time-related bottlenecks. For example, the bus bandwidth was underutilized, using less than half of its capacity when the ALU was busy, which negatively affected the overall performance and efficiency. To address such issues, we adopt a different approach that aims to maximize resource utilization while still maintaining the design’s compact area efficiency.
4.1. FSM-Oriented Hardware Design
As implied by its name,
poly__mul includes multiplications between polynomials on a ring
. To ease the complexity of the multiplications, conventional methods employ fast Fourier transform (FFT) or number theoretic transform (NTT) [
19,
20,
21,
22,
23,
24,
25]. However, NTRU does not use such operations for two major reasons. First, the quotient rings used in NTRU exhibit properties that are not directly supportive of FFT/NTT, as such approaches demand polynomials to have degrees of power of two [
26,
27]. However, NTRU variants use polynomials with degrees that are prime numbers, thus not powers of two. Previous research [
28] extends the polynomials to higher degrees of powers of two but results in more computation than the naive multiplications. The second reason is that the predefined modulus used in NTRU is rather simple and can be efficiently computed using specialized operation sequences. For instance, NTRU frequently uses the modulo 3, which only uses 1, 0, and −1 as coefficients, so any computation between such values can be easily managed by zeroization and bit-flip operations.
We, therefore, choose to naively compute polynomial operations, instead of employing additional techniques as prior work did, by extending the polynomials and using FFT/NTT. The obvious but crucial bottleneck of our approach is the increase in conditional branches within the algorithm, which are needed in finding the inverse polynomials and coefficient swappings. This is the reason why we select FSM-oriented designs. To efficiently handle these conditional branches, our hardware implementation of NTRU leverages finite state machines (FSMs) for the computation of sub-functions. Each FSM manages a pool of basic arithmetic units (i.e., multipliers and adders) to process internal operations in parallel. We carefully select the number of basic arithmetic units by a cycle-accurate analysis of a group of internal operations within sub-functions. The group of internal operations is based on the conditional branches within the sub-function, resulting in a more fine-grained analysis. In cases where the inherent parallelism of the internal operations is less than the number of available units, all the needed arithmetic units are allocated to maximize parallel processing. Otherwise, although the sub-function cannot be processed as a full parallel, all the units in the pool are pipelined so that multiple operations can be processed in each cycle, thereby minimizing the latency. Our FSM-oriented design enabled us to achieve a balance between performance and the hardware area, resulting in an efficient implementation.
4.2. Latency Profiling Sub-Functions for Acceleration
In the context of hardware acceleration, the process of choosing a specific sub-function to be optimized and sped up through hardware is an essential task that needs to be performed first. To identify the specific sub-functions that have the potential to significantly reduce the overall execution time of NTRU-KEM, a comprehensive latency profiling analysis was conducted on four distinct variants of NTRU-KEM with different parameter configurations. This process involved a detailed examination of the performance characteristics of each sub-function, intending to determine which ones may be optimized for improved efficiency. We used the NIST submission version of NTRU-KEM with an i5-8500 CPU at 2.5 GHz clock frequency.
Table 2 describes the result of the profiling. For each variant, we analyzed the runtime latency of each of the three main functions and all of their sub-functions that reside within them. For en/decapsulation,
poly__mul,
poly__mul, and
poly__mul account for between 83 and 97% of the total runtime. Accordingly, the aforementioned existing NTRU-KEM accelerators that only accelerated these two functions [
13,
14,
15] aimed to boost the performance of the polynomial multiplication. However, in the case of
KEYGEN, other sub-functions,
poly__inv and
poly__inv, account for the biggest portion, over 86%, while
poly__mul only accounts for 12%.
Therefore, to accelerate the entire NTRU-KEM algorithm, poly__inv and poly__inv also need to be taken into consideration when designing the hardware. It is worth noting that all the poly_*_inv and poly_*_mul sub-functions inherently involve parallelism since the computation of each term in the resulting polynomial can be performed independently of the others. In addition, crypto_sort_int32 in encapsulation and KEYGEN is also selected to implement in the hardware since it can be processed in a parallel manner. Conversely, the sub-function named randombytes within the encapsulation and KEYGEN function is predominantly comprised of sequential operations. Also, due to its relatively minor contribution to the overall execution time, it has not been implemented as hardware. The randombytes sub-function is used or the seed generation before the KEYGEN and encapsulation function. And the SHA3-hash sub-function is also left to the software part because of the small execution time in the CPU. To efficiently process the above-selected two kinds of polynomial operations, the optimizations that we have devised will be presented in the following subsections.
4.3. Optimizing Bus Utilization
In our previous work [
18], we had allocated a computation array and a sufficient number of registers to prevent delays in the operations, focusing on operational efficiency. This setup allowed continuous computation in each clock cycle, especially during polynomial multiplication, involving both multiplication and addition operations. However, upon shifting our focus to the bus interface in this study, we discovered that its utilization was quite low. For instance,
Figure 3 shows that the bus utilization ratio was only about 25% during the
poly__mul sub-function using 1-ALU.
Given that polynomial multiplication is a significant part of the NTRU-KEM functions, requiring around 80,000 cycles for a single sub-function operation, this low bus utilization was a concern. To address this issue, we decided to make constructive use of the underutilized bus interface during these computational periods. Our strategy involved increasing both the computation array and the number of registers to expedite the operational time. In the 1 × 16 computation array of 1-ALU, the upper and lower 16-bit operations were processed sequentially. By doubling this array to a 2-ALU array, we could simultaneously process the upper and lower bits, allowing sequential operation of the corresponding addition array. As a result, utilizing the 1 × 16 computation array in this manner reduced the operational cycles to half. Not only did this modification reduce the cycles needed for operations by half, but it also increased the frequency of bus interface usage during the shorter operational cycle. Consequently, we achieved a 50% bus utilization rate and a 50% reduced clock cycle. To further maximize bus utilization, we applied the additional techniques detailed in
Section 4.4.
4.4. Parallel Sub-Function Scheduling
To minimize the overall processing time with limited resources in the NTRU-KEM function, we developed a parallel sub-function scheduling technique. This technique allows two different sub-functions to be executed simultaneously. For example, it is possible to perform polynomial multiplication while also carrying out polynomial inversion or sorting tasks concurrently. This not only enables parallel execution but also makes efficient use of previously underutilized bus interfaces during polynomial multiplication tasks. To achieve this, we conducted an in-depth data flow analysis of each sub-function, synchronizing the timing of the bus interface usage across different sub-functions. The goal was to optimize resource utilization, particularly during the execution of the polynomial multiplication sub-function. The next three subsections provide a comprehensive explanation of the techniques.
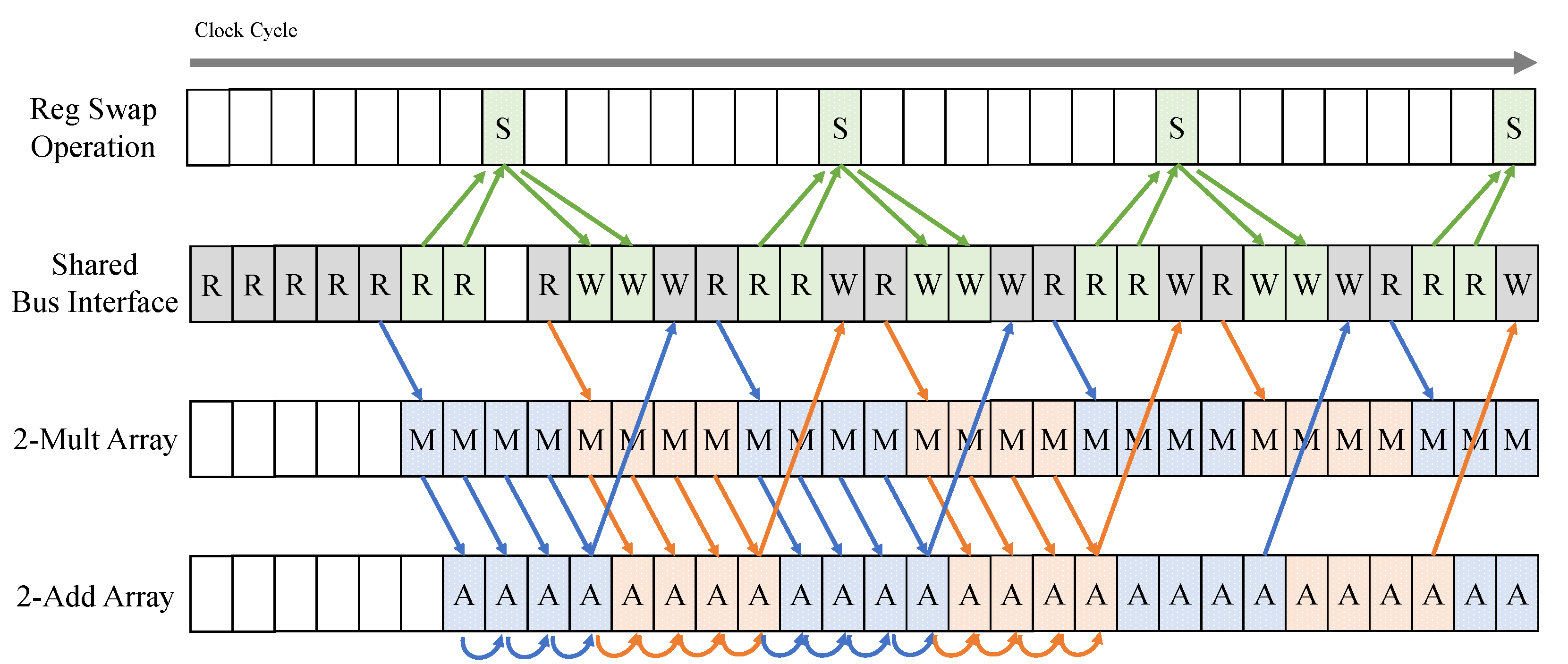
4.4.1. Key Generation Scheduling
The
KEYGEN function in NTRU-KEM includes a series of
poly_inv and
poly_mul sub-functions. NTRU utilizes an efficient almost inverse algorithm [
29], which calculates almost an inverse of a polynomial that yields an exact result across all NTRU-KEM functions. This inverse calculation primarily consists of iterating a swap operation based on the highest degree of a non-zero coefficient in each polynomial. Notably, the
poly_inv sub-function does not require the use of multiplication or addition arrays. This is because it operates on coefficients that are only 1 or 2 bits in size associated with the polynomial inverse sub-functions within the
or
ring modulus. For the polynomial inverse in the
ring modulus, the
poly__inv result is achieved by combining the
poly__inv and
poly__inv_to__inv sub-functions. In these processes, we primarily use bit operations,
reg_array, and the swap operation within the FSM.
4.4.2. Encapsulation Scheduling
In the encapsulation function of our design, we implemented a parallel scheduling strategy for both the poly_mul and crypto_sort_int32 sub-functions. Initially, the function receives seed data (r, m) and public key data . The poly_mul sub-function works with r and , while the crypto_sort_int32 processes m, making it feasible for these functions to operate simultaneously. However, efficient parallelization is challenging due to the limitations of the bus interface. Both sub-functions have idle time in the bus interface. The bus utilization rates are 50% for poly_mul and 80% for crypto_sort_int32. To manage their scheduling, the intervals of bus usage for poly_mul are spaced out in two-cycle units. Although the ALU operates every cycle, the output is stored in memory every four cycles, with one cycle for loading new data and another for storing results.
As depicted in
Figure 4, we maximized bus utilization by aligning the scheduling of the
poly_mul and
crypto_sort_int32 sub-functions. This was performed by creating two-cycle intervals in which the bus interface is idle, during which the
crypto_sort_int32 sub-function operates. The bus interface for
crypto_sort_int32 was designed to match these two-cycle intervals of the
poly_mul sub-function for optimal scheduling. By thoroughly analyzing the bus interface requirements of both sub-functions, we achieved efficient parallel scheduling. This led to a remarkable bus utilization rate of approximately 97% for the encapsulation function using the HPS4096821 parameter. This optimization significantly improved our design’s performance, eliminating the need for extra resources to increase the bus interface’s bit-width.
4.4.3. Decapsulation Scheduling
In the decapsulation function, poly__mul, poly__mul, and poly__mul sub-functions are scheduled in a parallel and pipelined manner. Each of these sub-functions, which perform polynomial multiplication, has a bus interface utilization rate of about 50%. A key challenge is simultaneously executing two polynomial multiplication sub-functions, as this not only requires bus utilization but also additional ALU resources.
On analyzing these sub-functions, we found that they operate with different ring moduli. The and rings require a 16-bit integer multiplier and adder, while the ring works with 2-bit data and coefficients in the range [0,1,2]. This allows the poly__mul sub-function to be executed using bitwise operators, eliminating the need for an ALU. Using this knowledge, we parallelized the poly__mul operation with the textttpoly__mul and poly__mul sub-functions. Despite sharing the same bus utilization rate, the unique characteristics of the poly__mul allowed for efficient parallel scheduling.
Moreover, the data for the poly__mul sub-function become available from the timing of completing half of the poly__mul sub-function, allowing for immediate input to the subsequent poly__mul sub-function. Similarly, starting from the timing of completing half of the poly__mul sub-function, the input data for the poly__mul sub-function could be obtained. We applied a pipelined approach to coordinate these three sub-functions effectively.
4.5. Optimizing Reg_Array Utilization with Combined Structure
In this section, we aim to explain our techniques that reduce the design area while preserving the performance enhancements achieved in the earlier sections. Our goal is to develop an area-efficient design that balances both performance improvement and area conservation. We implemented an integrated management approach for controlling the registers in FSMs. This involved allocating registers to arrays that were not in use at a particular time. This strategy, linked to the parallel sub-function scheduling technique described previously, effectively reduces the number of control registers needed. For instance, in the KEYGEN and encapsulation functions, the polynomial inversion and sorting sub-functions are never executed simultaneously as they are both scheduled alongside polynomial multiplication sub-functions. Thus, combining the control registers for these sub-functions does not hinder performance.
In the decapsulation function, we initially allocated a register array of 56 for storing intermediate data during the parallel and pipelined scheduling of polynomial multiplication sub-functions. However, we found that in various scenarios, such as in KEYGEN for polynomial inversion and multiplication, in encapsulation for sorting and polynomial multiplication, and in decapsulation for two parallel polynomial multiplication sub-functions, fewer registers were used (44, 40, and 56, respectively). Consequently, we were able to combine the control registers for two sub-functions into these 12 unused register arrays. This approach not only reduced the total number of registers required in the entire accelerator but also improved the utilization rate of the existing registers. Through this integrated management, we achieve a decrease in the design area without compromising performance, aligning with the goal of an area-efficient design.
5. Evaluation
To evaluate our design, we integrated the hardware part as an ASIC operation at 1 GHz over 45 nm processing technology. We used HDL language and the Design Compiler 2017.09-SP2 tool to design and obtain the synthesized results. For the software part, we evaluated over an Intel core i5-8500 CPU @2.5 GHz with 32 GB main memory, using a single core only.
5.1. Impact of Our Optimization Methods
Table 3 shows a gradual representation of our optimization process for our hardware implementation starting from our previous work’s design (v1 [
18]) (i.e., how we reached our optimal design). Note that all but the three functions performed by our hardware part are executed by our software part with consistent performance, no matter which entry of
Table 3 is used. Each ALU consists of an array of 16 multipliers and 16 adders. Each multiplier can perform 1 × 16-bit multiplications, while the adder can handle 16-bit additions. Note that the number of registers mentioned in the table
only refers to the general purpose registers—some extra registers are used in the FSMs.
Increasing the number of ALUs to four enables 1.33× better efficiency on average, in terms of the time × area metric compared to the single ALU reference. The number of registers is increased accordingly to meet the maximum needs of the overall computation (i.e., it cannot be reduced). However, note that such an approach induces a linear increase in the area usage, while the latency of each function is reduced with a smaller scale. This is due to the bottleneck induced at the bus interface, as its bandwidth is fixed at 64 bits. Increasing the number of ALUs requires more data movement—having four ALUs demands almost full bandwidth usage to compute the multiplications during poly_mul, making it difficult to perform other tasks since all tasks need data to pass the bus interface. Consequently, parallelizing the sub-function scheduling becomes infeasible and leaves several registers unused, which, in turn, leads to reduced resource utilization.
We, therefore, select a design with 2 ALUs (v4) and apply parallel sub-function scheduling, maintaining the same design area as v2 but with enhanced bus interface utilization. As a result, we obtained even better performance compared to the 4-ALU design (v3) for all sub-functions. As a final stage, we also added our reg_Array technique and reached our optimized design (v5). While the overall latency remains similar, the area is reduced, thus resulting in better performance in terms of time × area compared to all the other variants.
5.2. Performance Comparison with Prior Work
When comparing with prior work [
15], we assumed that the pre-/post-processing steps, such as generating seed and hashing, are executed in the software part, which also has the small execution time discussed in
Section 4.2. Prior work considered only the seed generation as a software part. In our approach, hashing is considered as a pre-/post-processing step, because it is performed either before encapsulation or after decapsulation, rather than during the hardware operation. Therefore, for a fair comparison, we included the time taken for hashing in our latency calculations, as shown in
Table 4.
Table 4 shows the performance of our design and existing ASIC accelerators, with ours outperforming the others by 1.82×–52.87× in terms of the time × area metric. Antognazza et al. [
15] focused on accelerating the encapsulation and decapsulation functions of NTRU-KEM. They proposed two sets of designs:
x-net, which is a performance-centric design set, and
comba, one that focuses on area efficiency. For each set, these authors designed separate accelerators for each of the four parameters; thus, single designs cannot be used for a generic purpose (i.e., supporting all parameters). Their design areas for each parameter of NTRU-KEM ranged from 99.99
to 762.17
when combining the encapsulation module and the decapsulation module together.
In contrast, our optimized design (v5) can perform NTRU computation over all four parameters, offering a more generic purpose usage. Our design also supports not only encapsulation and decapsulation but also
KEYGEN. All the above extra features are supported in a single design with an efficient area usage of 39.60
. Note that even when compared to the area efficient version of
comba, our design uses at least 2.87× less area, while demonstrating, on average, 17.66× faster performance in terms of latency. Compared to the
x-net version, our accelerator exhibited an average performance that was 7.69 times slower but achieved an average design area that was 15.98 times smaller. In terms of the time × area, our accelerator exhibits superior efficiency, surpassing that of both the
x-net and
comba accelerator versions by average factors of 2.09 and 48.66 across all parameters, respectively. It is worth noting that the mitigation of side-channel attacks (SCA) is beyond the scope of this work. However, future research could explore applying and optimizing the methods mentioned in [
30] to mitigate SCA. Given our design’s efficiency in terms of the time × area metric compared to previous works, we believe that our design will outperform others even after incorporating methods to mitigate SCA.