Model and Fuzzy Controller Design Approaches for Stability of Modern Robot Manipulators
Abstract
:1. Introduction
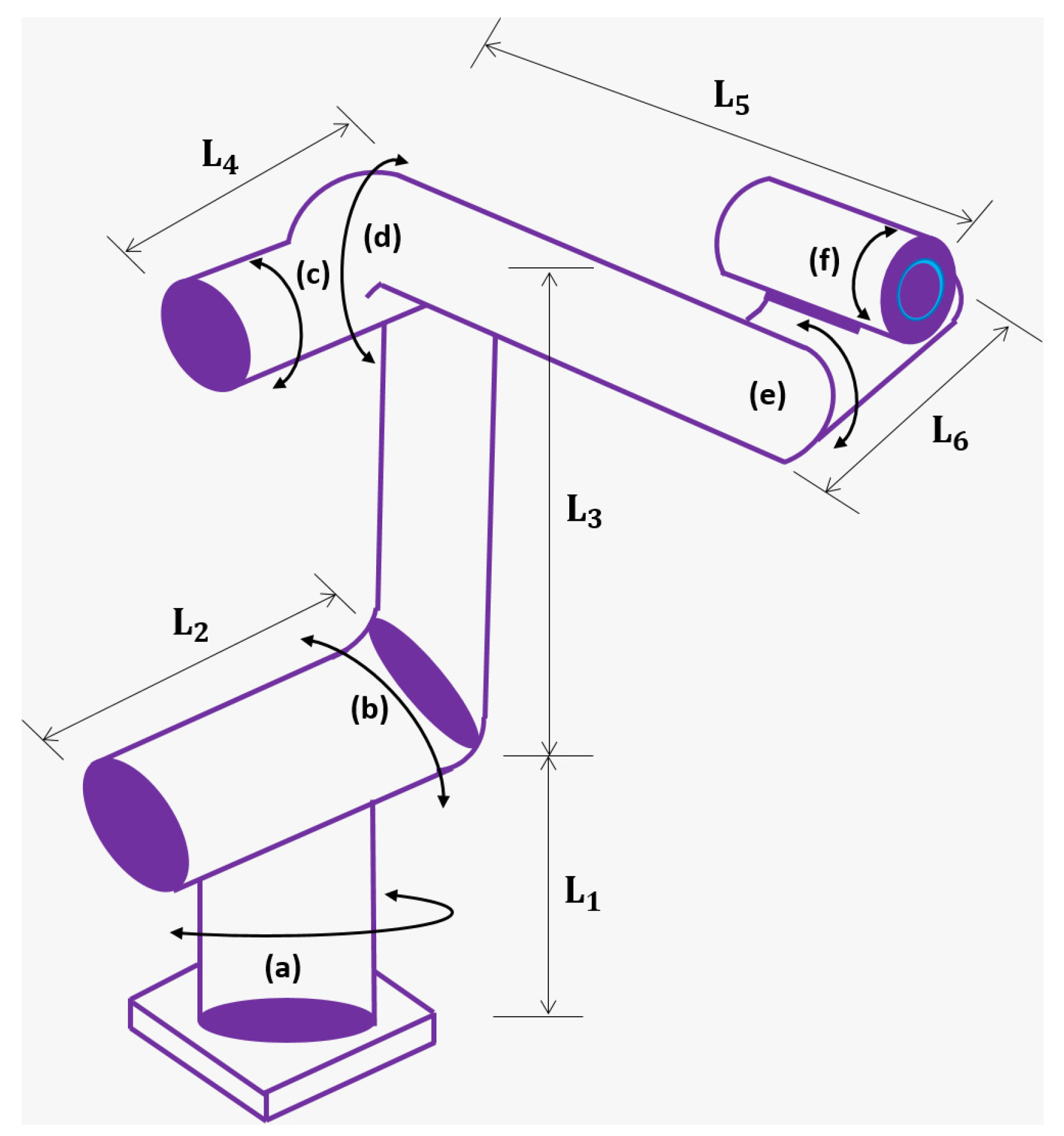
2. Evaluation of Different Parameters of Industrial Robots
3. Mathematical Model for Contemporary Robot Manipulators
4. Controller Design for Stability using Fuzzy Logic
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, J.; Gao, F.; Huang, C.; Zhao, J. Whole-body motion planning for a six-legged robot walking on rugged terrain. Appl. Sci. 2019, 9, 5284. [Google Scholar] [CrossRef]
- Hao, Q.; Wang, Z.; Wang, J.; Chen, G. Stability-guaranteed and high terrain adaptability static gait for quadruped robots. Sensors 2020, 20, 4911. [Google Scholar] [CrossRef] [PubMed]
- James, J.W.; Nathan, F.L. Slip detection for grasp stabilization with a multifingered tactile robot hand. IEEE Trans. Robot. 2020, 37, 506–519. [Google Scholar] [CrossRef]
- Kaymak, Ç.; Uçar, A.; Güzeliş, C. Development of a New Robust Stable Walking Algorithm for a Humanoid Robot Using Deep Reinforcement Learning with Multi-Sensor Data Fusion. Electronics 2023, 12, 568. [Google Scholar] [CrossRef]
- Nazir, A.; Xu, P.; Seo, J. Rock-and-walk manipulation: Object locomotion by passive rolling dynamics and periodic active control. IEEE Trans. Robot. 2022, 38, 2354–2369. [Google Scholar] [CrossRef]
- Rana, D.S.; Kaushal, D. Modelling, stability analysis and control of flexible single link robotic manipulator. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2014, 3, 7390–7401. [Google Scholar]
- Saeed, B.N. Introduction to Robotics Analysis, Systems, Applications; Prentice Hall: Hoboken, NJ, USA, 2001. [Google Scholar]
- Liao, B.; Lou, Y.; Li, Z. Acceleration analysis and optimal design of a 3-degree-of-freedom co-axis parallel manipulator for pick-and-place applications. Adv. Mech. Eng. 2018, 10, 1687814018768166. [Google Scholar] [CrossRef]
- Thomas, M.J.; Joy, M.L.; Sudheer, A.P. Kinematic and dynamic analysis of a 3-PRUS spatial parallel manipulator. Chin. J. Mech. Eng. 2020, 33, 13. [Google Scholar] [CrossRef]
- Helwa, M.K.; Heins, A.; Schoellig, A.P. Provably robust learning-based approach for high-accuracy tracking control of lagrangian systems. IEEE Robot. Autom. Lett. 2019, 4, 1587–1594. [Google Scholar] [CrossRef]
- Hui, J.; Pan, M.; Zhao, R.; Luo, L.; Wu, L. The closed-form motion equation of redundant actuation parallel robot with joint friction: An application of the Udwadia–Kalaba approach. Nonlinear Dyn. 2018, 93, 689–703. [Google Scholar] [CrossRef]
- He, Y.; Chen, J.; Gao, J.; Cui, C.; Yang, Z.; Chen, X.; Chen, Y.; Zhang, K.; Tang, H. Research on Motion Simulation of Wafer Handling Robot Based on SCARA. In Proceedings of the 2018 19th International Conference on Electronic Packaging Technology (ICEPT), Shanghai, China, 8–11 August 2018; pp. 734–739. [Google Scholar]
- Farid, Y.; Siciliano, B.; Ruggiero, F. Review and descriptive investigation of the connection between bipedal locomotion and non-prehensile manipulation. Annu. Rev. Control 2022, 53, 51–69. [Google Scholar] [CrossRef]
- Kang, B.; Chu, J.; Mills, J.K. Design of high speed planar parallel manipulator and multiple simultaneous specification control. In Proceedings of the 2001 ICRA. IEEE International Conference on Robotics and Automation (Cat. No. 01CH37164), Seoul, Republic of Korea, 21–26 May 2001; Volume 3, pp. 2723–2728. [Google Scholar]
- Hojati, M.; Baktash, A. Hybrid stepper motor with two rows of teeth on a cup-shaped rotor and a two-part stator. Precis. Eng. 2022, 73, 228–233. [Google Scholar] [CrossRef]
- Namazov, M. Fuzzy logic control design for 2-link robot manipulator in MATLAB/Simulink via robotics toolbox. In Proceedings of the 2018 Global Smart Industry Conference (GloSIC), Chelyabinsk, Russia, 13–15 November 2018; pp. 1–5. [Google Scholar]
- Mendonça, M.; Kondo, H.S.; de Souza, L.B.; Palácios, R.H.C.; de Almeida, J.P.L.S. Semi-Unknown Environments Exploration Inspired by Swarm Robotics using Fuzzy Cognitive Maps. In Proceedings of the 2019 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), New Orleans, LO, USA, 23–26 June 2019; pp. 1–8. [Google Scholar]
- Selaka, H.S.; Perera, K.A.T.S.; Deepal, M.A.W.T.; Sanjeewa, P.D.R.; Sirithunge, H.C.; Jayasekara, A.G.B.P. Fuzzy-Bot: A Food Serving Robot as a Teaching and Learning Platform for Fuzzy Logic. In Proceedings of the 2018 Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 30 May–1 June 2018; pp. 565–570. [Google Scholar]
- Singh, N.H.; Thongam, K. Mobile robot navigation using fuzzy logic in static environments. Procedia Comput. Sci. 2018, 125, 11–17. [Google Scholar] [CrossRef]
- Yilmaz, B.M.; Tatlicioglu, E.; Savran, A.; Alci, M. Adaptive fuzzy logic with self-tuned membership functions based repetitive learning control of robotic manipulators. Appl. Soft Comput. 2021, 104, 107183. [Google Scholar] [CrossRef]
- Saleem, O.; Iqbal, J. Fuzzy-Immune-Regulated Adaptive Degree-of-Stability LQR for a Self-Balancing Robotic Mechanism: Design and HIL Realization. IEEE Robot. Autom. Lett. 2023, 8, 4577–4584. [Google Scholar] [CrossRef]
- Saleem, O.; Iqbal, J.; Afzal, M.S. A robust variable-structure LQI controller for under-actuated systems via flexible online adaptation of performance-index weights. PLoS ONE 2023, 18, e0283079. [Google Scholar] [CrossRef] [PubMed]
- ABB Robotics. Product Specification CRB 15000; ABB Robotics: Zurich, Switzerland, 2022. [Google Scholar]
- Available online: www.maxpowergears.com (accessed on 20 January 2023).
- Available online: https://www.abb-conversations.com/2017/07/abb-motor-sets-world-record-in-energy-efficiency/ (accessed on 27 January 2023).
- Sariyildiz, E.; Sekiguchi, H.; Nozaki, T.; Ugurlu, B.; Ohnishi, K. A stability analysis for the acceleration-based robust position control of robot manipulators via disturbance observer. IEEE/ASME Trans. Mechatron. 2018, 23, 2369–2378. [Google Scholar] [CrossRef]
- Tvoroshenko, I.S.; Gorokhovatskyi, V.O. Effective tuning of membership function parameters in fuzzy systems based on multi-valued interval logic. Telecommun. Radio Eng. 2020, 79, 149–163. [Google Scholar] [CrossRef]
- Sutcliffe, G.; Pelletier, F.J. JGXYZ: An ATP system for gap and glut logics. In Automated Deduction–CADE 27: 27th International Conference on Automated Deduction, Natal, Brazil, 27–30 August 2019; Proceedings 27; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 526–537. [Google Scholar]
- Available online: https://www.researchgate.net/figure/Block-Diagram-of-Fuzzy-Logic-Controller_fig4_286765408 (accessed on 27 January 2023).
- Yahyaei, M.; Jam, J.E.; Hosnavi, R. Controlling the navigation of automatic guided vehicle (AGV) using integrated fuzzy logic controller with programmable logic controller (IFLPLC)—Stage 1. Int. J. Adv. Manuf. Technol. 2010, 47, 795–807. [Google Scholar] [CrossRef]
- Krishan, K. Computer-Based Industrial Control; PHI Private Ltd.: Delhi, India, 1997. [Google Scholar]





| Link | Length | Mass | Inner Diameter | Outer Diameter |
|---|---|---|---|---|
| 1st-link | 0.265 | 4.21 | 0.103 | 0.135 |
| 2nd-link | 0.444 | 6.76 | 0.0985 | 0.130 |
| 3rd-link | 0.110 | 1.67 | 0.0985 | 0.130 |
| 4th-link | 0.470 | 7.2 | 0.0985 | 0.130 |
| 5th-link | 0.101 | 1.2 | 0.074 | 0.105 |
| 6th-link | 0.08 | 0.96 | 0.074 | 0.105 |
| Parameter | Formula | Value |
|---|---|---|
| Stiffness | Stiffness, 0.0533933 Stiffness, 0.0624217 Stiffness, 0.0310255 Stiffness, 0.0644157357 Stiffness, 0.0163124297 Stiffness, 0.0145902 | |
| Deflection | Deflection, 0.0138 Deflection, 0.03099 Deflection, 0.00959 Deflection, 0.0492 Deflection, 0.0123 Deflection, 0.00139 | |
| Damping | Amplitude reduction factor = | Damping, 0.043 Damping, 0.019 Damping, 0.220 Damping, 0.0176 Damping, 0.7696 Damping, 0.6499 |
| Target Input Parameters | Reference | Value |
|---|---|---|
| Armature input voltage | [23] | 24 |
| Gearbox efficiency | [24] | 0.94 |
| Motor efficiency | [25] | 98.80 |
| Target Input Parameters | Formula | Value |
|---|---|---|
| Armature resistance | 12 | |
| Motor torque constant | 0.11 | |
| Back e.m.f torque constant | 0.11 |
| Link | Acceleration | ||
|---|---|---|---|
| 1st-link | 3.42 | 2.6608 | 0.0151738 |
| 2nd-link | 0.4634 | 21.322 | 0.0224789 |
| 3rd-link | 18.05 | 0.5051 | 0.0055532 |
| 4th-link | 0.16424 | 57.2572 | 0.02394 |
| 5th-link | 14.96 | 0.5998 | 0.002475 |
| 6th-link | 1471.96 | 0.0061 | 0.00198012 |
| Acceleration | State | Moment of Inertia | State | Deflection | State | Stability | State |
|---|---|---|---|---|---|---|---|
| 0.16424 | Low | 0.0061 | Low | 0.00139 | Low | 19,370.20875 | Medium |
| 0.16424 | Low | 0.0061 | Low | 0.025 | Medium | 1076.983607 | Medium |
| 0.16424 | Low | 0.0061 | Low | 0.0492 | High | 547.2477676 | Low |
| 0.16424 | Low | 27 | Medium | 0.00139 | Low | 4.376232347 | Low |
| 0.16424 | Low | 27 | Medium | 0.025 | Medium | 0.243318519 | Low |
| 0.16424 | Low | 27 | Medium | 0.0492 | High | 0.123637459 | Low |
| 0.16424 | Low | 57.5 | High | 0.00139 | Low | 2.054926494 | Low |
| 0.16424 | Low | 57.5 | High | 0.025 | Medium | 0.114253913 | Low |
| 0.16424 | Low | 57.5 | High | 0.0492 | High | 0.05805585 | Low |
| 686 | Medium | 0.0061 | Low | 0.00139 | Low | 80,905,767.19 | High |
| 686 | Medium | 0.0061 | Low | 0.025 | Medium | 4,498,360.656 | High |
| 686 | Medium | 0.0061 | Low | 0.0492 | High | 2,285,752.366 | High |
| 686 | Medium | 27 | Medium | 0.00139 | Low | 18,278.71037 | Medium |
| 686 | Medium | 27 | Medium | 0.025 | Medium | 1016.296296 | Medium |
| 686 | Medium | 27 | Medium | 0.0492 | High | 516.4107197 | Low |
| 686 | Medium | 57.5 | High | 0.00139 | Low | 8583.046606 | Medium |
| 686 | Medium | 57.5 | High | 0.025 | Medium | 477.2173913 | Low |
| 686 | Medium | 57.5 | High | 0.0492 | High | 242.4885118 | Low |
| 1472 | High | 0.0061 | Low | 0.00139 | Low | 173,605,378 | High |
| 1472 | High | 0.0061 | Low | 0.025 | Medium | 9,652,459.016 | High |
| 1472 | High | 0.0061 | Low | 0.0492 | High | 4,904,704.785 | High |
| 1472 | High | 27 | Medium | 0.00139 | Low | 39,221.95577 | Medium |
| 1472 | High | 27 | Medium | 0.025 | Medium | 2180.740741 | Medium |
| 1472 | High | 27 | Medium | 0.0492 | High | 1108.09997 | Medium |
| 1472 | High | 57.5 | High | 0.00139 | Low | 18,417.26619 | Medium |
| 1472 | High | 57.5 | High | 0.025 | Medium | 1024 | Medium |
| 1472 | High | 57.5 | High | 0.0492 | High | 520.3252033 | Low |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mustary, S.; Kashem, M.A.; Chowdhury, M.A.; Uddin, J. Model and Fuzzy Controller Design Approaches for Stability of Modern Robot Manipulators. Computers 2023, 12, 190. https://doi.org/10.3390/computers12100190
Mustary S, Kashem MA, Chowdhury MA, Uddin J. Model and Fuzzy Controller Design Approaches for Stability of Modern Robot Manipulators. Computers. 2023; 12(10):190. https://doi.org/10.3390/computers12100190
Chicago/Turabian StyleMustary, Shabnom, Mohammod Abul Kashem, Mohammad Asaduzzaman Chowdhury, and Jia Uddin. 2023. "Model and Fuzzy Controller Design Approaches for Stability of Modern Robot Manipulators" Computers 12, no. 10: 190. https://doi.org/10.3390/computers12100190
APA StyleMustary, S., Kashem, M. A., Chowdhury, M. A., & Uddin, J. (2023). Model and Fuzzy Controller Design Approaches for Stability of Modern Robot Manipulators. Computers, 12(10), 190. https://doi.org/10.3390/computers12100190









