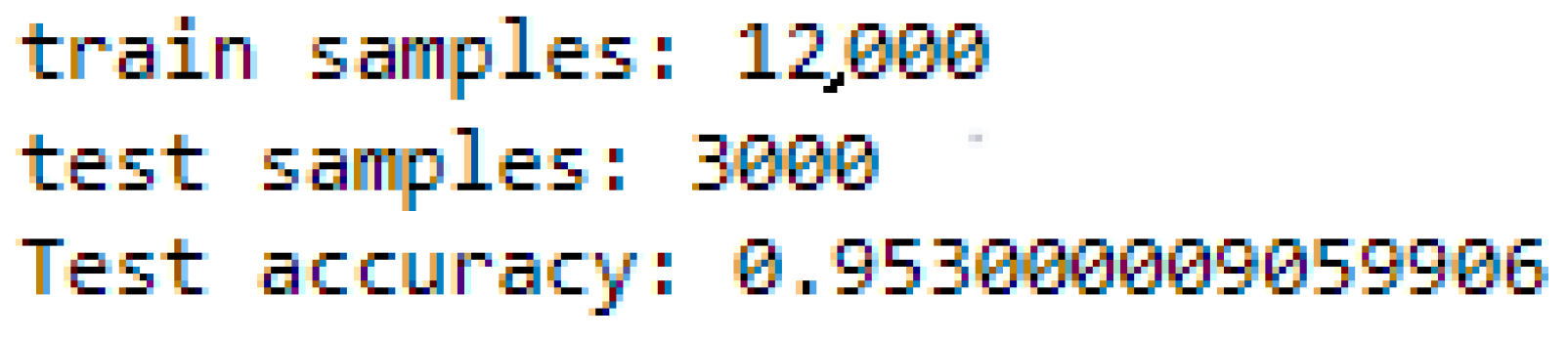Identification of Heart Arrhythmias by Utilizing a Deep Learning Approach of the ECG Signals on Edge Devices

Abstract

Accurate and timely detection of cardiac arrhythmias is crucial in reducing treatment times and, ultimately, preventing serious life-threatening complications, such as the incidence of a stroke. This becomes of major importance, especially during the diagnostic process, where there is limited access to cardiologists, such as in hospital emergency departments. The proposed lightweight solution uses a novel classifier, consistently designed and implemented, based on a 2D convolutional neural network (CNN) and properly optimized in terms of storage and computational complexity, thus making it suitable for deployment on edge devices capable of operating in hospital emergency departments, providing privacy, portability, and constant operation. The experiments on the MIT-BIH arrhythmia database, show that the proposed 2D-CNN obtains an overall accuracy of 95.3%, mean sensitivity of 95.27%, mean specificity of 98.82%, and a One-vs-Rest ROC-AUC score of 0.9934. Moreover, the results and metrics based on the NVIDIA^® Jetson Nano^™ platform show that the proposed method achieved excellent performance and speed, and would be particularly useful in the clinical practice for continuous real-time (RT) monitoring scenarios.

1. Introduction

Cardiovascular disease (CVD) is a batch of diseases impacting one or many parts of the heart and/or blood vessels. Cardiovascular diseases include heart or blood vessel conditions that narrow or block blood vessels (Coronary Heart Disease, Cardiac Valvular Diseases, Pericardial Diseases, Cardiac Muscular Diseases, Congenital Heart Diseases) leading to heart attack, angina, and strokes as well as conditions that affect the heart’s muscle, valves or cause abnormal rhythms (Cardiac Arrhythmias). Cardiovascular disease (CVD) is the leading cause of death worldwide each year, accounting for 32% or about 17.9 million people [1]. Due to the small amount of progress in heart disease prediction systems, the mortality rate has increased, and recent studies show that people with coronary artery disease are more susceptible to viral COVID-19 infections [2]. Thus, there is a need to detect such cardiac abnormalities at the time they occur. For the most part, this is done by recording electrophysiological signals, such as an electrocardiogram (ECG), and photoplethysmogram (PPG) waveforms, which are known as time series signals depicting electrical activities.

This work, which is an extended version of a previously published conference paper of ours, describes a new classifier based on a 2D convolutional neural network (CNN). [3]. The model is designed, implemented, and optimized in terms of storage and computational complexity, thus making it suitable for deployment on edge devices operating in the field of Emergency Departments (ED). The corresponding methodology uses ECG Lead II signals obtained from the publicly available MIT-BIH arrhythmia database on PhysioNet and segmented into heartbeats [4]. The ANSI/AAMI EC57 standard was used to define five types of heartbeats: normal pulse (N), supraventricular ectopic pulse (S), ventricular ectopic pulse (V), a fusion of ventricular and normal pulse (F), and paced pulse, a fusion of paced and normal pulse, or pulse that cannot be classified (Q) [5]. A QRS detection algorithm was used to identify R peaks in the ECG strips based on the annotation files for each of the individual recordings. These one-dimensional segmented data were converted into grayscale images for deep neural network training via CNN, while the trained model was then adapted to ONNX (Open Neural Network Exchange Format), followed by conversion via the NVIDIA^® Jetson Nano^™ Devkit to a TensorRT engine ready for inference on handheld and other edge computing devices. Experiments based on the MIT-BIH arrhythmia database demonstrated that the proposed 2D-CNN exhibits an overall accuracy of 95.3%, an average sensitivity of 95.27%, a mean specificity of 98.82%, and a ROC-AUC One-vs-Rest score of 0.9934. Moreover, the proposed method achieved excellent performance and would be particularly useful in clinical practice for continuous monitoring.

The paper is organized as follows: Section 2 depicts relevant work in literature and presents formal problem formulations regarding real-time arrhythmia classifications; Section 3 presents the system architecture and the proposed 2D-CNN model, in addition to a depiction of the adaptation of our model to be executed on edge devices; Section 4 is comprised of the experimental results; Section 5 presents corresponding discussions; and Section 6 concludes our work and provides recommendations for future research.

2. Literature Review

As with the majority of heart diseases, the correct classification of heartbeats is fundamental and prediction is extremely difficult since the morphology and spatio-temporal characteristics of electrophysiological signals are highly dynamic and differ between individuals due to factors such as age, gender, health status, and the recording conditions which determines the signal’s strength [6,7]. Here, new classifiers are required such as 1D or 2D convolutional neural networks—CNNs and AI transformers with optimized storage and computational complexity, suitable for deployment on low resource edge devices.

Such research works are related to deep learning models which can segment and quantify the 3D geometry of ascending thoracic aortic aneurysms with high accuracy [8], in addition to CT imaging, modeling, and flow simulations required to virtually plan and improve transcatheter aortic valve implantations [9].

To classify ECG waveforms, A. Farooq et al. in [10] proposed a technique using LabVIEW, k-mean clustering, and Arduino boards for the collection of data. The advantages of this implementation are that it is based on real data and the original signal is noisy, which is comparable to a real case implementation. Conversely, the sample of patients is only three, and most importantly, the evaluation response time is close to half a minute, which makes it unsuitable for real-time monitoring and processing in an Emergency Department environment. H. Abayaratne et al. in [11] utilize a RNN-LSTM based model for the classification part of their study. They included 96,265 samples from the MIT-BIH database to classify 15 arrhythmia classes with 94.7% accuracy which is an impressive feat, but the inference time is 6.8ms while utilizing the GPU. Discrete Wavelet Transform (DWT) and Support Vector Machines (SVMs) are proposed in [12] by D. Azariadi et al. to efficiently extract features and classify the heartbeats respectively, achieving 98.9% accuracy. All the above approaches, however, are impractical for edge/IoT devices due to their significantly high computational complexity.

In the field of machine learning techniques, deep learning emerges as a common solution for different classification issues. Advanced models capable of classifying different types of arrhythmias have been developed. S. Sakib et al. [13] in their study used a 1D CNN to eliminate the pre-processing and feature extraction steps of classifying four arrhythmia types. They achieved 96.04% accuracy, but this was with an inference time of 100 ms using a power-hungry consumer-grade processor (Core-i7). On the other hand, Ribeiro, H et al. in [14] used a Raspberry Pi (ARM Cortex A53) for the inference of the quantized neural network, and by sending data through a mobile application, achieved an accuracy of 99.6%, however the inference time varied between 4.76 ± 0.04 ms. Wenzhuo Li et al. [15] using identical DL techniques, proposed a 1D Convolution Neural Network to tackle the classification problem but this time used an automated machine learning (AutoML) tool for Neural Network Intelligence (NNI) to minimize the model size and lower power consumption. The study achieved 98.35% accuracy, classifying five arrhythmia types with an inference time of 7.08 ms. Rui Hu et al. [16] used an ECG arrhythmia detection algorithm based on CNN and a transformer taking continuous ECG segments as input. Despite the high accuracy of the model, 99.12% overall, the implementation is yet to be applied to edge or any other wearable devices.

To tackle the above limitations and improve existing work, our implementation uses a two-dimensional neural network (2d CNN) alongside the NVIDIA^® Jetson Nano^™, an edge device with strong computational capabilities for the training and inference of the proposed model.

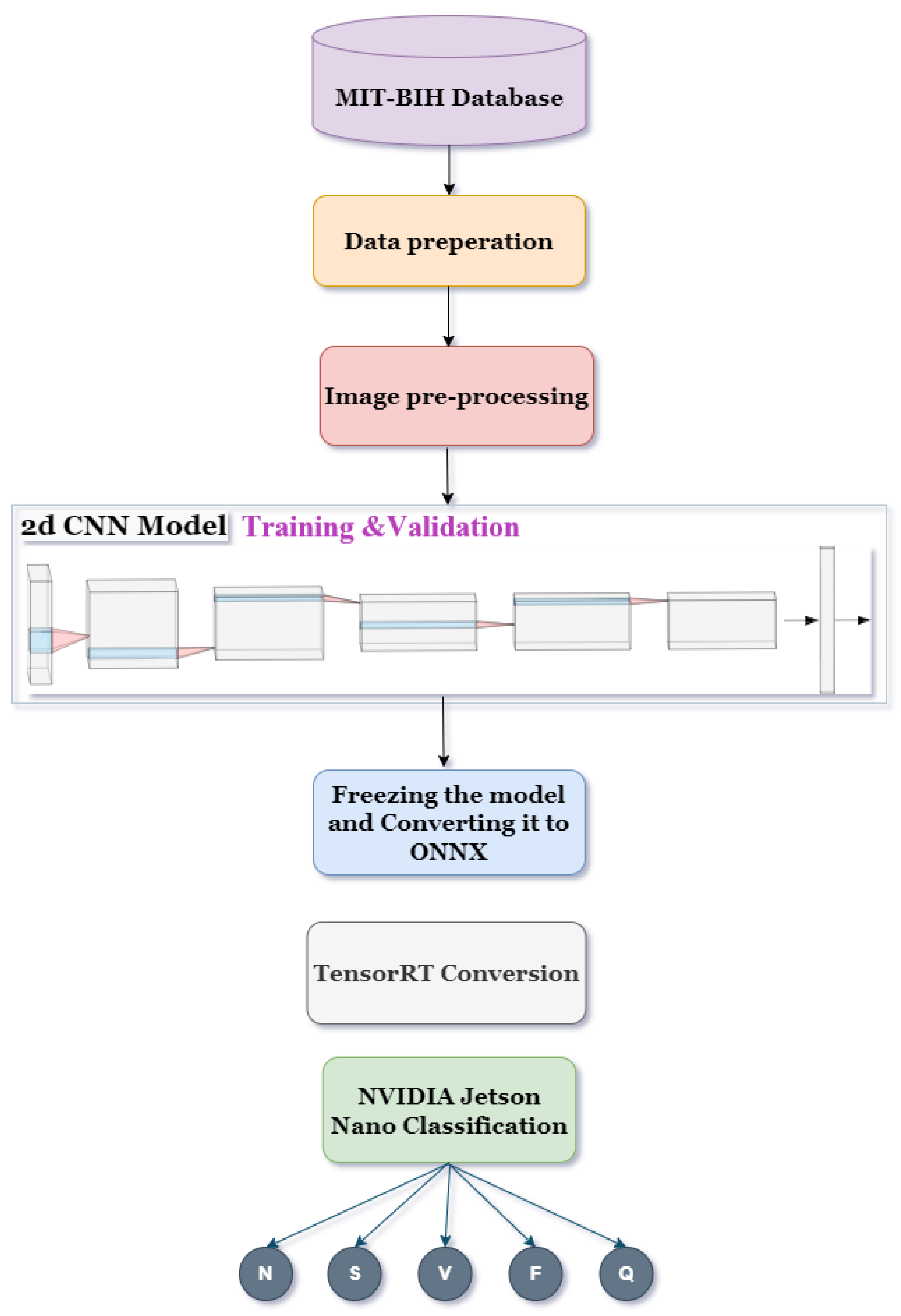
3. System Architecture

The proposed implementation of a remote, real-time monitoring system utilizing the NVIDIA^® Jetson Nano^™ edge device encapsulates a two-layer architecture, as shown in Figure 1. This dev kit costs around EUR 150 (at the time of publishing this paper). It is not wearable, but it is sufficiently portable with the dimensions 100 × 80 × 29 mm.

The Sensor/Patient Layer is composed of a wearable IoT device or devices which are capable of collecting and transmitting the ECG signals of patients in the Emergency Department (ED). These devices perform the sensing operation in a real-time manner and transmit the ECG signals via a USB Bluetooth adapter, or any other communication protocol, to the Jetson Nano without the need for online access. Several wearables can transmit data simultaneously to a single access point (Jetson Nano).

On the Edge Device Layer, the NVIDIA^® Jetson Nano^™ operates as the backbone of the proposed real-time monitoring system. It receives ECG signals, pre-processes the data, and feeds it to the trained model. With the NVIDIA^® TensorRT^™ library, we ensure the optimization of the model, so it meets the low latency needs of ED patient monitoring. Furthermore, it is possible to create multiple contexts of the same engine and map them to distinct streams for performing parallel executions of the inference [17]. This way, all patients in multiple departments can be monitored in real-time and assisted by medical personnel.

The following are key definitions of the associated priorities and goals of our study:

• Implementation of techniques to reduce overfitting, underfitting, and the imbalance of the MIT-BIH dataset.
• Performance analysis of the proposed 2d CNN framework and comparisons with other popular deep learning techniques.
• Conversion of the model to ONNX and TensorRT formats.
• Performance comparison as far as the inference is concerned between the converted and non-converted models.

The implementation process is illustrated in abstract view (see Figure 2) to demonstrate the steps that were followed.

3.1. Data Collection

The ECG signals were obtained from the publicly available MIT-BIH arrhythmia database from physionet.org [4]. The database contains 48 h two-channel recordings of 47 volunteers. Each record has a duration of 30 min, 360 Hz sampling rate, bandpass filtered at 0.1–100 Hz, and the two channels are the Modified Limb II and one of the Modified Leads: V1, V2, V4, or V5. Modified Limb II was selected in this work due to the inconsistency in the position of the second lead [18]. Each beat in every ECG recording was annotated by independent experts to indicate the type of arrhythmia prevalent at that beat.

3.2. ECG Categorization

In our implementation, the Advancement of Medical Instrumentation (ANSI/AAMI EC57) standard was followed. It states that each heartbeat can be categorized into five distinct types: normal beats (N), supraventricular ectopic beats (SVEB), ventricular ectopic beats (VEB), fusion beats (F), and unclassifiable or unknown beats (Q) [5]. The categorization and the mapping of the beats to MIT-BIH annotations/classes are demonstrated in

Table 1. Mapping between MIT-BIH beat annotations and ANSI/AAMI EC57 categories.

ANSI/AAMI Category	MIT-BIH Class	Annotation of MIT-BIH Beats
Normal beats (N)	N	Normal beat
	L	Left bundle branch block beat
	R	Right bundle branch block beat
	e	Atrial escape beat
	j	Nodal (junctional) escape beat
Supraventricular ectopic beats (SVEB)	A	Atrial premature beat
	a	Aberrated atrial premature beat
	J	Nodal (junctional) premature beat
	S	Supraventricular premature beat
Ventricular ectopic beats (VEB)	V	Premature Ventricular contraction
	E	Ventricular escape beat
Fusion beats (F)	F	Fusion of ventricular and normal beat
Unknown beats (Q)	/	Paced beat
	f	Fusion of paced and normal beat
	Q	Unclassified beat

.

3.3. Data Preparation

Each record was segmented into its heartbeats using the WFDB Toolbox [19]. This tool extracted annotated beats by finding the QRS complex of each beat on the signal. Segmented heartbeat examples can be seen in Figure 3. The total number of samples/images used for both training and testing was 15,000. The data were categorized into 5 different classes and the sampling frequency was 125 Hz.

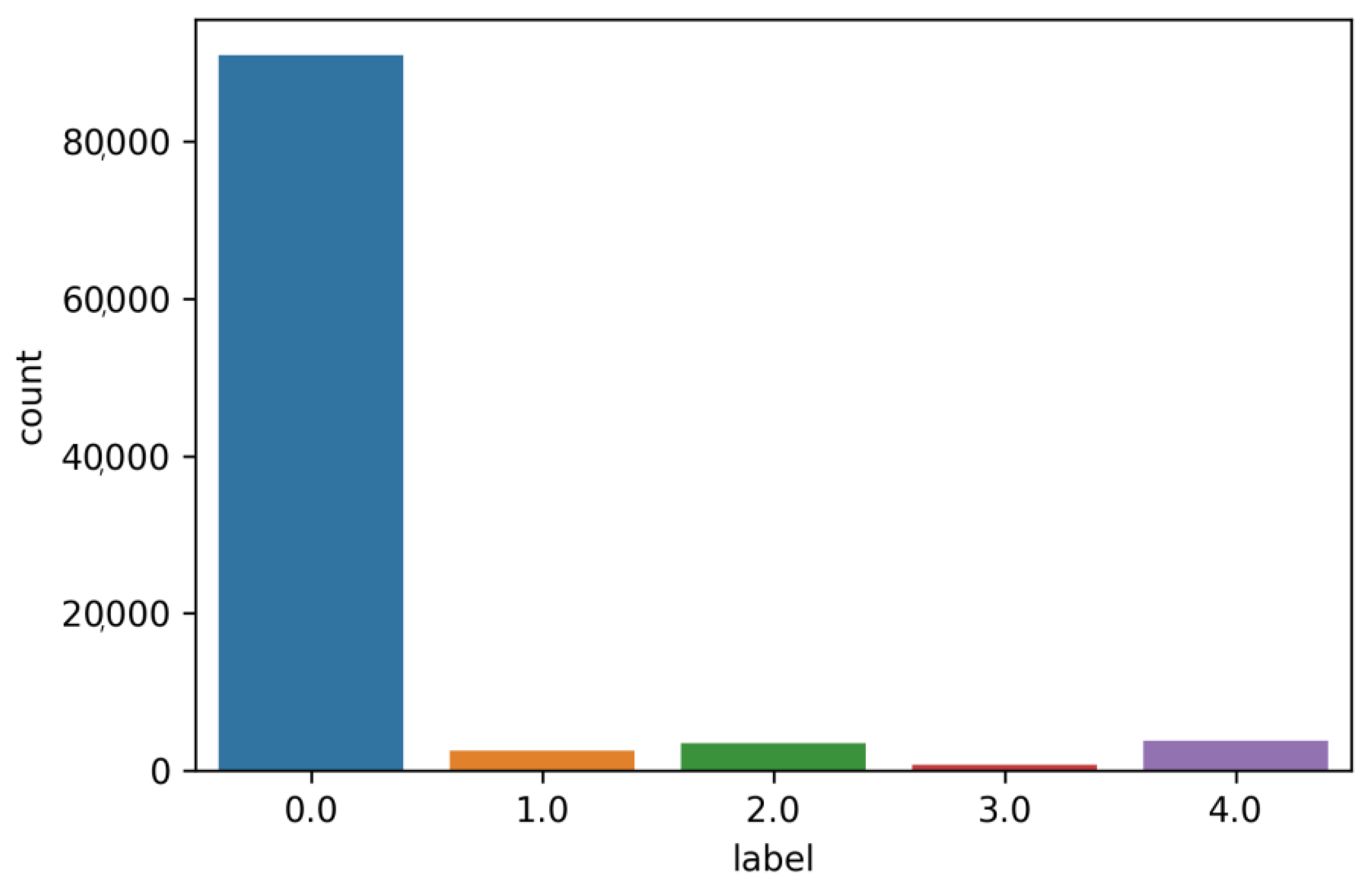
Furthermore, the original dataset was highly imbalanced (Figure 4) between the different arrhythmia classes. To combat this, Random Undersampling and the Synthetic Minority Oversampling Technique were used.

3.3.1. Random Undersampling

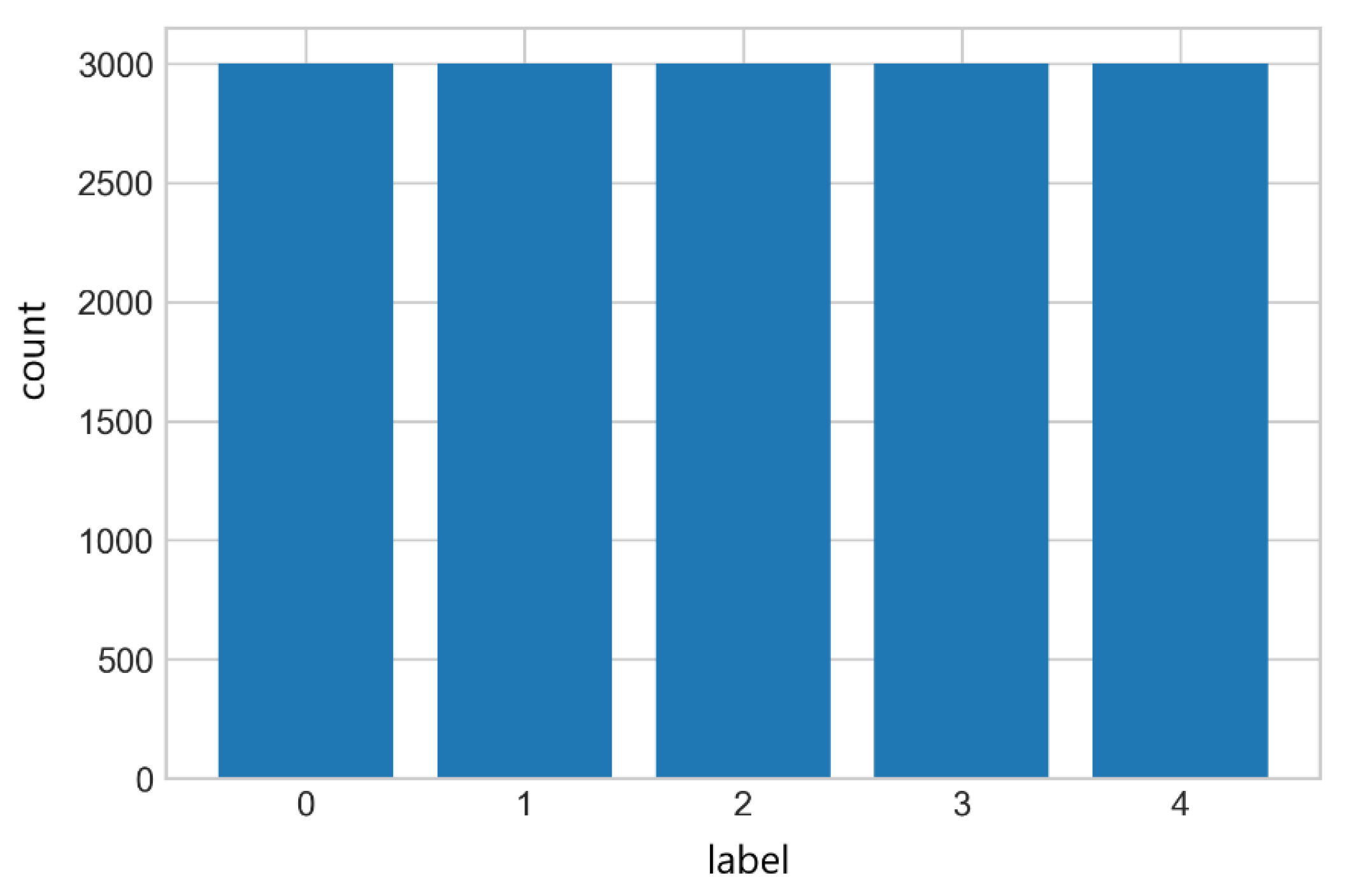
Undersampling is one of the simplest strategies to handle imbalanced data. Random undersampling involves randomly selecting examples from the majority class to delete from the training dataset [20]. This has the effect of reducing the number of examples in the majority class in the transformed version of the training dataset. This process can be repeated until the desired class distribution is achieved, such as an equal number of examples for each class.

3.3.2. Synthetic Minority Oversampling Technique (SMOTE)

In contrast to undersampling, the SMOTE algorithm carries out an oversampling approach to rebalance the original training set. Instead of applying a simple replication of the minority class instances, the key idea of SMOTE is to introduce synthetic examples. This new data is created by interpolation between several minority class instances that are within a defined neighborhood [21].

The results after applying the above techniques can be seen in Figure 5.

3.4. Image Pre-Processing

The ECG signals were converted to 2D images to skip the filtering and feature extraction processes using Pillow and OpenCV libraries. Furthermore, each image was also resized to 128 × 128 grayscale as color is not an important factor when differentiating arrhythmia types, as can be seen in Figure 6.

3.5. Proposed 2D Convolution Neural Network

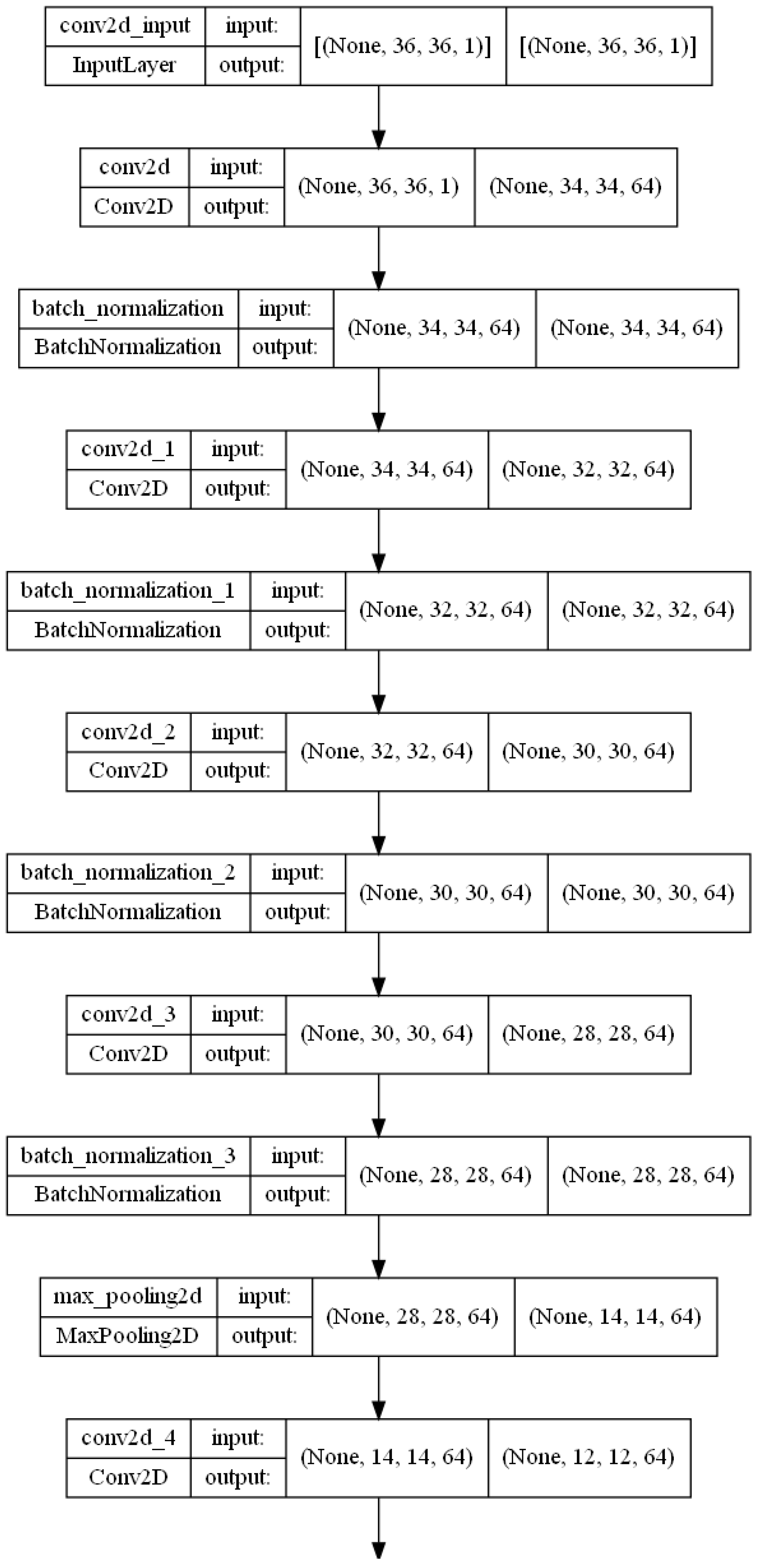
In this paper, a 2D-Convolutional Neural Network is used to train the ECG arrhythmia classifier on the MIT-BIH dataset. Convolutional Neural Networks are a class of feed-forward neural networks modeled on the visual layer of mammals [22,23]. They operate on 2D matrices and have shown great success in a variety of fields, such as image processing, speech recognition, etc. The proposed architecture includes six convolution layers, two pooling layers, and a fully connected layer. The dropout function is also applied to avoid over-fitting [24]. Before the last dense layer, we also implemented one hidden layer using the dropout function, and the neurons in the output layer corresponded to each arrhythmia type. The whole architecture of the proposed model is shown in Figure 7. A more detailed overview can be found in Figure 8.

All the data was divided into two parts for the training and testing stage using the Pareto principle: 80% training data, and 20% testing data. Scatterplots for the Training and Testing datasets can be found in Figure 9 and Figure 10.

3.5.1. Maxpooling and Flatten Layer

Pooling operations are employed to reduce the spatial dimension of the input sample while retaining significant information. This decreases the size of learning parameters, thus further reducing the cost of computation. Max pooling was used in the pooling layers. Convolution and pooling layers represent feature extraction steps. The pooling operation can be average, max, or sum [25]. In this implementation, max pooling was utilized. After the last max-pooling layer follows the flatten layer. The flatten layer converts the data of the extraction part to a 1D-vector format.

3.5.2. Batch Normalization

Batch normalization enables every layer of the network to learn a little more independently of the other layers. The batch normalization layer aims to standardize the input data by reducing internal covariate shifts [26].

3.5.3. Activation Functions

The activation function for all the layers is Exponential Linear Unit (ELU) except for the last dense layer where SoftMax [27] was applied. The SoftMax activation function transforms the raw outputs of the neural network into a vector of probabilities, essentially a probability distribution over the input classes. The rectified linear activation function, or ReLU for short, is a piecewise linear function that will output the input directly if it is positive, otherwise, it will output zero. It has become the default activation function for many types of neural networks because models that use it are easier to train and often perform better [28].

3.5.4. Regularization

An efficient regularization method called a dropout was employed. This strategy was proposed by Srivastava et al. [24]. During the training process, the dropout is conducted by maintaining the neuron active with a certain probability P or by setting it to 0. In our study, we set the hyperparameter to 0.50 because it outputs the maximum amount of regularization [29].

A regression model that uses an L1 regularization technique is called Lasso Regression (Equation (1)) and a model which uses L2 is called Ridge Regression (Equation (2)). The key difference between these two is the penalty term. Ridge regression adds a “squared magnitude” of coefficient as the penalty term to the loss function. Lasso Regression (Least Absolute Shrinkage and Selection Operator) adds “absolute value of magnitude” of the coefficient as the penalty term to the loss function [30].

$$\mathrm{Loss}=\mathrm{Error}(\mathrm{y},\hat{\mathrm{y}})+\mathsf{\lambda }{{\displaystyle \sum }}_{i=0}^n\left|w_i\right|$$

(1)

$$\mathrm{Loss}=\mathrm{Error}(\mathrm{y},\hat{\mathrm{y}})+\mathsf{\lambda }{{\displaystyle \sum }}_{i=0}^n{w}_i^2$$

(2)

3.6. IoT Platform—Edge Implementation

The NVIDIA^® Jetson Nano^™ provides a relatively large processing capability being equipped with 128-core Maxwell GPU, Quad-core ARM A57 @1.43 GHz CPU, and 4 GB LPDDR4 25.6 GB/s memory, while having low power consumption. The Jetson platform is well-supported with the JetPack Software Development Kit (SDK), containing developer tools and libraries for many deep learning applications. In the second part of our implementation, we “froze” the trained model and converted it to the ONNX Framework [31]. Furthermore, we utilized the Nvidia TensorRT platform, the cuDNN toolkit, and the TensorRT module to optimize the network models and significantly accelerate the inference phase. We also applied post-training quantization using an 8-bit half-precision floating-point format (FP8) instead of the 64-bit single-precision (FP64) to further improve the latency.

4. Experimental Results—Evaluation Metrics

The primary goal of the proposed system is to accurately predict the presence of arrhythmia and classify it from the ECG samples obtained in real-time using low-cost Edge devices without the need for complex cloud infrastructure. The arrhythmia classifier is evaluated on 3000 heartbeats.

The cardiac arrhythmia classification is evaluated by the following metrics:

• Confusion Matrix
• Accuracy
• Sensitivity (or Recall, or True Positive Rate)
• Specificity (or True Negative Rate)
• Precision (or Positive Predictive Value)
• Negative Predictive Value
• False Discovery Rate
• Fall out (or False Positive Rate)
• Categorical Cross-Entropy Loss
• f1-score
• AUC-ROC Curve (AUROC)
• One-vs-Rest ROC AUC Scores
• One-vs-One ROC AUC Scores

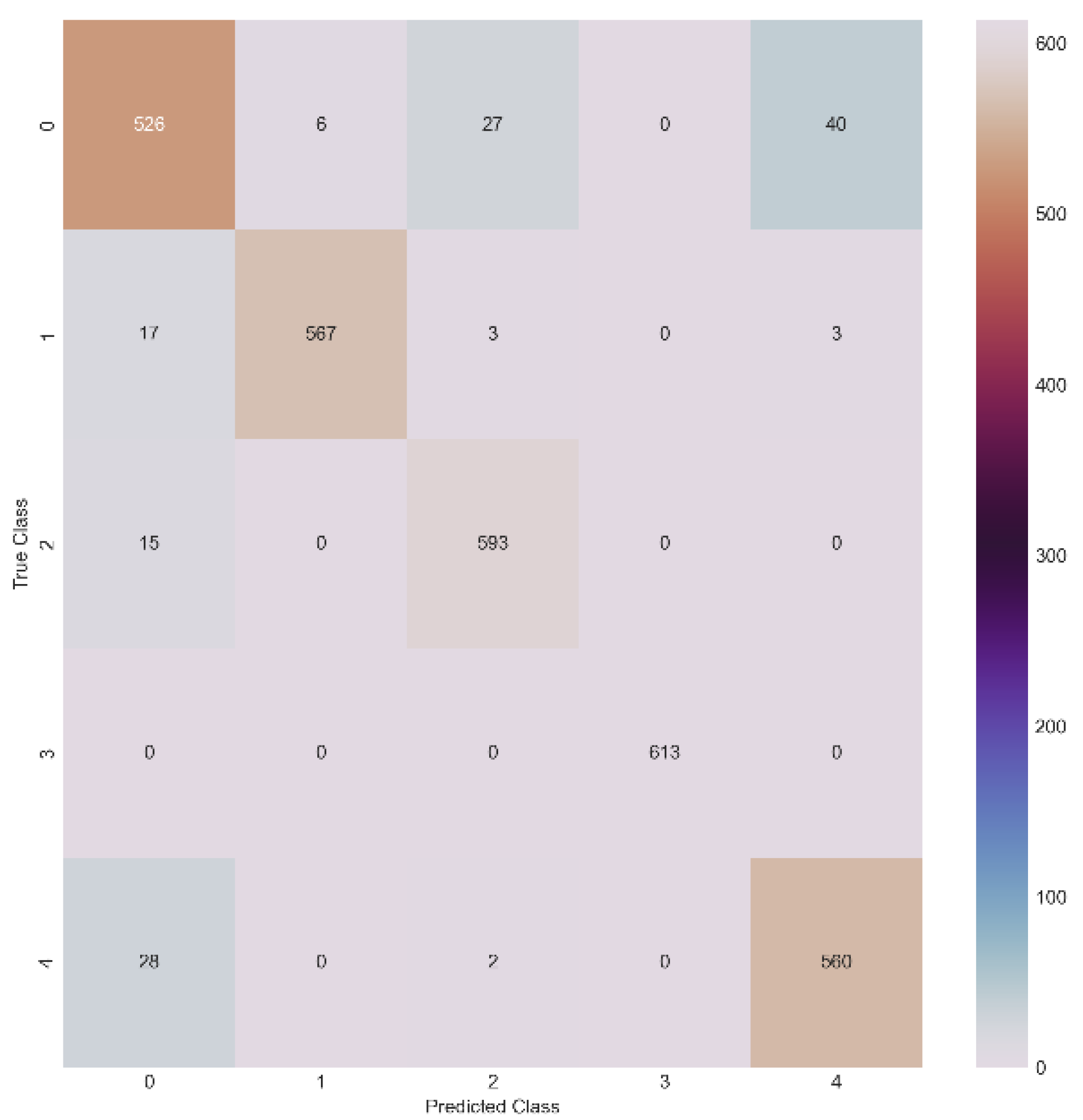
4.1. Confusion Matrix

A confusion matrix, also known as an error matrix, is a specific table layout that allows visualization of the performance of an algorithm as far as its classification is concerned. The numbers/classes 0, 1, 2, 3, and 4 represent the N, S, V, F, and Q categories of the AAMI/ANSI standard [5] in all the following Tables/Figures. The confusion matrix in its general form can be seen in

Table 2. Confusion Matrix Explained.

		Prediction Values
		Positive	Negative
Real Values	Positive	True Positive (TP)	False Negative (FN) Type II Error	Sensitivity/Recall/True Positive Rate $\frac{TP}{\left(TP+FN\right)}$
	Negative	False Positive (FP) Type I Error	True Negative (TN)	Specificity/True Negative Rate $\frac{TN}{\left(TN+FP\right)}$
		Precision/Positive Predictive Value $\frac{TP}{\left(TP+FP\right)}$	Negative Predictive Value $\frac{TN}{\left(TN+FN\right)}$	Accuracy $\frac{TP+TN}{\left(TP+TN+FP+FN\right)}$

.

For multi-class classification problems TP, TN, FP, and FN are defined as follows:

• TP: where the predicted values match the actual values;
• TN: cases except for the values of the class for which we are computing the values, the sum of all columns and rows;
• FP: sum of values of the columns except for TP;
• FN: sum of values of the row except for TP.

Specifically for our implementation, the confusion matrix can be seen in Figure 11.

4.2. Accuracy

Accuracy in Equation (3) is essentially the fraction of the number of correct predictions and the total number of predictions.

$$Accuracy=\frac{Sum of correct predictions}{Total number of predictions}=\frac{TP+TN}{\left(TP+TN+FP+FN\right)}$$

(3)

The developed model has an accuracy of 95.30%, as shown in Figure 12, and per epoch, the evolution of the accuracy is shown in Figure 13.

4.3. Sensitivity/Recall

Sensitivity as shown in Equation (4) (also referred to as True Positive Rate or Recall) is the measure of positive examples that are flagged as positive by the classifier.

$$Sensitivity=\frac{TP}{\left(TP+FN\right)}$$

(4)

The sensitivity for each of the arrhythmia categories is shown in

Table 3. Sensitivity/Recall for the different classified arrhythmia categories.

0: ‘N—Normal Beats’	1: ‘S—Supraventricular Ectopic Beats’	2: ‘V— Ventricular Ectopic Beats’	3: ‘F—Fusion Beats’	4: ‘Q—Unknown Beats’
87.81%	96.10%	97.53%	100%	94.91%
Sensitivity/Recall Mean			95.27%

.

4.4. Specificity

Specificity or True Positive Rate (Equation (5)) is the measure of negative examples flagged as negative by the classifier.

$$Specificity=\frac{TN}{\left(TN+FP\right)}$$

(5)

In this particular implementation, the specificity for each of the categories is shown in

Table 4. Specificity for the different classified arrhythmia categories.

0: ‘N—Normal Beats’	1: ‘S—Supraventricular Ectopic Beats’	2: ‘V— Ventricular Ectopic Beats’	3: ‘F—Fusion Beats’	4: ‘Q—Unknown Beats’
97.50%	99.75%	98.66%	100%	98.21%
Specificity Mean			98.82%

.

4.5. Precision

Precision, or Positive Predictive Value, as shown in Equation (6) is the ratio of the total number of correctly classified positive classes to the total number of predicted positive classes. It shows the correctness achieved in the positive prediction.

$$Precision=\frac{TP}{\left(TP+FP\right)}$$

(6)

For our proposed 2d-cnn model, the precision is shown in

Table 5. Precision for the different classified arrhythmia categories.

0: ‘N—Normal Beats’	1: ‘S—Supraventricular Ectopic Beats’	2: ‘V— Ventricular Ectopic Beats’	3: ‘F—Fusion Beats’	4: ‘Q—Unknown Beats’
89.76%	98.95%	94.88%	100%	92.86%
Precision Mean			95.29%

.

4.6. Negative Predictive Value

The Negative Predictive Value (NPV) is defined by Equation (7).

$$NPV=\frac{TN}{\left(TN+FN\right)}$$

(7)

and represents the probability that a pulse is correctly classified as not belonging to that category.

In this particular implementation, the Negative Predictive Value (NPV) for each of the categories is shown in

Table 6. Negative Predictive Value for the different classified arrhythmia categories.

0: ‘N—Normal Beats’	1: ‘S—Supraventricular Ectopic Beats’	2: ‘V— Ventricular Ectopic Beats’	3: ‘F—Fusion Beats’	4: ‘Q—Unknown Beats’
96.97%	99.05%	99.36%	100%	98.74%
Negative Predictive Value Mean			98.82%

.

4.7. False Discovery Rate

In statistics, the false discovery rate (FDR) is a method to measure the type I error rate in null hypothesis testing when conducting multiple comparisons. FDR is the expected ratio of the number of false positive classifications to the total number of positive classifications (rejections of the null hypothesis). This is defined as follows:

$$FDR=\frac{FP}{\left(TP+FP\right)}$$

(8)

The False Discovery Rate for each of the categories is shown in

Table 7. False Discovery Rate for the different classified arrhythmia categories.

0: ‘N—Normal Beats’	1: ‘S—Supraventricular Ectopic Beats’	2: ‘V— Ventricular Ectopic Beats’	3: ‘F—Fusion Beats’	4: ‘Q—Unknown Beats’
10.23%	1.04%	5.12%	0%	7.13%
False Discovery Rate Mean			4.70%

.

4.8. Fall out/False Positive Rate

This rate (fall-out or false positive rate—FPR) measures the percentage of false positive predictions against all positives in a classification problem. Its definition is as follows:

$$FPR=\frac{FP}{\left(FP+TN\right)}$$

(9)

In this particular implementation, the False Positive Rate for each of the categories is shown in

Table 8. Fall out for the different classified arrhythmia categories.

0: ‘N—Normal Beats’	1: ‘S—Supraventricular Ectopic Beats’	2: ‘V— Ventricular Ectopic Beats’	3: ‘F—Fusion Beats’	4: ‘Q—Unknown Beats’
2.49%	0.24%	1.33%	0%	1.78%
Fall out Mean			1.17%

.

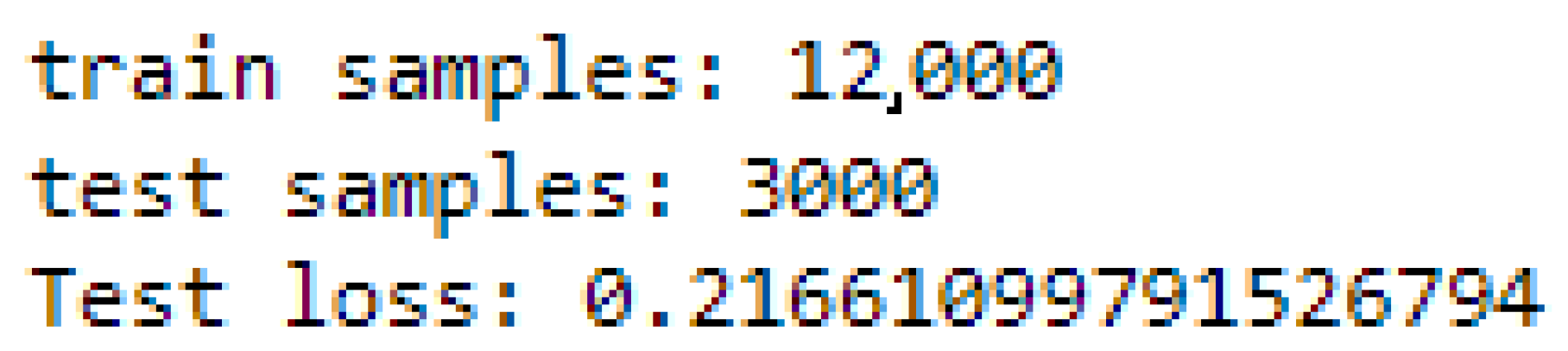
4.9. Categorical Cross-Entropy Loss

Also called SoftMax Loss. It is a SoftMax activation function plus a Cross-Entropy loss. Cross-entropy loss is used to adjust model weights during training. The goal is to minimize, i.e., the smaller the better the model. A perfect model has a cross-entropy loss of 0. The cross-entropy loss is defined as:

$$L_{CE}=-{{\displaystyle \sum }}_{i=1}^n{t}_i\log \left(p_i\right)\mathrm{for}\mathrm{n}\mathrm{classes}$$

(10)

where $t_i$ is the correct label and $p_i$ is the probability of the Softmax activation function for the n-th class.

Categorical cross-entropy is used when true labels are encoded in a one-hot manner. In digital circuits and machine learning, a one-hot is a group of bits among which the only allowed combinations of values are those with a single high (1) bit and all others low (0). In machine learning, in particular, one-hot coding is a commonly used method for dealing with categorical data. As many machine learning models need their input variables to be numeric, the categorical variables must be transformed in the data pre-processing stage.

In this specific implementation, the cross-entropy loss is 21.66% (Figure 14) and its evolution per epoch is shown in Figure 15.

4.10. f1-Score

f1-score is an overall measure of a model’s accuracy that combines precision and recall. A good f1-score (close to 1) means that there are a small number of false positives and false negatives. Thus, the true categories are correctly identified.

In this particular implementation the f1-score for each of the categories is shown in Figure 16:

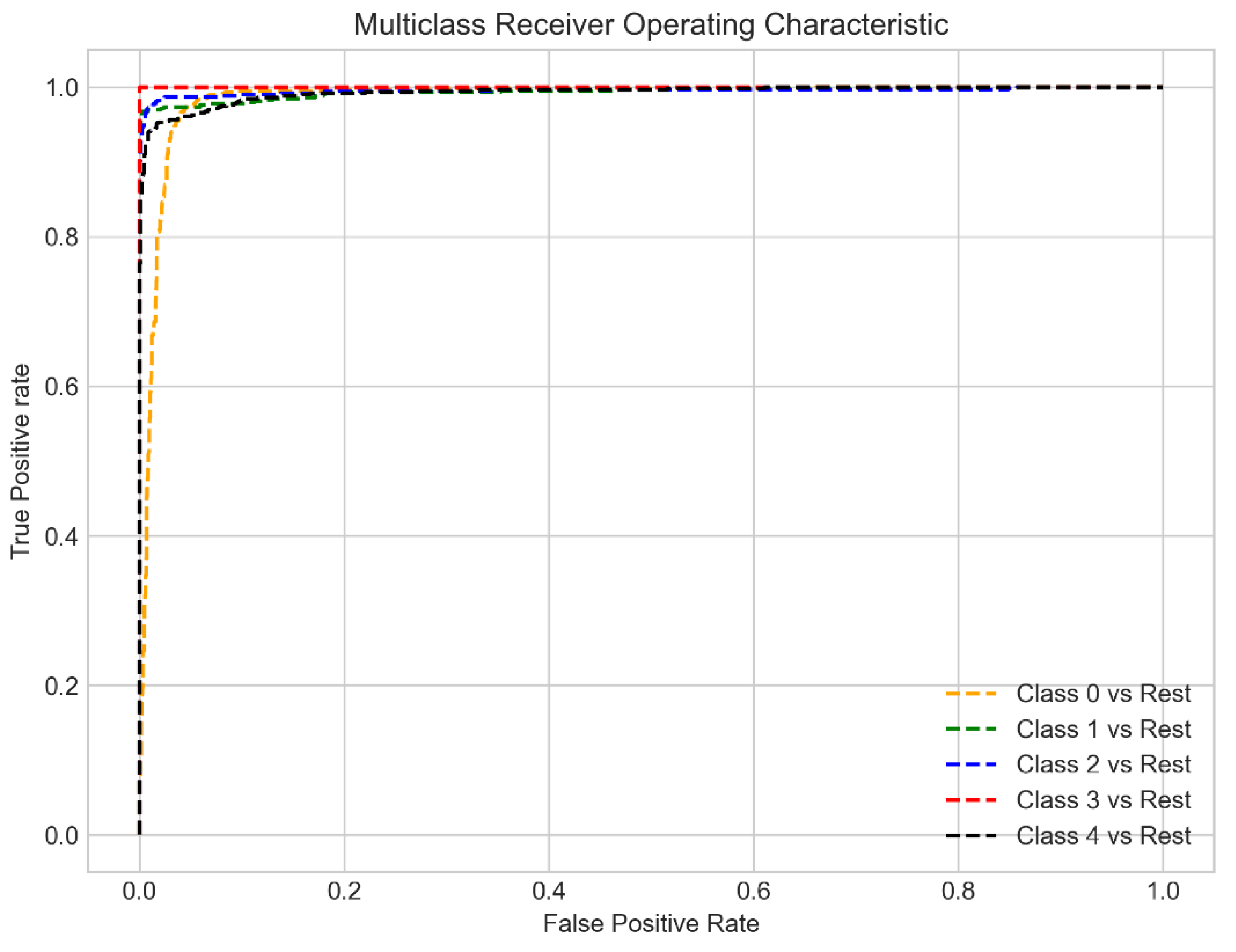
4.11. AUC-ROC Curves

The AUC—ROC curve (Area Under the Curve—Receiver Operating Characteristics) is a performance measurement of classification problems at various threshold settings. ROC is a probability curve and AUC represents the degree or measure of separability. It shows how well the model can discriminate between the different classes. The higher the AUC, the better the model is at discriminating between classes of cardiac arrhythmias.

In a multi-class model, it is possible to plot N number of AUC ROC curves for N classes, using the One-vs-Rest methodology discussed below.

The ROC curve is plotted with TPR (True Positive Rate) versus FPR (False Positive Rate), where TPR is on the y-axis and FPR is on the x-axis, as shown in Figure 17.

4.12. One-vs-Rest

OvR is a method for evaluating multi-class models by comparing each class to all others simultaneously. This method takes one class and considers it the “positive” class, while all others (the rest) are considered the “negative” class. In this way, it reduces the output of the multi-class classification to a binary classification output, and in this way, it is possible to use all known metrics for evaluation.

This is done for each class present in the data. Thus, for a 5-class data set 5 different OvR scores are obtained. Finally, the simple average (macro) or weighted average (weighted average) can be used to produce a final OvR score of the model.

In the implementation the One-vs-Rest ROC AUC (Figure 18) scores are:

4.13. One-vs-One

One-vs-One is similar to One-vs-Rest but, instead of comparing each class with the others, it compares all possible combinations of two classes in the data set. As in OvR, all OvO scores can be averaged to derive a final OvO model score.

The One-vs-One ROC AUC scores are presented in Figure 19.

5. Discussion

Regarding the approaches that were discussed in Section 2 (Literature Review): [12,13,14,15] achieves higher accuracy, [10] uses real patient data, and [11] classifies more arrhythmia types. All of the above are lacking in terms of fast, real-time inference which is crucial in an Emergency Department since most admitted patients are at significant risk of immediate fatal arrhythmias, such as ventricular fibrillation or asystole, and should receive continuous cardiac monitoring [32].

A detailed comparison between the implementations mentioned and our proposed solution can be seen in

Table 9. Comparison between other implementations and our proposed 2d CNN.

Reference	No. Classes	Database	Model-Method	Accuracy (%)	Other Notes
[10]	3 (healthy, unhealthy, not defined)	3 Private Patients	k-means	-	Classification Time: TM = 6250 ms
[11]	15 (N, SVPB, PVC, LBBB, RBBB, APB, AAP, NPB, PAC, AEB, FVB, NEB, VEB, FPB, PF)	MIT-BIH	RNN-LSTM	94.7%	Classification Time: 6.88 ms
[12]	2 (Normal/Abnormal)	MIT-BIH	SVM	98.9%	Classification Time: 29.25 ms
[13]	4 (Normal, Supraventricular, Ventricular, Fusion)	MIT-BIH	1D-CNN	96.26%	Classification Time: 100 ms with the best performance workstation
[14]	5 (N, S, V, F, Q)	MIT-BIH	1D-CNN	99.6%	Inference Time: 4.76 ms (lowest value)
[15]	5 (N, S, V, F, Q)	MIT-BIH	1D-CNN	98.35%	Classification Time: 7.08 ms
Our Work	5 (N, S, V, F, Q)	MIT-BIH	2D-CNN	95.30%	Classification Time: 1.476 ms

. It is evident that our work, when compared to existing multi-parameter monitor devices, has the major advantages of parallel and continuous monitoring, alerts for intervention teams, and compact size without relying on batteries. Furthermore, connectivity is a huge advantage since NVIDIA^® Jetson Nano^™ can transmit data through Wi-Fi, Bluetooth, or any other communication protocol, due to its support for a plethora of USB peripherals.

6. Conclusions

In this paper, we proposed an efficient method for the classification of ECG arrhythmias using two-dimensional convolution neural networks with images as input, and with improved techniques for speed and accuracy.

The proposed model achieved an ROC-AUC score of 0.9934, accuracy of 95.3%, mean specificity of 98.82%, and mean sensitivity of 95.27% with an inference time of 1.47 ms. The result of the classification of ECG arrhythmias shows that the conversion of the one-dimensional signal into two-dimensional ECG images and its modeling in a convolutional neural network can be an effective technique to support experts in diagnosing cardiovascular diseases through ECG signals. The five categories of cardiac arrhythmias could be grouped into three main categories: green (N, F, V), yellow (Q), and red (S). These categories can represent normal, abnormal, and potentially life-threatening states of the heart’s electrical activity, respectively. The transformation of the model into a corresponding TensorRT model enables the execution of edge computation. A potentially promising area is the deployment of the model in portable devices and real-time implementations, such as Holter machines or cardiography machines in emergency departments.

Despite the success the model achieved with this technique, there are still some weaknesses/problems that could improve the existing model. As mentioned, the total number of samples/images used for both training and testing is 15,000 images. Using the entire MIT-BIH database could significantly impact the accuracy of our model. At the edge of this implementation, NVIDIA^® Triton^™ inference servers and a dynamic application partitioning work scheduling framework (DAPWTS) could be used in conjunction with NVIDIA^® Jetson Nano^™ to fully leverage parallel processing at real-time speed using state-of-the-art models and devices.