Assessment of Gradient Descent Trained Rule-Fact Network Expert System Multi-Path Training Technique Performance
Abstract
:1. Introduction
2. Background
2.1. Expert Systems
2.2. Machine Learning Training and Gradient Descent
2.3. Gradient Descent Trained Expert Systems
2.4. Neural Networks and their Explainability Issues
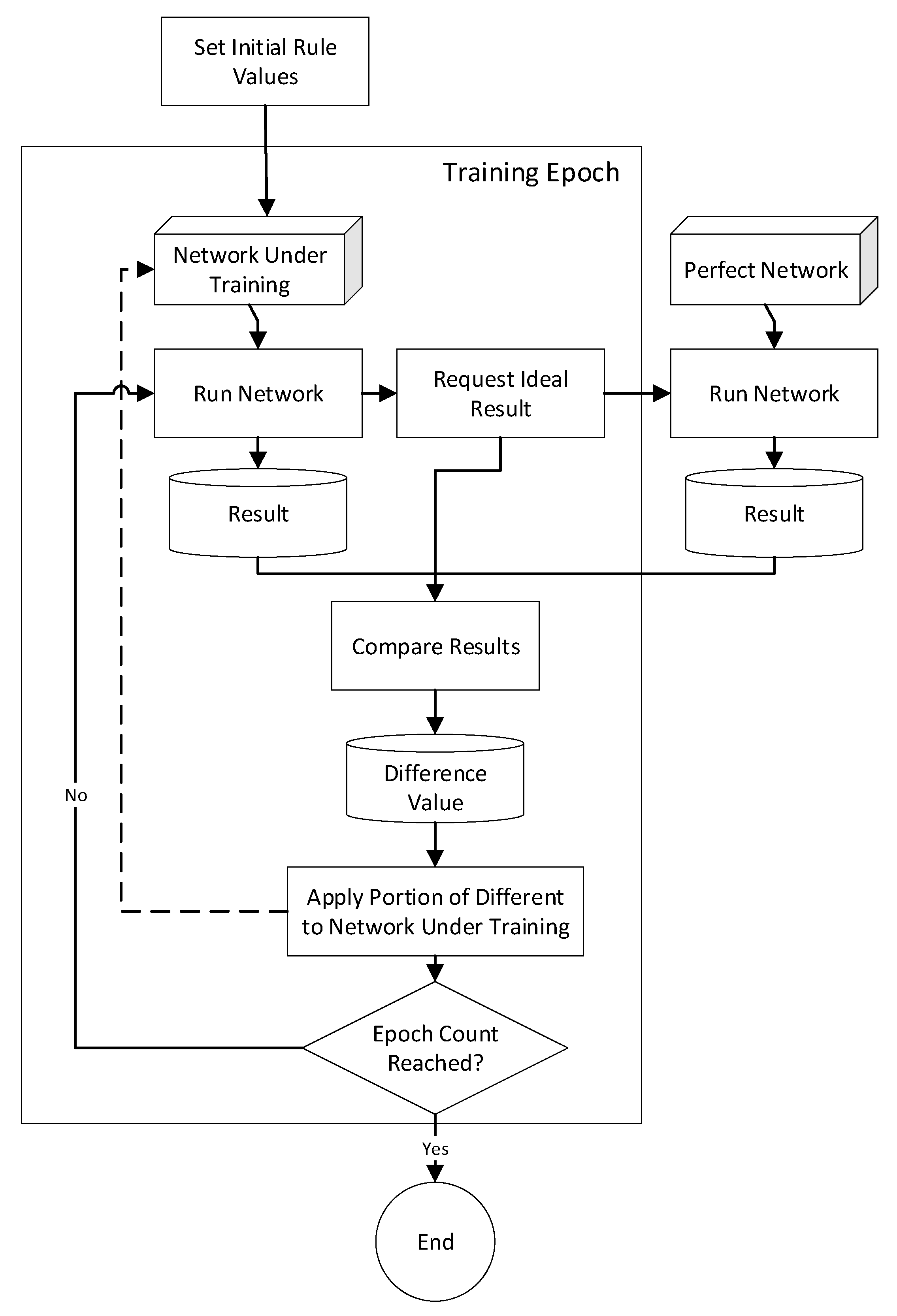
3. Experimental Design
3.1. Experimental System
3.2. Experimental Procedure
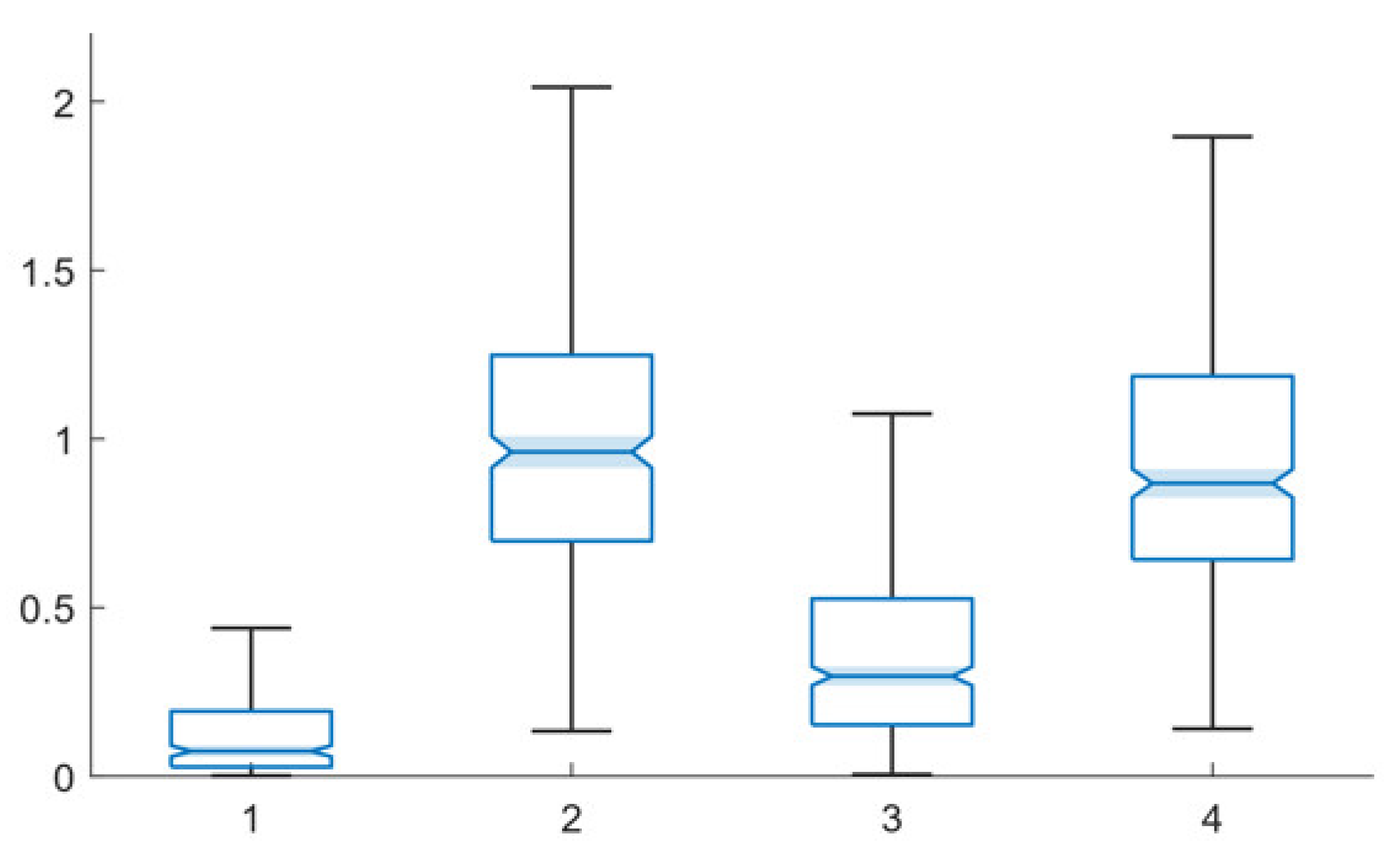
4. Network Types and System Performance
5. Training and System Performance
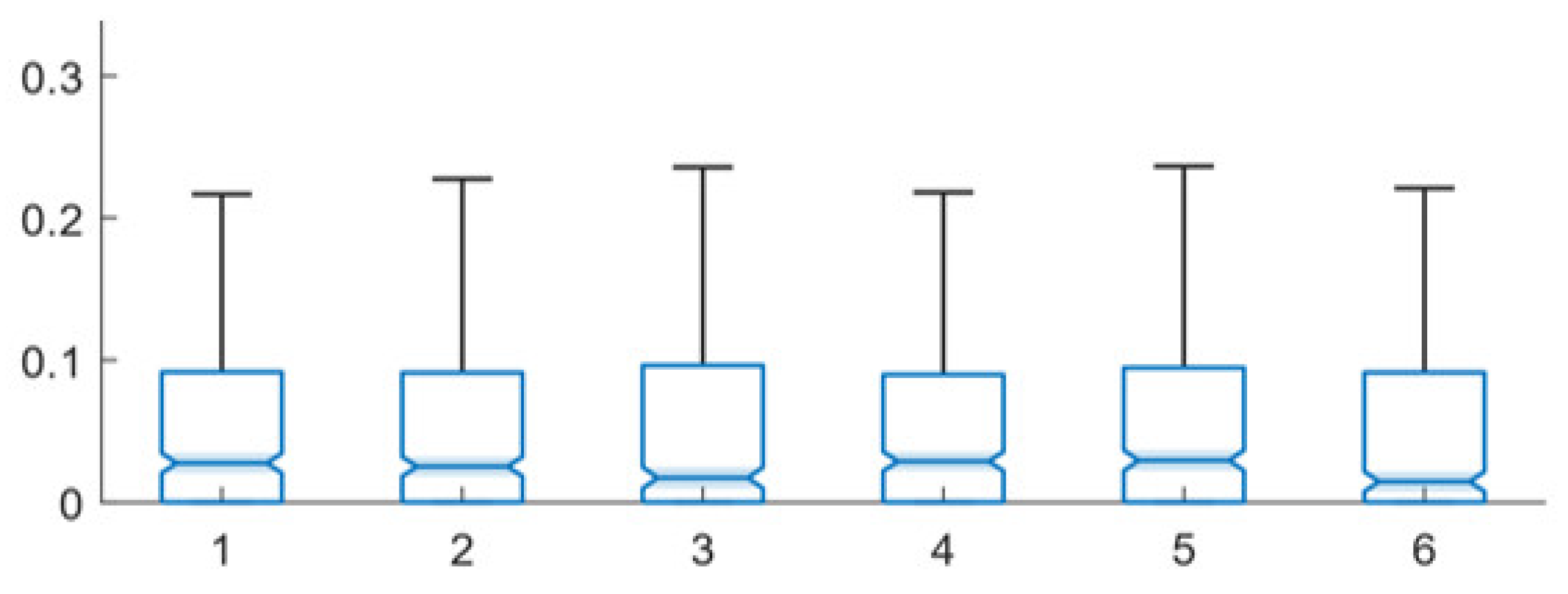
6. Velocity Levels and System Performance
7. Comparative Performance of the Single-Path and Multi-Path Techniques
7.1. Network Perturbation
7.2. Training Epochs
7.3. Training Velocity Levels
8. Algorithm Speed Assessment
9. Conclusions and Future Work
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Gradient Descent Rule-Fact Network Training Technique
| Variable | Meaning |
|---|---|
| Wi | Weighting for rule i |
| WR(m,h) | Weighting for each rule (m indicates the rule and h indicates which weight value) |
| {APT} | Set of all rules passed through |
| Ci | Contribution of rule i |
| {AC} | Set of all contributing rule nodes |
| RP | Perfect network result |
| RT | Training network result |
| V | Velocity |
| MAX | Function returning the largest value passed to it |
| Di | Difference applied to a given rule weighting |
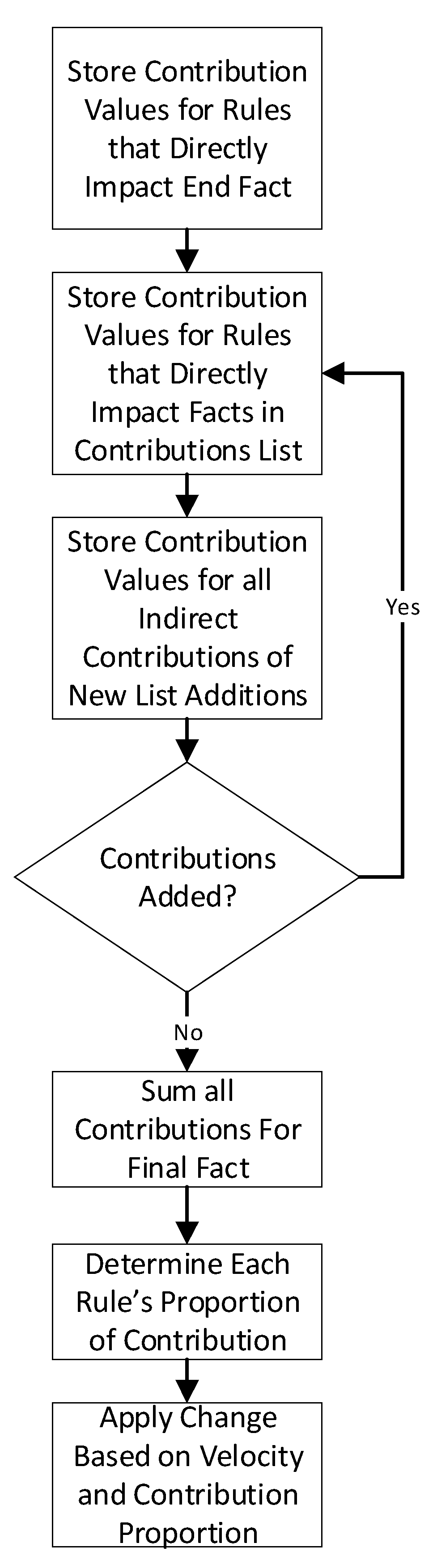
| Listing A1. Pseudocode for Algorithm. |
| Perfect Network Generation Using Relevant Parameters |
| { |
| Creation of Facts (including setting fact initial values) |
| Creation of Rules |
| Selection of Facts to Serve as Rule Inputs and Output |
| } |
| Creation of Network to be Trained |
| { |
| Copy rules and facts from perfect network |
| Apply network perturbations, if required for experimental condition |
| Reset all rule values |
| } |
| Training Process |
| { |
| For the specified number of training epochs |
| { |
| If training type = train path—same facts |
| { |
| Select input/output facts during first iteration, reuse throughout training |
| } |
| Elseif training type = train path—random facts |
| { |
| Select input/output facts during first iteration, reuse throughout training |
| Reset all fact values to new random values for the training epoch |
| } |
| Elseif training type = train multiple paths—same facts |
| { |
| Select input/output facts during each iteration |
| } |
| Elseif training type = train multiple paths—random facts |
| { |
| Select input/output facts during each iteration |
| Reset all fact values to new random values for the training epoch |
| } |
| Identify Contributing Rules |
| Run ideal network |
| Run network under training |
| Compare results of runs to determine error |
| Apply Part of Error Between Actual and Target Output to Contributing Rules |
| } |
| If fact values have been changed during training, reset to original values |
| } |
| Run Presentation Transaction to Collect Data |
Appendix B. Data Tables
| Mean | Median | Mean—High Err | Mean—Low Err | |
|---|---|---|---|---|
| Base Network | 0.058 | 0.025 | 0.183 | 0.023 |
| 10% Error Network | 0.067 | 0.032 | 0.186 | 0.025 |
| 25% Error Network | 0.059 | 0.018 | 0.184 | 0.018 |
| 50% Error Network | 0.060 | 0.025 | 0.182 | 0.021 |
| Random Network | 0.178 | 0.118 | 0.322 | 0.016 |
| 1% Augmented Network | 0.057 | 0.021 | 0.176 | 0.022 |
| 5% Augmented Network | 0.053 | 0.022 | 0.174 | 0.022 |
| 10% Augmented Network | 0.051 | 0.017 | 0.170 | 0.022 |
| 25% Augmented Network | 0.059 | 0.031 | 0.175 | 0.025 |
| 50% Augmented Network | 0.053 | 0.020 | 0.162 | 0.020 |
| Mean | Median | Mean—High Err | Mean—Low Err | |
|---|---|---|---|---|
| Base Network | 0.059 | 0.017 | 0.190 | 0.019 |
| 10% Error Network | 0.065 | 0.030 | 0.177 | 0.024 |
| 25% Error Network | 0.054 | 0.018 | 0.161 | 0.019 |
| 50% Error Network | 0.054 | 0.019 | 0.182 | 0.021 |
| Random Network | 0.170 | 0.095 | 0.322 | 0.023 |
| 1% Augmented Network | 0.050 | 0.017 | 0.166 | 0.020 |
| 5% Augmented Network | 0.056 | 0.019 | 0.174 | 0.019 |
| 10% Augmented Network | 0.058 | 0.025 | 0.196 | 0.023 |
| 25% Augmented Network | 0.059 | 0.020 | 0.184 | 0.021 |
| 50% Augmented Network | 0.062 | 0.022 | 0.189 | 0.021 |
| Mean | Median | Mean—High Err | Mean—Low Err | |
|---|---|---|---|---|
| 1 Epoch | 0.059 | 0.020 | 0.184 | 0.020 |
| 10 Epochs | 0.062 | 0.024 | 0.180 | 0.020 |
| 25 Epochs | 0.054 | 0.019 | 0.180 | 0.022 |
| 50 Epochs | 0.056 | 0.027 | 0.167 | 0.025 |
| 100 Epochs | 0.058 | 0.025 | 0.183 | 0.023 |
| 250 Epochs | 0.057 | 0.019 | 0.172 | 0.019 |
| 500 Epochs | 0.063 | 0.034 | 0.188 | 0.025 |
| 1000 Epochs | 0.048 | 0.013 | 0.181 | 0.020 |
| Mean | Median | Mean—High Err | Mean—Low Err | |
|---|---|---|---|---|
| 1 Epoch | 0.065 | 0.032 | 0.180 | 0.026 |
| 10 Epochs | 0.054 | 0.021 | 0.170 | 0.021 |
| 25 Epochs | 0.051 | 0.022 | 0.171 | 0.024 |
| 50 Epochs | 0.057 | 0.022 | 0.175 | 0.021 |
| 100 Epochs | 0.059 | 0.017 | 0.190 | 0.019 |
| 250 Epochs | 0.052 | 0.021 | 0.170 | 0.022 |
| 500 Epochs | 0.061 | 0.030 | 0.184 | 0.023 |
| 1000 Epochs | 0.065 | 0.030 | 0.196 | 0.025 |
| Velocity | Mean | Median | Mean—High Err | Mean—Low Err |
|---|---|---|---|---|
| 0.01 | 0.057 | 0.021 | 0.183 | 0.022 |
| 0.05 | 0.060 | 0.027 | 0.187 | 0.023 |
| 0.1 | 0.058 | 0.025 | 0.183 | 0.023 |
| 0.15 | 0.059 | 0.022 | 0.181 | 0.021 |
| 0.25 | 0.056 | 0.024 | 0.176 | 0.021 |
| 0.5 | 0.056 | 0.020 | 0.180 | 0.021 |
| Velocity | Mean | Median | Mean—High Err | Mean—Low Err |
|---|---|---|---|---|
| 0.01 | 0.058 | 0.028 | 0.175 | 0.024 |
| 0.05 | 0.056 | 0.025 | 0.171 | 0.023 |
| 0.1 | 0.059 | 0.017 | 0.190 | 0.019 |
| 0.15 | 0.057 | 0.029 | 0.170 | 0.024 |
| 0.25 | 0.062 | 0.029 | 0.183 | 0.025 |
| 0.5 | 0.055 | 0.015 | 0.178 | 0.019 |
References
- Straub, J. Expert system gradient descent style training: Development of a defensible artificial intelligence technique. Knowl. Based Syst. 2021, 228, 107275. [Google Scholar] [CrossRef]
- Mitra, S.; Pal, S.K. Neuro-fuzzy expert systems: Relevance, features and methodologies. IETE J. Res. 1996, 42, 335–347. [Google Scholar] [CrossRef]
- Zwass, V. Expert System. Available online: https://www.britannica.com/technology/expert-system (accessed on 24 February 2021).
- Lindsay, R.K.; Buchanan, B.G.; Feigenbaum, E.A.; Lederberg, J. DENDRAL: A case study of the first expert system for scientific hypothesis formation. Artif. Intell. 1993, 61, 209–261. [Google Scholar] [CrossRef] [Green Version]
- Styvaktakis, E.; Bollen, M.H.J.; Gu, I.Y.H. Expert system for classification and analysis of power system events. IEEE Trans. Power Deliv. 2002, 17, 423–428. [Google Scholar] [CrossRef]
- McKinion, J.M.; Lemmon, H.E. Expert systems for agriculture. Comput. Electron. Agric. 1985, 1, 31–40. [Google Scholar] [CrossRef]
- Kuehn, M.; Estad, J.; Straub, J.; Stokke, T.; Kerlin, S. An expert system for the prediction of student performance in an initial computer science course. In Proceedings of the IEEE International Conference on Electro Information Technology, Lincoln, NE, USA, 14–17 May 2017. [Google Scholar]
- Kalogirou, S. Expert systems and GIS: An application of land suitability evaluation. Comput. Environ. Urban Syst. 2002, 26, 89–112. [Google Scholar] [CrossRef]
- Waterman, D. A Guide to Expert Systems; Addison-Wesley Pub. Co.: Reading, MA, USA, 1986. [Google Scholar]
- Renders, J.M.; Themlin, J.M. Optimization of Fuzzy Expert Systems Using Genetic Algorithms and Neural Networks. IEEE Trans. Fuzzy Syst. 1995, 3, 300–312. [Google Scholar] [CrossRef]
- Sahin, S.; Tolun, M.R.; Hassanpour, R. Hybrid expert systems: A survey of current approaches and applications. Expert Syst. Appl. 2012, 39, 4609–4617. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Chohra, A.; Farah, A.; Belloucif, M. Neuro-fuzzy expert system E_S_CO_V for the obstacle avoidance behavior of intelligent autonomous vehicles. Adv. Robot. 1997, 12, 629–649. [Google Scholar] [CrossRef]
- Sandham, W.A.; Hamilton, D.J.; Japp, A.; Patterson, K. Neural network and neuro-fuzzy systems for improving diabetes therapy. In Proceedings of the 20th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Hong Kong, China, 1 November 1998; Institute of Electrical and Electronics Engineers (IEEE): Picataway, NJ, USA, 2002; pp. 1438–1441. [Google Scholar]
- Ephzibah, E.P.; Sundarapandian, V. A Neuro Fuzzy Expert System for Heart Disease Diagnosis. Comput. Sci. Eng. Int. J. 2012, 2, 17–23. [Google Scholar] [CrossRef]
- Das, S.; Ghosh, P.K.; Kar, S. Hypertension diagnosis: A comparative study using fuzzy expert system and neuro fuzzy system. In Proceedings of the IEEE International Conference on Fuzzy Systems, Hyderabad, India, 7–10 July 2013. [Google Scholar]
- Akinnuwesi, B.A.; Uzoka, F.M.E.; Osamiluyi, A.O. Neuro-Fuzzy Expert System for evaluating the performance of Distributed Software System Architecture. Expert Syst. Appl. 2013, 40, 3313–3327. [Google Scholar] [CrossRef]
- Rojas, R. The Backpropagation Algorithm. In Neural Networks; Springer: Berlin/Heidelberg, Germany, 1996; pp. 149–182. [Google Scholar]
- Battiti, R. Accelerated Backpropagation Learning: Two Optimization Methods. Complex Syst. 1989, 3, 331–342. [Google Scholar]
- Kosko, B.; Audhkhasi, K.; Osoba, O. Noise can speed backpropagation learning and deep bidirectional pretraining. Neural Netw. 2020, 129, 359–384. [Google Scholar] [CrossRef] [PubMed]
- Abbass, H.A. Speeding Up Backpropagation Using Multiobjective Evolutionary Algorithms. Neural Comput. 2003, 15, 2705–2726. [Google Scholar] [CrossRef]
- Aicher, C.; Foti, N.J.; Fox, E.B. Adaptively Truncating Backpropagation Through Time to Control Gradient Bias. In Proceedings of the 35th Uncertainty in Artificial Intelligence Conference, Tel Aviv, Israel, 22–25 July 2019; pp. 799–808. [Google Scholar]
- Chizat, L.; Bach, F. Implicit Bias of Gradient Descent for Wide Two-layer Neural Networks Trained with the Logistic Loss. Proc. Mach. Learn. Res. 2020, 125, 1–34. [Google Scholar]
- Kolen, J.F.; Pollack, J.B. Backpropagation is Sensitive to Initial Conditions. Complex Syst. 1990, 4, 269–280. [Google Scholar]
- Zhao, P.; Chen, P.Y.; Wang, S.; Lin, X. Towards query-efficient black-box adversary with zeroth-order natural gradient descent. Proc. AAAI Conf. Artif. Intell. 2020, 34, 6909–6916. [Google Scholar] [CrossRef]
- Wu, Z.; Ling, Q.; Chen, T.; Giannakis, G.B. Federated Variance-Reduced Stochastic Gradient Descent with Robustness to Byzantine Attacks. IEEE Trans. Signal Process. 2020, 68, 4583–4596. [Google Scholar] [CrossRef]
- Saffaran, A.; Azadi Moghaddam, M.; Kolahan, F. Optimization of backpropagation neural network-based models in EDM process using particle swarm optimization and simulated annealing algorithms. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 73. [Google Scholar] [CrossRef]
- Gupta, J.N.D.; Sexton, R.S. Comparing backpropagation with a genetic algorithm for neural network training. Omega 1999, 27, 679–684. [Google Scholar] [CrossRef]
- Basterrech, S.; Mohammed, S.; Rubino, G.; Soliman, M. Levenberg—Marquardt training algorithms for random neural networks. Comput. J. 2011, 54, 125–135. [Google Scholar] [CrossRef]
- Kim, S.; Ko, B.C. Building deep random ferns without backpropagation. IEEE Access 2020, 8, 8533–8542. [Google Scholar] [CrossRef]
- Ma, W.D.K.; Lewis, J.P.; Kleijn, W.B. The HSIC bottleneck: Deep learning without back-propagation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 5085–5092. [Google Scholar]
- Park, S.; Suh, T. Speculative Backpropagation for CNN Parallel Training. IEEE Access 2020, 8, 215365–215374. [Google Scholar] [CrossRef]
- Lee, C.; Sarwar, S.S.; Panda, P.; Srinivasan, G.; Roy, K. Enabling Spike-Based Backpropagation for Training Deep Neural Network Architectures. Front. Neurosci. 2020, 14, 119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mirsadeghi, M.; Shalchian, M.; Kheradpisheh, S.R.; Masquelier, T. STiDi-BP: Spike time displacement based error backpropagation in multilayer spiking neural networks. Neurocomputing 2021, 427, 131–140. [Google Scholar] [CrossRef]
- Straub, J. Machine learning performance validation and training using a ‘perfect’ expert system. MethodsX 2021, 8, 101477. [Google Scholar] [CrossRef]
- Li, J.; Huang, J.S. Dimensions of artificial intelligence anxiety based on the integrated fear acquisition theory. Technol. Soc. 2020, 63, 101410. [Google Scholar] [CrossRef]
- Gunning, D.; Stefik, M.; Choi, J.; Miller, T.; Stumpf, S.; Yang, G.Z. XAI-Explainable artificial intelligence. Sci. Robot. 2019, 4, eaay7120. [Google Scholar] [CrossRef] [Green Version]
- Eykholt, K.; Evtimov, I.; Fernandes, E.; Li, B.; Rahmati, A.; Xiao, C.; Prakash, A.; Kohno, T.; Song, D. Robust Physical-World Attacks on Deep Learning Models. arXiv 2017, arXiv:1707.08945. [Google Scholar]
- Gong, Y.; Poellabauer, C. Crafting Adversarial Examples for Speech Paralinguistics Applications. arXiv 2017, arXiv:1711.03280v2. [Google Scholar] [CrossRef]
- Sharif, M.; Bhagavatula, S.; Bauer, L.; Reiter, M.K. Accessorize to a Crime: Real and Stealthy Attacks on State-of-the-Art Face Recognition. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; ACM Press: New York, NY, USA, 2016; pp. 1528–1540. [Google Scholar]
- Doyle, T. Weapons of Math Destruction: How Big Data Increases Inequality and Threatens Democracy. Inf. Soc. 2017, 33, 301–302. [Google Scholar] [CrossRef]
- Noble, S.U. Algorithms of Oppression: How Search Engines Reinforce Racism Paperback; NYU Press: New York, NY, USA, 2018. [Google Scholar]
- Xu, F.; Uszkoreit, H.; Du, Y.; Fan, W.; Zhao, D.; Zhu, J. Explainable AI: A Brief Survey on History, Research Areas, Approaches and Challenges. In Proceedings of the CCF International Conference on Natural Language Processing and Chinese Computing 2019, Dunhuang, China, 9−14 October 2019. [Google Scholar]
- Barredo Arrieta, A.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; Garcia, S.; Gil-Lopez, S.; Molina, D.; Benjamins, R.; et al. Explainable Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef] [Green Version]
- Mahbooba, B.; Timilsina, M.; Sahal, R.; Serrano, M. Explainable Artificial Intelligence (XAI) to Enhance Trust Management in Intrusion Detection Systems Using Decision Tree Model. Complexity 2021, 2021, 1–11. [Google Scholar] [CrossRef]
- Gade, K.; Geyik, S.C.; Kenthapadi, K.; Mithal, V.; Taly, A. Explainable AI in Industry. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar]
- Mehdiyev, N.; Fettke, P. Explainable Artificial Intelligence for Process Mining: A General Overview and Application of a Novel Local Explanation Approach for Predictive Process Monitoring. arXiv 2020, arXiv:2009.02098. [Google Scholar]
- Van Lent, M.; Fisher, W.; Mancuso, M. An explainable artificial intelligence system for small-unit tactical behavior. In Proceedings of the 16th Conference on Innovative Applications of Artificial Intelligence, San Jose, CA, USA, 27–29 July 2004. [Google Scholar]
- Buhmann, A.; Fieseler, C. Towards a deliberative framework for responsible innovation in artificial intelligence. Technol. Soc. 2021, 64, 101475. [Google Scholar] [CrossRef]





| Model Hyperparameters | Experimental Parameters | Algorithm Hyperparameters | |||
|---|---|---|---|---|---|
| Facts | Rules | Network Perturbation | Training Epochs | Velocity | Training Approach |
| 100 | 100 | Base Random Augmented 1% Augmented 5% Augmented 10% Augmented 25% Augmented 50% Error 10% Error 25% Error 50% | 1 10 25 50 100 250 500 1000 | 0.01 0.05 0.10 0.15 0.25 0.50 | Multiple Paths—Same Facts Multiple Paths—Random Facts |
| Network | Training | Mean | Median | Mean—High Err | Mean—Low Err |
|---|---|---|---|---|---|
| Base | 1 | 0.051 | 0.010 | 0.204 | 0.018 |
| 25 | 0.061 | 0.023 | 0.197 | 0.023 | |
| 100 | 0.058 | 0.025 | 0.183 | 0.023 | |
| 250 | 0.057 | 0.023 | 0.176 | 0.023 | |
| 10% Error | 1 | 0.051 | 0.017 | 0.168 | 0.017 |
| 25 | 0.057 | 0.019 | 0.179 | 0.020 | |
| 100 | 0.067 | 0.032 | 0.186 | 0.025 | |
| 250 | 0.049 | 0.018 | 0.165 | 0.022 | |
| 25% Error | 1 | 0.048 | 0.017 | 0.165 | 0.020 |
| 25 | 0.058 | 0.029 | 0.175 | 0.026 | |
| 100 | 0.059 | 0.018 | 0.184 | 0.018 | |
| 250 | 0.057 | 0.025 | 0.175 | 0.023 | |
| 10% Augmented | 1 | 0.060 | 0.030 | 0.184 | 0.024 |
| 25 | 0.050 | 0.021 | 0.165 | 0.021 | |
| 100 | 0.051 | 0.017 | 0.170 | 0.022 | |
| 250 | 0.057 | 0.023 | 0.179 | 0.021 | |
| 25% Augmented | 1 | 0.058 | 0.021 | 0.168 | 0.018 |
| 25 | 0.061 | 0.032 | 0.177 | 0.025 | |
| 100 | 0.059 | 0.031 | 0.175 | 0.025 | |
| 250 | 0.058 | 0.027 | 0.171 | 0.023 | |
| Random | 1 | 0.191 | 0.161 | 0.293 | 0.019 |
| 25 | 0.182 | 0.111 | 0.341 | 0.015 | |
| 100 | 0.178 | 0.118 | 0.322 | 0.016 | |
| 250 | 0.197 | 0.148 | 0.342 | 0.016 |
| Network | Training | Mean | Median | Mean—High Err | Mean—Low Err |
|---|---|---|---|---|---|
| Base | 1 | 0.052 | 0.031 | 0.162 | 0.027 |
| 25 | 0.058 | 0.017 | 0.190 | 0.020 | |
| 100 | 0.059 | 0.017 | 0.190 | 0.019 | |
| 250 | 0.057 | 0.021 | 0.179 | 0.021 | |
| 10% Error | 1 | 0.059 | 0.025 | 0.165 | 0.019 |
| 25 | 0.054 | 0.021 | 0.186 | 0.023 | |
| 100 | 0.065 | 0.030 | 0.177 | 0.024 | |
| 250 | 0.064 | 0.029 | 0.193 | 0.024 | |
| 25% Error | 1 | 0.059 | 0.022 | 0.179 | 0.019 |
| 25 | 0.054 | 0.023 | 0.169 | 0.022 | |
| 100 | 0.054 | 0.018 | 0.161 | 0.019 | |
| 250 | 0.056 | 0.021 | 0.175 | 0.024 | |
| 10% Augmented | 1 | 0.063 | 0.019 | 0.193 | 0.017 |
| 25 | 0.062 | 0.027 | 0.181 | 0.022 | |
| 100 | 0.058 | 0.025 | 0.196 | 0.023 | |
| 250 | 0.058 | 0.025 | 0.178 | 0.024 | |
| 25% Augmented | 1 | 0.058 | 0.031 | 0.172 | 0.025 |
| 25 | 0.054 | 0.021 | 0.167 | 0.023 | |
| 100 | 0.059 | 0.020 | 0.184 | 0.021 | |
| 250 | 0.054 | 0.021 | 0.179 | 0.023 | |
| Random | 1 | 0.152 | 0.067 | 0.317 | 0.016 |
| 25 | 0.181 | 0.105 | 0.335 | 0.019 | |
| 100 | 0.170 | 0.095 | 0.322 | 0.023 | |
| 250 | 0.191 | 0.138 | 0.343 | 0.013 |
| Network | Velocity | Mean | Median | Mean—High Err | Mean—Low Err |
|---|---|---|---|---|---|
| Base | 0.01 | 0.057 | 0.021 | 0.183 | 0.022 |
| 10% Error | 0.01 | 0.060 | 0.026 | 0.177 | 0.022 |
| 25% Error | 0.01 | 0.066 | 0.029 | 0.186 | 0.023 |
| 10% Augmented | 0.01 | 0.055 | 0.019 | 0.195 | 0.021 |
| 25% Augmented | 0.01 | 0.053 | 0.020 | 0.170 | 0.021 |
| Random | 0.01 | 0.188 | 0.129 | 0.336 | 0.014 |
| Network | Velocity | Mean | Median | Mean—High Err | Mean—Low Err |
|---|---|---|---|---|---|
| Base | 0.25 | 0.056 | 0.024 | 0.176 | 0.021 |
| 10% Error | 0.25 | 0.053 | 0.020 | 0.185 | 0.023 |
| 25% Error | 0.25 | 0.057 | 0.019 | 0.195 | 0.020 |
| 10% Augmented | 0.25 | 0.050 | 0.015 | 0.175 | 0.021 |
| 25% Augmented | 0.25 | 0.055 | 0.023 | 0.178 | 0.023 |
| Random | 0.25 | 0.175 | 0.106 | 0.334 | 0.013 |
| Training | Velocity | Mean | Median | Mean—High Err | Mean—Low Err |
|---|---|---|---|---|---|
| Base | 0.01 | 0.058 | 0.028 | 0.175 | 0.024 |
| 10% Error | 0.01 | 0.061 | 0.025 | 0.189 | 0.022 |
| 25% Error | 0.01 | 0.053 | 0.027 | 0.164 | 0.023 |
| 10% Augmented | 0.01 | 0.053 | 0.020 | 0.173 | 0.020 |
| 25% Augmented | 0.01 | 0.057 | 0.019 | 0.177 | 0.020 |
| Random | 0.01 | 0.185 | 0.132 | 0.328 | 0.020 |
| Training | Velocity | Mean | Median | Mean—High Err | Mean—Low Err |
|---|---|---|---|---|---|
| Base | 0.25 | 0.062 | 0.029 | 0.183 | 0.025 |
| 10% Error | 0.25 | 0.057 | 0.025 | 0.178 | 0.025 |
| 25% Error | 0.25 | 0.057 | 0.023 | 0.178 | 0.023 |
| 10% Augmented | 0.25 | 0.063 | 0.028 | 0.194 | 0.023 |
| 25% Augmented | 0.25 | 0.059 | 0.024 | 0.174 | 0.024 |
| Random | 0.25 | 0.187 | 0.130 | 0.332 | 0.015 |
| Training | Velocity | Mean | Median | Mean—High Err | Mean—Low Err |
|---|---|---|---|---|---|
| 1 | 0.05 | 0.057 | 0.030 | 0.189 | 0.025 |
| 1 | 0.25 | 0.056 | 0.022 | 0.156 | 0.022 |
| 25 | 0.05 | 0.060 | 0.021 | 0.188 | 0.022 |
| 25 | 0.25 | 0.057 | 0.024 | 0.171 | 0.022 |
| 100 | 0.05 | 0.060 | 0.027 | 0.187 | 0.023 |
| 100 | 0.25 | 0.056 | 0.024 | 0.176 | 0.021 |
| 250 | 0.05 | 0.056 | 0.026 | 0.174 | 0.024 |
| 250 | 0.25 | 0.058 | 0.023 | 0.186 | 0.022 |
| Training | Velocity | Mean | Median | Mean—High Err | Mean—Low Err |
|---|---|---|---|---|---|
| 1 | 0.05 | 0.046 | 0.014 | 0.163 | 0.025 |
| 1 | 0.25 | 0.057 | 0.021 | 0.157 | 0.016 |
| 25 | 0.05 | 0.060 | 0.025 | 0.175 | 0.024 |
| 25 | 0.25 | 0.057 | 0.023 | 0.171 | 0.022 |
| 100 | 0.05 | 0.056 | 0.025 | 0.171 | 0.023 |
| 100 | 0.25 | 0.062 | 0.029 | 0.183 | 0.025 |
| 250 | 0.05 | 0.051 | 0.016 | 0.181 | 0.020 |
| 250 | 0.25 | 0.059 | 0.023 | 0.188 | 0.022 |
| Training | Network | Velocity | Mean | Median | Mean—High Err | Mean—Low Err |
|---|---|---|---|---|---|---|
| 25 Epoch | Base | 0.01 | 0.055 | 0.020 | 0.177 | 0.021 |
| 25 Epoch | Base | 0.1 | 0.061 | 0.023 | 0.197 | 0.023 |
| 25 Epoch | Base | 0.25 | 0.060 | 0.025 | 0.184 | 0.022 |
| 25 Epoch | 10% Error | 0.01 | 0.059 | 0.026 | 0.180 | 0.024 |
| 25 Epoch | 10% Error | 0.1 | 0.057 | 0.019 | 0.179 | 0.020 |
| 25 Epoch | 10% Error | 0.25 | 0.061 | 0.026 | 0.177 | 0.024 |
| 25 Epoch | 25% Error | 0.01 | 0.058 | 0.023 | 0.190 | 0.023 |
| 25 Epoch | 25% Error | 0.1 | 0.058 | 0.029 | 0.175 | 0.026 |
| 25 Epoch | 25% Error | 0.25 | 0.048 | 0.006 | 0.189 | 0.017 |
| 25 Epoch | 10% Augmented | 0.01 | 0.046 | 0.013 | 0.164 | 0.020 |
| 25 Epoch | 10% Augmented | 0.1 | 0.050 | 0.021 | 0.165 | 0.021 |
| 25 Epoch | 10% Augmented | 0.25 | 0.061 | 0.025 | 0.183 | 0.023 |
| 25 Epoch | 25% Augmented | 0.01 | 0.059 | 0.026 | 0.185 | 0.023 |
| 25 Epoch | 25% Augmented | 0.1 | 0.061 | 0.032 | 0.177 | 0.025 |
| 25 Epoch | 25% Augmented | 0.25 | 0.055 | 0.024 | 0.181 | 0.024 |
| 25 Epoch | Random | 0.01 | 0.173 | 0.135 | 0.315 | 0.016 |
| 25 Epoch | Random | 0.1 | 0.182 | 0.111 | 0.341 | 0.015 |
| 25 Epoch | Random | 0.25 | 0.186 | 0.121 | 0.331 | 0.015 |
| Training | Network | Velocity | Mean | Median | Mea—High Err | Mean—Low Err |
|---|---|---|---|---|---|---|
| 25 Epoch | Base | 0.01 | 0.055 | 0.021 | 0.172 | 0.023 |
| 25 Epoch | Base | 0.1 | 0.058 | 0.017 | 0.190 | 0.020 |
| 25 Epoch | Base | 0.25 | 0.066 | 0.030 | 0.185 | 0.024 |
| 25 Epoch | 10% Error | 0.01 | 0.057 | 0.024 | 0.183 | 0.021 |
| 25 Epoch | 10% Error | 0.1 | 0.054 | 0.021 | 0.186 | 0.023 |
| 25 Epoch | 10% Error | 0.25 | 0.062 | 0.026 | 0.179 | 0.022 |
| 25 Epoch | 25% Error | 0.01 | 0.053 | 0.014 | 0.180 | 0.018 |
| 25 Epoch | 25% Error | 0.1 | 0.054 | 0.023 | 0.169 | 0.022 |
| 25 Epoch | 25% Error | 0.25 | 0.056 | 0.022 | 0.173 | 0.022 |
| 25 Epoch | 10% Augmented | 0.01 | 0.057 | 0.024 | 0.182 | 0.022 |
| 25 Epoch | 10% Augmented | 0.1 | 0.062 | 0.027 | 0.181 | 0.022 |
| 25 Epoch | 10% Augmented | 0.25 | 0.059 | 0.026 | 0.178 | 0.023 |
| 25 Epoch | 25% Augmented | 0.01 | 0.058 | 0.021 | 0.189 | 0.021 |
| 25 Epoch | 25% Augmented | 0.1 | 0.054 | 0.021 | 0.167 | 0.023 |
| 25 Epoch | 25% Augmented | 0.25 | 0.055 | 0.017 | 0.170 | 0.019 |
| 25 Epoch | Random | 0.01 | 0.156 | 0.076 | 0.315 | 0.015 |
| 25 Epoch | Random | 0.1 | 0.181 | 0.105 | 0.335 | 0.019 |
| 25 Epoch | Random | 0.25 | 0.184 | 0.117 | 0.330 | 0.016 |
| Training Technique | Average Time |
|---|---|
| Train Path—Same Facts | 170,921.0 |
| Train Path—Random Facts | 995,436.0 |
| Train Multiple Paths—Same Facts | 376,210.8 |
| Train Multiple Paths—Random Facts | 925,475.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Straub, J. Assessment of Gradient Descent Trained Rule-Fact Network Expert System Multi-Path Training Technique Performance. Computers 2021, 10, 103. https://doi.org/10.3390/computers10080103
Straub J. Assessment of Gradient Descent Trained Rule-Fact Network Expert System Multi-Path Training Technique Performance. Computers. 2021; 10(8):103. https://doi.org/10.3390/computers10080103
Chicago/Turabian StyleStraub, Jeremy. 2021. "Assessment of Gradient Descent Trained Rule-Fact Network Expert System Multi-Path Training Technique Performance" Computers 10, no. 8: 103. https://doi.org/10.3390/computers10080103
APA StyleStraub, J. (2021). Assessment of Gradient Descent Trained Rule-Fact Network Expert System Multi-Path Training Technique Performance. Computers, 10(8), 103. https://doi.org/10.3390/computers10080103





