4.1. Experiment Setup
In the integrated evaluation framework, the RISC-V ecosystem with a dedicated hardware accelerator for decimal arithmetic is used along with several input samples for decimal computing. In this framework, the operations corresponding to the hardware part in the proposed methods are integrated as custom instructions in a Rocket Chip (one of the hardware implementations for RISC-V) [
33,
34], and they are executed in an accelerator through the Rocket Custom Coprocessor (RoCC) interface. These custom instructions can be used by implementing the corresponding hardware in the accelerator.
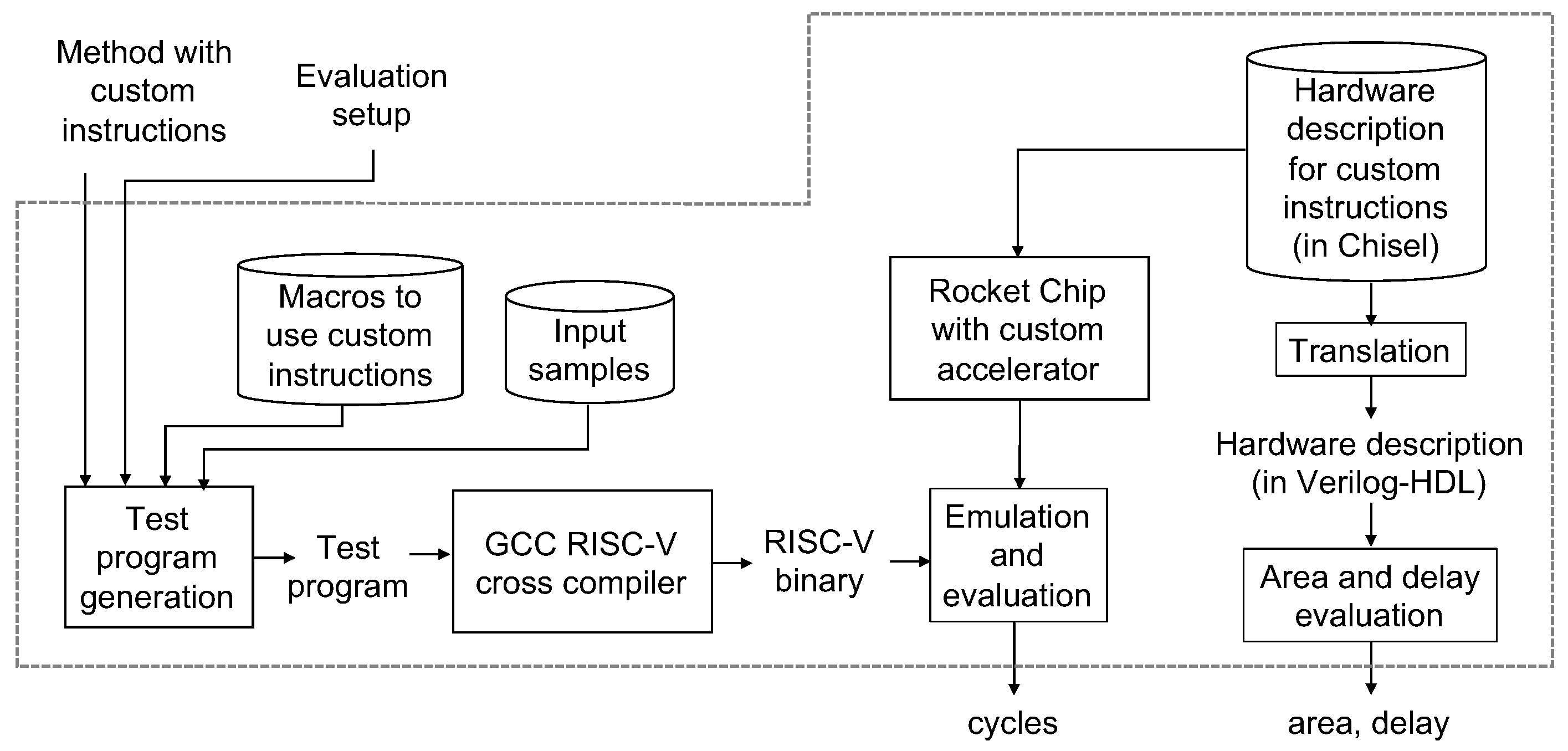
Figure 10 shows an overview of the RISC-V-based evaluation environment proposed in Reference [
21]. The framework uses RISC-V ecosystem with input samples as decimal arithmetic verification test cases. The ecosystem contains compilers, system libraries, OS kernels, and an emulator with the Rocket Chip. Given a program code for an arithmetic operation with custom instructions and an evaluation setup information, a test program is generated and it is complied to an executable by the GCC RISC-V cross compiler with optimization flag -O. The evaluation setup information can specify a precision (double or quad), types of input samples (rounding, overflow, normal, underflow, etc.), types of the arithmetic operation (addition, subtraction, multiplication or any other), the number of iterations, the pattern of output (execution time or number of cycles), etc. The cycle-accurate evaluation is possible with the framework. The hardware parts are also evaluated with the framework, where the hardware parts are integrated as custom instructions executed in an accelerator. The corresponding hardware is described in a hardware description language Chisel for the Rocket Chip, and it is translated into Verilog-HDL and evaluated with CAD tools.
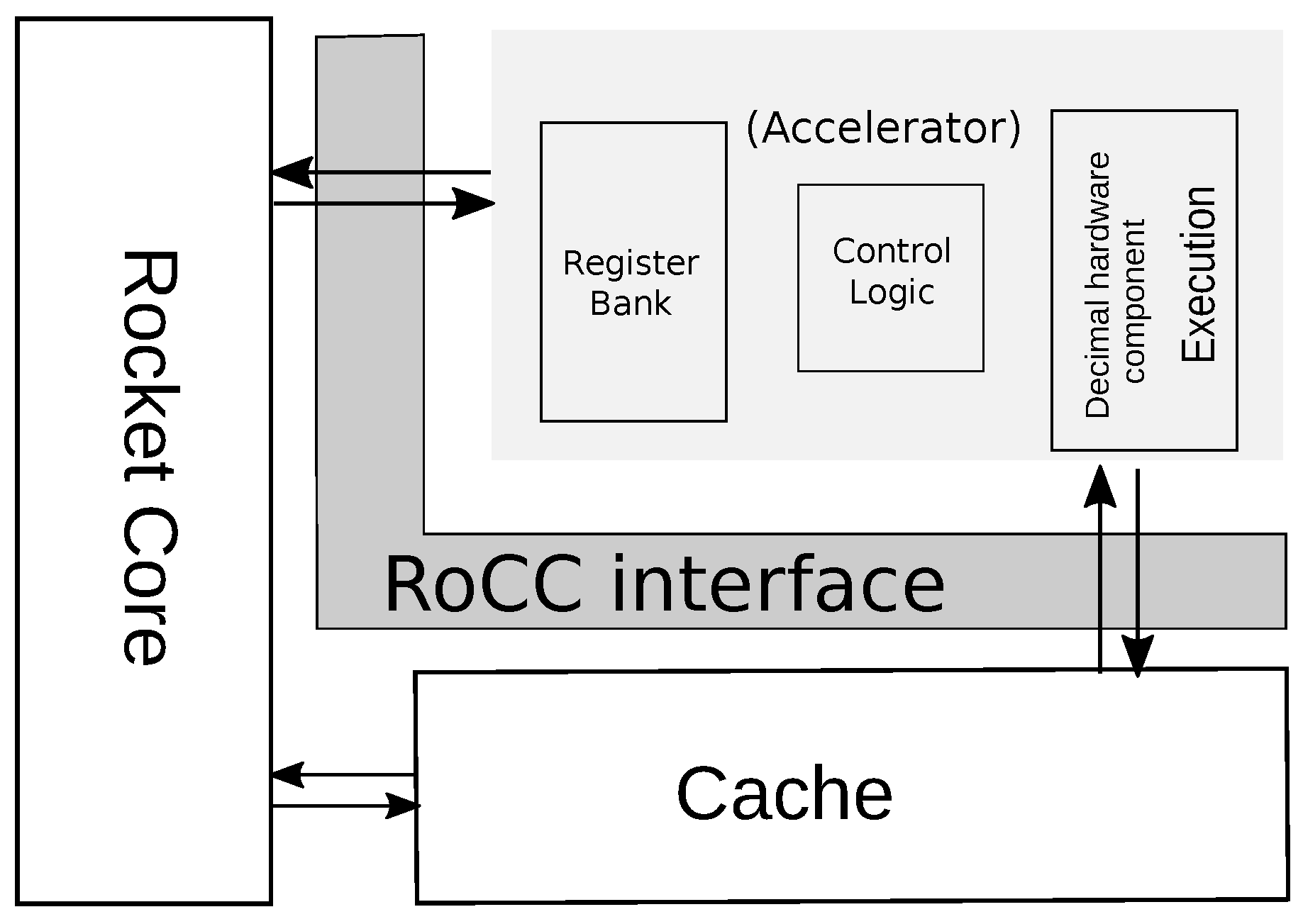
In the framework, the Rocket Chip contains Rocket core, which is a five-stage single-issue in-order scalar processor. The Rocket Chip also contains an accelerator which can be used by custom instructions whose opcodes are reserved in RISC-V ISA. The Rocket core and the accelerator have a decoupled communication through the RoCC interface as shown in
Figure 11. The commands for the accelerator including register values are generated by committed instructions in the Rocket core and sent to the accelerator, and they may write an integer register in response. The accelerator can also share the Rocket core’s data cache through the RoCC interface.
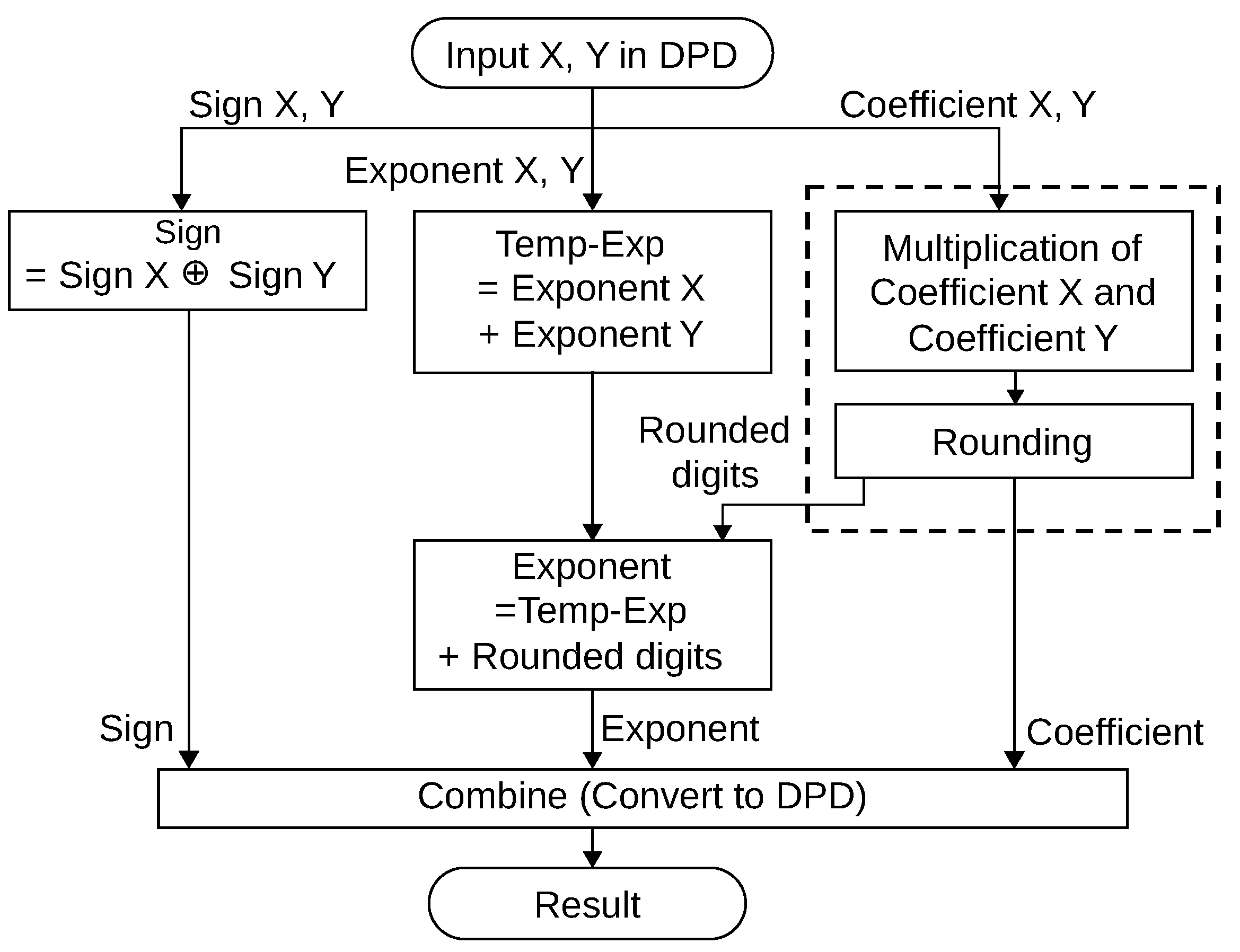
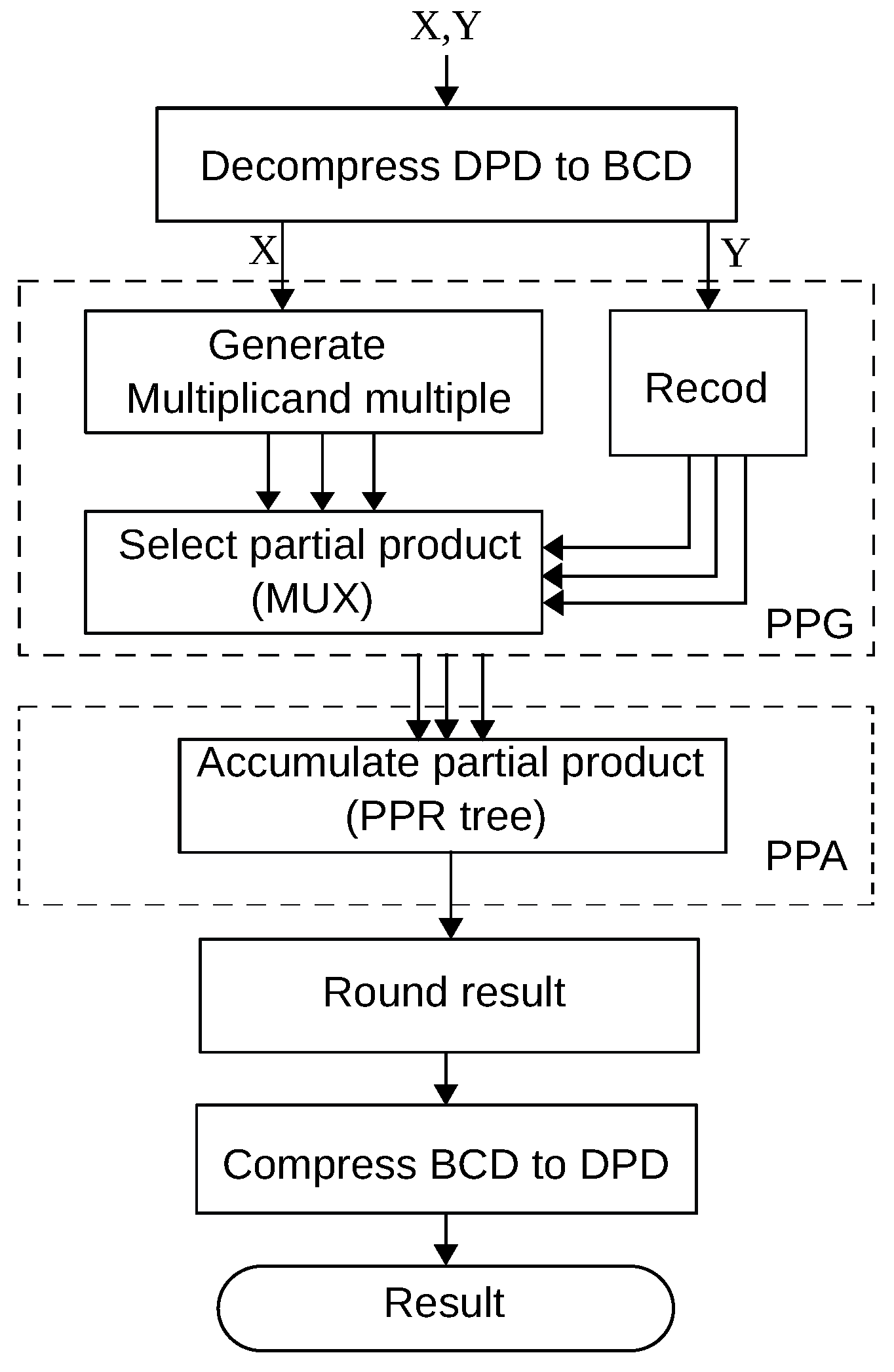
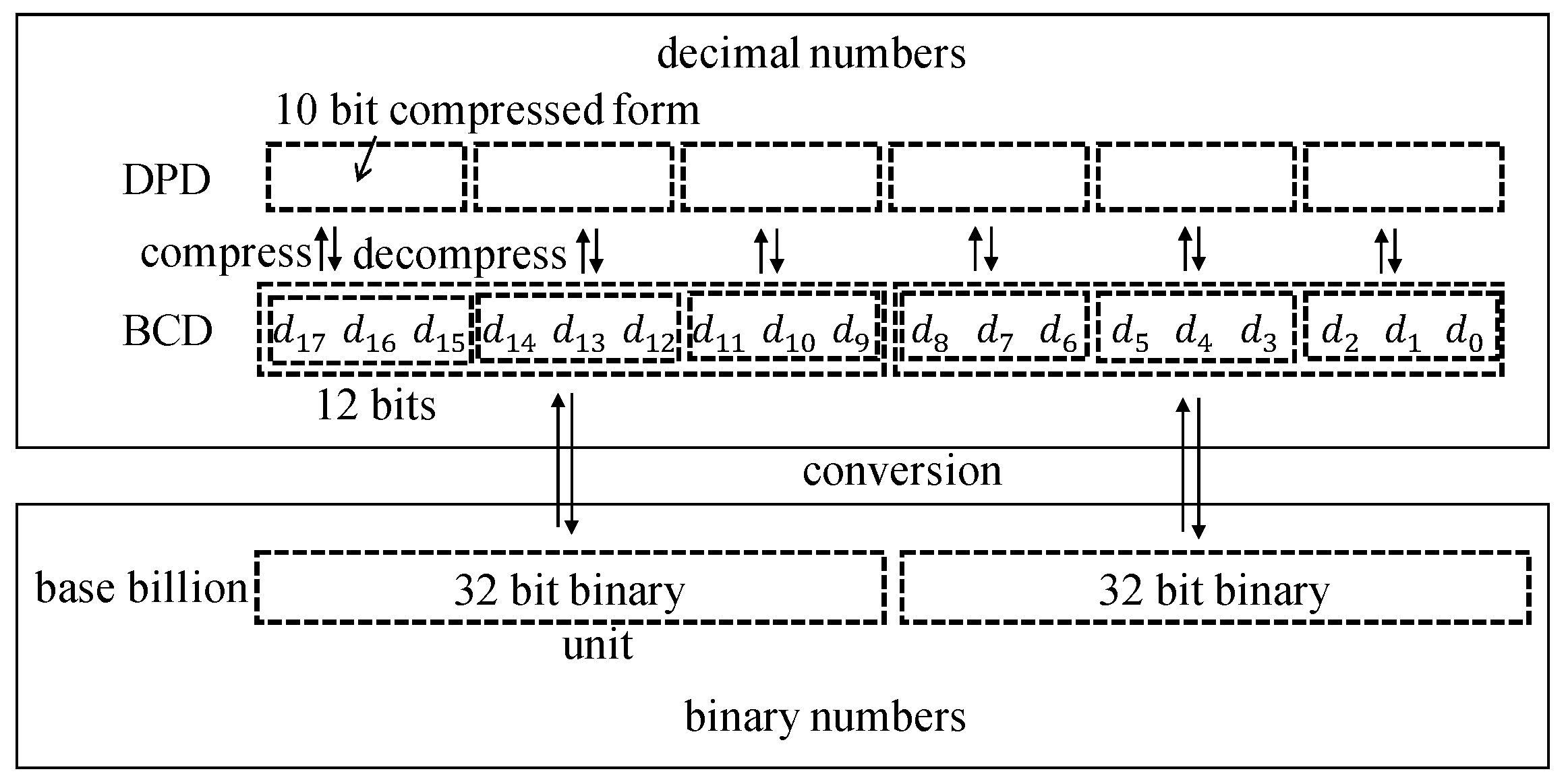
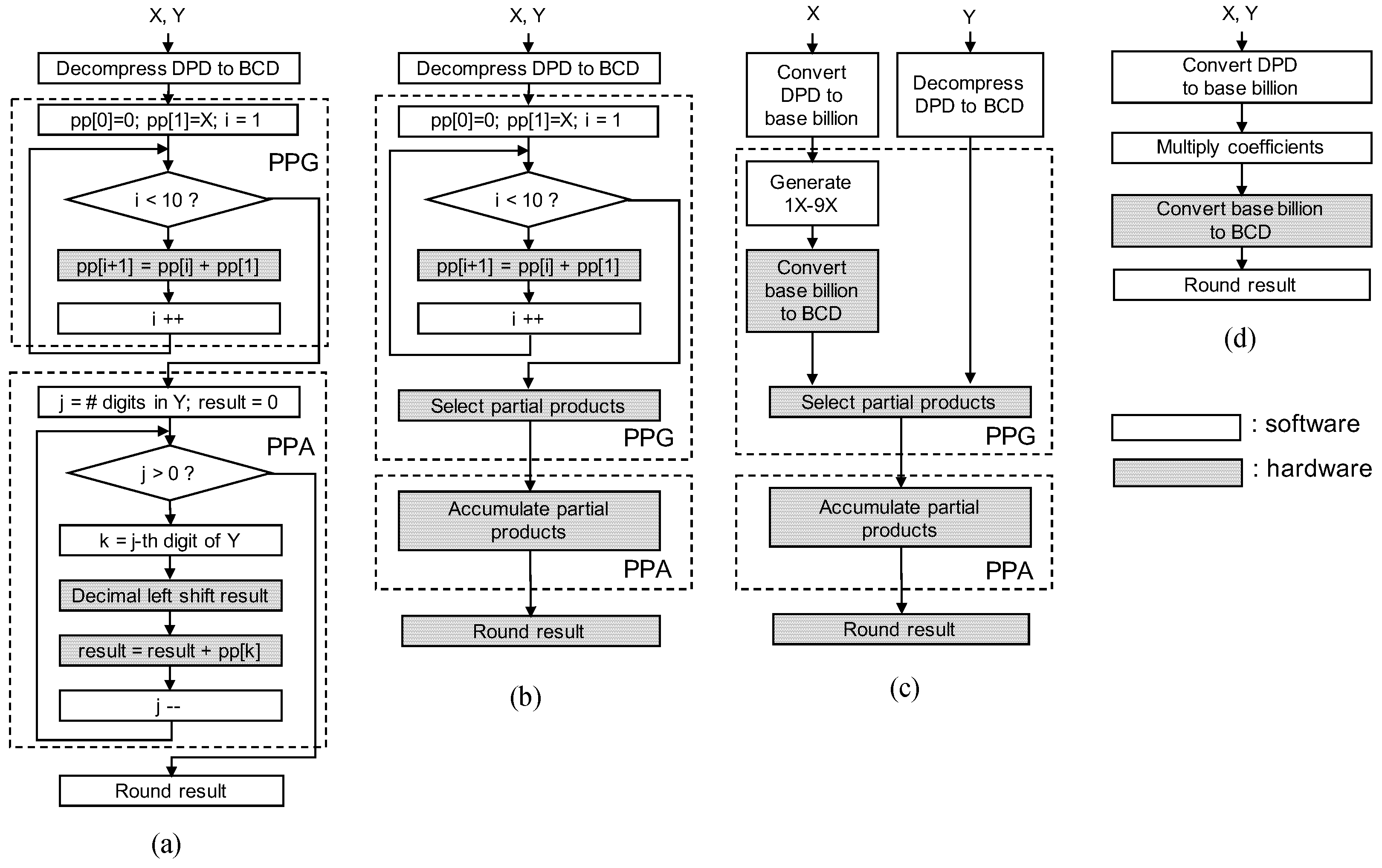
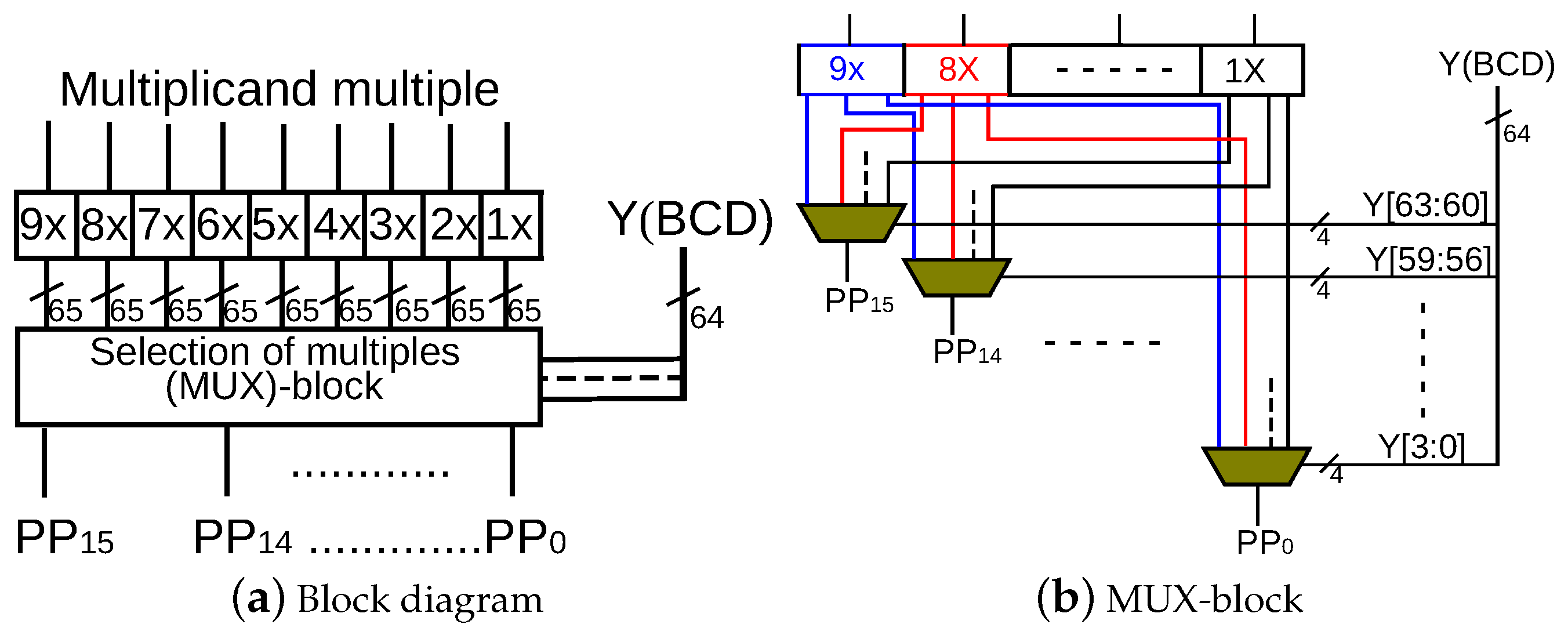
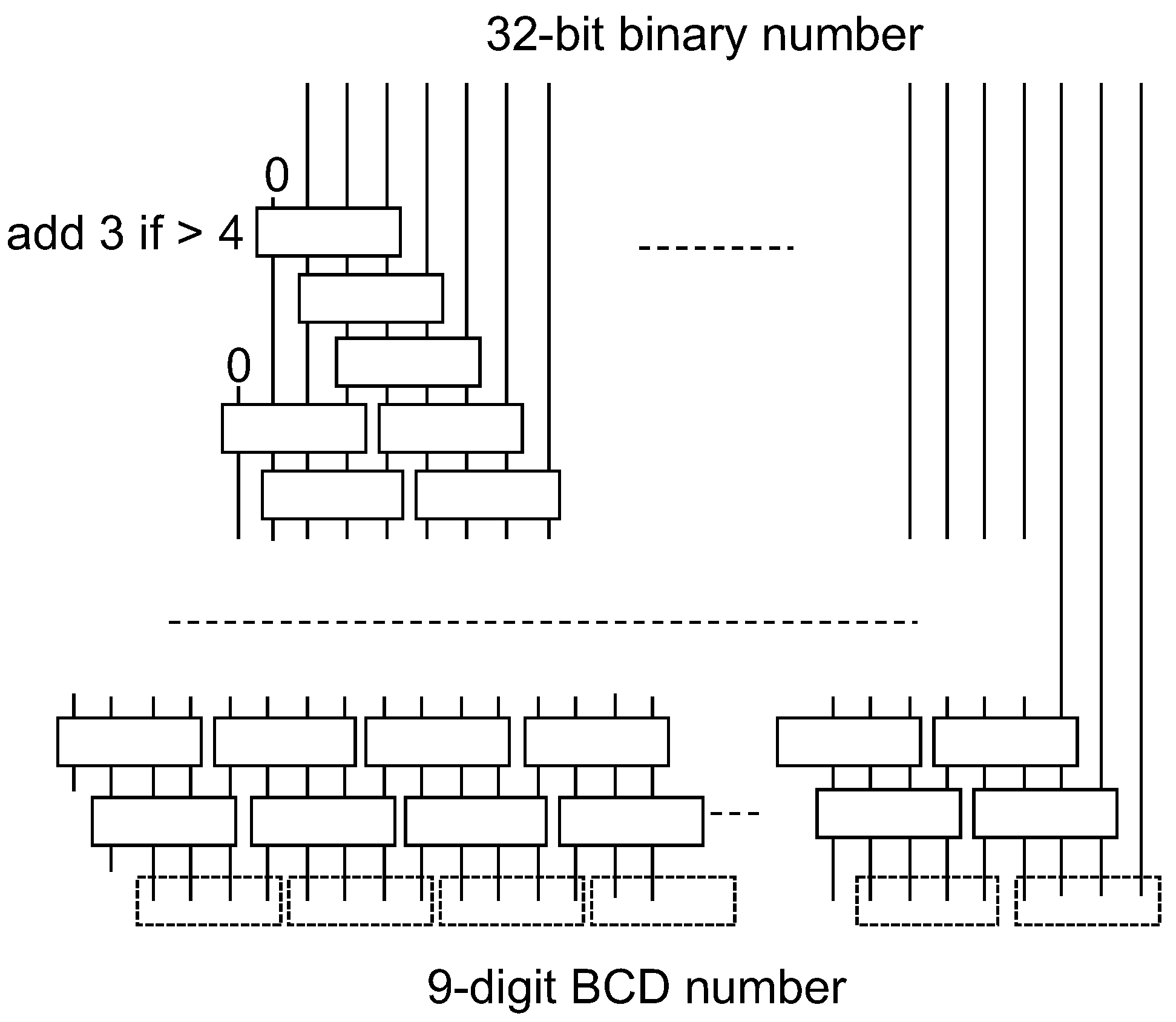
Cycle-accurate evaluation is possible for software-hardware co-design solutions for a 64-bit format, where a clock cycle is determined only considering a main processor (Rocket Chip). Custom instructions require multiple cycles according to their hardware implementation. Custom instructions corresponding to a decimal addition, partial product selection and accumulation, rounding for a decimal number, and conversion from base-billion to BCD formats have been implemented. Regarding the instruction for partial product selection and accumulation, the precomputed multiplicand multiples – are loaded on the accelerator and they are accumulated according to the value of a multiplier Y. Custom instructions are used from the program code through macros that include in-line assembly codes for the corresponding custom instructions.
The hardware intensive solution uses a coefficient multiplication [
31] and a rounding logic [
14] as dedicated hardware. Since the coefficient multiplication [
31] accepts BCD numbers as input coefficients, the hardware intensive solution includes a decompression from DPD to BCD as software.
The dedicated hardware parts for the proposed methods and the hardware intensive solution are translated from Chisel to Verilog-HDL, and their area and delay are evaluated by the logic synthesizer [
35] with a 90 nm standard cell library [
36]. Other hardware units used in the existing hardware solutions for decimal computing are also evaluated in the same environment.
As an input for the decimal multiplication, 8000 different samples were selected for the evaluation [
37,
38]. These samples include overflow, underflow, result (samples generating various results), rounding, and some other cases. The clock cycles for these samples are evaluated in the integrated evaluation framework.
4.2. Area and Delay Tradeoff
The integrated evaluation of all the proposed methods along with full software solution [
4] and the hardware intensive solution is presented in
Table 2. This table shows the average number of cycles required to execute a single multiplication operation. In the table, “Method” denotes the proposed methods, software and full hardware solutions, and the average number of cycles for the hardware part and total computation are denoted as “Hardware”, and “Total” columns, respectively. “Speed up” denotes the speedup achieved against the software solution [
4], while “Performance loss” denotes the performance loss against the the hardware intensive solution. It can be observed that good speedup from 1.43× to 2.37× can be achieved against thesoftware solution. Compared to the hardware intensive solution, performance losses are 16.8% to 49.7%. Method-2 is the fastest among the proposed methods. It achieves 2.37× speedup against the software solution that is 16.8% performance loss against the hardware intensive solution. Both Method-1 and Method-2 perform BCD-based calculations and do not require any conversion between binary and decimal numbers. Hence, the elimination of complicated conversion achieves significant execution speedup. On the other hand, Method-3 and Method-4 achieve acceleration by executing the conversion using hardware.
The execution cycle distributions of the 8000 samples used for the proposed methods, the software solution, and the hardware intensive solution are presented in
Figure 12. In all methods, some distributions with multiple peaks are observed. The software solution exhibits the widest distribution. It can be considered that the number of cycles depends on the input samples in the software solution and is distributed in a wide range. In contrast, the execution cycles of Method-2 and the hardware intensive solution are distributed in a narrow range with two peaks. (The input samples include a collection of very small numbers and relatively large numbers, which results in the two peaks [
38] observed.) This implies that not only the average performance but also the worst-case performance can be accelerated.
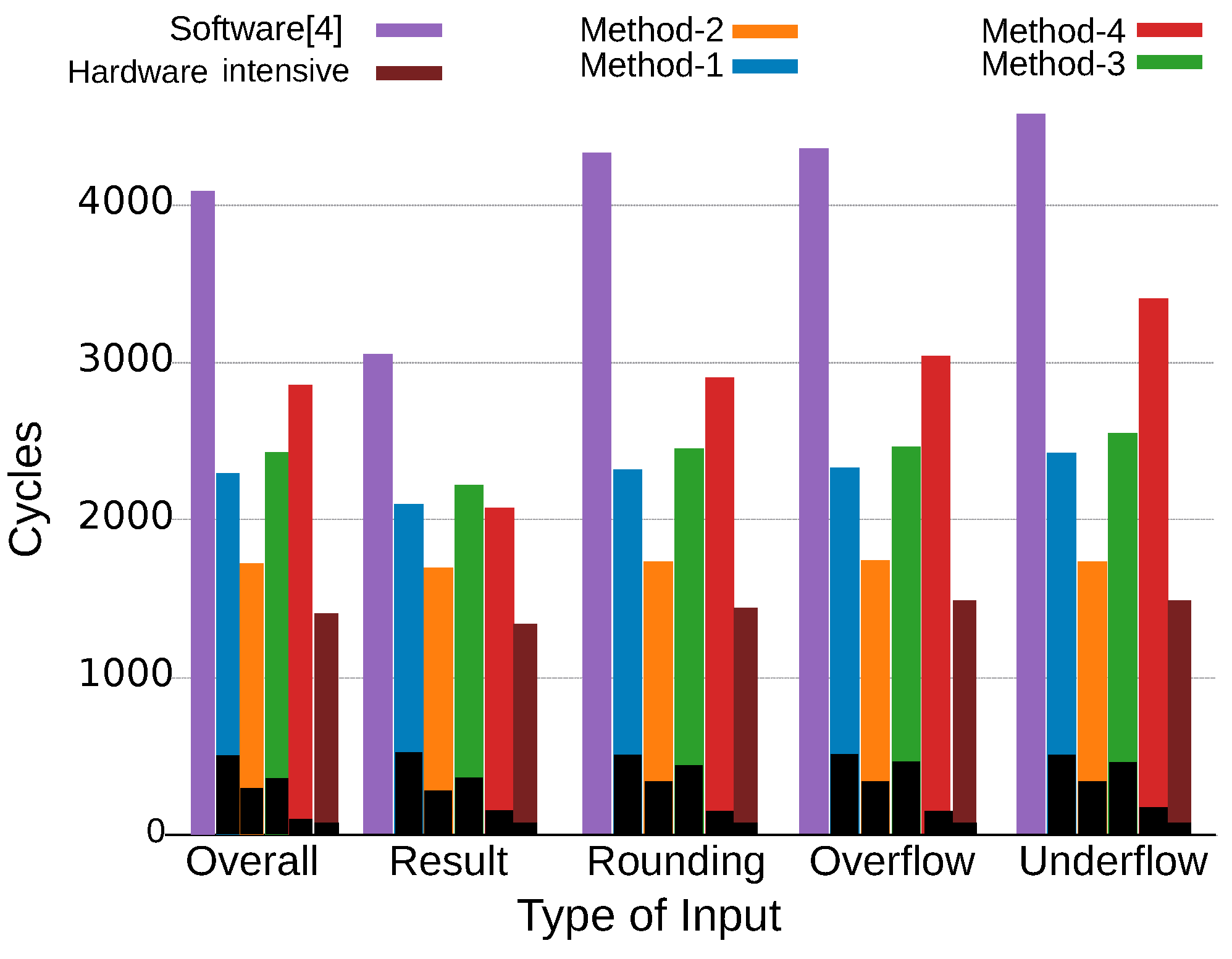
The performance of each input type was also analyzed. The average execution cycles for each input type are presented in
Figure 13, where each type has 2000 input samples. The average cycles for all input types are also shown in “Overall”. In the cases of rounding, overflow, and underflow types, the performance of the methods exhibits a trend similar to the overall trend. However, Method-4 is comparable with Method-1 regarding the “result” type. The “result” type generates various types of results, including many normal results without rounding, overflow, or underflow. That is, Method-4 is comparable with Method-1 for normal cases, and its performance is degraded only for special cases, such as rounding, overflow, and underflow. The number of execution cycles required for hardware by the proposed methods is in the following decreasing order: Method-1, Method-3, Method-2, and Method-4. This is because custom instructions are repeatedly called in Method-1, Method-2, and Method-3, whereas Method-4 called a few custom instructions. It can also be observed that the software solution is degraded more in the special cases than the proposed methods and the hardware intensive solution. Thus, hardware solutions can avoid performance degradation by mitigating input-dependent cycle inflation. Especially in Method-2 and the hardware intensive solution, the average number of cycles is almost the same for all the input types.
The area and delay of the hardware part for both 64-bit and 128-bit formats are presented in
Table 3,
Table 4 and
Table 5. In the proposed methods, the same hardware can be used repeatedly (e.g., BCD-CLA is repeatedly used in Method-1 and Method-2). In this case, the total delay for the hardware is evaluated by accumulating the delay of the target hardware according to the number of usage times. Since Method-1, Method-2, and Method-3 include PPG and PPA stages, these parts are evaluated in comparison with existing solutions [
27,
30,
31]. (In Method-1, although a partial product selection is included in the PPA stage, this is executed by software. Therefore, the hardware parts are clearly separated. (See
Figure 6a for details.)) In
Table 3 and
Table 4, the existing solutions have two BCD numbers as inputs. Finally, the total hardware overheads for the four proposed methods are compared with full hardware implementation. In the area evaluation (
Table 3,
Table 4 and
Table 5), the delay of the software routine for the proposed methods is not included to estimate hardware delay only.
The area overhead and the delay of the PPG for the proposed methods and existing hardware solutions are presented in
Table 3. The existing solutions fully realize the PPG stage with hardware, whereas the values for the proposed methods correspond to the hardware part in this stage. Hardware solutions based on several encodings have been previously proposed. Columns “M”, “A”, and “D” (also used in
Table 4) denote the method, area, and delay, respectively. The column “Architecture” shows the encodings or the architecture regarding the basic blocks for each method. (This column is also used in
Table 4 and
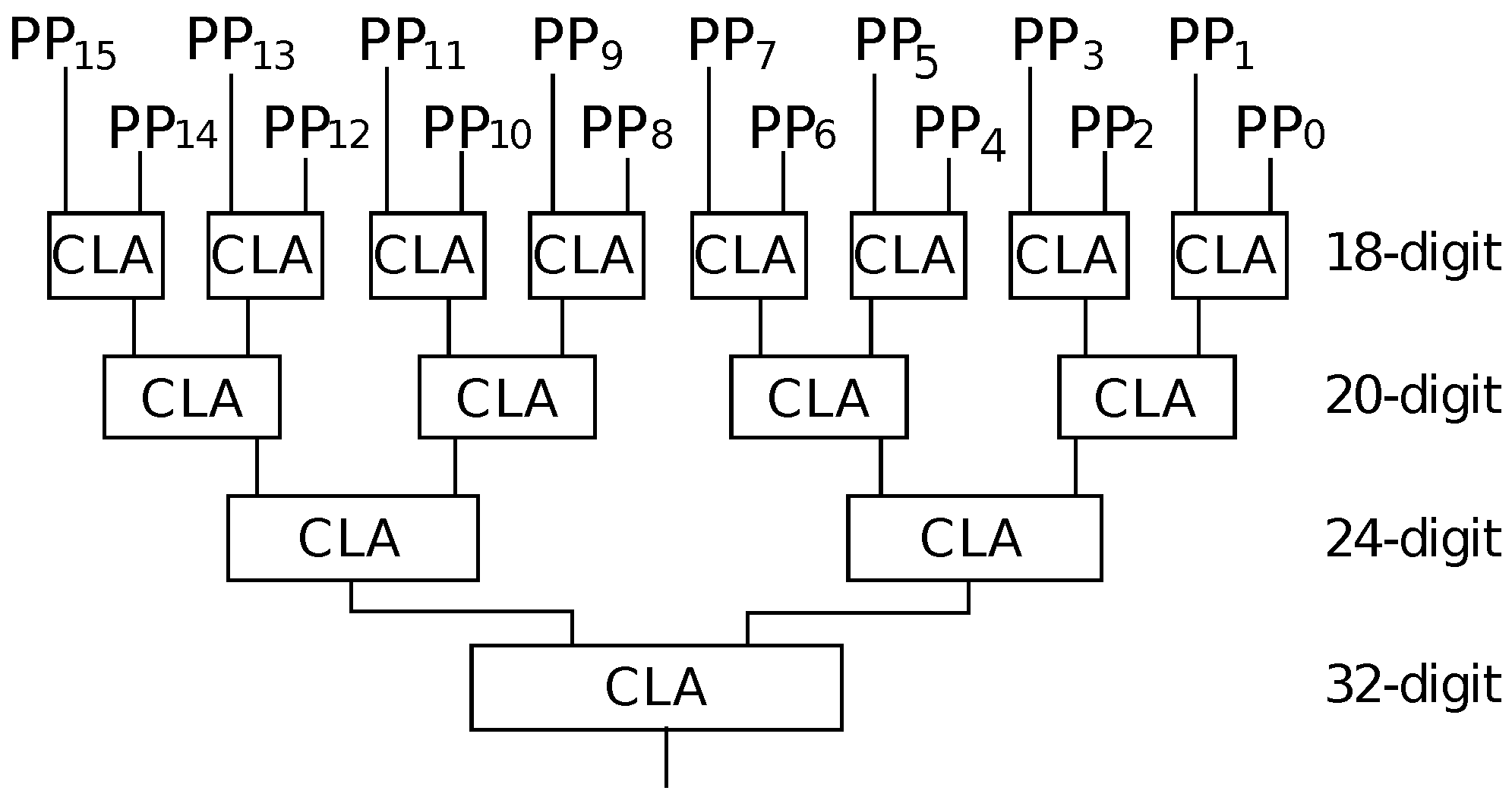
Table 5.) Method-1 has a very small area overhead, since it only requires one BCD-CLA, whereas Method-2 and Method-3 require more hardware for the parallel selection of PPs. However, compared with full hardware solutions, the area overheads of Method-2 and Method-3 are still small. The BCD-CLA is used repeatedly in Method-1 and Method-3. In these methods, larger delays are observed.
The area overhead and the delay of the PPA are presented in
Table 4. Similarly to the PPG, the values for the proposed methods correspond to the hardware part in the PPA stage. Method-1 requires only one BCD-CLA and has a very small area overhead. This BCD-CLA can also be used in the PPG stage, and it implies that no extra area overhead is required in the PPG stage. However, sequential accumulation is required, and a larger delay is observed. Method-2 and Method-3 adopt a parallel accumulator based on the 8421 CLA proposed in Reference [
27]. Hence, they exhibit the same area and delay.
The overall area overhead and delay of each method are presented in
Table 5, where conversion and rounding circuits are included with the PPG and PPA stages. Columns “Area”, “ARR”, and “Delay” denote area, the area reduction ratio compared with the most area-efficient existing solution, and execution time for both 64-bit and 128-bit formats, and column “Ratio(128/64)” denotes the execution time ratio of the 128-bit to the 64-bit format. Since Method-1 shares its BCD-CLA in both the PPG and PPA stages, an area for only one BCD-CLA is required. Method-1 and Method-4 have relatively less hardware requirements compared with full hardware solutions, whereas Method-2 and Method-3 require more hardware. Regarding delay, even though the proposed methods realize a part of the function as hardware, this hardware part exhibits higher delay than full hardware solutions.
The area-delay tradeoff for all the proposed methods, the software solution, and the hardware intensive solution is presented in
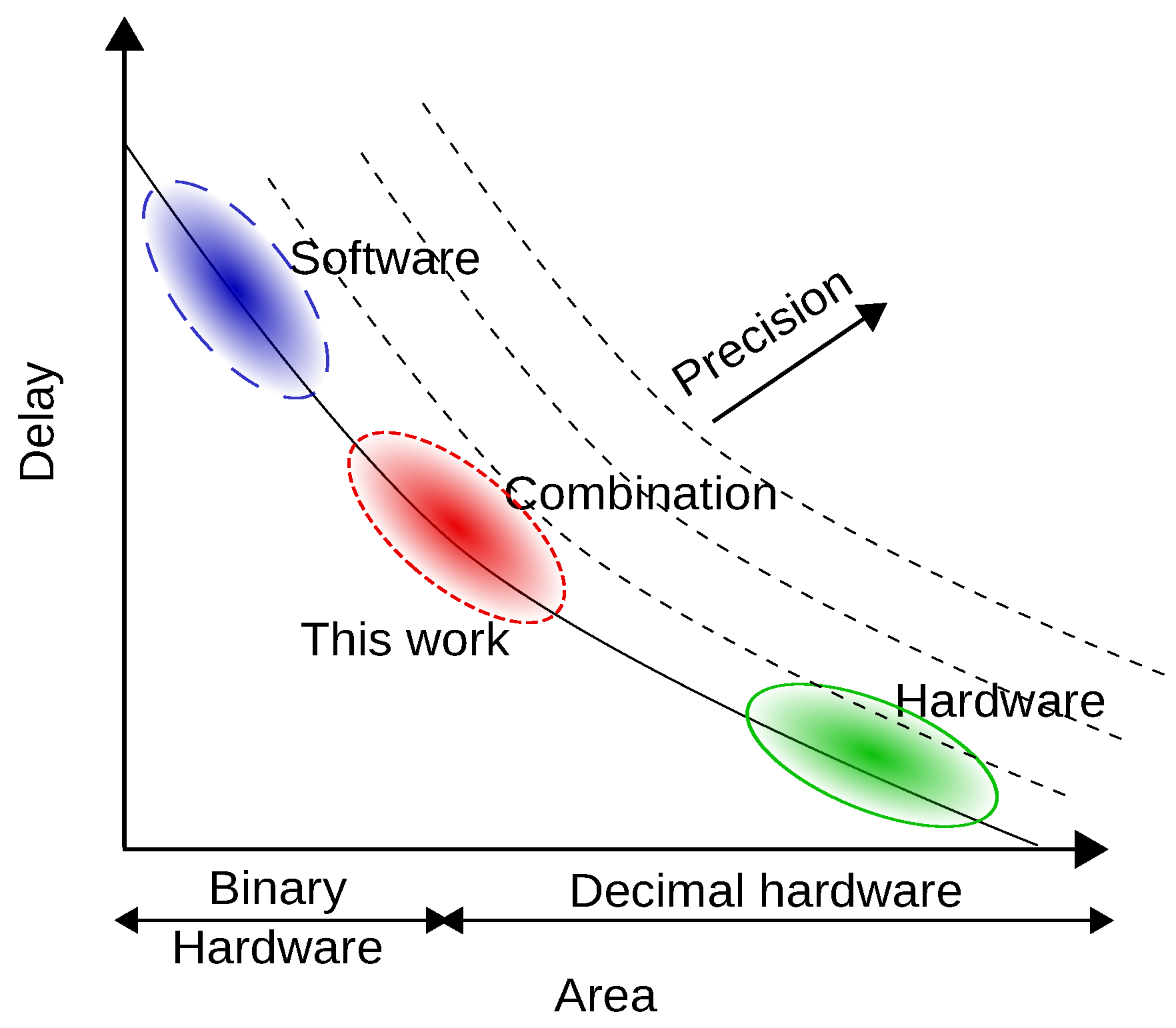
Figure 14. The delay has been obtained by the integrated evaluation framework. In this figure, the purple line is the tradeoff curve obtained by curve fitting using a inverse proportional model. The parameters are estimated using Trust-Region algorithm in MATLAB Curve Fitting Toolbox with custom function of
, where
x stands for the area. The fitting parameters
a,
b, and
c are set to
, 1495, and 1966, respectively. The curve shows the trend of the proposed methods in terms of speed and area tradeoff. Method-1 and Method-4 achieve speedup with a very small hardware overhead. However, to enhance the speed more, a huge area overhead is required in Method-2 and Method-3. From the figure, we get two Pareto points of Method-1 and Method-2 for the 64-bit precision.
Method-1 and Method-4 achieve moderate acceleration with a small area overhead (Method-4 is comparable with Method-1 for the normal type of inputs as previously analyzed). They reduces hardware overhead over 90% compared to the hardware intensive solution while losing less than 50% of performance. On the other hand, Method-2 achieves the fastest acceleration with a relatively large area overhead. It achieves 16.8% performance loss against the hardware intensive solution while reducing 12.2% of hardware overhead. Method-3 also achieves a moderate acceleration but it requires a large area overhead, and it does not exhibit any superior performance compared with the other methods.
Table 6 shows more detailed results for the execution time and the area overhead. Column “Method” denotes the solutions (the proposed methods, software, and the hardware intensive solutions) and hardware blocks or software routines in the solutions. Columns “Avg. # of cycles” and “Area” denote the average number of cycles and the hardware area, respectively. The two hardware components, PPS and PPA, are collectively used in a single custom instruction and their execution time is measured together in Method-2 and Method-3. These two hardware components require a very high area overhead though the corresponding instruction reduces the execution time. Rounding (Method-2, 3) and base-billion to BCD conversion (Method-3, 4) in hardware is a good substitution in terms of area overhead, where they reduce over 96% and 92% cycles, respectively, with reasonable area overhead. (The execution time for BCD conversions are compared between the software solution and Method-4 since both solutions require to convert 4 units of base-billion numbers.)