Hardware–Software Co-Design for Decimal Multiplication

Abstract

Decimal arithmetic using software is slow for very large-scale applications. On the other hand, when hardware is employed, extra area overhead is required. A balanced strategy can overcome both issues. Our proposed methods are compliant with the IEEE 754-2008 standard for decimal floating-point arithmetic and combinations of software and hardware. In our methods, software with some area-efficient decimal component (hardware) is used to design the multiplication process. Analysis in a RISC-V-based integrated co-design evaluation framework reveals that the proposed methods provide several Pareto points for decimal multiplication solutions. The total execution process is sped up by 1.43× to 2.37× compared with a full software solution. In addition, 7–97% less hardware is required compared with an area-efficient full hardware solution.

1. Introduction

Decimal arithmetic is very important for banking, commercial, and financial transactions. Moreover, it is widely used in scientific applications. A study by IBM has indicated that more than half of the numerical data in a commercial database are stored in decimal format [1]. Decimal arithmetic using hardware or software is typically much more complex and slower than its counterpart binary arithmetic. However, decimal arithmetic in binary logic causes some errors that change the actual value of the exact result. This is completely unacceptable in financial or other critical scientific operations. Thus, IEEE 754 (the Standard for Floating-point Arithmetic) has been revised to include decimal floating-point (DFP) formats and operations [2].

Programming languages, such as Java [3] and C [4,5], have their own package or library for calculating decimal arithmetic using software, which is realized with binary hardware units. We call it software (SW)-based decimal computing. However, these may not be sufficient for very large-scale applications, such as telco billing system, banking enterprise system, or a big e-commerce site. This is because the required computation time might not be acceptable when a large number of mathematical calculations have to be completed within a fixed amount of time.

There are a few modern processors with dedicated hardware for decimal arithmetic [6]. To the best of our knowledge, the first decimal accelerator was introduced by IBM in their mainframe computer [7]. Then, they implemented DFP into system z [8], zEnterprise [9], and power series [10]. FUJITSU also introduced decimal hardware in their SPARC64 processor [11]. We call this hardware (HW)-based decimal computing. Such a solution through hardware requires extra area overhead [12,13,14,15,16,17,18,19,20].

The aim of our study is presented in Figure 1, where the relationship of among area, delay, and precision are depicted. Our study is focused on a solution containing software functions, which is based on binary arithmetic, along with hardware components for dedicated decimal arithmetic. This combination is capable of balancing the hardware area overhead with delay. Based on the analysis of both the existing software and hardware solutions, four methods for decimal multiplication are proposed. Herein, using the RISC-V-based evaluation environment proposed in Reference [21], it is experimentally demonstrated that these approaches are capable of speeding up the total execution process by 1.43× to 2.37× compared with a standard software library. In addition, 7–97% less hardware area overhead is required compared with a hardware solution where a coefficient multiplication is fully implemented in hardware.

The key contribution of each method is summarized as follows:

Method-1 

is the most area-efficient solution, where the addition is supported by decimal hardware, and most operations are processed sequentially. It does not use any binary arithmetic and hence does not require time-consuming decimal-to-binary or binary-to-decimal conversion. It accelerates the execution process efficiently compared with software-based solutions.

Method-2 

achieves the highest speed where the sequential accumulation using a decimal adder in Method-1 is replaced by a parallel decimal multiplier. However, a large area overhead is required.

Method-3 

partially relies on binary arithmetic, where only the multiplicand suffers decimal-to-binary and binary-to-decimal conversion, and a parallel decimal multiplier is used as in Method-2. It can achieve moderate execution process speedup and requires a large area overhead.

Method-4 

achieves execution process speedup by adopting a hardware binary-to-decimal converter. Basic operations for multiplication rely on well-optimized binary arithmetic. It can also achieve well acceleration with a relatively low area overhead.

The rest of this paper is organized as follows. The DFP number and its standards with existing software and hardware solutions are briefly introduced and analyzed in Section 2. Based on our analyses, four different methods are described in Section 3. The hardware components required to implement our proposed methods are also discussed in Section 3. In Section 4, the proposed methods are evaluated in terms of area and delay. Finally, the conclusion is provided in Section 5.

2. Decimal Floating-Point Multiplication

In the DFP numbering system, a floating-point number is presented using radix-10. A number can be finite or a special value. Every finite number has three integer parameters, i.e., the sign, coefficient, and exponent. The numerical value of a finite number is given by:

$$\begin{array}{c}\hfill {(-1)}^{sign}\times coefficient\times {10}^{exponent}.\end{array}$$

(1)

According to the IEEE 754-2008 standard [2], two types of representations are allowed for specific formats (32, 64, and 128 bits). One is the binary integer decimal (BID) proposed by Intel [5] where the coefficient encoding is an unsigned binary integer. The other is a densely packed decimal (DPD) proposed by IBM [22], where the coefficient encoding is a compressed binary-coded decimal (BCD) format. Although the performance of BID-based software library has a faster performance than the DPD-based software library for a 64-bit operation, it is downgraded significantly for higher precision, such as 128-bit [23].

The IEEE 754-2008 compliant decimal multiplication process (for finite numbers) is presented in Figure 2. Two operands, the multiplicand X and the multiplier Y, are multiplied according to the following steps:

• The sign and temporal exponent are calculated from the signs and exponents of X and Y.
• A coefficient multiplication is performed.
• If the result exceeds the precision, a rounding operation using various rounding algorithms is applied [12,24,25].
• Finally, the exponents are adjusted accordingly.

In this paper, hardware–software co-design solutions for the multiplication of two coefficients and rounding of the coefficient product (a dotted rectangle in Figure 2) are considered, while relying on software for the rest parts. A brief overview of coefficient multiplication in the existing software and hardware-based solutions for decimal multiplication will be provided. For simplicity, the coefficients of multiplicand and multiplier are denoted by X and Y, instead of “coefficient X” and “coefficient Y” hereafter.

2.1. Software Library

The BID format can take advantage of the highly optimized binary multiplication since the coefficient is stored as a binary number in the BID format. A BID-based software library (Intel Decimal Floating-Point Math Library) uses binary arithmetic [5,26]. The multiplication is executed by multiplying the coefficients in binary logic.

In contrast, the DPD-based library (IBM decNumber C Library) uses a base-billion numbering system for internal calculation [4]. In the base-billion numbering system, one unit (digit) can represent one billion numbers, which corresponds to nine decimal digits. In this system, one unit is represented as a 32-bit binary number; hence, operations among units can be performed using binary arithmetic (i.e., software). A flow of the multiplication in such a system is presented in Figure 3. Initially, the DPD is converted to a base-billion number using a lookup table.Then, binary multiplications are performed among the units sequentially, and the result is accumulated. Subsequently, the accumulated result is converted to BCD. Although binary-based multiplication is efficiently handled by binary arithmetic, conversions between the BCD and base-billion number require complicated processes.

2.2. Hardware Solutions

IBM power and enterprise series (Power6, system z10, z196) have provided a full DFP accelerator. The accelerator supports several decimal operations with a set of registers [7,8,9,10].

A basic flow describing the multiplication of coefficients of multiplicand X and multiplier Y is presented in Figure 4, which involves two principal stages: the partial product generation (PPG) and the partial product accumulation (PPA), followed by a conversion from DPD to BCD. DPD is a compressed BCD and can be easily converted to BCD. Several variations of BCD encodings, such as signed-digit (SD) $[-6,6]$ and $[-7,7]$, redundant encodings XS-3 and ODD, and non-redundant encodings 8421, 4221, and 5211, are used internally [27,28,29,30,31].

Assume that Y has n decimal digits, and it is represented as $Y=y_{n-1}{y}_{n-2}\cdots y_1{y}_0$. Multiplication is obtained as:

$$X·Y=y_{n-1}·X·{10}^{n-1}+y_{n-2}·X·{10}^{n-2}+\cdots +y_1·X·{10}^1+y_0,$$

where $y_k·X$ ($k=1,\dots ,n-1$) is $1X$, $2X$, …, or $9X$, and it is called a partial product (PP).

In the PPG, the multiplicand multiples $1X$–$9X$ are calculated in advance. Several optimizations have been proposed with respect to this process [13,27,28,30,31]. For example, some easy multiples, such as $2X$ and $5X$, are calculated using combinational logic, and the rest are calculated by adding two precomputed multiples in parallel [13,14,31]. Then, the partial products $y_{n-1}·X$, $y_{n-2}·X$, …, $y_1·X$ are selected from precomputed multiplicand multiples.

In the PPA, the partial products are accumulated. Different types of adder, counter, compressor, and converter with various encodings are used to generate the final product. In Reference [31], both the 8421 Carry-lookahead adder (CLA) and 4221 Carry-save adder (CSA) tree have been proposed. A CSA tree with a counter and a compressor are used in References [30,32], whereas a signed-digit has been proposed in Reference [27]. Such high-performance dedicated decimal hardware units require a large area. Processor designers consider that this results in a very high cost.

3. Proposed Methods for Decimal Multiplication

Hardware-software co-design solutions for decimal multiplication are proposed in this section. Four methods (Method-1, Method-2, Method-3, and Method-4) are proposed, which provide several Pareto points in terms of area and delay. The DPD format is adopted to represent input and output decimal numbers, because, it is suitable for handling decimal numbers in dedicated decimal hardware.

In the hardware-software co-design solutions, number encodings is very important. In the proposed methods, BCD and base-billion formats, as well as DPD format, are used internally. The relationship among these three formats is presented in Figure 5. In the BCD format, every decimal digit is represented by 4 bits. In the DPD format, three decimal digits are compressed into 10 bits, because three decimal digits can represent only 1000 numbers (0–999). Although the DPD format compresses 12 bits of the BCD format into 10 bits, compression and decompression are very simple processes and do not require a significant amount of time (or hardware). In this paper, both the DPD and BCD formats are called decimal formats. In the base-billion format, nine decimal digits are converted into a 32-bit binary number. The 32-bit binary number is also called a unit in the base-billion numbering system. The base-billion format is regarded as a type of binary format. Although the conversion between binary and decimal numbers is time-consuming, binary arithmetic can be used without any hardware overhead, once the decimal numbers are converted into binary numbers.

The detailed design and features of the proposed methods are discussed below. The flow of these methods are presented in Figure 6.

3.1. Method-1

This method is oriented to a very low area, where only one BCD-CLA is required in the hardware part. This adder is used to generate multiplicand multiples and accumulate PPs. The basic multiplication operations rely only on decimal addition. The time-consuming decimal-to-binary or binary-to-decimal conversion is not required. First, both X and Y are decompressed into BCD from DPD. Hardware component BCD-CLA is used to generate multiplicand multiples $1X$ to $9X$ by adding the coefficient of X repeatedly (PPG). Then, the partial products are accumulated by adding and shifting the multiples according to the digits of Y (PPA). The sequential decimal operations using proposed hardware are managed by software. The first loop has a constant iteration count, whereas the iteration count of the second loop depends on the precision of the inputs. Thus, more time is required for higher precision. Rounding is less expensive to be handled by software, since the coefficient is in BCD format.

3.2. Method-2

Method-2 is the fastest among all methods. It is designed to speed up the latter half of Method-1 for higher precisions. Multiplicand multiples are obtained in the same way as in Method-1, whereas partial products are selected in parallel from multiplicand multiples. The sequential accumulation of the PPA in Method-1 is replaced by a parallel accumulator, and the final rounding is also performed by hardware. This method provides good execution acceleration due to the dedicated hardware.

3.3. Method-3

Method-3 (and also Method-4) achieves acceleration by adopting hardware for conversion. This method is different from Method-1 and Method-2, where acceleration is achieved by avoiding the time-consuming conversion. In Method-3, only multiplicand X suffers binary-to-decimal and decimal-to-binary conversions. Multiplicand multiples are obtained using binary arithmetic, and then they are converted into decimal numbers. The latter half is the same as Method-2.

3.4. Method-4

This method follows the process of IBM decNumber C Library [4] by replacing the time-consuming base-billion to BCD conversion parts with hardware. First, X and Y are converted to base billion numbers, and the multiplication between two base-billion numbers is performed by software. After that, the result is converted to BCD using the hardware, and the final result is rounded up using software.

3.5. Decimal Hardware Component Design

Five decimal hardware components are adopted to support the proposed co-design solutions. These are BCD-based carry-lookahead adder (BCD-CLA), partial product selector, parallel accumulator, conversion circuit from base billion number to BCD number (BCD converter), and rounding logic.

As shown in Figure 6, the gray blocks are for hardware components. Correspondence between hardware blocks and hardware components is summarized in

Table 1. Correspondences between hardware blocks and hardware components.

Method	Block	Component
Method-1, 2	pp[i + 1] = pp[i] + pp[1]
Method-1	Decimal left shift result	BCD-CLA
	result = result + pp[k]
Method-2, 3	Select partial products	Partial Product Selector
Method-2, 3	Accumulate Partial Products	Parallel Accumulator
Method-2, 3	Round result	Rounding Logic
Method-3, 4	Convert base billion to BCD	BCD Converter

. The functionality and block diagram of each of the hardware components are detailed below. As described below, partial product selector and parallel accumulator used in Method-2 and Method-3 have large area since they handle several values in parallel, and this is later verified in the experiment (see Section 4).

3.5.1. BCD-CLA

The BCD adder proposed in Reference [31] is adopted. This adder uses 8421 BCD encoding. Since 8421 BCD encoding has an unused combination of 4-bits (1010 to 1111), the adder includes a logic to handle such an unused combination. The basic component accepts two 4-bit (one decimal digit) BCD numbers with 1-bit carry and produces 4-bit (one decimal digit) sum in BCD with a single-bit carry-out. For multi-digit addition, a 4-digit CLA is built as a the basic block, where four digits are grouped together to calculate a group carry-propagation and generation. Then, a multi-digit CLA is implemented based on these primitive four-digit CLA blocks.

BCD-CLA is the base component for the parallel decimal multiplication. We also examined a delay efficient BCD-CLA proposed in Reference [31]. We compared BCD-CLA [31] and the delay-efficient BCD-CLA [31]. For the single-digit case, the delay-efficient BCD-CLA costs 533.2 $\mathsf{\mu }$m${}^2$ that requires an additional 193.9 $\mathsf{\mu }$m${}^2$ area overhead from the proposed component. So, the multi-digit case requires more area. As this study considers a co-design methodology where the delay improvement in hardware is not a considerable amount compared to the other part (software routine), we adopt the area efficient BCD-CLA [31].

3.5.2. Partial Product Selector

Figure 7a shows the partial product selector for 64-bit format. This component is used between multiplicand multiple generations and parallel accumulation of the multiplication process. In case of 64-bit format, each of 16 partial products is selected from 1X, 2X, …, 9X. The partial product selector is composed of nine registers for nine 65-bit multiplicand multiples and 16 nine-input multiplexers (MUXs), in case of 64-bit format. Signals of 16-digit multiplier (Y) in BCD are used as selection signals for 16 MUXs. Figure 7b shows the MUX network for generating sixteen partial products in parallel.

Alternatively to the partial product selector, it can be considered to adopt hardware to a whole PPG process. There are several proposals for such a hardware. In the process proposed in References [13,31], multiplicand multiples (1X–9X) are obtained by calculating some easy multipliers, like 2X and 5X, with combinational logic initially, and calculating the rest of the multiplicand multiples by adding two precomputed multiplicands in parallel [13,31]. This process is followed to avoid hard multiplication which cannot perform in constant time due to carry propagation. Some proposals generate 1X–5X in parallel instead of 1X–9X. In such case, multiplier digits need to be recoded into SD radix-10 $[-5,5]$ for selecting PPs [27,28,30]. In that case, all multiplicand multiple including only hard multiplication 3X can be generated in constant time by using XS-3 $[-3,12]$ [28,30] or using SD$[-6,6]$ [27]. All these processes require additional combinational logic for multiplicand multiple generation and internal conversion. To avoid the area overhead, we used CLAs to generate (1X–9X). Section 4 evaluate the area and delay of various alternative components for the partial product selector.

3.5.3. Parallel Accumulator

An area-efficient architecture is designed for this component. This component is a BCD-CLA tree shown in Figure 8. This component is adopted from Reference [31]. This BCD-CLA tree accumulates the partial products to generate the final coefficient product. BCD-CLAs are organized in a tree structure. To accumulate ($n=2^k)$ decimal numbers, a CLA tree with k stages is used, where ($n+2^i$)-digit CLAs are used in each i-th stage ($1\le i\le k$). Therefore, for a 64-bit operation, it requires 15 BCD-CLAs of (18–32) digits for a carry free partial product reduction in four stages.

Some other implementation of parallel accumulator have been proposed in References [28,30,31], where non-redundant decimal encoding formats, like 8421, 4221, and 5211, are used in References [28,30,31] and redundant formats, such as XS-3 and ODD, are used in References [29,30]. The signed-digit encoding, like $[-6,6]$, $[-7,7]$, are used in Reference [27]. All of these implementations perform better in terms of speed, however, considering the area-efficient solutions, we adopted this approach. Table 4 evaluates all the implementations.

3.5.4. BCD Converter

A base-billion to BCD converter converts one unit of a base billion number represented as a 32-bit binary number into a nine-digit BCD. The shift-and-add-3 algorithm [18] is applied. Figure 9 shows a block diagram, where each block is a small combinational logic that takes a 4-bit binary number and adds 3 if it is greater than 4. In the critical path, it takes 28 steps of this conversion blocks and a total of 141 blocks to convert a base-billion number to a BCD number.

A high-performance converter using digit splitting is proposed in References [19,20]. This is a design targeting digit by digit decimal multiplication where every stage of PPG requires conversion. One the other hand, in Reference [18], a base-thousand numbering system is introduced for the converter. Some other implementation proposes the lookup table for small scale conversion. As Method-3 and Method-2 are using base-billion numbering system, thus, we developed a converter for base-billion to BCD. Because base-thousand in software is slower than the base-billion for decimal multiplication [4] as most of the modern CPU has the 64-bit highly optimized binary multiplier to handle base-billion numbers directly.

3.5.5. Rounding Logic

When an intermediate product cannot be placed into the product coefficient, rounding is executed. Rounding to nearest, ties to even is adopted in the same way as in Reference [14]. The component includes a logic to determine whether it is round up or down, and an adder used for rounding-up. This is designed based on the definition of the IEEE-754 standard.

4. Experimental Results

The proposed methods are evaluated and compared with the existing software and hardware intensive solutions. The proposed methods are implemented on an RISC-V based integrated framework for the software–hardware co-design proposed in Reference [21] (The integrated framework is available at https://decimalarith.info.).

4.1. Experiment Setup

In the integrated evaluation framework, the RISC-V ecosystem with a dedicated hardware accelerator for decimal arithmetic is used along with several input samples for decimal computing. In this framework, the operations corresponding to the hardware part in the proposed methods are integrated as custom instructions in a Rocket Chip (one of the hardware implementations for RISC-V) [33,34], and they are executed in an accelerator through the Rocket Custom Coprocessor (RoCC) interface. These custom instructions can be used by implementing the corresponding hardware in the accelerator.

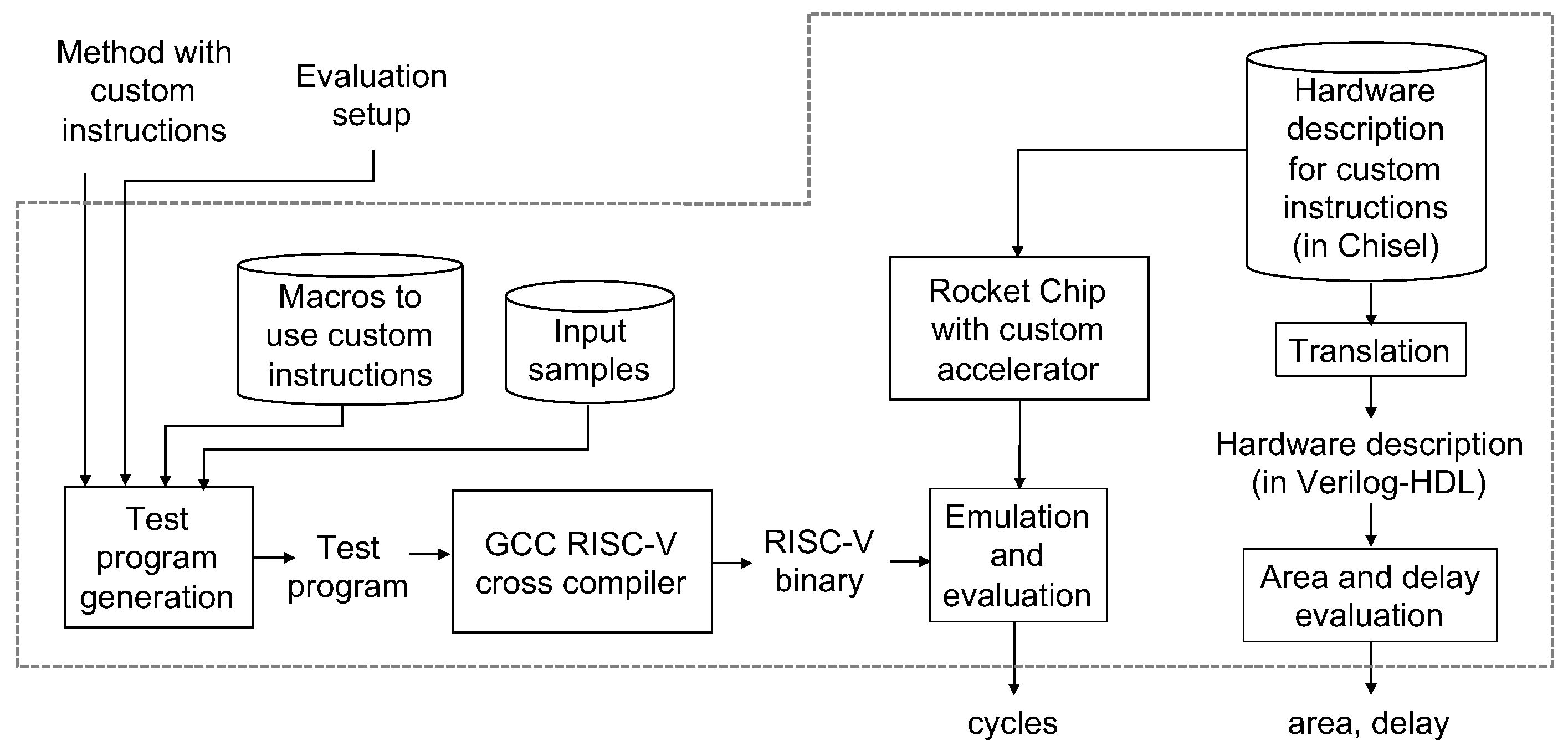
Figure 10 shows an overview of the RISC-V-based evaluation environment proposed in Reference [21]. The framework uses RISC-V ecosystem with input samples as decimal arithmetic verification test cases. The ecosystem contains compilers, system libraries, OS kernels, and an emulator with the Rocket Chip. Given a program code for an arithmetic operation with custom instructions and an evaluation setup information, a test program is generated and it is complied to an executable by the GCC RISC-V cross compiler with optimization flag -O. The evaluation setup information can specify a precision (double or quad), types of input samples (rounding, overflow, normal, underflow, etc.), types of the arithmetic operation (addition, subtraction, multiplication or any other), the number of iterations, the pattern of output (execution time or number of cycles), etc. The cycle-accurate evaluation is possible with the framework. The hardware parts are also evaluated with the framework, where the hardware parts are integrated as custom instructions executed in an accelerator. The corresponding hardware is described in a hardware description language Chisel for the Rocket Chip, and it is translated into Verilog-HDL and evaluated with CAD tools.

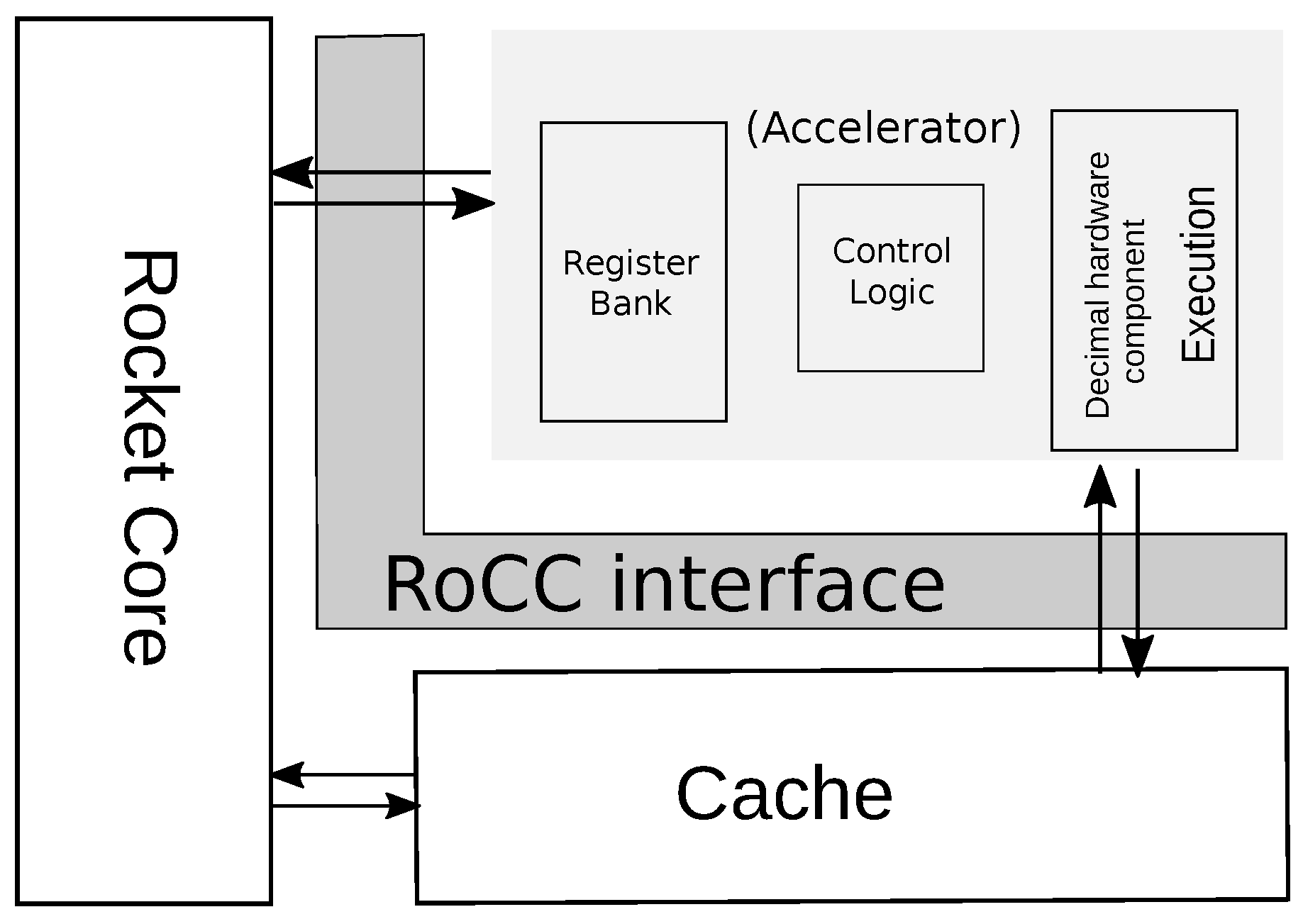
In the framework, the Rocket Chip contains Rocket core, which is a five-stage single-issue in-order scalar processor. The Rocket Chip also contains an accelerator which can be used by custom instructions whose opcodes are reserved in RISC-V ISA. The Rocket core and the accelerator have a decoupled communication through the RoCC interface as shown in Figure 11. The commands for the accelerator including register values are generated by committed instructions in the Rocket core and sent to the accelerator, and they may write an integer register in response. The accelerator can also share the Rocket core’s data cache through the RoCC interface.

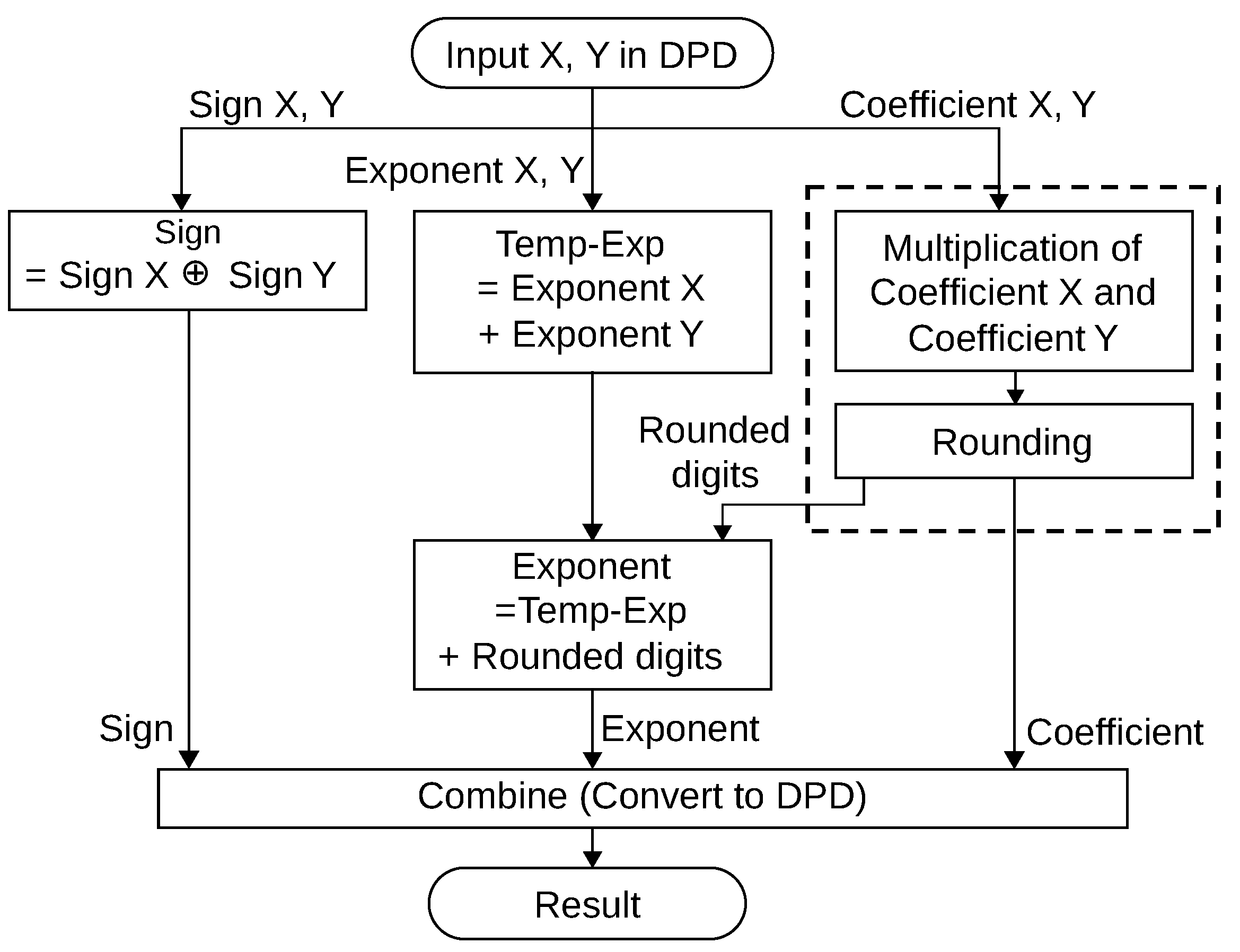
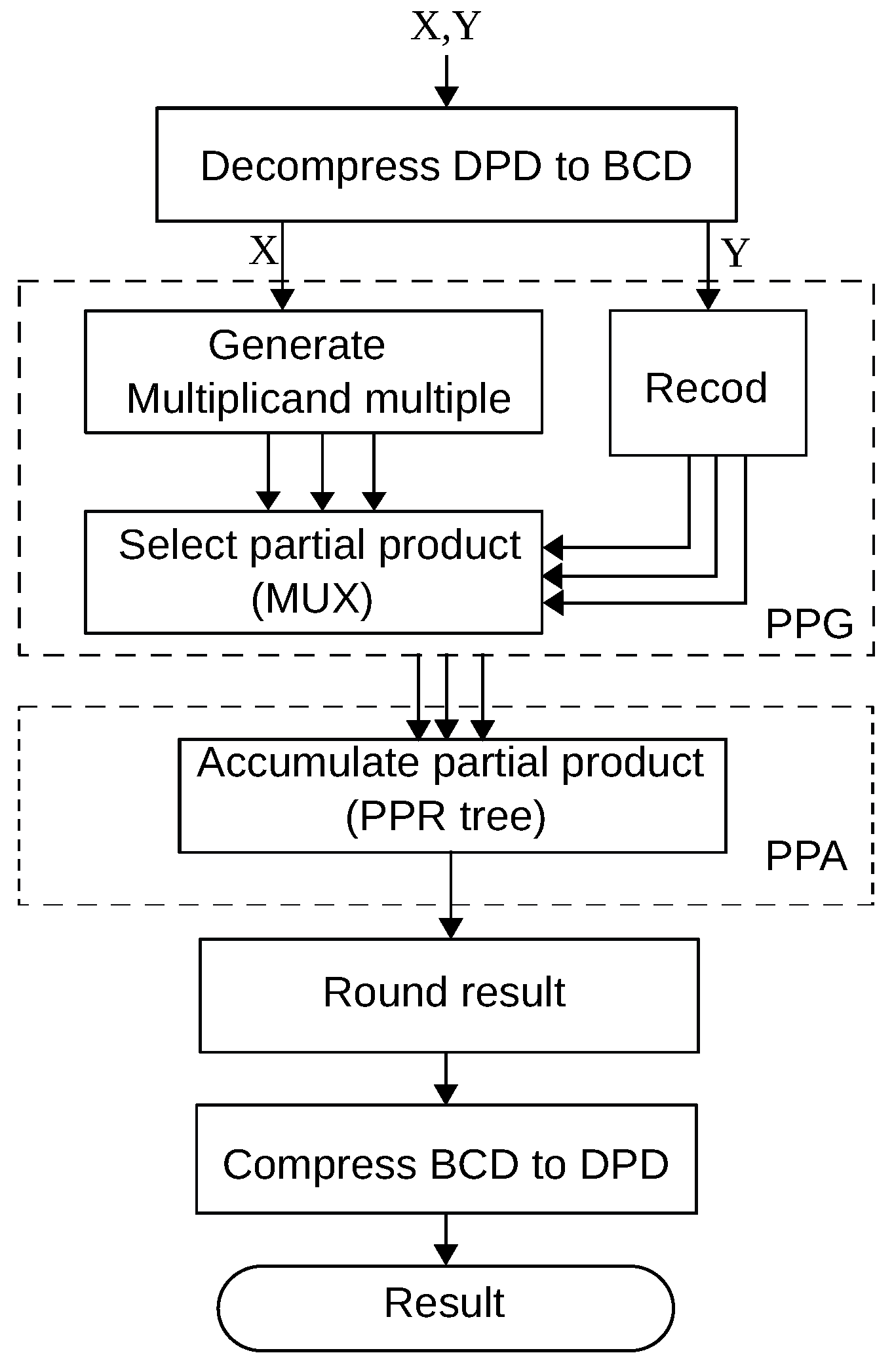
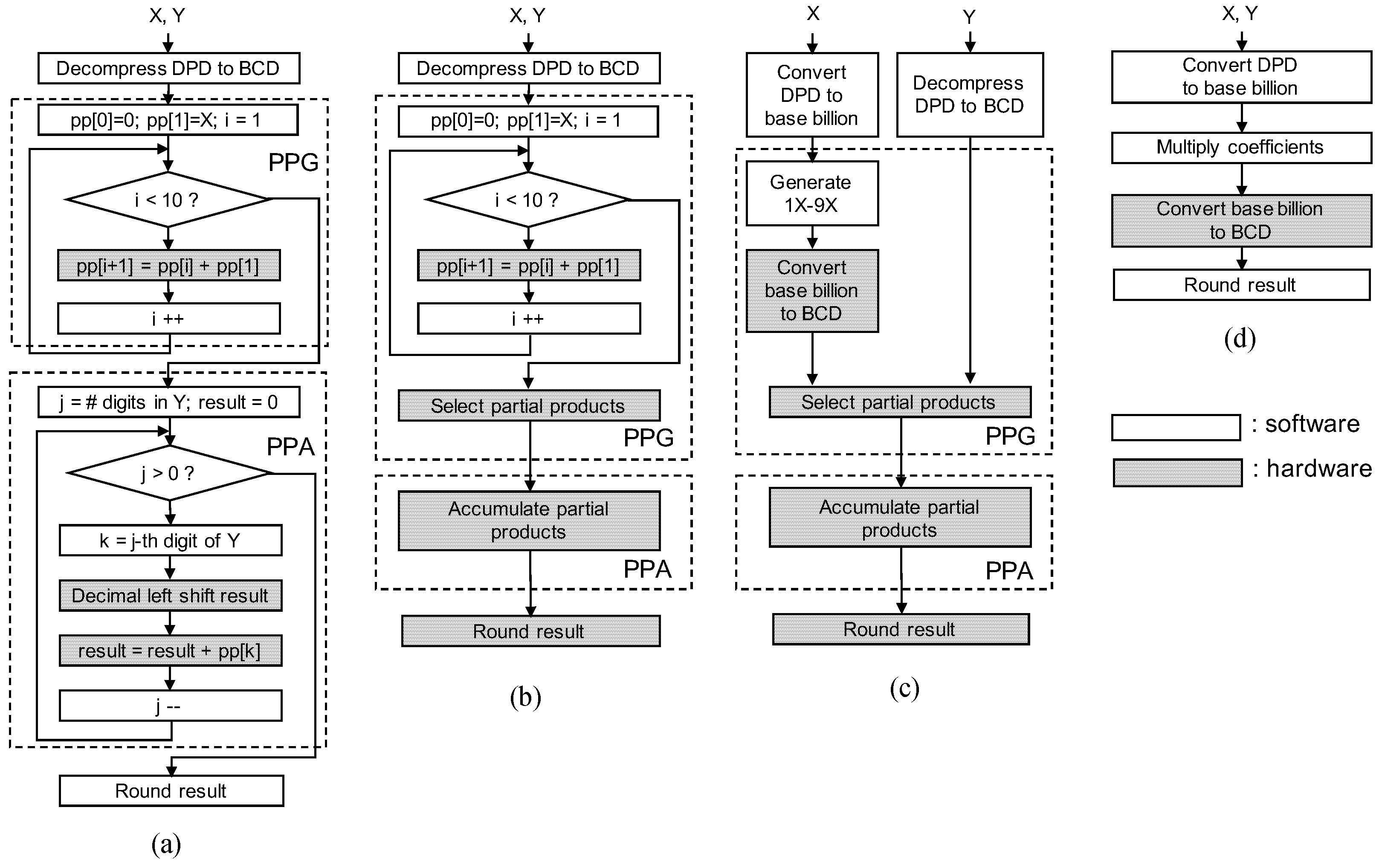
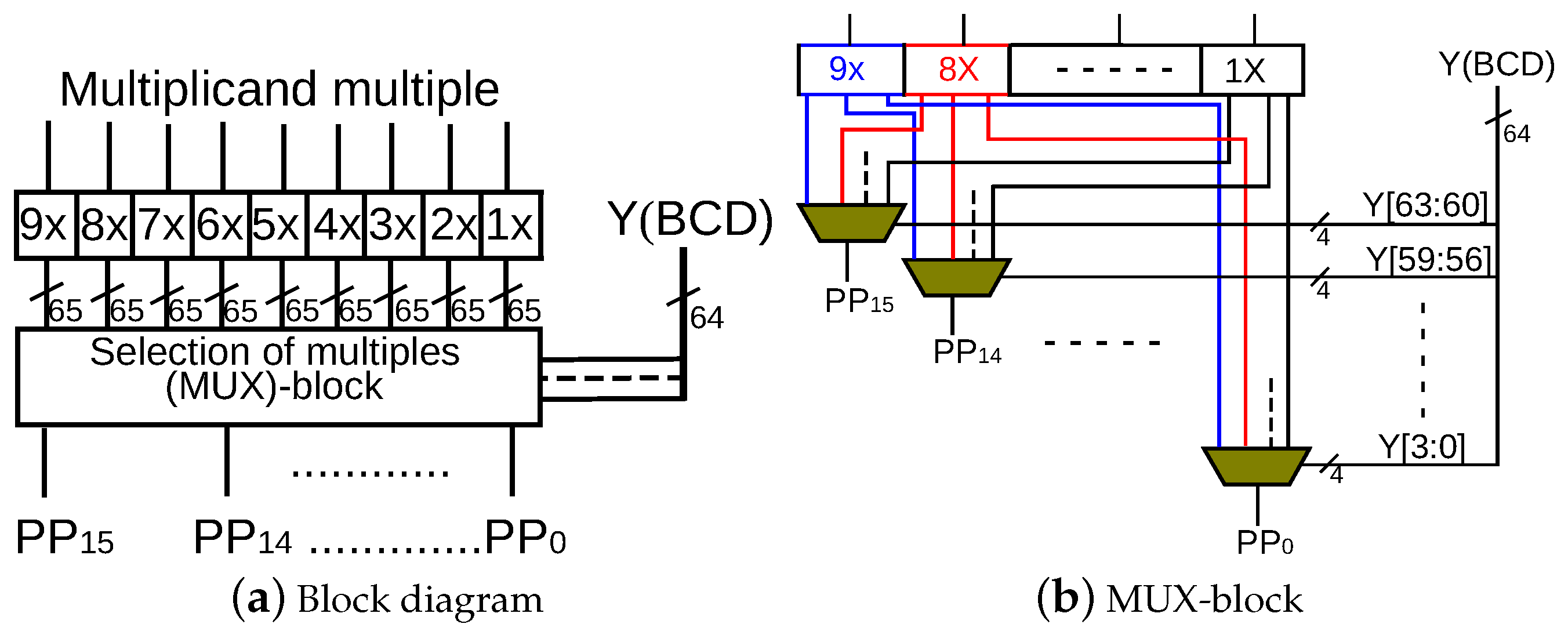
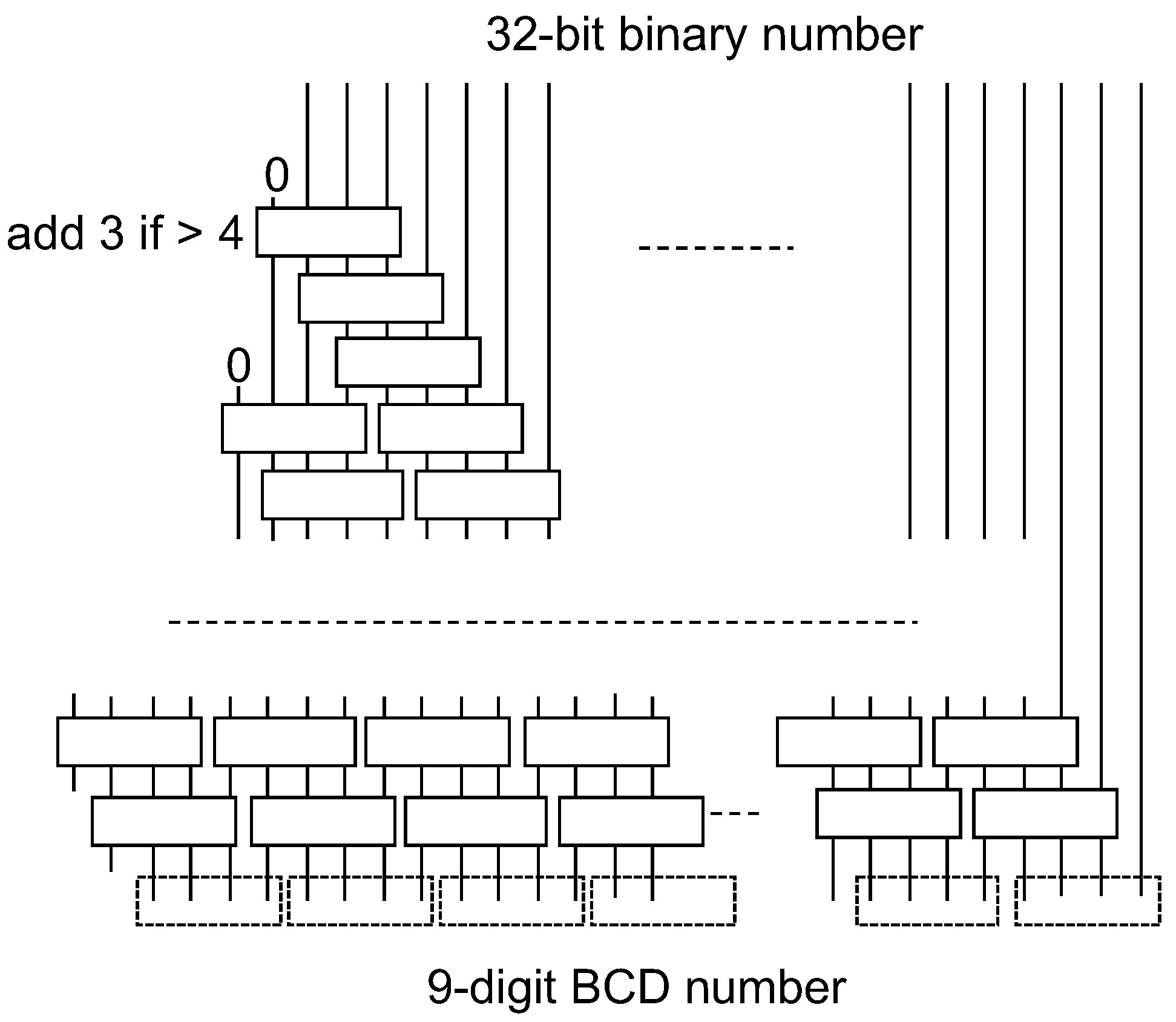
Cycle-accurate evaluation is possible for software-hardware co-design solutions for a 64-bit format, where a clock cycle is determined only considering a main processor (Rocket Chip). Custom instructions require multiple cycles according to their hardware implementation. Custom instructions corresponding to a decimal addition, partial product selection and accumulation, rounding for a decimal number, and conversion from base-billion to BCD formats have been implemented. Regarding the instruction for partial product selection and accumulation, the precomputed multiplicand multiples $1X$–$9X$ are loaded on the accelerator and they are accumulated according to the value of a multiplier Y. Custom instructions are used from the program code through macros that include in-line assembly codes for the corresponding custom instructions.

The hardware intensive solution uses a coefficient multiplication [31] and a rounding logic [14] as dedicated hardware. Since the coefficient multiplication [31] accepts BCD numbers as input coefficients, the hardware intensive solution includes a decompression from DPD to BCD as software.

The dedicated hardware parts for the proposed methods and the hardware intensive solution are translated from Chisel to Verilog-HDL, and their area and delay are evaluated by the logic synthesizer [35] with a 90 nm standard cell library [36]. Other hardware units used in the existing hardware solutions for decimal computing are also evaluated in the same environment.

As an input for the decimal multiplication, 8000 different samples were selected for the evaluation [37,38]. These samples include overflow, underflow, result (samples generating various results), rounding, and some other cases. The clock cycles for these samples are evaluated in the integrated evaluation framework.

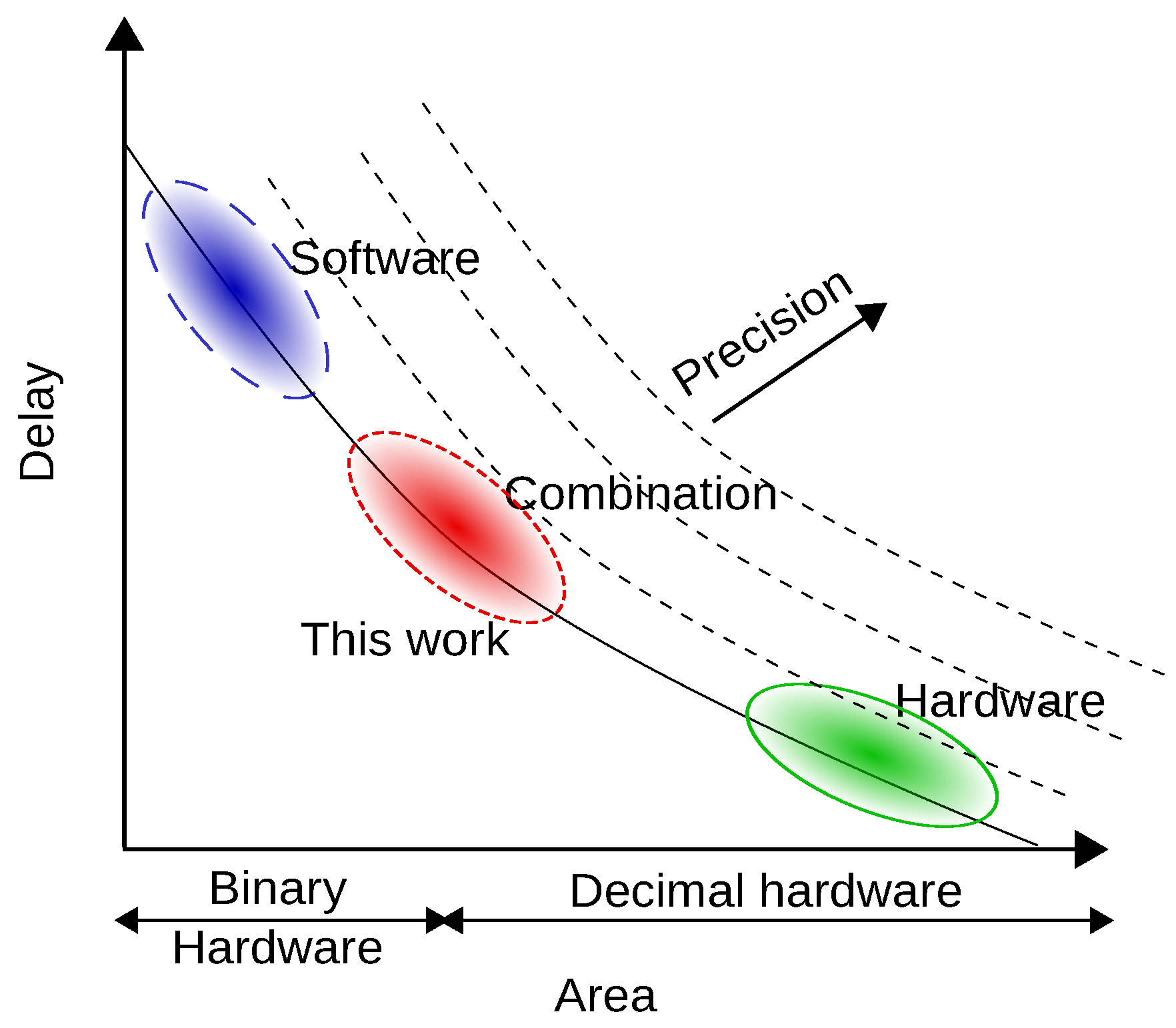
4.2. Area and Delay Tradeoff

The integrated evaluation of all the proposed methods along with full software solution [4] and the hardware intensive solution is presented in

Table 2. Execution cycles in integrated evaluation (64-bit).

Method	Avg. Number of Cycles		Speed Up	Performance
	Hardware	Total		Loss
Software [4]	0.00	4078.83	-	64.9%
Method-1	509.12	2288.74	1.78×	37.4%
Method-2	286.91	1723.72	2.37×	16.8%
Method-3	337.92	2420.01	1.69×	40.8%
Method-4	106.32	2852.50	1.43×	49.7%
Hardware intensive	86.40	1433.60	2.85×	-

. This table shows the average number of cycles required to execute a single multiplication operation. In the table, “Method” denotes the proposed methods, software and full hardware solutions, and the average number of cycles for the hardware part and total computation are denoted as “Hardware”, and “Total” columns, respectively. “Speed up” denotes the speedup achieved against the software solution [4], while “Performance loss” denotes the performance loss against the the hardware intensive solution. It can be observed that good speedup from 1.43× to 2.37× can be achieved against thesoftware solution. Compared to the hardware intensive solution, performance losses are 16.8% to 49.7%. Method-2 is the fastest among the proposed methods. It achieves 2.37× speedup against the software solution that is 16.8% performance loss against the hardware intensive solution. Both Method-1 and Method-2 perform BCD-based calculations and do not require any conversion between binary and decimal numbers. Hence, the elimination of complicated conversion achieves significant execution speedup. On the other hand, Method-3 and Method-4 achieve acceleration by executing the conversion using hardware.

The execution cycle distributions of the 8000 samples used for the proposed methods, the software solution, and the hardware intensive solution are presented in Figure 12. In all methods, some distributions with multiple peaks are observed. The software solution exhibits the widest distribution. It can be considered that the number of cycles depends on the input samples in the software solution and is distributed in a wide range. In contrast, the execution cycles of Method-2 and the hardware intensive solution are distributed in a narrow range with two peaks. (The input samples include a collection of very small numbers and relatively large numbers, which results in the two peaks [38] observed.) This implies that not only the average performance but also the worst-case performance can be accelerated.

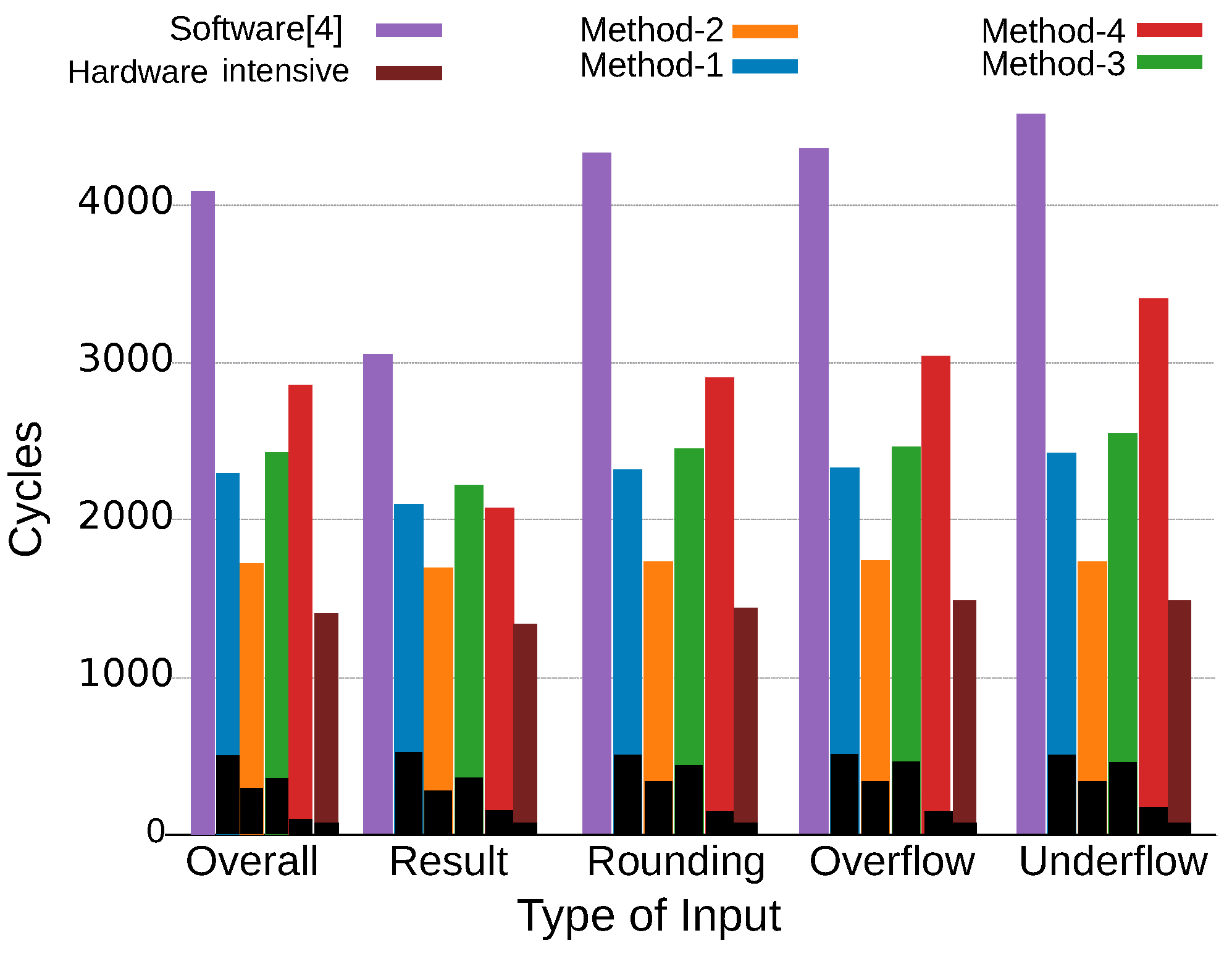
The performance of each input type was also analyzed. The average execution cycles for each input type are presented in Figure 13, where each type has 2000 input samples. The average cycles for all input types are also shown in “Overall”. In the cases of rounding, overflow, and underflow types, the performance of the methods exhibits a trend similar to the overall trend. However, Method-4 is comparable with Method-1 regarding the “result” type. The “result” type generates various types of results, including many normal results without rounding, overflow, or underflow. That is, Method-4 is comparable with Method-1 for normal cases, and its performance is degraded only for special cases, such as rounding, overflow, and underflow. The number of execution cycles required for hardware by the proposed methods is in the following decreasing order: Method-1, Method-3, Method-2, and Method-4. This is because custom instructions are repeatedly called in Method-1, Method-2, and Method-3, whereas Method-4 called a few custom instructions. It can also be observed that the software solution is degraded more in the special cases than the proposed methods and the hardware intensive solution. Thus, hardware solutions can avoid performance degradation by mitigating input-dependent cycle inflation. Especially in Method-2 and the hardware intensive solution, the average number of cycles is almost the same for all the input types.

The area and delay of the hardware part for both 64-bit and 128-bit formats are presented in

Table 3. Hardware overhead comparison (Partial Product Generation (PPG)).

M	Architecture	64-Bit Format		128-Bit Format
		A ($\mathsf{\mu }$m${}^2$)	D (ns)	A ($\mathsf{\mu }$m${}^2$)	D (ns)
[27]	Signed-digit	109,822	20.91	380,336	35.90
[30]	XS-3	106,078	19.39	371,940	25.21
[31]	8421-BCD	137,593	43.00	276,545	99.58
M-1	BCD-CLA	5459	63.00	11,270	117.10
M-2	BCD-CLA, PPS	88,290	67.33	228,094	123.66
M-3	Converter, PPS	99,428	4.66	250,734	6.56

PPS: Partial product selector.

,

Table 4. Hardware overhead comparison (partial product accumulation (PPA)).

M	Architecture	64-Bit Format		128-Bit Format
		A ($\mathsf{\mu }$m${}^2$)	D (ns)	A ($\mathsf{\mu }$m${}^2$)	D (ns)
[27]	Signed-digit	93,794	26.46	207,720	33.14
[30]	Hybrid BCD	94,268	36.68	230,929	130.25
[31]	8421 CLA tree	87,729	59.34	225,982	123.87
M-1	BCD-CLA	5459	112.00	11,270	416.40
M-2	PA	87,729	59.34	225,982	123.87
M-3	PA	87,729	59.34	225,982	123.87

PA: Parallel accumulator.

and

Table 5. Overall hardware overhead comparison.

M	Architecture	64-Bit Format			128-Bit Format			Ratio (128/64)
		A ($\mathsf{\mu }$m${}^2$)	R (%)	D (ns)	A ($\mathsf{\mu }$m${}^2$)	R (%)	D (ns)	A	D
[27]	Signed-digit	216,789	−1.53	47.37	614,779	−16.16	69.04	2.89	1.46
[30]	XS-3 and Hybrid BCD	213,519	0.00	56.07	629,592	−18.95	155.46	3.01	2.77
[31]	8421 addition, CLA tree	238,495	−10.47	102.34	529,250	0.00	229.83	2.23	2.25
M-1	BCD-CLA	5459	97.44	175.00	11,270	97.87	533.50	2.06	3.05
M-2	BCD-CLA, PP selector, PA	187,308	12.27	126.67	476,653	9.93	247.53	2.58	1.95
M-3	PP selector, PA	198,446	7.06	64.00	499,293	5.66	130.43	2.55	2.04
M-4	BB to BCD converter	16,596	92.22	42.53	33,910	93.59	150.60	2.04	3.54

M: Method, A: Area, D: Delay, R: Area reduction ratio, BB: Base Billion, PA: Parallel accumulator.

. In the proposed methods, the same hardware can be used repeatedly (e.g., BCD-CLA is repeatedly used in Method-1 and Method-2). In this case, the total delay for the hardware is evaluated by accumulating the delay of the target hardware according to the number of usage times. Since Method-1, Method-2, and Method-3 include PPG and PPA stages, these parts are evaluated in comparison with existing solutions [27,30,31]. (In Method-1, although a partial product selection is included in the PPA stage, this is executed by software. Therefore, the hardware parts are clearly separated. (See Figure 6a for details.)) In Table 3 and Table 4, the existing solutions have two BCD numbers as inputs. Finally, the total hardware overheads for the four proposed methods are compared with full hardware implementation. In the area evaluation (Table 3, Table 4 and Table 5), the delay of the software routine for the proposed methods is not included to estimate hardware delay only.

The area overhead and the delay of the PPG for the proposed methods and existing hardware solutions are presented in Table 3. The existing solutions fully realize the PPG stage with hardware, whereas the values for the proposed methods correspond to the hardware part in this stage. Hardware solutions based on several encodings have been previously proposed. Columns “M”, “A”, and “D” (also used in Table 4) denote the method, area, and delay, respectively. The column “Architecture” shows the encodings or the architecture regarding the basic blocks for each method. 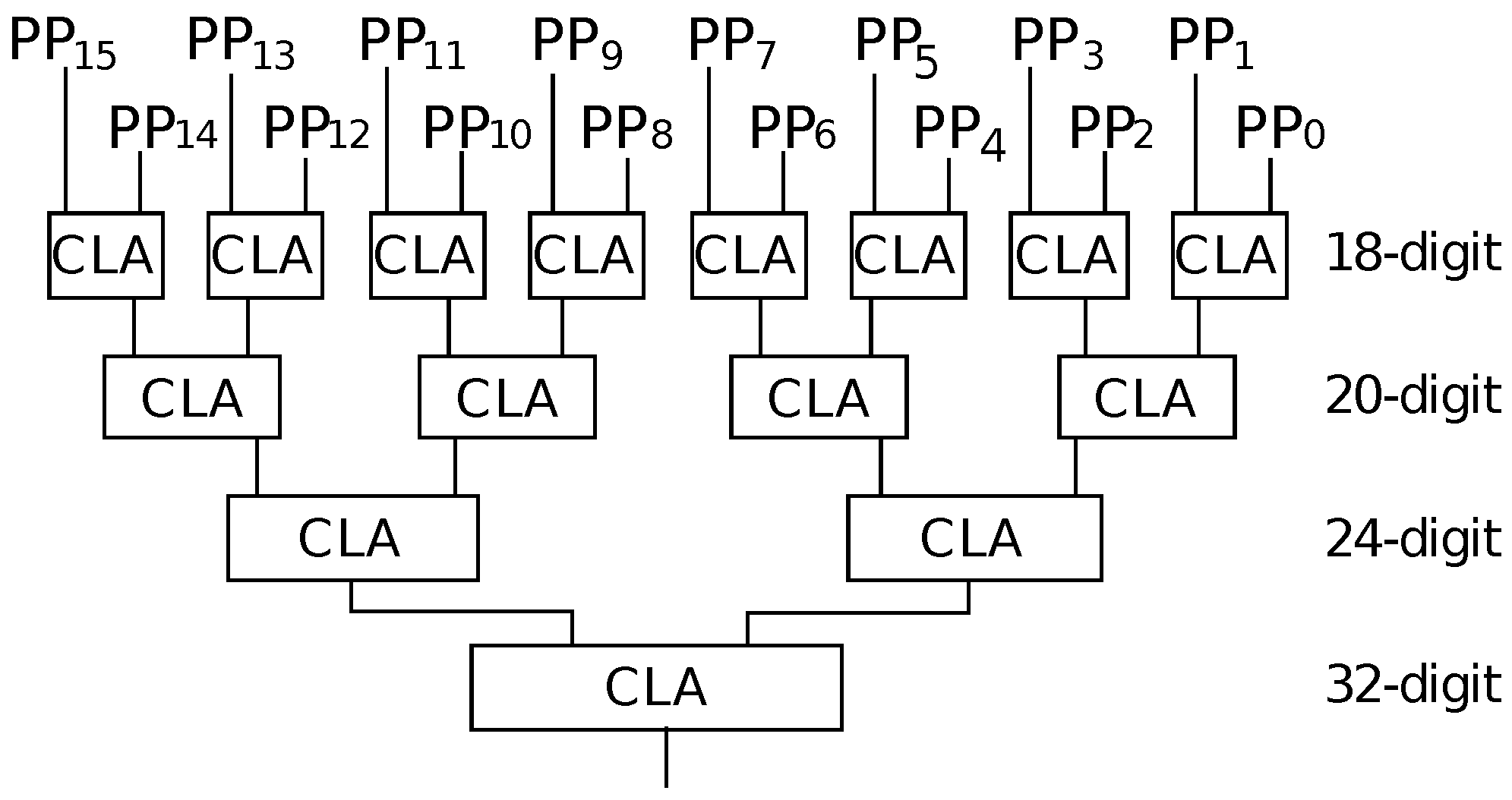(This column is also used in Table 4 and Table 5.) Method-1 has a very small area overhead, since it only requires one BCD-CLA, whereas Method-2 and Method-3 require more hardware for the parallel selection of PPs. However, compared with full hardware solutions, the area overheads of Method-2 and Method-3 are still small. The BCD-CLA is used repeatedly in Method-1 and Method-3. In these methods, larger delays are observed.

The area overhead and the delay of the PPA are presented in Table 4. Similarly to the PPG, the values for the proposed methods correspond to the hardware part in the PPA stage. Method-1 requires only one BCD-CLA and has a very small area overhead. This BCD-CLA can also be used in the PPG stage, and it implies that no extra area overhead is required in the PPG stage. However, sequential accumulation is required, and a larger delay is observed. Method-2 and Method-3 adopt a parallel accumulator based on the 8421 CLA proposed in Reference [27]. Hence, they exhibit the same area and delay.

The overall area overhead and delay of each method are presented in Table 5, where conversion and rounding circuits are included with the PPG and PPA stages. Columns “Area”, “ARR”, and “Delay” denote area, the area reduction ratio compared with the most area-efficient existing solution, and execution time for both 64-bit and 128-bit formats, and column “Ratio(128/64)” denotes the execution time ratio of the 128-bit to the 64-bit format. Since Method-1 shares its BCD-CLA in both the PPG and PPA stages, an area for only one BCD-CLA is required. Method-1 and Method-4 have relatively less hardware requirements compared with full hardware solutions, whereas Method-2 and Method-3 require more hardware. Regarding delay, even though the proposed methods realize a part of the function as hardware, this hardware part exhibits higher delay than full hardware solutions.

The area-delay tradeoff for all the proposed methods, the software solution, and the hardware intensive solution is presented in Figure 14. The delay has been obtained by the integrated evaluation framework. In this figure, the purple line is the tradeoff curve obtained by curve fitting using a inverse proportional model. The parameters are estimated using Trust-Region algorithm in MATLAB Curve Fitting Toolbox with custom function of $f\left(x\right)=a/(x+b)+c$, where x stands for the area. The fitting parameters a, b, and c are set to $4.191\times {10}^6$, 1495, and 1966, respectively. The curve shows the trend of the proposed methods in terms of speed and area tradeoff. Method-1 and Method-4 achieve speedup with a very small hardware overhead. However, to enhance the speed more, a huge area overhead is required in Method-2 and Method-3. From the figure, we get two Pareto points of Method-1 and Method-2 for the 64-bit precision.

Method-1 and Method-4 achieve moderate acceleration with a small area overhead (Method-4 is comparable with Method-1 for the normal type of inputs as previously analyzed). They reduces hardware overhead over 90% compared to the hardware intensive solution while losing less than 50% of performance. On the other hand, Method-2 achieves the fastest acceleration with a relatively large area overhead. It achieves 16.8% performance loss against the hardware intensive solution while reducing 12.2% of hardware overhead. Method-3 also achieves a moderate acceleration but it requires a large area overhead, and it does not exhibit any superior performance compared with the other methods.

Table 6. Execution time and area overhead (64-bit).

Method	Avg. # Cycles	Area ($\mathsf{\mu }$m${}^2$)
Software [4]	4078.83	-
DPD to base-billion conversion	606.36	-
exception check (NaN, Infinity, etc.)	109.32	-
base-billion multiplication	647.66	-
base-billion to BCD conversion	1474.68	-
rounding	795.7	-
Method-1 (total)	2288.74	5459
addition in PPG	178.48	5459
shift & addition in partial product accumulation	330.63	-
Method-2 (total)	1723.72	187,308
addition in Partial product generation	178.48	5459
Partial product selection	81.22	82,831
Partial product accumulation		87,727
rounding	27.20	11,288
Method-3 (total)	2420.01	198,446
conversion to BCD	229.50	16,596
Partial product selection	81.22	82,831
Partial product accumulation		87,729
rounding	27.20	11,288
Method-4 (total)	2852.50	16,596
conversion to BCD	106.32	16,596
Hardware intensive	1433.60	235,424
coefficient multiplication	86.40	235,424

shows more detailed results for the execution time and the area overhead. Column “Method” denotes the solutions (the proposed methods, software, and the hardware intensive solutions) and hardware blocks or software routines in the solutions. Columns “Avg. # of cycles” and “Area” denote the average number of cycles and the hardware area, respectively. The two hardware components, PPS and PPA, are collectively used in a single custom instruction and their execution time is measured together in Method-2 and Method-3. These two hardware components require a very high area overhead though the corresponding instruction reduces the execution time. Rounding (Method-2, 3) and base-billion to BCD conversion (Method-3, 4) in hardware is a good substitution in terms of area overhead, where they reduce over 96% and 92% cycles, respectively, with reasonable area overhead. (The execution time for BCD conversions are compared between the software solution and Method-4 since both solutions require to convert 4 units of base-billion numbers.)

4.3. Discussion

We proposed four methods for hardware–software co-design of decimal multiplication to find new Pareto points in terms of speed and area overhead. Method-1 and Method-4 achieved acceleration with a small area overhead, whereas Method-2 achieved the highest speedup with a large area overhead. Such speedup was obtained by either avoiding conversion or executing conversion in hardware. That shows the conversion between binary and decimal numbers is a bottleneck for a decimal computation in software solutions. In Method-1, a small decimal adder brings acceleration by avoiding binary–decimal conversions, while Method-4 uses a dedicated hardware for a binary to decimal conversion. Method-2 is also a Pareto point, where the highest speed-up is achieved using a powerful parallel accumulator with a large area overhead. We tried another combination of dedicated hardware units in Method-3, but it cannot be a Pareto point. Two methods, Method-1 and Method-2, can be selected considering a hardware constraint or a requirement of speed-up.

5. Conclusions

In this paper, four methods were presented, which provide several Pareto points in terms of area, and delay for decimal multiplication. These methods use both software and hardware to reduce hardware overhead and increase computation speed simultaneously. An RISC-V-based integrated evaluation framework was used to evaluate the proposed methods. Experiments on an RISC-V-based environment for a 64-bit format proved that the proposed methods can achieve 1.43× to 2.37× execution speedup compared with an existing software solution. They can also achieve a 7–97% area reduction compared with the existing full hardware decimal multiplier.

Besides the decimal multiplication, we intend to develop other decimal arithmetic based on SW–HW co-design. Currently, the proposed multiplication is designed using C language with the library decNumber C, and we plan to include other popular programming languages, like Java BigDecimal Class and Python decimal module, using decimal accelerator support.

Future Vision

From an architectural point of view, there are numerous research opportunities to improve and extend the proposed decimal co-design-based arithmetic discussed in Section 3. This study establishes decimal multiplication co-design using hardware component, however, to enhance these tracks, research is needed to examine combined decimal/binary multiplier with a co-design approach.

The IEEE standard for floating-point arithmetic (IEEE 754) again revised in 2019 to include additional demands in computing [39]. This study introduces decimal multiplication using a combination of software and hardware, and we believe this study established to satisfy the current needs and focus the interests of both commercial and personal users in decimal arithmetic. Though the market has a choice, as continued research decreases the performance gap between binary and decimal computing, we may very well see decimal applications replacing binary applications in certain computing area.