A Comparison of Singlet Oxygen Explicit Dosimetry (SOED) and Singlet Oxygen Luminescence Dosimetry (SOLD) for Photofrin-Mediated Photodynamic Therapy
Abstract
:1. Introduction
2. Materials and Methods
2.1. SOED Model In Vitro and In Vivo
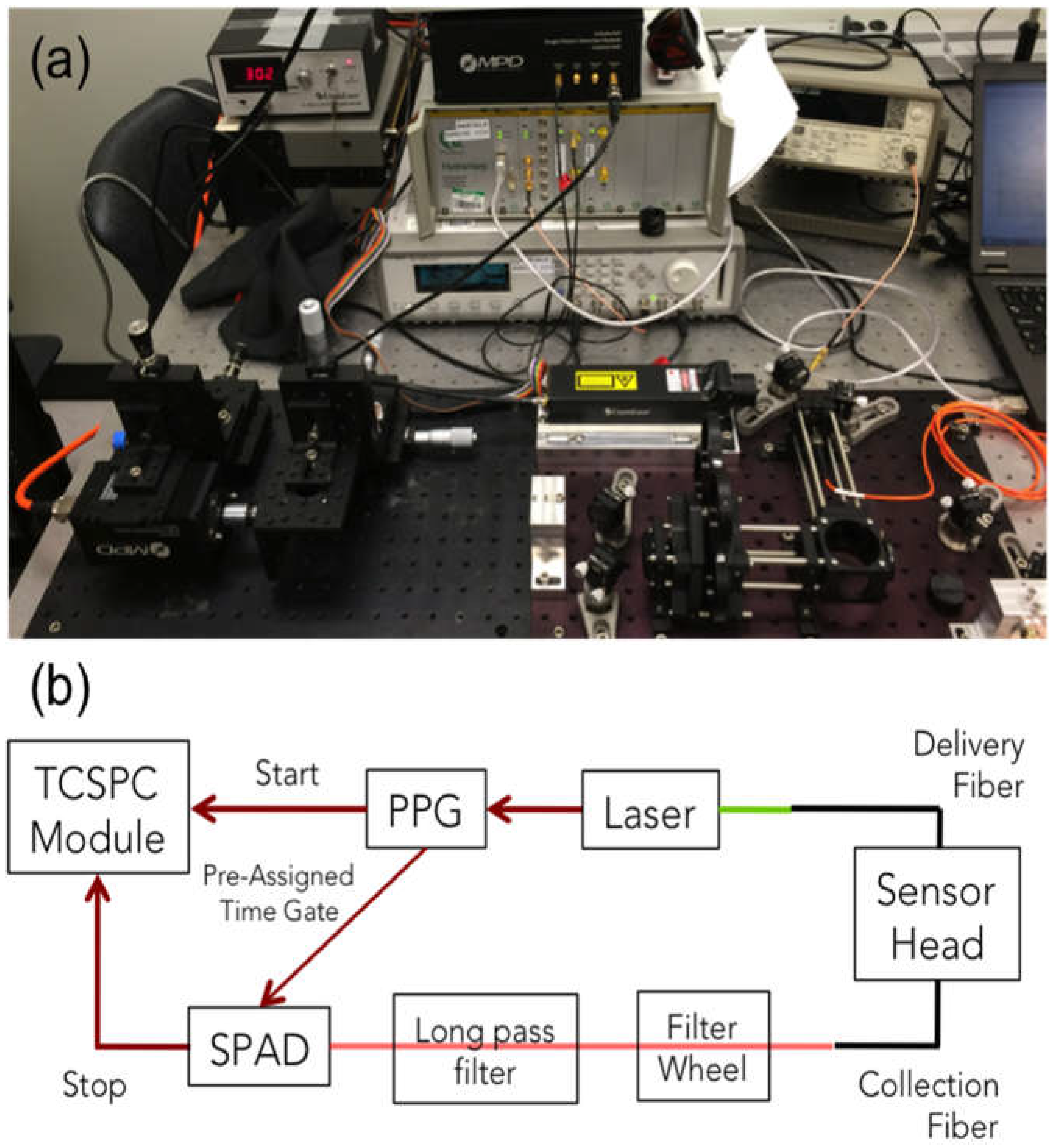
2.2. SOLD Instrumentation
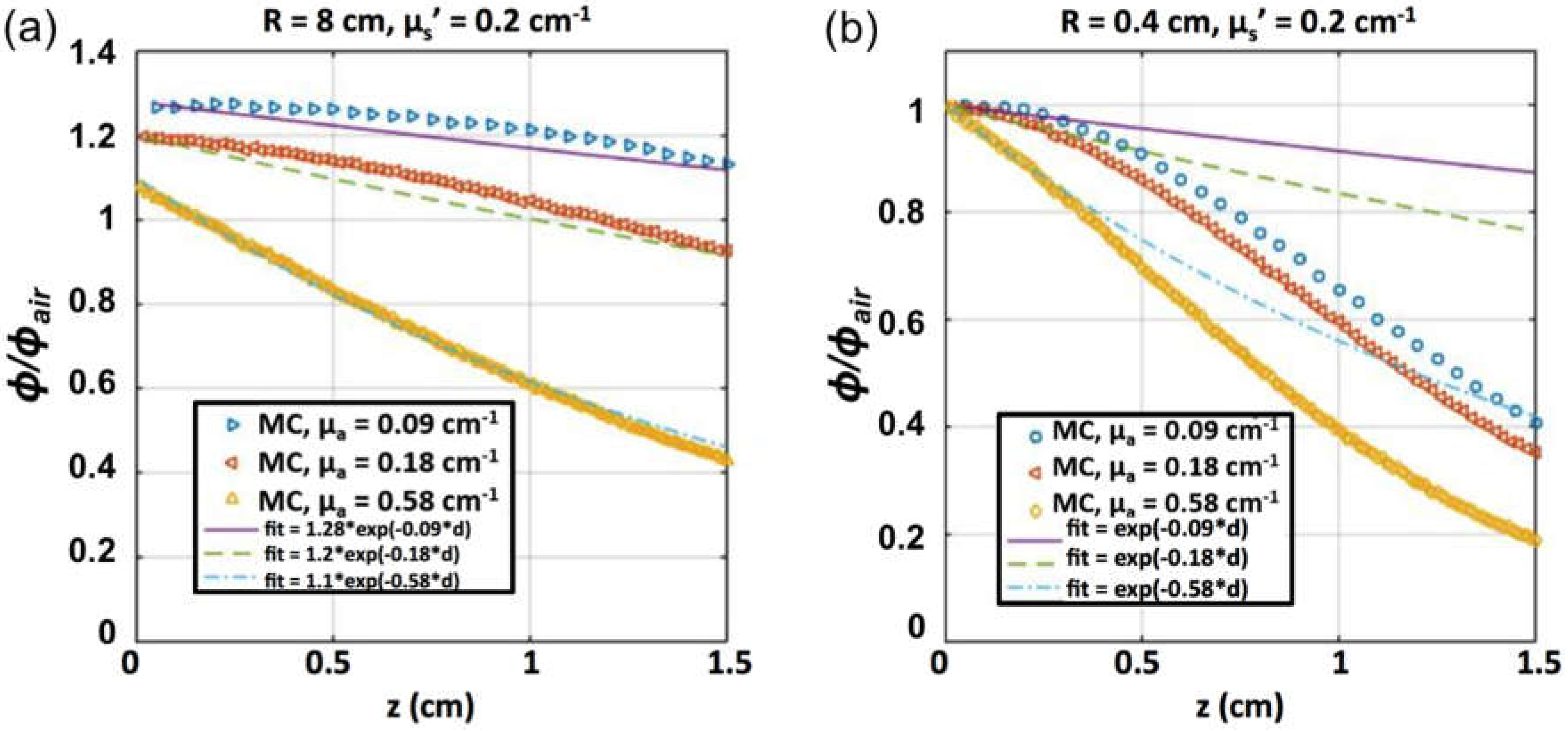
2.3. Measurements in Tissue-Simulating Phantoms
2.4. Comparison of 630 nm and 523 nm SOED
3. Results
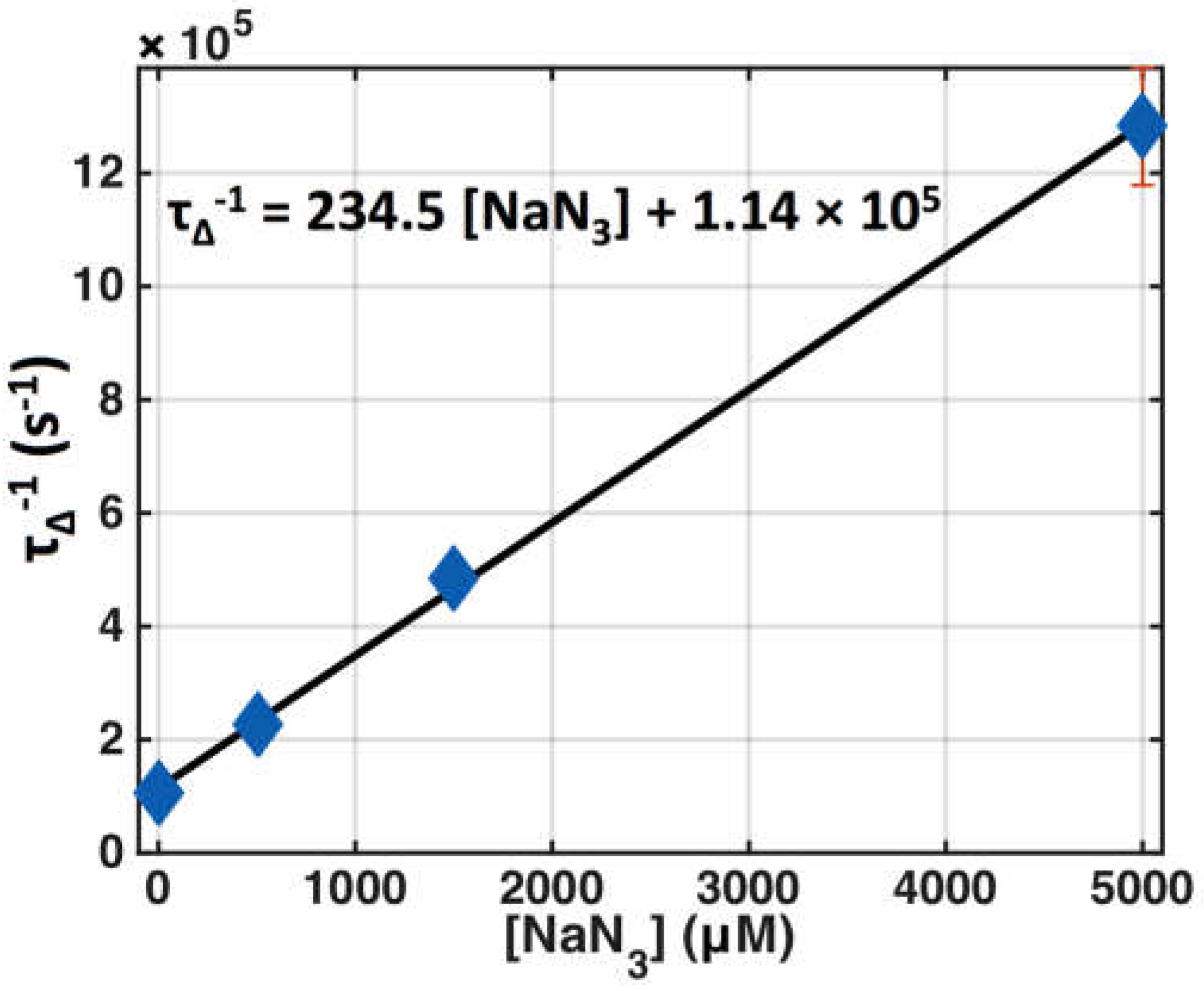
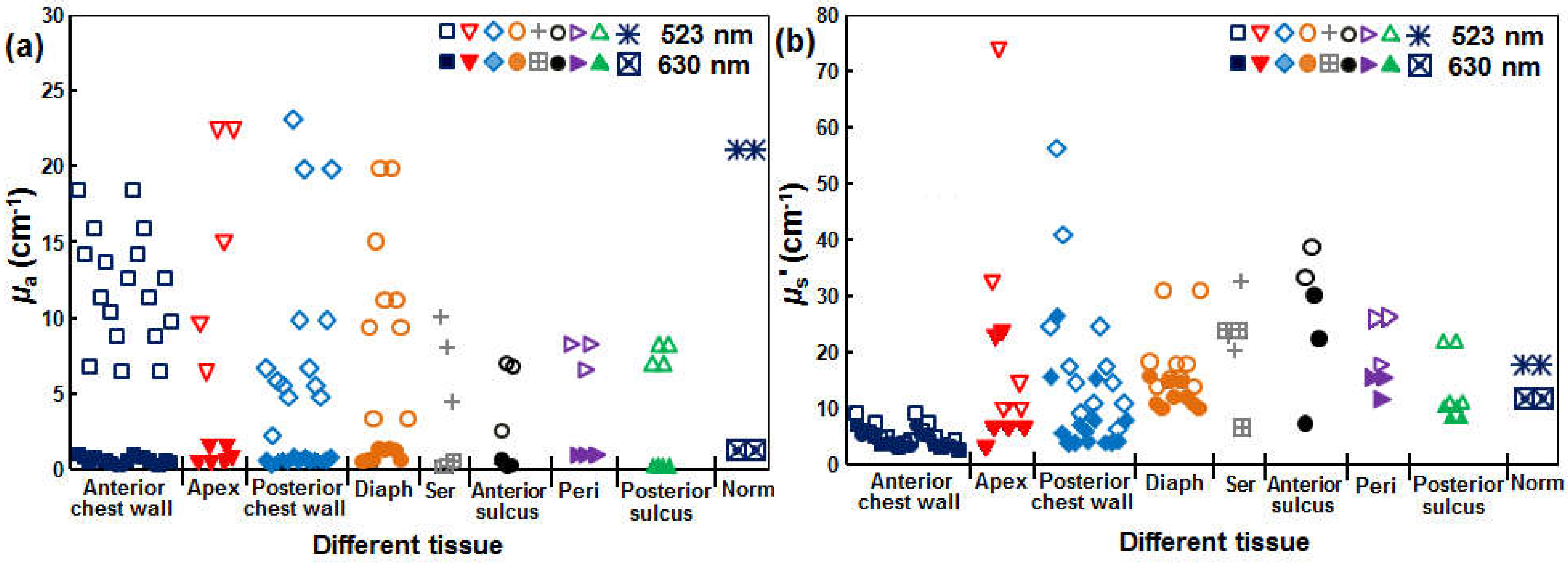
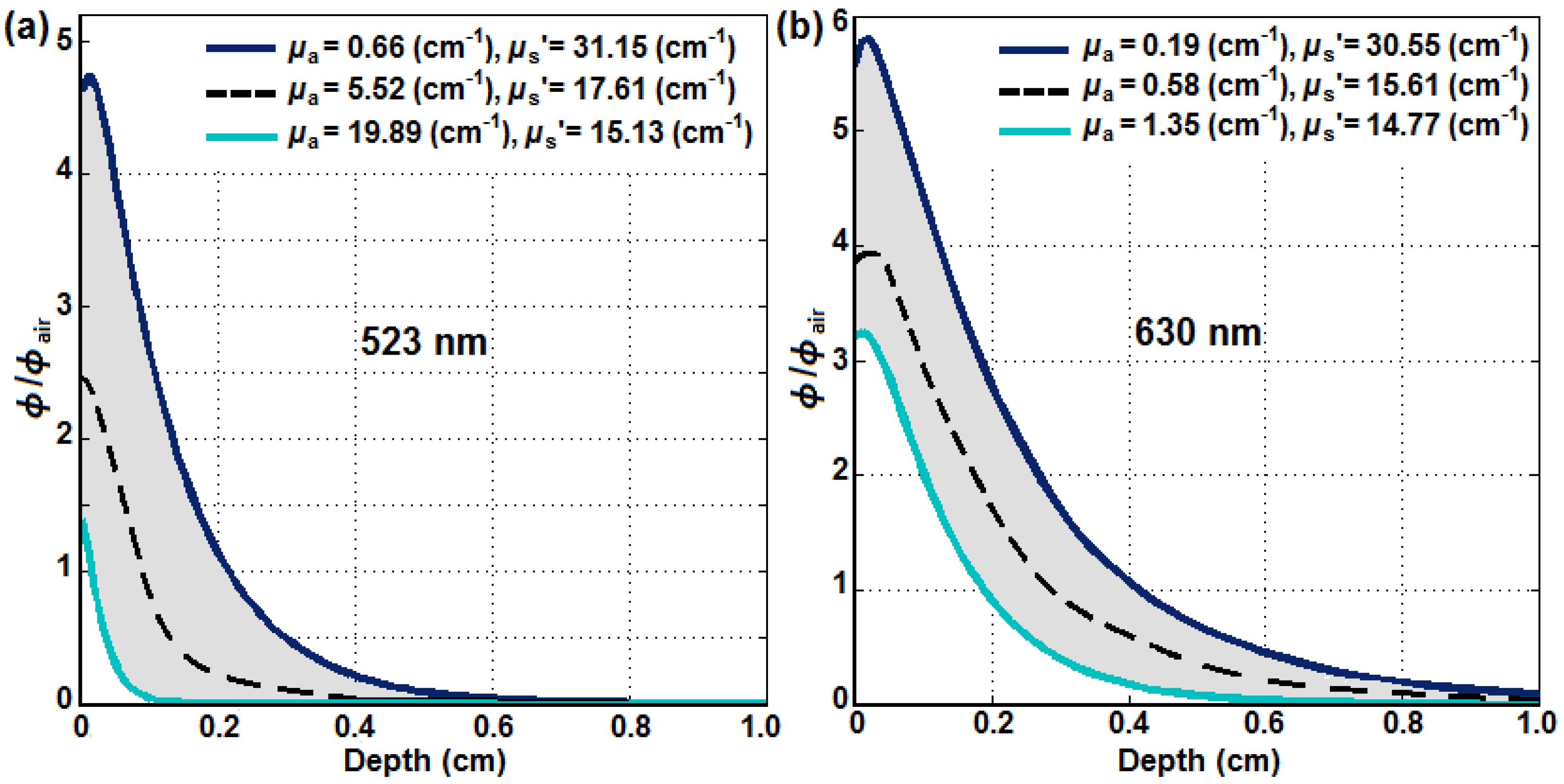
3.1. SOED Photophysical Parameters
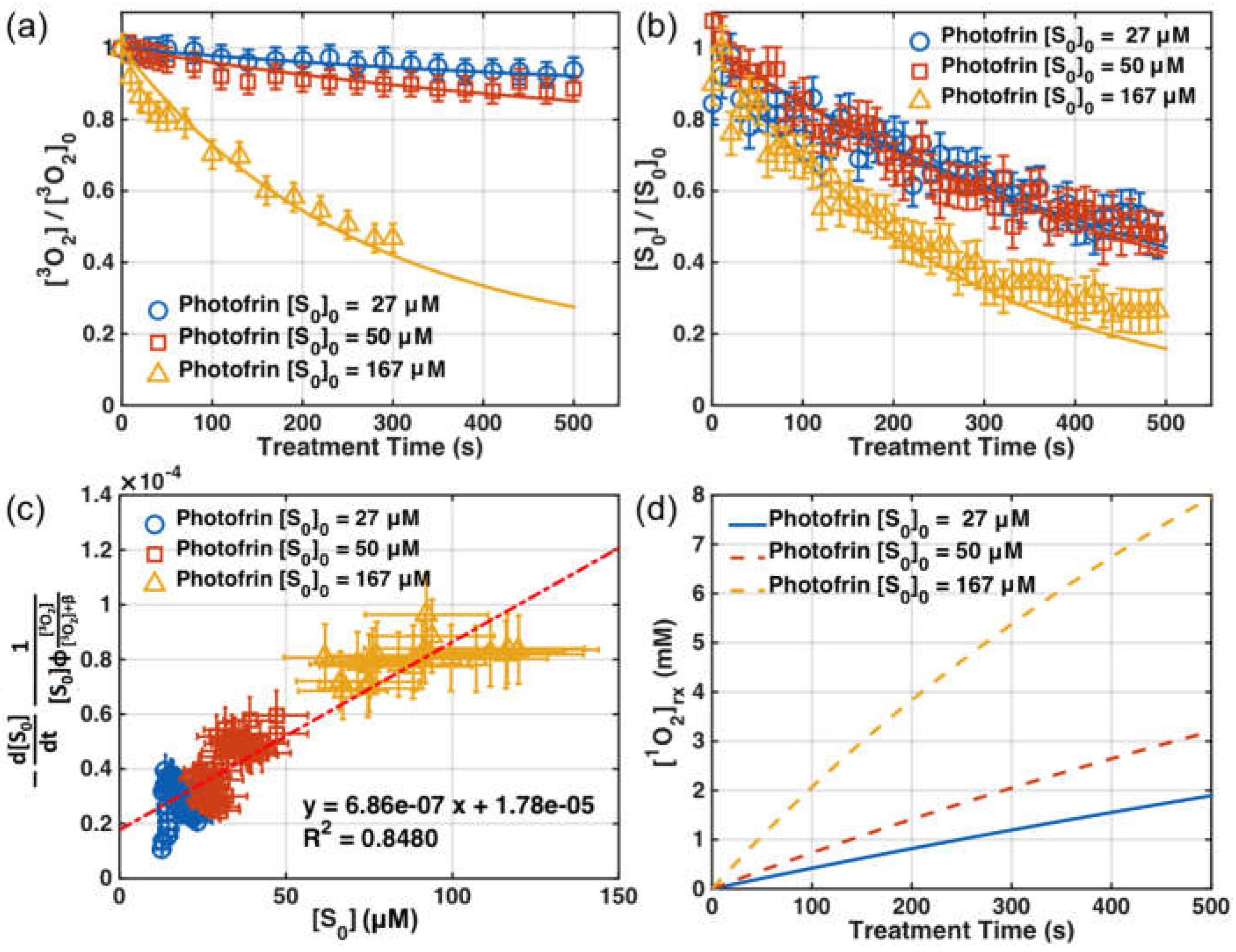
3.2. SOED in Phantom
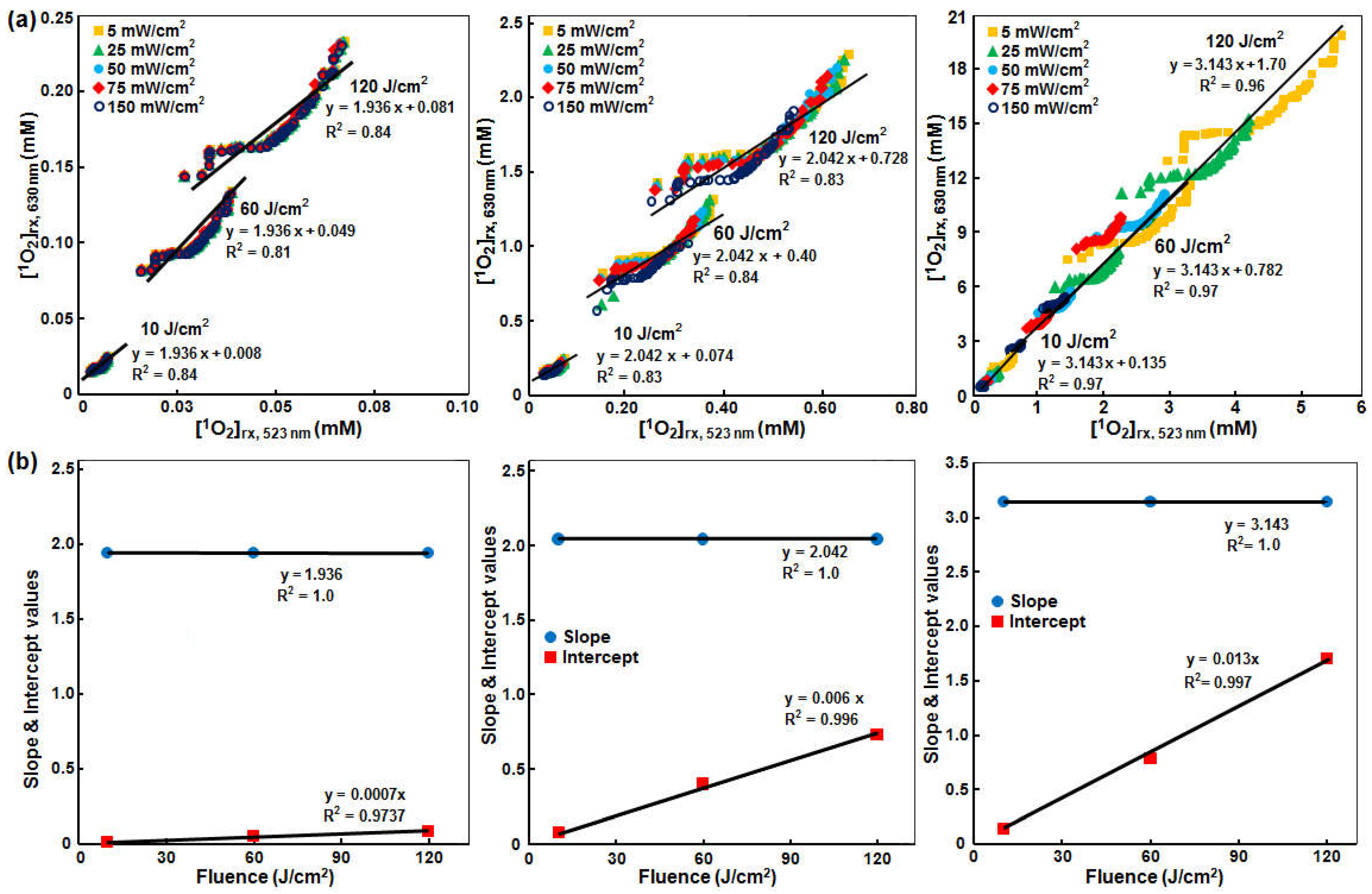
3.3. SOED/SOLD Comparison in Solution
4. Discussion
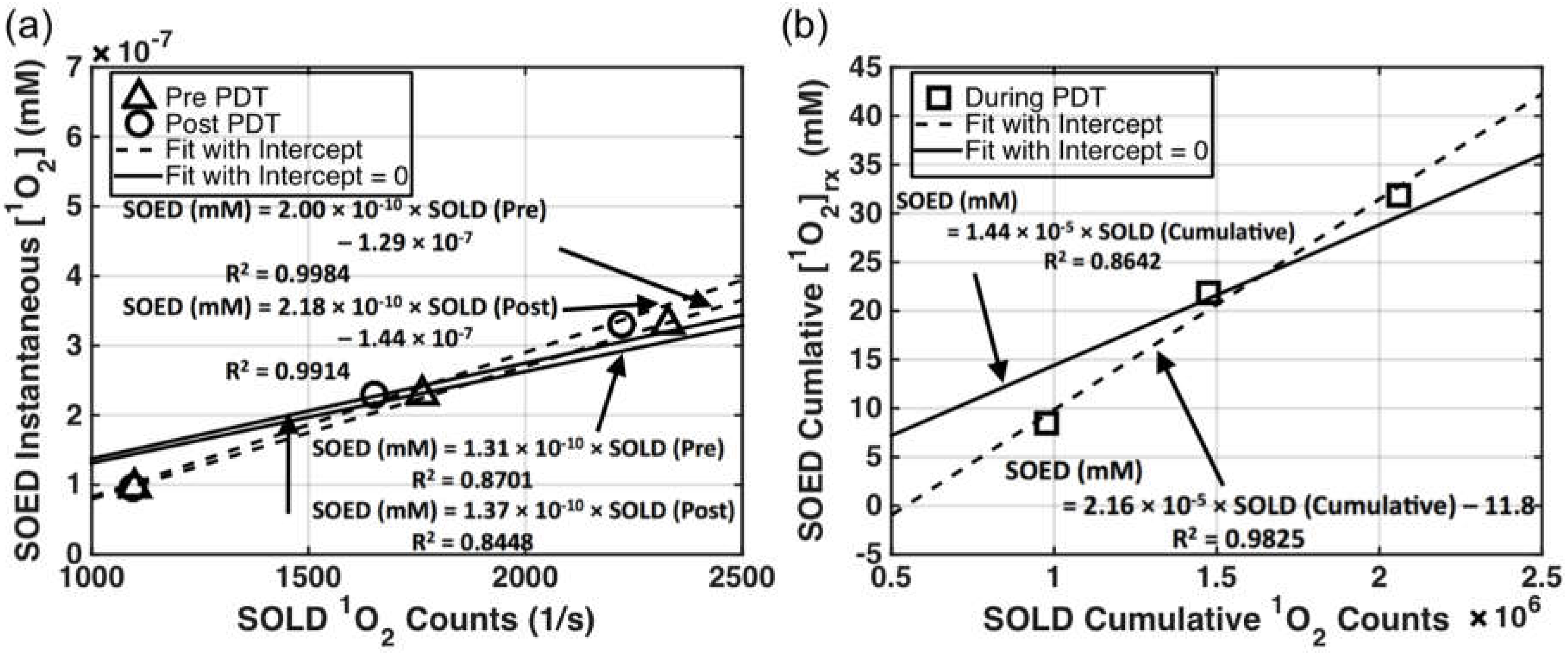
4.1. SOED and SOLD Intercomparison
4.2. Feasibility of Using SOLD at 523 nm for Predicting [1O2]rx at 630 nm
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PS | Photosensitizer |
| SOED | Singlet Oxygen Explicit Dosimetry |
| SOLD | Singlet Oxygen Luminescence Dosimetry |
References
- Zhu, T.C.; Finlay, J.C. The role of photodynamic therapy (PDT) Physics. Med. Phys. 2008, 35, 3127–3136. [Google Scholar] [CrossRef] [PubMed]
- Wilson, B.C.; Patterson, M.S. The physics, Biophysics, and technology of photodynamic therapy. Phys. Med. Biol. 2008, 53, R61–R109. [Google Scholar] [CrossRef] [PubMed]
- Dougherty, T.J. Photodynamic Therapy. Photochem. Photobiol. 1993, 58, 896–900. [Google Scholar] [CrossRef]
- Foote, C.S. Definition of type I and type II photosensitized oxidation. Photochem. Photobiol. 1991. [Google Scholar] [CrossRef]
- Foote, C.S. Photosensitized Oxidation and Singlet Oxygen: Consequences in Biological Systems. In Free Radicals in Biology; Pryor, W.A., Ed.; Academic Press: New York, NY, USA, 1976; pp. 85–133. [Google Scholar]
- Weishaupt, K.R.; Gomer, C.J.; Dougherty, T.J. Identification of singlet oxygen as the cytotoxic agent in photo-activation of a murine tumor. Can. Res. 1976, 36, 2326–2392. [Google Scholar]
- Zhou, X.; Pogue, B.W.; Chen, B.; Demidenko, E.; Joshi, R.; Hoopes, J.; Hasan, T. Pretreatment photosensitizer dosimetry reduces variation in tumor response. IJROBP 2006, 64, 1211–1220. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.K.; Finlay, J.C.; Busch, T.M.; Hahn, S.M.; Zhu, T.C. Explicit dosimetry for photodynamic therapy: Macroscopic singlet oxygen modeling. J. Biophotonics 2010, 3, 304–318. [Google Scholar] [CrossRef] [PubMed]
- Foster, T.H.; Murant, R.S.; Bryant, R.G.; Knox, R.S.; Gibson, S.L.; Hilf, R. Oxygen Consumption and Diffusion Effects in Photodynamic Therapy. Radiat. Res. 1991, 126, 296–303. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.-H.; Feng, Y.; Lu, J.Q.; Allison, R.R.; Cuenca, R.E.; Downie, G.H.; Sibata, C.H. Modeling of a Type II Photofrin-mediated Photodynamic Therapy Process in a Heterogeneous Tissue Phantom. Photochem. Photobiol. 2005, 81, 1460–1468. [Google Scholar] [CrossRef] [PubMed]
- Sandell, J.L.; Zhu, T.C. A review of in vivo optical properties of human tissues and its impact on PDT. J. Biophoton. 2011, 4, 773–787. [Google Scholar] [CrossRef]
- Finlay, J.C.; Mitra, S.; Patterson, M.S.; Foster, T.H. Photobleaching kinetics of Photofrin in vivo and in multicell tumour spheroids indicate two simultaneous bleaching mechanisms. Phys. Med. Biol. 2004, 49, 4837–4860. [Google Scholar] [CrossRef] [PubMed]
- Moan, J.; Berg, K. The photodegradation of porphyrins in cells can be used to estimate the lifetime of singlet oxygen. Photochem. Photobiol. 1991, 53, 549–553. [Google Scholar] [CrossRef] [PubMed]
- Penjweini, R.; Liu, B.; Kim, M.M.; Zhu, T.C. Explicit dosimetry for 2-(1-Hexyloxyethyl)-2-devinyl pyropheophorbide-a (HPPH) mediated photodynamic therapy: Macroscopic singlet oxygen modeling. J. Biomed. Opt. 2015. [Google Scholar] [CrossRef] [PubMed]
- Qiu, H.; Kim, M.M.; Penjweini, R.; Zhu, T.C. Macroscopic singlet oxygen modeling for dosimetry of Photofrin-mediated photodynamic therapy: An in vivo study. J. Biomed. Opt. 2016. [Google Scholar] [CrossRef] [PubMed]
- Zhu, T.C.; Kim, M.M.; Liang, X.; Finlay, J.C.; Busch, T.M. In vivo singlet oxygen threshold doses for PDT. Photon Lasers Med. 2015, 4, 59–71. [Google Scholar] [CrossRef] [PubMed]
- Jarvi, M.T.; Niedre, M.J.; Patterson, M.S.; Wilson, B.C. Singlet Oxygen Luminescence Dosimetry (SOLD) for Photodynamic Therapy: Current Status, Challenges and Future Prospects. Photochem. Photobiol. 2006, 82, 1198–1210. [Google Scholar] [CrossRef] [PubMed]
- Niedre, M.J.; Yu, C.S.; Patterson, M.S.; Wilson, B.C. Singlet oxygen luminescence as an in vivo photodynamic therapy dose metric: Validation in normal mouse skin with topical amino-levulinic acid. Br. J. Cancer 2005, 92, 298–304. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.M.; Ghogare, A.A.; Greer, A.; Zhu, T.C. On the in vivo photocheical rate parameters for PDT reactive oxygen species modeling. Phys. Med. Biol. 2016, in press. [Google Scholar]
- Wang, H.W.; Putt, M.E.; Emanuele, M.J.; Shin, D.B.; Glatstein, E.; Yodh, A.G.; Busch, T.M. Treatment-induced changes in tumor oxygenation predict photodynamic therapy outcome. Can. Res. 2004, 64, 7553–7561. [Google Scholar] [CrossRef] [PubMed]
- Gemmell, N.R.; McCarthy, A.; Kim, M.M.; Veilleux, I.; Zhu, T.C.; Buller, G.S.; Wilson, B.C.; Hadfield, R.H. A compact fiber-optic probe-based singlet oxygen luminescence detection system. J. Biophotonics 2016. [Google Scholar] [CrossRef] [PubMed]
- Gemmell, N.R.; McCarthy, A.; Liu, B.; Tanner, M.G.; Dorenbos, S.N.; Zwiller, V.; Patterson, M.S.; Buller, G.S.; Wilson, B.C.; Hadfield, R.H. Singlet oxygen luminescence detection with a fiber-coupled superconducting nanowire single-photon detector. Opt. Express 2013, 21, 5005–5013. [Google Scholar] [CrossRef] [PubMed]
- Jarvi, M.T.; Niedre, M.J.; Patterson, M.S.; Wilson, B.C. The influences of oxygen depletion and photosensitizer triplet-state dynamic during photodynamic therapy on accurate singlet oxygen luminescence monitoring and analysis of treatment dose response. Photochem. Photobiol. 2011, 87, 223–234. [Google Scholar] [CrossRef] [PubMed]
- Zhu, T.C.; Liu, B.; Penjweini, R. Study of tissue oxygen supply rate in a macroscopic photodynamic therapy singlet oxygen model. J. Biomed. Opt. 2015. [Google Scholar] [CrossRef] [PubMed]
- Finlay, J.C.; Conover, D.L.; Hull, E.L.; Foster, T.H. Porphyrin bleaching and PDT-induced spectral changes are irradiance dependent in ALA-sensitized normal rat skin in vivo. Photochem. Photobiol. 2001, 73, 54–63. [Google Scholar] [CrossRef]
- Gallagher-Colombo, S.M.; Quon, H.; Malloy, K.M.; Ahn, P.H.; Cengel, K.C.; Simone, C.B.; Chalian, A.A.; O’Malley, B.W.; Weinstein, G.S.; Zhu, T.C.; et al. Measuring the physiologic properties of oral lesions receiving fractionated photodynamic therapy. Photochem. Photobiol. 2015, 91, 1210–1218. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.-W.; Zhu, T.C.; Putt, M.E.; Solonenko, M.; Metz, J.; Dimofte, A.; Miles, J.; Fraker, D.L.; Glatstein, E.; Hahn, S.M.; et al. Broadband reflectance measurements of light penetration, blood oxygenation, hemoglobin concentration, and drug concentration in human intraperitoneal tissues before and after photodynamic therapy. J. Biomed. Opt. 2005. [Google Scholar] [CrossRef] [PubMed]
- Ong, Y.H.; Zhu, T.C. An analytic function for predicting light fluence rate of circular fields on a semi-infinite turbid medium. Opt. Express 2016, 24, 26261–26281. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML-Monte Carlo modeling of light transport in multi-layered tissues. Comput. Methods Programs Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Jacques, S.L.; Wang, L. Monte Carlo modeling of light transport in tissues. In Optical-Thermal Response of Laser-Irradiated Tissue; Welch, A.J., van Gemert, M.J.C., Eds.; Springer: Plenum, NY, USA, 1995; pp. 73–100. [Google Scholar]
- Prahl, S.A.; Keijzer, M.; Jacques, S.L.; Welch, A.J. A Monte Carlo model of light propagation in tissue. SPIE Inst. Ser. 1989, 5, 102–111. [Google Scholar]
- Wilson, B.C.; Adam, G. A Monte Carlo model for the absorption and flux distributions of light in tissue. Med. Phys. 1983, 10, 824–830. [Google Scholar] [CrossRef] [PubMed]
- Hahn, S.M.; Putt, M.E.; Metz, J.; Shin, D.B.; Rickter, E.; Menon, C.; Smith, D.; Glatstein, E.; Fraker, D.L.; Busch, T.M. Photofrin uptake in the tumor and normal tissues of patients receiving intraperitoneal photodynamic therapy. Clin. Cancer Res. 2006, 12, 5464–5470. [Google Scholar] [CrossRef] [PubMed]
- Georgakoudi, I.; Nichols, M.G.; Foster, T.H. The mechanism of photofrin photobleaching and its consequences for photodynamic dosimetry. Photochem. Photobiol. 1997, 65, 135–144. [Google Scholar] [CrossRef] [PubMed]
- Dysart, J.S.; Singh, G.; Patterson, M.S. Calculation of singlet oxygen dose from photosensitizer fluorescence and photobleaching during mTHPC photodynamic therapy of MLL cells. Photochem. Photobiol. 2005, 81, 196–205. [Google Scholar] [CrossRef] [PubMed]
- Lovell, J.F.; Liu, T.W.; Chen, J.; Zheng, G. Activatable Photosensitizers for imaging and therapy. Chem. Rev. 2010, 110, 2839–2857. [Google Scholar] [CrossRef] [PubMed]
- Mitra, S.; Foster, T.H. Photophysical parameters, photosensitizer retention and tissue optical properties completely account for the higher photodynamic efficacy of meso-tetra-hydroxyphenyl-chlorin vs. photofrin. Photochem. Photobiol. 2005, 81, 849–859. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, F.; Helman, W.P.; Ross, A.B. Rate constants for the decay and reactions of the lowest electronically excited singlet state of molecular oxygen in solution. An expanded and revised compilation. J. Phys. Chem. Ref. Data 1995, 24, 663–667. [Google Scholar] [CrossRef]
- Zhu, T.C.; Dimofte, A.; Hahn, S.M.; Lustig, R.A. Light dosimetry at tissue surfaces for small circular fields. Proc. SPIE 2003, 4952, 56–67. [Google Scholar]
- Weston, M.A.; Patterson, M.S. Calculation of singlet oxygen dose using explicit and implicit dose metrics during benzoporphyrin derivative monoacid ring A (BPD-MA)-PDT in vitro and correlation with MLL cell survival. Photochem. Photobiol. 2011, 87, 1129–1137. [Google Scholar] [CrossRef] [PubMed]
| Parameter | Definition | In Vitro | In Vivo |
|---|---|---|---|
| ε (cm−1·μM−1) | Photosensitizer extinction coefficient | 0.0035 at 632 nm (1) 0.0089 at 523 nm (1) | |
| β (μM) | Oxygen-quenching threshold concentration * | 11.9 [34] | |
| δ (μM) | Low-concentration correction | 25 ± 4.3 (2) | 33 [15] |
| ξ (cm2·mW−1·s−1) | Specific oxygen consumption rate | 10.3 × 10−3 (3) at 632 nm 24.8 × 10−3 (4) at 523 nm | 3.7 × 10−3 [34] at 632 nm 8.99 × 10−3 (5) at 523 nm |
| σ (μM−1) | Specific photobleaching ratio where σ = k1τΔ * | (6.6 ± 7) × 10−5 (2) | 7.6 × 10−5 [8,34] |
| τΔ (s) | Singlet oxygen lifetime * | (9.4 ± 0.2) × 10−6 (6) | 1.6 × 10−7 [35] |
| τt (s) | Triplet state lifetime * | (0.43 ± 0.03) × 10−6 (7) | 1.5 × 10−6 (7) |
| ΦΔ | Singlet oxygen quantum yield | 0.56 [36,37] | 0.20 [19] |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.M.; Penjweini, R.; Gemmell, N.R.; Veilleux, I.; McCarthy, A.; Buller, G.S.; Hadfield, R.H.; Wilson, B.C.; Zhu, T.C. A Comparison of Singlet Oxygen Explicit Dosimetry (SOED) and Singlet Oxygen Luminescence Dosimetry (SOLD) for Photofrin-Mediated Photodynamic Therapy. Cancers 2016, 8, 109. https://doi.org/10.3390/cancers8120109
Kim MM, Penjweini R, Gemmell NR, Veilleux I, McCarthy A, Buller GS, Hadfield RH, Wilson BC, Zhu TC. A Comparison of Singlet Oxygen Explicit Dosimetry (SOED) and Singlet Oxygen Luminescence Dosimetry (SOLD) for Photofrin-Mediated Photodynamic Therapy. Cancers. 2016; 8(12):109. https://doi.org/10.3390/cancers8120109
Chicago/Turabian StyleKim, Michele M., Rozhin Penjweini, Nathan R. Gemmell, Israel Veilleux, Aongus McCarthy, Gerald S. Buller, Robert H. Hadfield, Brian C. Wilson, and Timothy C. Zhu. 2016. "A Comparison of Singlet Oxygen Explicit Dosimetry (SOED) and Singlet Oxygen Luminescence Dosimetry (SOLD) for Photofrin-Mediated Photodynamic Therapy" Cancers 8, no. 12: 109. https://doi.org/10.3390/cancers8120109
APA StyleKim, M. M., Penjweini, R., Gemmell, N. R., Veilleux, I., McCarthy, A., Buller, G. S., Hadfield, R. H., Wilson, B. C., & Zhu, T. C. (2016). A Comparison of Singlet Oxygen Explicit Dosimetry (SOED) and Singlet Oxygen Luminescence Dosimetry (SOLD) for Photofrin-Mediated Photodynamic Therapy. Cancers, 8(12), 109. https://doi.org/10.3390/cancers8120109






