Using the Tissue Impulse Response Function to Streamline Fractionated MRgFUS-Induced Hyperthermia
Simple Summary
Abstract
1. Introduction
2. Material and Methods
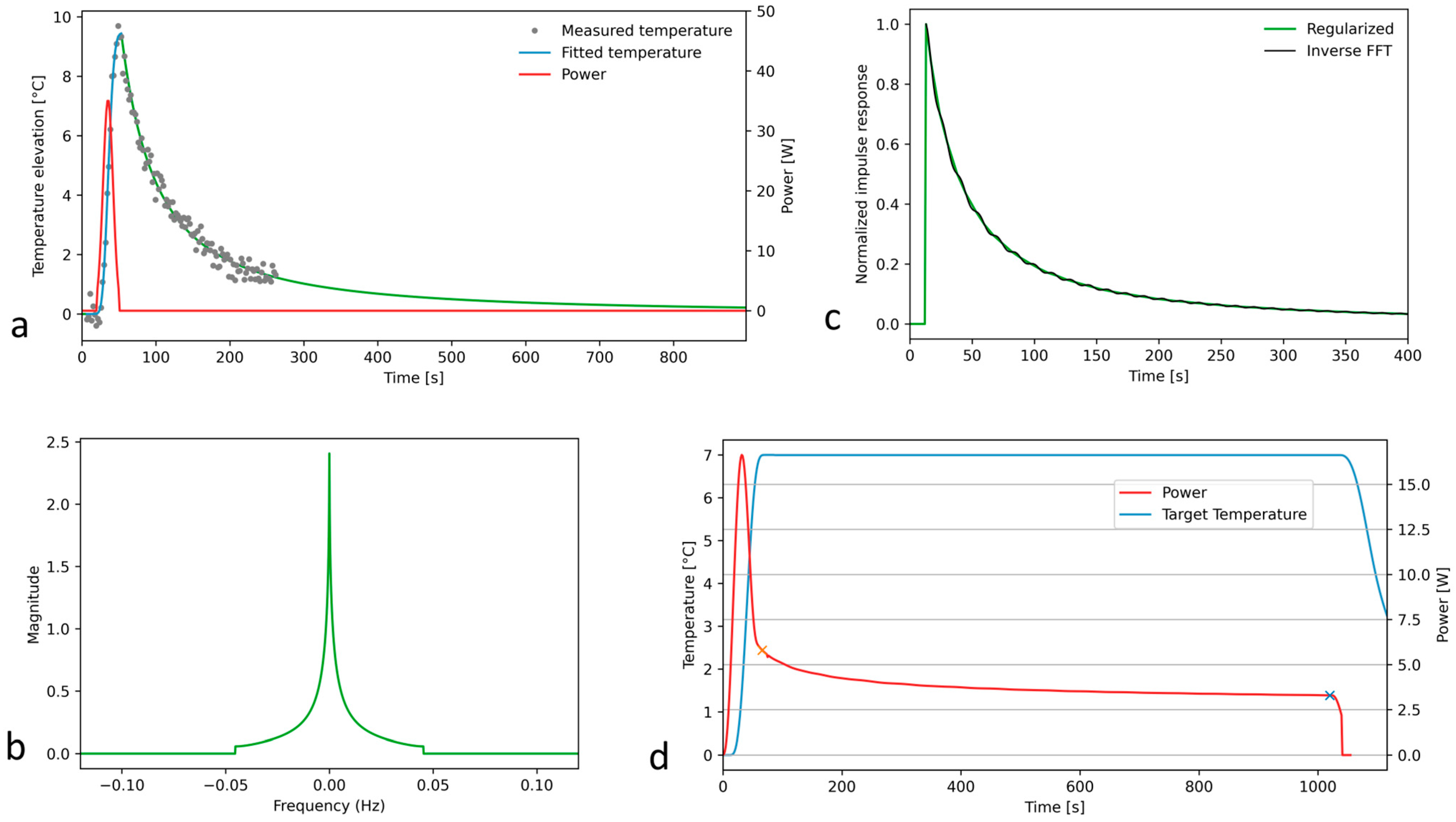
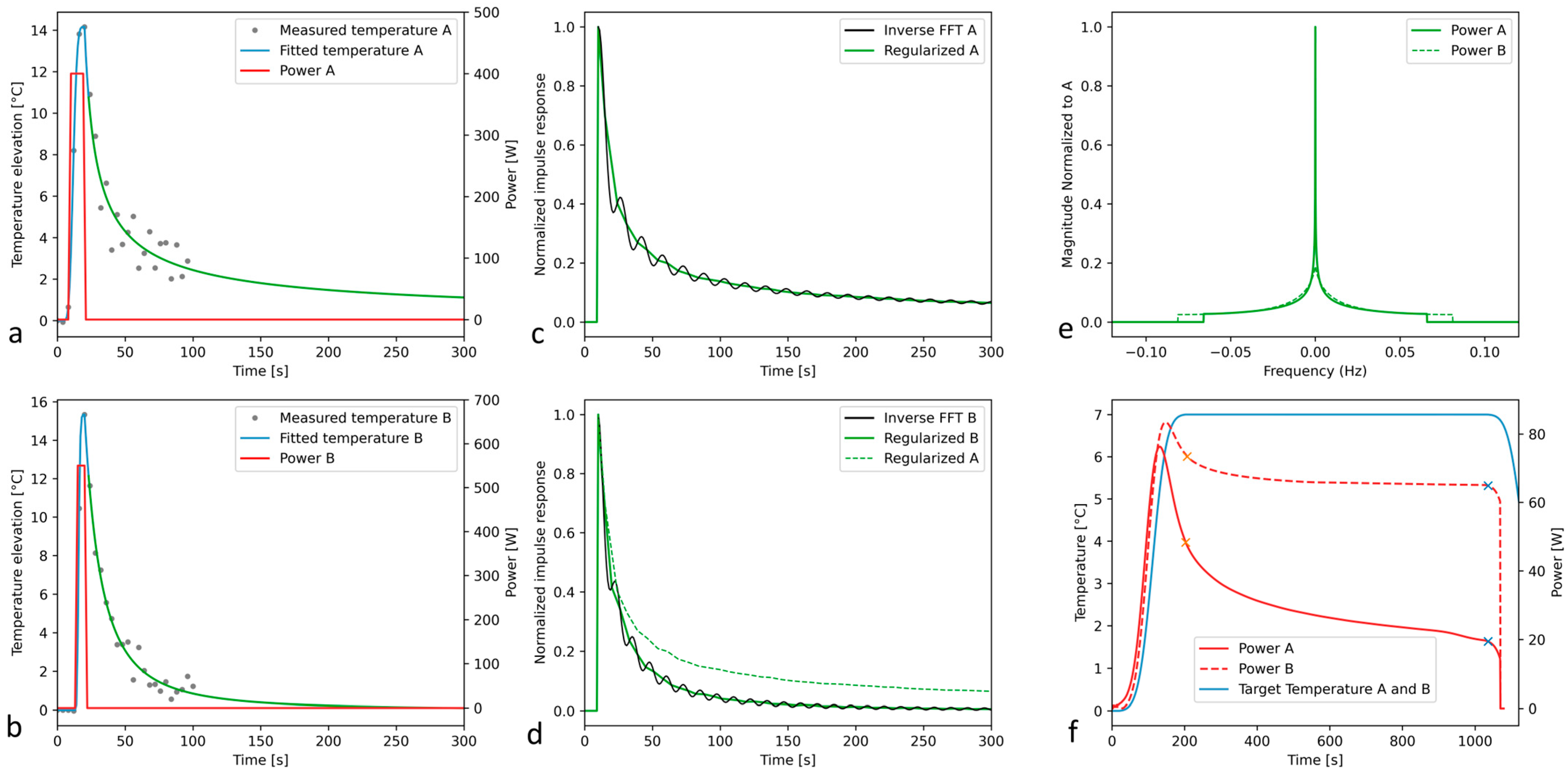
2.1. Theory
- The excitation of the system with a Gaussian input;
- Recording and denoising the MR thermometry data for this quasi-impulse response;
- The deconvolution of the quasi-impulse temperature response and the Gaussian acoustic input;
- The truncation of the 1D Fourier spectrum;
- Filtering out the truncation-related oscillations of Green’s function;
- The deconvolution of the target temperature elevation and Green’s function to obtain the prescribed acoustic power for steady-state long hyperthermia.
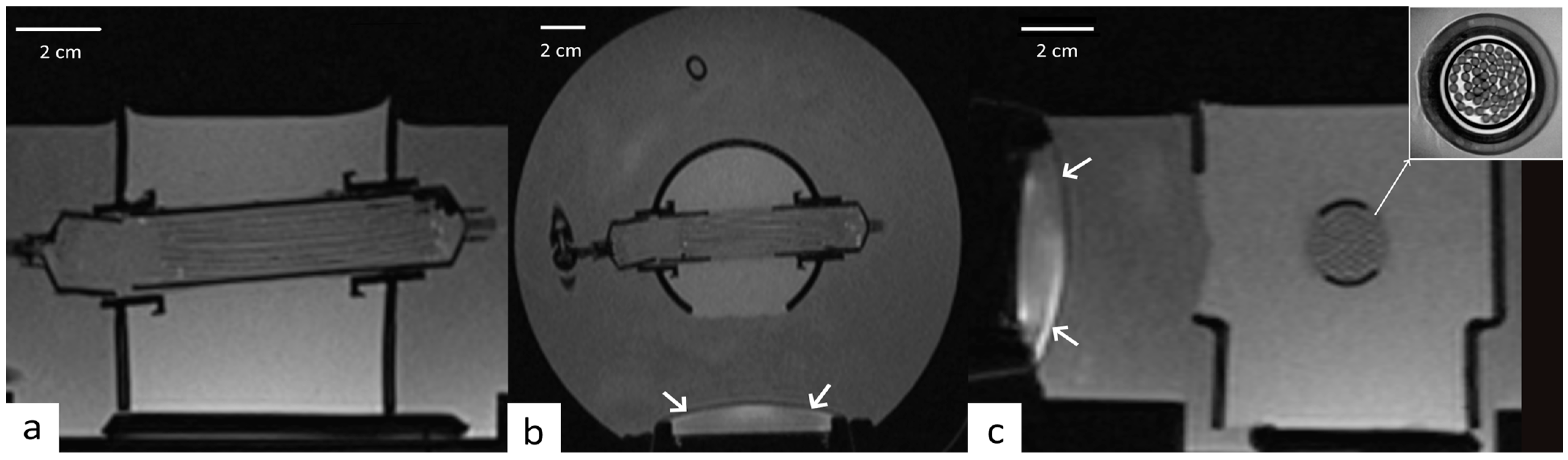
2.2. Perfused Phantom
2.3. MRI Guidance of Local Hyperthermia
2.4. Focused Ultrasound
2.5. Experimental Procedure on Perfused Phantom
2.6. Comparison Experiments
2.7. Retrospective Analysis of MRgFUS Thalamotomy Data
3. Results
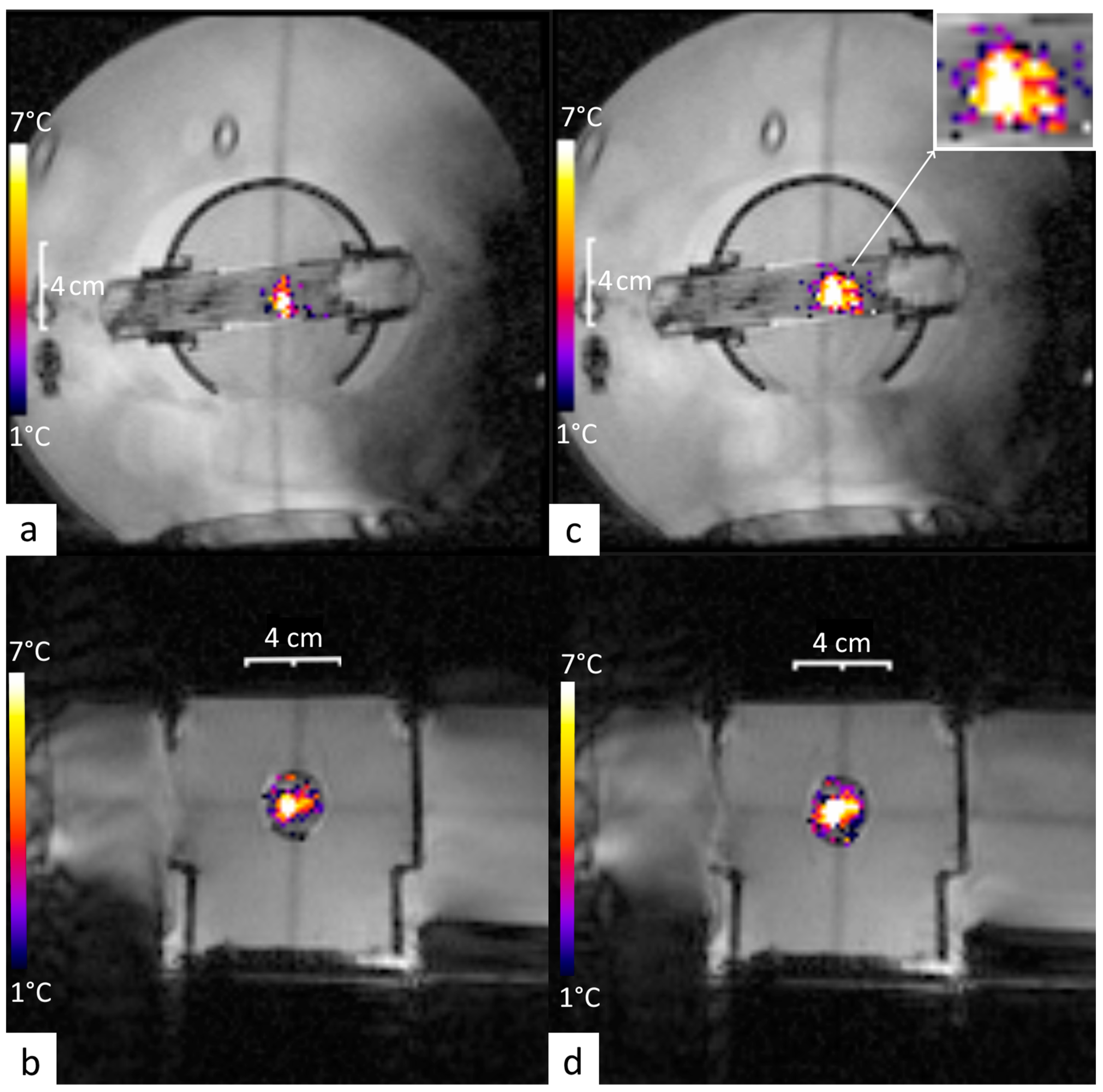
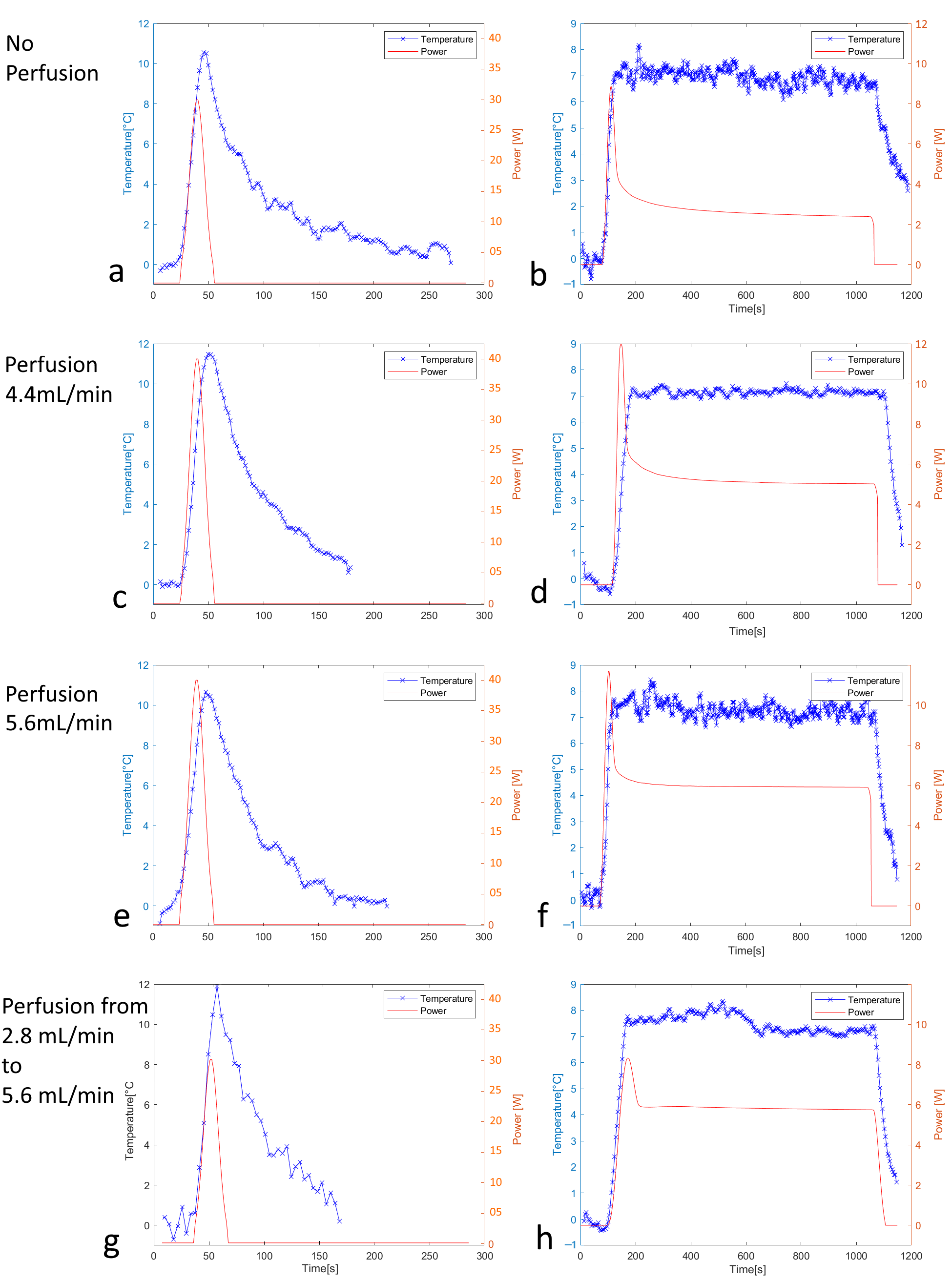
3.1. Off-Line Hyperthermia Control in Perfused Phantoms
3.2. Conventional On-Line Control Loop Versus the New Approach Using the Impulse Response Formalism
3.3. Retrospective Analysis of Clinical MRgFUS VIM–Thalamotomy Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MRgFUS | Magnetic Resonance-guided Focused Ultrasound |
| HT | Hyperthermia |
| RT | Radiation Therapy |
| MR | Magnetic Resonance |
| MRI | Magnetic Resonance Imaging |
| SAR | Specific Absorption Rate |
| HIFU | High-Intensity Focused Ultrasound |
| GGF | Generalized Gaussian Function |
| AUC | Area Under Curve |
| PTFE | Polytetrafluoroethylene |
| PRFS | Proton Resonance Frequency Shift |
| GRE | Gradient Echo |
| EPI | Echo-Planar Imaging |
| FOV | Field Of View |
| TR | Repetition Time |
| TE | Echo Time |
| BW | Bandwidth |
| TtoSS | Time to Steady-State |
References
- Datta, N.R.; Ordonez, S.G.; Gaipl, U.S.; Paulides, M.M.; Crezee, H.; Gellermann, J.; Marder, D.; Puric, E.; Bodis, S. Local hyperthermia combined with radiotherapy and-/or chemotherapy: Recent advances and promises for the future. Cancer Treat. Rev. 2015, 41, 742–753. [Google Scholar] [CrossRef]
- Dewhirst, M.W.; Vujaskovic, Z.; Jones, E.; Thrall, D. Re-setting the biologic rationale for thermal therapy. Int. J. Hyperth. 2005, 21, 779–790. [Google Scholar] [CrossRef]
- Crezee, J.; van Leeuwen, C.M.; Oei, A.L.; van Heerden, L.E.; Bel, A.; Stalpers, L.J.; Ghadjar, P.; Franken, N.A.; Kok, H.P. Biological modelling of the radiation dose escalation effect of regional hyperthermia in cervical cancer. Radiat. Oncol. 2016, 11, 14. [Google Scholar] [CrossRef] [PubMed]
- Issels, R.D. Hyperthermia adds to chemotherapy. Eur. J. Cancer 2008, 44, 2546–2554. [Google Scholar] [CrossRef]
- Kampinga, H.H.; Dikomey, E. Hyperthermic radiosensitization: Mode of action and clinical relevance. Int. J. Radiat. Biol. 2001, 77, 399–408. [Google Scholar] [CrossRef]
- Landon, C.D.; Park, J.Y.; Needham, D.; Dewhirst, M.W. Nanoscale Drug Delivery and Hyperthermia: The Materials Design and Preclinical and Clinical Testing of Low Temperature-Sensitive Liposomes Used in Combination with Mild Hyperthermia in the Treatment of Local Cancer. Open Nanomed. J. 2011, 3, 38–64. [Google Scholar] [CrossRef]
- Vujaskovic, Z.; Song, C.W. Physiological mechanisms underlying heat-induced radiosensitization. Int. J. Hyperth. 2004, 20, 163–174. [Google Scholar] [CrossRef]
- Benfante, V.; Stefano, A.; Ali, M.; Laudicella, R.; Arancio, W.; Cucchiara, A.; Caruso, F.; Cammarata, F.P.; Coronnello, C.; Russo, G.; et al. An Overview of In Vitro Assays of (64)Cu-, (68)Ga-, (125)I-, and (99m)Tc-Labelled Radiopharmaceuticals Using Radiometric Counters in the Era of Radiotheranostics. Diagnostics 2023, 13, 1210. [Google Scholar] [CrossRef]
- Van Dieren, L.; Quisenaerts, T.; Licata, M.; Beddok, A.; Lellouch, A.G.; Ysebaert, D.; Saldien, V.; Peeters, M.; Gorbaslieva, I. Combined Radiotherapy and Hyperthermia: A Systematic Review of Immunological Synergies for Amplifying Radiation-Induced Abscopal Effects. Cancers 2024, 16, 3656. [Google Scholar] [CrossRef] [PubMed]
- Kaur, P.; Hurwitz, M.D.; Krishnan, S.; Asea, A. Combined hyperthermia and radiotherapy for the treatment of cancer. Cancers 2011, 3, 3799–3823. [Google Scholar] [CrossRef]
- Zhu, L.; Lam, D.; Pacia, C.P.; Gach, H.M.; Partanen, A.; Talcott, M.R.; Greco, S.C.; Zoberi, I.; Hallahan, D.E.; Chen, H.; et al. Characterization of magnetic resonance-guided high-intensity focused ultrasound (MRgHIFU)-induced large-volume hyperthermia in deep and superficial targets in a porcine model. Int. J. Hyperth. 2020, 37, 1159–1173. [Google Scholar] [CrossRef] [PubMed]
- Petrusca, L.; Viallon, M.; Breguet, R.; Terraz, S.; Manasseh, G.; Auboiroux, V.; Goget, T.; Baboi, L.; Gross, P.; Sekins, K.M.; et al. An experimental model to investigate the targeting accuracy of MR-guided focused ultrasound ablation in liver. J. Transl. Med. 2014, 12, 12. [Google Scholar] [CrossRef] [PubMed]
- Baust, J.M.; Rabin, Y.; Polascik, T.J.; Santucci, K.L.; Snyder, K.K.; Van Buskirk, R.G.; Baust, J.G. Defeating Cancers’ Adaptive Defensive Strategies Using Thermal Therapies: Examining Cancer’s Therapeutic Resistance, Ablative, and Computational Modeling Strategies as a means for Improving Therapeutic Outcome. Technol. Cancer Res. Treat. 2018, 17, 1533033818762207. [Google Scholar] [CrossRef] [PubMed]
- Melodelima, D.; Salomir, R.; Mougenot, C.; Prat, F.; Theillere, Y.; Moonen, C.; Cathignol, D. Intraluminal ultrasound applicator compatible with magnetic resonance imaging “real-time” temperature mapping for the treatment of oesophageal tumours: An ex vivo study. Med. Phys. 2004, 31, 236–244. [Google Scholar] [CrossRef]
- Moonen, C.T.; Quesson, B.; Salomir, R.; Vimeux, F.C.; de Zwart, J.A.; van Vaals, J.J.; Grenier, N.; Palussiere, J. Thermal therapies in interventional MR imaging. Focused ultrasound. Neuroimaging Clin. N. Am. 2001, 11, 737–747. [Google Scholar] [PubMed]
- Ellis, S.; Rieke, V.; Kohi, M.; Westphalen, A.C. Clinical applications for magnetic resonance guided high intensity focused ultrasound (MRgHIFU): Present and future. J. Med. Imaging Radiat. Oncol. 2013, 57, 391–399. [Google Scholar] [CrossRef]
- Zhu, L.; Huang, Y.; Lam, D.; Gach, H.M.; Zoberi, I.; Hallahan, D.E.; Grigsby, P.W.; Chen, H.; Altman, M.B. Targetability of cervical cancer by magnetic resonance-guided high-intensity focused ultrasound (MRgHIFU)-mediated hyperthermia (HT) for patients receiving radiation therapy. Int. J. Hyperth. 2021, 38, 498–510. [Google Scholar] [CrossRef]
- Zhu, L.; Partanen, A.; Talcott, M.R.; Gach, H.M.; Greco, S.C.; Henke, L.E.; Contreras, J.A.; Zoberi, I.; Hallahan, D.E.; Chen, H.; et al. Feasibility and safety assessment of magnetic resonance-guided high-intensity focused ultrasound (MRgHIFU)-mediated mild hyperthermia in pelvic targets evaluated using an in vivo porcine model. Int. J. Hyperth. 2019, 36, 1147–1159. [Google Scholar] [CrossRef] [PubMed]
- Gorny, K.R.; Hangiandreou, N.J.; Hesley, G.K.; Gostout, B.S.; McGee, K.P.; Felmlee, J.P. MR guided focused ultrasound: Technical acceptance measures for a clinical system. Phys. Med. Biol. 2006, 51, 3155–3173. [Google Scholar] [CrossRef]
- Mohr-Sasson, A.; Machtinger, R.; Mashiach, R.; Nir, O.; Inbar, Y.; Maliyanker, N.; Goldenberg, M.; Rabinovici, J. Long-term outcome of MR-guided focused ultrasound treatment and laparoscopic myomectomy for symptomatic uterine fibroid tumors. Am. J. Obstet. Gynecol. 2018, 219, 375.e1–375.e7. [Google Scholar] [CrossRef]
- Quinn, S.D.; Vedelago, J.; Gedroyc, W.; Regan, L. Safety and five-year re-intervention following magnetic resonance-guided focused ultrasound (MRgFUS) for uterine fibroids. Eur. J. Obstet. Gynecol. Reprod. Biol. 2014, 182, 247–251. [Google Scholar] [CrossRef]
- Peek, M.C.; Ahmed, M.; Napoli, A.; ten Haken, B.; McWilliams, S.; Usiskin, S.I.; Pinder, S.E.; van Hemelrijck, M.; Douek, M. Systematic review of high-intensity focused ultrasound ablation in the treatment of breast cancer. Br. J. Surg. 2015, 102, 873–882; discussion 882. [Google Scholar] [CrossRef] [PubMed]
- Peek, M.C.L.; Ahmed, M.; Scudder, J.; Baker, R.; Charalampoudis, P.; Pinder, S.E.; Douek, M.; Collaborators, H.-F. High-intensity focused ultrasound in the treatment of breast fibroadenomata (HIFU-F trial). Int. J. Hyperth. 2018, 34, 1002–1009. [Google Scholar] [CrossRef] [PubMed]
- Ghai, S.; Perlis, N.; Lindner, U.; Hlasny, E.; Haider, M.A.; Finelli, A.; Zlotta, A.R.; Kulkarni, G.S.; van der Kwast, T.H.; McCluskey, S.A.; et al. Magnetic resonance guided focused high frequency ultrasound ablation for focal therapy in prostate cancer—Phase 1 trial. Eur. Radiol. 2018, 28, 4281–4287. [Google Scholar] [CrossRef]
- Jolesz, F.A. MRI-guided focused ultrasound surgery. Annu. Rev. Med. 2009, 60, 417–430. [Google Scholar] [CrossRef]
- Marien, A.; Gill, I.; Ukimura, O.; Betrouni, N.; Villers, A. Target ablation—Image-guided therapy in prostate cancer. Urol. Oncol. 2014, 32, 912–923. [Google Scholar] [CrossRef] [PubMed]
- Rau, B.; Gaestel, M.; Wust, P.; Stahl, J.; Mansmann, U.; Schlag, P.M.; Benndorf, R. Preoperative treatment of rectal cancer with radiation, chemotherapy and hyperthermia: Analysis of treatment efficacy and heat-shock response. Radiat. Res. 1999, 151, 479–488. [Google Scholar] [CrossRef] [PubMed]
- Rueff, L.E.; Raman, S.S. Clinical and Technical Aspects of MR-Guided High Intensity Focused Ultrasound for Treatment of Symptomatic Uterine Fibroids. Semin. Interv. Radiol. 2013, 30, 347–353. [Google Scholar] [CrossRef]
- Zhou, Y.F. High intensity focused ultrasound in clinical tumor ablation. World J. Clin. Oncol. 2011, 2, 8–27. [Google Scholar] [CrossRef]
- Dababou, S.; Marrocchio, C.; Scipione, R.; Erasmus, H.P.; Ghanouni, P.; Anzidei, M.; Catalano, C.; Napoli, A. High-Intensity Focused Ultrasound for Pain Management in Patients with Cancer. Radiographics 2018, 38, 603–623. [Google Scholar] [CrossRef]
- Huisman, M.; Verkooijen, H.M.; van der Linden, Y.M.; van den Bosch, M.A.; van Vulpen, M. Effectiveness of Repeat Radiotherapy for Painful Bone Metastases in Clinical Practice: A 10 Year Historical Cohort Study. Clin. Oncol. 2015, 27, 472–478. [Google Scholar] [CrossRef]
- Hurwitz, M.D.; Ghanouni, P.; Kanaev, S.V.; Iozeffi, D.; Gianfelice, D.; Fennessy, F.M.; Kuten, A.; Meyer, J.E.; LeBlang, S.D.; Roberts, A.; et al. Magnetic resonance-guided focused ultrasound for patients with painful bone metastases: Phase III trial results. J. Natl. Cancer Inst. 2014, 106, dju082. [Google Scholar] [CrossRef] [PubMed]
- Napoli, A.; Anzidei, M.; Marincola, B.C.; Brachetti, G.; Ciolina, F.; Cartocci, G.; Marsecano, C.; Zaccagna, F.; Marchetti, L.; Cortesi, E.; et al. Primary pain palliation and local tumor control in bone metastases treated with magnetic resonance-guided focused ultrasound. Investig. Radiol. 2013, 48, 351–358. [Google Scholar] [CrossRef] [PubMed]
- Frazier, N.; Payne, A.; de Bever, J.; Dillon, C.; Panda, A.; Subrahmanyam, N.; Ghandehari, H. High intensity focused ultrasound hyperthermia for enhanced macromolecular delivery. J. Control. Release 2016, 241, 186–193. [Google Scholar] [CrossRef] [PubMed]
- Frazier, N.; Ghandehari, H. Hyperthermia approaches for enhanced delivery of nanomedicines to solid tumors. Biotechnol. Bioeng. 2015, 112, 1967–1983. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Partanen, A.; Pichardo, S.; Staruch, R.; Perry, K.; McGuffin, M.; Huang, Y.; Chan, K.K.; Wong, S.; Czarnota, G.; et al. Mild hyperthermia with magnetic resonance- guided high intensity focused ultrasound combined with salvage chemoradiation for recurrent rectal cancer. Int. J. Hyperth. 2024, 41, 2365385. [Google Scholar] [CrossRef] [PubMed]
- Guillemin, P.C.; Sinden, D.; M’Rad, Y.; Schwenke, M.; Le Guevelou, J.; Uiterwijk, J.W.E.; Lorton, O.; Scheffler, M.; Poletti, P.A.; Jenne, J.; et al. A Novel Concept of Transperineal Focused Ultrasound Transducer for Prostate Cancer Local Deep Hyperthermia Treatments. Cancers 2022, 15, 163. [Google Scholar] [CrossRef]
- Piras, A.; Corso, R.; Benfante, V.; Ali, M.; Laudicella, R.; Alongi, P.; D’Aviero, A.; Cusumano, D.; Boldrini, L.; Salvaggio, G. Artificial Intelligence and Statistical Models for the Prediction of Radiotherapy Toxicity in Prostate Cancer: A Systematic Review. Appl. Sci. 2024, 14, 10947. [Google Scholar] [CrossRef]
- Guillemin, P.C. Magnetic resonance-guided ultrasound hyperthermia for prostate cancer radiotherapy: An immobilization device embedding the ultrasound applicator. 3D Print. Med. 2021, 6, 55–67. [Google Scholar] [CrossRef]
- Gao, B.; Langer, S.; Corry, P.M. Application of the time-dependent Green’s function and Fourier transforms to the solution of the bioheat equation. Int. J. Hyperth. 1995, 11, 267–285. [Google Scholar] [CrossRef] [PubMed]
- Yeung, C.J.; Atalar, E. A Green’s function approach to local rf heating in interventional MRI. Med. Phys. 2001, 28, 826–832. [Google Scholar] [CrossRef] [PubMed]
- Kou, H.S.; Shih, T.C.; Lin, W.L. Effect of the directional blood flow on thermal dose distribution during thermal therapy: An application of a Green’s function based on the porous model. Phys. Med. Biol. 2003, 48, 1577–1589. [Google Scholar] [CrossRef] [PubMed]
- Freeman, N.J.; Odeen, H.; Parker, D.L. 3D-specific absorption rate estimation from high-intensity focused ultrasound sonications using the Green’s function heat kernel. Med. Phys. 2018, 45, 3109–3119. [Google Scholar] [CrossRef] [PubMed]
- Hofstetter, L.W.; Odeen, H.; Bolster, B.D., Jr.; Christensen, D.A.; Payne, A.; Parker, D.L. Magnetic resonance shear wave elastography using transient acoustic radiation force excitations and sinusoidal displacement encoding. Phys. Med. Biol. 2021, 66, 055027. [Google Scholar] [CrossRef] [PubMed]
- Alex, D.; Ronit, B.; Vincent, P.H.; Shlomo, S. Analytical properties of generalized Gaussian distributions. J. Stat. Distrib. Appl. 2018, 5, 6. [Google Scholar] [CrossRef]
- Adam, H.A. Green’s Function for the Heat Equation. Fluid Mech. 2017, 4, 2. [Google Scholar] [CrossRef]
- Jorgensen, C.S.; Paaske, W.P. Physical and mechanical properties of ePTFE stretch vascular grafts determined by time-resolved scanning acoustic microscopy. Eur. J. Vasc. Endovasc. Surg. 1998, 15, 416–422. [Google Scholar] [CrossRef]
- Brandner, D.M.; Cai, X.; Foiret, J.; Ferrara, K.W.; Zagar, B.G. Estimation of Tissue Attenuation from Ultrasonic B-Mode Images-Spectral-Log-Difference and Method-of-Moments Algorithms Compared. Sensors 2021, 21, 2548. [Google Scholar] [CrossRef]
- Buchs, J.B.; Buhler, L.; Morel, P. A new disposable perfusion machine, nuclear magnetic resonance compatible, to test the marginal organs and the kidneys from non-heart-beating donors before transplantation. Interact. Cardiovasc. Thorac. Surg. 2007, 6, 421–424. [Google Scholar] [CrossRef]
- Lorton, O.; Guillemin, P.; Holman, R.; Desgranges, S.; Gui, L.; Crowe, L.A.; Terraz, S.; Nastasi, A.; Lazeyras, F.; Contino-Pepin, C.; et al. Enhancement of HIFU thermal therapy in perfused tissue models using micron-sized FTAC-stabilized PFOB-core endovascular sonosensitizers. Int. J. Hyperth. 2020, 37, 1116–1130. [Google Scholar] [CrossRef]
- Holman, R.; Gui, L.; Lorton, O.; Guillemin, P.; Desgranges, S.; Contino-Pepin, C.; Salomir, R. PFOB sonosensitive microdroplets: Determining their interaction radii with focused ultrasound using MR thermometry and a Gaussian convolution kernel computation. Int. J. Hyperth. 2022, 39, 108–119. [Google Scholar] [CrossRef] [PubMed]
- van Vulpen, M.; Raaymakers, B.W.; de Leeuw, A.A.; van de Kamer, J.B.; van Moorselaar, R.J.; Hobbelink, M.G.; Battermann, J.J.; Lagendijk, J.J. Prostate perfusion in patients with locally advanced prostate carcinoma treated with different hyperthermia techniques. J. Urol. 2002, 168, 1597–1602. [Google Scholar] [CrossRef] [PubMed]
- Guillemin, P.C.; Gui, L.; Lorton, O.; Zilli, T.; Crowe, L.A.; Desgranges, S.; Montet, X.; Terraz, S.; Miralbell, R.; Salomir, R.; et al. Mild hyperthermia by MR-guided focused ultrasound in an ex vivo model of osteolytic bone tumour: Optimization of the spatio-temporal control of the delivered temperature. J. Transl. Med. 2019, 17, 350. [Google Scholar] [CrossRef] [PubMed]
- Heinonen, I.; Brothers, R.M.; Kemppainen, J.; Knuuti, J.; Kalliokoski, K.K.; Crandall, C.G. Local heating, but not indirect whole body heating, increases human skeletal muscle blood flow. J. Appl. Physiol. 2011, 111, 818–824. [Google Scholar] [CrossRef]
- Horsman, M.R. Tissue physiology and the response to heat. Int. J. Hyperth. 2006, 22, 197–203. [Google Scholar] [CrossRef] [PubMed]
- Pearson, J.; Low, D.A.; Stohr, E.; Kalsi, K.; Ali, L.; Barker, H.; Gonzalez-Alonso, J. Hemodynamic responses to heat stress in the resting and exercising human leg: Insight into the effect of temperature on skeletal muscle blood flow. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2011, 300, R663–R673. [Google Scholar] [CrossRef] [PubMed]
- Kok, H.P.; Crezee, J.; Franken, N.A.; Stalpers, L.J.; Barendsen, G.W.; Bel, A. Quantifying the combined effect of radiation therapy and hyperthermia in terms of equivalent dose distributions. Int. J. Radiat. Oncol. Biol. Phys. 2014, 88, 739–745. [Google Scholar] [CrossRef]
- Delabrousse, E.; Salomir, R.; Birer, A.; Paquet, C.; Mithieux, F.; Chapelon, J.Y.; Cotton, F.; Lafon, C. Automatic temperature control for MR-guided interstitial ultrasound ablation in liver using a percutaneous applicator: Ex vivo and in vivo initial studies. Magn. Reson. Med. 2010, 63, 667–679. [Google Scholar] [CrossRef]
- Zou, X.; Dong, H.; Qian, S.Y. Influence of dynamic tissue properties on temperature elevation and lesions during HIFU scanning therapy: Numerical simulation. Chin. Phys. B 2020, 29, 034305. [Google Scholar] [CrossRef]

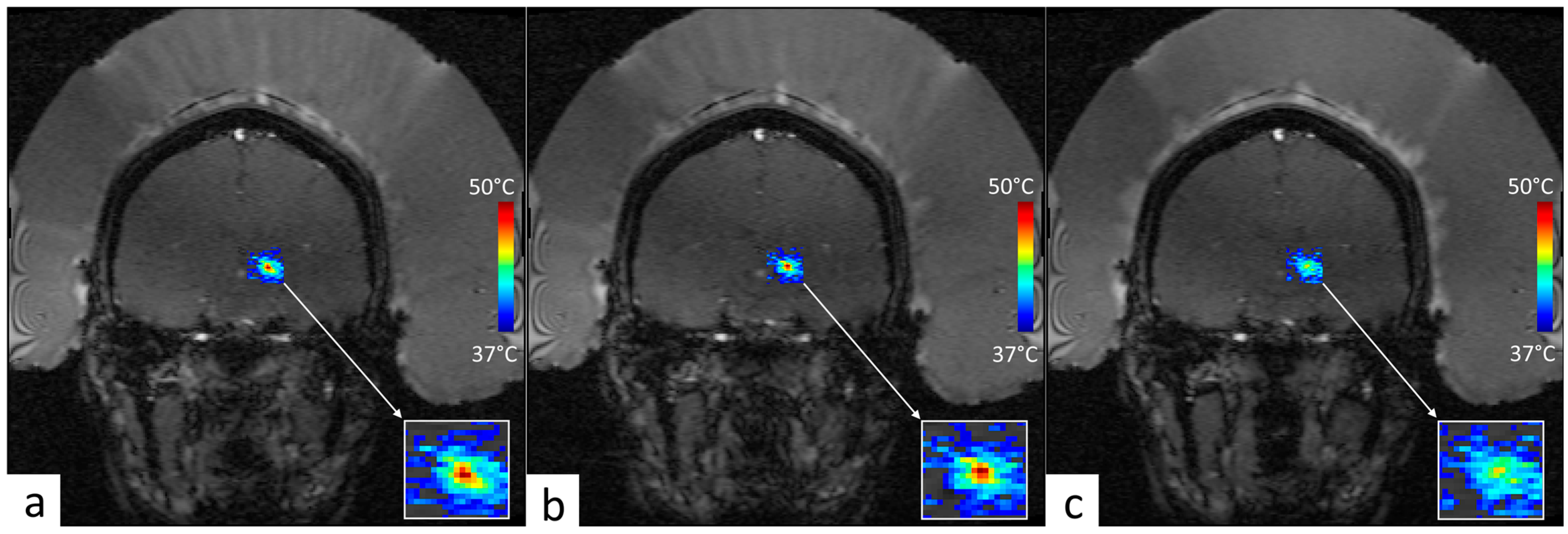
| #ID | Age | Skull Density Ratio | Number of Active Elements | Active Surface of Transducer [cm2] | Electronic Steering ML, AP, SI [mm] | Measured Acoustic Power [W] | Sonication Duration [s] | Measured Energy [kJ] | Peak Temperature Elevation [°C] |
|---|---|---|---|---|---|---|---|---|---|
| A | 76 | 0.56 | 933 | 347.8 | 0, 0, 0 | 395.8 | 12.0 | 4.38 | 14.2 |
| B | 48 | 0.45 | 912 | 335.7 | −1.6, −0.5, 0.5 | 540.3 | 8.0 | 3.81 | 15.3 |
| Perfusion | N | Mean (°C) | STD (°C) | Drift (10−3 °C/s) (Min–Max) | TtoSS (Sampling Points) | TtoSS(s) |
|---|---|---|---|---|---|---|
| no | 10 | 6.94 | 0.35 | 0.6 (0.2–1.4) | 22 | 59.4 |
| low | 10 | 7.29 | 0.32 | 0.7 (0.3–1.4) | 16 | 43.2 |
| high | 10 | 7.09 | 0.33 | 0.9 (0.4–1.6) | 15 | 40.5 |
| Perfusion | N | Mean (°C) | STD (°C) | Drift (10−3 °C/s) (Min–Max) | TtoSS (Sampling Points) | TtoSS (s) |
|---|---|---|---|---|---|---|
| no | 5 | 7.08 | 0.65 | 7.0 (1.8–9.6) | 68 | 183.6 |
| low | 5 | 8.03 | 0.72 | 8.3 (0.9–13.0) | 49 | 132.3 |
| high | 5 | 8.29 | 1.06 | 8.3 (3.6–9.2) | 51 | 140.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guillemin, P.C.; M’Rad, Y.; Dipasquale, G.; Lorton, O.; Fleury, V.; Momjian, S.; Borich, A.; Crowe, L.A.; Zilli, T.; Boudabbous, S.; et al. Using the Tissue Impulse Response Function to Streamline Fractionated MRgFUS-Induced Hyperthermia. Cancers 2025, 17, 515. https://doi.org/10.3390/cancers17030515
Guillemin PC, M’Rad Y, Dipasquale G, Lorton O, Fleury V, Momjian S, Borich A, Crowe LA, Zilli T, Boudabbous S, et al. Using the Tissue Impulse Response Function to Streamline Fractionated MRgFUS-Induced Hyperthermia. Cancers. 2025; 17(3):515. https://doi.org/10.3390/cancers17030515
Chicago/Turabian StyleGuillemin, Pauline C., Yacine M’Rad, Giovanna Dipasquale, Orane Lorton, Vanessa Fleury, Shahan Momjian, Anna Borich, Lindsey A. Crowe, Thomas Zilli, Sana Boudabbous, and et al. 2025. "Using the Tissue Impulse Response Function to Streamline Fractionated MRgFUS-Induced Hyperthermia" Cancers 17, no. 3: 515. https://doi.org/10.3390/cancers17030515
APA StyleGuillemin, P. C., M’Rad, Y., Dipasquale, G., Lorton, O., Fleury, V., Momjian, S., Borich, A., Crowe, L. A., Zilli, T., Boudabbous, S., & Salomir, R. (2025). Using the Tissue Impulse Response Function to Streamline Fractionated MRgFUS-Induced Hyperthermia. Cancers, 17(3), 515. https://doi.org/10.3390/cancers17030515







