Investigating the Limits of Predictability of Magnetic Resonance Imaging-Based Mathematical Models of Tumor Growth
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Biophysical Model of Tumor Growth and Angiogenesis
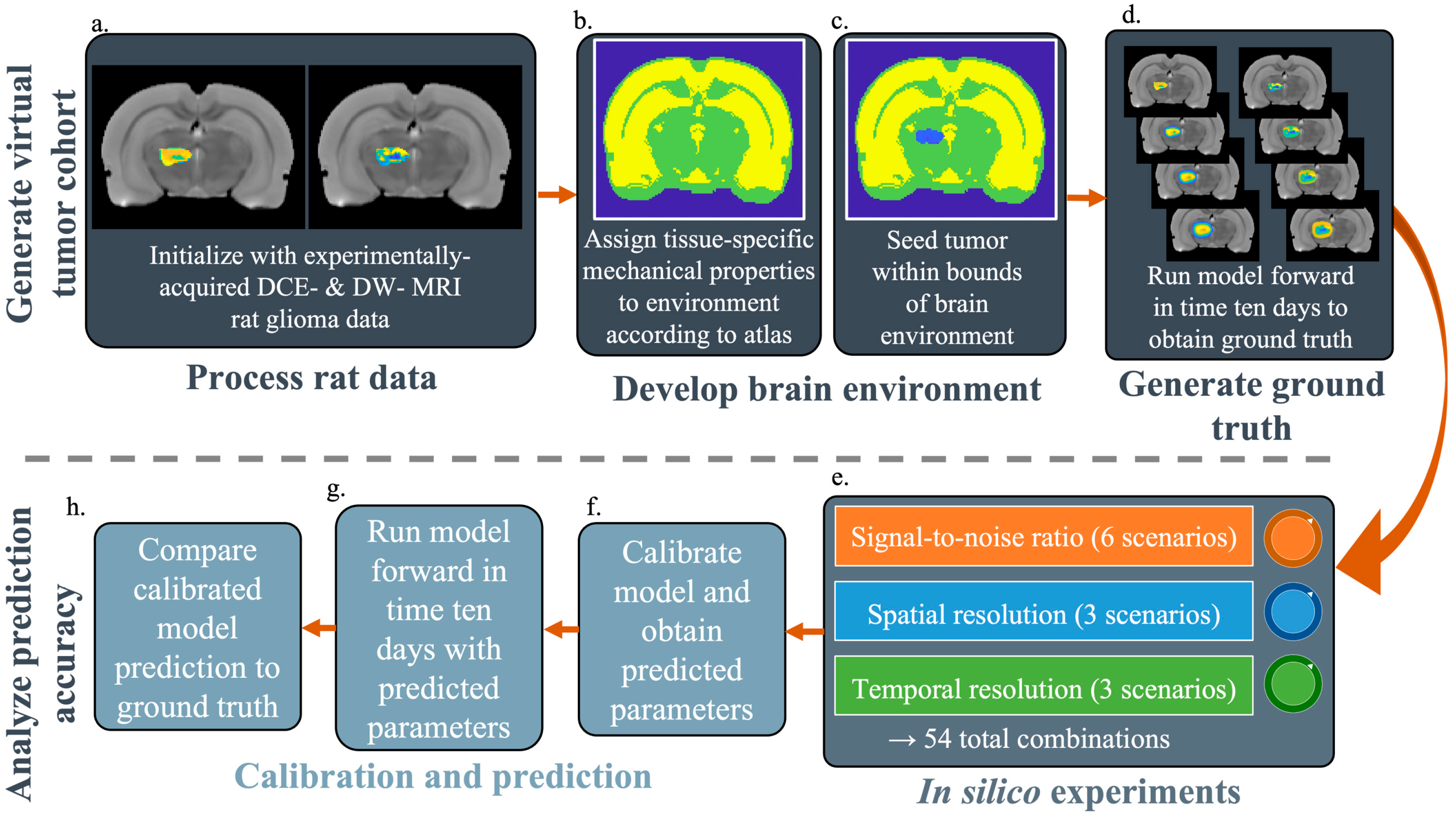
2.2. Generate Virtual Tumor Cohort for In Silico Experiments
2.2.1. Experimental Data Used to Initialize the Simulations
2.2.2. Establishing the Computational Domain
2.2.3. Generating SR-Specific Ground Truth Tumors to Compare Against the Model Predictions
2.3. Quantifying the Accuracy of Model Predictions for Specific SNR, SR, and TR Combinations
2.3.1. In Silico Experiments
2.3.2. Calibration and Prediction
2.4. Error Quantification and Statistical Analyses
3. Results
3.1. Representative Ground Truth Images
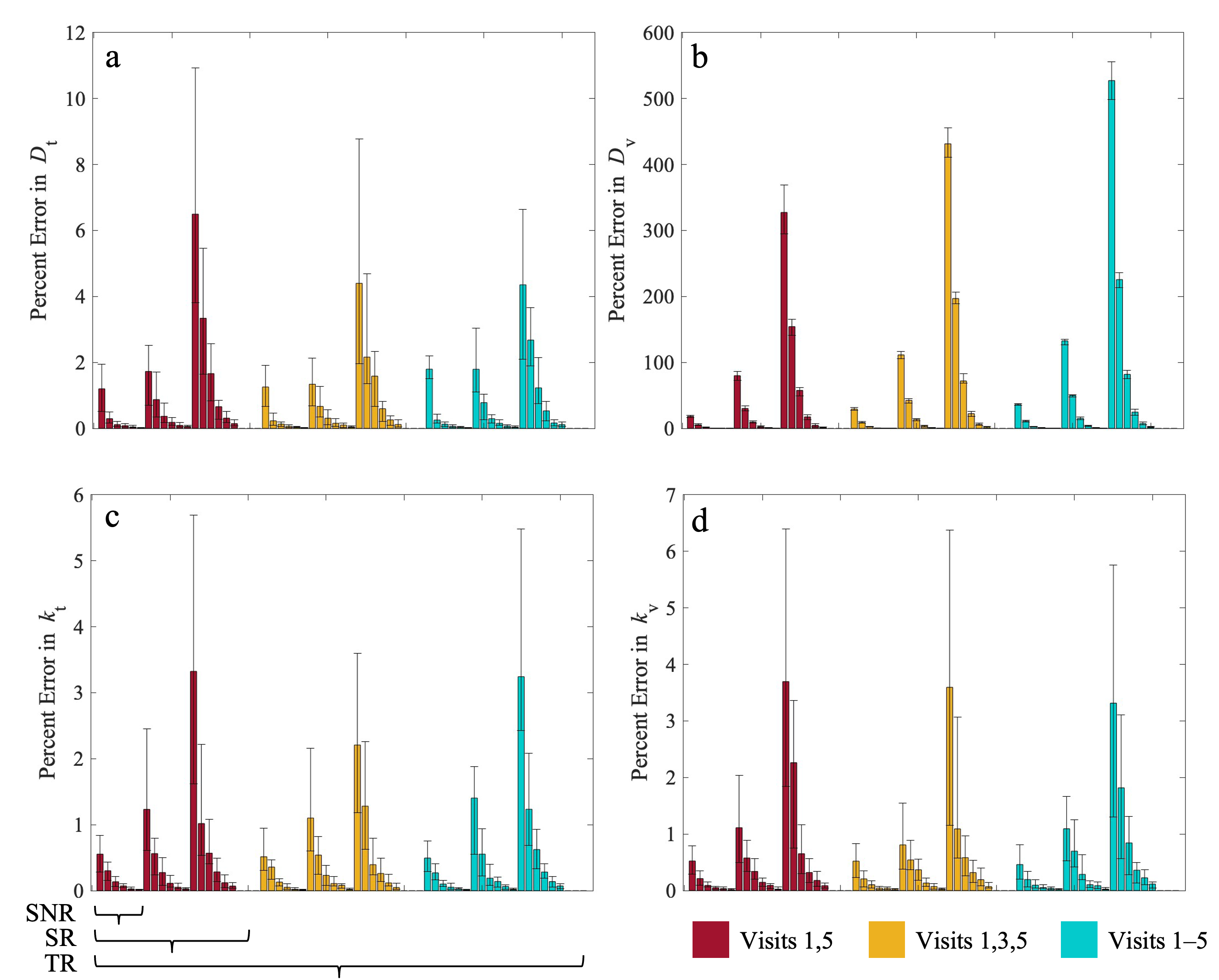
3.2. Error in Estimated Parameters
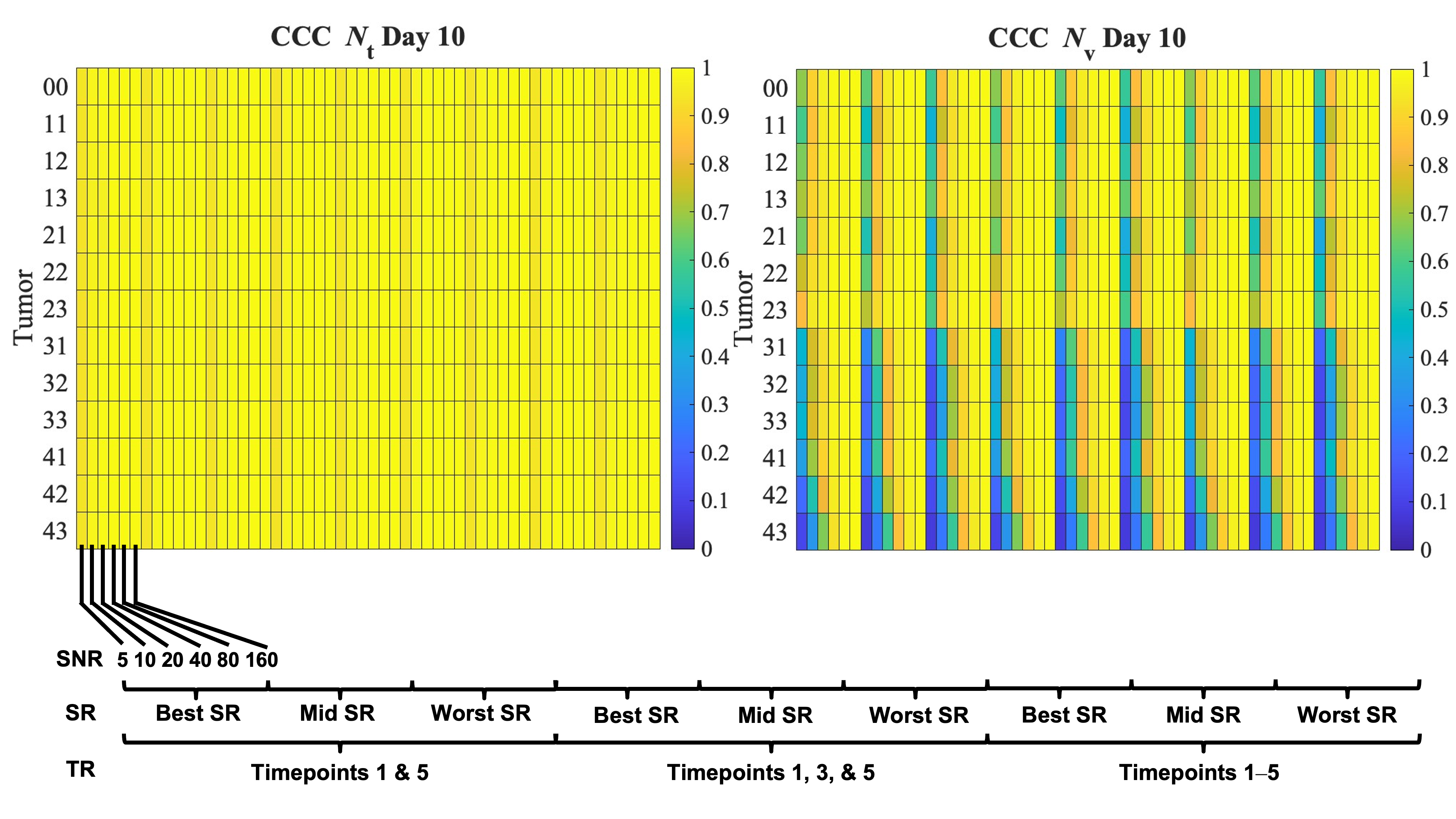
3.3. Error in Tumor Growth Predictions
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SNR | Signal-to-noise ratio |
| SR | Spatial resolution |
| TR | Temporal resolution |
| MRI | Magnetic resonance imaging |
| CCC | Concordance correlation coefficient |
References
- Noiphithak, R.; Veerasarn, K. Clinical Predictors for Survival and Treatment Outcome of High-Grade Glioma in Prasat Neurological Institute. Asian J. Neurosurg. 2017, 12, 28–33. [Google Scholar] [CrossRef]
- Rutter, E.M.; Banks, H.T.; Flores, K.B. Estimating Intratumoral Heterogeneity from Spatiotemporal Data. J. Math. Biol. 2018, 77, 1999–2022. [Google Scholar] [CrossRef]
- Phillips, C.M.; Lima, E.A.B.F.; Wu, C.; Jarrett, A.M.; Zhou, Z.; Elshafeey, N.; Ma, J.; Rauch, G.M.; Yankeelov, T.E. Assessing the Identifiability of Model Selection Frameworks for the Prediction of Patient Outcomes in the Clinical Breast Cancer Setting. J. Comput. Sci. 2023, 69, 102006. [Google Scholar] [CrossRef] [PubMed]
- Hiremath, K.C.; Atakishi, K.; Lima, E.A.B.F.; Farhat, M.; Panthi, B.; Langshaw, H.; Shanker, M.D.; Talpur, W.; Thrower, S.; Goldman, J.; et al. Identifiability and Model Selection Frameworks for Models of High-Grade Glioma Response to Chemoradiation. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2025, 383, 20240212. [Google Scholar] [CrossRef]
- Le, M.; Delingette, H.; Kalpathy-Cramer, J.; Gerstner, E.R.; Batchelor, T.; Unkelbach, J.; Ayache, N. Personalized Radiotherapy Planning Based on a Computational Tumor Growth Model. IEEE Trans. Med. Imaging 2017, 36, 815–825. [Google Scholar] [CrossRef]
- Hawkins-Daarud, A.; Johnston, S.K.; Swanson, K.R. Quantifying Uncertainty and Robustness in a Biomathematical Model–Based Patient-Specific Response Metric for Glioblastoma. JCO Clin. Cancer Inf. 2019, 3, 1–8. [Google Scholar] [CrossRef]
- Hormuth, D.A.; Jarrett, A.M.; Feng, X.; Yankeelov, T.E. Calibrating a Predictive Model of Tumor Growth and Angiogenesis with Quantitative MRI. Ann. Biomed. Eng. 2019, 47, 1539–1551. [Google Scholar] [CrossRef]
- Burger, M.; Di Francesco, M.; Pietschmann, J.; Schlake, B. Nonlinear Cross-Diffusion with Size Exclusion. SIAM J. Math. Anal. 2010, 42, 2842–2871. [Google Scholar] [CrossRef]
- Hormuth, D.A.; Eldridge, S.L.; Weis, J.A.; Miga, M.I.; Yankeelov, T.E. Mechanically Coupled Reaction-Diffusion Model to Predict Glioma Growth: Methodological Details. Methods Mol. Biol. 2018, 1711, 225–241. [Google Scholar] [CrossRef] [PubMed]
- Hormuth, D.A.; Weis, J.A.; Barnes, S.L.; Miga, M.I.; Rericha, E.C.; Quaranta, V.; Yankeelov, T.E. A Mechanically Coupled Reaction–Diffusion Model That Incorporates Intra-Tumoural Heterogeneity to Predict in Vivo Glioma Growth. J. R. Soc. Interface 2017, 14, 20161010. [Google Scholar] [CrossRef] [PubMed]
- Albrecht, J.; Polenz, D.; Kühl, A.A.; Rogasch, J.M.M.; Leder, A.; Sauer, I.M.; Babos, M.; Mócsai, G.; Beindorff, N.; Steffen, I.G.; et al. Diffusion-Weighted Magnetic Resonance Imaging Using a Preclinical 1 T PET/MRI in Healthy and Tumor-Bearing Rats. EJNMMI Res. 2019, 9, 21. [Google Scholar] [CrossRef]
- Hormuth, D.A.; Jarrett, A.M.; Davis, T.; Yankeelov, T.E. Towards an Image-Informed Mathematical Model of In Vivo Response to Fractionated Radiation Therapy. Cancers 2021, 13, 1765. [Google Scholar] [CrossRef] [PubMed]
- Hormuth, D.A.; Skinner, J.T.; Does, M.D.; Yankeelov, T.E. A Comparison of Individual and Population-Derived Vascular Input Functions for Quantitative DCE-MRI in Rats. Magn. Reson. Imaging 2014, 32, 397–401. [Google Scholar] [CrossRef]
- Valdés-Hernández, P.A.; Sumiyoshi, A.; Nonaka, H.; Haga, R.; Aubert-Vásquez, E.; Ogawa, T.; Iturria-Medina, Y.; Riera, J.J.; Kawashima, R. An in Vivo MRI Template Set for Morphometry, Tissue Segmentation, and fMRI Localization in Rats. Front. Neuroinfor. 2011, 5, 26. [Google Scholar] [CrossRef]
- Glen, S. Concordance Correlation Coefficient: Definition & Interpretations. Available online: https://www.statisticshowto.com/concordance-correlation-coefficient/ (accessed on 13 July 2023).
- Xiao, Y.; Thomas, L.; Chaplain, M. Calibrating Models of Cancer Invasion: Parameter Estimation Using Approximate Bayesian Computation and Gradient Matching. Available online: https://royalsocietypublishing.org/doi/epdf/10.1098/rsos.202237 (accessed on 5 September 2024).
- Handl, J.; Kell, D.B.; Knowles, J. Multiobjective Optimization in Bioinformatics and Computational Biology. IEEE/ACM Trans. Comput. Biol. Bioinform. 2007, 4, 279–292. [Google Scholar] [CrossRef] [PubMed]
- Sobol′, I.M. Global Sensitivity Indices for Nonlinear Mathematical Models and Their Monte Carlo Estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- van de Ven, R.C.G.; Hogers, B.; van den Maagdenberg, A.M.J.M.; de Groot, H.J.M.; Ferrari, M.D.; Frants, R.R.; Poelmann, R.E.; van der Weerd, L.; Kiihne, S.R. T1 Relaxation in in Vivo Mouse Brain at Ultra-high Field. Magn. Reson. Med. 2007, 58, 390–395. [Google Scholar] [CrossRef]
- DiFrancesco, M.W.; Rasmussen, J.M.; Yuan, W.; Pratt, R.; Dunn, S.; Dardzinski, B.J.; Holland, S.K. Comparison of SNR and CNR for in Vivo Mouse Brain Imaging at 3 and 7 T Using Well Matched Scanner Configurations. Med. Phys. 2008, 35, 3972–3978. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Lin, Y.-J.; Lin, S.-H.; Tsai, C.-C.; Lin, Y.-C.; Cheng, J.-S.; Wang, J.-J. The Effect of Spatial Resolution on the Reproducibility of Diffusion Imaging When Controlled Signal to Noise Ratio. Biomed. J. 2019, 42, 268–276. [Google Scholar] [CrossRef]
- Kennedy, M.C.; O’Hagan, A. Bayesian Calibration of Computer Models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2001, 63, 425–464. [Google Scholar] [CrossRef]
- Kimpton, L.M.; Paun, L.M.; Colebank, M.J.; Volodina, V. Challenges and Opportunities in Uncertainty Quantification for Healthcare and Biological Systems. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2025, 383, 20240232. [Google Scholar] [CrossRef]
- Jackson, P.R.; Hawkins-Daarud, A.; Partridge, S.C.; Kinahan, P.E.; Swanson, K.R. Simulating Magnetic Resonance Images Based on a Model of Tumor Growth Incorporating Microenvironment. Proceedings of Medical Imaging 2018, Houston, TX, USA, 11–15 February 2018; Society of Photo-Optical Instrumentation Engineers: Bellingham, WA, USA, 2018; Volume 10577, pp. 310–318. [Google Scholar]
- Abadi, E.; Segars, W.P.; Tsui, B.M.W.; Kinahan, P.E.; Bottenus, N.; Frangi, A.F.; Maidment, A.; Lo, J.; Samei, E. Virtual Clinical Trials in Medical Imaging: A Review. J. Med. Imaging 2020, 7, 042805. [Google Scholar] [CrossRef]
- Han, S.; Liu, Y.; Cai, S.J.; Qian, M.; Ding, J.; Larion, M.; Gilbert, M.R.; Yang, C. IDH Mutation in Glioma: Molecular Mechanisms and Potential Therapeutic Targets. Br. J. Cancer 2020, 122, 1580–1589. [Google Scholar] [CrossRef]
- Yan, H.; Parsons, D.W.; Jin, G.; McLendon, R.; Rasheed, B.A.; Yuan, W.; Kos, I.; Batinic-Haberle, I.; Jones, S.; Riggins, G.J.; et al. IDH1 and IDH2 Mutations in Gliomas. N. Engl. J. Med. 2009, 360, 765–773. [Google Scholar] [CrossRef]
- Verhaak, R.G.W.; Hoadley, K.A.; Purdom, E.; Wang, V.; Qi, Y.; Wilkerson, M.D.; Miller, C.R.; Ding, L.; Golub, T.; Mesirov, J.P.; et al. Integrated Genomic Analysis Identifies Clinically Relevant Subtypes of Glioblastoma Characterized by Abnormalities in PDGFRA, IDH1, EGFR, and NF1. Cancer Cell 2010, 17, 98–110. [Google Scholar] [CrossRef]
- Barth, R.F. Rat Brain Tumor Models in Experimental Neuro-Oncology: The 9L, C6, T9, F98, RG2 (D74), RT-2 and CNS-1 Gliomas. J. Neuro-Oncol. 1998, 36, 91–102. [Google Scholar] [CrossRef] [PubMed]
- Hormuth, D.A.; Farhat, M.; Panthi, B.; Langshaw, H.; Shanker, M.D.; Talpur, W.; Thrower, S.; Goldman, J.; Ty, S.; Custer, C.; et al. Forecasting Chemoradiation Response Midtreatment for High-Grade Gliomas Through Patient-Specific Biology-Based Modeling. Int. J. Radiat. Oncol. Biol. Phys. 2025. [Google Scholar] [CrossRef]
- Kapteyn, M.G.; Pretorius, J.V.R.; Willcox, K.E. A Probabilistic Graphical Model Foundation for Enabling Predictive Digital Twins at Scale. Nat. Comput. Sci. 2021, 1, 337–347. [Google Scholar] [CrossRef] [PubMed]
- National Academy of Engineering; National Academies of Sciences, Engineering, and Medicine. Foundational Research Gaps and Future Directions for Digital Twins; The National Academies Press: Washington, DC, USA, 2023; ISBN 978-0-309-71169-2. [Google Scholar]
- Lipková, J.; Angelikopoulos, P.; Wu, S.; Alberts, E.; Wiestler, B.; Diehl, C.; Preibisch, C.; Pyka, T.; Combs, S.E.; Hadjidoukas, P.; et al. Personalized Radiotherapy Design for Glioblastoma: Integrating Mathematical Tumor Models, Multimodal Scans, and Bayesian Inference. IEEE Trans. Med. Imaging 2019, 38, 1875–1884. [Google Scholar] [CrossRef] [PubMed]
- Neal, M.L.; Trister, A.D.; Cloke, T.; Sodt, R.; Ahn, S.; Baldock, A.L.; Bridge, C.A.; Lai, A.; Cloughesy, T.F.; Mrugala, M.M.; et al. Discriminating Survival Outcomes in Patients with Glioblastoma Using a Simulation-Based, Patient-Specific Response Metric. PLoS ONE 2013, 8, e51951. [Google Scholar] [CrossRef]
- Wu, C.; Jarrett, A.M.; Zhou, Z.; Elshafeey, N.; Adrada, B.E.; Candelaria, R.P.; Mohamed, R.M.M.; Boge, M.; Huo, L.; White, J.B.; et al. MRI-Based Digital Models Forecast Patient-Specific Treatment Responses to Neoadjuvant Chemotherapy in Triple-Negative Breast Cancer. Cancer Res. 2022, 82, 3394–3404. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Summers, R.M.; Yao, J. Kidney Tumor Growth Prediction by Coupling Reaction-Diffusion and Biomechanical Model. Biomed. Eng. IEEE Trans. 2013, 60, 169–173. [Google Scholar] [CrossRef]
- Sel, K.; Hawkins-Daarud, A.; Chaudhuri, A.; Osman, D.; Bahai, A.; Paydarfar, D.; Willcox, K.; Chung, C.; Jafari, R. Survey and Perspective on Verification, Validation, and Uncertainty Quantification of Digital Twins for Precision Medicine. npj Digit. Med. 2025, 8, 40. [Google Scholar] [CrossRef] [PubMed]
- Cho, H.; Lewis, A.L.; Storey, K.M. Bayesian Information-Theoretic Calibration of Radiotherapy Sensitivity Parameters for Informing Effective Scanning Protocols in Cancer. J. Clin. Med. 2020, 9, 3208. [Google Scholar] [CrossRef] [PubMed]
- Cho, H.; Lewis, A.L.; Storey, K.M.; Zittle, A.C.; Cho, H.; Lewis, A.L.; Storey, K.M.; Zittle, A.C. An Adaptive Information-Theoretic Experimental Design Procedure for High-to-Low Fidelity Calibration of Prostate Cancer Models. Math. Biosci. Eng. 2023, 20, 17986–18017. [Google Scholar] [CrossRef]
- Partridge, S.C.; McDonald, E.S. Diffusion Weighted MRI of the Breast: Protocol Optimization, Guidelines for Interpretation, and Potential Clinical Applications. Magn. Reson. Imaging Clin. N. Am. 2013, 21, 601–624. [Google Scholar] [CrossRef]
- Shusharina, N.; Maier, S.E.; Lam, M.B.; Kaza, E. Optimal Setup and Parameters of Diffusion-Weighted Magnetic Resonance Imaging for Translational Evaluation of a Tumor Progression Model for Soft Tissue Sarcomas. Adv. Radiat. Oncol. 2025, 10, 101661. [Google Scholar] [CrossRef]
- McDonald, B.A.; Vedam, S.; Yang, J.; Wang, J.; Castillo, P.; Lee, B.; Sobremonte, A.; Ahmed, S.; Ding, Y.; Mohamed, A.S.R.; et al. Initial Feasibility and Clinical Implementation of Daily MR-Guided Adaptive Head and Neck Cancer Radiation Therapy on a 1.5T MR-Linac System: Prospective R-IDEAL 2a/2b Systematic Clinical Evaluation of Technical Innovation. Int. J. Radiat. Oncol. Biol. Phys. 2021, 109, 1606–1618. [Google Scholar] [CrossRef]




| Parameter or Variable | Description | How Assigned |
|---|---|---|
| Nt(x,t) | fraction of tumor cells per voxel | Initialized at Day 1 with murine DW-MRI data |
| Nv(x,t) | fraction of vasculature per voxel | Initialized at Day 1 with murine DCE-MRI data |
| Dt,0 | diffusion coefficient of tumor cells | Calibrated |
| Dv,0 | diffusion coefficient of vasculature | Calibrated |
| kt | proliferation rate of tumor cells | Calibrated |
| kv | proliferation rate of vasculature | Calibrated |
| θmin | minimum carrying capacity | Set to 0.1 |
| θmax | maximum carrying capacity | Set to 0.9716 |
| θtot | total carrying capacity | Set to θmax + θmin |
| Nthresh | Nv fraction at which max Nt can be supported | Set to 0.022 |
| kd,v | Vasculature death rate | Set to 0.125 day−1 |
| coefficient representing the impact of von Mises stress on diffusion | Set to 0.25 | |
| d(x,t) | Normalized distance to periphery | Calculated |
| σvm | von Mises stress | Calculated |
| Acquisition Parameter | Values |
|---|---|
| Signal-to-noise ratio (SNR) | 5, 10, 20, 40, 80, 160 |
| Spatial resolution (SR) | 0.008 mm3, 0.063 mm3, 0.50 mm3 |
| Temporal resolution (TR) | 5, 3, or 2 timepoints used during calibration |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
LaMonica, M.F.; Yankeelov, T.E.; Hormuth, D.A., II. Investigating the Limits of Predictability of Magnetic Resonance Imaging-Based Mathematical Models of Tumor Growth. Cancers 2025, 17, 3361. https://doi.org/10.3390/cancers17203361
LaMonica MF, Yankeelov TE, Hormuth DA II. Investigating the Limits of Predictability of Magnetic Resonance Imaging-Based Mathematical Models of Tumor Growth. Cancers. 2025; 17(20):3361. https://doi.org/10.3390/cancers17203361
Chicago/Turabian StyleLaMonica, Megan F., Thomas E. Yankeelov, and David A. Hormuth, II. 2025. "Investigating the Limits of Predictability of Magnetic Resonance Imaging-Based Mathematical Models of Tumor Growth" Cancers 17, no. 20: 3361. https://doi.org/10.3390/cancers17203361
APA StyleLaMonica, M. F., Yankeelov, T. E., & Hormuth, D. A., II. (2025). Investigating the Limits of Predictability of Magnetic Resonance Imaging-Based Mathematical Models of Tumor Growth. Cancers, 17(20), 3361. https://doi.org/10.3390/cancers17203361





