Comparison of a Multi-Scenario Robustness Evaluation Method with Measurements for Proton Teletherapy †
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
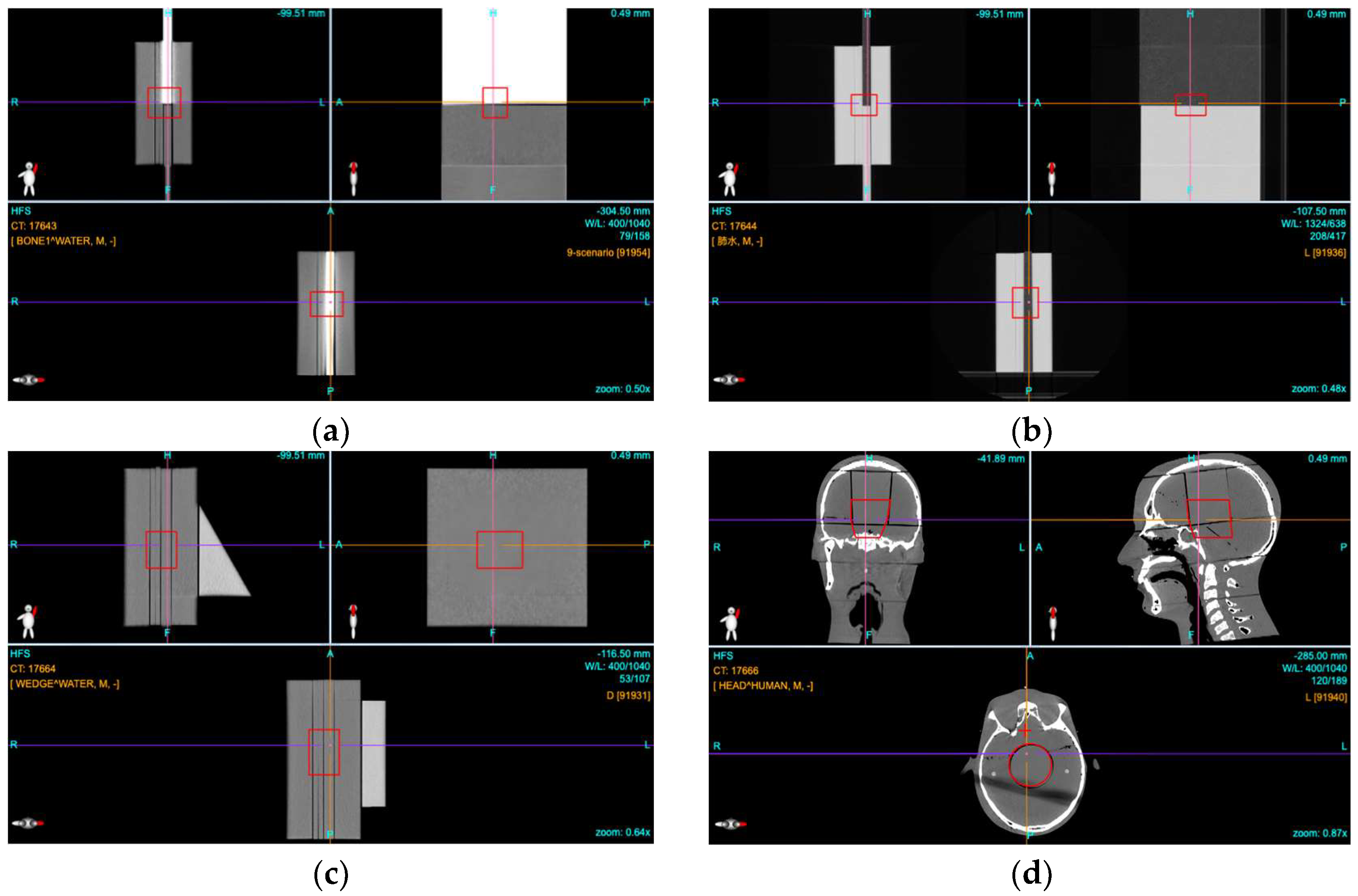
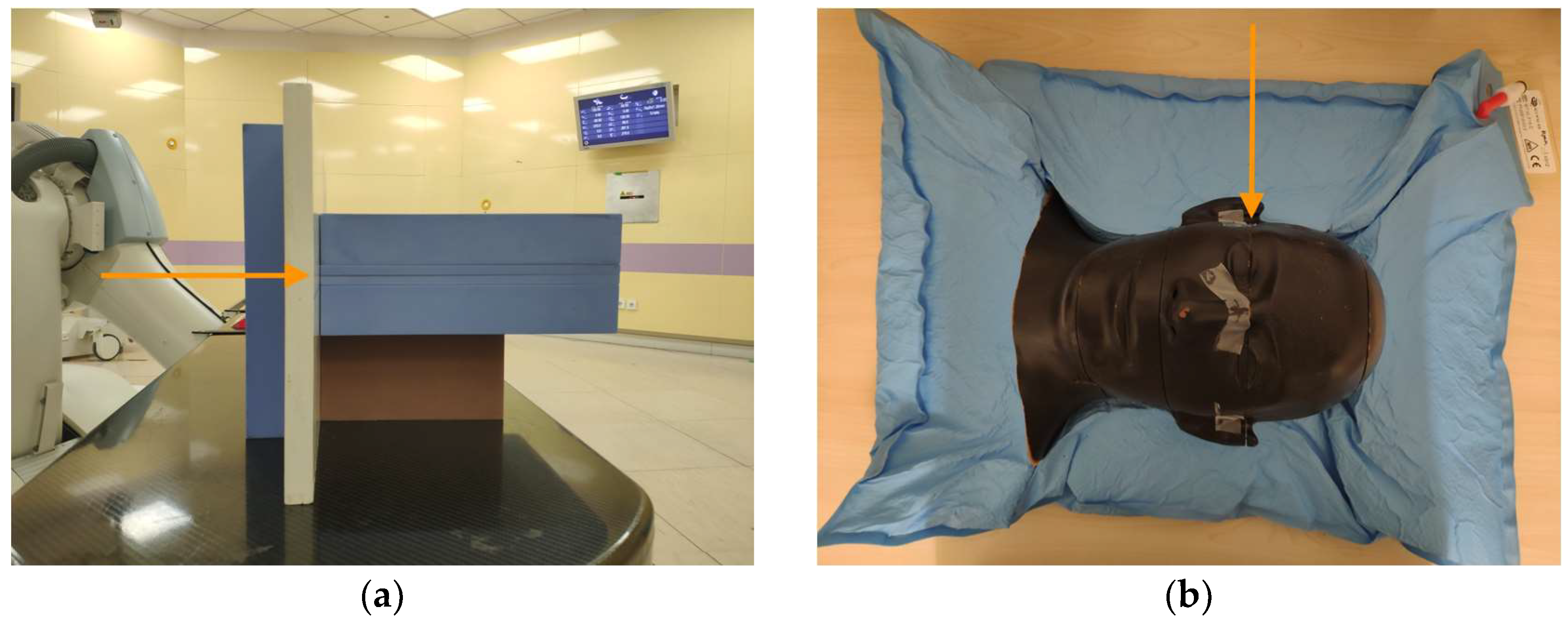
2.1. Phantom Planning
2.2. DVH Analysis
2.3. Maximum and Minimum Doses
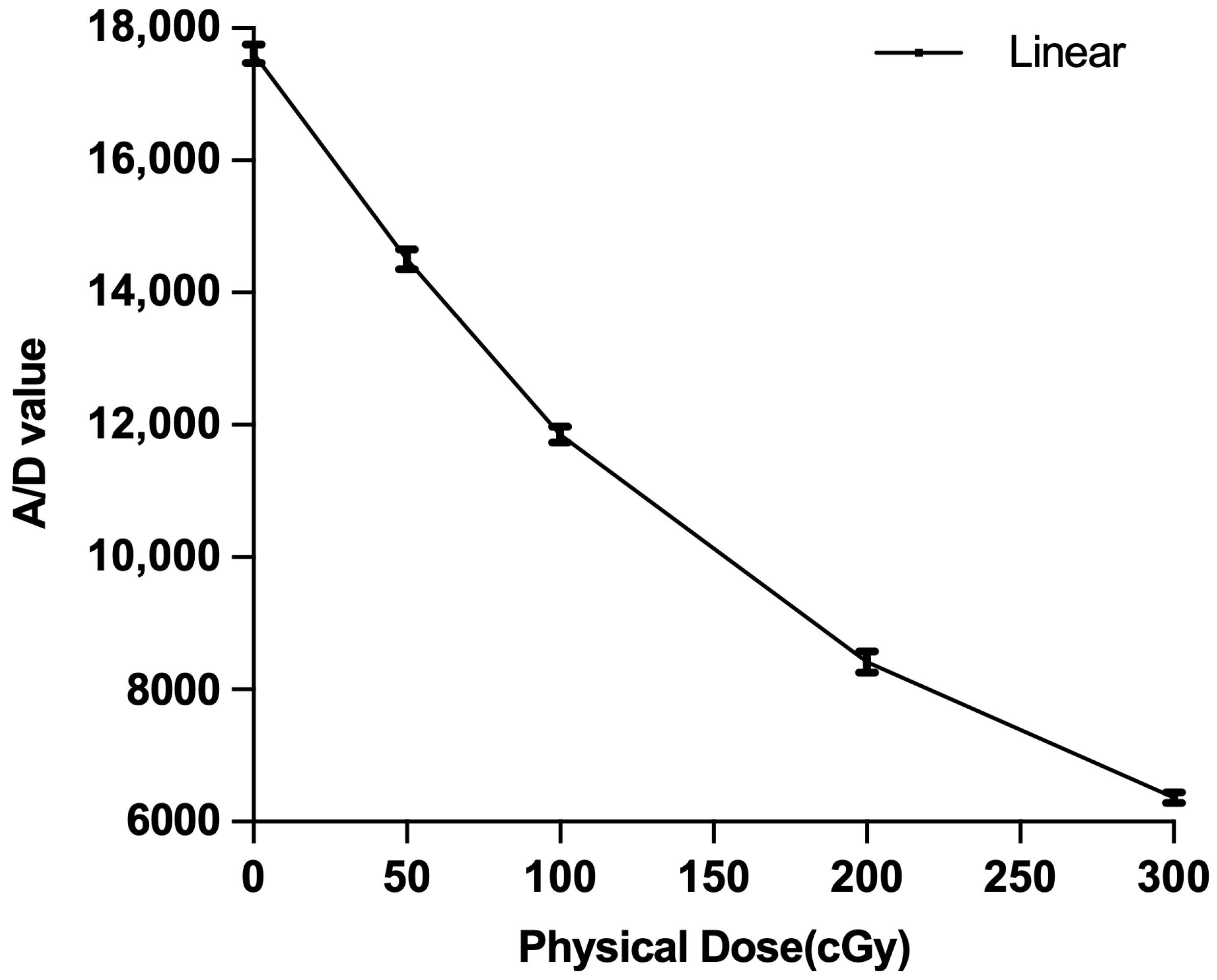
2.4. Film Dosimetry
2.5. Comparison of Measured to Calculated Profiles
3. Results
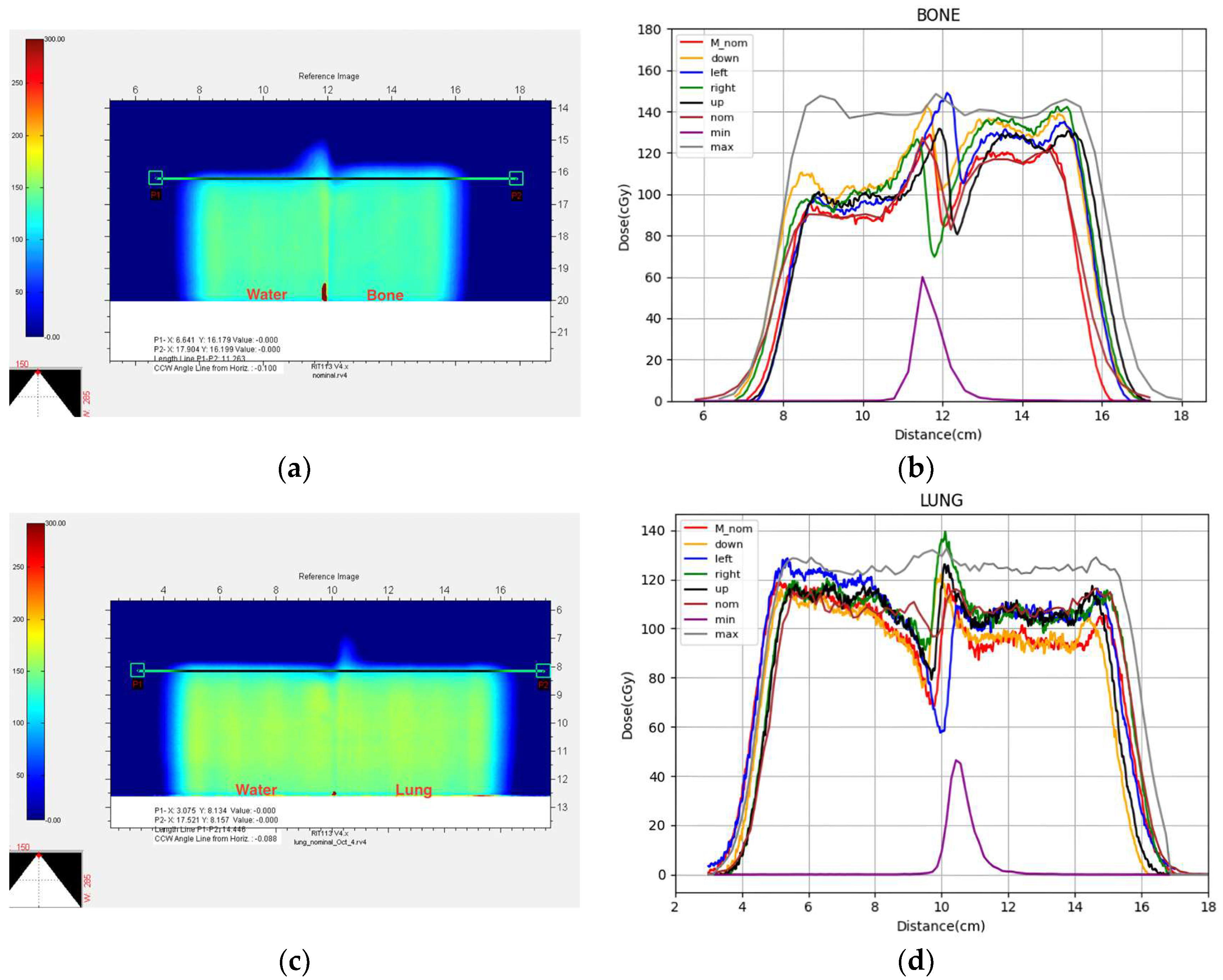
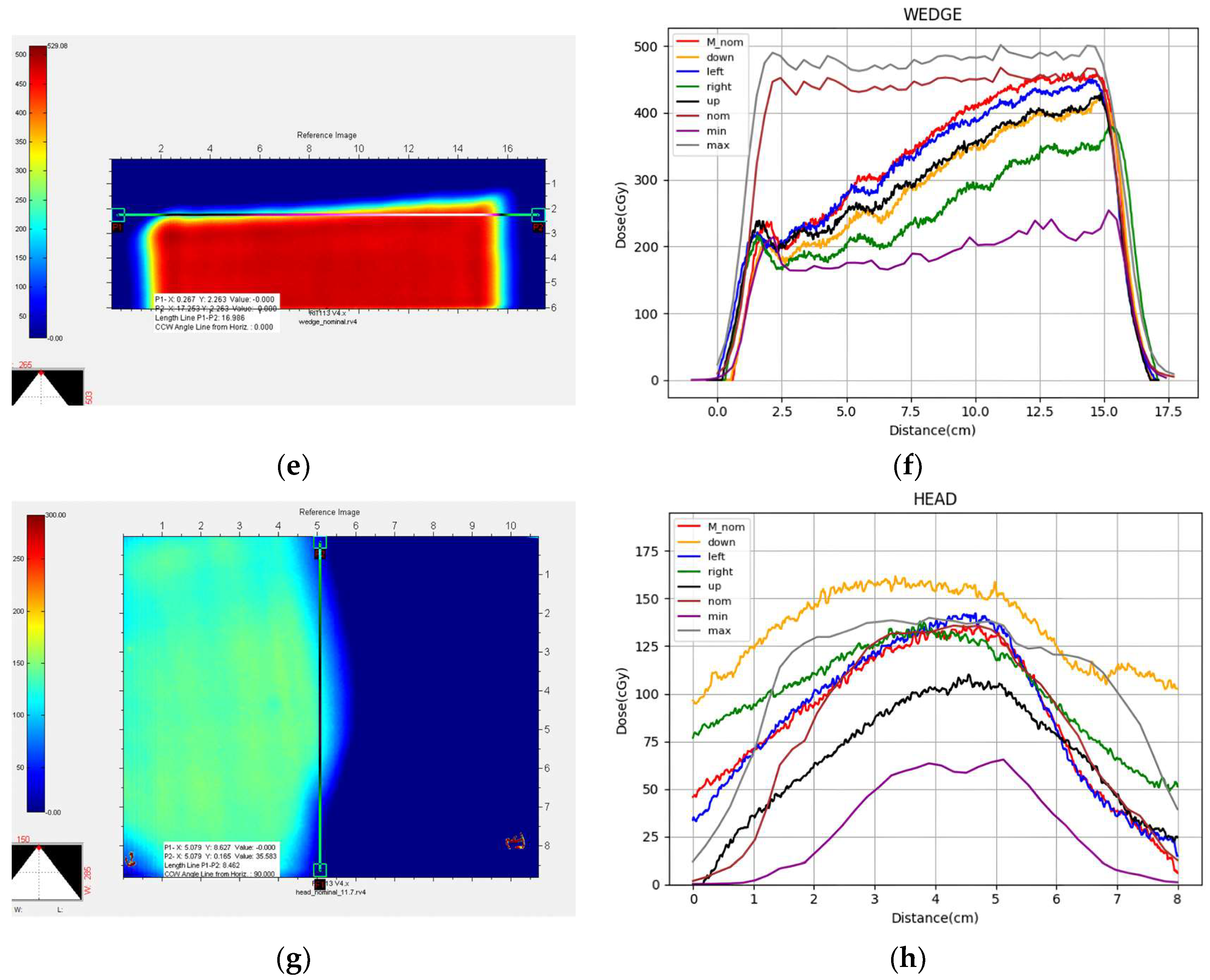
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Dmin | the minimum dose delivered to 100% of the specified volume of interest (also known as D100%) |
| Dmax | the maximum dose delivered to any part of the volume of interest (also known as D0%) |
| DRBE | RBE weighted dose |
| DVH | dose volume histogram |
| LET | linear energy transfer |
| OAR | organ at risk |
| PMMA | polymethylmethacrylate |
| PTV | planning target volume |
| RBE | relative biological effectiveness |
| TPS | treatment planning system |
| V95 | the volume receiving 95% of the specified dose |
| XCT | X ray computed tomography |
References
- Karlsson, K.; Lax, I.; Lindbäck, E.; Poludniowski, G. Accuracy of the dose-shift approximation in estimating the delivered dose in SBRT of lung tumors considering setup errors and breathing motions. Acta Oncol. 2017, 56, 1189–1196. [Google Scholar] [CrossRef] [PubMed]
- Korevaar, E.W.; Habraken, S.J.M.; Scandurra, D.; Kierkels, R.G.J.; Unipan, M.; Eenink, M.G.C.; Steenbakkers, R.J.H.M.; Peeters, S.G.; Zindler, J.D.; Hoogeman, M.; et al. Practical robustness evaluation in radiotherapy-A photon and proton-proof alternative to PTV-based plan evaluation. Radiother. Oncol. 2019, 141, 267–274. [Google Scholar] [CrossRef] [PubMed]
- Moyers, M.F.; Miller, D.W.; Bush, D.A.; Slater, J.D. Methodologies and tools for proton beam design for lung tumors. Int. J. Radiat. Oncol. Biol. Phys. 2001, 49, 1429–1438. [Google Scholar] [CrossRef] [PubMed]
- Unkelbach, J.; Paganetti, H. Robust Proton Treatment Planning: Physical and Biological Optimization. Semin. Radiat. Oncol. 2018, 28, 88–96. [Google Scholar] [CrossRef]
- Engelsman, M.; Kooy, H.M. Target volume dose considerations in proton beam treatment planning for lung tumors. Med. Phys. 2005, 32, 3549–3557. [Google Scholar] [CrossRef]
- Wei, L.; Xiaodong, Z.; Yupeng, L.; Radhe, M. Robust optimization of intensity modulated proton therapy. Med. Phys. 2012, 39, 1079–1091. [Google Scholar] [CrossRef]
- Goitein, M. Limitations of two-dimensional treatment planning programs. Med. Phys. 1982, 9, 580–586. [Google Scholar] [CrossRef]
- Moyers, M.F.; Toth, T.L.; Sadagopan, R.; Chvetsov, A.; Unkelbach, J.; Mohan, R.; Lesyna, D.; Lin, L.; Li, Z.; Poenisch, F.; et al. Physical Uncertainties in the Planning and Delivery of Light lon Beam Treatments. Am. Assoc. Phys. Med. 2020, 202, 1. [Google Scholar]
- Goitein, M. Calculation of the uncertainty in the dose delivered during radiation therapy. Med. Phys. 1985, 12, 608–612. [Google Scholar] [CrossRef]
- Stuschke, M.; Kaiser, A.; Abu, J.J.; Pöttgen, C.; Levegrün, S.; Farr, J. Multi-scenario based robust intensity-modulated proton therapy (IMPT) plans can account for set-up errors more effectively in terms of normal tissue sparing than planning target volume (PTV) based intensity-modulated photon plans in the head and neck region. Radiat. Oncol. 2013, 8, 145. [Google Scholar] [CrossRef]
- Sterpin, E.; Rivas, S.T.; Van den Heuvel, F.; George, B.; Lee, J.A.; Souris, K. Development of robustness evaluation strategies for enabling statistically consistent reporting. Phys. Med. Biol. 2021, 66, 45002. [Google Scholar] [CrossRef]
- Noufal, M.P.; Widesott, L.; Sharma, S.D.; Righetto, R.; Cianchetti, M.; Schwarz, M. The Role of Plan Robustness Evaluation in Comparing Protons and Photons Plans—An Application on IMPT and IMRT Plans in Skull Base Chordomas. J. Med. Phys. 2020, 45, 206–214. [Google Scholar] [CrossRef]
- Yock, A.D.; Mohan, R.; Flampouri, S.; Bosch, W.; Taylor, P.A.; Gladstone, D.; Kim, S.; Sohn, J.; Wallace, R.; Xiao, Y.; et al. Robustness Analysis for External Beam Radiation Therapy Treatment Plans: Describing Uncertainty Scenarios and Reporting Their Dosimetric Consequences. Pract. Radiat. Oncol. 2019, 9, 200–207. [Google Scholar] [CrossRef] [PubMed]
- Rana, S.; Rosenfeld, A.B. Small spot size versus large spot size: Effect on plan quality for lung cancer in pencil beam scanning proton therapy. J. Appl. Clin. Med. Phys. 2022, 23, e13512. [Google Scholar] [CrossRef]
- Ödén, J.; Eriksson, K.; Toma-Dasu, I. Incorporation of relative biological effectiveness uncertainties into proton plan robustness evaluation. Acta Oncol. 2017, 56, 769–778. [Google Scholar] [CrossRef] [PubMed]
- Ödén, J.; Toma-Dasu, I.; Nyström, P.W.; Traneus, E.; Dasu, A. Spatial correlation of linear energy transfer and relative biological effectiveness with suspected treatment-related toxicities following proton therapy for intracranial tumors. Med. Phys. 2020, 47, 342–351. [Google Scholar] [CrossRef] [PubMed]
- Moyers, M.F.; Saganti, P.B.; Nelson, G.A. EVA space suit proton and electron threshold energy measurements by XCT and range shifting. Radiat. Meas. 2006, 41, 1216–1226. [Google Scholar] [CrossRef]
- Zeitlin, C.; Guetersloh, S.B.; Heilbronn, L.H.; Miller, J.; Shavers, M. Radiation tests of the extravehicular mobility unit space suit for the international space station using energetic protons. Radiat. Meas. 2006, 41, 1158–1172. [Google Scholar] [CrossRef][Green Version]
- Benton, E.R.; Benton, E.V.; Frank, A.L.; Moyers, M.F. Characterization of the radiation shielding properties of US and Russian EVA suits using passive detectors. Radiat. Meas. 2006, 41, 1191–1201. [Google Scholar] [CrossRef]
- Moyers, M.F.; Lin, J.; Li, J.; Chen, H.; Shen, Z. Optimization of the planning process with an in-house treatment information management, and planning system. Radiat. Med. Prot. 2022, 3, 102–107. [Google Scholar] [CrossRef]
- Yepes, P.; Randeniya, S.; Taddei, P.J.; Newhauser, W.D. A track-repeating algorithm for fast Monte Carlo dose calculations of proton radiotherapy. Nucl. Technol. 2009, 168, 736–740. [Google Scholar] [CrossRef]
- Wang, Q.; Schlegel, N.; Moyers, M.; Lin, J.; Hong, L.; Chen, H.; Johnson, A.; Li, J.; Shen, Z.M.; Xu, M.; et al. Validation of the Fast Dose Calculator for Shanghai Proton and Heavy Ion Center. Biomed. Phys. Eng. Express 2018, 4, 65007. [Google Scholar] [CrossRef]
- Wang, Q.; Zhu, C.; Bai, X.; Deng, Y.; Schlegel, N.; Adair, A.; Chen, Z.; Li, Y.; Moyers, M.; Yepes, P. Automatic phase space generation for Monte Carlo calculations of intensity modulated particle therapy. Biomed. Phys. Eng. Express 2020, 6, 25001. [Google Scholar] [CrossRef]
- Trofimov, A.; Unkelbach, J.; Delaney, T.F.; Bortfeld, T. Visualization of a variety of possible dosimetric outcomes in radiation therapy using dose-volume histogram bands. Pract. Radiat. Oncol. 2012, 2, 164–171. [Google Scholar] [CrossRef] [PubMed]
- Mason, D. SU-E-T-33: Pydicom: An Open Source DICOM Library. Version 2.2. Available online: https://github.com/pydicom/pydicom (accessed on 12 September 2021).
- Castriconi, R.; Ciocca, M.; Mirandola, A.; Sini, C.; Broggi, S.; Schwarz, M.; Fracchiolla, F.; Martisikova, M.; Arico, G.; Mettivier, G.; et al. Dose-response of EBT3 radiochromic films to proton and carbon ion clinical beams. Phys. Med. Biol. 2017, 62, 377–393. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Sheng, Y.; Huang, Z.; Shahnazi, K. EBT3 and EDR2 film dosimetry for scanning carbon ion beams. Chin. J. Radiol. Med. Prot. 2018, 38, 705–709. [Google Scholar]
- International Atomic Energy Agency (IAEA). Absorbed Dose Determination in External Beam Radiotherapy: An International Code of Practice for Dosimetry Based on Standards of Absorbed Dose to Water; Technical Reports Series No. 398; Revised and Updated Version V.11b, 23 April 2004; International Atomic Energy Agency: Vienna, Austria, 2000; Available online: https://www.iaea.org/publications/15048/absorbed-dose-determination-in-external-beam-radiotherapy (accessed on 12 August 2025). [CrossRef]
- Casanova, B.V.; Pasquino, M.; Russo, G.; Grosso, P.; Cante, D.; Sciacero, P.; Girelli, G.; La Porta, M.R.; Tofani, S. Dosimetric characterization and use of GAFCHROMIC EBT3 film for IMRT dose verification. J. Appl. Clin. Med. Phys. 2013, 14, 4111. [Google Scholar] [CrossRef]
- Wen, N.; Lu, S.; Kim, J.; Qin, Y.; Huang, Y.; Zhao, B.; Liu, C.; Chetty, I.J. Precise film dosimetry for stereotactic radiosurgery and stereotactic body radiotherapy quality assurance using Gafchromic™ EBT3 films. Radiat. Oncol. 2016, 11, 132. [Google Scholar] [CrossRef]
- Saini, J.; Traneus, E.; Maes, D.; Regmi, R.; Bowen, S.R.; Bloch, C.; Wong, T. Advanced Proton Beam Dosimetry Part I: Review and performance evaluation of dose calculation algorithms. Transl. Lung Cancer Res. 2018, 7, 171–179. [Google Scholar] [CrossRef]
- Goitein, M. Radiation Oncology: A Physicist’s-Eye View; Springer: New York, NY, USA, 2008; pp. 14–22. [Google Scholar]

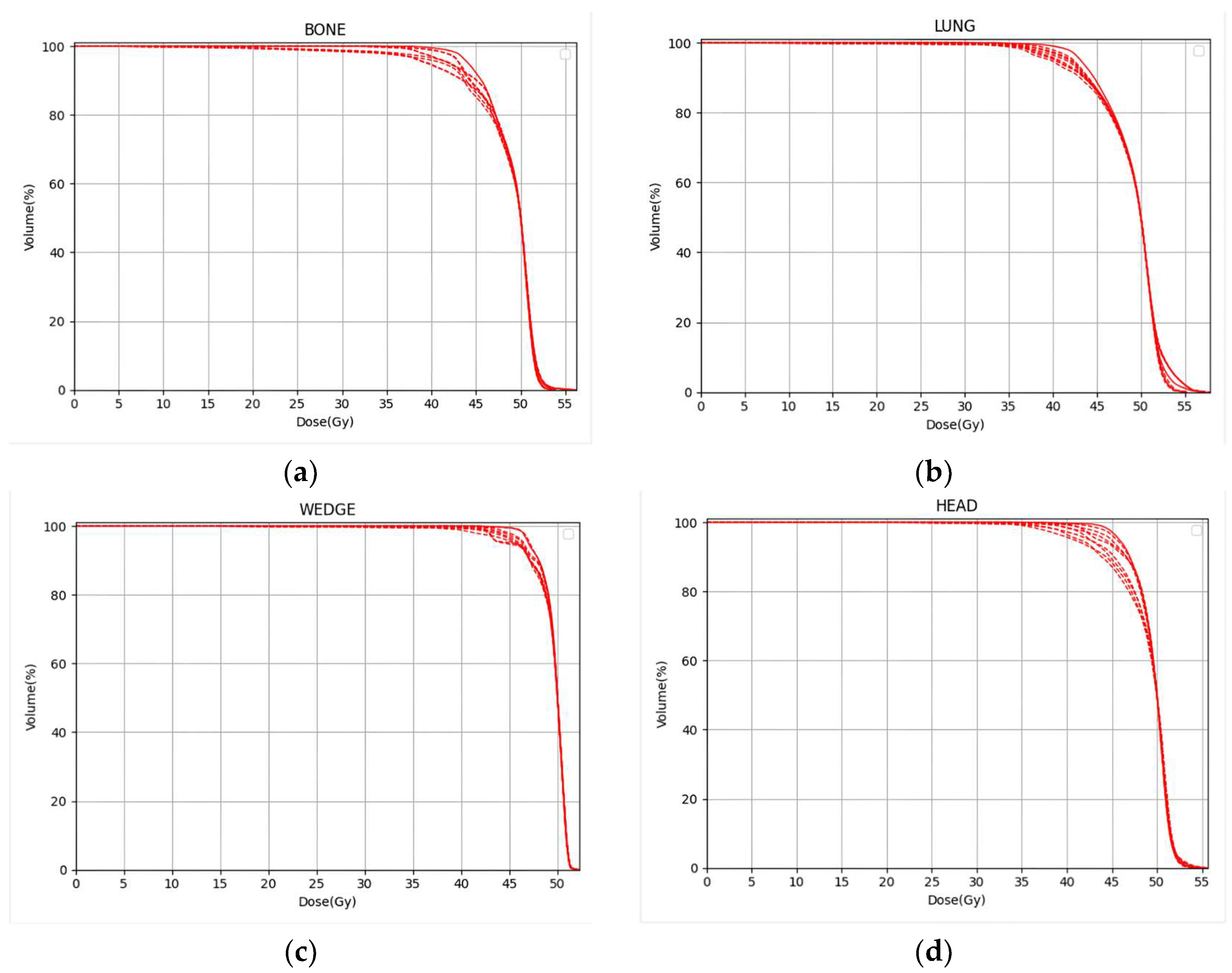
| V95% | |||
|---|---|---|---|
| Bone | 4.28 Gy–37.94 Gy | 52.46 Gy–56.34 Gy | 86.07–98.60% |
| Lung | 4.20 Gy–38.82 Gy | 55.16 Gy–57.83 Gy | 85.49–98.80% |
| Wedge | 11.83 Gy–41.90 Gy | 51.96 Gy–52.27 Gy | 97.63–99.68% |
| Head | 19.56 Gy–37.33 Gy | 53.93 Gy–55.62 Gy | 85.77–99.06% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Moyers, M.F.; Shen, Z. Comparison of a Multi-Scenario Robustness Evaluation Method with Measurements for Proton Teletherapy. Cancers 2025, 17, 2927. https://doi.org/10.3390/cancers17172927
Yang Q, Moyers MF, Shen Z. Comparison of a Multi-Scenario Robustness Evaluation Method with Measurements for Proton Teletherapy. Cancers. 2025; 17(17):2927. https://doi.org/10.3390/cancers17172927
Chicago/Turabian StyleYang, Qiangxing, Michael F. Moyers, and Zhuangming Shen. 2025. "Comparison of a Multi-Scenario Robustness Evaluation Method with Measurements for Proton Teletherapy" Cancers 17, no. 17: 2927. https://doi.org/10.3390/cancers17172927
APA StyleYang, Q., Moyers, M. F., & Shen, Z. (2025). Comparison of a Multi-Scenario Robustness Evaluation Method with Measurements for Proton Teletherapy. Cancers, 17(17), 2927. https://doi.org/10.3390/cancers17172927






