A Deep Learning Model Integrating Clinical and MRI Features Improves Risk Stratification and Reduces Unnecessary Biopsies in Men with Suspected Prostate Cancer
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
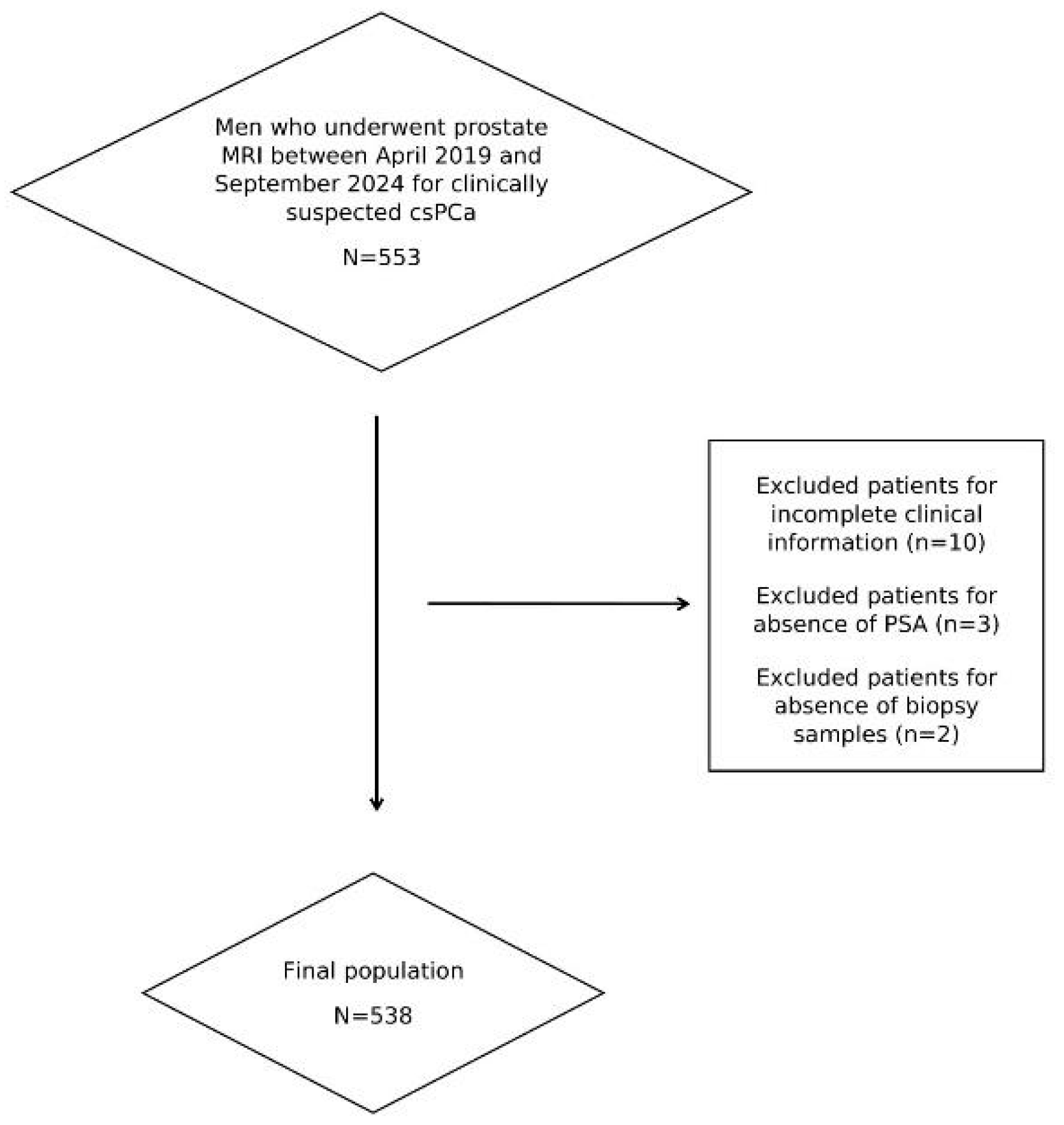
2.1. Study Population and Standard of Reference
2.2. MRI Protocol and MRI Analysis
2.3. Dataset Building and Definition of the Models
2.4. Pre-Processing
2.5. Building, Training, and Testing
- is the ground truth label
- p ∈ (0,1) is the predicted probability of the positive class.
- The first moment is the exponentially decaying average of past gradients (akin to momentum).
- The second moment is the exponentially decaying average of the squared gradients.
2.6. Data Analysis
3. Results
3.1. Study Population and MRI Results
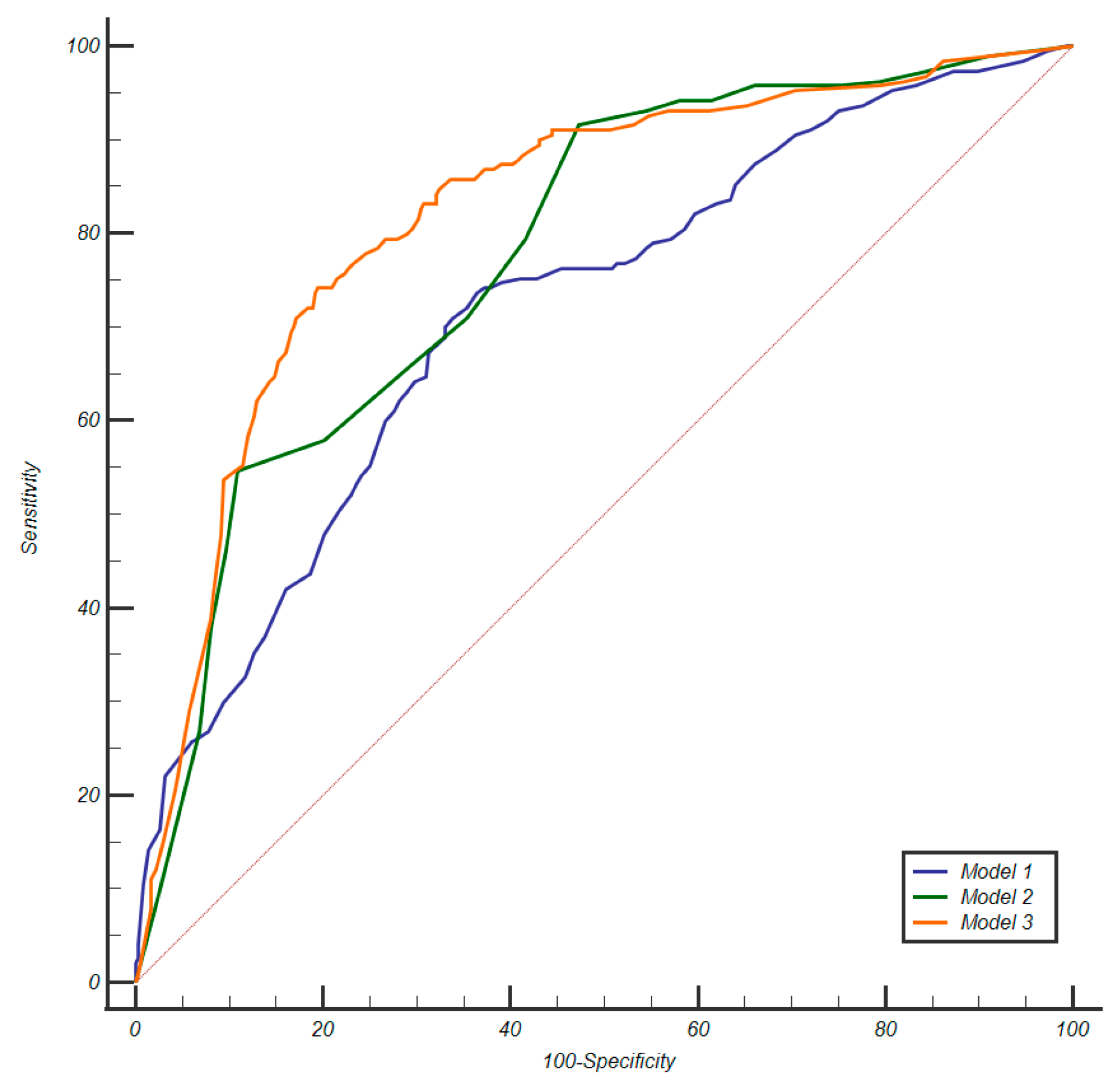
3.2. Calibration and Discrimination
3.3. Clinical Impact
4. Discussion
5. Conclusions
Declaration of Generative AI and AI-Assisted Technologies in the Writing Process
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cornford, P.; van den Bergh, R.C.; Briers, E.; Van den Broeck, T.; Brunckhorst, O.; Darraugh, J.; Eberli, D.; De Meerleer, G.; De Santis, M.; Farolfi, A.; et al. EAU-EANM-ESTRO-ESUR-ISUP-SIOG guidelines on prostate cancer—2024 update. Part I: Screening, diagnosis, and local treatment with curative intent. Eur. Urol. 2024, 86, 148–163. [Google Scholar] [CrossRef] [PubMed]
- Sathianathen, N.J.; Omer, A.; Harriss, E.; Davies, L.; Kasivisvanathan, V.; Punwani, S.; Moore, C.M.; Kastner, C.; Barrett, T.; Van Den Bergh, R.C.N.; et al. Negative predictive value of multiparametric magnetic resonance imaging in the detection of clinically significant prostate cancer in the prostate imaging reporting and data system era: A systematic review and meta-analysis. Eur. Urol. 2020, 78, 402–414. [Google Scholar] [CrossRef]
- Hamm, C.A.; Asbach, P.; Pöhlmann, A.; Schoots, I.G.; Kasivisvanathan, V.; Henkel, T.O.; Johannsen, M.; Speck, T.; Baur, A.D.J.; Haas, M.; et al. Oncological safety of MRI-informed biopsy decision-making in men with suspected prostate cancer. JAMA Oncol. 2025, 11, 145–153. [Google Scholar] [CrossRef] [PubMed]
- Kasivisvanathan, V.; Chan, V.W.-S.; Clement, K.D.; Levis, B.; Ng, A.; Asif, A.; Haider, M.A.; Emberton, M.; Pond, G.R.; Agarwal, R.; et al. VISION: An individual patient data meta-analysis of randomised trials comparing magnetic resonance imaging targeted biopsy with standard transrectal ultrasound guided biopsy in the detection of prostate cancer. Eur. Urol. 2025, 87, 512–523. [Google Scholar] [CrossRef]
- Mazzone, E.; Stabile, A.; Pellegrino, F.; Basile, G.; Cignoli, D.; Cirulli, G.O.; Sorce, G.; Barletta, F.; Scuderi, S.; Bravi, C.A.; et al. Positive predictive value of prostate imaging reporting and data system version 2 for the detection of clinically significant prostate cancer: A systematic review and meta-analysis. Eur. Urol. Oncol. 2021, 4, 697–713. [Google Scholar] [CrossRef]
- Girometti, R.; Giannarini, G.; Greco, F.; Isola, M.; Cereser, L.; Como, G.; Sioletic, S.; Pizzolitto, S.; Crestani, A.; Ficarra, V.; et al. Interreader agreement of PI-RADS v. 2 in assessing prostate cancer with multiparametric MRI: A study using whole-mount histology as the standard of reference. J. Magn. Reson. Imaging 2019, 49, 546–555. [Google Scholar] [CrossRef]
- Zanelli, E.; Giannarini, G.; Cereser, L.; Zuiani, C.; Como, G.; Pizzolitto, S.; Crestani, A.; Valotto, C.; Ficarra, V.; Girometti, R. Head-to-head comparison between multiparametric MRI, the partin tables, memorial sloan kettering cancer center nomogram, and CAPRA score in predicting extraprostatic cancer in patients undergoing radical prostatectomy. J. Magn. Reson. Imaging 2019, 50, 1604–1613. [Google Scholar] [CrossRef] [PubMed]
- Osses, D.F.; Roobol, M.J.; Schoots, I.G. Prediction medicine: Biomarkers, risk calculators and magnetic resonance imaging as risk stratification tools in prostate cancer diagnosis. Int. J. Mol. Sci. 2019, 20, 1637. [Google Scholar] [CrossRef]
- Mannaerts, C.K.; Gayet, M.; Verbeek, J.F.; Engelbrecht, M.R.; Savci-Heijink, C.D.; Jager, G.J.; Gielens, M.P.; van der Linden, H.; Beerlage, H.P.; de Reijke, T.M.; et al. Prostate cancer risk assessment in biopsy-naïve patients: The Rotterdam prostate cancer risk calculator in multiparametric magnetic resonance imaging-transrectal ultrasound (TRUS) fusion biopsy and systematic TRUS biopsy. Eur. Urol. Oncol. 2018, 1, 109–117. [Google Scholar] [CrossRef]
- Saba, K.; Wettstein, M.S.; Lieger, L.; Hötker, A.M.; Donati, O.F.; Moch, H.; Ankerst, D.P.; Poyet, C.; Sulser, T.; Eberli, D.; et al. External validation and comparison of prostate cancer risk calculators incorporating multiparametric magnetic resonance imaging for prediction of clinically significant prostate cancer. J. Urol. 2020, 203, 719–726. [Google Scholar] [CrossRef]
- Sarao, V.; Veritti, D.; De Nardin, A.; Misciagna, M.; Foresti, G.; Lanzetta, P. Explainable artificial intelligence model for the detection of geographic atrophy using colour retinal photographs. BMJ Open Ophthalmol. 2023, 8, e001411. [Google Scholar] [CrossRef] [PubMed]
- Madni, H.A.; Shujat, H.; De Nardin, A.; Zottin, S.; Foresti, G.L. Unsupervised Brain MRI Anomaly Detection via Inter-Realization Channels. Int. J. Neural Syst. 2025; 2550047, online ahead of print. [Google Scholar] [CrossRef]
- Parekh, S.; Ratnani, P.; Falagario, U.; Lundon, D.; Kewlani, D.; Nasri, J.; Dovey, Z.; Stroumbakis, D.; Ranti, D.; Grauer, R.; et al. The Mount Sinai prebiopsy risk calculator for predicting any prostate cancer and clinically significant prostate cancer: Development of a risk predictive tool and validation with advanced neural networking, prostate magnetic resonance imaging outcome database, and European randomized study of screening for prostate cancer risk calculator. Eur. Urol. Open Sci. 2022, 41, 45–54. [Google Scholar] [PubMed]
- Stephan, C.; Jung, K.; Cammann, H.; Vogel, B.; Brux, B.; Kristiansen, G.; Rudolph, B.; Hauptmann, S.; Lein, M.; Schnorr, D.; et al. An artificial neural network considerably improves the diagnostic power of percent free prostate-specific antigen in prostate cancer diagnosis: Results of a 5-year investigation. Int. J. Cancer 2002, 99, 466–473. [Google Scholar] [CrossRef]
- Babaian, R.; Fritsche, H.; Ayala, A.; Bhadkamkar, V.; Johnston, D.A.; Naccarato, W.; Zhang, Z. Performance of a neural network in detecting prostate cancer in the prostate-specific antigen reflex range of 2.5 to 4.0 ng/mL. Urology 2000, 56, 1000–1006. [Google Scholar] [CrossRef]
- Turkbey, B.; Rosenkrantz, A.B.; Haider, M.A.; Padhani, A.R.; Villeirs, G.; Macura, K.J.; Tempany, C.M.; Choyke, P.L.; Cornud, F.; Margolis, D.J.; et al. Prostate Imaging Reporting and Data System Version 2.1: 2019 Update of Prostate Imaging Reporting and Data System Version 2. Eur. Urol. 2019, 76, 340–351. [Google Scholar] [CrossRef]
- Epstein, J.I.; Egevad, L.; Amin, M.B.; Delahunt, B.; Srigley, J.R.; Humphrey, P.A.; Grading Committee. The 2014 International Society of Urological Pathology (ISUP) consensus conference on Gleason grading of prostatic carcinoma: Definition of grading patterns and proposal for a new grading system. Am. J. Surg. Pathol. 2016, 40, 244–252. [Google Scholar] [CrossRef]
- de Rooij, M.; Israël, B.; Tummers, M.; Ahmed, H.U.; Barrett, T.; Giganti, F.; Hamm, B.; Løgager, V.; Padhani, A.; Panebianco, V.; et al. ESUR/ESUI consensus statements on multi-parametric MRI for the detection of clinically significant prostate cancer: Quality requirements for image acquisition, interpretation and radiologists’ training. Eur. Radiol. 2020, 30, 5404–5416. [Google Scholar] [CrossRef]
- Mao, A.; Mohri, M.; Zhong, Y. Cross-entropy loss functions: Theoretical analysis and applications. In Proceedings of the 40th International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023; pp. 23803–23828. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference for Learning Representations, ICLR, San Diego, CA, USA, 7–9 May 2015. Poster. [Google Scholar]
- Park, S.H.; Han, K.; Lee, J.-G. Conceptual Review of Outcome Metrics and Measures Used in Clinical Evaluation of Artificial Intelligence in Radiology. Radiol. Med. 2024, 129, 1644–1655. [Google Scholar] [CrossRef] [PubMed]
- Obuchowski, N.A. Fundamentals of Clinical Research for Radiologists: ROC Analysis. AJR Am. J. Roentgenol. 2005, 184, 364–372. [Google Scholar] [CrossRef]
- Vickers, A.J.; Elkin, E.B. Decision curve analysis: A novel method for evaluating prediction models. Med. Decis. Mak. 2006, 26, 565–574. [Google Scholar] [CrossRef]
- Penzkofer, T.; Padhani, A.R.; Turkbey, B.; Haider, M.A.; Huisman, H.; Walz, J.; Salomon, G.; Schoots, I.G.; Richenberg, J.; Villeirs, G.; et al. ESUR/ESUI position paper: Developing artificial intelligence for precision diagnosis of prostate cancer using magnetic resonance imaging. Eur. Radiol. 2021, 31, 9567–9578. [Google Scholar] [CrossRef] [PubMed]
- Padhani, A.R.; Haider, M.A.; Rouviere, O. Balancing the benefits and harms of MRI-directed biopsy pathways. Eur. Radiol. 2022, 32, 2326–2329. [Google Scholar] [CrossRef]
- Davik, P.; Remmers, S.; Elschot, M.; Roobol, M.J.; Bathen, T.F.; Bertilsson, H. Performance of magnetic resonance imaging-based prostate cancer risk calculators and decision strategies in two large European medical centres. BJU Int. 2024, 133, 278–288. [Google Scholar] [CrossRef]
- Mortezavi, A.; Palsdottir, T.; Eklund, M.; Chellappa, V.; Murugan, S.K.; Saba, K.; Ankerst, D.P.; Haug, E.S.; Nordström, T. Head-to-head comparison of conventional, and image-and biomarker-based prostate cancer risk calculators. Eur. Urol. Focus 2021, 7, 546–553. [Google Scholar] [CrossRef] [PubMed]
- Alberts, A.R.; Roobol, M.J.; Verbeek, J.F.; Schoots, I.G.; Chiu, P.K.; Osses, D.F.; Tijsterman, J.D.; Beerlage, H.P.; Mannaerts, C.K.; Schimmöller, L.; et al. Prediction of high-grade prostate cancer following multiparametric magnetic resonance imaging: Improving the Rotterdam European randomized study of screening for prostate cancer risk calculators. Eur. Urol. 2019, 75, 310–318. [Google Scholar] [CrossRef] [PubMed]
- Giganti, F.; Moore, C.M.; Robertson, N.L.; McCartan, N.; Jameson, C.; Bott, S.R.J.; Winkler, M.; Gambarota, G.; Whitcher, B.; Castro, R.; et al. MRI findings in men on active surveillance for prostate cancer: Does dutasteride make MRI visible lesions less conspicuous? Results from a placebo-controlled, randomised clinical trial. Eur. Radiol. 2017, 27, 4767–4774. [Google Scholar] [CrossRef]
- Purysko, A.S.; Bullen, J.; Valdez, R.; Austhof, E.; D’Ippolito, G.; Klein, E.A. Influence of 5-alpha reductase inhibitors on prostate cancer detection with magnetic resonance imaging: A matched cohort study. J. Urol. 2021, 206, 1139–1146. [Google Scholar] [CrossRef]
- Wu, X.-J.; Zhi, Y.; Zheng, J.; He, P.; Zhou, X.-Z.; Li, W.-B.; Zhou, Z.-S. Dutasteride on benign prostatic hyperplasia: A meta-analysis on randomized clinical trials in 6460 patients. Urology 2014, 83, 539–543. [Google Scholar] [CrossRef]
- Eklund, M.; Jäderling, F.; Discacciati, A.; Bergman, M.; Annerstedt, M.; Aly, M.; Glaessgen, A.; Carlsson, S.; Grönberg, H.; Nordström, T. MRI-Targeted or Standard Biopsy in Prostate Cancer Screening. N. Engl. J. Med. 2021, 385, 908–920. [Google Scholar] [CrossRef]
- Auvinen, A.; Tammela, T.L.; Mirtti, T.; Lilja, H.; Tolonen, T.; Kenttämies, A.; Rinta-Kiikka, I.; Lehtimäki, T.; Natunen, K.; Nevalainen, J.; et al. Prostate Cancer Screening with PSA, Kallikrein Panel, and MRI: The ProScreen Randomized Trial. JAMA 2024, 331, 1452–1459. [Google Scholar] [CrossRef]
- Rebbeck, T.R.; Devesa, S.S.; Chang, B.L.; Bunker, C.H.; Cheng, I.; Cooney, K.; Eeles, R.; Fernandez, P.; Giri, V.N.; Gueye, S.M.; et al. Global patterns of prostate cancer incidence, aggressiveness, and mortality in men of African descent. Prostate Cancer 2013, 2013, 560857. [Google Scholar] [CrossRef] [PubMed]



| Training Set | Test Set | |||||
|---|---|---|---|---|---|---|
| Median Value | Range, IQR | Rate | Median Value | Range, IQR | Rate | |
| Age | 67 | 43–84; (61–73) | - | 66 | 49–80; (61–72) | - |
| PSA (ng/mL) | 8.52 | 0.36–157; (4.3–9.3) | - | 8.75 | 2–106; (4.9–8.9) | - |
| PSAD (ng/mL/mL) | 0.15 | 0.002–1.98; (0.08–0.18) | - | 0.17 | 0.03–2.6; (0.08–0.17) | - |
| Men with prior negative biopsy | - | - | 93/430 = 0.22 | - | - | 25/108 = 0.23 |
| Positive DRE | - | - | 128/430 = 0.3 | - | - | 34/108 = 0.31 |
| Family history of prostate cancer | - | - | 76/430 = 0.18 | - | - | 16/108 = 0.15 |
| Ongoing therapy for the prostate | - | - | 164/430 = 0.38 | - | - | 45/108 = 0.41 |
| Prostate volume (mL) | 60 | 15–291; (38–73) | - | 61.5 | 12–200; (37.75–80.5) | - |
| PI-RADS category of the index lesion | ||||||
| PI-RADS 1 | 56/430 = 0.13 | 14/108 = 0.13 | ||||
| PI-RADS 2 | 41/430 = 0.10 | 12/108 = 0.11 | ||||
| PI-RADS 3 | 56/430 = 0.13 | 17/108 = 0.16 | ||||
| PI-RADS 4 | 159/430 = 0.37 | 41/108 = 0.38 | ||||
| PI-RADS 5 | 118/430 = 0.27 | 24/108 = 0.22 | ||||
| Site of visible index lesions on MRI | ||||||
| Base | 70/380 = 0.18 | 24/94 = 0.25 | ||||
| Mid-gland | 161/380 = 0.43 | 40/94 = 0.43 | ||||
| Apex | 80/380 = 0.21 | 15/94 = 0.16 | ||||
| 69/380 = 0.18 | 15/94 = 0.16 | |||||
| Size of MRI-visible lesions | 13,7 | 4–47; (8–17) | - | 12 | 4–35; (7–15) | - |
| Prostate cancer: histology | ||||||
| No cancer | - | - | 192/430 = 0.45 | - | - | 50/108 = 0.46 |
| GG1 | - | - | 85/430 = 0.20 | - | - | 21/108 = 0.09 |
| GG2 | - | - | 66/430 = 0.15 | - | - | 15/108 = 0.14 |
| GG3 | - | - | 47/430 = 0.11 | - | - | 13/108 = 0.12 |
| GG4 | - | - | 21/430 = 0.05 | - | - | 5/108 = 0.05 |
| GG5 | - | - | 19/430 = 0.04 | - | - | 4/108 = 0.04 |
| Prostate cancer: T stage on MRI | ||||||
| ≤T2 | 95/153 = 0.62 | 20/37 = 0.54 | ||||
| T3a | 43/153 = 0.28 | 17/37 = 0.46 | ||||
| T3b | 10/153 = 0.07 | 0 | ||||
| T4 | 5/153 = 0.03 | 0 | ||||
| Variable | Univariable Analysis | Multivariable Analysis | |||
|---|---|---|---|---|---|
| Prevalence in the Cohort (%) | Prevalence in Men with csPCa (%) | p | OR (95%CI) | p | |
| Age ≥ 65 years | 334/538 (62.1%) | 141/190 (74.2%) | <0.0001 | 2.32 (1.42–3.50) | 0.0005 |
| PSA ≥ 10 ng/mL | 111/538 (20.6%) | 51/190 (26.8%) | 0.0086 | - | - |
| PSAD ≥ ng/mL/mL | 196/538 (36.4%) | 99/190 (52.1%) | <0.0001 | 2.70 (176–4.14) | <0.0001 |
| Positive DRE | 162/538 (30.1%) | 78/190 (41%) | 0.0002 | 1.73 (1.12–2.67) | 0.0126 |
| Prior negative biopsy | 118/538 (21.9%) | 25/190 (13.2%) | 0.0003 | 0.43 (0.24–0.76) | 0.0036 |
| Ongoing therapy with alpha-blockers or 5-alpha reductase inhibitors | 209/538 (38.8%) | 64/190 (33.7%) | 0.0697 | - | - |
| Family history of csPCa | 92/538 (17.1%) | 27/190 (14.2%) | 0.1888 | - | - |
| Prostate volume on MRI | 0.0018 | - | - | ||
| 1st quartile (12–38 mL) | 138/538 (25.6%) | 65/190 (34.2%) | |||
| 2nd quartile (39–52 mL) | 137/538 (25.5%) | 51/190 (26.8%) | |||
| 3rd quartile (53–73 mL) | 129/538 (24%) | 39/190 (20.5%) | |||
| 4th quartile (74–291 mL) | 134/538 (24.9%) | 35/190 (18.5%) | |||
| Lesion site on MRI | 0.0001 | - | - | ||
| No visible lesions | 65/538 (11.4%) | 5/190 (2.6%) | |||
| Base | 105/538 (19.6%) | 39/190 (20.6%) | |||
| Mid-gland | 214/538 (39.8%) | 79/190 (41.6%) | |||
| Apex | 97/538 (18.4%) | 38/190 (20%) | |||
| More sites involved | 57/538 (10.8%) | 29/190 (15.2%) | |||
| Lesion size on MRI | <0.0001 | - | - | ||
| Non visible | 65/538 (12.1%) | 5/190 (2.6%) | |||
| <1 cm | 173/538 (32.2%) | 38/190 (20%) | |||
| 1–1.9 cm | 217/538 (40.3%) | 96/190 (50.5%) | |||
| 2–2.9 cm | 54/538 (10%) | 27/190 (14.2%) | |||
| ≥3 cm | 29/538 (5.4%) | 24/190 (12.7%) | |||
| PI-RADS category | <0.0001 | 10.32 (5.83–18.27) | <0.0001 | ||
| 1–3 | 199/538 (37%) | 16/190 (8.4%) | |||
| 4–5 | 339/538 (63%) | 174/190 (91.6%) | |||
| Model | AUC (95%CI) | Threshold | Sensitivity % (95%CI) | Specificity % (95%CI) | NPV % (95%CI) | PPV % (95%CI) | ISUP Grading Group (GG) of Missed csPCa |
|---|---|---|---|---|---|---|---|
| Model 1 | 0.716 (0.676–0.754) | Confidence ≥ 0.27 | 87.4 (81.8–91.7) | 33.9 (28.9–39.1) | 83.1 (84.7–92.7) | 41.9 (39.6–44.2) | 14/24 GG2 6/24 GG3 1/24 GG4 3/24 GG5 |
| Model 2 | 0.778 (0.740–0.812) | Confidence ≥ 0.21, corresponding to PI-RADS ≥ 4 | 91.6 (86.6–95.1) | 52.6 (47.2–57.9) | 91.9 (87.6–94.8) | 51.3 (48.3–54.3) | 13/24 GG2 3/24 GG3 |
| Model 3 | 0.822 (0.787–0.853) | Confidence ≥ 0.32 | 86.8 (81.2–91.3) | 62.6 (57.3–67.7) | 89.7 (85.7–92.7) | 55.9 (52.2–59.5) | 19/24 GG2 6/24 GG3 |
| Biopsy Strategies | Net Benefit | ||||
|---|---|---|---|---|---|
| 10% | 15% | 20% | 25% | 30% | |
| Model 1 | 0.261 | 0.233 | 0.202 | 0.166 | 0.125 |
| Model 2 | 0.289 | 0.269 | 0.247 | 0.221 | 0.192 |
| Model 3 | 0.280 | 0.264 | 0.246 | 0.226 | 0.203 |
| Treat all (biopsying any lesion) | 0.281 | 0.239 | 0.191 | 0.138 | 0.076 |
| Treat none (biopsying no lesions) | 0 | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bacchetti, E.; De Nardin, A.; Giannarini, G.; Cereser, L.; Zuiani, C.; Crestani, A.; Girometti, R.; Foresti, G.L. A Deep Learning Model Integrating Clinical and MRI Features Improves Risk Stratification and Reduces Unnecessary Biopsies in Men with Suspected Prostate Cancer. Cancers 2025, 17, 2257. https://doi.org/10.3390/cancers17132257
Bacchetti E, De Nardin A, Giannarini G, Cereser L, Zuiani C, Crestani A, Girometti R, Foresti GL. A Deep Learning Model Integrating Clinical and MRI Features Improves Risk Stratification and Reduces Unnecessary Biopsies in Men with Suspected Prostate Cancer. Cancers. 2025; 17(13):2257. https://doi.org/10.3390/cancers17132257
Chicago/Turabian StyleBacchetti, Emiliano, Axel De Nardin, Gianluca Giannarini, Lorenzo Cereser, Chiara Zuiani, Alessandro Crestani, Rossano Girometti, and Gian Luca Foresti. 2025. "A Deep Learning Model Integrating Clinical and MRI Features Improves Risk Stratification and Reduces Unnecessary Biopsies in Men with Suspected Prostate Cancer" Cancers 17, no. 13: 2257. https://doi.org/10.3390/cancers17132257
APA StyleBacchetti, E., De Nardin, A., Giannarini, G., Cereser, L., Zuiani, C., Crestani, A., Girometti, R., & Foresti, G. L. (2025). A Deep Learning Model Integrating Clinical and MRI Features Improves Risk Stratification and Reduces Unnecessary Biopsies in Men with Suspected Prostate Cancer. Cancers, 17(13), 2257. https://doi.org/10.3390/cancers17132257






