Experimental and Computational Analysis of High-Intensity Focused Ultrasound Thermal Ablation in Breast Cancer Cells: Monolayers vs. Spheroids
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
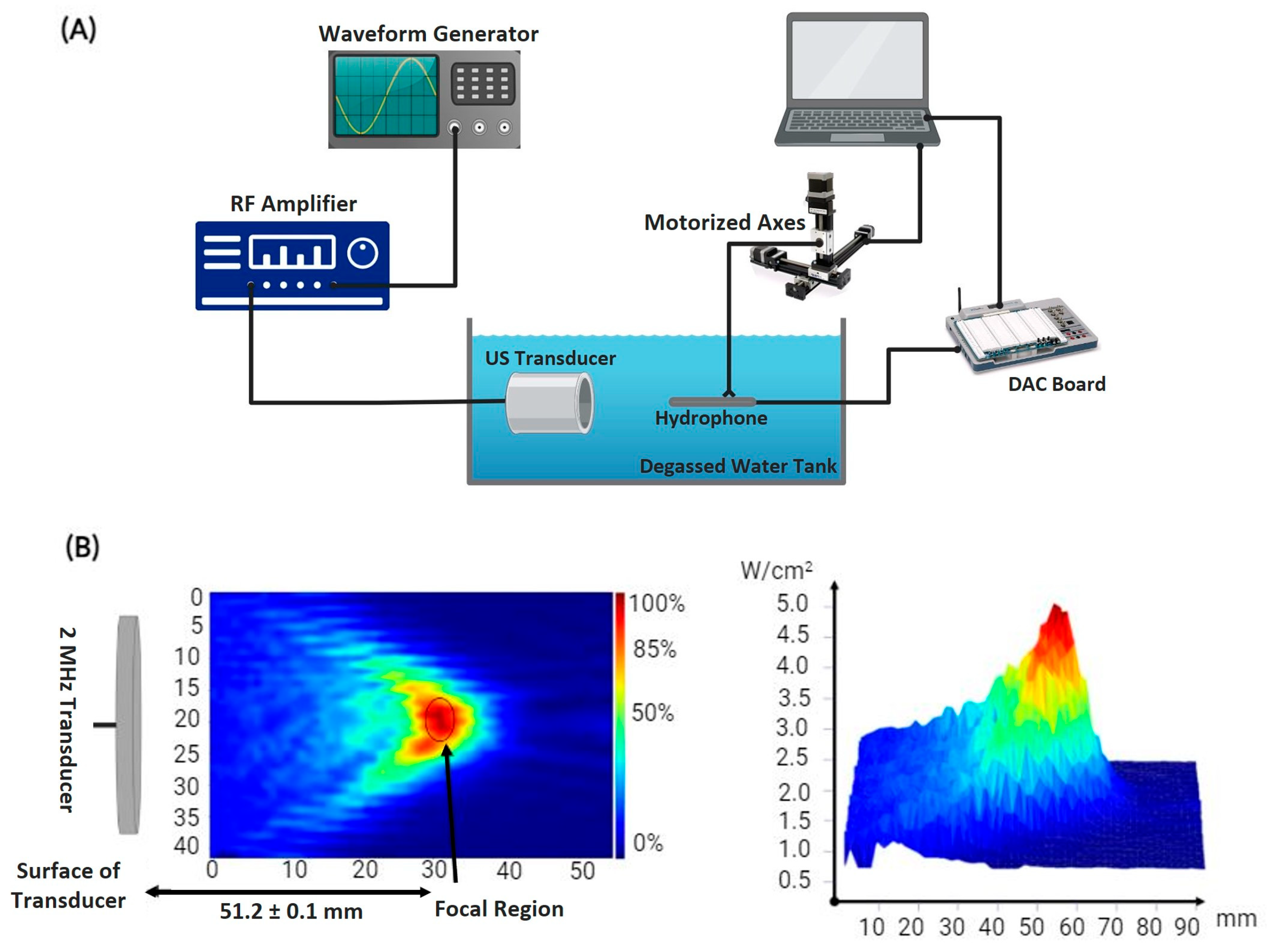
2.1. HIFU Mapping and Characterization
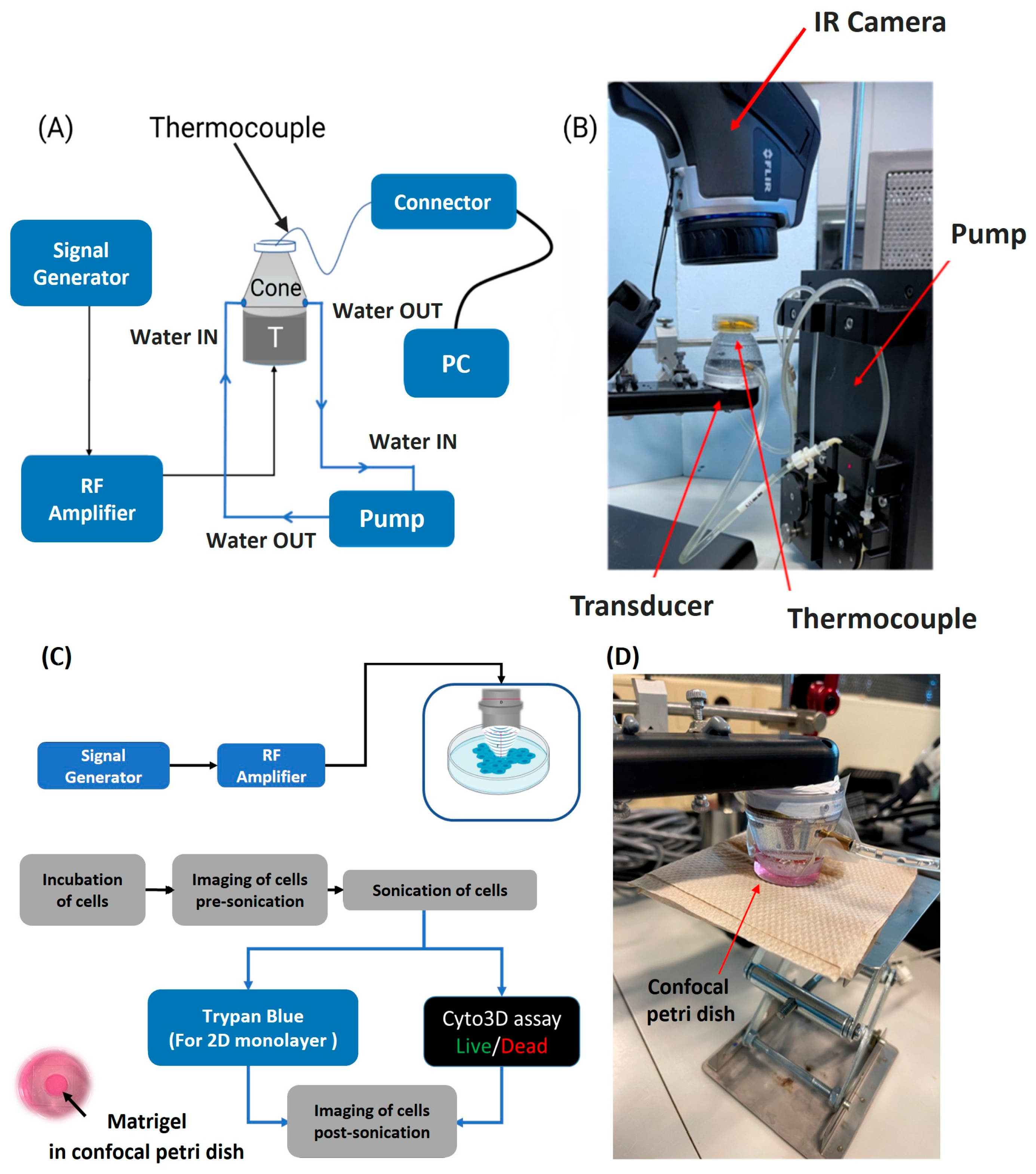
2.2. Temperature Acquisition
2.3. Two-Dimensional and Three-Dimensional Tumor Cell Culturing
2.4. Ultrasound Sonication and Cellular Ablation
2.5. Statistical Analysis
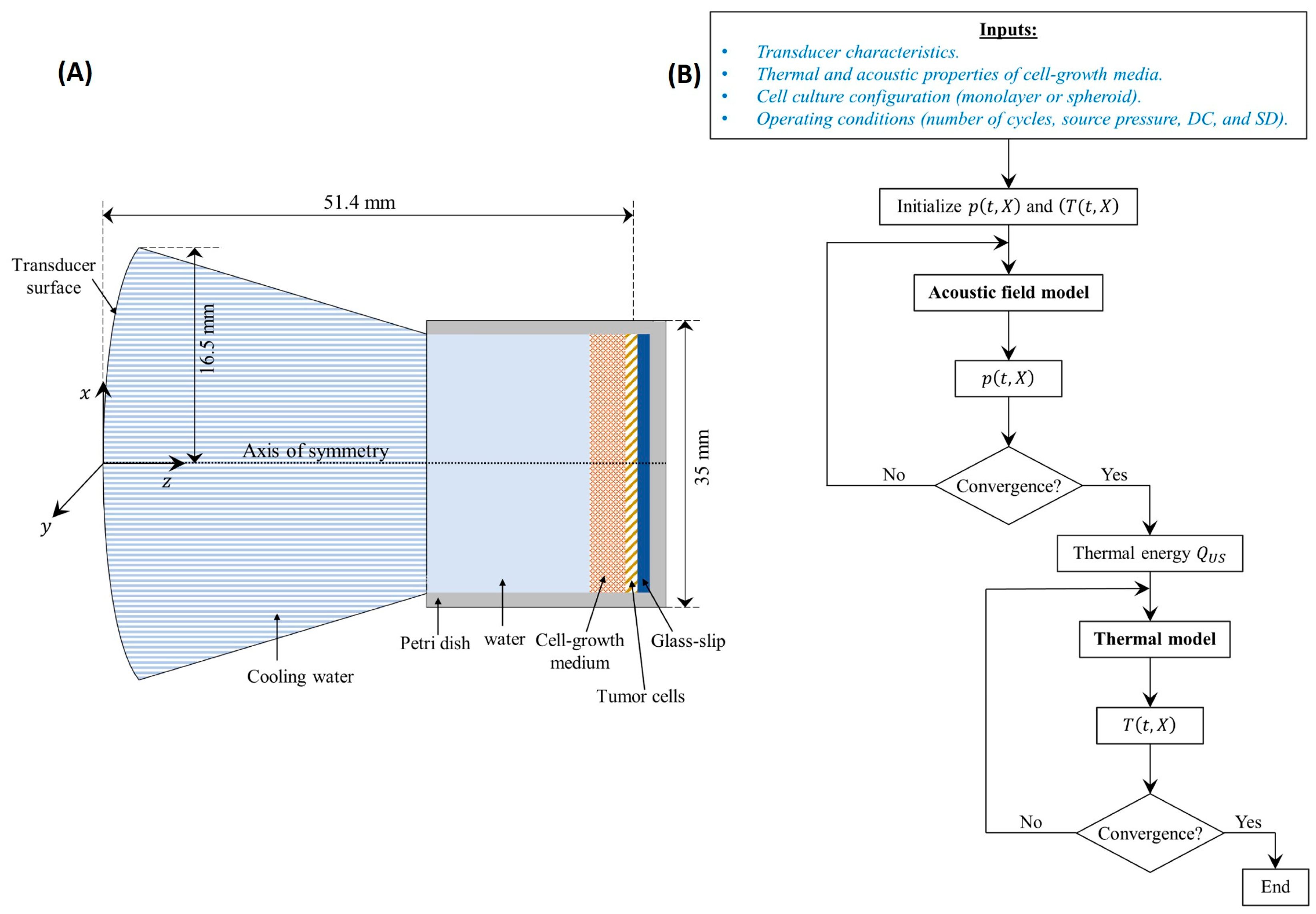
2.6. Computational Modeling
2.6.1. Computational Domain
2.6.2. Acoustic Field Model Coupled with the Thermal Model
3. Results
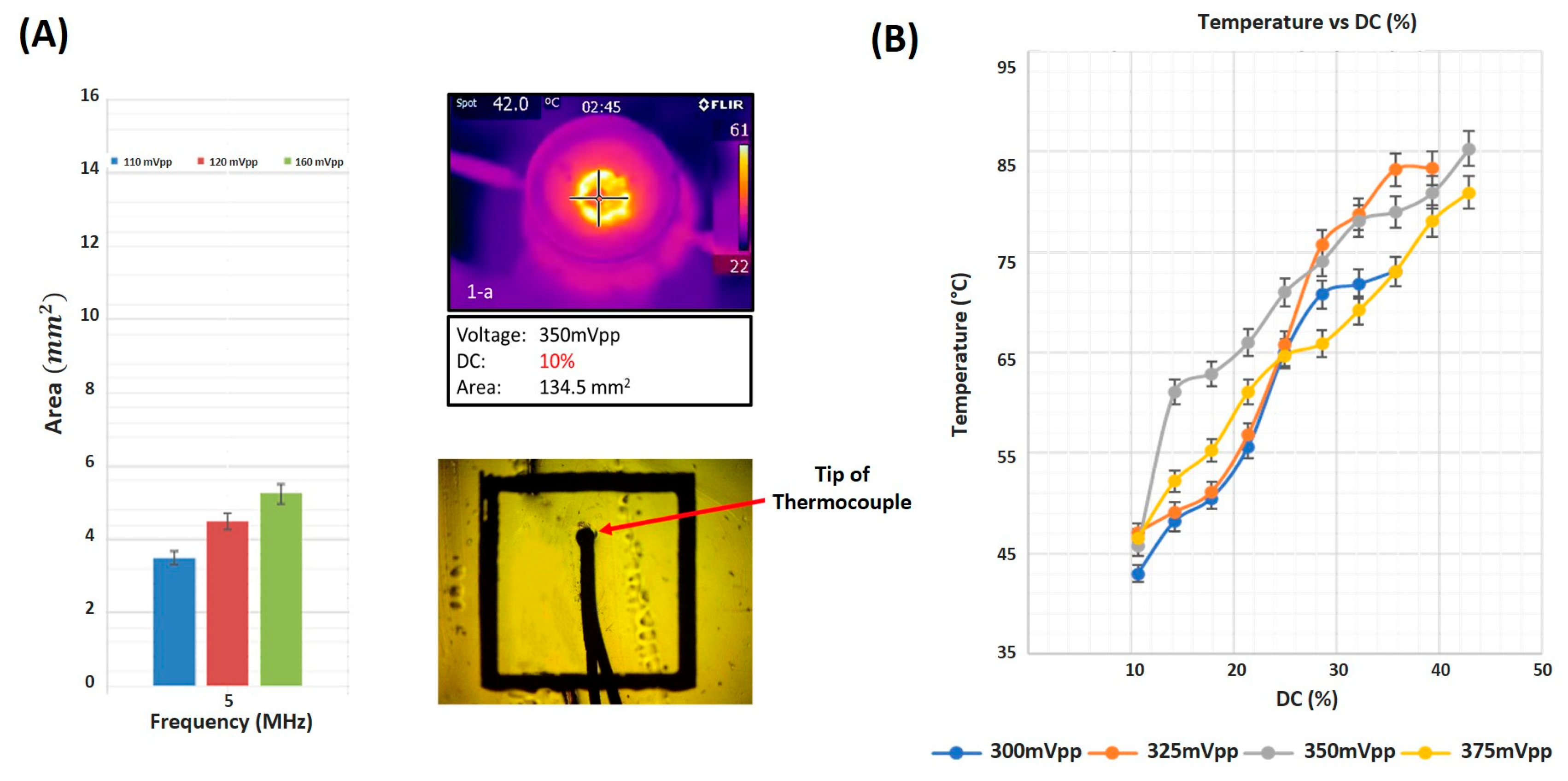
3.1. Focal Area and Temperature Measurements
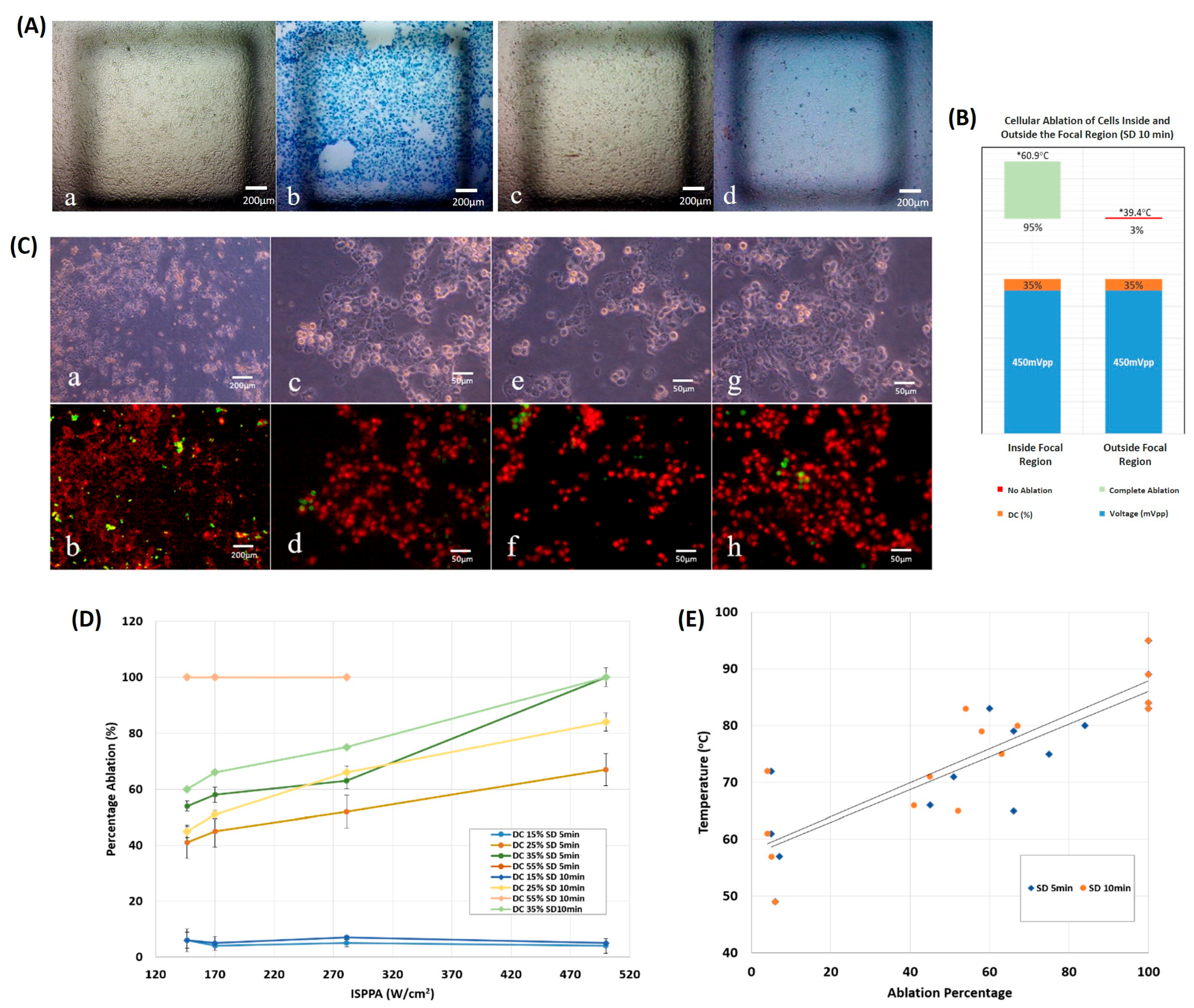
3.2. Cellular Ablation Using HIFU
3.2.1. On 2D Cultures
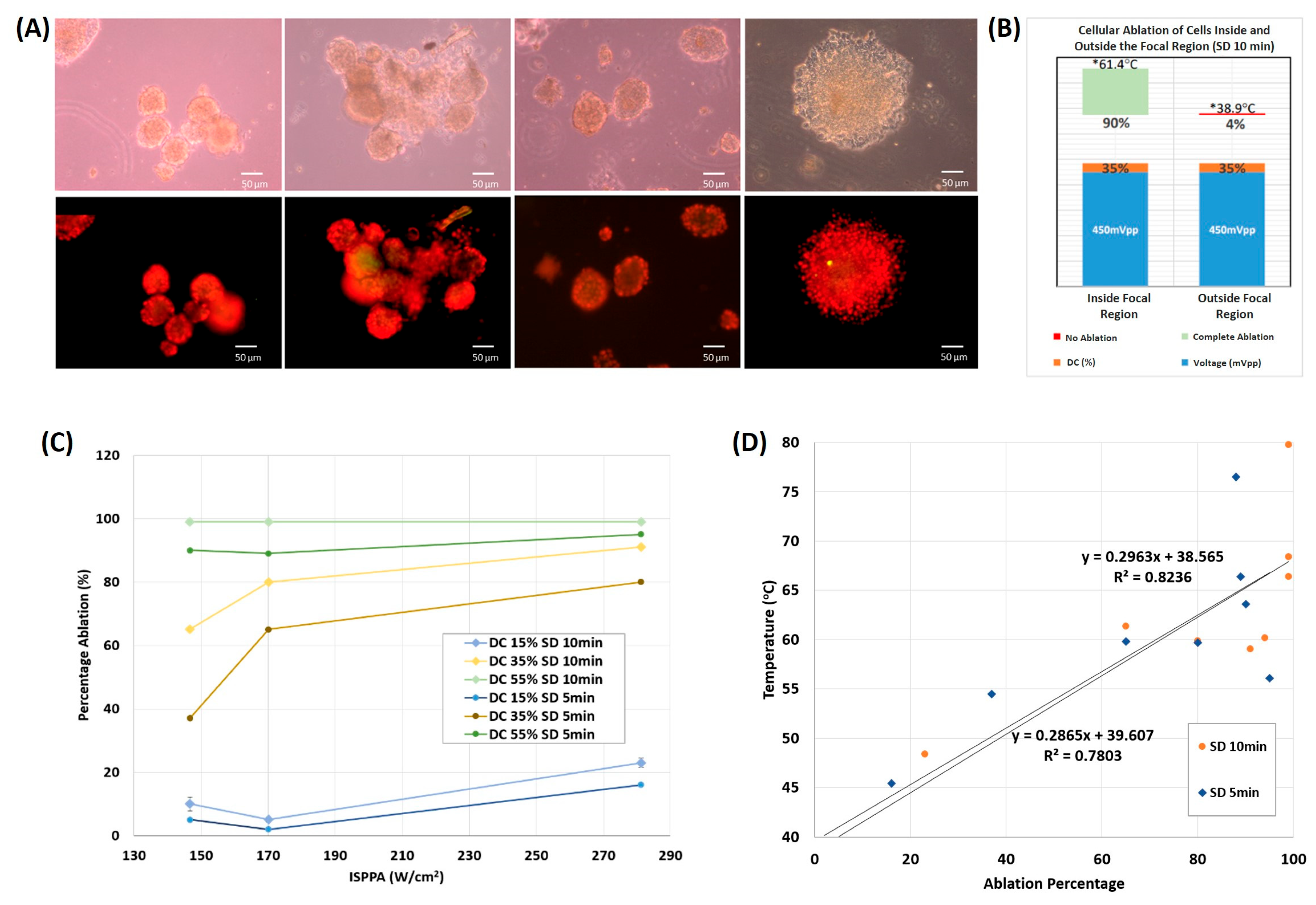
3.2.2. On 3D Cultures
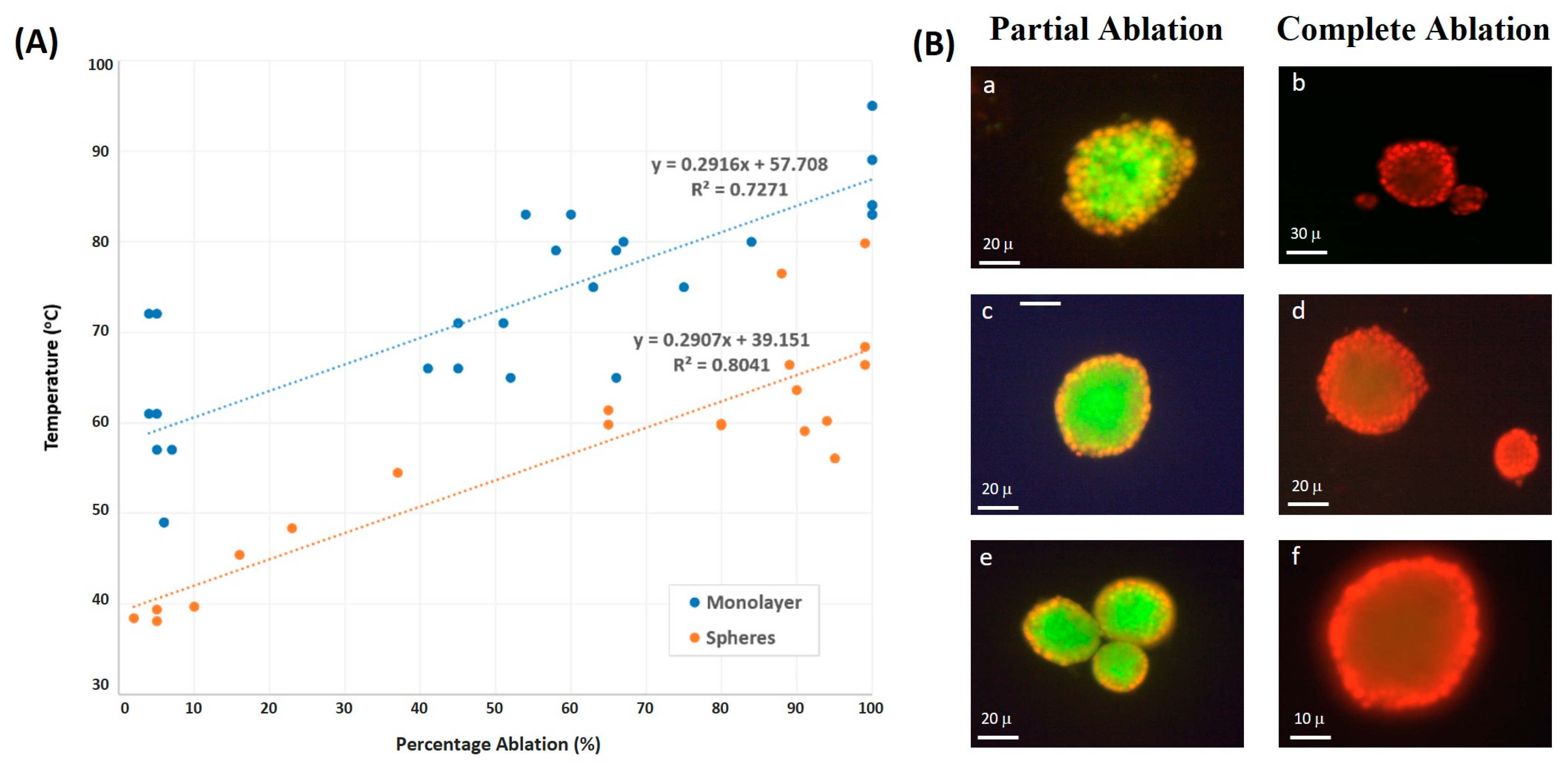
3.3. Spheroid vs. Monolayer Thermal Culture Ablation
3.4. Numerical Simulations
4. Discussion
4.1. Duty Cycle Affects Degree of Cellular Ablation
4.2. Monolayer vs. Spheroid Ablation Temperature
4.3. Partial and Complete Cellular Ablation in Spheroids
4.4. Model Validation
4.5. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zulkifli, D.; Manan, H.A.; Yahya, N.; Hamid, H.A. The applications of high-intensity focused ultrasound (HIFU) ablative therapy in the treatment of primary breast cancer: A systematic review. Diagnostics 2023, 13, 2595. [Google Scholar] [CrossRef] [PubMed]
- Nazari, S.S.; Mukherjee, P. An overview of mammographic density and its association with breast cancer. Breast Cancer 2018, 25, 259–267. [Google Scholar] [CrossRef]
- Singh, M.; Dalal, M.; Sodhi, G.S. Estimation of clinical size of breast tumour lesions using contrast enhanced magnetic resonance imaging: Delineation of tumour boundaries. In Proceedings of the Summer Biomechanics, Bioengineering and Biotransport Conference, Virtual, 14–18 June 2021. [Google Scholar]
- Habli, Z.; Zantout, A.; El-Sabban, M.; Khraiche, M.L. Investigating malignancy-dependent mechanical properties of breast cancer cells. In Proceedings of the 2023 45th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Sydney, Australia, 24–27 July 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Habli, Z.; AlChamaa, W.; Saab, R.; Kadara, H.; Khraiche, M.L. Circulating Tumor Cell Detection Technologies and Clinical Utility: Challenges and Opportunities. Cancers 2020, 12, 1930. [Google Scholar] [CrossRef] [PubMed]
- Vogl, T.J.; Farshid, P.; Naguib, N.N.; Zangos, S. Thermal ablation therapies in patients with breast cancer liver metastases: A review. Eur. Radiol. 2013, 23, 797–804. [Google Scholar] [CrossRef]
- van de Voort, E.M.; Struik, G.M.; Birnie, E.; Moelker, A.; Verhoef, C.; Klem, T.M. Thermal ablation as an alternative for surgical resection of small (≤2 cm) breast cancers: A meta-analysis. Clin. Breast Cancer 2021, 21, e715–e730. [Google Scholar] [CrossRef]
- Kinoshita, T. RFA experiences, indications and clinical outcomes. Int. J. Clin. Oncol. 2019, 24, 603–607. [Google Scholar] [CrossRef] [PubMed]
- Benjamin, D.J. The efficacy of surgical treatment of cancer–20 years later. Med. Hypotheses 2014, 82, 412–420. [Google Scholar] [CrossRef]
- Singh, M.; Singh, T.; Soni, S. Pre-operative assessment of ablation margins for variable blood perfusion metrics in a magnetic resonance imaging based complex breast tumour anatomy: Simulation paradigms in thermal therapies. Comput. Methods Programs Biomed. 2021, 198, 105781. [Google Scholar] [CrossRef]
- Ahmed, M.; Goldberg, S.N. Basic science research in thermal ablation. Surg. Oncol. Clin. 2011, 20, 237–258. [Google Scholar] [CrossRef]
- Khraiche, M.L.; Phillips, W.B.; Jackson, N.; Muthuswamy, J. Sustained elevation of activity of developing neurons grown on polyimide microelectrode arrays (MEA) in response to ultrasound exposure. Microsyst. Technol. 2017, 23, 3671–3683. [Google Scholar] [CrossRef]
- Narayanan, G.; Daye, D.; Wilson, N.M.; Noman, R.; Mahendra, A.M.; Doshi, M.H. Ablation in Pancreatic Cancer: Past, Present and Future. Cancers 2021, 13, 2511. [Google Scholar] [CrossRef]
- Maloney, E.; Hwang, J.H. Emerging HIFU applications in cancer therapy. Int. J. Hyperth. 2015, 31, 302–309. [Google Scholar] [CrossRef]
- van den Bijgaart, R.J.; Eikelenboom, D.C.; Hoogenboom, M.; Fütterer, J.J.; den Brok, M.H.; Adema, G.J. Thermal and mechanical high-intensity focused ultrasound: Perspectives on tumor ablation, immune effects and combination strategies. Cancer Immunol. Immunother. 2017, 66, 247–258. [Google Scholar] [CrossRef] [PubMed]
- Todd, N.; McDannold, N.; Borsook, D. Targeted manipulation of pain neural networks: The potential of focused ultrasound for treatment of chronic pain. Neurosci. Biobehav. Rev. 2020, 115, 238–250. [Google Scholar] [CrossRef] [PubMed]
- Singh, M. Incorporating vascular-stasis based blood perfusion to evaluate the thermal signatures of cell-death using modified Arrhenius equation with regeneration of living tissues during nanoparticle-assisted thermal therapy. Int. Commun. Heat Mass Transf. 2022, 135, 106046. [Google Scholar] [CrossRef]
- Izadifar, Z.; Babyn, P.; Chapman, D. Ultrasound cavitation/microbubble detection and medical applications. J. Med. Biol. Eng. 2019, 39, 259–276. [Google Scholar] [CrossRef]
- Orsi, F.; Arnone, P.; Chen, W.; Zhang, L. High intensity focused ultrasound ablation: A new therapeutic option for solid tumors. J. Cancer Res. Ther. 2010, 6, 414–420. [Google Scholar] [PubMed]
- Kapałczyńska, M.; Kolenda, T.; Przybyła, W.; Zajączkowska, M.; Teresiak, A.; Filas, V.; Ibbs, M.; Bliźniak, R.; Łuczewski, Ł.; Lamperska, K. 2D and 3D cell cultures–A comparison of different types of cancer cell cultures. Arch. Med. Sci. 2018, 14, 910–919. [Google Scholar] [CrossRef]
- Roy, M.; Alix, C.; Bouakaz, A.; Serrière, S.; Escoffre, J.-M. Tumor Spheroids as Model to Design Acoustically Mediated Drug Therapies: A Review. Pharmaceutics 2023, 15, 806. [Google Scholar] [CrossRef] [PubMed]
- Vantangoli, M.M.; Madnick, S.J.; Huse, S.M.; Weston, P.; Boekelheide, K. MCF-7 human breast cancer cells form differentiated microtissues in scaffold-free hydrogels. PLoS ONE 2015, 10, e0135426. [Google Scholar] [CrossRef]
- El Hassan, R.; Lawand, N.; Al-Chaer, E.; Khraiche, M. Frequency dependent, reversible focused ultrasound suppression of evoked potentials in the reflex arc in an anesthetized animal. J. Peripher. Nerv. Syst. 2022, 27, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Tiennot, T.; Kamimura, H.A.; Lee, S.A.; Aurup, C.; Konofagou, E.E. Numerical modeling of ultrasound heating for the correction of viscous heating artifacts in soft tissue temperature measurements. Appl. Phys. Lett. 2019, 114, 203702. [Google Scholar] [CrossRef] [PubMed]
- Fry, W.J.; Fry, R.B. Determination of absolute sound levels and acoustic absorption coefficients by thermocouple probes—Theory. J. Acoust. Soc. Am. 1954, 26, 294–310. [Google Scholar] [CrossRef]
- Parker, K.J. Ultrasonic attenuation and absorption in liver tissue. Ultrasound Med. Biol. 1983, 9, 363–369. [Google Scholar] [CrossRef] [PubMed]
- Morris, H.; Rivens, I.; Shaw, A.; Ter Haar, G. Investigation of the viscous heating artefact arising from the use of thermocouples in a focused ultrasound field. Phys. Med. Biol. 2008, 53, 4759. [Google Scholar] [CrossRef]
- Karaböce, B.; Çetin, E.; Durmuş, H.O. Investigation of temperature rise in tissue—Mimicking material induced by a HIFU transducer. In Proceedings of the 2016 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Benevento, Italy, 15–18 May 2016; pp. 1–6. [Google Scholar]
- Jones, D.; Brischke, C. Performance of Bio-Based Building Materials; Woodhead Publishing: Cambridge, UK, 2017. [Google Scholar]
- Khraiche, M.L.; Rogul, J.; Muthuswamy, J. Design and Development of Microscale Thickness Shear Mode (TSM) Resonators for Sensing Neuronal Adhesion. Front. Neurosci. 2019, 13, 518. [Google Scholar] [CrossRef]
- Secomski, W.; Bilmin, K.; Kujawska, T.; Nowicki, A.; Grieb, P.; Lewin, P.A. In vitro ultrasound experiments: Standing wave and multiple reflections influence on the outcome. Ultrasonics 2017, 77, 203–213. [Google Scholar] [CrossRef]
- O’Reilly, M.A.; Huang, Y.; Hynynen, K. The impact of standing wave effects on transcranial focused ultrasound disruption of the blood–brain barrier in a rat model. Phys. Med. Biol. 2010, 55, 5251. [Google Scholar] [CrossRef]
- Khraiche, M.; Muthuswamy, J. Multi-modal biochip for simultaneous, real-time measurement of adhesion and electrical activity of neurons in culture. Lab Chip 2012, 12, 2930–2941. [Google Scholar] [CrossRef]
- Anastasiadis, P.; Mohammadabadi, A.; Fishman, M.J.; Smith, J.A.; Nguyen, B.A.; Hersh, D.S.; Frenkel, V. Design, characterization and evaluation of a laser-guided focused ultrasound system for preclinical investigations. BioMed. Eng. OnLine 2019, 18, 36. [Google Scholar] [CrossRef] [PubMed]
- Badawe, H.M.; El Hassan, R.H.; Khraiche, M.L. Modeling ultrasound modulation of neural function in a single cell. Heliyon 2023, 9, e22522. [Google Scholar] [CrossRef]
- ter Haar, G.; Coussios, C. High intensity focused ultrasound: Physical principles and devices. Int. J. Hyperth. 2007, 23, 89–104. [Google Scholar] [CrossRef] [PubMed]
- Bachu, V.S.; Kedda, J.; Suk, I.; Green, J.J.; Tyler, B. High-intensity focused ultrasound: A review of mechanisms and clinical applications. Ann. Biomed. Eng. 2021, 49, 1975–1991. [Google Scholar] [CrossRef] [PubMed]
- Badawe, H.; Khraiche, M. Modeling of Calcium-dependent Low Intensity Low Frequency Ultrasound Modulation of a Hodgkin–Huxley Neuron. In Proceedings of the 2023 45th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Sydney, Australia, 24–27 July 2023. [Google Scholar]
- Gupta, P.; Srivastava, A. Non-Fourier transient thermal analysis of biological tissue phantoms subjected to high intensity focused ultrasound. Int. J. Heat Mass Transf. 2019, 136, 1052–1063. [Google Scholar] [CrossRef]
- Lean, H.Q.; Zhou, Y. Acoustic field of phased-array ultrasound transducer with the focus/foci shifting. J. Med. Biol. Eng. 2019, 39, 919–931. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, B.; Chen, Q.; Wang, L.; Bai, Y. Cellular Automata Modeling of Propagation and Absorption of Acoustic Waves in Impedance Tube; Universitätsbibliothek der RWTH Aachen: Aachen, Germany, 2019. [Google Scholar]
- Červenka, M.; Bednařík, M. A versatile computational approach for the numerical modelling of parametric acoustic array. J. Acoust. Soc. Am. 2019, 146, 2163–2169. [Google Scholar] [CrossRef] [PubMed]
- Doinikov, A.A.; Novell, A.; Calmon, P.; Bouakaz, A. Simulations and measurements of 3-D ultrasonic fields radiated by phased-array transducers using the westervelt equation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1470–1477. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Zhou, Y. Simulation of non-linear acoustic field and thermal pattern of phased-array high-intensity focused ultrasound (HIFU). Int. J. Hyperth. 2016, 32, 569–582. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Haddadi, S.; Ahmadian, M.T. Analysis of nonlinear acoustic wave propagation in HIFU treatment using Westervelt equation. Sci. Iran. 2018, 25, 2087–2097. [Google Scholar] [CrossRef]
- Cai, W.; Chen, W.; Fang, J.; Holm, S. A survey on fractional derivative modeling of power-law frequency-dependent viscous dissipative and scattering attenuation in acoustic wave propagation. Appl. Mech. Rev. 2018, 70, 030802. [Google Scholar] [CrossRef]
- Hamilton, M.F. Comparison of three transient solutions for the axial pressure in a focused sound beam. J. Acoust. Soc. Am. 1992, 92, 527–532. [Google Scholar] [CrossRef]
- Roohi, R.; Baroumand, S.; Hosseinie, R.; Ahmadi, G. Numerical simulation of HIFU with dual transducers: The implementation of dual-phase lag bioheat and non-linear Westervelt equations. Int. Commun. Heat Mass Transf. 2021, 120, 105002. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef] [PubMed]
- Singh, M. Modified Pennes bioheat equation with heterogeneous blood perfusion: A newer perspective. Int. J. Heat Mass Transf. 2024, 218, 124698. [Google Scholar] [CrossRef]
- Andreozzi, A.; Iasiello, M.; Tucci, C. An overview of mathematical models and modulated-heating protocols for thermal ablation. Adv. Heat Transf. 2020, 52, 489–541. [Google Scholar]
- Cafarchio, A.; Iasiello, M.; Brunese, M.C.; Francica, G.; Rocca, A.; Andreozzi, A. Emprint Microwave Thermoablation System: Bridging Thermal Ablation Efficacy between Human Patients and Porcine Models through Mathematical Correlation. Bioengineering 2023, 10, 1057. [Google Scholar] [CrossRef] [PubMed]
- Trujillo, M.; Berjano, E. Review of the mathematical functions used to model the temperature dependence of electrical and thermal conductivities of biological tissue in radiofrequency ablation. Int. J. Hyperth. 2013, 29, 590–597. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; Wiley: New York, NY, USA, 1996; Volume 6. [Google Scholar]
- Gupta, P.; Srivastava, A. Numerical analysis of thermal response of tissues subjected to high intensity focused ultrasound. Int. J. Hyperth. 2018, 35, 419–434. [Google Scholar] [CrossRef]
- Zhu, Q.; Liu, C.; Liu, L.; Li, Y. Effect of pulse parameters on ablation efficiency in dual-frequency HIFU therapy. Ultrasonics 2023, 134, 107064. [Google Scholar] [CrossRef]
- Wang, Y.-N.; Khokhlova, T.; Bailey, M.; Hwang, J.H.; Khokhlova, V. Histological and biochemical analysis of mechanical and thermal bioeffects in boiling histotripsy lesions induced by high intensity focused ultrasound. Ultrasound Med. Biol. 2013, 39, 424–438. [Google Scholar] [CrossRef]
- Pahk, K.J.; Heo, J.; Joung, C.; Pahk, K. Noninvasive mechanical destruction of liver tissue and tissue decellularisation by pressure-modulated shockwave histotripsy. Front. Immunol. 2023, 14, 1150416. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.; Gupta, A.; Matuwana, D.; Amante, J.J.; Kearney, C.J.; Rotello, V.M. In vitro cell culture models for ultrasound treatments using collagen-based scaffolds. MethodsX 2022, 9, 101909. [Google Scholar] [CrossRef]
- Özsoy, Ç.; Lafci, B.; Reiss, M.; Deán-Ben, X.L.; Razansky, D. Real-time assessment of high-intensity focused ultrasound heating and cavitation with hybrid optoacoustic ultrasound imaging. Photoacoustics 2023, 31, 100508. [Google Scholar] [CrossRef] [PubMed]
- Leenhardt, R.; Camus, M.; Mestas, J.; Jeljeli, M.; Abou Ali, E.; Chouzenoux, S.; Bordacahar, B.; Nicco, C.; Batteux, F.; Lafon, C. Ultrasound-induced Cavitation enhances the efficacy of Chemotherapy in a 3D Model of Pancreatic Ductal Adenocarcinoma with its microenvironment. Sci. Rep. 2019, 9, 18916. [Google Scholar] [CrossRef] [PubMed]
- Ciuti, P.; Dezhkunov, N.; Francescutto, A.; Calligaris, F.; Sturman, F. Study into mechanisms of the enhancement of multibubble sonoluminescence emission in interacting fields of different frequencies. Ultrason. Sonochem. 2003, 10, 337–341. [Google Scholar] [CrossRef]
- Yildirim, A.; Shi, D.; Roy, S.; Blum, N.T.; Chattaraj, R.; Cha, J.N.; Goodwin, A.P. Nanoparticle-mediated acoustic cavitation enables high intensity focused ultrasound ablation without tissue heating. ACS Appl. Mater. Interfaces 2018, 10, 36786–36795. [Google Scholar] [CrossRef] [PubMed]
- Landgraf, L.; Kozlowski, A.; Zhang, X.; Fournelle, M.; Becker, F.-J.; Tretbar, S.; Melzer, A. Focused ultrasound treatment of a spheroid in vitro tumour model. Cells 2022, 11, 1518. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Cunitz, B.W.; Dunmire, B.; Wang, Y.N.; Karl, S.G.; Warren, C.; Mitchell, S.; Hwang, J.H. Characterization and Ex Vivo evaluation of an extracorporeal high-intensity focused ultrasound (HIFU) system. J. Appl. Clin. Med. Phys. 2021, 22, 345–359. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, D.; Zhao, W. Beneficial response of eldly patients with advanced pancreatic cancer after HIFU treatment. Chin. J. Clin. 2012, 6, 7784–7786. [Google Scholar]
- Sofuni, A.; Moriyasu, F.; Sano, T.; Yamada, K.; Itokawa, F.; Tsuchiya, T.; Tsuji, S.; Kurihara, T.; Ishii, K.; Itoi, T. The current potential of high-intensity focused ultrasound for pancreatic carcinoma. J. Hepato-Biliary-Pancreat. Sci. 2011, 18, 295–303. [Google Scholar] [CrossRef]
- Khokhlova, T.D.; Wang, Y.-N.; Simon, J.C.; Cunitz, B.W.; Starr, F.; Paun, M.; Crum, L.A.; Bailey, M.R.; Khokhlova, V.A. Ultrasound-guided tissue fractionation by high intensity focused ultrasound in an in vivo porcine liver model. Proc. Natl. Acad. Sci. USA 2014, 111, 8161–8166. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Hunter, K.S.; Shandas, R. Wave scattering from encapsulated microbubbles subject to high-frequency ultrasound: Contribution of higher-order scattering modes. J. Acoust. Soc. Am. 2009, 126, 1766–1775. [Google Scholar] [CrossRef] [PubMed]
- Mohanty, K.; Papadopoulou, V.; Newsome, I.G.; Shelton, S.; Dayton, P.A.; Muller, M. Ultrasound multiple scattering with microbubbles can differentiate between tumor and healthy tissue in vivo. Phys. Med. Biol. 2019, 64, 115022. [Google Scholar] [CrossRef] [PubMed]

| Layer | (kg/m3) | (J/kg∙K) | (W/m∙K) | (m/s) | (Np/m) | (−) | (−) |
|---|---|---|---|---|---|---|---|
| Water | 1000 | 4180 | 0.615 | 1520 | 2.8 × 10−4 | 3.5 | 2 |
| DMEM | 1023 | 3800 | 0.13 | 1560 | - | - | - |
| Hydrogel | 1060 | 3770 | 0.53 | 1560 | - | - | - |
| Cells | 1066 | 3610 | 0.442 | 1423 | 0.57 | - | 0.75 |
| Glass | 2500 | 880 | 1.1 | 4500 | 0.27 | 6.8 | 1.32 |
| Petri Dish | 1000 | 1350 | 0.165 | 2000 | 0.27 | 6.8 | 1.32 |
| Configuration | DC (%) | Pressure at the Source (MPa) | Experimental Maximum Temperature (°C) | Numerical Maximum Temperature (°C) | Error (%) |
|---|---|---|---|---|---|
| Monolayer | 15 | 0.433 | 49.0 | 46.6 | 5.0 |
| 0.661 | 72.0 | 71.2 | 1.1 | ||
| 30 | 0.433 | 74.5 | 88.1 | 15.0 | |
| Spheroids | 15 | 0.433 | 38.0 | 40.6 | 6.8 |
| 30 | 0.433 | 54.5 | 58.0 | 6.4 | |
| 55 | 0.433 | 63.3 | 63.5 | 0.3 |
| Configuration | DC (%) | Pressure at the Source (MPa) | Final Temperature Range (°C) |
|---|---|---|---|
| Monolayer | 15 | 0.433 | (46.53; 46.59) |
| 0.661 | (55.13; 71.21) | ||
| 30 | 0.433 | (88.00; 88.11) | |
| 0.661 | (74.01; 95.71) | ||
| Spheroids | 15 | 0.433 | (40.55; 40.6) |
| 0.661 | (42.9; 55.41) | ||
| 30 | 0.433 | (57.88; 57.96) | |
| 0.661 | (48.01; 62.01) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badawe, H.M.; Harouz, J.P.; Raad, P.; Abu, K.; Freije, A.; Ghali, K.; Abou-Kheir, W.; Khraiche, M.L. Experimental and Computational Analysis of High-Intensity Focused Ultrasound Thermal Ablation in Breast Cancer Cells: Monolayers vs. Spheroids. Cancers 2024, 16, 1274. https://doi.org/10.3390/cancers16071274
Badawe HM, Harouz JP, Raad P, Abu K, Freije A, Ghali K, Abou-Kheir W, Khraiche ML. Experimental and Computational Analysis of High-Intensity Focused Ultrasound Thermal Ablation in Breast Cancer Cells: Monolayers vs. Spheroids. Cancers. 2024; 16(7):1274. https://doi.org/10.3390/cancers16071274
Chicago/Turabian StyleBadawe, Heba M., Jean Paul Harouz, Petra Raad, Kareem Abu, Anthony Freije, Kamel Ghali, Wassim Abou-Kheir, and Massoud L. Khraiche. 2024. "Experimental and Computational Analysis of High-Intensity Focused Ultrasound Thermal Ablation in Breast Cancer Cells: Monolayers vs. Spheroids" Cancers 16, no. 7: 1274. https://doi.org/10.3390/cancers16071274
APA StyleBadawe, H. M., Harouz, J. P., Raad, P., Abu, K., Freije, A., Ghali, K., Abou-Kheir, W., & Khraiche, M. L. (2024). Experimental and Computational Analysis of High-Intensity Focused Ultrasound Thermal Ablation in Breast Cancer Cells: Monolayers vs. Spheroids. Cancers, 16(7), 1274. https://doi.org/10.3390/cancers16071274






