Comparing Performances of Predictive Models of Toxicity after Radiotherapy for Breast Cancer Using Different Machine Learning Approaches
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Patient Characteristics, Endpoint Definition, and Available Variables
2.2. Data Preprocessing
2.3. Statistical and ML Methods
2.4. Metrics to Compare ML Methods
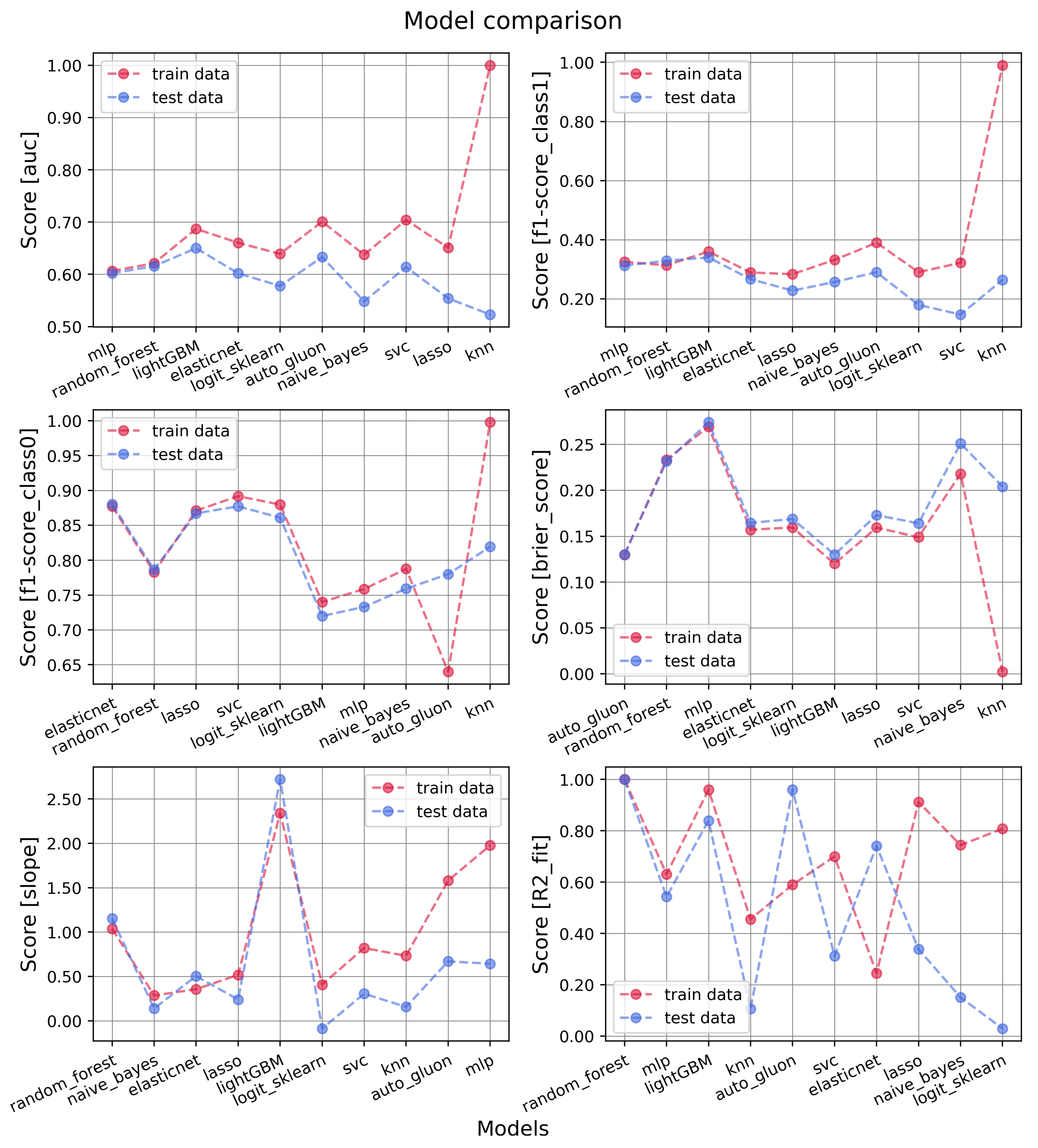
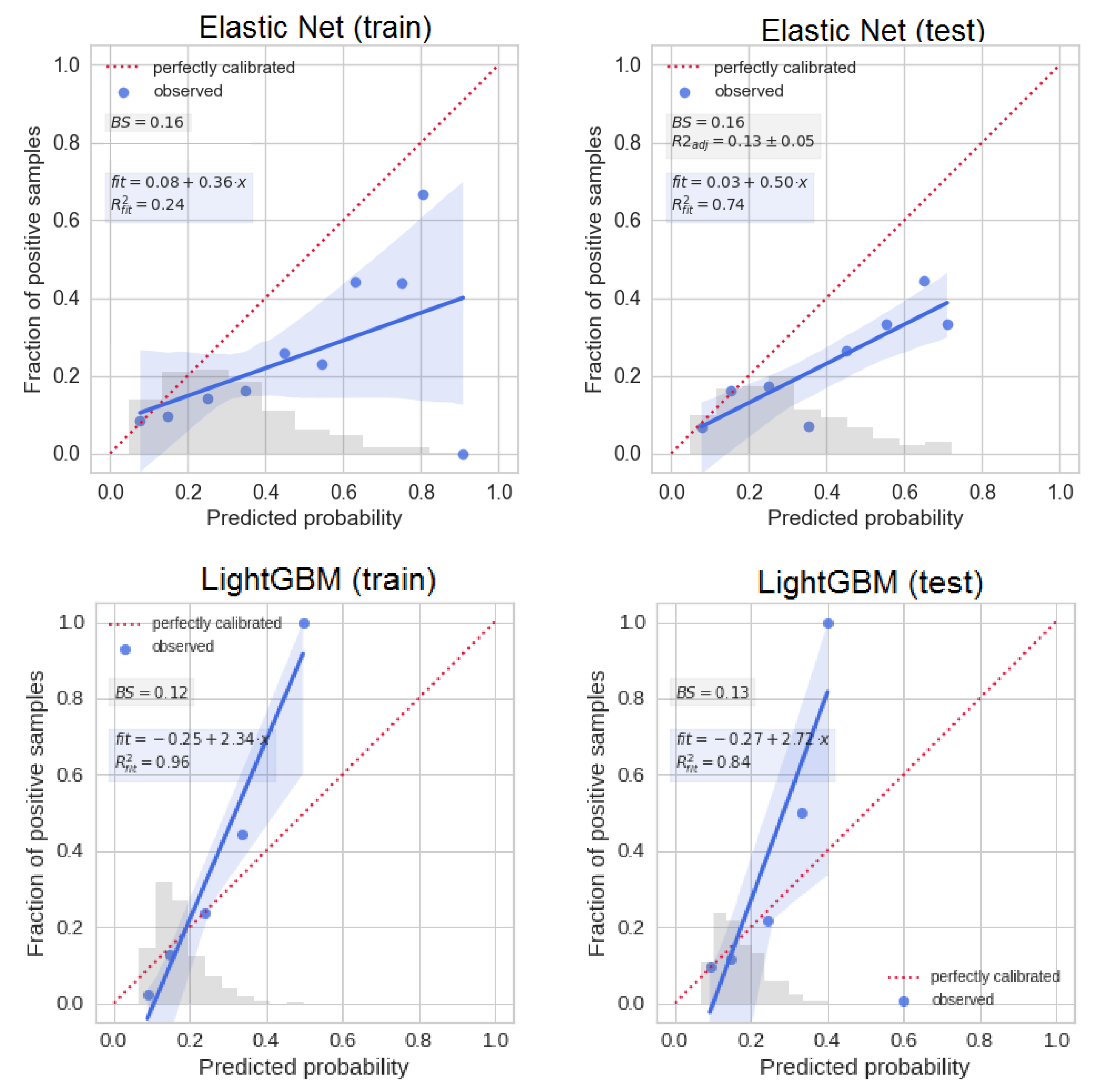
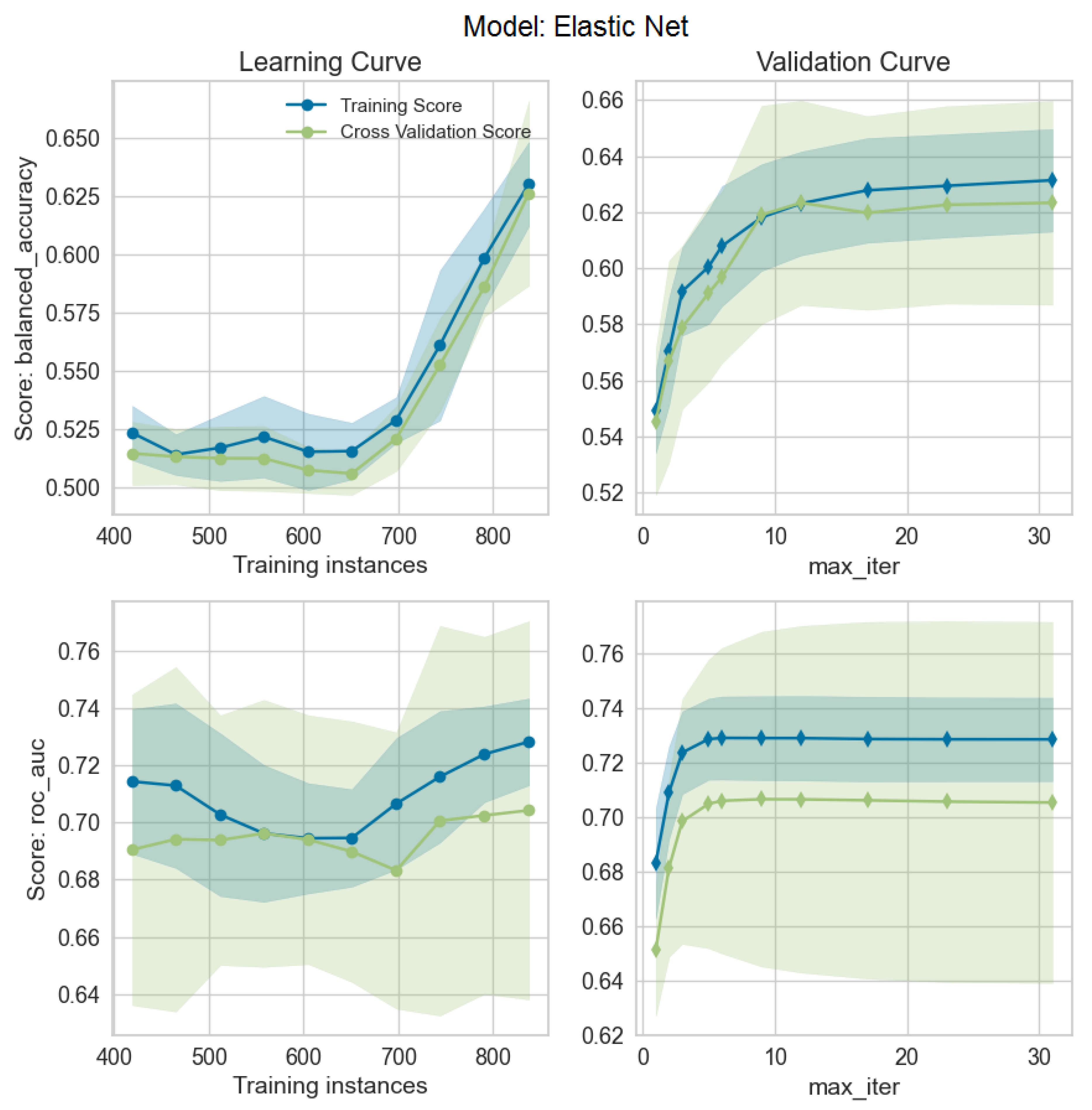
3. Results
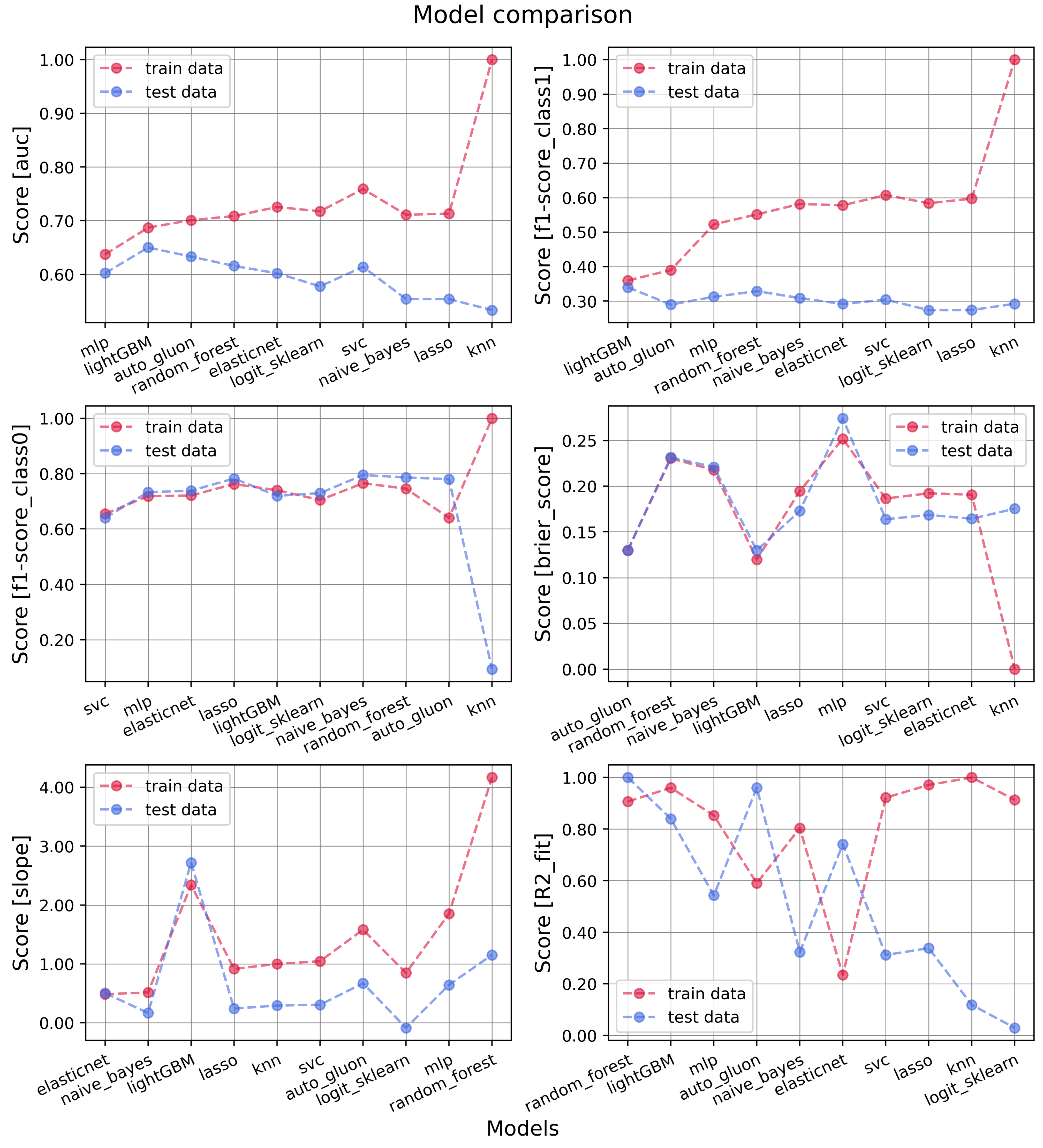
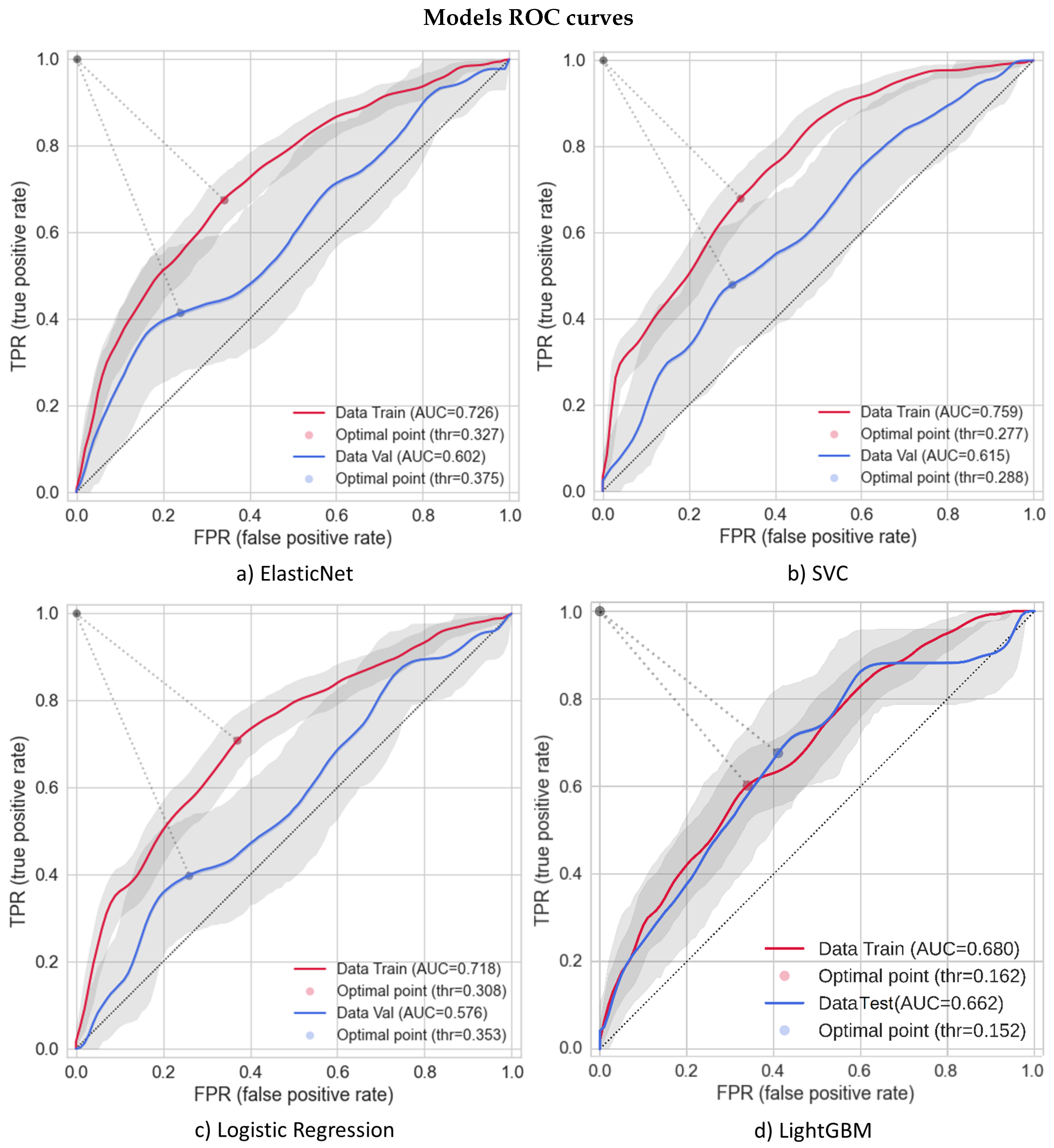
3.1. Models’ Performances
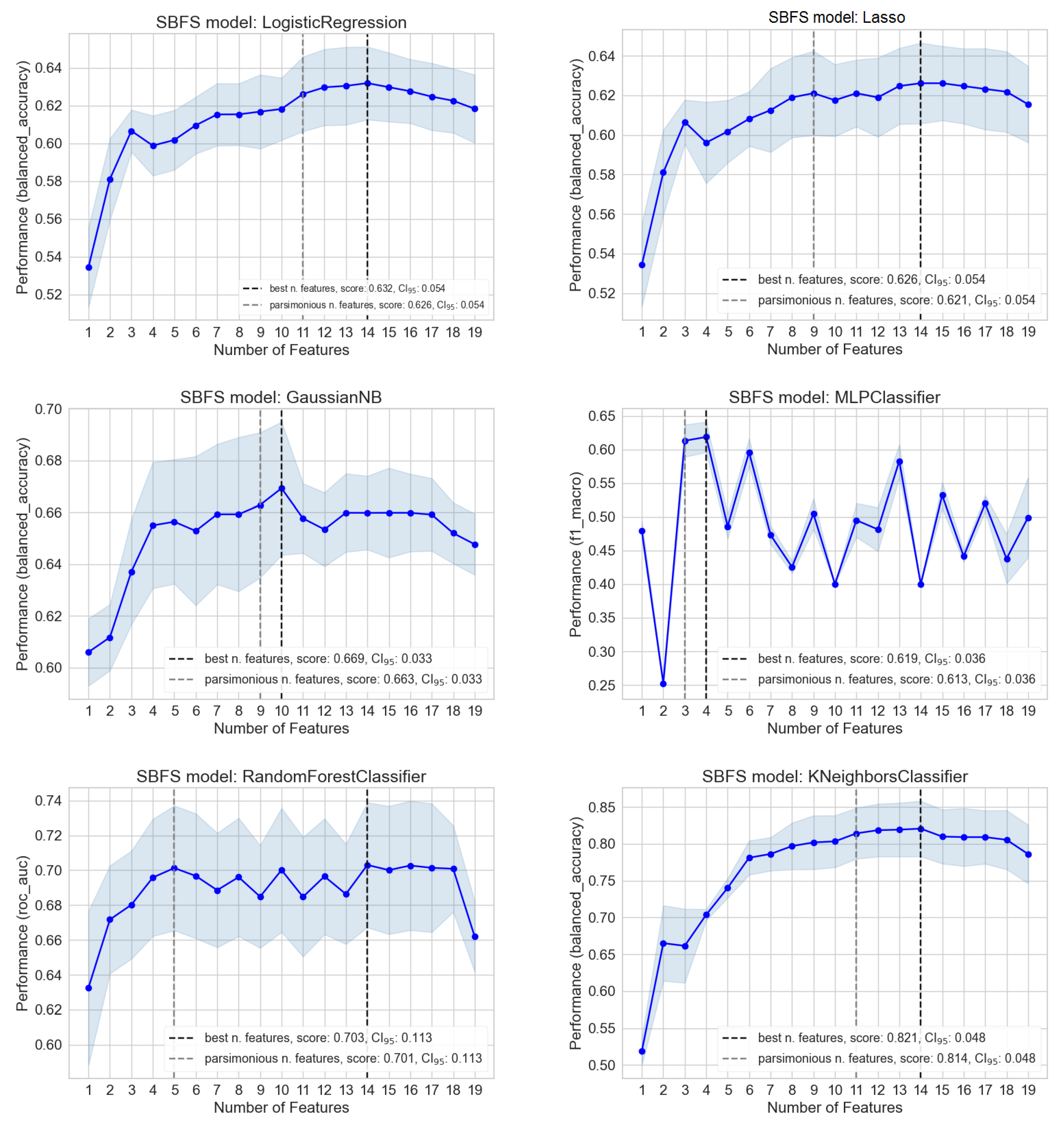
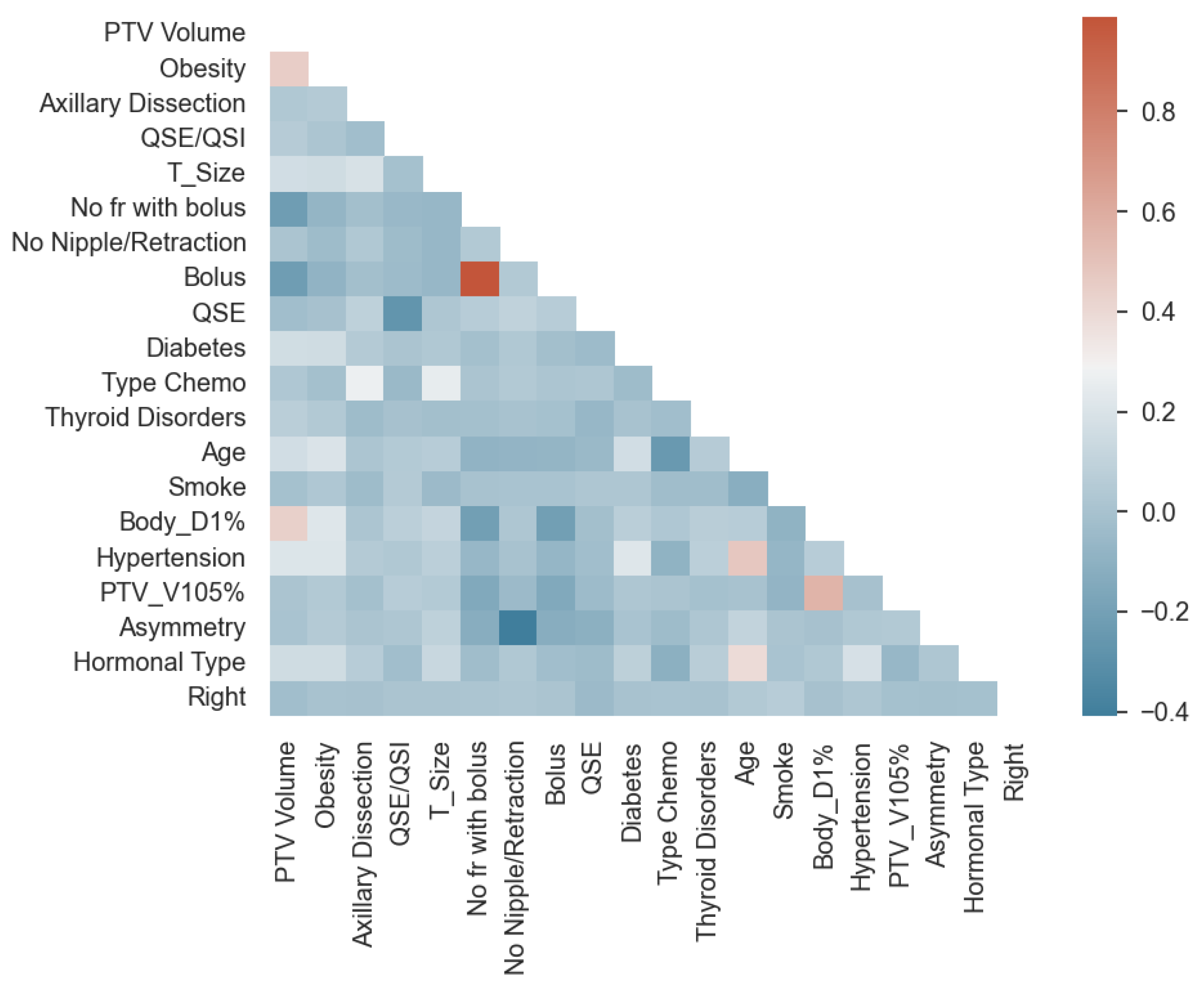
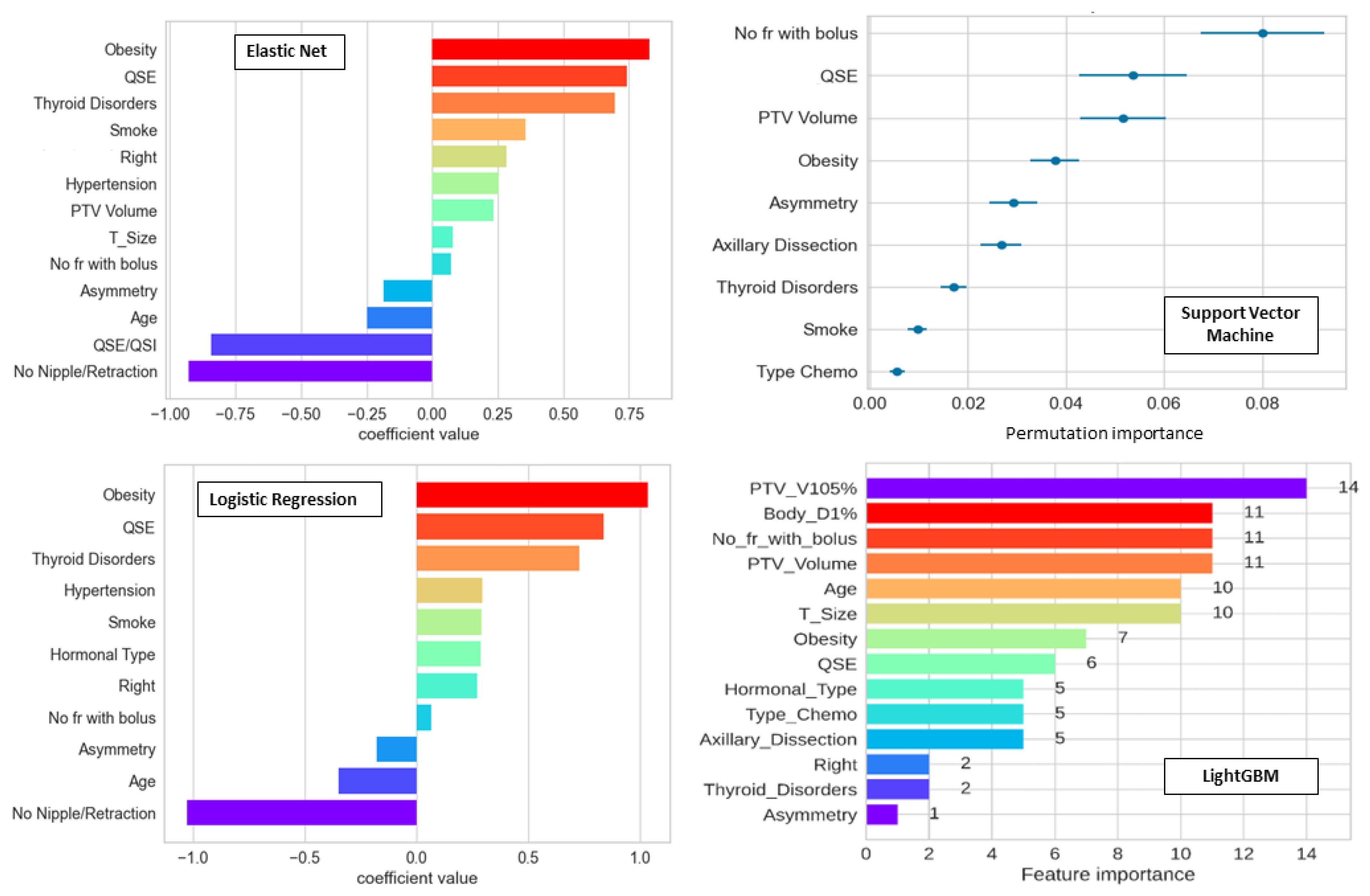
3.2. Importance and Number of Selected Features: Measuring Redundancy
3.3. Bootstrap-Based Logistic Regression with Small Number of Features
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1
| Model | Hyperparameters |
|---|---|
| LightGBM | objective: binary, metric: binary error, boosting type: gbdt, |
| lambda l1: 4.17, lambda l2: 7.20, num leaves: 2, min child samples: 2, max depth: 10, bagging freq: 6, | |
| min data in leaf: 84, bagging fraction: 0.57, learning rate: 0.20, feature fraction: 0.65 | |
| AutoGluon | eval metric: roc auc, sample weight: auto weight, num bag folds: 2, |
| num bag sets: 3, num stack levels: 1, presets: best quality | |
| RF | criterion: gini, max leaf nodes: 17, bootstrap: True, ccp alpha: 0.02, class weight: balanced, max depth: 7, |
| min samples split: 12, min samples leaf: 7, n estimators: 75, min impurity decrease: 0.0 | |
| SVC | class weight: balanced, probability: True, C: 0.8, kernel: poly, degree: 3 |
| MLP | solver: Adam, max iter: 5000, learning rate: adaptive, epsilon: , |
| activation: relu, alpha: 1.0, hidden layer sizes: 5, learning rate init: 0.001 | |
| ElasticNet | fit intercept: True, max iter: 1000, penalty: ElasticNet, solver: Saga, C: 4.83, l1 ratio: 0.70 |
| LR | C: 1, solver: newton-cg, fit intercept: True, max iter: 1000, penalty: none |
| Lasso | fit intercept: True, intercept scaling: 1, max iter: 1000, penalty: l1, C: 4.83, solver: saga |
| GNB | priors: None, var smoothing: 0.001 |
| KNN | algorithm: auto, p: 1, leaf size: 30, metric: minkowski, n neighbors: 17, weights: distance |
| Metric/Model | AUC Internal Test | ||||||
|---|---|---|---|---|---|---|---|
| Balacc | f1 Weight | f1 Macro | AUC | AUC | AUC | AUC | |
| Balacc | f1 Weight | f1 Macro | AUC | Balacc | f1 Weight | f1 Macro | |
| Random Forest | 0.579 | 0.599 | 0.573 | 0.590 | 0.612 | 0.616 | 0.616 |
| SVC | 0.541 | 0.524 | 0.537 | 0.614 | 0.562 | 0.547 | 0.562 |
| MLP sklearn | 0.471 | 0.494 | 0.602 | 0.424 | 0.577 | 0.577 | 0.577 |
| ElasticNet | 0.602 | 0.555 | 0.602 | 0.514 | 0.513 | 0.513 | 0.513 |
| LR sklearn | 0.578 | 0.578 | 0.531 | 0.513 | 0.513 | 0.513 | 0.513 |
| Lasso | 0.554 | 0.554 | 0.554 | 0.554 | 0.513 | 0.513 | 0.513 |
| Naïve Bayes | 0.548 | 0.554 | 0.495 | 0.521 | 0.547 | 0.548 | 0.547 |
| KNN | 0.523 | 0.459 | 0.467 | 0.533 | 0.486 | 0.486 | 0.486 |
| Variables | High Variance | High LR p-Value | High Correlation |
|---|---|---|---|
| Age | 1 | 1 | 1 |
| Axillary Dissection | 1 | 1 | 1 |
| Quadrant position | 1 | 1 | 1 |
| T Size | 1 | 1 | 1 |
| Chemo | 1 | - | |
| Type Chemo | 1 | 1 | 1 |
| AB monoclonal | 1 | - | |
| Hormonal Therapy | 1 | - | |
| Bilateral RT | - | ||
| Right | 1 | 1 | - |
| No fr with bolus | 1 | 1 | 1 |
| Bolus | 1 | 1 | - |
| PTV Volume | 1 | 1 | 1 |
| PTV V105% | 1 | 1 | 1 |
| Body D1% | 1 | 1 | 1 |
| Obesity | 1 | 1 | 1 |
| Diabetes | 1 | 1 | 1 |
| Hypertension | 1 | 1 | 1 |
| Thyroid Disorders | 1 | 1 | 1 |
| Smoke | 1 | 1 | 1 |
| Alcohol | 1 | - | |
| Asymmetry | 1 | 1 | 1 |
| Overall Cosmesis | 1 | - | |
| No Nipple/Retraction | 1 | 1 | 1 |
| Hormonal Type | 1 | 1 | 1 |
Appendix A.2. Computational Resources and Running Time Spent
References
- Fiorino, C.; Jeraj, R.; Clark, C.H.; Garibaldi, C.; Georg, D.; Muren, L.; van Elmpt, W.; Bortfeld, T.; Jornet, N. Grand challenges for medical physics in radiation oncology. Radiother. Oncol. 2020, 153, 7–14. [Google Scholar] [CrossRef]
- Fiorino, C.; Guckenberger, M.; Schwarz, M.; van der Heide, U.A.; Heijmen, B. Technology-driven research for radiotherapy innovation. Mol. Oncol. 2020, 14, 1500–1513. [Google Scholar] [CrossRef]
- Siddique, S.; Chow, J.C. Artificial intelligence in radiotherapy. Rep. Pract. Oncol. Radiother. 2020, 25, 656–666. [Google Scholar] [CrossRef]
- Ho, D. Artificial intelligence in cancer therapy. Science 2020, 367, 982–983. [Google Scholar] [CrossRef] [PubMed]
- Chow, J.C.L. Artificial Intelligence in Radiotherapy and Patient Care. In Artificial Intelligence in Medicine; Springer International Publishing: Cham, Switzerland, 2021; pp. 1–13. [Google Scholar] [CrossRef]
- Darby, S.; McGale, P.; Correa, C.; Taylor, C.; Arriagada, R.; Clarke, M.; Cutter, D.; Davies, C.; Ewertz, M.; Godwin, J.; et al. Effect of radiotherapy after breast-conserving surgery on 10-year recurrence and 15-year breast cancer death: Meta-analysis of individual patient data for 10801 women in 17 randomised trials. Lancet 2011, 378, 1707–1716. [Google Scholar] [CrossRef] [PubMed]
- Shah, C.; Al-Hilli, Z.; Vicini, F. Advances in Breast Cancer Radiotherapy: Implications for Current and Future Practice. JCO Oncol. Pract. 2021, 17, 697–706. [Google Scholar] [CrossRef]
- Seibold, P.; Webb, A.; Aguado-Barrera, M.E.; Azria, D.; Bourgier, C.; Brengues, M.; Briers, E.; Bultijnck, R.; Calvo-Crespo, P.; Carballo, A.; et al. REQUITE: A prospective multicentre cohort study of patients undergoing radiotherapy for breast, lung or prostate cancer. Radiother. Oncol. 2019, 138, 59–67. [Google Scholar] [CrossRef]
- McGale, P.; Taylor, C.; Correa, C.; Cutter, D.; Duane, F.; Ewertz, M.; Gray, R.; Mannu, G.; Peto, R.; Whelan, T.; et al. Effect of radiotherapy after mastectomy and axillary surgery on 10-year recurrence and 20-year breast cancer mortality: Meta-analysis of individual patient data for 8135 women in 22 randomised trials. Lancet 2014, 383, 2127–2135. [Google Scholar] [CrossRef]
- Cox, J.D.; Stetz, J.; Pajak, T.F. Toxicity criteria of the Radiation Therapy Oncology Group (RTOG) and the European organization for research and treatment of cancer (EORTC). Int. J. Radiat. Oncol. Biol. Phys. 1995, 31, 1341–1346. [Google Scholar] [CrossRef] [PubMed]
- Chan, R.J.; Larsen, E.; Chan, P. Re-examining the Evidence in Radiation Dermatitis Management Literature: An Overview and a Critical Appraisal of Systematic Reviews. Int. J. Radiat. Oncol. Biol. Phys. 2012, 84, e357–e362. [Google Scholar] [CrossRef]
- Tesselaar, E.; Flejmer, A.M.; Farnebo, S.; Dasu, A. Changes in skin microcirculation during radiation therapy for breast cancer. Acta Oncol. 2017, 56, 1072–1080. [Google Scholar] [CrossRef]
- Avanzo, M.; Pirrone, G.; Vinante, L.; Caroli, A.; Stancanello, J.; Drigo, A.; Massarut, S.; Mileto, M.; Urbani, M.; Trovo, M.; et al. Electron Density and Biologically Effective Dose (BED) Radiomics-Based Machine Learning Models to Predict Late Radiation-Induced Subcutaneous Fibrosis. Front. Oncol. 2020, 10, 490. [Google Scholar] [CrossRef] [PubMed]
- Rancati, T.; Fiorino, C. Modelling Radiotherapy Side Effects: Practical Applications for Planning Optimisation; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar] [CrossRef]
- Harbeck, N. Breast cancer is a systemic disease optimally treated by a multidisciplinary team. Nat. Rev. Dis. Prim. 2020, 6, 30. [Google Scholar] [CrossRef] [PubMed]
- The radiotherapeutic injury—A complex ‘wound’. Radiother. Oncol. 2002, 63, 129–145. [CrossRef]
- Isaksson, L.J.; Pepa, M.; Zaffaroni, M.; Marvaso, G.; Alterio, D.; Volpe, S.; Corrao, G.; Augugliaro, M.; Starzyńska, A.; Leonardi, M.C.; et al. Machine Learning-Based Models for Prediction of Toxicity Outcomes in Radiotherapy. Front. Oncol. 2020, 10, 790. [Google Scholar] [CrossRef]
- Fiorino, C.; Rancati, T. Artificial intelligence applied to medicine: There is an “elephant in the room”. Phys. Med. 2022, 98, 8–10. [Google Scholar] [CrossRef]
- Mbah, C.; Thierens, H.; Thas, O.; Neve, J.D.; Chang-Claude, J.; Seibold, P.; Botma, A.; West, C.; Ruyck, K.D. Pitfalls in Prediction Modeling for Normal Tissue Toxicity in Radiation Therapy: An Illustration With the Individual Radiation Sensitivity and Mammary Carcinoma Risk Factor Investigation Cohorts. Int. J. Radiat. Oncol. Biol. Phys. 2016, 95, 1466–1476. [Google Scholar] [CrossRef] [PubMed]
- Reddy, J.; Lindsay, W.; Berlind, C.; Ahern, C.; Smith, B. Applying a Machine Learning Approach to Predict Acute Toxicities During Radiation for Breast Cancer Patients. Int. J. Radiat. Oncol. Biol. Phys. 2018, 102, S59. [Google Scholar] [CrossRef]
- Saednia, K.; Tabbarah, S.; Lagree, A.; Wu, T.; Klein, J.; Garcia, E.; Hall, M.; Chow, E.; Rakovitch, E.; Childs, C.; et al. Quantitative Thermal Imaging Biomarkers to Detect Acute Skin Toxicity from Breast Radiotherapy Using Supervised Machine Learning. Int. J. Radiat. Oncol. Biol. Phys. 2020, 106, 1071–1083. [Google Scholar] [CrossRef]
- Rattay, T.; Seibold, P.; Aguado-Barrera, M.E.; Altabas, M.; Azria, D.; Barnett, G.C.; Bultijnck, R.; Chang-Claude, J.; Choudhury, A.; Coles, C.E.; et al. External Validation of a Predictive Model for Acute Skin Radiation Toxicity in the REQUITE Breast Cohort. Front. Oncol. 2020, 10, 575909. [Google Scholar] [CrossRef]
- Aldraimli, M.; Osman, S.O.S.; Grishchuck, D.; Ingram, S.P.; Lyon, R.; Mistry, A.; Oliveira, J.; Samuel, R.; Shelley, L.E.A.; Soria, D.; et al. Development and Optimization of a Machine-Learning Prediction Model for Acute Desquamation After Breast Radiation Therapy in the Multicenter REQUITE Cohort. Adv. Radiat. Oncol. 2022, 7, 100890. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, H.; Xu, L.Y.; Ren, Y.; Deng, W.; Feng, H.; Yang, Z.; Ma, S.; Ni, Q.; Kuang, Y. A Machine Learning Framework for Early Prediction of Radiation Dermatitis in Patients with Breast Cancer Receiving Radiation Treatment: A Multicenter Retrospective Analysis Study. Int. J. Radiat. Oncol. Biol. Phys. 2022, 114, e119. [Google Scholar] [CrossRef]
- Cilla, S.; Romano, C.; Macchia, G.; Boccardi, M.; Pezzulla, D.; Buwenge, M.; Castelnuovo, A.D.; Bracone, F.; Curtis, A.D.; Cerletti, C.; et al. Machine-learning prediction model for acute skin toxicity after breast radiation therapy using spectrophotometry. Front. Oncol. 2023, 12, 1044358. [Google Scholar] [CrossRef] [PubMed]
- Fodor, A.; Brombin, C.; Mangili, P.; Borroni, F.; Pasetti, M.; Tummineri, R.; Zerbetto, F.; Longobardi, B.; Perna, L.; Dell’Oca, I.; et al. Impact of molecular subtype on 1325 early-stage breast cancer patients homogeneously treated with hypofractionated radiotherapy without boost: Should the indications for radiotherapy be more personalized? Breast 2021, 55, 45–54. [Google Scholar] [CrossRef] [PubMed]
- Fodor, A.; Brombin, C.; Mangili, P.; Tummineri, R.; Pasetti, M.; Zerbetto, F.; Longobardi, B.; Galvan, A.S.; Deantoni, C.L.; Dell’Oca, I.; et al. Toxicity of Hypofractionated Whole Breast Radiotherapy Without Boost and Timescale of Late Skin Responses in a Large Cohort of Early-Stage Breast Cancer Patients. Clin. Breast Cancer 2022, 22, e480–e487. [Google Scholar] [CrossRef] [PubMed]
- Ahsan, M.; Mahmud, M.; Saha, P.; Gupta, K.; Siddique, Z. Effect of Data Scaling Methods on Machine Learning Algorithms and Model Performance. Technologies 2021, 9, 52. [Google Scholar] [CrossRef]
- Steyerberg, E. Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating; Springer: New York, NY, USA, 2009; Volume 19, Chapter 11. Selection of Main Effects. [Google Scholar] [CrossRef]
- Palumbo, D.; Mori, M.; Prato, F.; Crippa, S.; Belfiori, G.; Reni, M.; Mushtaq, J.; Aleotti, F.; Guazzarotti, G.; Cao, R.; et al. Prediction of Early Distant Recurrence in Upfront Resectable Pancreatic Adenocarcinoma: A Multidisciplinary, Machine Learning-Based Approach. Cancers 2021, 13, 4938. [Google Scholar] [CrossRef]
- Friedman, J.H.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef]
- Goldberger, J.; Hinton, G.E.; Roweis, S.; Salakhutdinov, R.R. Neighbourhood Components Analysis. In Proceedings of the 17th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 1 December 2004; Advances in Neural Information Processing Systems. Saul, L., Weiss, Y., Bottou, L., Eds.; MIT Press: Cambridge, MA, USA, 2004; Volume 17. [Google Scholar]
- Schölkopf, B.; Smola, A.J.; Williamson, R.C.; Bartlett, P.L. New Support Vector Algorithms. Neural Comput. 2000, 12, 1207–1245. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Zhang, H. Exploring conditions for the optimality of naive Bayes. Int. J. Pattern Recognit. Artif. Intell. 2005, 19, 183–198. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; Teh, Y.W., Titterington, M., Eds.; Chia Laguna Resort: Chia, Italy, 2010; Volune 9, pp. 249–256. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finely, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIP 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Erickson, N.; Mueller, J.; Shirkov, A.; Zhang, H.; Larroy, P.; Li, M.; Smola, A. AutoGluon-Tabular: Robust and Accurate AutoML for Structured Data. arXiv 2020, arXiv:2003.06505. [Google Scholar] [CrossRef]
- Uddin, S.; Khan, A.; Hossain, M.E.; Moni, M.A. Comparing different supervised machine learning algorithms for disease prediction. BMC Med. Inform. Decis. Mak. 2019, 19, 281. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. arXiv 2016, arXiv:1602.04938. [Google Scholar] [CrossRef]
- Mori, M.; Passoni, P.; Incerti, E.; Bettinardi, V.; Broggi, S.; Reni, M.; Whybra, P.; Spezi, E.; Vanoli, E.; Gianolli, L.; et al. Training and validation of a robust PET radiomic-based index to predict distant-relapse-free-survival after radio-chemotherapy for locally advanced pancreatic cancer. Radiother. Oncol. 2020, 153. [Google Scholar] [CrossRef]
- Naqa, I.E.; Bradley, J.; Blanco, A.I.; Lindsay, P.E.; Vicic, M.; Hope, A.; Deasy, J.O. Multivariable modeling of radiotherapy outcomes, including dose–volume and clinical factors. Int. J. Radiat. Oncol. Biol. Phys. 2006, 64, 1275–1286. [Google Scholar] [CrossRef]
- Palorini, F.; Rancati, T.; Cozzarini, C.; Improta, I.; Carillo, V.; Avuzzi, B.; Borca, V.C.; Botti, A.; Esposti, C.D.; Franco, P.; et al. Multi-variable models of large International Prostate Symptom Score worsening at the end of therapy in prostate cancer radiotherapy. Radiother. Oncol. 2016, 118, 92–98. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar] [CrossRef]
- Avanzo, M.; Stancanello, J.; Naqa, I.E. Beyond imaging: The promise of radiomics. Phys. Med. 2017, 38, 122–139. [Google Scholar] [CrossRef]
- Rossi, L.; Bijman, R.; Schillemans, W.; Aluwini, S.; Cavedon, C.; Witte, M.; Incrocci, L.; Heijmen, B. Texture analysis of 3D dose distributions for predictive modelling of toxicity rates in radiotherapy. Radiother. Oncol. 2018, 129, 548–553. [Google Scholar] [CrossRef]
- Placidi, L.; Gioscio, E.; Garibaldi, C.; Rancati, T.; Fanizzi, A.; Maestri, D.; Massafra, R.; Menghi, E.; Mirandola, A.; Reggiori, G.; et al. A Multicentre Evaluation of Dosiomics Features Reproducibility, Stability and Sensitivity. Cancers 2021, 13, 3835. [Google Scholar] [CrossRef] [PubMed]
- Yahya, N.; Ebert, M.A.; Bulsara, M.; House, M.J.; Kennedy, A.; Joseph, D.J.; Denham, J.W. Statistical-learning strategies generate only modestly performing predictive models for urinary symptoms following external beam radiotherapy of the prostate: A comparison of conventional and machine-learning methods. Med. Phys. 2016, 43, 2040–2052. [Google Scholar] [CrossRef] [PubMed]
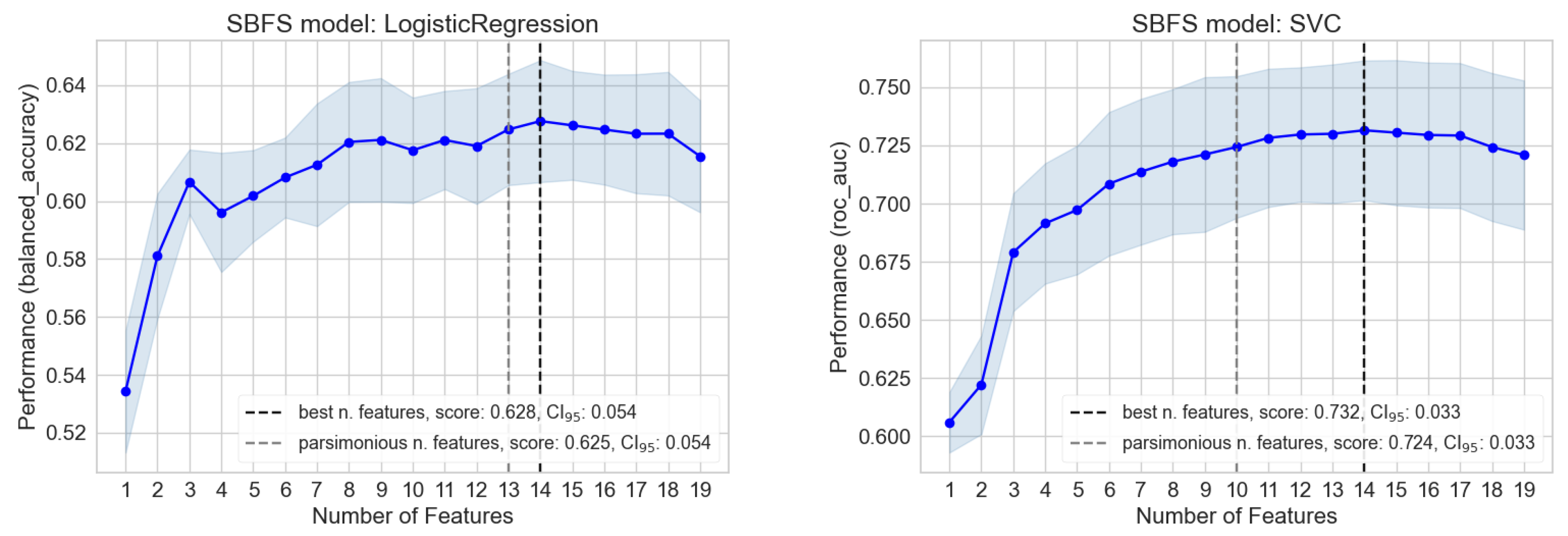
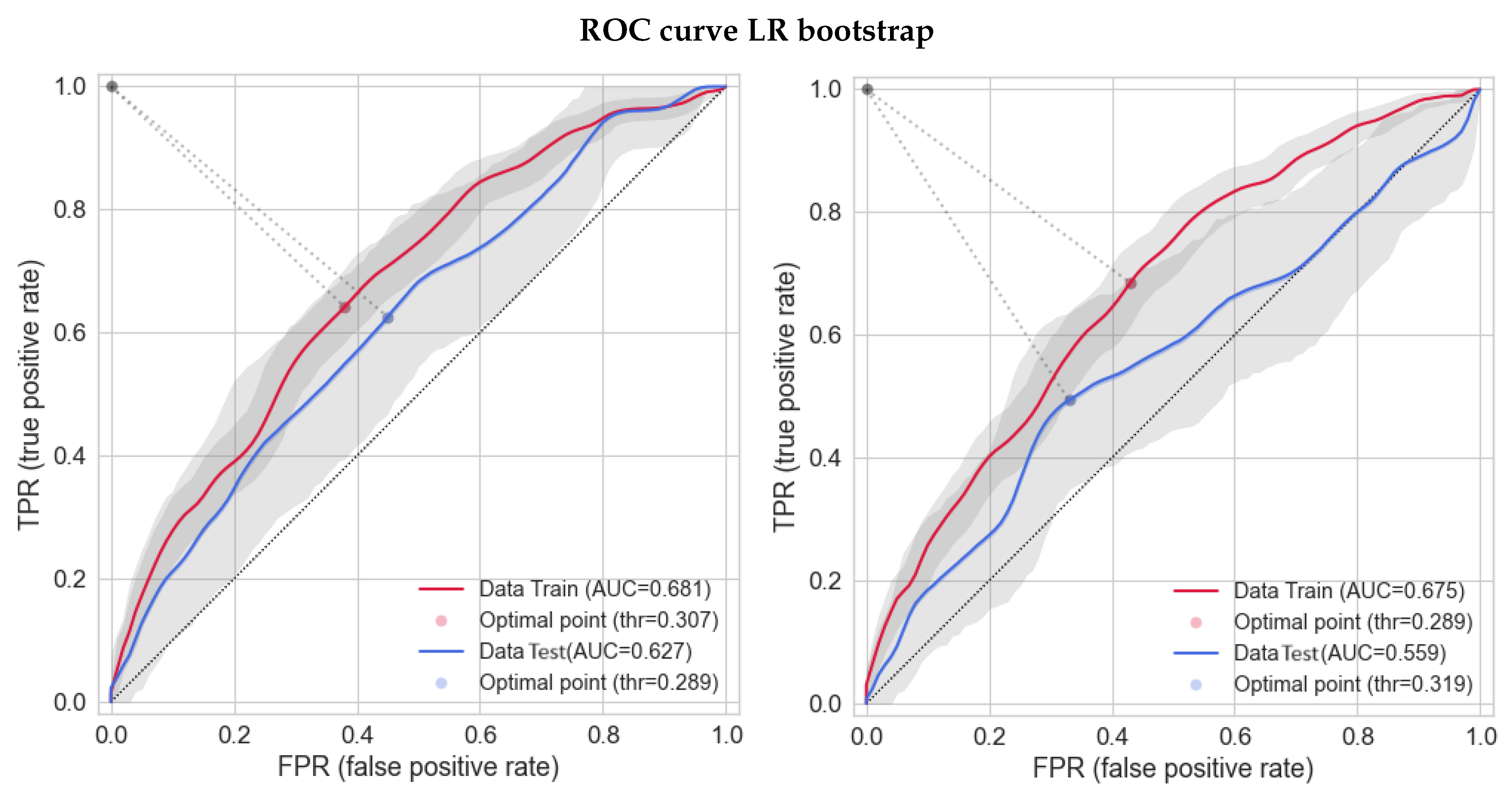
| Column Names | No | Yes | NA | %No | %Yes | %NA |
|---|---|---|---|---|---|---|
| Axillary Dissection | 1073 | 241 | 0 | 82 | 17 | 0 |
| Type Chemo | 1022 | 292 | 0 | 78 | 21 | 0 |
| Right | 677 | 637 | 0 | 52 | 47 | 0 |
| Bolus | 1007 | 307 | 0 | 77 | 22 | 0 |
| Obesity | 959 | 313 | 42 | 73 | 23 | 3 |
| Diabetes | 1119 | 79 | 116 | 85 | 6 | 8 |
| Hypertension | 751 | 450 | 113 | 57 | 33 | 8 |
| Thyroid Disorders | 1018 | 178 | 118 | 78 | 13 | 8 |
| Smoke | 1054 | 260 | 0 | 80 | 19 | 0 |
| No Nipple/Retraction | 124 | 1190 | 0 | 9 | 90 | 0 |
| Hormonal Type | 582 | 732 | 0 | 44 | 54 | 0 |
| Quadrant Position | Count | %Count |
|---|---|---|
| QSE * | 597 | 45.4 |
| QSI | 223 | 17.0 |
| QIE | 142 | 10.8 |
| QSE/QSI * | 100 | 7.6 |
| QII | 96 | 7.3 |
| Q retroareolar | 54 | 4.1 |
| QIE/QII | 47 | 3.6 |
| QSE/QIE | 42 | 3.2 |
| QSI/QII | 12 | 0.9 |
| NA | 1 | 0.1 |
| Column Names | Median | IQR | Mean | Std | Min | Max | Count NA |
|---|---|---|---|---|---|---|---|
| Age | 62.16 | [51.57, 70.65] | 61.32 | 11.92 | 27.98 | 91.20 | 0 |
| T Size | 1.30 | [0.9, 1.8] | 1.43 | 0.80 | 0.00 | 6.70 | 14 |
| No fr with bolus | 0.00 | [0.0, 0.0] | 1.64 | 3.07 | 0.00 | 15.00 | 41 |
| PTV Volume | 642.25 | [445.62, 914.47] | 709.51 | 359.56 | 114.80 | 2649.00 | 0 |
| PTV V105% | 2.46 | [1.07, 4.39] | 3.32 | 3.45 | 0.00 | 33.63 | 0 |
| Body D1% | 41.02 | [40.78, 41.27] | 41.03 | 0.42 | 38.37 | 46.23 | 0 |
| Asymmetry | 1.00 | [1.0, 2.0] | 1.22 | 0.83 | 0.00 | 3.00 | 0 |
| Model | Acronym | Reference Paper | Description |
|---|---|---|---|
| Logistic Regression * | LR | [31] | The event probability is a function of a linear combination of independent variables. |
| Lasso | Lasso | [31] | It is part of the same typology of models of LR, differing for the chosen penalty. |
| ElasticNet | ElasticNet | [31] | It is a combination of LR and Lasso, regarding the chosen penalty. |
| k-Nearest Neighbors | KNN | [32] | It is a nonparametric classifier, which uses proximity methods to distinguish between classes. |
| Support Vector Machines | SVM | [33,34] | It is an algorithm that classifies through the choice of a N-dimensional hyperplane. |
| Gaussian Naïve Bayes | GNB | [35] | It is part of the so-called probabilistic classifiers, based on the Bayes’ theorem with the assumption of a strong independence between input features and of a normal distribution for each class. |
| Multi-Layer Perceptron | MLP 1 | [36] | It is a feedforward artificial neural network (ANN) with multiple layers where the mapping between input and output layers is a nonlinear activation function. |
| Random Forest | RF | [37] | It combines multiple decision trees, constructed independently, to reach one final result. |
| Light Gradient Boosting Machine | LightGBM | [38] | Development of RF. It is a gradient-boosting based algorithm, which builds multiple decision trees one after another. |
| AutoGluon | AutoGluon | [39] | It is an AutoML code, focused on automated stack ensembling of individually trained classifiers to reduce their intrinsic error, here used as a comparison with the other codes. |
| Model | Train | Test | n. Features | ||
|---|---|---|---|---|---|
| LightGBM | 0.162 | 0.130 | 14 | - | - |
| AutoGluon | 0.177 | 0.090 | 19 | - | - |
| LR 3 Variables | 0.294 | 0.283 | 3 | - | - |
| Random Forest | 0.511 | 0.509 | 5 | AUC | f1 macro |
| SVC | 0.250 | 0.294 | 10 | AUC | AUC |
| MLP | 0.500 | 0.489 | 3 | f1 macro | f1 macro |
| ElasticNet | 0.322 | 0.406 | 13 | balanced acc. | balanced acc. |
| LR Multivariable | 0.303 | 0.415 | 11 | balanced acc. | balanced acc. |
| LR 4 Variables | 0.264 | 0.327 | 4 | - | - |
| Lasso | 0.356 | 0.475 | 9 | balanced acc. | balanced acc. |
| Naïve Bayes | 0.448 | 0.469 | 9 | f1 weight | f1 weight |
| KNN | 0.010 | 0.517 | 10 | AUC | AUC |
| Train | Internal Test | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Precision | Specificity | Sensitivity | f | f | AUC | Precision | Specificity | Sensitivity | f | f | AUC |
| LightGBM | 0.249 | 0.662 | 0.608 | 0.760 | 0.350 | 0.680 | 0.248 | 0.673 | 0.588 | 0.770 | 0.350 | 0.662 |
| AutoGluon | 0.249 | 0.481 | 0.935 | 0.640 | 0.390 | 0.701 | 0.216 | 0.712 | 0.431 | 0.780 | 0.290 | 0.633 |
| LR 3 variables | 0.438 | 0.583 | 0.693 | 0.680 | 0.540 | 0.681 | 0.205 | 0.568 | 0.608 | 0.690 | 0.310 | 0.627 |
| Random Forest | 0.511 | 0.714 | 0.599 | 0.746 | 0.551 | 0.709 | 0.245 | 0.709 | 0.329 | 0.787 | 0.329 | 0.616 |
| SVC | 0.472 | 0.522 | 0.854 | 0.655 | 0.607 | 0.759 | 0.206 | 0.514 | 0.583 | 0.640 | 0.304 | 0.614 |
| MLP sklearn | 0.474 | 0.678 | 0.582 | 0.719 | 0.522 | 0.637 | 0.225 | 0.637 | 0.510 | 0.733 | 0.312 | 0.602 |
| ElasticNet | 0.497 | 0.651 | 0.691 | 0.721 | 0.578 | 0.725 | 0.219 | 0.658 | 0.437 | 0.738 | 0.292 | 0.602 |
| LR sklearn | 0.487 | 0.618 | 0.728 | 0.705 | 0.584 | 0.717 | 0.204 | 0.647 | 0.417 | 0.730 | 0.274 | 0.578 |
| LR 4 variables | 0.417 | 0.487 | 0.783 | 0.610 | 0.540 | 0.675 | 0.169 | 0.471 | 0.588 | 0.610 | 0.260 | 0.559 |
| Lasso | 0.542 | 0.720 | 0.665 | 0.763 | 0.597 | 0.713 | 0.224 | 0.733 | 0.354 | 0.783 | 0.274 | 0.554 |
| Naïve Bayes | 0.542 | 0.735 | 0.627 | 0.765 | 0.582 | 0.711 | 0.253 | 0.747 | 0.396 | 0.795 | 0.309 | 0.554 |
| KNN | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.173 | 0.050 | 0.917 | 0.290 | 0.094 | 0.533 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ubeira-Gabellini, M.G.; Mori, M.; Palazzo, G.; Cicchetti, A.; Mangili, P.; Pavarini, M.; Rancati, T.; Fodor, A.; del Vecchio, A.; Di Muzio, N.G.; et al. Comparing Performances of Predictive Models of Toxicity after Radiotherapy for Breast Cancer Using Different Machine Learning Approaches. Cancers 2024, 16, 934. https://doi.org/10.3390/cancers16050934
Ubeira-Gabellini MG, Mori M, Palazzo G, Cicchetti A, Mangili P, Pavarini M, Rancati T, Fodor A, del Vecchio A, Di Muzio NG, et al. Comparing Performances of Predictive Models of Toxicity after Radiotherapy for Breast Cancer Using Different Machine Learning Approaches. Cancers. 2024; 16(5):934. https://doi.org/10.3390/cancers16050934
Chicago/Turabian StyleUbeira-Gabellini, Maria Giulia, Martina Mori, Gabriele Palazzo, Alessandro Cicchetti, Paola Mangili, Maddalena Pavarini, Tiziana Rancati, Andrei Fodor, Antonella del Vecchio, Nadia Gisella Di Muzio, and et al. 2024. "Comparing Performances of Predictive Models of Toxicity after Radiotherapy for Breast Cancer Using Different Machine Learning Approaches" Cancers 16, no. 5: 934. https://doi.org/10.3390/cancers16050934
APA StyleUbeira-Gabellini, M. G., Mori, M., Palazzo, G., Cicchetti, A., Mangili, P., Pavarini, M., Rancati, T., Fodor, A., del Vecchio, A., Di Muzio, N. G., & Fiorino, C. (2024). Comparing Performances of Predictive Models of Toxicity after Radiotherapy for Breast Cancer Using Different Machine Learning Approaches. Cancers, 16(5), 934. https://doi.org/10.3390/cancers16050934







