Signature Genes Selection and Functional Analysis of Astrocytoma Phenotypes: A Comparative Study
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Pre-Processing, Quality Control, Normalisation and Initial Inspection of the Data
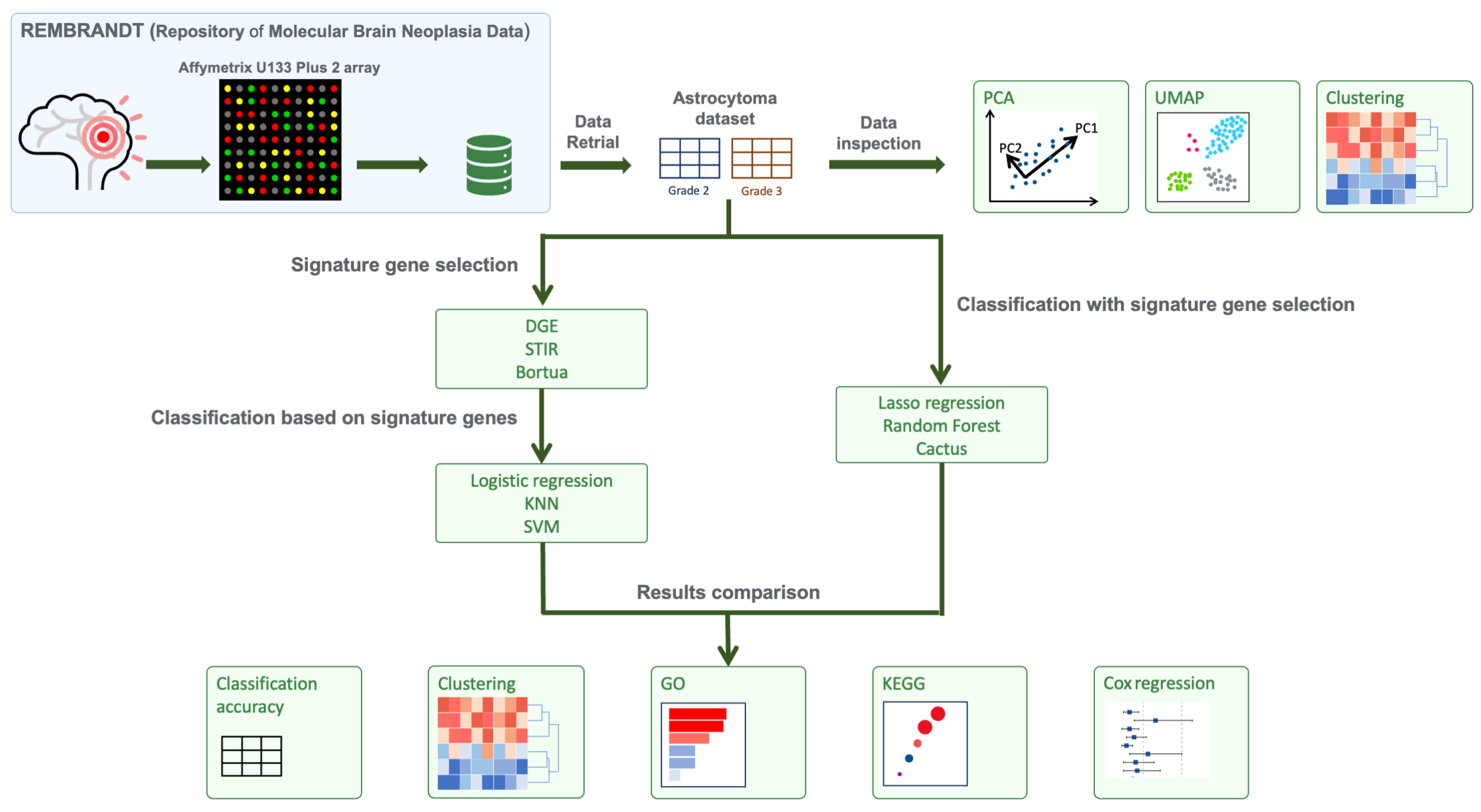
2.3. Overview of the Comparison of Feature Selection and Classification Methods
2.4. Signature Gene Selection
2.4.1. Differential Gene Expression
2.4.2. STIR-STatistical Inference RelieF
2.4.3. Boruta Algorithm
2.5. Classification Based on Selected Signature Genes
2.6. Classification with Selection of Signature Genes
2.6.1. Random Forest (RF)
2.6.2. LASSO (Least Absolute Shrinkage and Selection Operator)
2.6.3. CACTUS (Comprehensive Abstraction and Classification Tool for Uncovering Structures)
2.7. Comparison of the Overall Results
2.7.1. Performance Metrics
2.7.2. Concordance in the Signature Gene Sets
2.7.3. Concordance in the Biological Pathways Identified by Gene Set Enrichment Analyses
2.7.4. Signature Gene Sets as Prognostic Biomarkers
3. Results
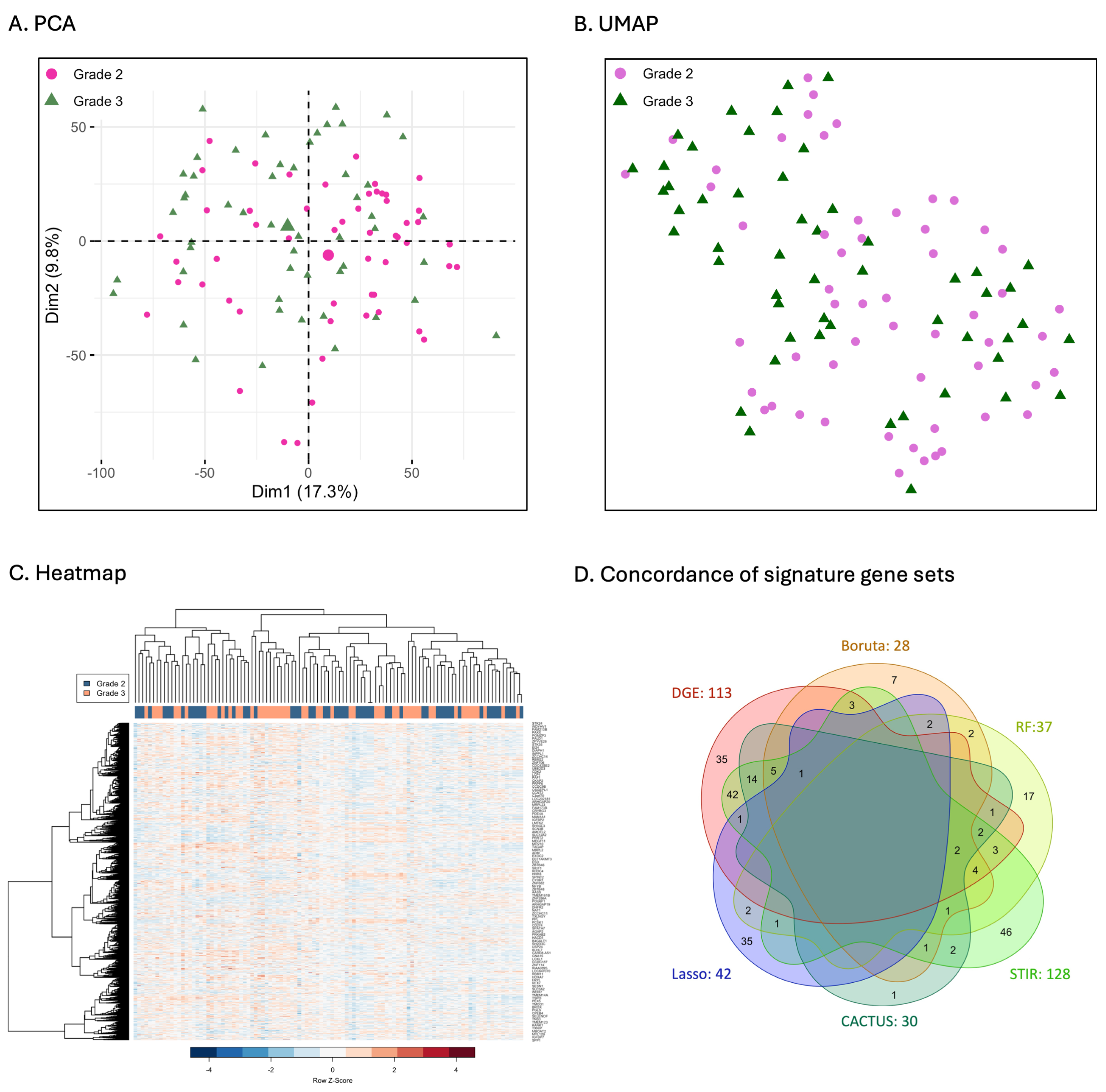
3.1. Data Overview
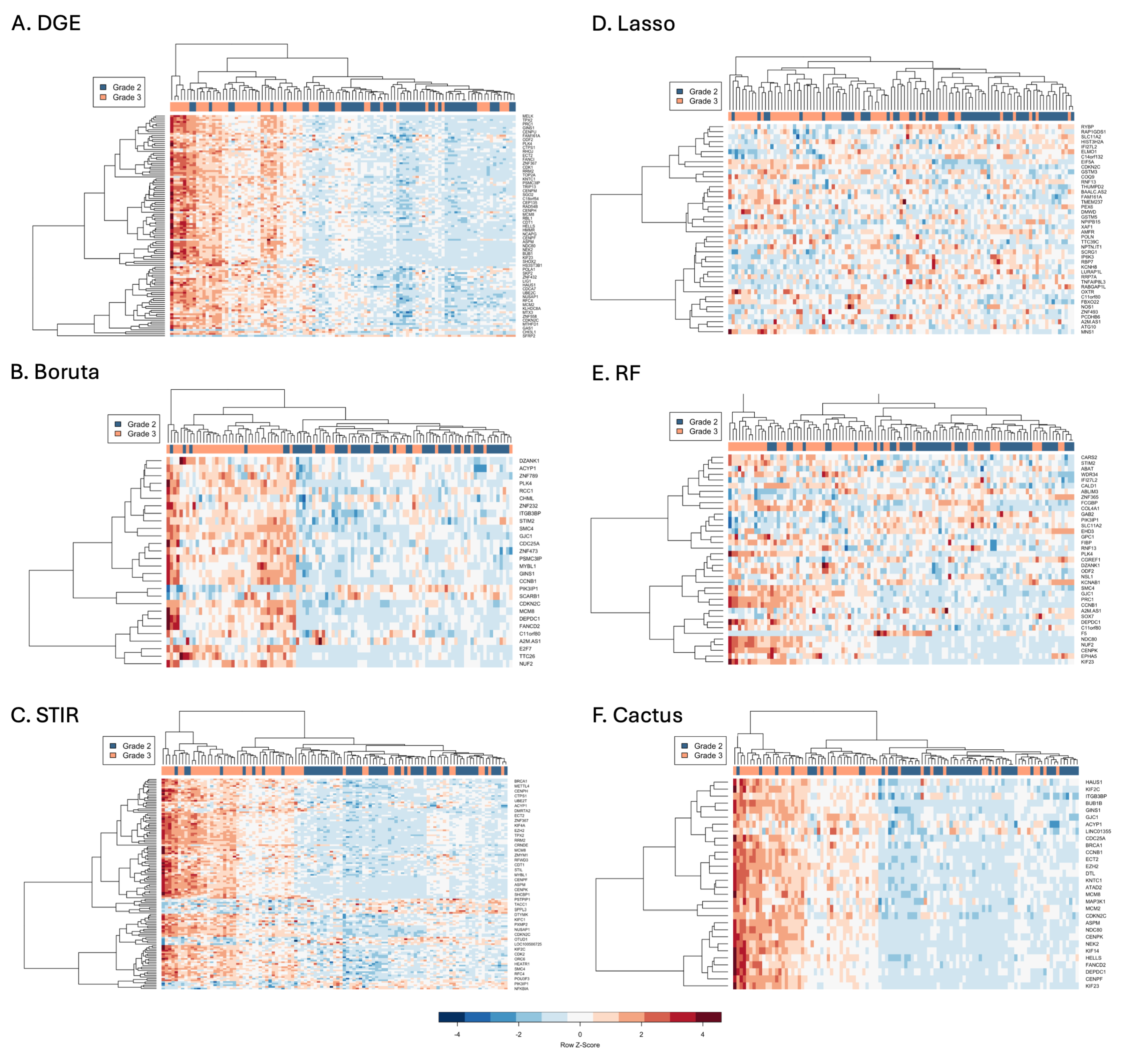
3.2. Comparison of Signature Genes Selection
3.3. Comparison of Clustering of Astrocytoma Based on Gene Expression Patterns
3.4. Signature Genes Based Classification
3.5. Signature Genes and Their Pathways and Functions
3.5.1. Gene Ontology (GO) Enrichment Analyses
3.5.2. KEGG Pathway Enrichment Analyses
3.6. Signature Genes and Their Prognostic Value as Biomarkers
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BA | Balanced Accuracy |
| CACTUS | Comprehensive Abstraction and Classification Tool for Uncovering Structure |
| CDKN2A/B | Cyclin-Dependent Kinase Inhibitor 2A/B |
| GO | Gene Onthology |
| IDH | Isocitrate Dehydrogenase |
| DGE | Differential Gene Expression |
| KEGG | Kyoto Encyclopedia of Genes and Genomes |
| KNN | K-Nearest Neighbors |
| PCA | Principal Component Analysis |
| QC | Quality Control |
| REMBRANDT | REpository for Molecular BRAin Neoplasia DaTa |
| STIR | STatistical Inference RelieF |
| SVM | Support Vector Machines |
| UMAP | Uniform Manifold Approximation and Projection |
| WHO | World Health Organisation |
References
- Molinaro, A.M.; Taylor, J.W.; Wiencke, J.K.; Wrensch, M.R. Genetic and molecular epidemiology of adult diffuse glioma. Nat. Rev. Neurol. 2019, 15, 405–417. [Google Scholar] [CrossRef] [PubMed]
- Boon, K.; Edwards, J.B.; Eberhart, C.G.; Riggins, G.J. Identification of associated genes including cell surface markers. BMC Cancer 2004, 4, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Brandes, A.A. Adding temozolomide to radiotherapy prolongs survival in people with glioblastoma. Cancer Treat. Rev. 2005, 31, 577–581. [Google Scholar] [CrossRef] [PubMed]
- Johnson, D.R.; Galanis, E. Medical management of high-grade: Current and emerging therapies. In Seminars in Oncology; Elsevier: Amsterdam, The Netherlands, 2014; Volume 41, pp. 511–522. [Google Scholar]
- Kohzuki, H.; Matsuda, M.; Miki, S.; Shibuya, M.; Ishikawa, E.; Matsumura, A. Diffusely infiltrating cerebellar anaplastic effectively controlled with bevacizumab: Case report and literature review. World Neurosurg. 2018, 115, 181–185. [Google Scholar] [CrossRef] [PubMed]
- Reardon, D.A.; Brandes, A.A.; Omuro, A.; Mulholland, P.; Lim, M.; Wick, A.; Baehring, J.; Ahluwalia, M.S.; Roth, P.; Bähr, O.; et al. Effect of nivolumab vs bevacizumab in patients with recurrent glioblastoma: The CheckMate 143 phase 3 randomized clinical trial. JAMA Oncol. 2020, 6, 1003–1010. [Google Scholar] [CrossRef]
- Torp, S.H.; Solheim, O.; Skjulsvik, A.J. The WHO 2021 Classification of Central Nervous System tumours: A practical update on what neurosurgeons need to know—A minireview. Acta Neurochir. 2022, 164, 2453–2464. [Google Scholar] [CrossRef]
- Sejda, A.; Grajkowska, W.; Trubicka, J.; Szutowicz, E.; Wojdacz, T.; Kloc, W.; Iżycka-Świeszewska, E. WHO CNS5 2021 classification of gliomas: A practical review and road signs for diagnosing pathologists and proper patho-clinical and neuro-oncological cooperation. Folia Neuropathol. 2022, 60, 137–152. [Google Scholar] [CrossRef]
- Network, C.G.A.R. Comprehensive, integrative genomic analysis of diffuse lower-grade gliomas. N. Engl. J. Med. 2015, 372, 2481–2498. [Google Scholar]
- Hira, Z.M.; Gillies, D.F. A review of feature selection and feature extraction methods applied on microarray data. Adv. Bioinform. 2015, 2015, 198363. [Google Scholar] [CrossRef]
- Jirapech-Umpai, T.; Aitken, S. Feature selection and classification for microarray data analysis: Evolutionary methods for identifying predictive genes. BMC Bioinform. 2005, 6, 1–11. [Google Scholar] [CrossRef]
- Ahmad Zamri, N.; Aziz, N.A.A.; Bhuvaneswari, T.; Abdul Aziz, N.H.; Ghazali, A.K. Feature selection of microarray data using simulated Kalman filter with mutation. Processes 2023, 11, 2409. [Google Scholar] [CrossRef]
- Aziz, R.; Verma, C.; Srivastava, N. A novel approach for dimension reduction of microarray. Comput. Biol. Chem. 2017, 71, 161–169. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Xie, W.; Liu, T. Efficient feature selection and classification for microarray data. PLoS ONE 2018, 13, e0202167. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Bø, T.H.; Jonassen, I.; Myklebost, O.; Hovig, E. Tumor classification and marker gene prediction by feature selection and fuzzy c-means clustering using microarray data. BMC Bioinform. 2003, 4, 60. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Tang, J.; Liu, H. Feature Selection. In Encyclopedia of Machine Learning and Data Mining; Springer: Boston, MA, USA, 2017; Volume 10. [Google Scholar]
- Gusev, Y.; Bhuvaneshwar, K.; Song, L.; Zenklusen, J.C.; Fine, H.; Madhavan, S. The REMBRANDT study, a large collection of genomic data from brain cancer patients. Sci. Data 2018, 5, 180158. [Google Scholar] [CrossRef] [PubMed]
- Nuechterlein, N.; Shapiro, L.G.; Holland, E.C.; Cimino, P.J. Machine learning modeling of genome-wide copy number alteration signatures reliably predicts IDH mutational status in adult diffuse glioma. Acta Neuropathol. Commun. 2021, 9, 191. [Google Scholar] [CrossRef]
- Wilson, C.L.; Miller, C.J. Simpleaffy: A BioConductor package for Affymetrix Quality Control and data analysis. Bioinformatics 2005, 21, 3683–3685. [Google Scholar] [CrossRef]
- Gautier, L.; Cope, L.; Bolstad, B.M.; Irizarry, R.A. affy—Analysis of Affymetrix GeneChip data at the probe level. Bioinformatics 2004, 20, 307–315. [Google Scholar] [CrossRef]
- Irizarry, R.A. The Analysis of Gene Expression Data: Methods and Software; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Warnes, M.G.R.; Bolker, B.; Bonebakker, L.; Gentleman, R.; Huber, W.; Liaw, A. Package ‘gplots’. In Various R Programming Tools for Plotting Data; R Foundation for Statistical Computing: Vienna, Austria, 2016; pp. 112–119. [Google Scholar]
- Le, T.T.; Urbanowicz, R.J.; Moore, J.H.; McKinney, B.A. Statistical inference relief (STIR) feature selection. Bioinformatics 2019, 35, 1358–1365. [Google Scholar] [CrossRef]
- Kursa, M.B.; Jankowski, A.; Rudnicki, W.R. Boruta–a system for feature selection. Fundam. Inform. 2010, 101, 271–285. [Google Scholar] [CrossRef]
- Gherardini, L.; Varma, V.R.; Capała, K.; Woods, R.; Sousa, J. CACTUS: A Comprehensive Abstraction and Classification Tool for Uncovering Structures. Acm Trans. Intell. Syst. Technol. 2024, 15, 1–23. [Google Scholar] [CrossRef]
- Ritchie, M.E.; Phipson, B.; Wu, D.; Hu, Y.; Law, C.W.; Shi, W.; Smyth, G.K. limma powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res. 2015, 43, e47. [Google Scholar] [CrossRef] [PubMed]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. (Methodol.) 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Kira, K.; Rendell, L.A. The feature selection problem: Traditional methods and a new algorithm. In Proceedings of the Tenth National Conference on Artificial Intelligence, San Jose, CA, USA, 12–16 July 1992; pp. 129–134. [Google Scholar]
- Kira, K.; Rendell, L.A. A practical approach to feature selection. In Machine Learning Proceedings 1992; Elsevier: Amsterdam, The Netherlands, 1992; pp. 249–256. [Google Scholar]
- Urbanowicz, R.J.; Olson, R.S.; Schmitt, P.; Meeker, M.; Moore, J.H. Benchmarking relief-based feature selection methods for bioinformatics data mining. J. Biomed. Inform. 2018, 85, 168–188. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Dimitriadou, E.; Hornik, K.; Leisch, F.; Meyer, D.; Weingessel, A.; Leisch, M.F. Package ‘e1071’. R Software Package. 2009. Available online: http://cran.rproject.org/web/packages/e1071/index.html (accessed on 6 August 2024).
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010, 33, 1. [Google Scholar] [CrossRef]
- Yu, G.; Wang, L.G.; Han, Y.; He, Q.Y. clusterProfiler: An R package for comparing biological themes among gene clusters. Omics J. Integr. Biol. 2012, 16, 284–287. [Google Scholar] [CrossRef]
- Therneau, T.M. A Package for Survival Analysis in R. R Package Version 3.7-0. 2024. Available online: https://cran.r-project.org/web/packages/survival/vignettes/survival.pdf (accessed on 6 August 2024).
- Wood, H. IDH1 vaccine shows potential in astrocytoma. Nat. Rev. Neurol. 2021, 17, 262. [Google Scholar]
- Li, P.; Xu, Z.; Liu, T.; Liu, Q.; Zhou, H.; Meng, S.; Feng, Z.; Tang, Y.; Liu, C.; Feng, J.; et al. Circular RNA sequencing reveals serum exosome circular RNA panel for high-grade diagnosis. Clin. Chem. 2022, 68, 332–343. [Google Scholar] [CrossRef]
- Bagley, S.J.; Kothari, S.; Rahman, R.; Lee, E.Q.; Dunn, G.P.; Galanis, E.; Chang, S.M.; Nabors, L.B.; Ahluwalia, M.S.; Stupp, R.; et al. Glioblastoma Clinical Trials: Current Landscape and Opportunities for Improvement. Clin. Cancer Res. 2022, 28, 594–602. [Google Scholar] [CrossRef] [PubMed]
- Lexe, G.; Monaco, J.; Doyle, S.; Basavanhally, A.; Reddy, A.; Seiler, M.; Ganesan, S.; Bhanot, G.; Madabhushi, A. Towards improved cancer diagnosis and prognosis using analysis of gene expression data and computer aided imaging. Exp. Biol. Med. 2009, 234, 860–879. [Google Scholar]
- Bumgarner, R. Overview of DNA microarrays: Types, applications, and their future. Curr. Protoc. Mol. Biol. 2013, 101, 22.1.1–22.1.11. [Google Scholar] [CrossRef] [PubMed]
- Parkinson, H.; Kapushesky, M.; Shojatalab, M.; Abeygunawardena, N.; Coulson, R.; Farne, A.; Holloway, E.; Kolesnykov, N.; Lilja, P.; Lukk, M.; et al. ArrayExpress—A public database of microarray experiments and gene expression profiles. Nucleic Acids Res. 2007, 35, D747–D750. [Google Scholar] [CrossRef] [PubMed]
- Clough, E.; Barrett, T. The gene expression omnibus database. In Statistical Genomics: Methods and Protocols; Springer: New York, NY, USA, 2016; pp. 93–110. [Google Scholar]
- Smyth, G.K. Linear models and empirical bayes methods for assessing differential expression in microarray experiments. Stat. Appl. Genet. Mol. Biol. 2004, 3. [Google Scholar] [CrossRef] [PubMed]
- Saeys, Y.; Inza, I.; Larranaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef]
- Allan, K.; Jordan, R.C.; Ang, L.C.; Taylor, M.; Young, B. Overexpression of Cyclin A and Cyclin B1Proteins in s. Arch. Pathol. Lab. Med. 2000, 124, 216–220. [Google Scholar] [CrossRef]
- Dai, P.; Xiong, L.; Wei, Y.; Wei, X.; Zhou, X.; Zhao, J.; Tang, H. A pancancer analysis of the oncogenic role of cyclin B1 (CCNB1) in human tumors. Sci. Rep. 2023, 13, 16226. [Google Scholar] [CrossRef]
- Cui, K.; Chen, J.H.; Zou, Y.F.; Zhang, S.Y.; Wu, B.; Jing, K.; Li, L.W.; Xia, L.; Sun, C.; Dong, Y.L. Hub biomarkers for the diagnosis and treatment of glioblastoma based on microarray technology. Technol. Cancer Res. Treat. 2021, 20, 1533033821990368. [Google Scholar] [CrossRef]
- Mokgautsi, N.; Kuo, Y.C.; Tang, S.L.; Liu, F.C.; Chen, S.J.; Wu, A.T.; Huang, H.S. Anticancer Activities of 9-chloro-6-(piperazin-1-yl)-11H-indeno [1, 2-c] quinolin-11-one (SJ10) in Glioblastoma Multiforme (GBM) Chemoradioresistant Cell Cycle-Related Oncogenic Signatures. Cancers 2022, 14, 262. [Google Scholar] [CrossRef]
- Tschan, M.; Peters, U.; Cajot, J.; Betticher, D.; Fey, M.; Tobler, A. The cyclin-dependent kinase inhibitors p18INK4c and p19INK4d are highly expressed in CD34+ progenitor and acute myeloid leukaemic cells but not in normal differentiated myeloid cells. Br. J. Haematol. 1999, 106, 644–651. [Google Scholar] [CrossRef] [PubMed]
- Ashida, S.; Nakagawa, H.; Katagiri, T.; Furihata, M.; Iiizumi, M.; Anazawa, Y.; Tsunoda, T.; Takata, R.; Kasahara, K.; Miki, T.; et al. Molecular features of the transition from prostatic intraepithelial neoplasia (PIN) to prostate cancer: Genome-wide gene-expression profiles of prostate cancers and PINs. Cancer Res. 2004, 64, 5963–5972. [Google Scholar] [CrossRef] [PubMed]
- Korshunov, A.; Shishkina, L.; Golanov, A. Immunohistochemical analysis of p16INK4a, p14ARF, p18INK4c, p21CIP1, p27KIP1 and p73 expression in 271 meningiomas correlation with tumor grade and clinical outcome. Int. J. Cancer 2003, 104, 728–734. [Google Scholar] [CrossRef] [PubMed]
- Santarius, T.; Kirsch, M.; Nikas, D.; Imitola, J.; Black, P. Molecular analysis of alterations of the p18INK4c gene in human meningiomas. Neuropathol. Appl. Neurobiol. 2000, 26, 67–75. [Google Scholar] [CrossRef]
- Scrideli, C.A.; Carlotti, C.G.; Okamoto, O.K.; Andrade, V.S.; Cortez, M.A.; Motta, F.J.; Lucio-Eterovic, A.K.; Neder, L.; Rosemberg, S.; Oba-Shinjo, S.M.; et al. Gene expression profile analysis of primary glioblastomas and non-neoplastic brain tissue: Identification of potential target genes by oligonucleotide microarray and real-time quantitative PCR. J. Neuro-Oncol. 2008, 88, 281–291. [Google Scholar] [CrossRef]
- Seifert, M.; Schackert, G.; Temme, A.; Schröck, E.; Deutsch, A.; Klink, B. Molecular characterization of progression towards secondary glioblastomas utilizing patient-matched tumor pairs. Cancers 2020, 12, 1696. [Google Scholar] [CrossRef]
- Radebold, K.; Horakova, E.; Gloeckner, J.; Ortega, G.; Spray, D.; Vieweger, H.; Siebert, K.; Manuelidis, L.; Geibel, J. Gap junctional channels regulate acid secretion in the mammalian gastric gland. J. Membr. Biol. 2001, 183, 147–153. [Google Scholar] [CrossRef]
- Iwata, F.; Joh, T.; Ueda, F.; Yokoyama, Y.; Itoh, M. Role of gap junctions in inhibiting ischemia-reperfusion injury of rat gastric mucosa. Am. J. Physiol.-Gastrointest. Liver Physiol. 1998, 275, G883–G888. [Google Scholar] [CrossRef]
- Sirnes, S.; Honne, H.; Ahmed, D.; Danielsen, S.A.; Rognum, T.O.; Meling, G.I.; Leithe, E.; Rivedal, E.; Lothe, R.A.; Lind, G.E. DNA methylation analyses of the connexin gene family reveal silencing of GJC1 (Connexin45) by promoter hypermethylation in colorectal cancer. Epigenetics 2011, 6, 602–609. [Google Scholar] [CrossRef]
- Li, Z.H.; Guan, Y.L.; Liu, Q.; Wang, Y.; Cui, R.; Wang, Y.J. Astrocytoma progression scoring system based on the WHO 2016 criteria. Sci. Rep. 2019, 9, 96. [Google Scholar] [CrossRef]
- Bao, Z.S.; Li, M.Y.; Wang, J.Y.; Zhang, C.B.; Wang, H.J.; Yan, W.; Liu, Y.W.; Zhang, W.; Chen, L.; Jiang, T. Prognostic value of a nine-gene signature in glioma patients based on mRNA expression profiling. Cns Neurosci. Ther. 2014, 20, 112–118. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Wei, J.; Li, Z.; Tian, Y.; Du, C. Bioinformatical analysis of gene expression signatures of different glioma subtypes. Oncol. Lett. 2018, 15, 2807–2814. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Zhu, Z.; Li, J.; Yao, J.; Jiang, H.; Ran, R.; Li, X.; Li, Z. Expression and prognostic value of long non-coding RNA H19 in glioma via integrated bioinformatics analyses. Aging 2020, 12, 3407. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; He, D.; Yang, P.; He, J.; Zhang, Y. Genome-wide expression profiling of glioblastoma using a large combined cohort. Sci. Rep. 2018, 8, 15104. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Zhou, J.; Zhong, D.; Zhou, Y.; Zhang, W.; Wu, W.; Zhao, Z.; Wang, W.; Xu, W.; He, L.; et al. Overexpression of SMC4 activates TGFβ/Smad signaling and promotes aggressive phenotype in glioma cells. Oncogenesis 2017, 6, e301. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; He, Z.; Chen, Y. Comprehensive analysis reveals a 4-gene signature in predicting response to temozolomide in low-grade glioma patients. Cancer Control 2019, 26, 1073274819855118. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, Y.; Li, J.; Qu, F.; Fu, X.; Liu, S.; Wang, X.; Xie, Y.; Zhang, X. RFC2: A prognosis biomarker correlated with the immune signature in diffuse lower-grade gliomas. Sci. Rep. 2022, 12, 3122. [Google Scholar] [CrossRef]
- Zhang, Y.A.; Zhou, Y.; Luo, X.; Song, K.; Ma, X.; Sathe, A.; Girard, L.; Xiao, G.; Gazdar, A.F. SHOX2 is a potent independent biomarker to predict survival of WHO grade II–III diffuse gliomas. eBioMedicine 2016, 13, 80–89. [Google Scholar] [CrossRef]
- Cho, S.Y.; Kim, S.; Kim, G.; Singh, P.; Kim, D.W. Integrative analysis of KIF4A, 9, 18A, and 23 and their clinical significance in low-grade glioma and glioblastoma. Sci. Rep. 2019, 9, 4599. [Google Scholar] [CrossRef]
- Zhou, H.Y.; Wang, Y.C.; Wang, T.; Wu, W.; Cao, Y.Y.; Zhang, B.C.; Wang, M.D.; Mao, P. CCNA2 and NEK2 regulate glioblastoma progression by targeting the cell cycle. Oncol. Lett. 2024, 27, 1–16. [Google Scholar] [CrossRef]
- Huo, Z.; Guo, L.; Shao, W.; Ding, Q.; Guo, Y.; Xu, Q. CRNDE, an enhancer RNA of prognostic value in glioma, correlates with immune infiltration: A pan-cancer analysis. Eur. J. Inflamm. 2023, 21, 1721727X221138068. [Google Scholar] [CrossRef]
- Wang, B.; Ma, Q.; Wang, X.; Guo, K.; Liu, Z.; Li, G. TGIF1 overexpression promotes glioma progression and worsens patient prognosis. Cancer Med. 2022, 11, 5113–5128. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Zhang, L.; Song, S.; Xu, L.; Yan, Y.; Wu, H.; Tong, X.; Yan, H. Elevated GAS2L3 expression correlates with poor prognosis in patients with glioma: A study based on bioinformatics and immunohistochemical analysis. Front. Genet. 2021, 12, 649270. [Google Scholar] [CrossRef] [PubMed]





| Gene | Description | Adjusted p-Value | Selection Algorithm | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ACYP1 | Acylphosphatase 1 | 0.47 | 7.38 | 7.85 | DGE | Boruta | STIR | CACTUS | |||
| CCNB1 | Cyclin B1 | 0.91 | 6.69 | 7.60 | DGE | Boruta | STIR | RF | CACTUS | ||
| CDKN2C | Cyclin Dependent Kinase Inhibitor 2C | 1.19 | 8.72 | 9.91 | DGE | Boruta | STIR | LASSO | CACTUS | ||
| CENPK | Centromere Protein K | 0.95 | 5.28 | 6.23 | DGE | STIR | RF | CACTUS | |||
| DEPDC1 | DEP Domain Containing 1 | 0.43 | 5.98 | 6.41 | Boruta | STIR | RF | CACTUS | |||
| FANCD2 | FA Complementation Group D2 | 0.50 | 5.56 | 6.06 | DGE | Boruta | STIR | CACTUS | |||
| GINS1 | GINS Complex Subunit 1 | 0.75 | 7.25 | 8.00 | DGE | Boruta | STIR | CACTUS | |||
| GJC1 | Gap Junction Protein Gamma 1 | 0.97 | 7.29 | 8.26 | DGE | Boruta | STIR | RF | CACTUS | ||
| ITGB3BP | Integrin Subunit Beta 3 Binding Protein | 0.57 | 7.94 | 8.52 | DGE | Boruta | STIR | CACTUS | |||
| MCM8 | Minichromosome Maintenance 8 Homologous | 0.60 | 6.13 | 6.73 | DGE | Boruta | STIR | CACTUS | |||
| NDC80 | NDC80 Kinetochore Complex Component | 1.00 | 5.25 | 6.24 | DGE | STIR | RF | CACTUS | |||
| NUF2 | NUF2 Component Of NDC80 Kinetochore Complex | 1.05 | 5.16 | 6.21 | DGE | Boruta | STIR | RF | |||
| PIK3IP1 | Phosphoinositide-3-Kinase Interacting Protein1 | 10.1 | 9.82 | DGE | Boruta | STIR | RF | ||||
| PLK4 | Polo Like Kinase 4 | 0.30 | 7.83 | 8.13 | DGE | Boruta | STIR | RF | |||
| SMC4 | Structural Maintenance Of Chromosomes 4 | 1.10 | 7.67 | 8.78 | DGE | Boruta | STIR | RF | |||
| Classification | Selection | Sensitivity | Specificity | Balanced Accuracy |
|---|---|---|---|---|
| KNN | All genes | 0.923 | 0.462 | 0.692 |
| DGE | 0.538 | 0.769 | 0.654 | |
| Boruta | 0.923 | 0.769 | 0.846 | |
| STIR | 0.692 | 0.692 | 0.692 | |
| Logistic regression | All genes | 0.692 | 0.385 | 0.538 |
| DGE | 0.615 | 0.615 | 0.615 | |
| Boruta | 0.462 | 0.615 | 0.538 | |
| STIR | 0.462 | 0.615 | 0.538 | |
| SVM radial kernel | All genes | 0.692 | 0.769 | 0.731 |
| DGE | 0.846 | 0.769 | 0.808 | |
| Boruta | 0.769 | 0.769 | 0.769 | |
| STIR | 0.769 | 0.615 | 0.692 | |
| SVM sigmoid kernel | All genes | 0.769 | 0.615 | 0.692 |
| DGE | 0.769 | 0.615 | 0.692 | |
| Boruta | 0.923 | 0.692 | 0.808 | |
| STIR | 0.923 | 0.615 | 0.769 | |
| Random Forest | 0.714 | 0.667 | 0.691 | |
| LASSO Regression | 0.714 | 0.583 | 0.649 | |
| CACTUS | 0.818 | 0.673 | 0.746 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drozdz, A.; McInerney, C.E.; Prise, K.M.; Spence, V.J.; Sousa, J. Signature Genes Selection and Functional Analysis of Astrocytoma Phenotypes: A Comparative Study. Cancers 2024, 16, 3263. https://doi.org/10.3390/cancers16193263
Drozdz A, McInerney CE, Prise KM, Spence VJ, Sousa J. Signature Genes Selection and Functional Analysis of Astrocytoma Phenotypes: A Comparative Study. Cancers. 2024; 16(19):3263. https://doi.org/10.3390/cancers16193263
Chicago/Turabian StyleDrozdz, Anna, Caitriona E. McInerney, Kevin M. Prise, Veronica J. Spence, and Jose Sousa. 2024. "Signature Genes Selection and Functional Analysis of Astrocytoma Phenotypes: A Comparative Study" Cancers 16, no. 19: 3263. https://doi.org/10.3390/cancers16193263
APA StyleDrozdz, A., McInerney, C. E., Prise, K. M., Spence, V. J., & Sousa, J. (2024). Signature Genes Selection and Functional Analysis of Astrocytoma Phenotypes: A Comparative Study. Cancers, 16(19), 3263. https://doi.org/10.3390/cancers16193263






